Survivability of Suddenly Loaded Arrays of Micropillars
Abstract
:1. Introduction
2. Model Description and Computational Scheme
2.1. Pillars
2.2. Load Transfer Rules Reflecting Substrate Rigidities
2.3. Survivability and Survival Function
2.4. Computational Scheme
2.5. Survival Function Estimate
3. Results and Discussion
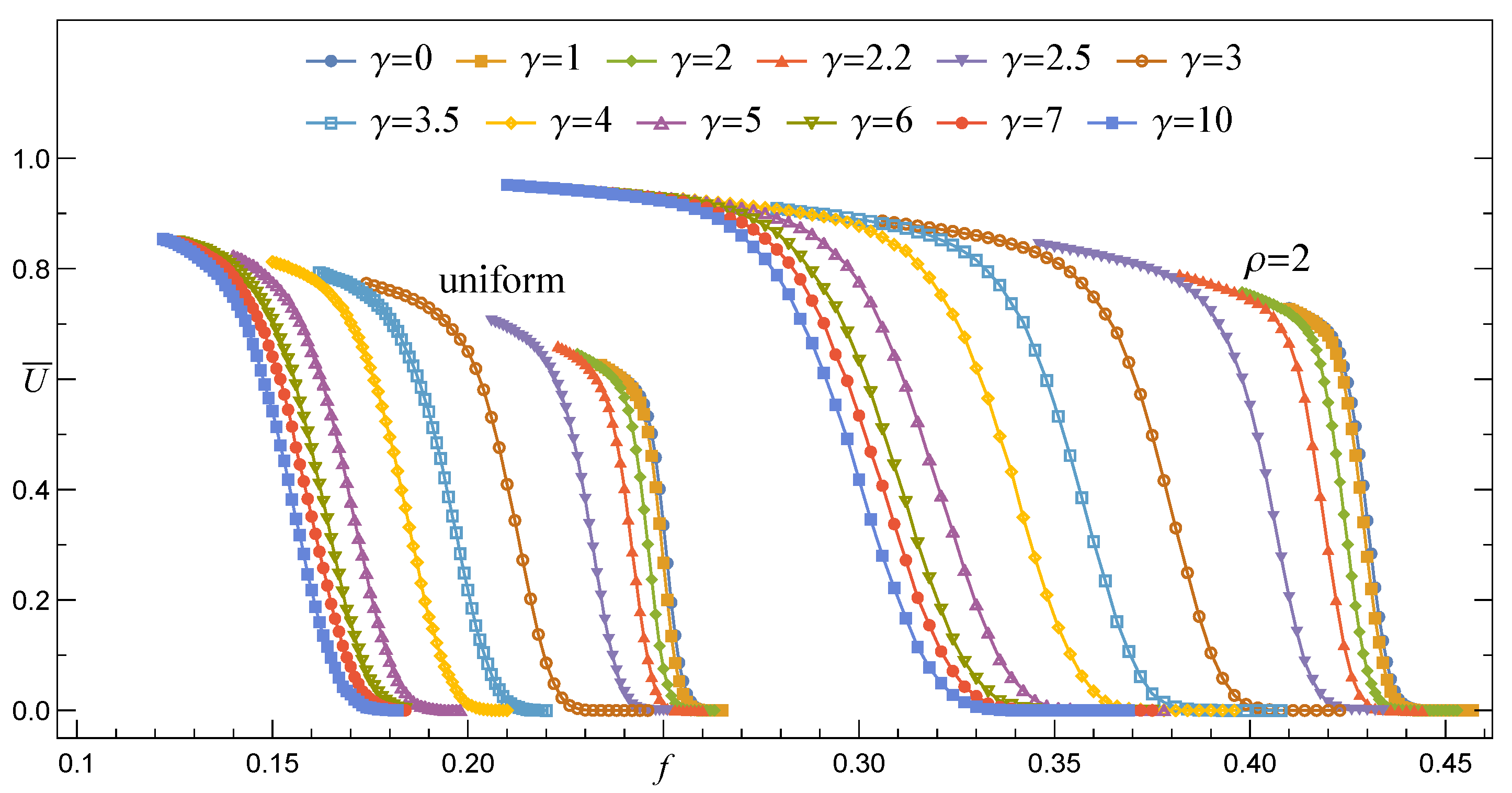
3.1. Empirical Survival Functions Referring to the Range-of-Load-Transfer Limits
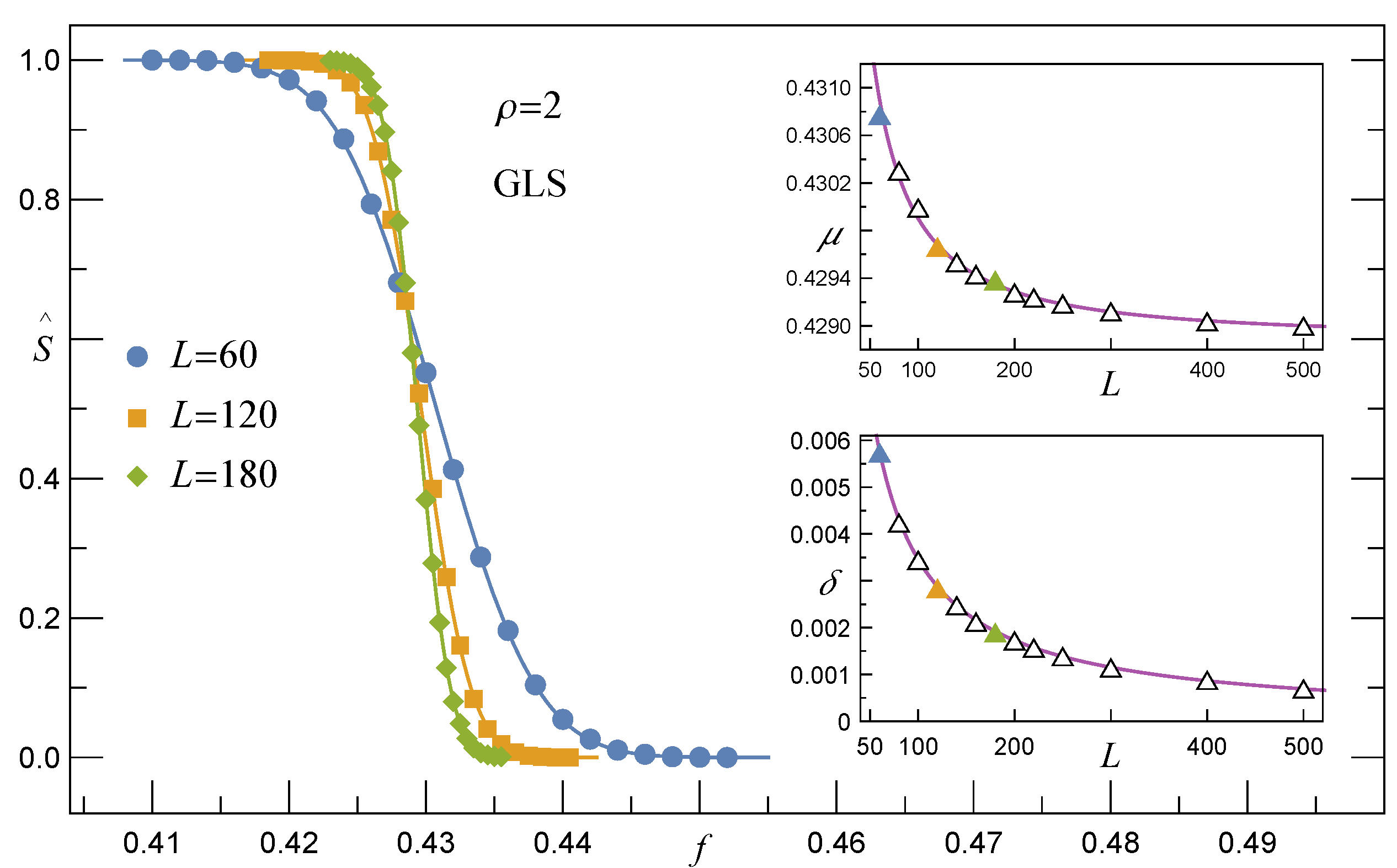
3.1.1. Survival Function under the GLS Rule, RV()
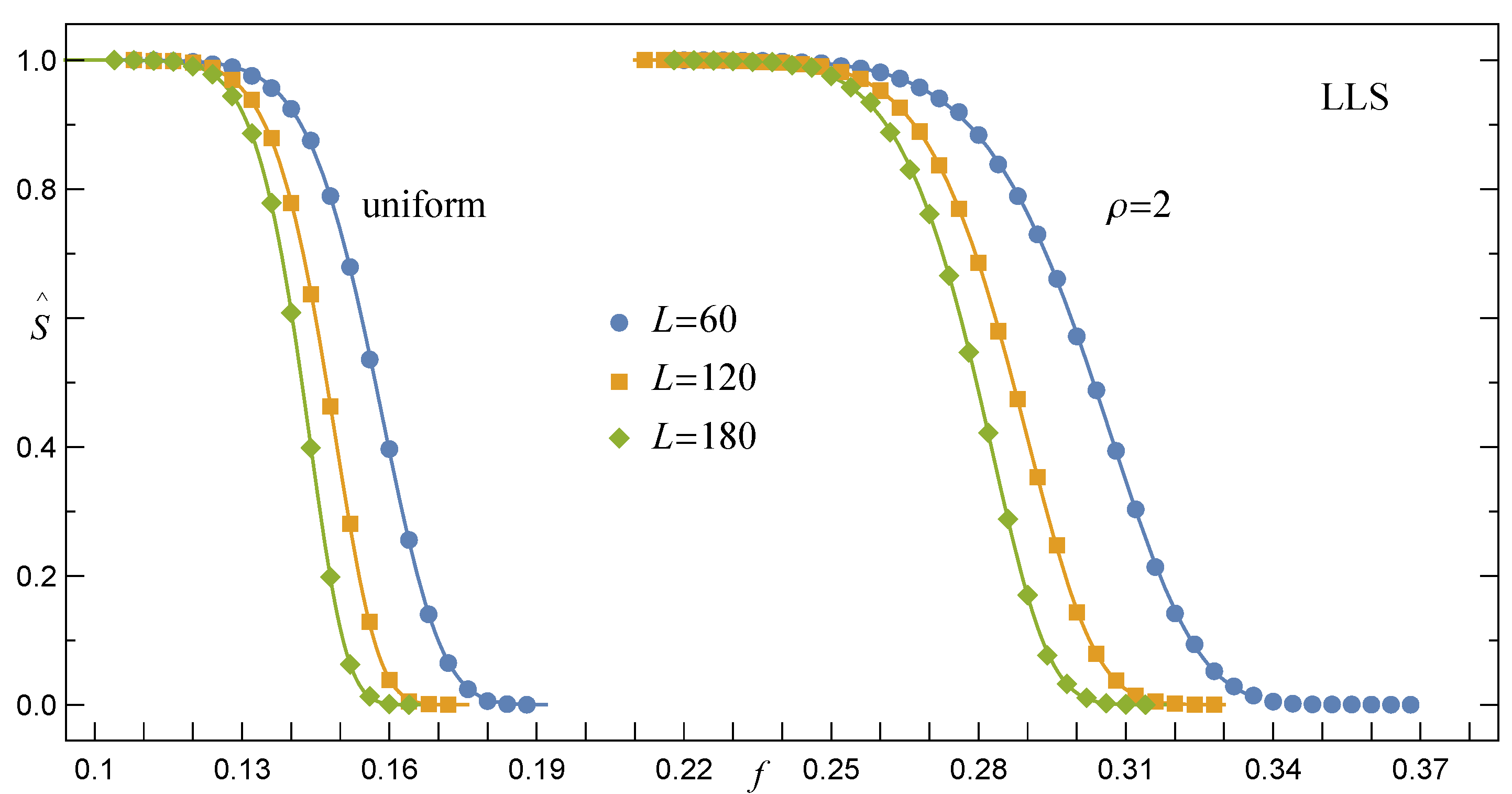
3.1.2. Survival Function under the LLS Rule, RV()
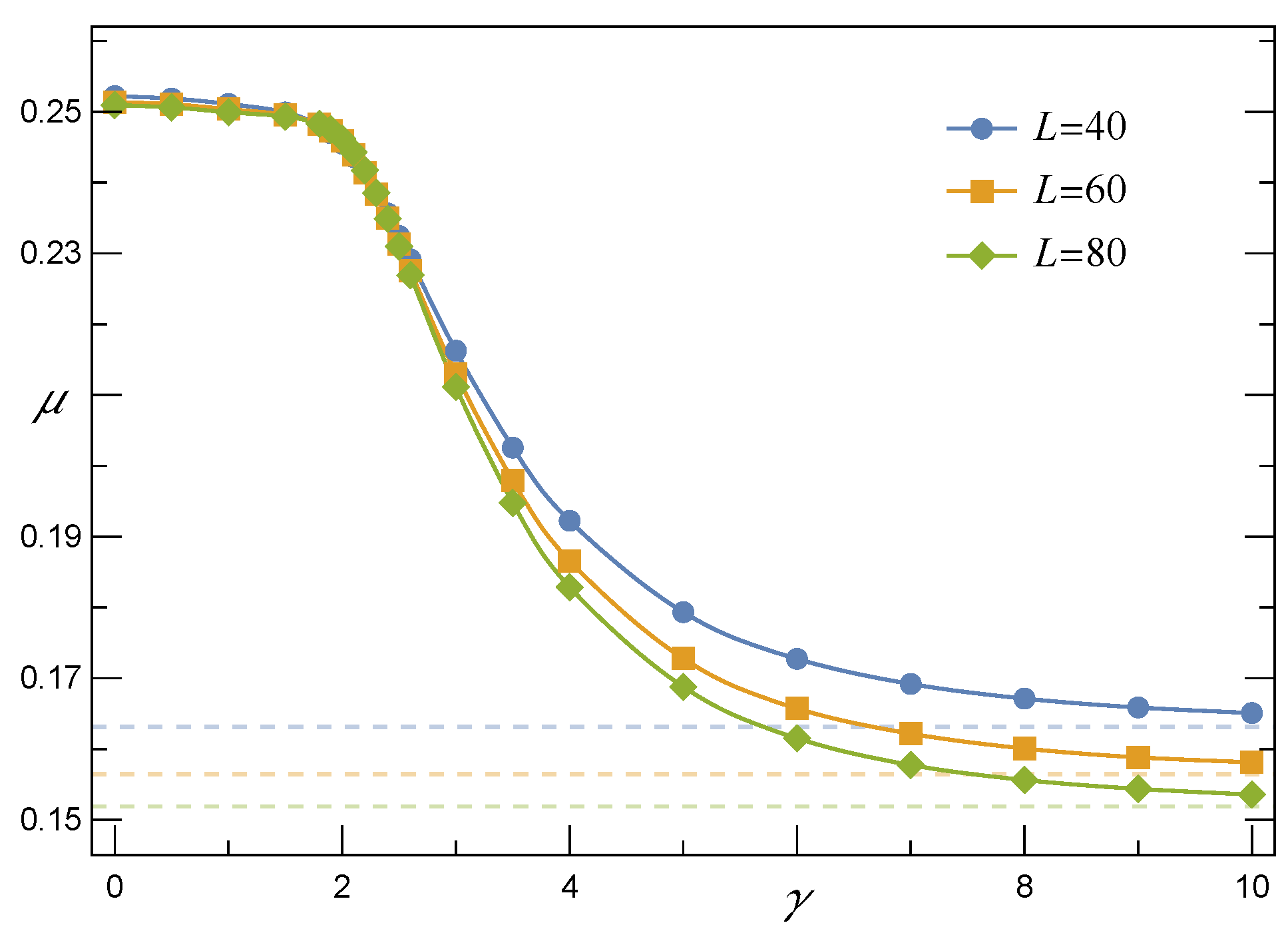
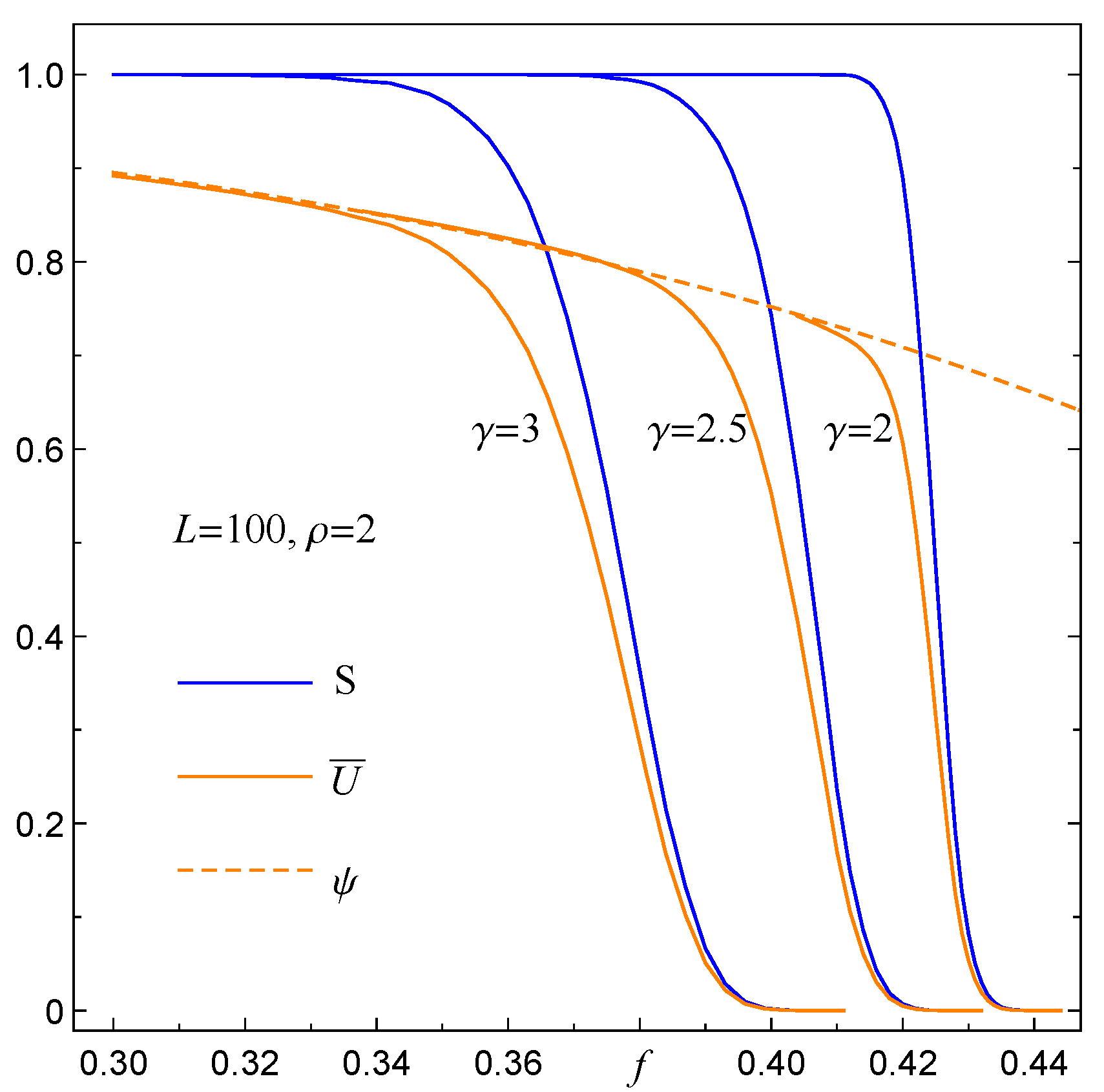
3.2. Empirical Survival Function for Intermediate Ranges of Load Transfer
3.3. Fraction of Surviving Pillars
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chekurov, N.; Grigoras, K.; Peltonen, A.; Franssila, S.; Tittonen, I. The fabrication silicon nanostructures by local gallium implantation and cryogenic deep reactive ion etching. Nanotechnology 2009, 20, 65307. [Google Scholar] [CrossRef] [Green Version]
- Sievila, P.; Chekurov, N.; Tittonen, I. The fabrication of silicon nanostructures by focused-ion-beam implantation and TMAH wet etching. Nanotechnology 2010, 21, 145301. [Google Scholar] [CrossRef]
- Park, J.E.; Won, S.; Cho, W.; Kim, J.G.; Jhang, S.; Lee, J.G.; Wie, J.J. Fabrication and applications of stimuli-responsive micro/nanopillar arrays. J. Polym. Sci. 2021, 59, 1491. [Google Scholar] [CrossRef]
- Schoen, I.; Hu, W.; Klotzsch, E.; Vogel, V. Probing Cellular Traction Forces by Micropillar Arrays: Contribution of Substrate Warping to Pillar Deflection. Nano Lett. 2010, 10, 1823–1830. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiu, X.; Lo, J.C.C.; Lee, S.W.R.; Liou, Y.; Chiu, P. Evaluation and Benchmarking of Cu Pillar Micro-bumps with Printed Polymer Core. In Proceedings of the 2019 International Conference on Electronics Packaging (ICEP), Niigata, Japan, 17–20 April 2019; pp. 24–27. [Google Scholar] [CrossRef]
- Harding, F.J.; Surdo, S.; Delalat, B.; Cozzi, C.; Elnathan, R.; Gronthos, S.; Voelcker, N.H.; Barillaro, G. Ordered Silicon Pillar Arrays Prepared by Electrochemical Micromachining: Substrates for High-Efficiency Cell Transfection. ACS Appl. Mater. Interfaces 2016, 8, 29197–29202. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Li, X.; Shao, J.; An, N.; Tian, H.; Wang, C.; Han, T.; Wang, L.; Lu, B. High-Performance Piezoelectric Nanogenerators with Imprinted P(VDF-TrFE)/BaTiO3 Nanocomposite Micropillars for Self-Powered Flexible Sensors. Small 2017, 13, 1604245. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.-Y.; Yun, T.G.; Qaiser, N.; Paik, H.; Roh, H.S.; Hong, J.; Hong, S.; Han, S.M.; No, K. Vertically aligned P(VDF-TrFE) core-shell structures on flexible pillar arrays. Sci. Rep. 2015, 5, 10728. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Shao, J.; Tian, H.; Li, X.; Tian, Y.; Wang, C. Flexible three-axial tactile sensors with microstructure-enhanced piezoelectric effect and specially-arranged piezoelectric arrays. Smart Mater. Struct. 2018, 27, 025018. [Google Scholar] [CrossRef]
- Taloni, A.; Vodret, M.; Costantini, G.; Zapperi, S. Size effects on the fracture of microscale and nanoscale materials. Nat. Rev. Mater. 2018, 3, 211–224. [Google Scholar] [CrossRef]
- Greer, J.R.; Jang, D.; Kim, J.-Y.; Burek, M.J. Emergence of New Mechanical Functionality in Material via Size Reduction. Adv. Funct. Mater. 2009, 19, 2880–2886. [Google Scholar] [CrossRef]
- Jang, D.; Greer, J.R. Transition from a strong-yet-brittle to a stronger-and-ductile state by size reduction of metallic glasses. Nat. Mater. 2010, 9, 215–219. [Google Scholar] [CrossRef] [PubMed]
- Uchic, M.D.; Dimiduk, D.M.; Florando, J.N.; Nix, W.D. Sample Dimensions Influence Strength and Crystal Plasticity. Science 2004, 305, 986–989. [Google Scholar] [CrossRef]
- Shan, Z.W.; Mishra, R.K.; Syed Asif, S.A.; Warren, O.L.; Minor, A.M. Mechanical annealing and source-limited deformation in submicrometre-diameter Ni crystals. Nat. Mater. 2008, 7, 115–119. [Google Scholar] [CrossRef] [PubMed]
- Biswas, S.; Chakrabarti, B.K. Crossover behaviors in one and two dimensional heterogeneous load sharing fiber bundle models. Eur. Phys. J. B 2013, 86, 160. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, S.; Chakrabarti, B.K.; Hansen, A. Crossover behavior in a mixed-mode fiber bundle model. Phys. Rev. E 2005, 71, 036149. [Google Scholar] [CrossRef] [Green Version]
- Roy, S.; Biswas, S.; Ray, P. Modes of failure in disordered solids. Phys. Rev. E 2017, 96, 063003. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.-H.; Kim, B.J.; Jeong, H. Universality class of the fiber bundle model on complex networks. Phys. Rev. Lett. 2005, 94, 025501. [Google Scholar] [CrossRef] [Green Version]
- Roy, S.; Goswami, S. Fiber Bundle Model Under Heterogeneous Loading. J. Stat. Phys. 2018, 170, 1197–1214. [Google Scholar] [CrossRef] [Green Version]
- Biswas, S.; Sen, P. Effect of localized loading on failure threshold of fiber bundles. Physica A 2018, 509, 1087–1094. [Google Scholar] [CrossRef] [Green Version]
- Biswas, S.; Sen, P. Maximizing the Strength of Fiber Bundles under Uniform Loading. Phys. Rev. Lett. 2015, 115, 155501. [Google Scholar] [CrossRef] [Green Version]
- Derda, T.; Domanski, Z. Enhanced strength of cyclically preloaded arrays of pillars. Acta Mech. 2020, 231, 3145–3155. [Google Scholar] [CrossRef]
- Lee, J.-A.; Lee, D.-H.; Seok, M.-Y.; Choi, I.-C.; Han, H.N.; Tsui, T.Y.; Ramamurty, U.; Jang, J.-I. Significant strengthening of nanocrystalline Ni sub-micron pillar by cyclic loading in elastic regime. Scr. Mater. 2017, 140, 31–34. [Google Scholar] [CrossRef]
- Domanski, Z. Spreading of Failures in Small-World Networks: A Connectivity-Dependent Load Sharing Fibre Bundle Model. Front. Phys. 2020, 8, 469. [Google Scholar] [CrossRef]
- Hansen, A.; Hemmer, P.C.; Pradhan, S. The Fiber Bundle Model: Modeling Failure in Materials; Wiley-VCH: Weinheim, Germany, 2015. [Google Scholar]
- Pradhan, S.; Hansen, A.; Chakrabarti, B.K. Failure Processes in Elastic Fiber Bundles. Rev. Mod. Phys. 2010, 82, 499–555. [Google Scholar] [CrossRef] [Green Version]
- Chakrabarti, B.K.; Biswas, S.; Pradhan, S. Cooperative Dynamics in the Fiber Bundle Model. Front. Phys. 2021, 8, 613392. [Google Scholar] [CrossRef]
- Hao, S.; Yang, H.; Liang, X. Catastrophic Failure and Critical Scaling Laws of Fiber Bundle Material. Materials 2017, 10, 515. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sinha, S.; Roy, S.; Hansen, A. Crack localization and the interplay between stress enhancement and thermal noise. Physica A 2021, 569, 125782. [Google Scholar] [CrossRef]
- Kukla, S.; Siedlecka, U. A Fractional Single-Phase-Lag Model of Heat Conduction for Describing Propagation of the Maximum Temperature in a Finite Medium. Entropy 2018, 20, 876. [Google Scholar] [CrossRef] [Green Version]
- Hidalgo, R.C.; Moreno, J.; Kun, F.; Herrmann, H.J. Fracture model with variable range of interaction. Phys. Rev. E 2002, 65, 046148. [Google Scholar] [CrossRef] [Green Version]
- Biswas, S.; Goehring, L. Interface propagation in fiber bundles: Local, mean-field and intermediate range-dependent statistics. New J. Phys. 2016, 18, 103048. [Google Scholar] [CrossRef] [Green Version]
- Yewande, O.E.; Moreno, Y.; Kun, F.; Hidalgo, R.C.; Herrmann, H.J. Time evolution of damage under variable ranges of load transfer. Phys. Rev. E 2003, 68, 026116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krings, A. CHAPTER 5–System Survivability. In Information Assurance; Qian, Y., Joshi, J., Tipper, D., Krishnamurthy, P., Eds.; Morgan Kaufmann: Burlington, MA, USA, 2008; pp. 113–145. [Google Scholar] [CrossRef]
- McCartney, L.N.; Smith, R.L. Statistical Theory of the Strength of Fiber Bundles. J. Appl. Mech. 1983, 50, 601–608. [Google Scholar] [CrossRef]
- Smith, R.L. The Asymptotic Distribution of the Strength of a Series-Parallel System with Equal Load-Sharing. Ann. Probab. 1982, 10, 137–171. [Google Scholar] [CrossRef]
- Porwal, P.K.; Beyerlein, I.J.; Phoenix, S.L. Statistical strength of a twisted fiber bundle: An extension of Daniels equal-load-sharing parallel bundle theory. J. Mech. Mater. Struct. 2006, 1, 1425–1447. [Google Scholar] [CrossRef]
- Derda, T. Statistical analysis of mechanical damage in arrays of mixed nanopillars. J. Appl. Math. Comput. Mech. 2015, 14, 43–53. [Google Scholar] [CrossRef] [Green Version]
- Azzalini, A. The Skew-Normal and Related Families; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Domanski, Z. Damage Statistics in Progressively Compressed Arrays of Nano-pillars. Eng. Lett. 2019, 27, 18–23. [Google Scholar]
- Hao, D.-P.; Tang, G.; Xun, Z.-P.; Xia, H.; Han, K. Simulation of finite size effects of the fiber bundle model. Physica A 2018, 490, 338–346. [Google Scholar] [CrossRef]
- Alava, M.J.; Nukala, P.K.V.V.; Zapperi, S. Statistical models of fracture. Adv. Phys. 2006, 55, 349–476. [Google Scholar] [CrossRef] [Green Version]

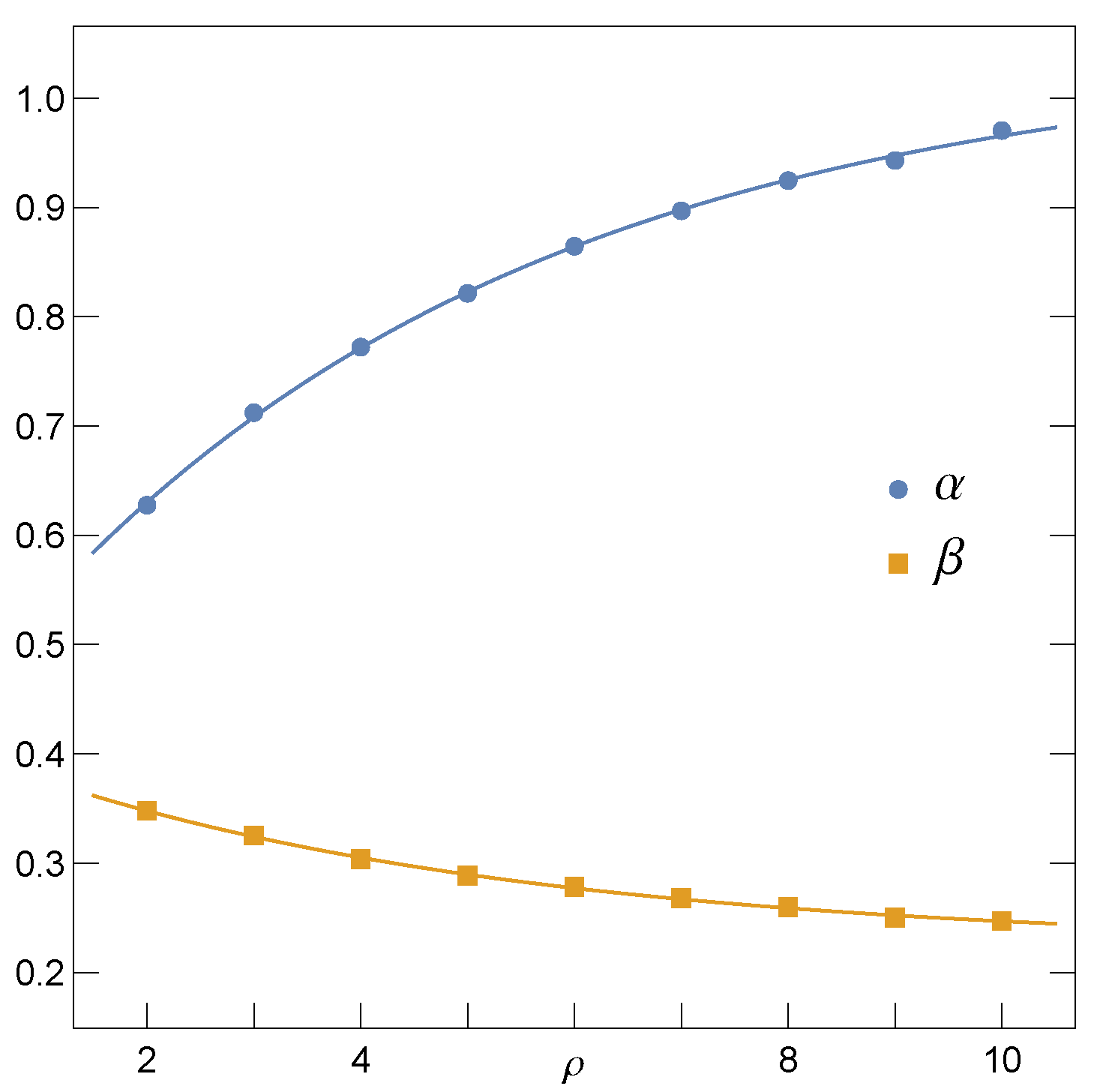



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derda, T.; Domanski, Z. Survivability of Suddenly Loaded Arrays of Micropillars. Materials 2021, 14, 7173. https://doi.org/10.3390/ma14237173
Derda T, Domanski Z. Survivability of Suddenly Loaded Arrays of Micropillars. Materials. 2021; 14(23):7173. https://doi.org/10.3390/ma14237173
Chicago/Turabian StyleDerda, Tomasz, and Zbigniew Domanski. 2021. "Survivability of Suddenly Loaded Arrays of Micropillars" Materials 14, no. 23: 7173. https://doi.org/10.3390/ma14237173
APA StyleDerda, T., & Domanski, Z. (2021). Survivability of Suddenly Loaded Arrays of Micropillars. Materials, 14(23), 7173. https://doi.org/10.3390/ma14237173





