Anisotropy of Mechanical Properties and Residual Stress in Additively Manufactured 316L Specimens
Abstract
:1. Introduction
2. Materials and Experimental Methods
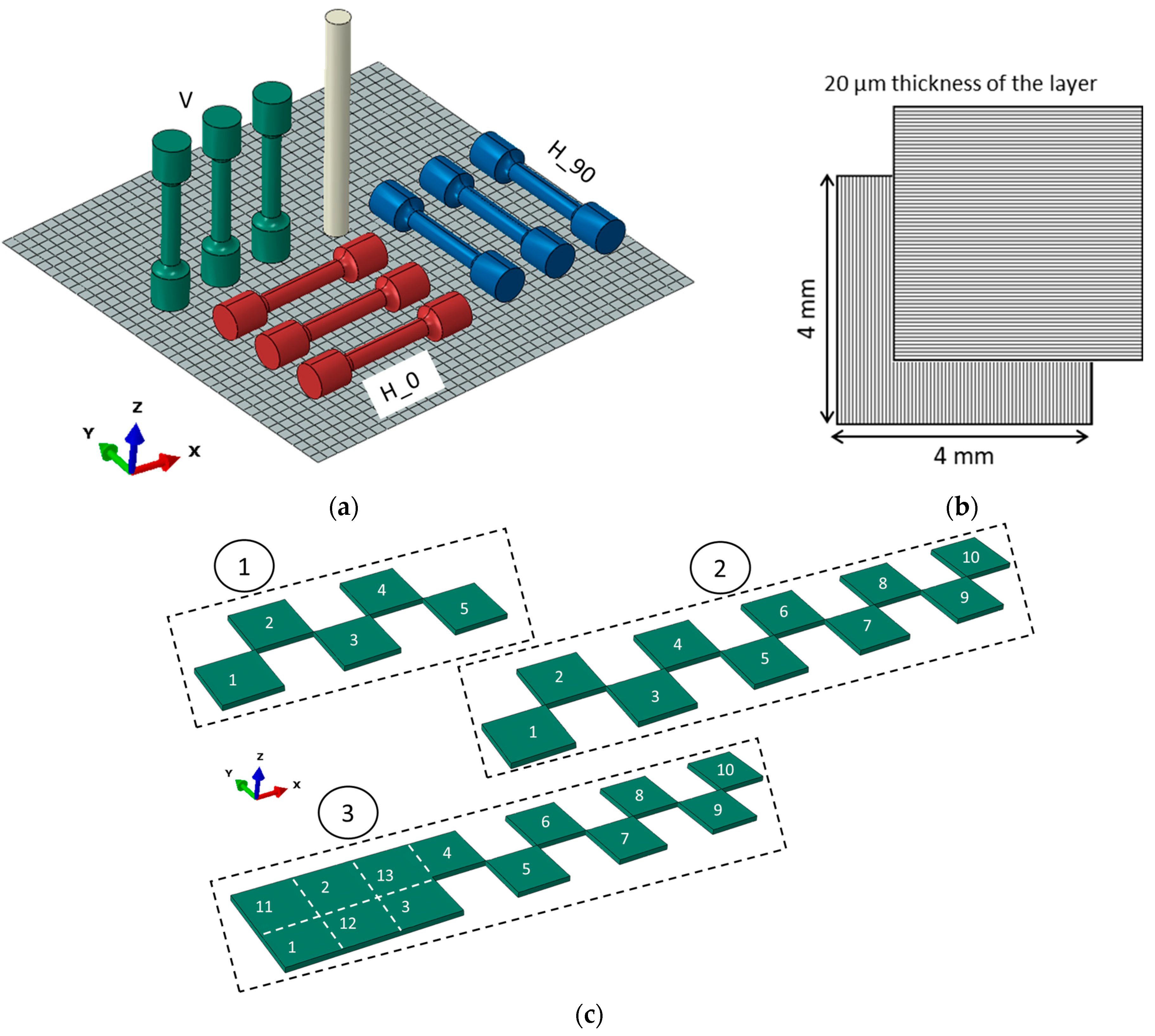
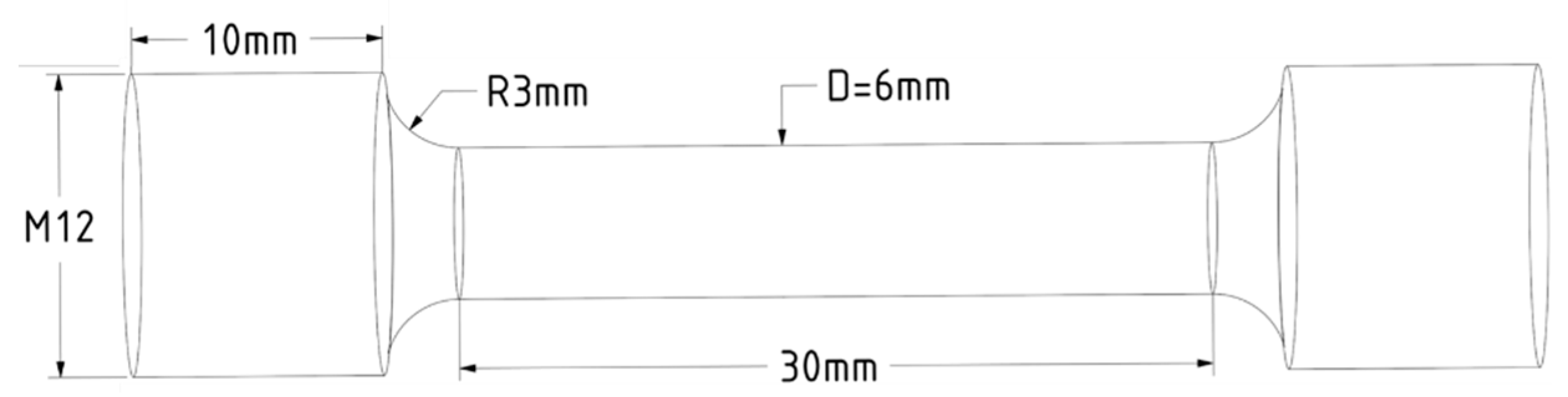
2.1. Selection and Preparation of the Specimens
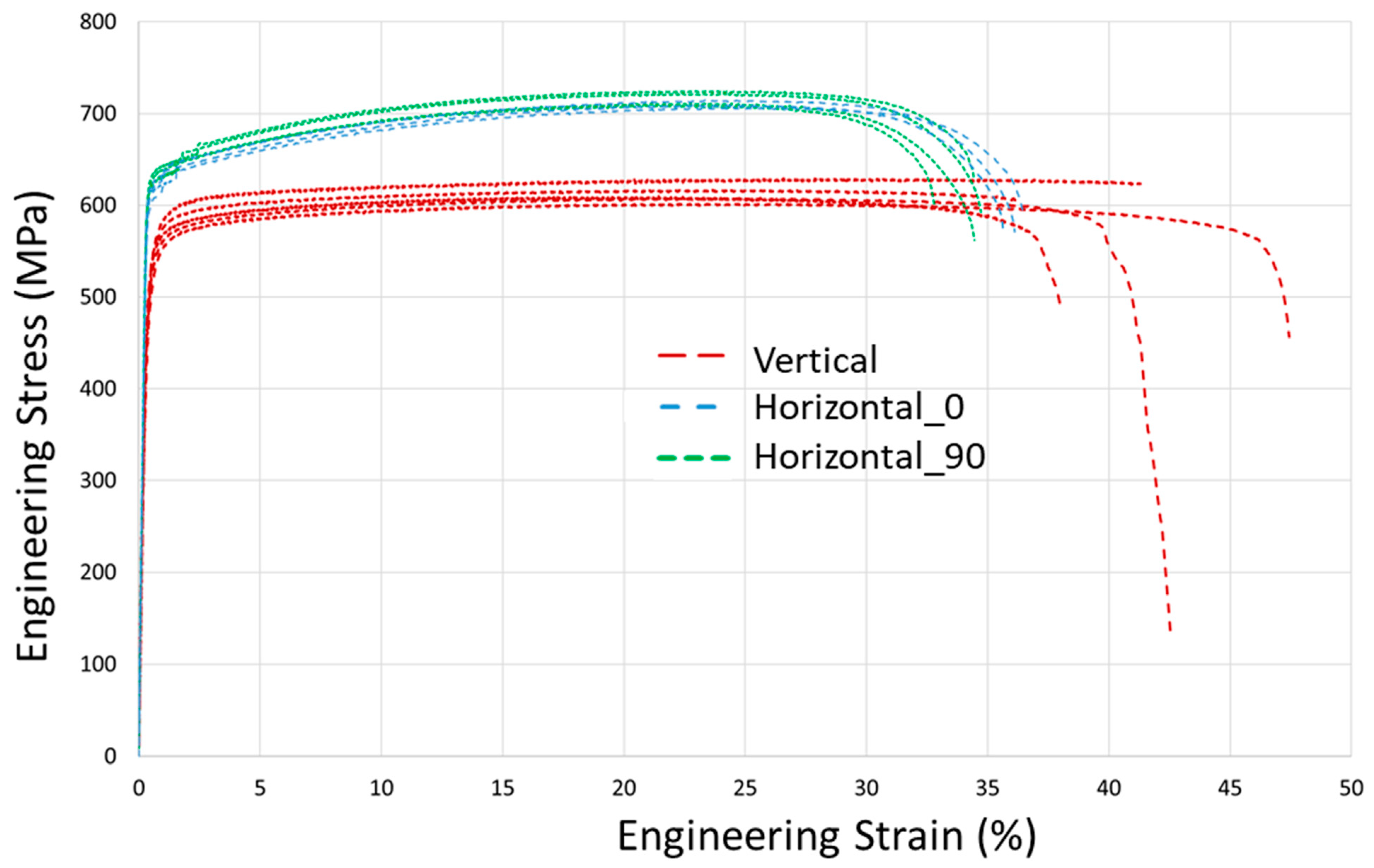
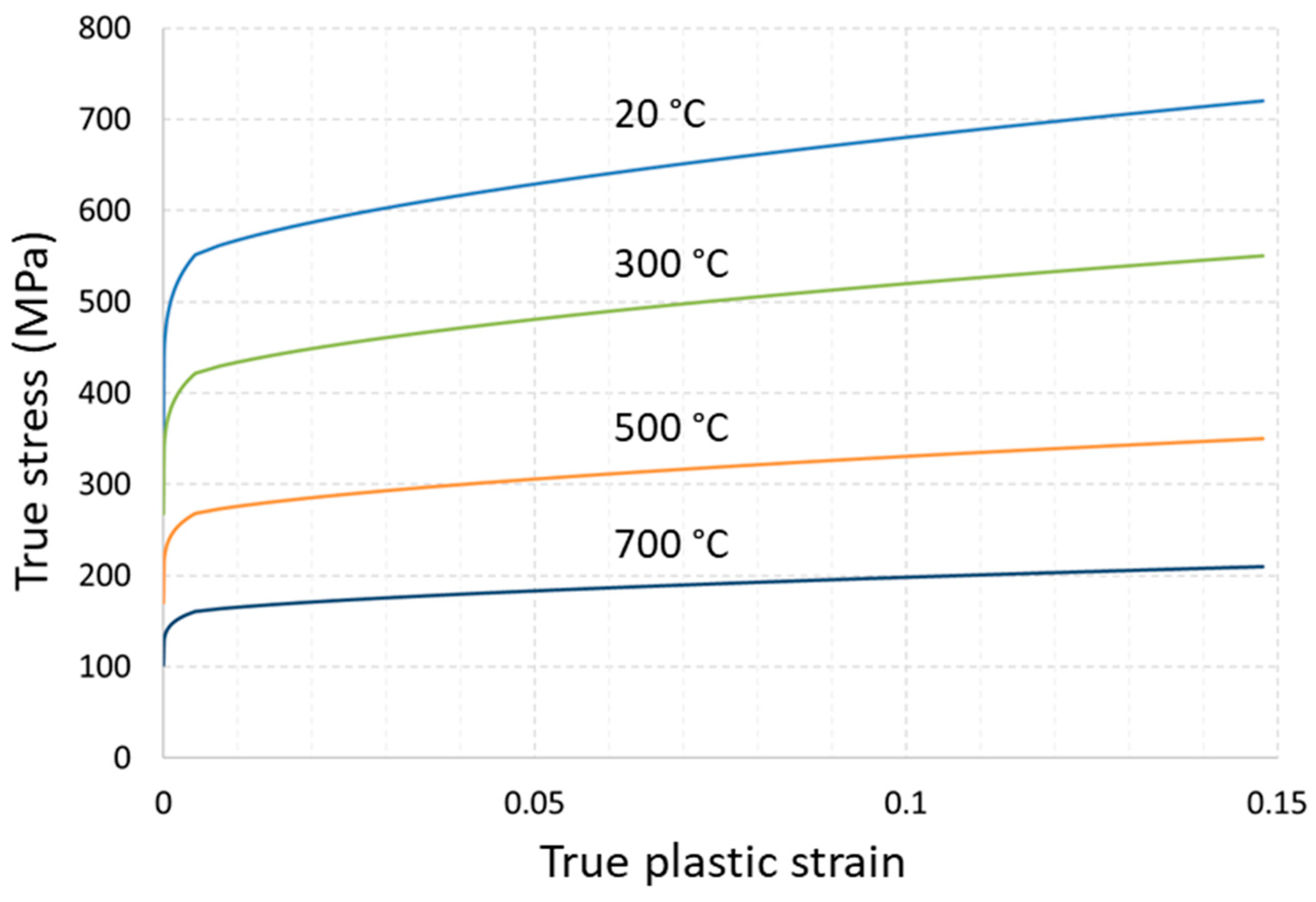
2.2. Tensile Tests
2.3. Validation Experiment
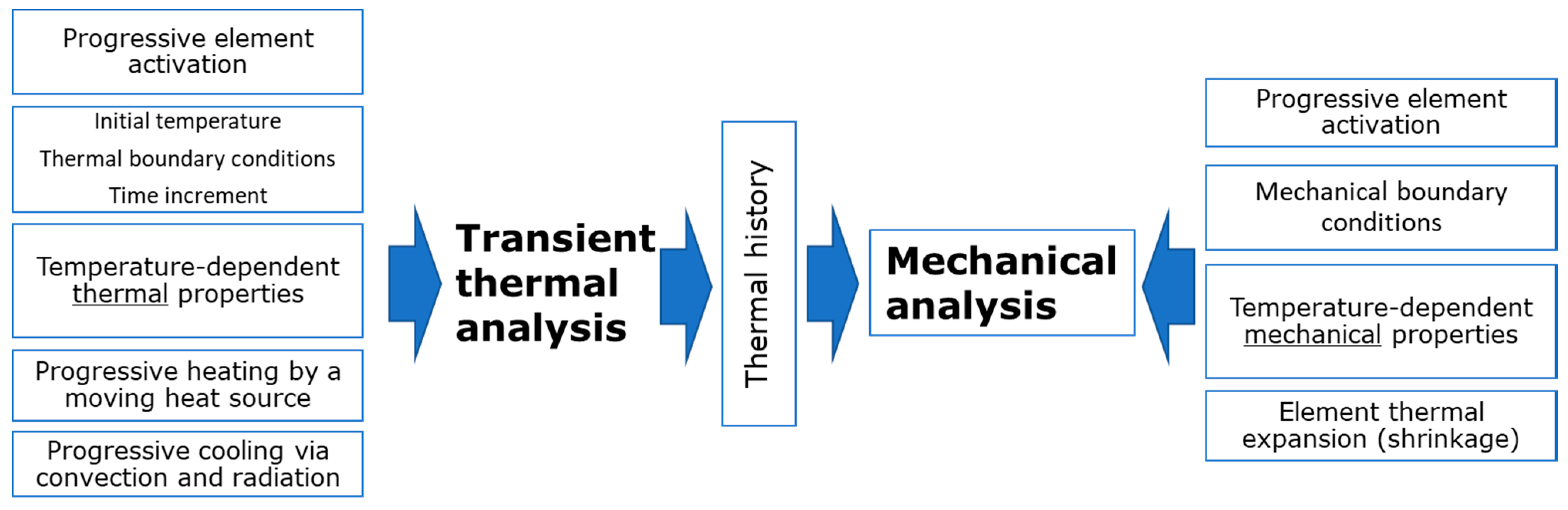
3. Simulation Approach
3.1. General Details
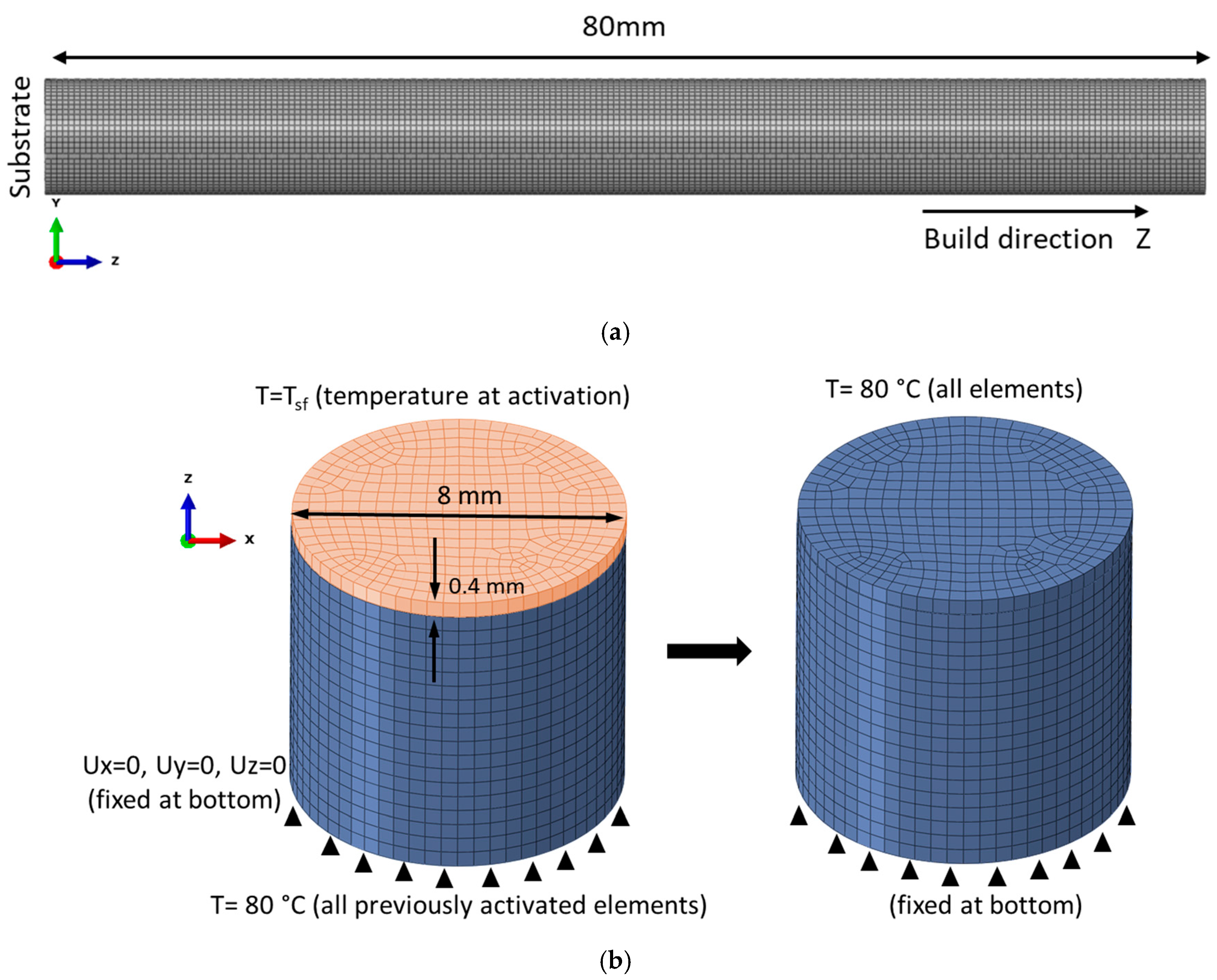
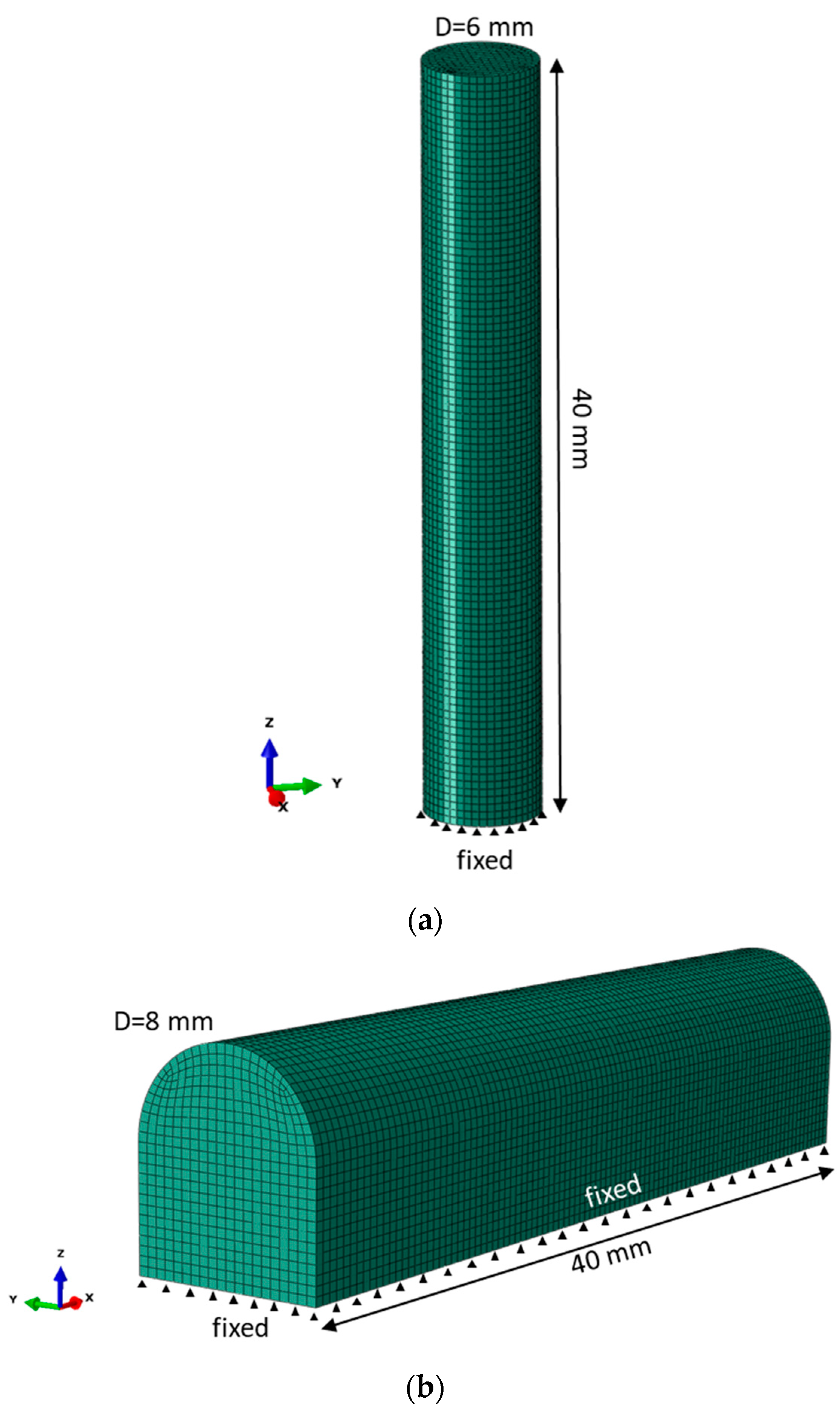
3.2. Finite Element Model
4. Simulation Results
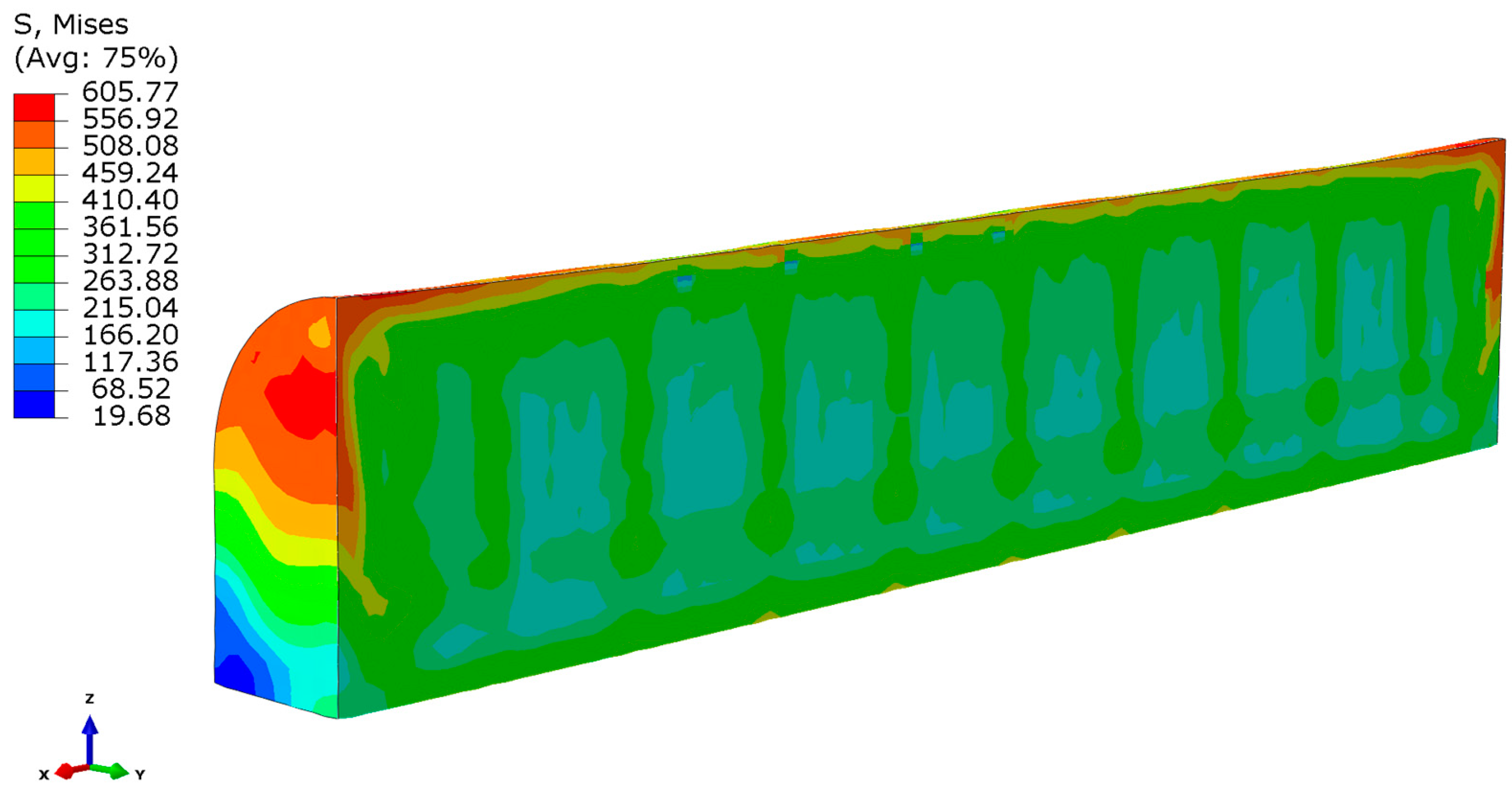
4.1. Simulation Results of Validation Problem
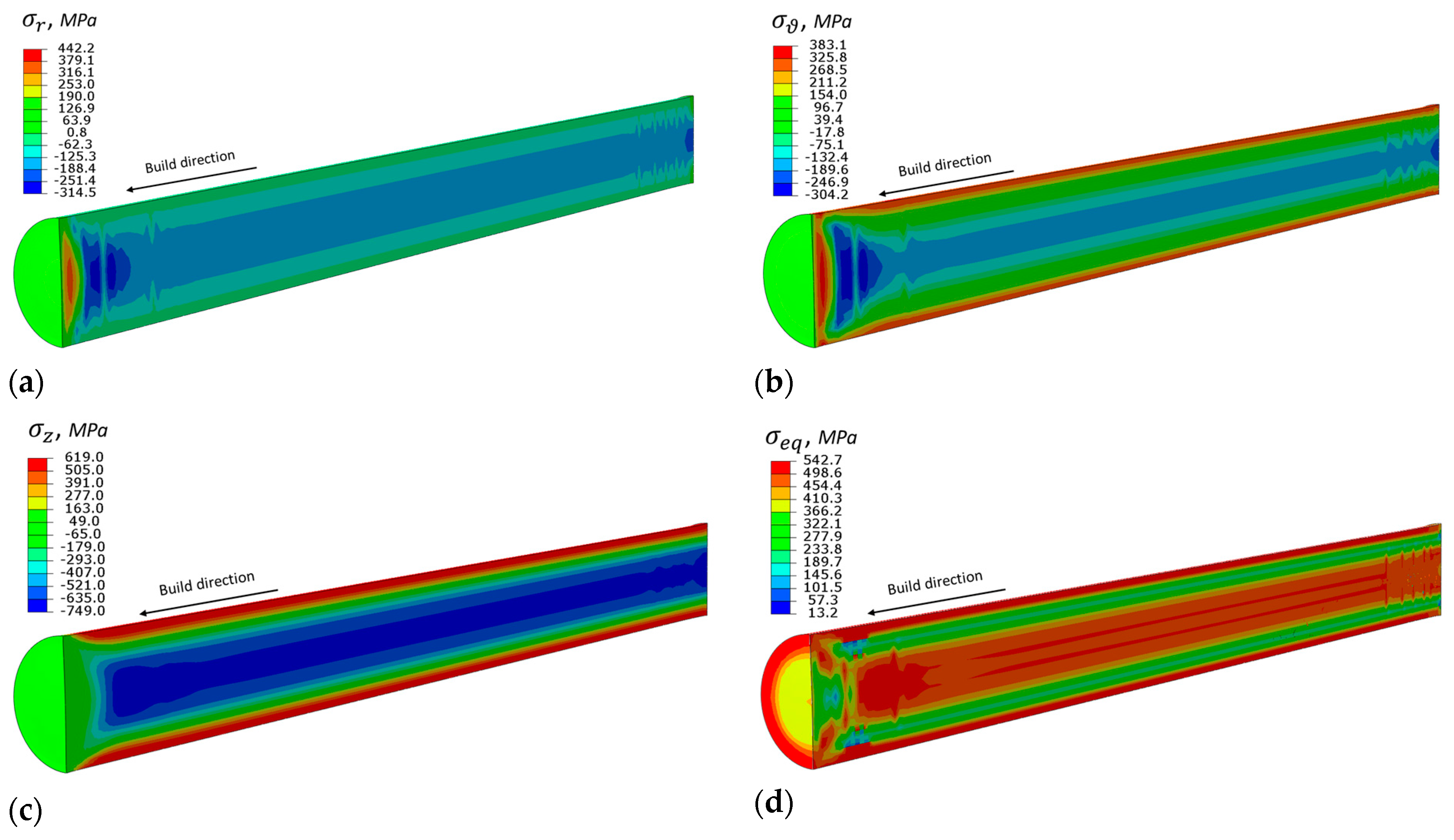
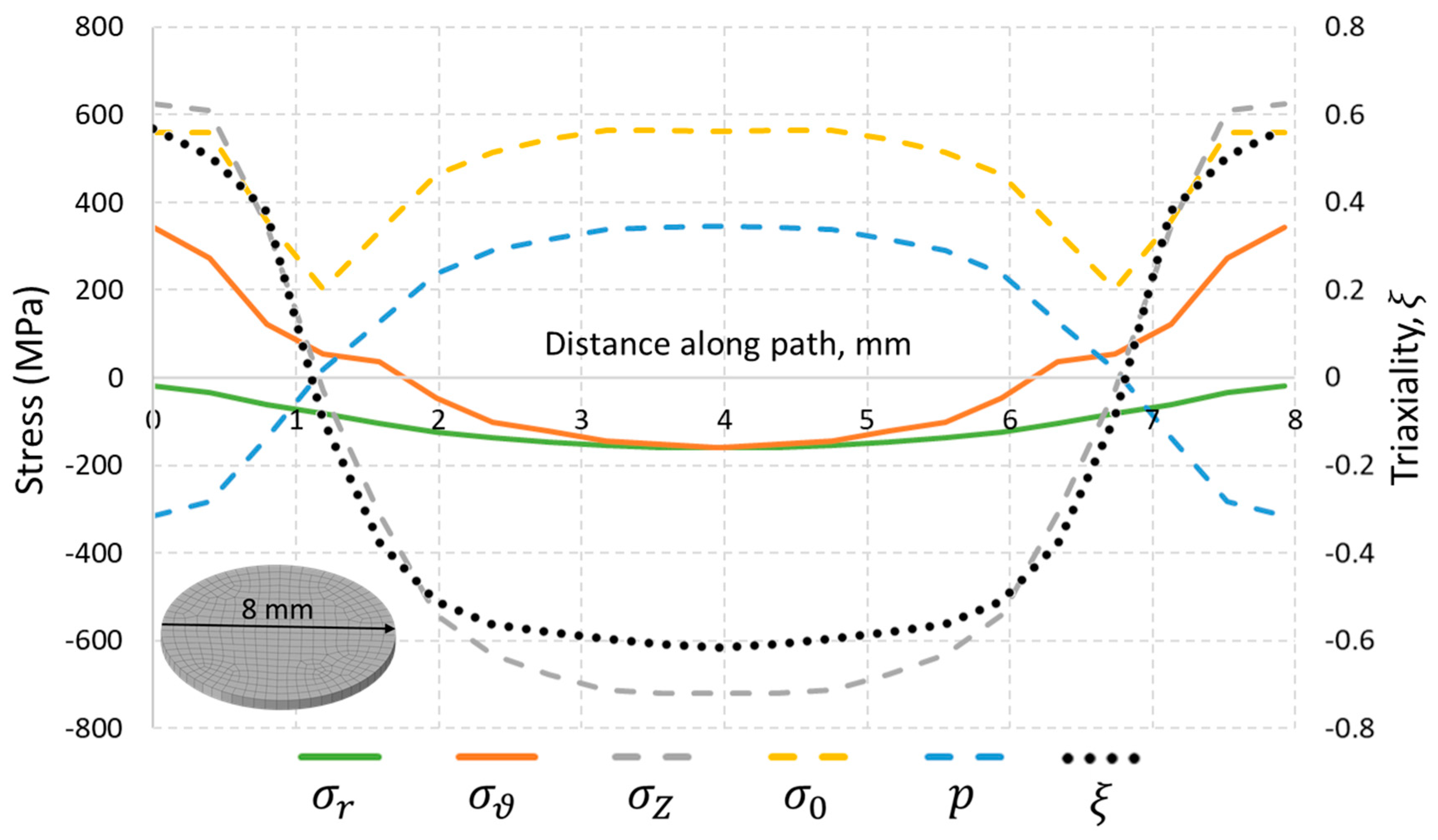
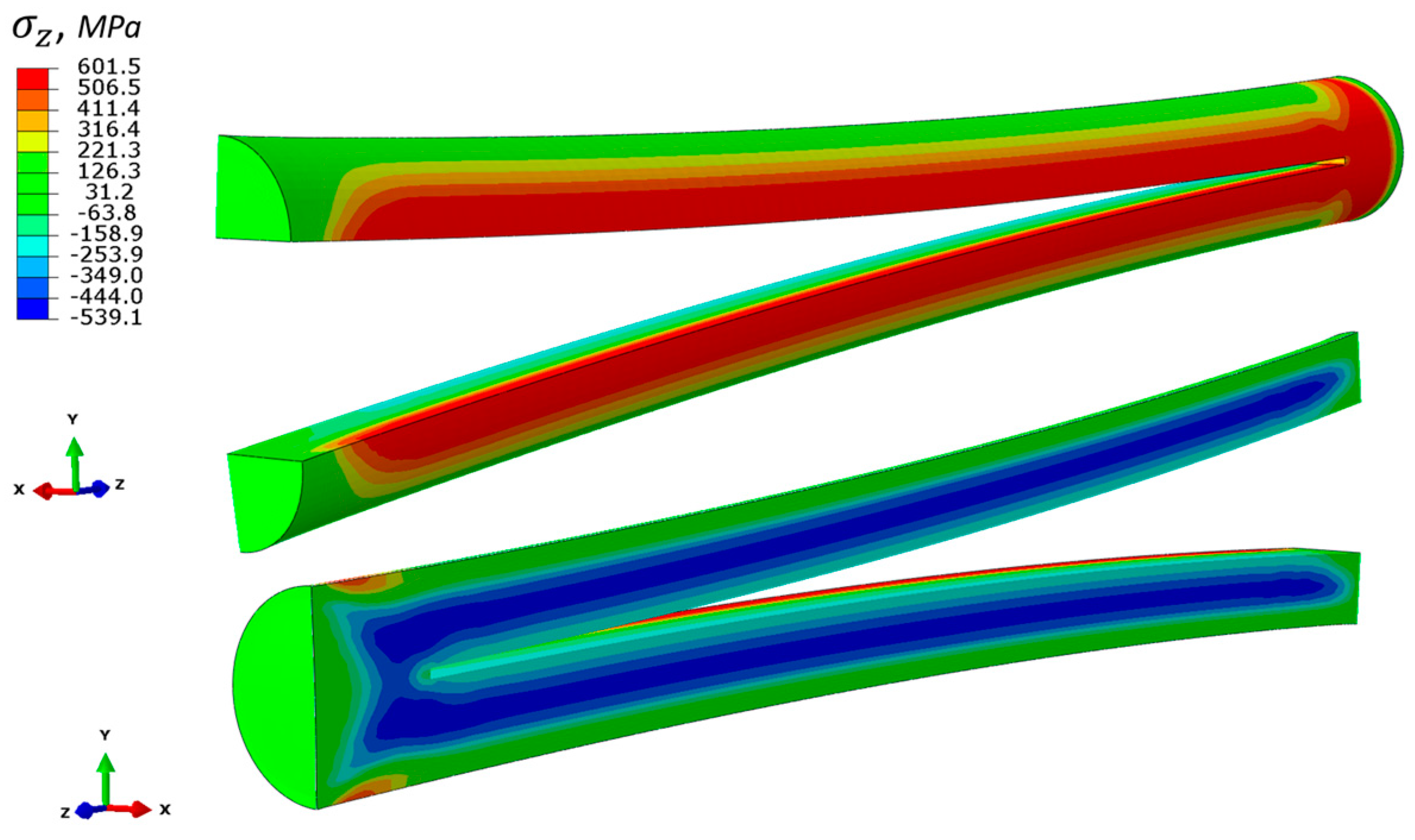
4.2. Residual Stress in Horizontal Specimen
4.3. Virtual Tensile Test of Vertical Specimen
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.M.; Voisin, T.; McKeown, J.; Ye, J.; Calta, N.; Li, Z.; Zeng, Z.; Zhang, Y.; Chen, W.; Roehling, T.T.; et al. Additively manufactured hierarchical stainless steels with high strength and ductility. Nat. Mater. 2017, 17, 63–71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ummethala, R.; Karamched, P.S.; Rathinavelu, S.; Singh, N.; Aggarwal, A.; Sun, K.; Ivanov, E.; Kollo, L.; Okulov, I.; Eckert, J.; et al. Selective laser melting of high-strength, low-modulus Ti–35Nb–7Zr–5Ta alloy. Materialia 2020, 14, 100941. [Google Scholar] [CrossRef]
- Karimi, J.; Suryanarayana, C.; Okulov, I.; Prashanth, K. Selective laser melting of Ti6Al4V: Effect of laser re-melting. Mater. Sci. Eng. A 2020, 805, 140558. [Google Scholar] [CrossRef]
- Tolosa, I.; Garciandía, F.; Zubiri, F.; Zapirain, F.; Esnaola, A. Study of mechanical properties of AISI 316 stainless steel processed by “selective laser melting”, following different manufacturing strategies. Int. J. Adv. Manuf. Technol. 2010, 51, 639–647. [Google Scholar] [CrossRef]
- Lavery, N.P.; Cherry, J.; Mehmood, S.; Davies, H.; Girling, B.; Sackett, E.; Brown, S.; Sienz, J. Effects of hot isostatic pressing on the elastic modulus and tensile properties of 316L parts made by powder bed laser fusion. Mater. Sci. Eng. A 2017, 693, 186–213. [Google Scholar] [CrossRef] [Green Version]
- Garlea, E.; Choo, H.; Sluss, C.C.; Koehler, M.R.; Bridges, R.L.; Xiao, X.; Ren, Y.; Jared, B.H. Variation of elastic mechanical properties with texture, porosity, and defect characteristics in laser powder bed fusion 316L stainless steel. Mater. Sci. Eng. A 2019, 763, 138032. [Google Scholar] [CrossRef]
- Jeon, J.M.; Park, J.M.; Yu, J.-H.; Kim, J.G.; Seong, Y.; Park, S.H.; Kim, H.S. Effects of microstructure and internal defects on mechanical anisotropy and asymmetry of selective laser-melted 316L austenitic stainless steel. Mater. Sci. Eng. A 2019, 763, 138152. [Google Scholar] [CrossRef]
- Prasad, M.R.G.; Biswas, A.; Geenen, K.; Amin, W.; Gao, S.; Lian, J.; Röttger, A.; Vajragupta, N.; Hartmaier, A. Influence of Pore Characteristics on Anisotropic Mechanical Behavior of Laser Powder Bed Fusion–Manufactured Metal by Micromechanical Modeling. Adv. Eng. Mater. 2020, 22, 2000641. [Google Scholar] [CrossRef]
- Hitzler, L.; Hirsch, J.; Heine, B.; Merkel, M.; Hall, W.; Öchsner, A. On the Anisotropic Mechanical Properties of Selective Laser-Melted Stainless Steel. Materials 2017, 10, 1136. [Google Scholar] [CrossRef] [Green Version]
- Niendorf, T.; Leuders, S.; Riemer, A.; Richard, H.A.; Tröster, T.; Schwarze, D. Highly Anisotropic Steel Processed by Selective Laser Melting. Met. Mater. Trans. A 2013, 44, 794–796. [Google Scholar] [CrossRef] [Green Version]
- Geiger, F.; Kunze, K.; Etter, T. Tailoring the texture of IN738LC processed by selective laser melting (SLM) by specific scanning strategies. Mater. Sci. Eng. A 2016, 661, 240–246. [Google Scholar] [CrossRef]
- Mainprice, D.; Bachmann, F.; Hielscher, R.; Schaeben, H.; Lloyd, G. Calculating anisotropic piezoelectric properties from texture data using the MTEX open source package. Geol. Soc. Spéc. Publ. 2015, 409, 223–249. [Google Scholar] [CrossRef] [Green Version]
- Im, Y.-D.; Kim, K.-H.; Jung, K.-H.; Lee, Y.-K.; Song, K.-H. Anisotropic Mechanical Behavior of Additive Manufactured AISI 316L Steel. Met. Mater. Trans. A 2019, 50, 2014–2021. [Google Scholar] [CrossRef]
- Charmi, A.; Falkenberg, R.; Ávila, L.; Mohr, G.; Sommer, K.; Ulbricht, A.; Sprengel, M.; Neumann, R.S.; Skrotzki, B.; Evans, A. Mechanical anisotropy of additively manufactured stainless steel 316L: An experimental and numerical study. Mater. Sci. Eng. A 2021, 799, 140154. [Google Scholar] [CrossRef]
- Röttger, A.; Boes, J.; Theisen, W.; Thiele, M.; Esen, C.; Edelmann, A.; Hellmann, R. Microstructure and mechanical properties of 316L austenitic stainless steel processed by different SLM devices. Int. J. Adv. Manuf. Technol. 2020, 108, 769–783. [Google Scholar] [CrossRef]
- Kurzynowski, T.; Gruber, K.; Stopyra, W.; Kuźnicka, B.; Chlebus, E. Correlation between process parameters, microstructure and properties of 316 L stainless steel processed by selective laser melting. Mater. Sci. Eng. A 2018, 718, 64–73. [Google Scholar] [CrossRef]
- Zhang, B.; Dembinski, L.; Coddet, C. The study of the laser parameters and environment variables effect on mechanical properties of high compact parts elaborated by selective laser melting 316L powder. Mater. Sci. Eng. A 2013, 584, 21–31. [Google Scholar] [CrossRef]
- Krawitz, A.D.; Holden, T.M. The Measurement of Residual Stresses Using Neutron Diffraction. MRS Bull. 1990, 15, 57–64. [Google Scholar] [CrossRef]
- Wu, A.S.; Brown, D.W.; Kumar, M.; Gallegos, G.F.; King, W.E. An Experimental Investigation into Additive Manufacturing-Induced Residual Stresses in 316L Stainless Steel. Met. Mater. Trans. A 2014, 45, 6260–6270. [Google Scholar] [CrossRef]
- Song, X.; Xie, M.; Hofmann, F.; Illston, T.; Connolley, T.; Reinhard, C.T.; Atwood, R.C.; Connor, L.D.; Drakopoulos, M.; Frampton, L.; et al. Residual stresses and microstructure in Powder Bed Direct Laser Deposition (PB DLD) samples. Int. J. Mater. Form. 2015, 8, 245–254. [Google Scholar] [CrossRef]
- Withers, P.; Bhadeshia, H.K.D.H. Residual stress. Part 1—Measurement techniques. Mater. Sci. Technol. 2001, 17, 355–365. [Google Scholar] [CrossRef]
- Chao, Q.; Thomas, S.; Birbilis, N.; Cizek, P.; Hodgson, P.D.; Fabijanic, D. The effect of post-processing heat treatment on the microstructure, residual stress and mechanical properties of selective laser melted 316L stainless steel. Mater. Sci. Eng. A 2021, 821, 141611. [Google Scholar] [CrossRef]
- Suryawanshi, J.; Prashanth, K.; Ramamurty, U. Mechanical behavior of selective laser melted 316L stainless steel. Mater. Sci. Eng. A 2017, 696, 113–121. [Google Scholar] [CrossRef]
- Ronneberg, T.; Davies, C.M.; Hooper, P.A. Revealing relationships between porosity, microstructure and mechanical properties of laser powder bed fusion 316L stainless steel through heat treatment. Mater. Des. 2020, 189, 108481. [Google Scholar] [CrossRef]
- Chen, W.; Voisin, T.; Zhang, Y.; Florien, J.-B.; Spadaccini, C.M.; McDowell, D.L.; Zhu, T.; Wang, Y.M. Microscale residual stresses in additively manufactured stainless steel. Nat. Commun. 2019, 10, 4338. [Google Scholar] [CrossRef] [Green Version]
- Dye, D.; Stone, H.; Reed, R. Intergranular and interphase microstresses. Curr. Opin. Solid State Mater. Sci. 2001, 5, 31–37. [Google Scholar] [CrossRef]
- Rangaswamy, P.; Griffith, M.; Prime, M.; Holden, T.; Rogge, R.; Edwards, J.; Sebring, R. Residual stresses in LENS® components using neutron diffraction and contour method. Mater. Sci. Eng. A 2005, 399, 72–83. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Yadroitsava, I. Evaluation of residual stress in stainless steel 316L and Ti6Al4V samples produced by selective laser melting. Virtual Phys. Prototyp. 2015, 10, 67–76. [Google Scholar] [CrossRef]
- Denlinger, E.R.; Irwin, J.; Michaleris, P. Thermomechanical Modeling of Additive Manufacturing Large Parts. J. Manuf. Sci. Eng. 2014, 136, 061007. [Google Scholar] [CrossRef]
- Kruth, J.-P.; Deckers, J.; Yasa, E.; Wauthlé, R. Assessing and comparing influencing factors of residual stresses in selective laser melting using a novel analysis method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2012, 226, 980–991. [Google Scholar] [CrossRef]
- Costa, L.; Vilar, R.; Réti, T.; Deus, A. Rapid tooling by laser powder deposition: Process simulation using finite element analysis. Acta Mater. 2005, 53, 3987–3999. [Google Scholar] [CrossRef]
- Mukherjee, T.; Zhang, W.; DebRoy, T. An improved prediction of residual stresses and distortion in additive manufacturing. Comput. Mater. Sci. 2017, 126, 360–372. [Google Scholar] [CrossRef] [Green Version]
- Dunbar, A.J.; Denlinger, E.R.; Gouge, M.F.; Michaleris, P. Experimental validation of finite element modeling for laser powder bed fusion deformation. Addit. Manuf. 2016, 12, 108–120. [Google Scholar] [CrossRef]
- Bugatti, M.; Semeraro, Q. Limitations of the inherent strain method in simulating powder bed fusion processes. Addit. Manuf. 2018, 23, 329–346. [Google Scholar] [CrossRef]
- Lu, X.; Lin, X.; Chiumenti, M.; Cervera, M.; Hu, Y.; Ji, X.; Ma, L.; Huang, W. In situ measurements and thermo-mechanical simulation of Ti–6Al–4V laser solid forming processes. Int. J. Mech. Sci. 2019, 153–154, 119–130. [Google Scholar] [CrossRef]
- Williams, R.J.; Davies, C.M.; Hooper, P.A. A pragmatic part scale model for residual stress and distortion prediction in powder bed fusion. Addit. Manuf. 2018, 22, 416–425. [Google Scholar] [CrossRef]
- Acevedo, R.B.; Kantarowska, K.; Santos, E.C.; Fredel, M.C. Residual stress measurement techniques for Ti6Al4V parts fabricated using selective laser melting: State of the art review. Rapid Prototyp. J. 2020. [Google Scholar] [CrossRef]
- Yang, Y.; Allen, M.; London, T.; Oancea, V. Residual Strain Predictions for a Powder Bed Fusion Inconel 625 Single Cantilever Part. Integr. Mater. Manuf. Innov. 2019, 8, 294–304. [Google Scholar] [CrossRef] [Green Version]
- Narvan, M.; Ghasemi, A.; Fereiduni, E.; Kendrish, S.; Elbestawi, M. Part deflection and residual stresses in laser powder bed fusion of H13 tool steel. Mater. Des. 2021, 204, 109659. [Google Scholar] [CrossRef]
- Filimonov, A.M.; Rogozin, O.A.; Firsov, D.G.; Kuzminova, Y.O.; Sergeev, S.N.; Zhilyaev, A.P.; Lerner, M.I.; Toropkov, N.E.; Simonov, A.P.; Binkov, I.I.; et al. Hardening of Additive Manufactured 316L Stainless Steel by Using Bimodal Powder Containing Nanoscale Fraction. Materials 2020, 14, 115. [Google Scholar] [CrossRef]
- Song, X.; Feih, S.; Zhai, W.; Sun, C.-N.; Li, F.; Maiti, R.; Wei, J.; Yang, Y.; Oancea, V.; Brandt, L.R.; et al. Advances in additive manufacturing process simulation: Residual stresses and distortion predictions in complex metallic components. Mater. Des. 2020, 193, 108779. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, K.; Tan, P.; Tor, S.B.; Chua, C.K.; Leong, K.F. Modeling temperature and residual stress fields in selective laser melting. Int. J. Mech. Sci. 2018, 136, 24–35. [Google Scholar] [CrossRef]
- Shan, X.; Davies, C.; Wangsdan, T.; O’Dowd, N.; Nikbin, K. Thermo-mechanical modelling of a single-bead-on-plate weld using the finite element method. Int. J. Press. Vessel. Pip. 2009, 86, 110–121. [Google Scholar] [CrossRef]
- Hossain, S.; Truman, C.; Smith, D.; Daymond, M. Application of quenching to create highly triaxial residual stresses in type 316H stainless steels. Int. J. Mech. Sci. 2005, 48, 235–243. [Google Scholar] [CrossRef]
- Williams, R.J.; Hooper, P.; Davies, C. Finite element prediction and validation of residual stress profiles in 316L samples manufactured by laser powder bed fusion. Procedia Struct. Integr. 2018, 13, 1353–1358. [Google Scholar] [CrossRef]
- Williams, R.J.; Vecchiato, F.; Kelleher, J.; Wenman, M.R.; Hooper, P.A.; Davies, C. Effects of heat treatment on residual stresses in the laser powder bed fusion of 316L stainless steel: Finite element predictions and neutron diffraction measurements. J. Manuf. Process. 2020, 57, 641–653. [Google Scholar] [CrossRef]




| PBF Parameter | Values |
|---|---|
| Laser power | 113 W |
| Laser spot diameter | 55 µm |
| Hatch spacing | 80 µm |
| Layer thickness | 20 µm |
| Laser scan speed | 750 mm/s |
| Gas speed (Ar) | 2.5 m/s |
| Oxygen level | <0.3 at. % |
| Pressure in chamber | 1 bar |
| Spec. # | Young’s Modulus, GPa | YTS, MPa (0.2% Offset) | UTS, MPa | Elongation at Fracture, % | Reduction of Cross-Sectional Area at Fracture, % |
|---|---|---|---|---|---|
| V_1 | 160 | 535 | 630 | 41 | 48 |
| V_2 | 163 | 535 | 615 | 37 | 46 |
| V_3 | 157 | 530 | 610 | 38 | 43 |
| V_4 | 161 | 535 | 615 | 46 | 42 |
| V_5 | 159 | 525 | 605 | 36 | 40 |
| V_6 | 152 | 510 | 600 | 36 | 41 |
| Average | 158.7 | 528.3 | 612.5 | 39.0 | 43.3 |
| Standard deviation | 3.8 | 9.8 | 10.4 | 3.6 | 3.1 |
| Spec. # | Young’s Modulus, GPa | YTS, MPa (0.2% Offset) | UTS, MPa | Elongation at Fracture, % | Reduction of Cross-Sectional Area at Fracture, % |
|---|---|---|---|---|---|
| H_0_1 | 200 | 630 | 725 | 32 | 58 |
| H_0_2 | 198 | 615 | 710 | 31 | 55 |
| H_0_3 | 201 | 610 | 705 | 30 | 56 |
| H_0_4 | 185 | 610 | 705 | 30 | 54 |
| Average | 196 | 616.2 | 711.2 | 30.8 | 55.8 |
| Standard deviation | 7.4 | 9.5 | 9.5 | 0.8 | 1.7 |
| Spec. # | Young’s Modulus, GPa | YTS, MPa 1234567 (0.2% Offset) | UTS, MPa | Elongation at Fracture, % | Reduction of Cross-Sectional Area at Fracture, % |
|---|---|---|---|---|---|
| H_90_1 | 199 | 615 | 705 | 29 | 52 |
| H_90_2 | 211 | 620 | 705 | 30 | 58 |
| H_90_3 | 188 | 605 | 695 | 28 | 56 |
| H_90_4 | 198 | 610 | 700 | 28 | 49 |
| Average | 199.0 | 612.5 | 701.3 | 28.8 | 53.7 |
| Standard deviation | 9.4 | 6.5 | 4.8 | 0.8 | 4.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fedorenko, A.; Fedulov, B.; Kuzminova, Y.; Evlashin, S.; Staroverov, O.; Tretyakov, M.; Lomakin, E.; Akhatov, I. Anisotropy of Mechanical Properties and Residual Stress in Additively Manufactured 316L Specimens. Materials 2021, 14, 7176. https://doi.org/10.3390/ma14237176
Fedorenko A, Fedulov B, Kuzminova Y, Evlashin S, Staroverov O, Tretyakov M, Lomakin E, Akhatov I. Anisotropy of Mechanical Properties and Residual Stress in Additively Manufactured 316L Specimens. Materials. 2021; 14(23):7176. https://doi.org/10.3390/ma14237176
Chicago/Turabian StyleFedorenko, Alexey, Boris Fedulov, Yulia Kuzminova, Stanislav Evlashin, Oleg Staroverov, Mikhail Tretyakov, Evgeny Lomakin, and Iskander Akhatov. 2021. "Anisotropy of Mechanical Properties and Residual Stress in Additively Manufactured 316L Specimens" Materials 14, no. 23: 7176. https://doi.org/10.3390/ma14237176
APA StyleFedorenko, A., Fedulov, B., Kuzminova, Y., Evlashin, S., Staroverov, O., Tretyakov, M., Lomakin, E., & Akhatov, I. (2021). Anisotropy of Mechanical Properties and Residual Stress in Additively Manufactured 316L Specimens. Materials, 14(23), 7176. https://doi.org/10.3390/ma14237176








