Geometrical Investigation of Piezoelectric Patches for Broadband Energy Harvesting in Non-Deterministic Composite Plates
Abstract
:1. Introduction
2. Methodology
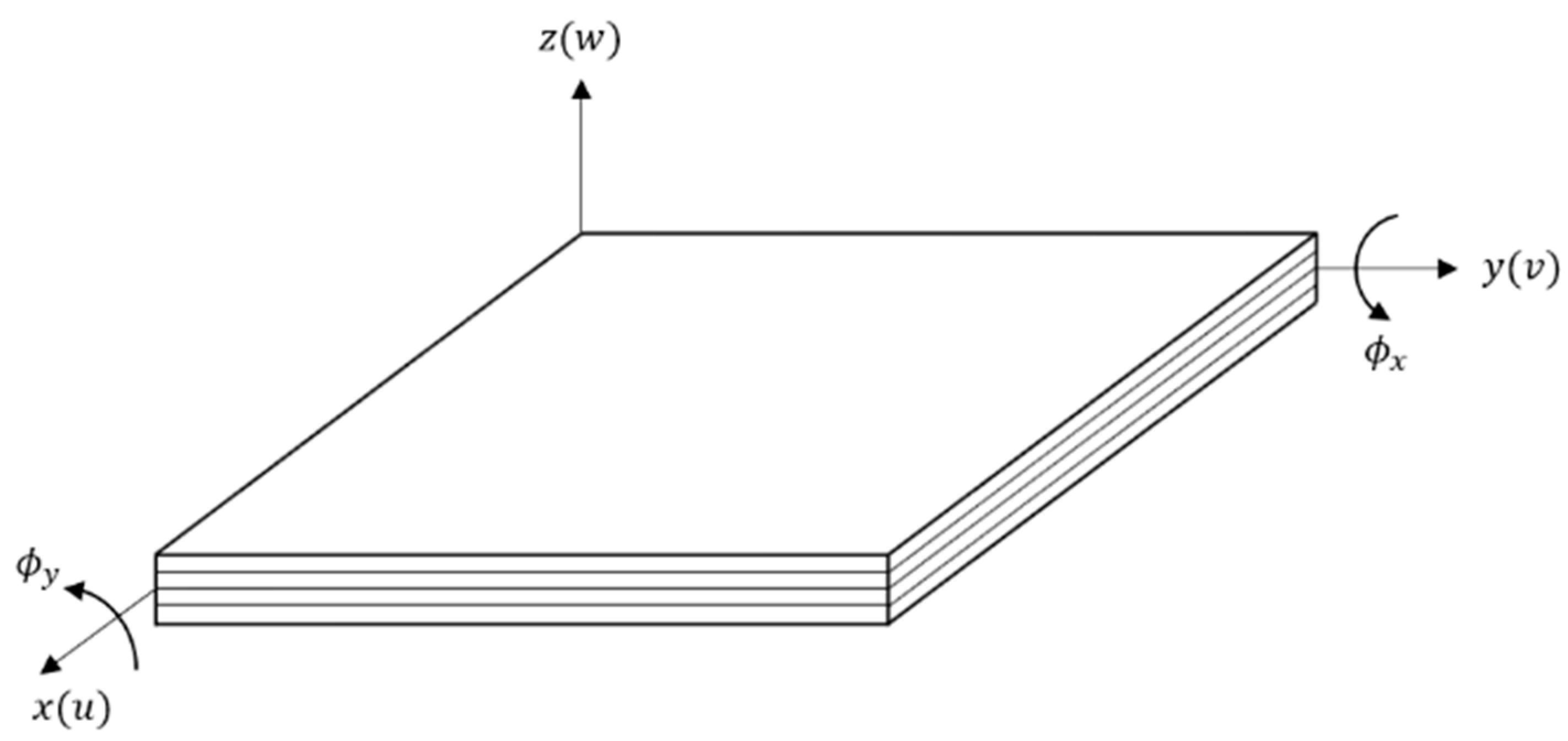
2.1. Theory of Laminated Composite Plates
2.1.1. Strain-Displacement Relationship
2.1.2. Constitutive Equations of a Lamina
2.2. Model Construction
2.2.1. Composite Laminated Plate
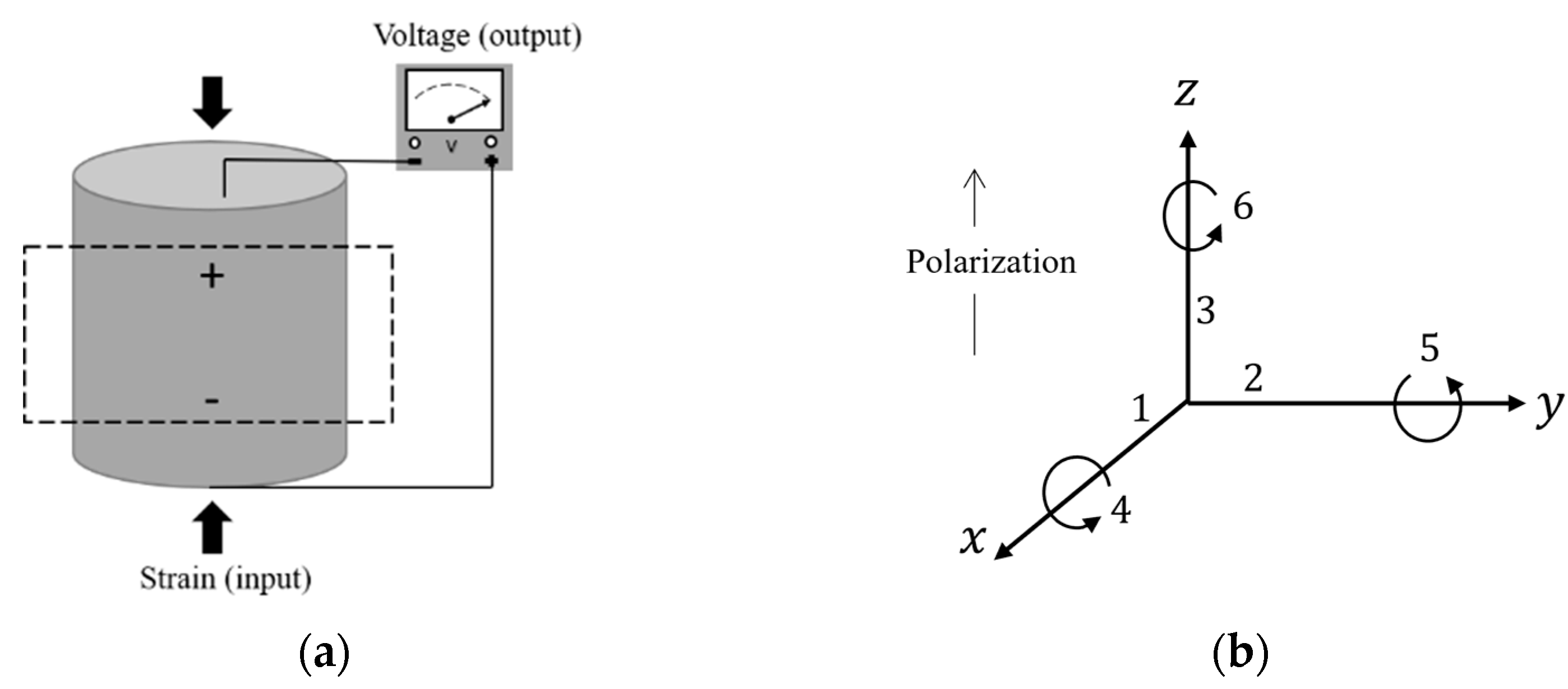
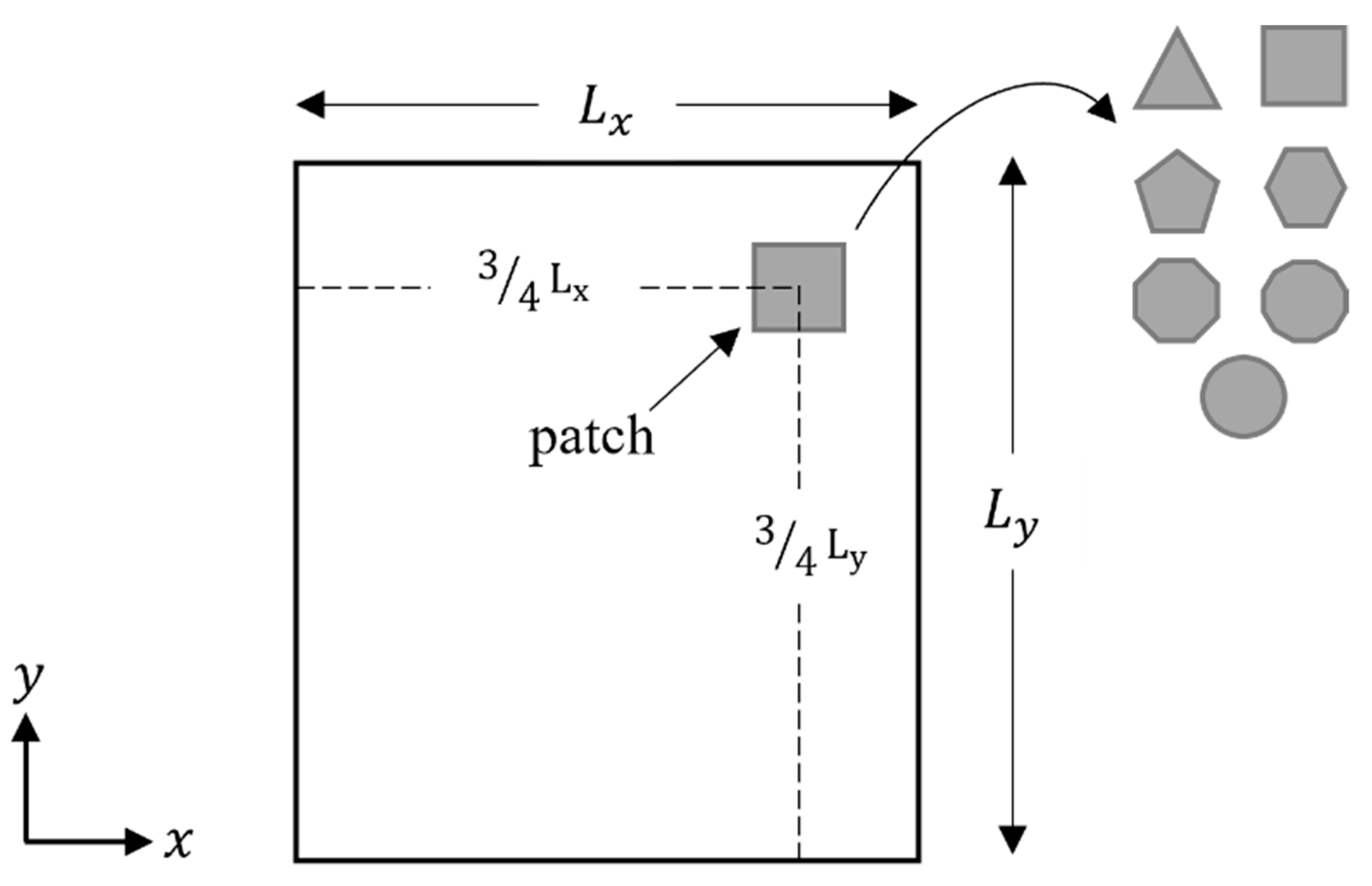
2.2.2. Piezoelectric Patches
- (i)
- (ii)
- Transverse Mode : indicates the polarization in the 3-direction per unit stress applied in the 1-direction. Or, induced strain in the 1-direction per unit electric field applied in the 3-direction [32]
- (iii)
- Shear Mode : indicates the polarization developed in the 1-direction per unit shear stress 5 applied (shear around the 2-direction) when there are no other external stresses.
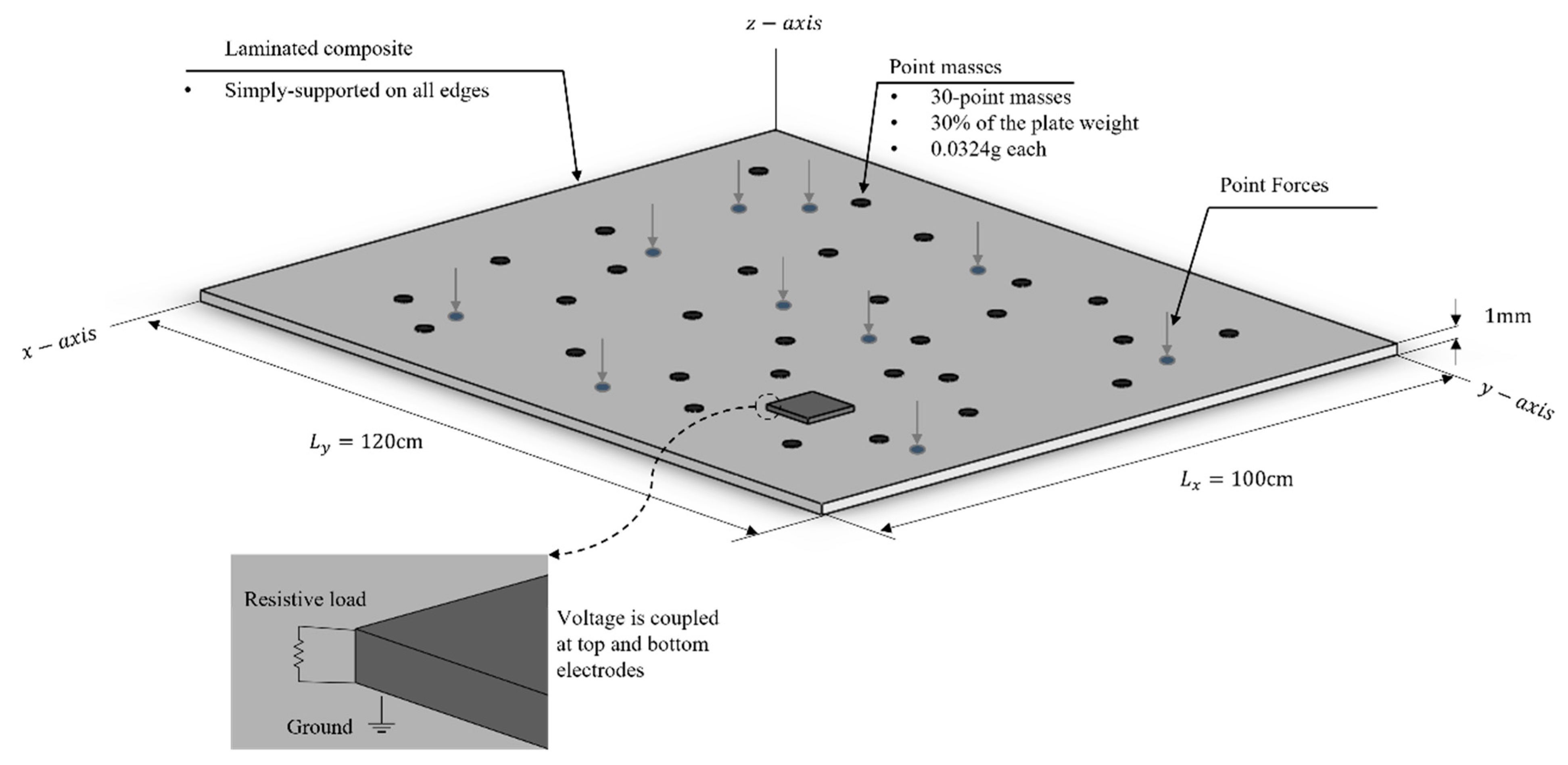
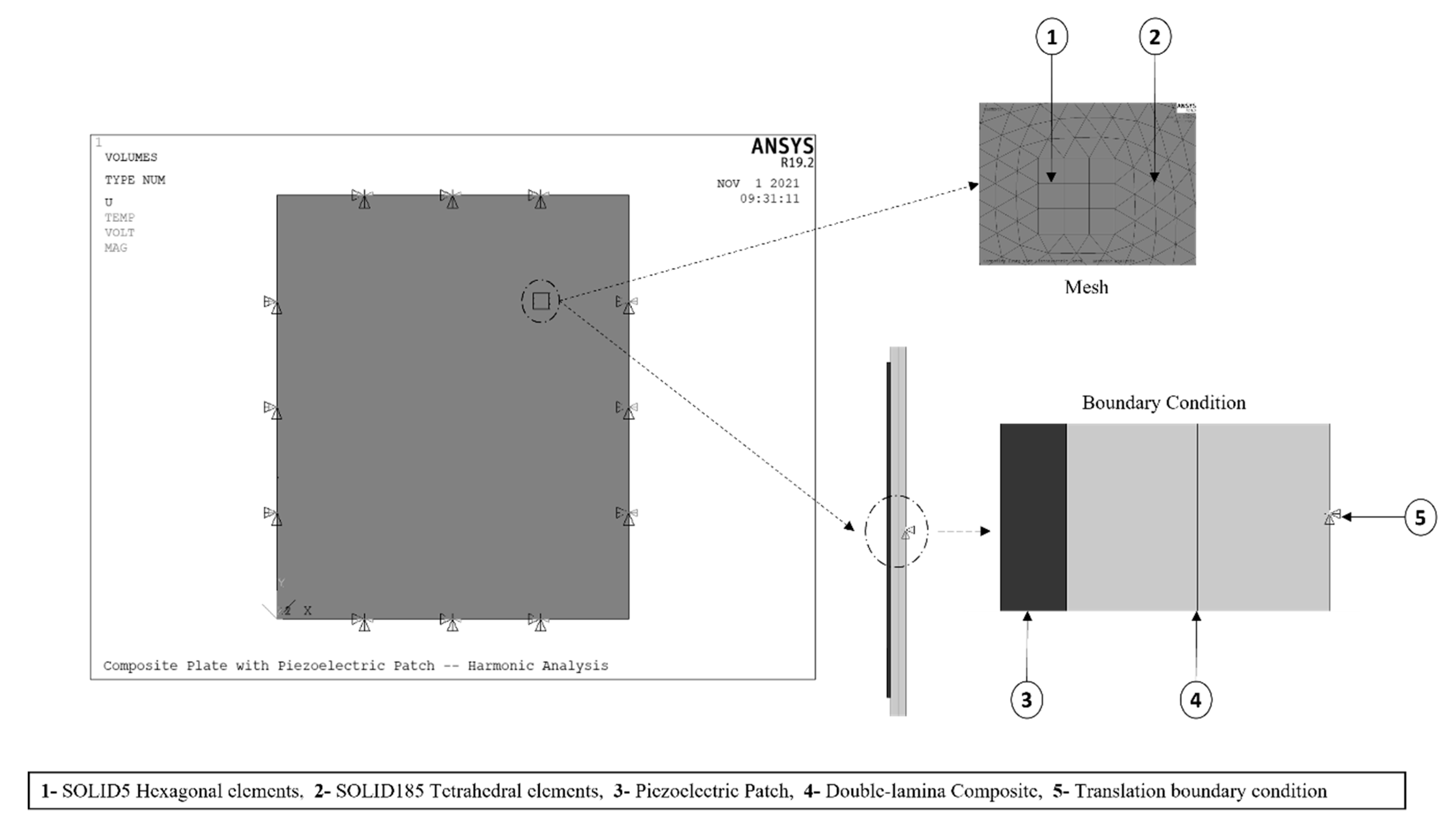
2.2.3. FE Model Components and Randomization
2.2.4. Randomization
2.2.5. Elements and Mesh
2.2.6. Boundary Condition
3. Results and Analysis
3.1. Single-Lamina Composite
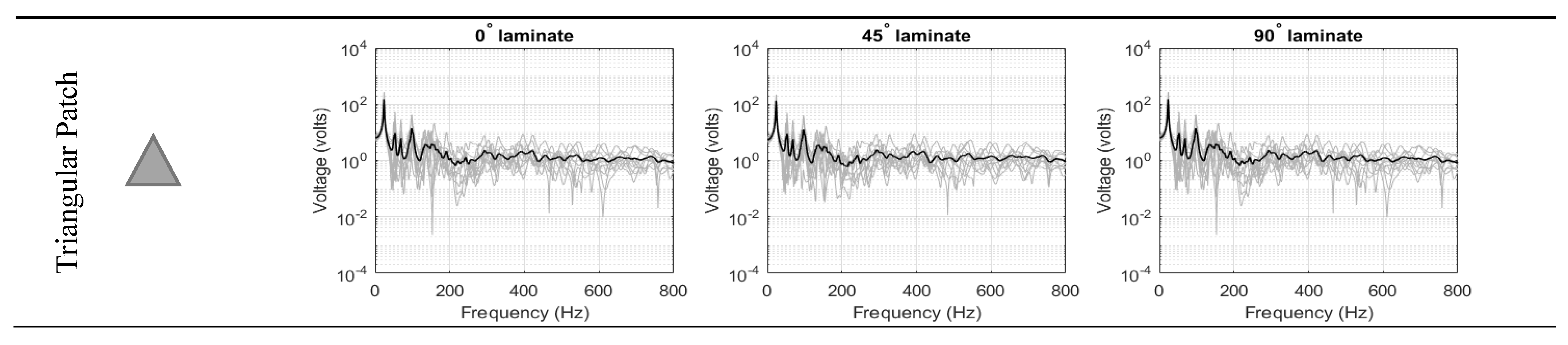
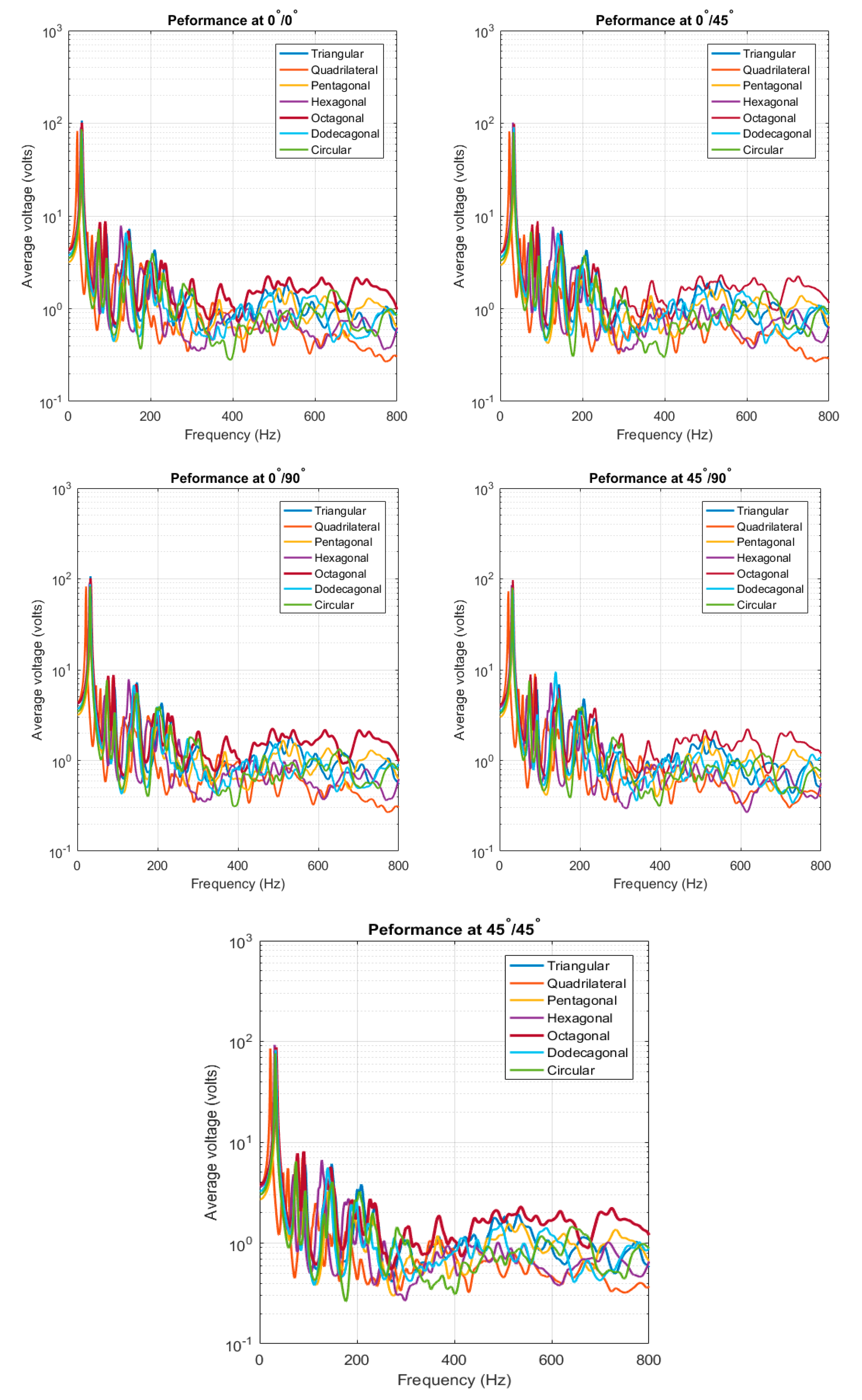
3.1.1. Ensemble-Average Voltage Response of Single-Lamina
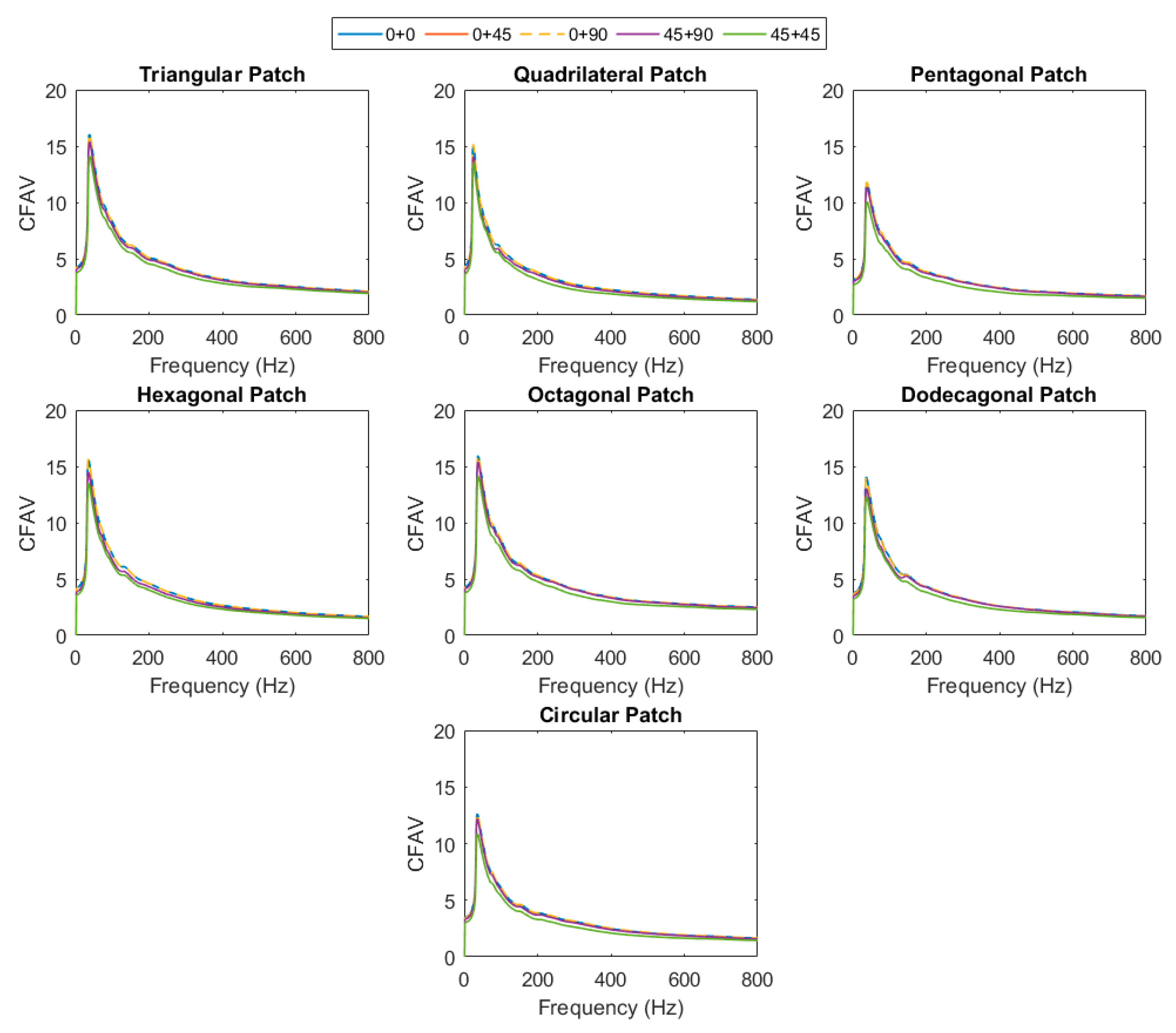
3.1.2. CFAV of Single-Lamina for Optimal Fiber Orientation
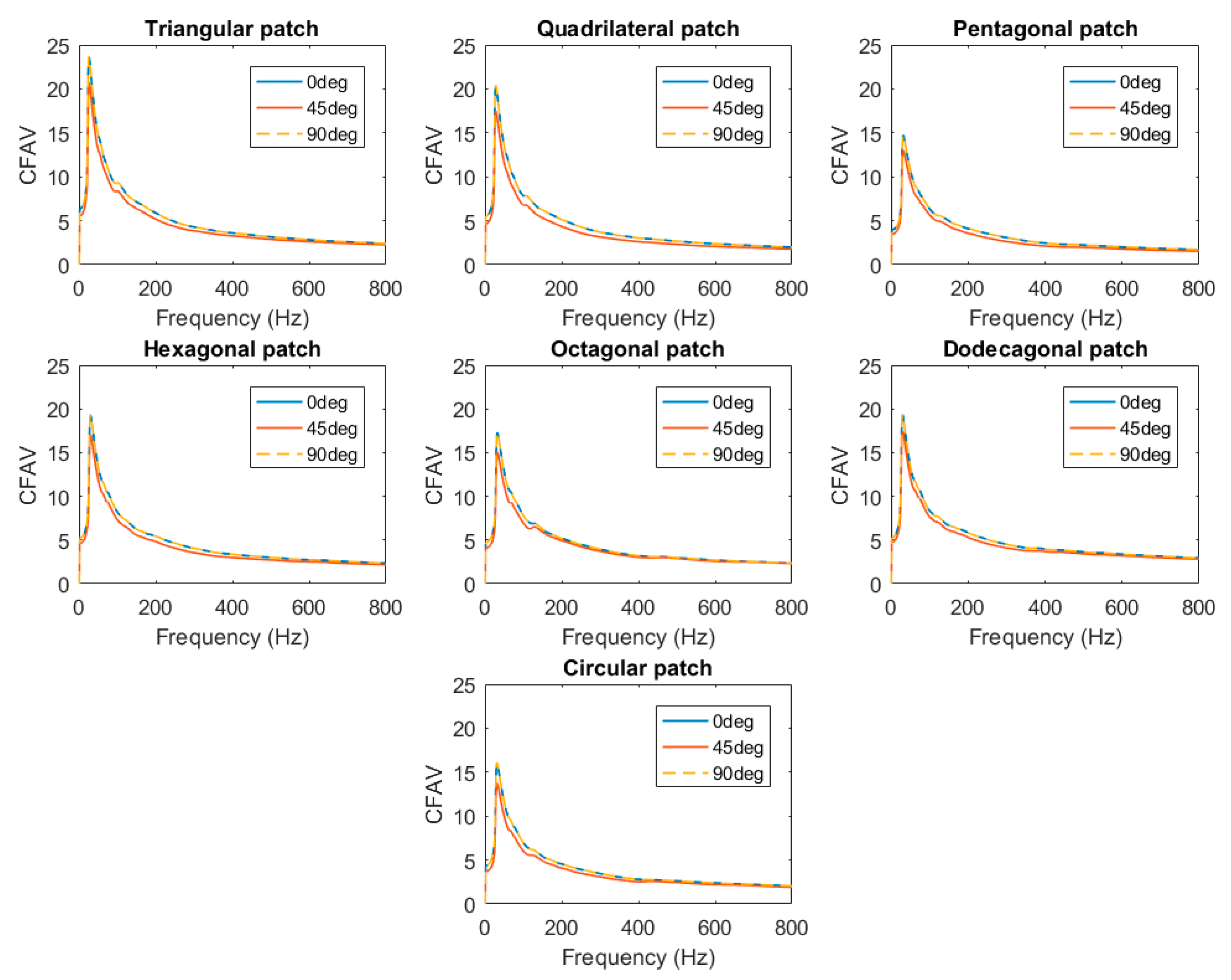
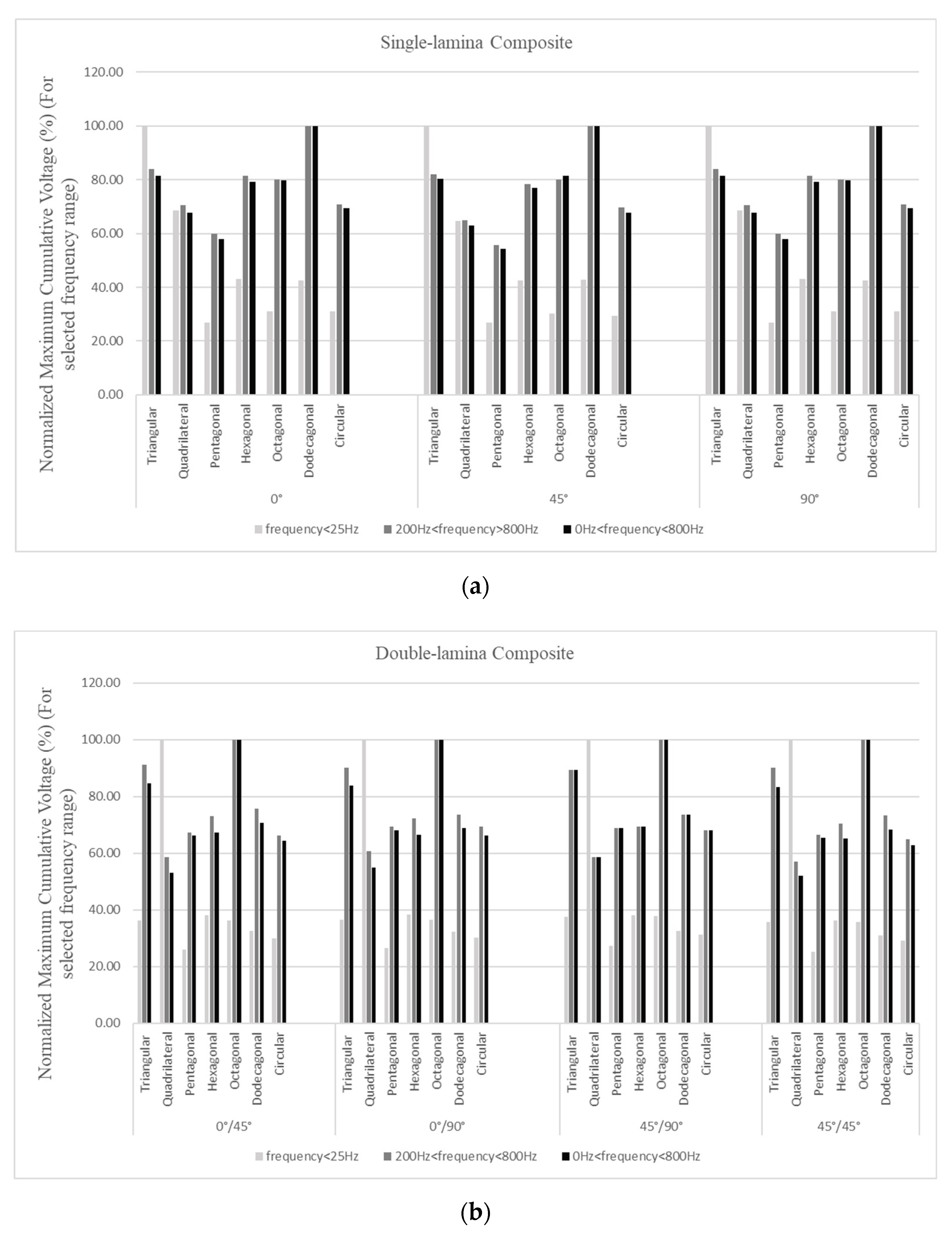
3.1.3. CFAV of Single-Lamina for Optimal Piezoelectric Shape
3.2. Double-Layer Lamina
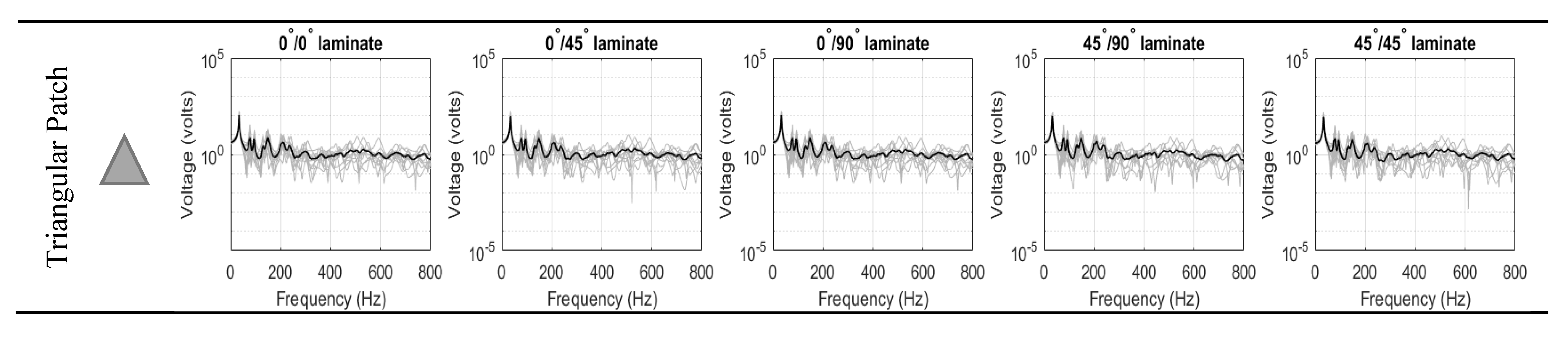
3.2.1. Ensemble-Average Voltage Response of Double-Lamina
3.2.2. CFAV of Double-Lamina for Optimal FIBER orientation
3.2.3. CFAV of Double-Lamina for Optimal Piezoelectric Shape
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Wei, C.; Jing, X. A comprehensive review on vibration energy harvesting: Modelling and realization. Renew. Sustain. Energy Rev. 2017, 74, 1–18. [Google Scholar] [CrossRef]
- Liu, H.; Fu, H.; Sun, L.; Lee, C.; Yeatman, E.M. Hybrid energy harvesting technology: From materials, structural design, system integration to applications. Renew. Sustain. Energy Rev. 2021, 137, 110473. [Google Scholar] [CrossRef]
- Zou, H.-X.; Zhao, L.-C.; Gao, Q.-H.; Zuo, L.; Liu, M.; Tan, T.; Wei, K.-X.; Zhang, W.-M. Mechanical modulations for enhancing energy harvesting: Principles, methods and applications. Appl. Energy 2019, 255, 113871. [Google Scholar] [CrossRef]
- Wang, X. Piezoelectric nanogenerators—Harvesting ambient mechanical energy at the nanometer scale. Nano Energy 2012, 1, 13–24. [Google Scholar] [CrossRef]
- Chen, J.; Qiu, Q.; Han, Y.; Lau, D. Piezoelectric materials for sustainable building structures: Fundamentals and applications. Renew. Sustain. Energy Rev. 2019, 101, 14–25. [Google Scholar] [CrossRef]
- Ali, F.; Raza, W.; Li, X.; Gul, H.; Kim, K.-H. Piezoelectric energy harvesters for biomedical applications. Nano Energy 2019, 57, 879–902. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K. A piezoelectric vibration based generator for wireless electronics. Smart Mater. Struct. 2004, 13, 1131–1142. [Google Scholar] [CrossRef] [Green Version]
- Casciati, S.; Faravelli, L.; Chen, Z. Energy harvesting and power management of wireless sensors for structural control applications in civil engineering. Smart Struct. Syst. 2012, 10, 299–312. [Google Scholar] [CrossRef]
- Bodaghi, M.; Damanpack, A.; Aghdam, M.; Shakeri, M. Non-linear active control of FG beams in thermal environments subjected to blast loads with integrated FGP sensor/actuator layers. Compos. Struct. 2012, 94, 3612–3623. [Google Scholar] [CrossRef]
- Sezer, N.; Koç, M. A comprehensive review on the state-of-the-art of piezoelectric energy harvesting. Nano Energy 2021, 80, 105567. [Google Scholar] [CrossRef]
- Truitt, A.; Mahmoodi, S.N. A review on active wind energy harvesting designs. Int. J. Precis. Eng. Manuf. 2013, 14, 1667–1675. [Google Scholar] [CrossRef]
- Park, J.; Lee, S.; Kwak, B.M. Design optimization of piezoelectric energy harvester subject to tip excitation. J. Mech. Sci. Technol. 2012, 26, 137–143. [Google Scholar] [CrossRef]
- Wein, F.; Kaltenbacher, M.; Stingl, M. Topology optimization of a cantilevered piezoelectric energy harvester using stress norm constraints. Struct. Multidiscip. Optim. 2013, 48, 173–185. [Google Scholar] [CrossRef]
- Liang, Z.; Xu, C.; Ren, B.; Di, W.; Li, L.; Luo, H.; Chen, Z.; Su, J. Optimization of cantilevered piezoelectric energy harvester with a fixed resonance frequency. Sci. China Ser. E Technol. Sci. 2014, 57, 1093–1100. [Google Scholar] [CrossRef]
- Kim, C.; Lee, J. Topology optimum design of unimorph piezoelectric cantilevered Mindlin plates as a vibrating electric harvester. J. Mech. Sci. Technol. 2014, 28, 4131–4138. [Google Scholar] [CrossRef]
- Sordo, G.; Serra, E.; Schmid, U.; Iannacci, J. Optimization method for designing multimodal piezoelectric MEMS energy harvesters. Microsyst. Technol. 2016, 22, 1811–1820. [Google Scholar] [CrossRef]
- Song, J.; Zhao, G.; Li, B.; Wang, J. Design optimization of PVDF-based piezoelectric energy harvesters. Heliyon 2017, 3, e00377. [Google Scholar] [CrossRef]
- Izadgoshasb, I.; Lim, Y.Y.; Lake, N.; Tang, L.; Padilla, R.V.; Kashiwao, T. Optimizing orientation of piezoelectric cantilever beam for harvesting energy from human walking. Energy Convers. Manag. 2018, 161, 66–73. [Google Scholar] [CrossRef]
- Kim, T.; Ko, Y.; Yoo, C.; Choi, B.; Han, S.; Kim, N. Design optimisation of wide-band piezoelectric energy harvesters for self-powered devices. Energy Convers. Manag. 2020, 225, 113443. [Google Scholar] [CrossRef]
- Ichige, R.; Kuriyama, N.; Umino, Y.; Tsukamoto, T.; Suzuki, T. Size optimization of metamaterial structure for elastic layer of a piezoelectric vibration energy harvester. Sens. Actuators A Phys. 2021, 318, 112488. [Google Scholar] [CrossRef]
- Peralta, P.; Ruiz, R.; Natarajan, S.; Atroshchenko, E. Parametric study and shape optimization of piezoelectric energy harvesters by isogeometric analysis and kriging metamodeling. J. Sound Vib. 2020, 484, 115521. [Google Scholar] [CrossRef]
- Muthalif, A.G.A.; Wahid, A.N. Estimation and measurement of effective line mobility on a non-deterministic thin plate excited by a piezoelectric patch. J. Vibroengineering 2020, 22, 98–110. [Google Scholar] [CrossRef]
- Muthalif, A.G.; Wahid, A.N.; Nor, K.A. Estimating ensemble average power delivered by a piezoelectric patch actuator to a non-deterministic subsystem. J. Sound Vib. 2014, 333, 1149–1162. [Google Scholar] [CrossRef]
- Muthalif, A.G.A.; Langley, R.S. Active control of high-frequency vibration: Optimisation using the hybrid modelling method. J. Sound Vib. 2012, 331, 2969–2983. [Google Scholar] [CrossRef]
- Cotoni, V.; Shorter, P.; Langley, R. Numerical and experimental validation of a hybrid finite element-statistical energy analysis method. J. Acoust. Soc. Am. 2007, 122, 259–270. [Google Scholar] [CrossRef] [PubMed]
- Shastry, S.N.; Swamy, S.S. Study on high frequency vibrations using statistical energy analysis for different composite materials. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 925, p. 012044. [Google Scholar]
- Seçgin, A. Numerical determination of statistical energy analysis parameters of directly coupled composite plates using a modal-based approach. J. Sound Vib. 2013, 332, 361–377. [Google Scholar] [CrossRef]
- Ngo-Cong, D.; Mai-Duy, N.; Karunasena, W.; Tran-Cong, T. Free vibration analysis of laminated composite plates based on FSDT using one-dimensional IRBFN method. Comput. Struct. 2011, 89, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Soares, C.A.M.; Soares, C.M.M.; Freitas, M.J.M. (Eds.) Mechanics of Composite Materials and Structures; Springer: Dordrecht, The Netherlands, 1999. [Google Scholar] [CrossRef]
- Benjeddou, A. Field-dependent nonlinear piezoelectricity: A focused review. Int. J. Smart Nano Mater. 2018, 9, 68–84. [Google Scholar] [CrossRef] [Green Version]
- Fakhzan, M.A.; Muthalif, A.G.; Lumpur, K. Vibration based energy harvesting using piezoelectric material. In Proceedings of the 2011 4th International Conference on Mechatronics: Integrated Engineering for Industrial and Societal Development, ICOM’11—Conference Proceedings, Kuala Lumpur, Malaysia, 17–19 May 2011; pp. 17–19. [Google Scholar]
- Trindade, M.A.; Benjeddou, A. Finite element characterisation of multilayer d31 piezoelectric macro-fibre composites. Compos. Struct. 2016, 151, 47–57. [Google Scholar] [CrossRef]
- ANSYS® Academic Mechanical, Release 17.0, Help System, Element Reference, Ansys, Inc. Canonsburg, PA, USA, 2020.
- Bodaghi, M.; Damanpack, A.; Aghdam, M.; Shakeri, M. Geometrically non-linear transient thermo-elastic response of FG beams integrated with a pair of FG piezoelectric sensors. Compos. Struct. 2014, 107, 48–59. [Google Scholar] [CrossRef]
- Chilabi, H.J.; Salleh, H.; Supeni, E.E.; As’Arry, A.B.; Rezali, K.A.M.; Atrah, A.B. Harvesting energy from planetary gear using piezoelectric material. Energies 2020, 13, 223. [Google Scholar] [CrossRef] [Green Version]





| Laminated Composite Plate | |||
|---|---|---|---|
| Model | Fiber Orientation | ||
| Single-lamina composite |  | ||
| Double-lamina composite | Model A |  | |
| Model B |  | ||
| Model C |  | ||
| Model D |  | ||
| Model E |  | ||
| Length | ||
| Width | ||
| Ply Thickness | ||
| Material | Epoxy-Glass | |
| Modulus of elasticity | ||
| Shear modulus | ||
| Poisson’s ration | ||
| Density | ||
| Material Property | Coefficient/Shape | Value |
|---|---|---|
|
Compliance Matrix (/N) | ||
|
Relative Permittivity Matrix (F/m) | ||
| Piezoelectric Strain Matrix ( C/N) | ||
| Density (kg/m3) | ||
| Side Length () | Triangular | |
| Quadrilateral | ||
| Pentagonal | ||
| Hexagonal | ||
| Octagonal | ||
| Dodecagonal | ||
| Circular |
| Orientation | Mode 1 | Mode 2 | Mode 3 | Mode 4 | |
|---|---|---|---|---|---|
| Single | 7.8076 | 16.281 | 21.992 | 26.242 | |
| 8.2785 | 17.486 | 22.536 | 29.368 | ||
| 7.8076 | 16.281 | 21.922 | 26.242 | ||
| Double | 12.265 | 23.161 | 30.253 | 37.537 | |
| 13.764 | 25.899 | 31.451 | 43.243 | ||
| 12.265 | 23.161 | 30.253 | 37.537 | ||
| 12.019 | 23.711 | 30.196 | 40.927 | ||
| 13.263 | 26.130 | 31.791 | 45.171 | ||
| Mode Shape |  | 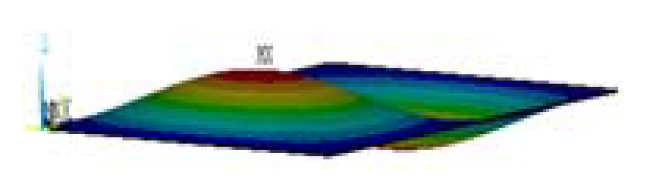 | 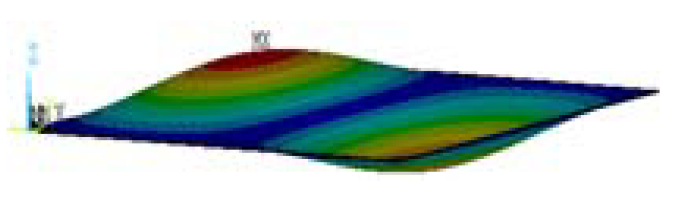 |  | |
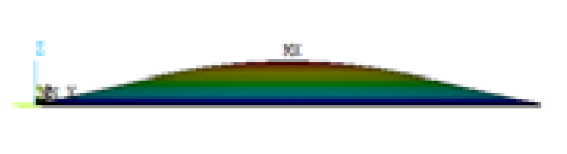 |  |  |  | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muthalif, A.G.A.; Ali, A.; Renno, J.; Wahid, A.N.; Nor, K.A.M.; Nordin, N.H.D. Geometrical Investigation of Piezoelectric Patches for Broadband Energy Harvesting in Non-Deterministic Composite Plates . Materials 2021, 14, 7370. https://doi.org/10.3390/ma14237370
Muthalif AGA, Ali A, Renno J, Wahid AN, Nor KAM, Nordin NHD. Geometrical Investigation of Piezoelectric Patches for Broadband Energy Harvesting in Non-Deterministic Composite Plates . Materials. 2021; 14(23):7370. https://doi.org/10.3390/ma14237370
Chicago/Turabian StyleMuthalif, Asan G. A., Abdelrahman Ali, Jamil Renno, Azni N. Wahid, Khairul A. M. Nor, and Nor Hidayati Diyana Nordin. 2021. "Geometrical Investigation of Piezoelectric Patches for Broadband Energy Harvesting in Non-Deterministic Composite Plates " Materials 14, no. 23: 7370. https://doi.org/10.3390/ma14237370
APA StyleMuthalif, A. G. A., Ali, A., Renno, J., Wahid, A. N., Nor, K. A. M., & Nordin, N. H. D. (2021). Geometrical Investigation of Piezoelectric Patches for Broadband Energy Harvesting in Non-Deterministic Composite Plates . Materials, 14(23), 7370. https://doi.org/10.3390/ma14237370






