Study of the Mechanical, Sound Absorption and Thermal Properties of Cellular Rubber Composites Filled with a Silica Nanofiller
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Measurement Methodology
2.2.1. Curing Characteristics
2.2.2. Rubber Processing Analysis
2.2.3. Optical Microscopy
2.2.4. Rebound Resilience
2.2.5. Compression Testing
2.2.6. Mechanical Vibration Damping Testing
2.2.7. Sound Absorption Measurements
2.2.8. Thermal Conductivity
2.2.9. Thermogravimetric Analysis
3. Results and Discussion
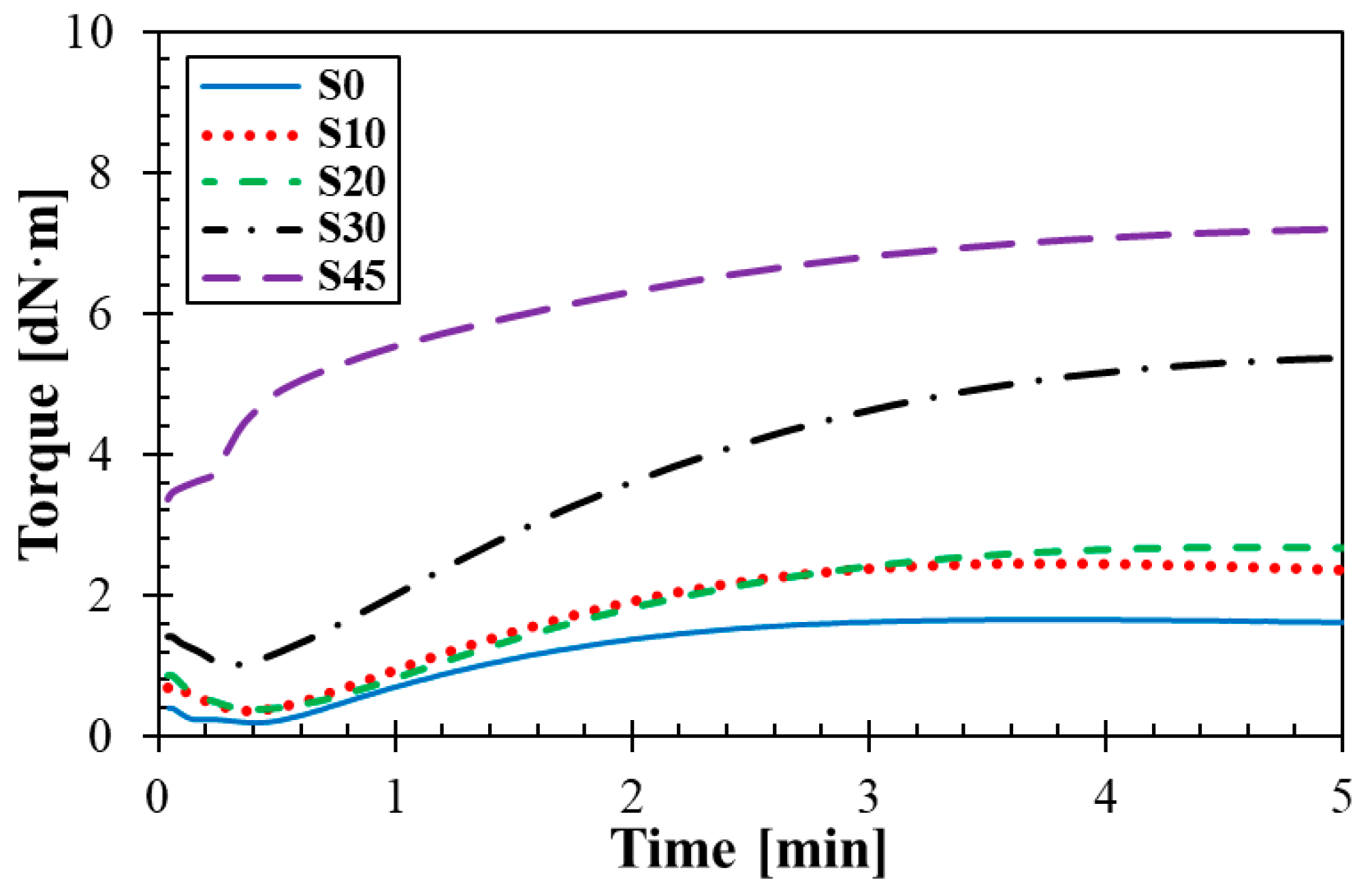
3.1. Curing Characteristics
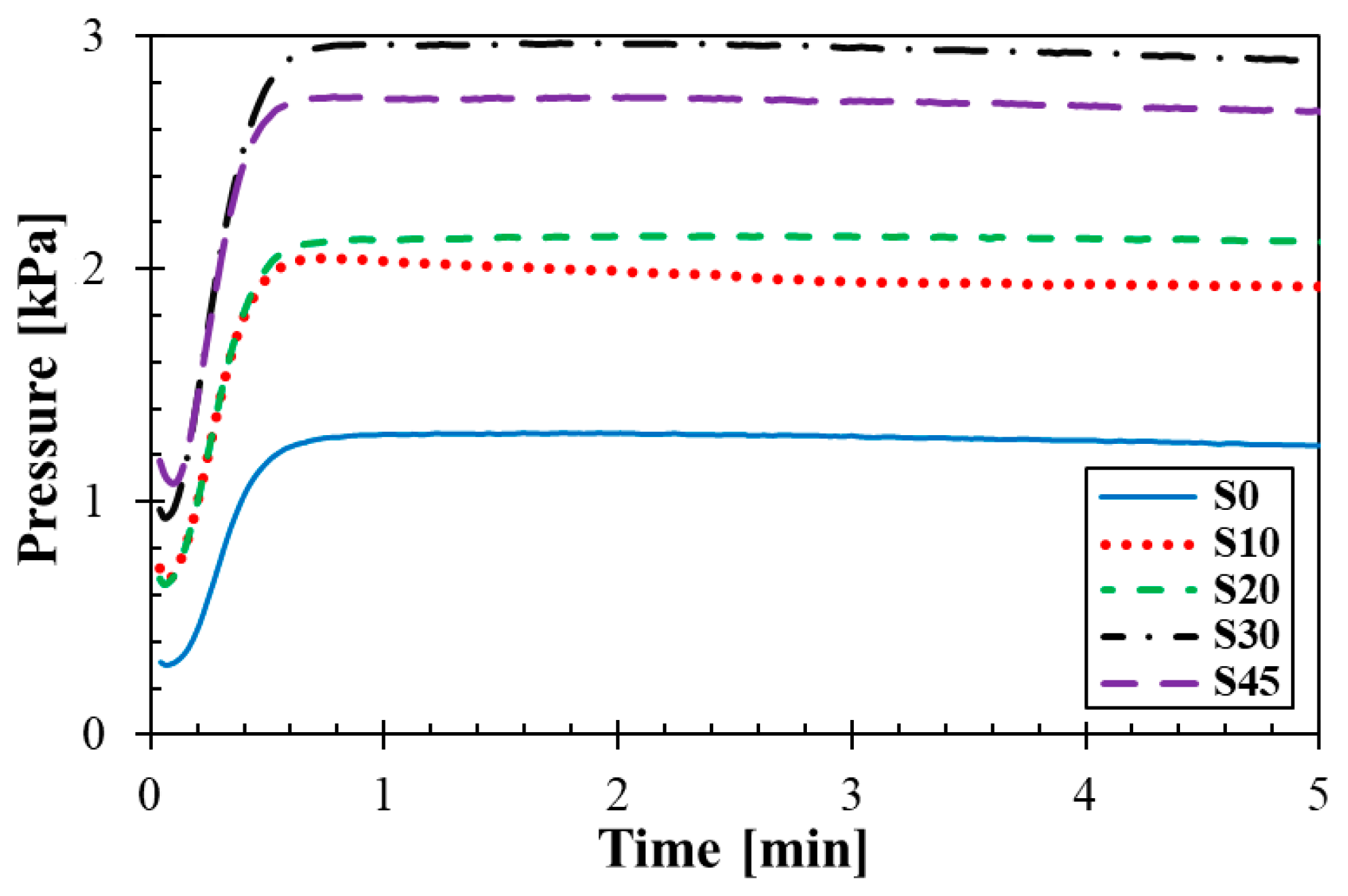
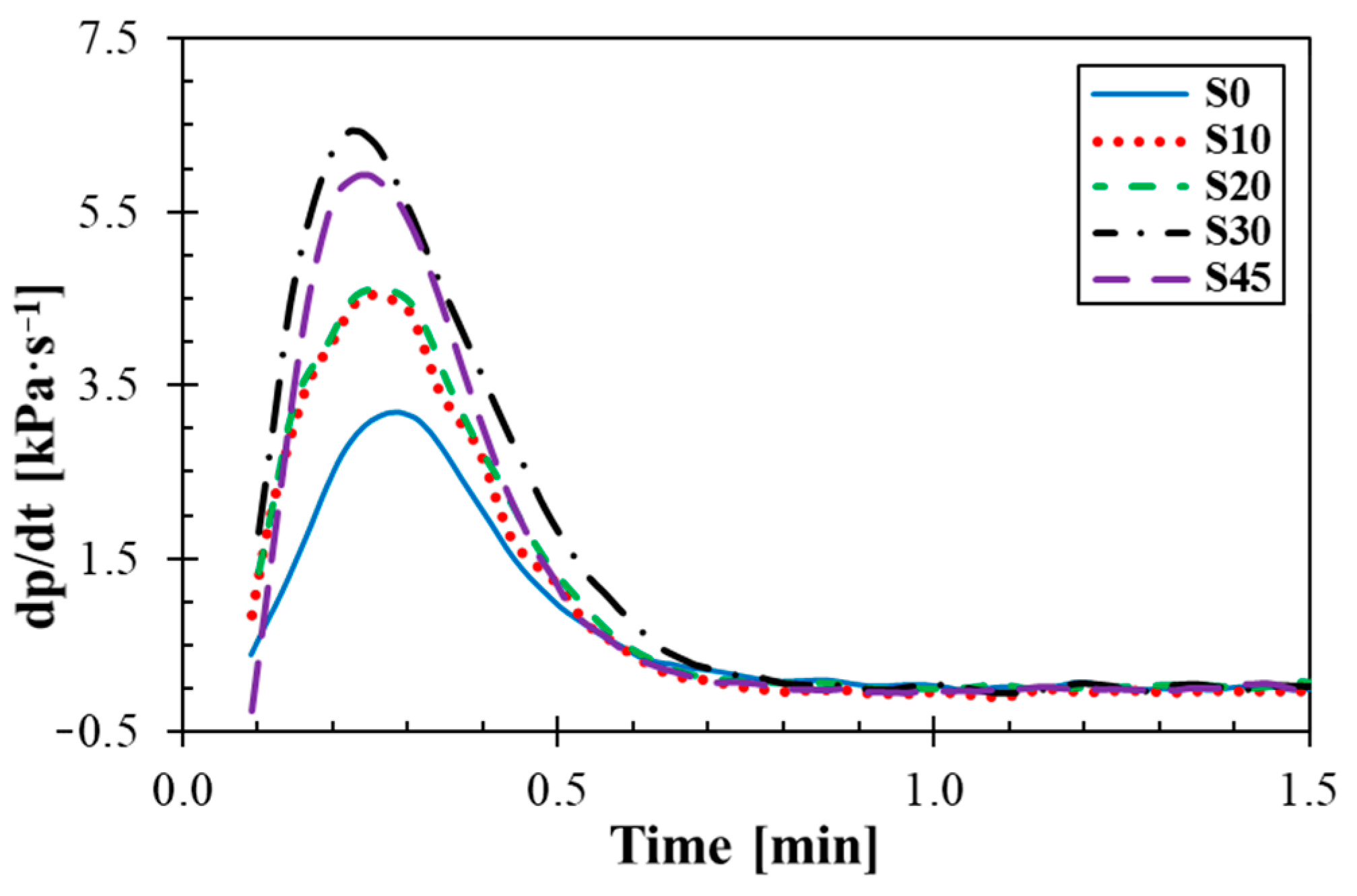
3.2. Rubber Processing Analysis
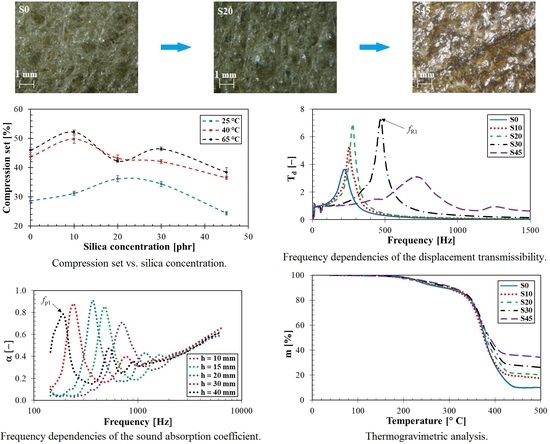
3.3. Optical Microscopy
3.4. Mechanical Properties
3.4.1. Rebound Resilience
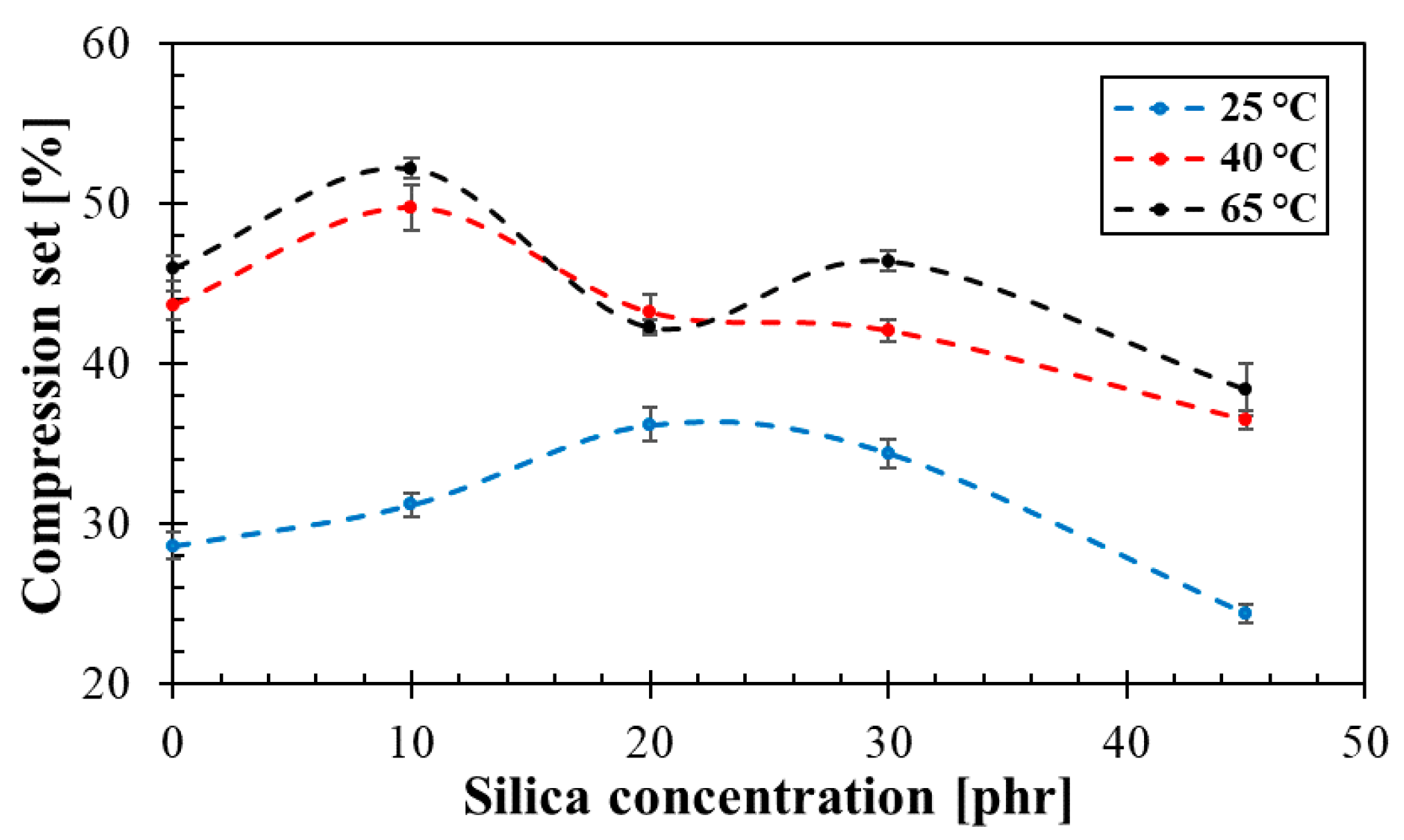
3.4.2. Compression Testing
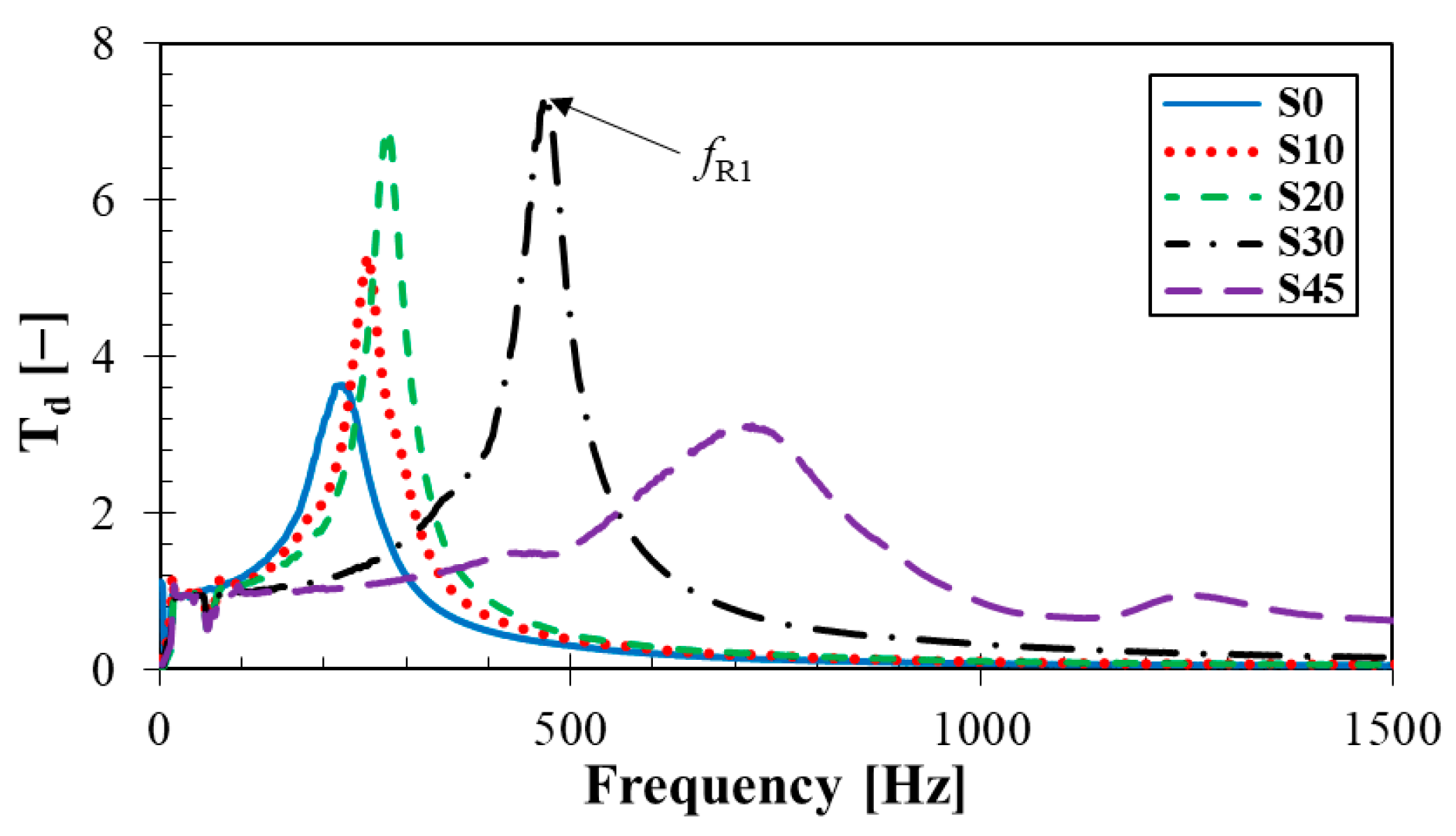
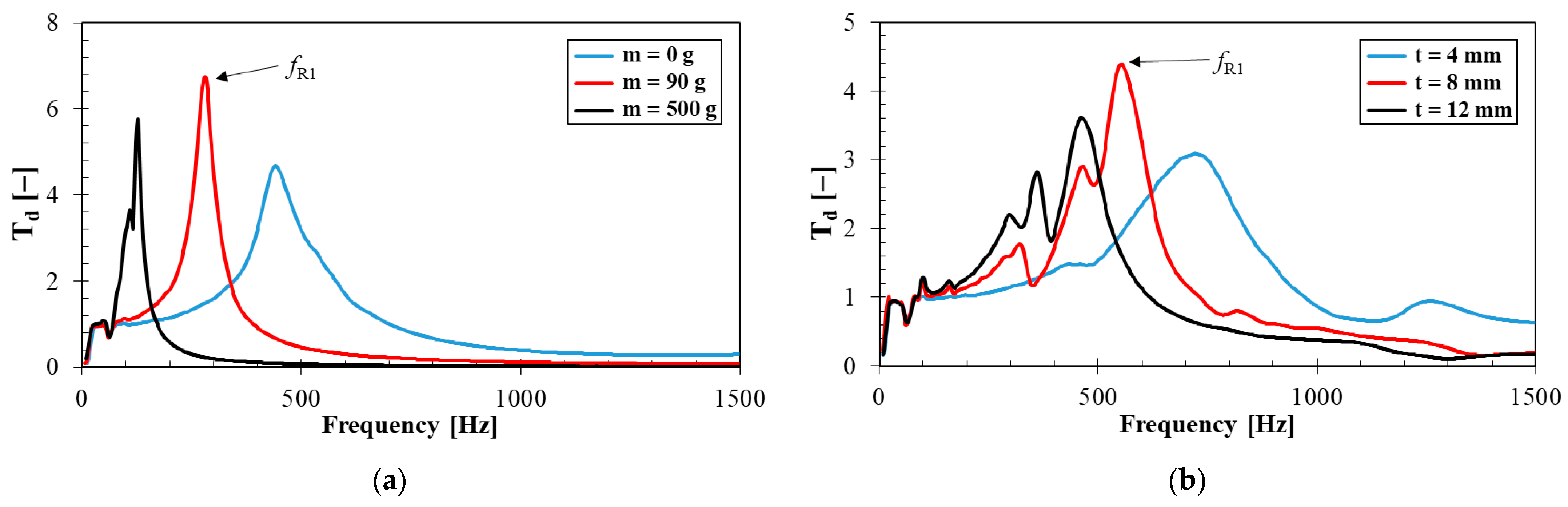
3.4.3. Mechanical Vibration Damping Testing
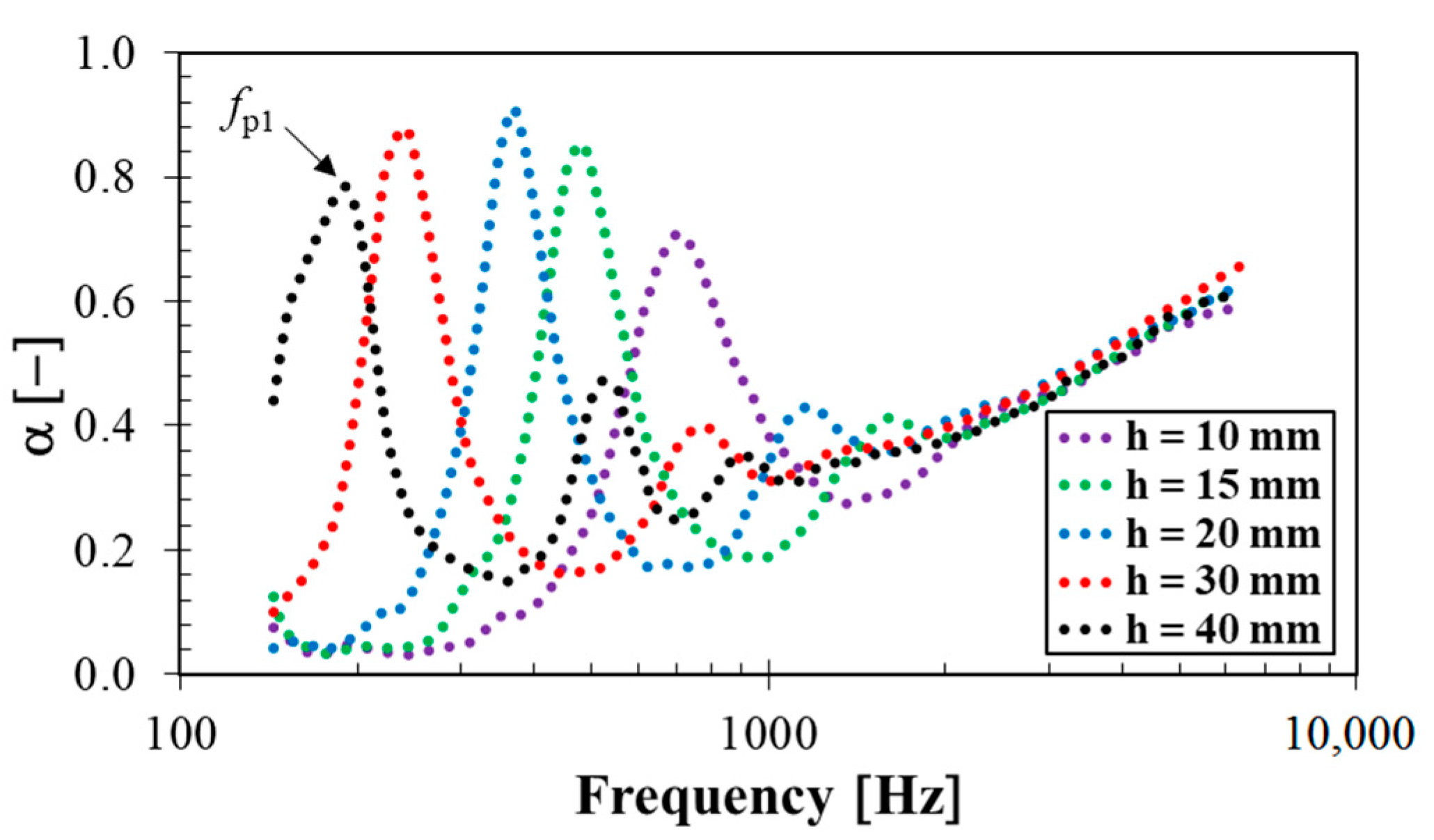
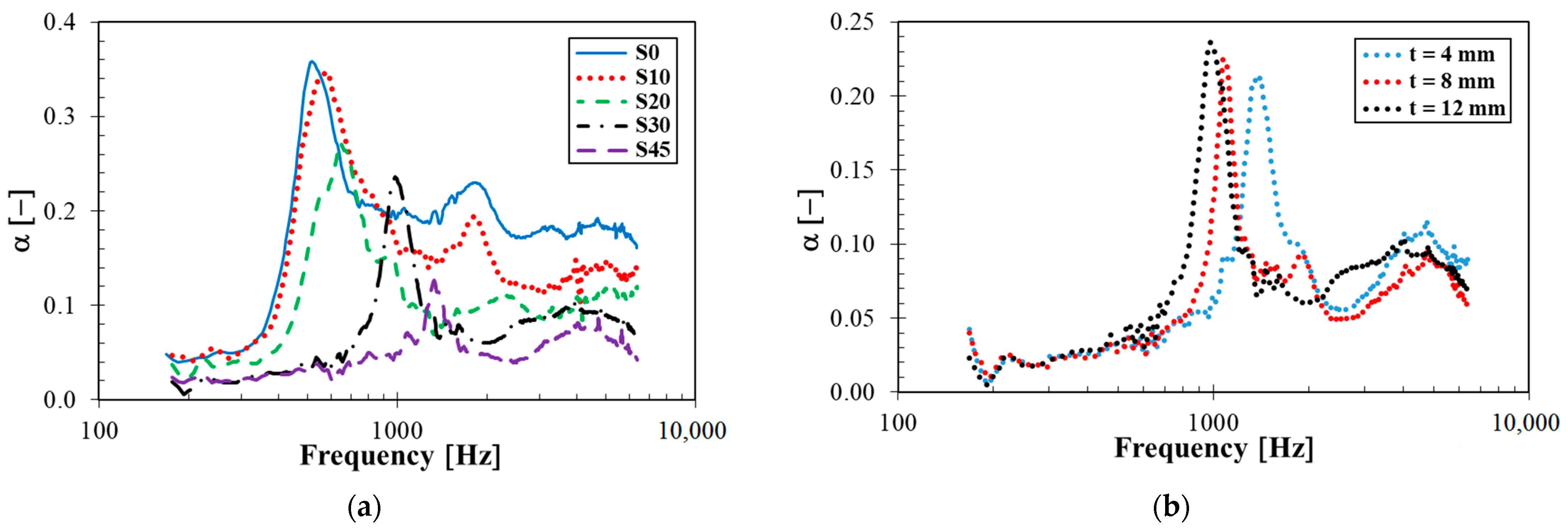
3.5. Sound Absorption Properties
3.6. Thermal Properties
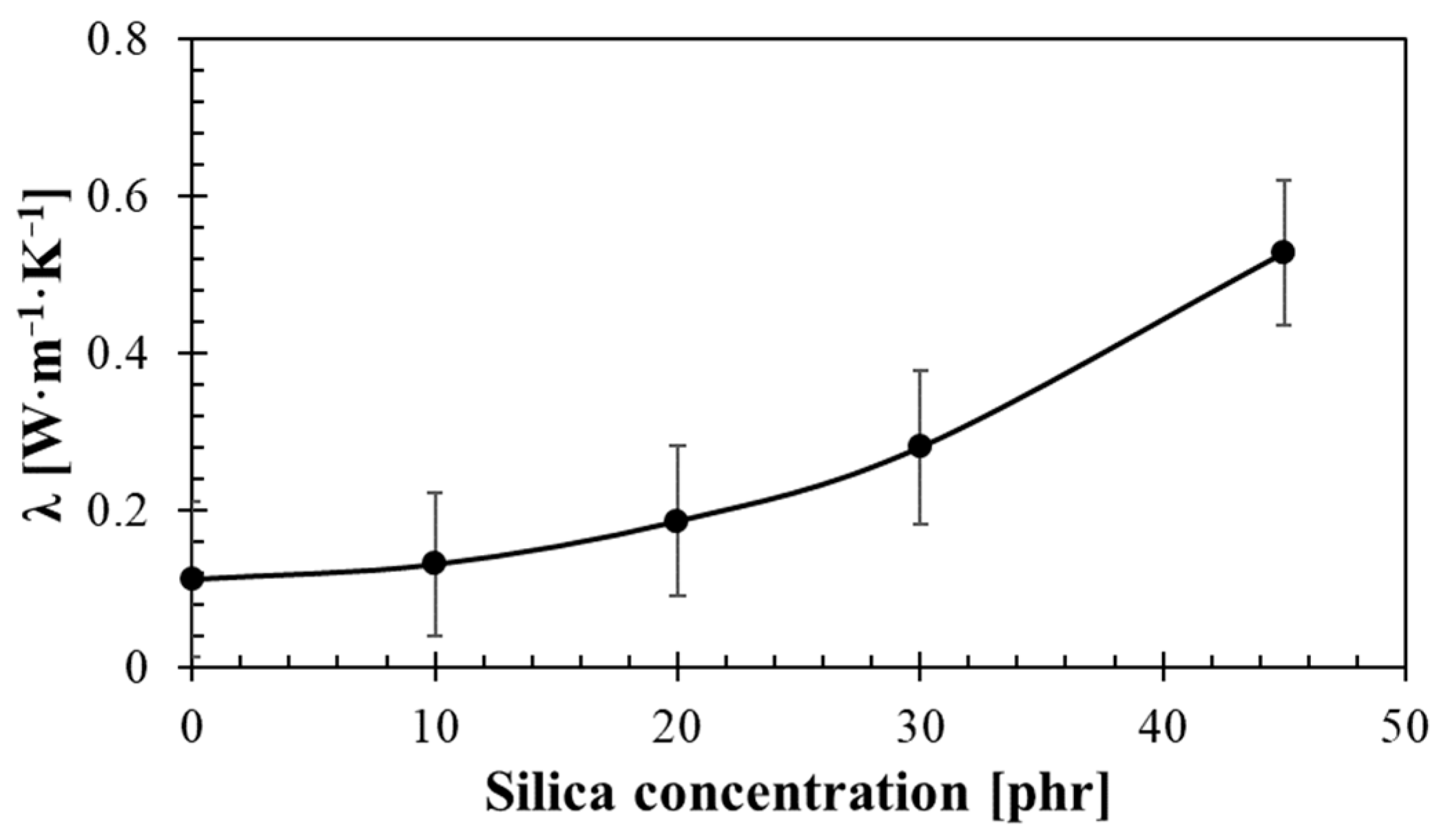
3.6.1. Thermal Conductivity
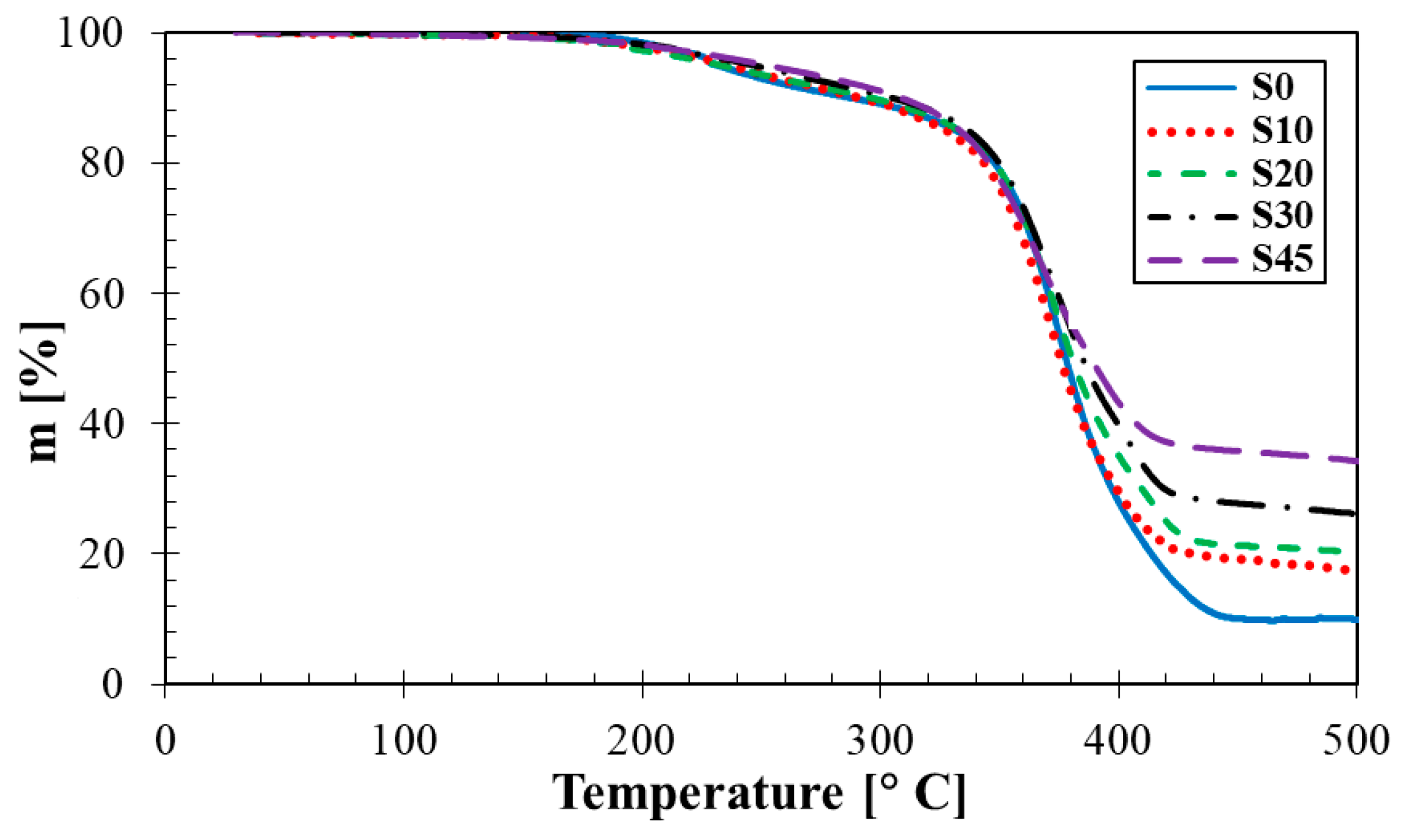
3.6.2. Thermogravimetric Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shizok, K. Natural Rubber: From the Odyssey of the Hevea Tree to the Age of Transport, 1st ed.; A Smithers Group Company: Shawbury, UK, 2015; pp. 3–4. [Google Scholar]
- Gent, A.N.; Kawahara, S.; Zhao, J. Crystalization and strength of natural rubber and synthetic cis-1,4 polyisoprene. Rubber Chem. Technol. 1998, 71, 668–678. [Google Scholar] [CrossRef]
- Parrella, F.W.; Gaspari, A.A. Natural rubber latex protein reduction with an emphasis on enzyme treatment. Methods 2002, 27, 77–86. [Google Scholar] [CrossRef]
- Nie, Y.; Gu, Z.; Wei, Y.; Hao, T.; Zhou, Z. Features of strain-induced crystallization of natural rubber revealed by experiments and simulations. Polym. J. 2017, 49, 309–317. [Google Scholar] [CrossRef]
- Chenal, J.-M.; Gauthier, C.; Chazeaur, L.; Guy, L.; Bomaly, Y. Parameters governing strain induced crystallization in filled natural rubber. Polymer 2007, 48, 6893–6901. [Google Scholar] [CrossRef] [Green Version]
- Sarkawi, S.; Dierkes, W.K.; Noordermeer, J.W.M. Reinforcement of natural rubber by precipitated silica: The influence of processing temperature. Rubber Chem. Tech. 2014, 87, 103–119. [Google Scholar] [CrossRef] [Green Version]
- Morton, M. Rubber Technology, 3rd ed.; Springer Science+Business Media: Dordrech, OH, USA, 1999; pp. 30–47. [Google Scholar]
- Alan, N.G. Engineering with Rubber—How to Design Rubber Components, 3rd ed.; Hanscher Publischers: Ohio, OH, USA, 2012; pp. 18–20. [Google Scholar]
- Thomas, S.; Stephen, R. Rubber Nanocomposites Preparation, Properties and Applications, 1st ed.; John Wiley & Sons Pte Ltd.: Singapore, 2010; pp. 21–39. [Google Scholar]
- Hewitt, N. Compositeing Precipitated Silica in Elastomers, 1st ed.; William Andrew Publishing/Plastics Design Library: New York, NY, USA, 2007; pp. 1–9. [Google Scholar]
- Cassagnau, P. Melt rheology of organoclay and fumed silica nanocomposites. Polymer 2008, 49, 2183–2196. [Google Scholar] [CrossRef] [Green Version]
- Wilgis, T.A.; Heinrich, G.K. Reinforcement of Polymer Nano-Composites—Theory, Experiments and Applications, 1st ed.; Cambridge University Press: Cambridge, UK, 2009; pp. 96–100. [Google Scholar]
- Leung, S.N.; Wong, A.; Park, C.B.; Zhong, J.H. Ideal surface geometries of nucleating agents to enhance cell nucleation in polymeric foaming processes. J. Appl. Polym. Sci. 2008, 108, 3997–4003. [Google Scholar] [CrossRef]
- Arthur, H.L. Handbook of Plastics Foams, 1st ed.; Elsevier Books: Cambridge, UK, 1995; pp. 246–250. [Google Scholar]
- Nijib, N.N.; Ariff, Z.M.; Manan, N.A.; Bakar, A.A.; Sipaut, C.S. Effect of blowing agent concentration on cell morphology and impact properties of natural rubber foam. J. Phys. Sci. 2009, 20, 13–25. [Google Scholar]
- Gayathri, R.; Vasanthakumari, R.; Padmanabhan, C. Sound absorption, thermal and mechanical behavior of polyurethane foam modified with nano silica, nano clay and crumb rubber fillers. Int. J. Sci. Eng. Res. 2013, 4, 301–308. [Google Scholar]
- Pang, Y.; Cao, Y.; Zheng, W.; Park, C.B. A comprehensive review of cell structure variation and general rules for polymer microcellular foams. Chem. Eng. J. 2021, 430, 132662. [Google Scholar] [CrossRef]
- Park, C.B.; Baldwin, D.F.; Suh, N.P. Effect of the pressure drop rate on cell nucleation in continuous processing of microcellular polymers. Polym. Eng. Sci. 1995, 35, 432–440. [Google Scholar] [CrossRef]
- Bayat, H.; Fasihi, M.; Zare, Y.; Rhee, K.Y. An experimental study on one-step and two-step foaming of natural rubber/silica nanocomposites. Nanotechnol. Rev. 2020, 9, 427–435. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, G.; Zhang, G.; Shi, Q.; Tang, B.; Wu, Z. Study on foaming water-swellable EPDM rubber. J. App. Polym. Sci. 2002, 84, 3712–3717. [Google Scholar] [CrossRef]
- Panploo, K.; Chalermsinsuwan, B.; Poompradus, S. Natural rubber latex foam with particulate fillers for carbon dioxide adsorption and regeneration. RSC Adv. 2019, 9, 28916–28923. [Google Scholar] [CrossRef] [Green Version]
- Sombatsompop, N.; Thongsang, S.; Markpin, T.; Wimolmala, E. Fly ash particles and precipitated silica as fillers in rubbers. I. Untreated fillers in natural rubber and styrene–butadiene rubber compounds. J. Appl. Polym. Sci. 2004, 93, 2119–2130. [Google Scholar] [CrossRef]
- Rodriguez-Vear, R.; Genovese, K.; Rayas, J.A.; Mendoza-Santoyo, F. Vibration Analysis at Microscale by Talbot Fringe Projection Method. Strain 2009, 45, 249–258. [Google Scholar] [CrossRef]
- Prasopdee, T.; Smitthipong, W. Effect of fillers on the recovery of rubber foam: From theory to applications. Polymer 2020, 12, 2745. [Google Scholar] [CrossRef]
- Rao, S.S. Mechanical Vibrations, 5th ed.; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2011; pp. 281–287. [Google Scholar]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Lopes, V., Jr. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Liu, K.; Liu, J. The damped dynamic vibration absorbers: Revisited and next result. J. Sound Vib. 2005, 284, 1181–1189. [Google Scholar] [CrossRef]
- Stephen, N. On energy harvesting from ambient vibration. J. Sound Vib. 2006, 293, 409–425. [Google Scholar] [CrossRef] [Green Version]
- Vette, A.H.; Wu, N.; Masani, K.; Popovic, M.R. Low-intensity functional electrical stimulation can increase multidirectional trunk stiffness in able-bodied individuals during sitting. Med. Eng. Phys. 2015, 37, 777–782. [Google Scholar] [CrossRef] [PubMed]
- Sgard, F.; Castel, F.; Atalla, N. Use of a hybrid adaptive finite element/modal approach to assess the sound absorption of porous materials with meso-heterogeneities. Appl. Acoust. 2011, 72, 157–168. [Google Scholar] [CrossRef]
- Tiwari, W.; Shukla, A.; Bose, A. Acoustic properties of cenosphere reinforced cement and asphalt concrete. Appl. Acoust. 2004, 65, 263–275. [Google Scholar] [CrossRef]
- Okudaira, Y.; Kurihara, Y.; Ando, H.; Satoh, M.; Miyanami, K. Sound absorption measurements for evaluating dynamic physical properties of a powder bad. Powder Tech. 1993, 77, 39–48. [Google Scholar] [CrossRef]
- Yanagida, T.; Matchett, A.J.; Coulthard, J.M.; Asmar, B.N.; Langston, P.A.; Walters, J.K. Dynamic measurements for the stiffness of loosely packed powder beds. AIChE J. 2002, 48, 2510–2517. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO 10534-2, Acoustics-Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes-Part 2: Transfer-Function Method; ISO/TC 43/SC2 Building Acoustics; CEN, European Committee for Standardization: Brussels, Belgium, 1998; pp. 10534–10542. [Google Scholar]
- Han, F.S.; Seiffert, G.; Zhao, Y.Y.; Gibbs, B. Acoustic absorption behaviour of an open-celled alluminium foam. J. Phys. D Appl. Phys. 2003, 36, 294–302. [Google Scholar] [CrossRef] [Green Version]
- Júnior, J.H.S.A.; Júnior, H.L.O.; Amico, S.C.; Amado, F.D.R. Study of hybrid intralaminate curaua/glass composites. Mater. Des. 2012, 42, 111–117. [Google Scholar] [CrossRef]
- Rajoria, H.; Jalili, N. Passive Vibration Damping Enhancement using Carbon Nanotube-epoxy Reinforced Composites. Compos. Sci. Tech. 2005, 65, 2079–2093. [Google Scholar] [CrossRef]
- Kalauni, K.; Pawar, S.J. A review on the taxonomy, factors associated with sound absorption and theoretical modeling of porous sound absorbing materials. J. Porous Mater. 2019, 26, 1795–1819. [Google Scholar] [CrossRef]

| Ingredients | Rubber Designation | ||||
|---|---|---|---|---|---|
| S0 | S10 | S20 | S30 | S45 | |
| Loading (phr) | |||||
| SMR–20 | 100 | 100 | 100 | 100 | 100 |
| Silika KS–408 | 0 | 10 | 20 | 30 | 45 |
| ZnO | 2 | 2 | 2 | 2 | 2 |
| Vulkanox 4020 | 1 | 1 | 1 | 1 | 1 |
| Porofor ADC | 5 | 5 | 5 | 5 | 5 |
| Nyflex 228 | 10 | 10 | 10 | 10 | 10 |
| Stearic acid | 1 | 1 | 1 | 1 | 1 |
| TBBS | 1 | 1 | 1 | 1 | 1 |
| Sulphur OT33 | 2 | 2 | 2 | 2 | 2 |
| Rubber Type | MH [dN·m] | ML [dN·m] | ts1 [min] | t90 [min] |
|---|---|---|---|---|
| S0 | 1.67 | 0.20 | 0.54 | 1.76 |
| S10 | 2.45 | 0.37 | 0.57 | 1.73 |
| S20 | 2.67 | 0.41 | 1.09 | 2.31 |
| S30 | 5.28 | 1.03 | 0.87 | 3.36 |
| S45 | 7.14 | 3.37 | 0.31 | 3.54 |
| Rubber Type | Resilience [%] |
|---|---|
| S0 | 51 ± 1 |
| S10 | 48 ± 1 |
| S20 | 44 ± 1 |
| S30 | 41 ± 1 |
| S45 | 35 ± 1 |
| Rubber Type | t [mm] | m [g] | ||
|---|---|---|---|---|
| 0 | 90 | 500 | ||
| S0 | 4 | 399 ± 13 | 218 ± 10 | 100 ± 5 |
| 8 | 192 ± 8 | 115 ± 5 | 62 ± 3 | |
| 12 | 176 ± 6 | 80 ± 3 | 55 ± 2 | |
| S10 | 4 | 417 ± 15 | 251 ± 11 | 106 ± 4 |
| 8 | 235 ± 10 | 122 ± 4 | 70 ± 3 | |
| 12 | 220 ± 9 | 103 ± 4 | 59 ± 2 | |
| S20 | 4 | 434 ± 14 | 279 ± 12 | 120 ± 5 |
| 8 | 294 ± 12 | 178 ± 6 | 77 ± 3 | |
| 12 | 257 ± 11 | 146 ± 4 | 73 ± 3 | |
| S30 | 4 | 525 ± 15 | 468 ± 18 | 196 ± 6 |
| 8 | 436 ± 16 | 343 ± 11 | 140 ± 4 | |
| 12 | 396 ± 13 | 278 ± 9 | 119 ± 4 | |
| S45 | 4 | 1239 ± 25 | 721 ± 20 | 284 ± 9 |
| 8 | 804 ± 19 | 548 ± 15 | 201 ± 7 | |
| 12 | 545 ± 14 | 457 ± 12 | 154 ± 5 | |
| Quantity | h [mm] | ||||
|---|---|---|---|---|---|
| 10 | 15 | 20 | 30 | 40 | |
| NRC [–] | 0.259 | 0.359 | 0.302 | 0.458 | 0.384 |
| fp1 [Hz] | 696 | 480 | 364 | 244 | 184 |
| αfp1 [–] | 0.709 | 0.854 | 0.911 | 0.879 | 0.784 |
| c [m·s−1] | 27.8 | 28.8 | 29.1 | 29.3 | 29.4 |
| K [MPa] | 0.132 | 0.141 | 0.144 | 0.146 | 0.147 |
| Rubber Type | t [mm] | ||
|---|---|---|---|
| 4 | 8 | 12 | |
| S0 | 0.086 | 0.113 | 0.182 |
| S10 | 0.066 | 0.107 | 0.158 |
| S20 | 0.065 | 0.098 | 0.110 |
| S30 | 0.047 | 0.067 | 0.084 |
| S45 | 0.028 | 0.030 | 0.037 |
| Rubber Type | ∆m [% w/w] |
|---|---|
| S0 | 90.42 ± 0.40 |
| S10 | 83.29 ± 0.53 |
| S20 | 79.34 ± 0.43 |
| S30 | 73.33 ± 0.58 |
| S45 | 66.63 ± 0.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pöschl, M.; Vašina, M. Study of the Mechanical, Sound Absorption and Thermal Properties of Cellular Rubber Composites Filled with a Silica Nanofiller. Materials 2021, 14, 7450. https://doi.org/10.3390/ma14237450
Pöschl M, Vašina M. Study of the Mechanical, Sound Absorption and Thermal Properties of Cellular Rubber Composites Filled with a Silica Nanofiller. Materials. 2021; 14(23):7450. https://doi.org/10.3390/ma14237450
Chicago/Turabian StylePöschl, Marek, and Martin Vašina. 2021. "Study of the Mechanical, Sound Absorption and Thermal Properties of Cellular Rubber Composites Filled with a Silica Nanofiller" Materials 14, no. 23: 7450. https://doi.org/10.3390/ma14237450
APA StylePöschl, M., & Vašina, M. (2021). Study of the Mechanical, Sound Absorption and Thermal Properties of Cellular Rubber Composites Filled with a Silica Nanofiller. Materials, 14(23), 7450. https://doi.org/10.3390/ma14237450