The Influence of Different Lay-Up Parameters on the Fatigue Response of Carbon/Epoxy Laminates under Internal Multiaxial Stress States
Abstract
:1. Introduction
2. Materials and Methods
2.1. Selection of Material
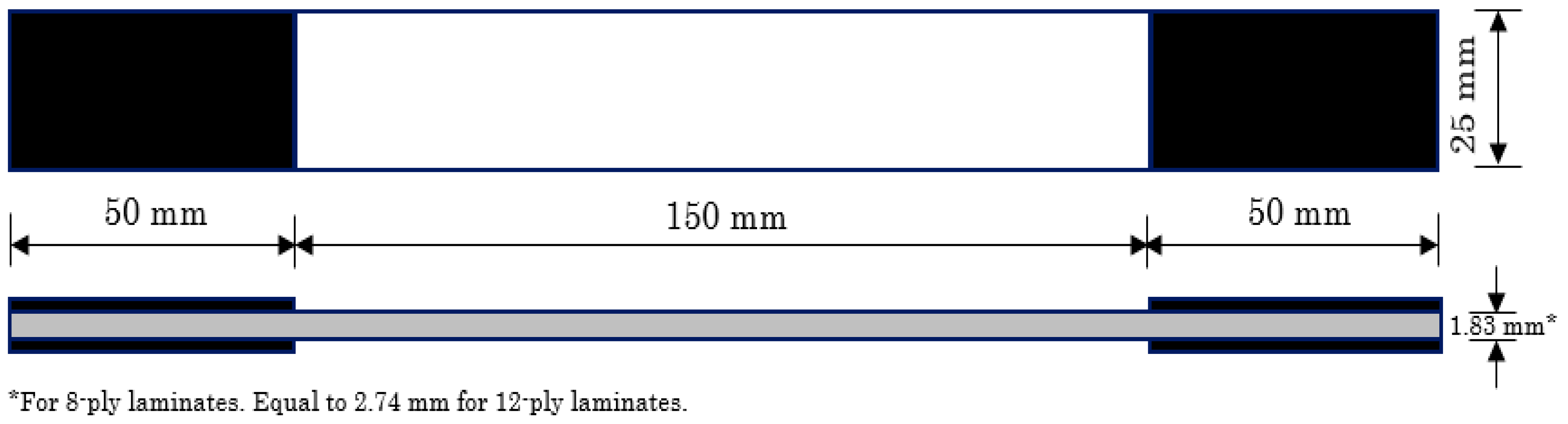
2.2. Experimental Details
3. Results and Discussion
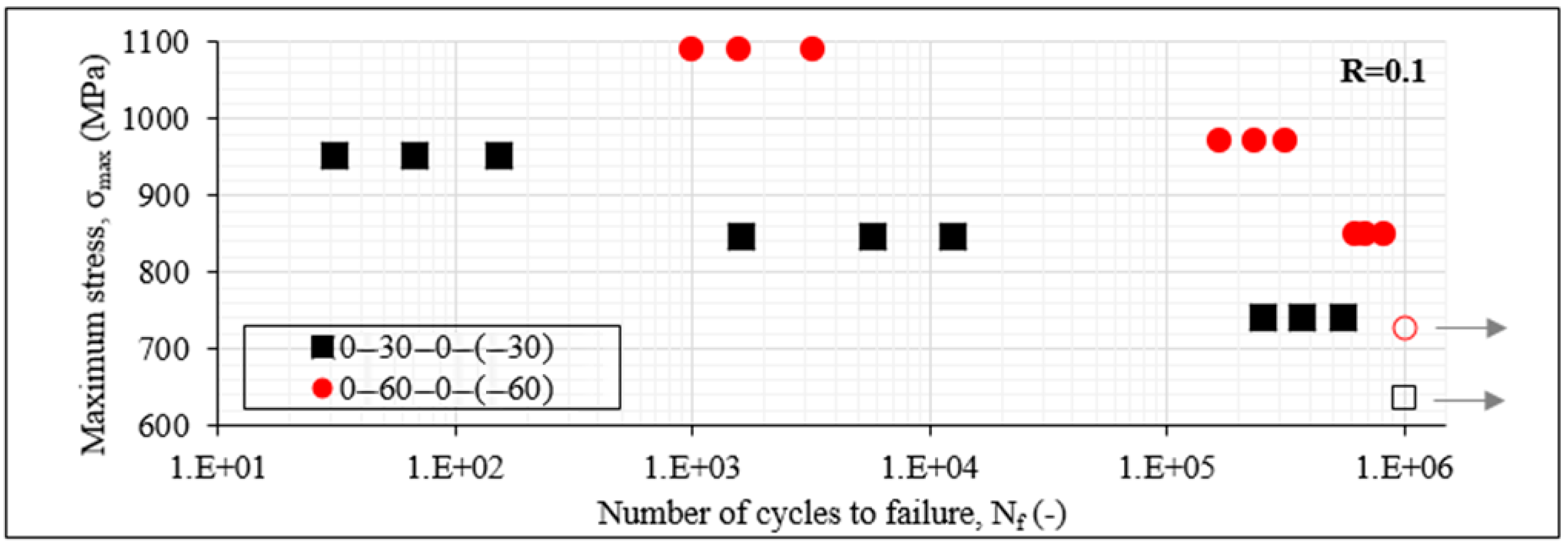
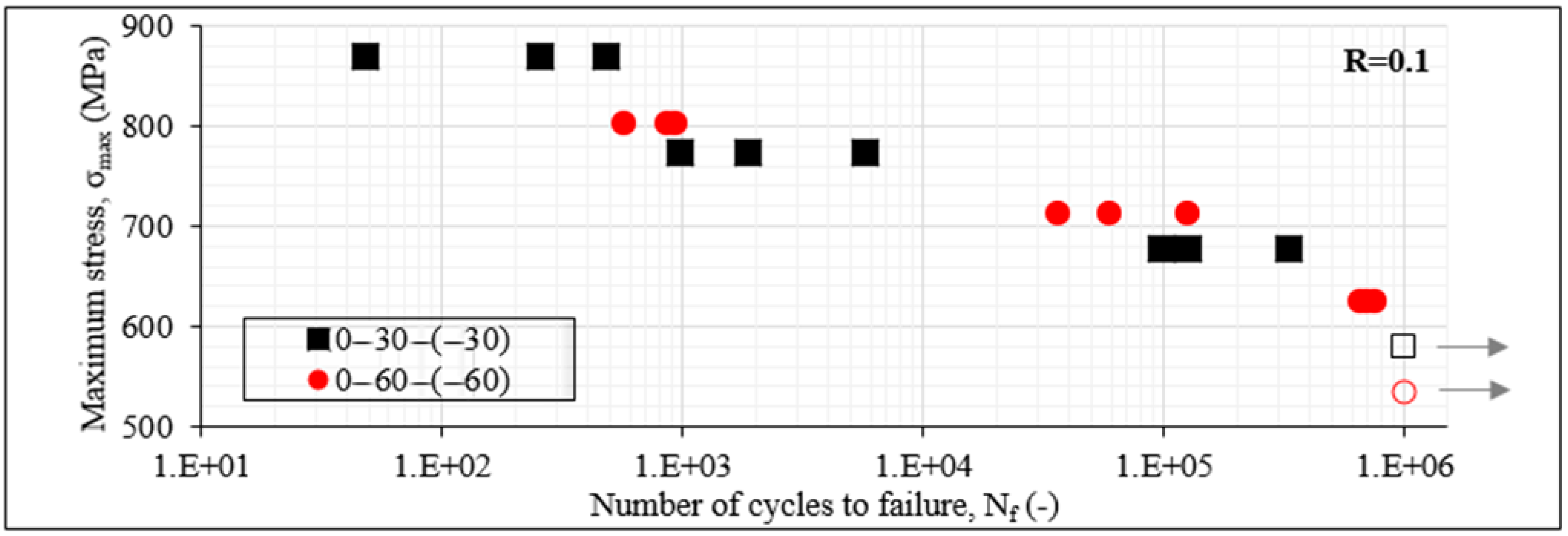
3.1. S-Nf Data
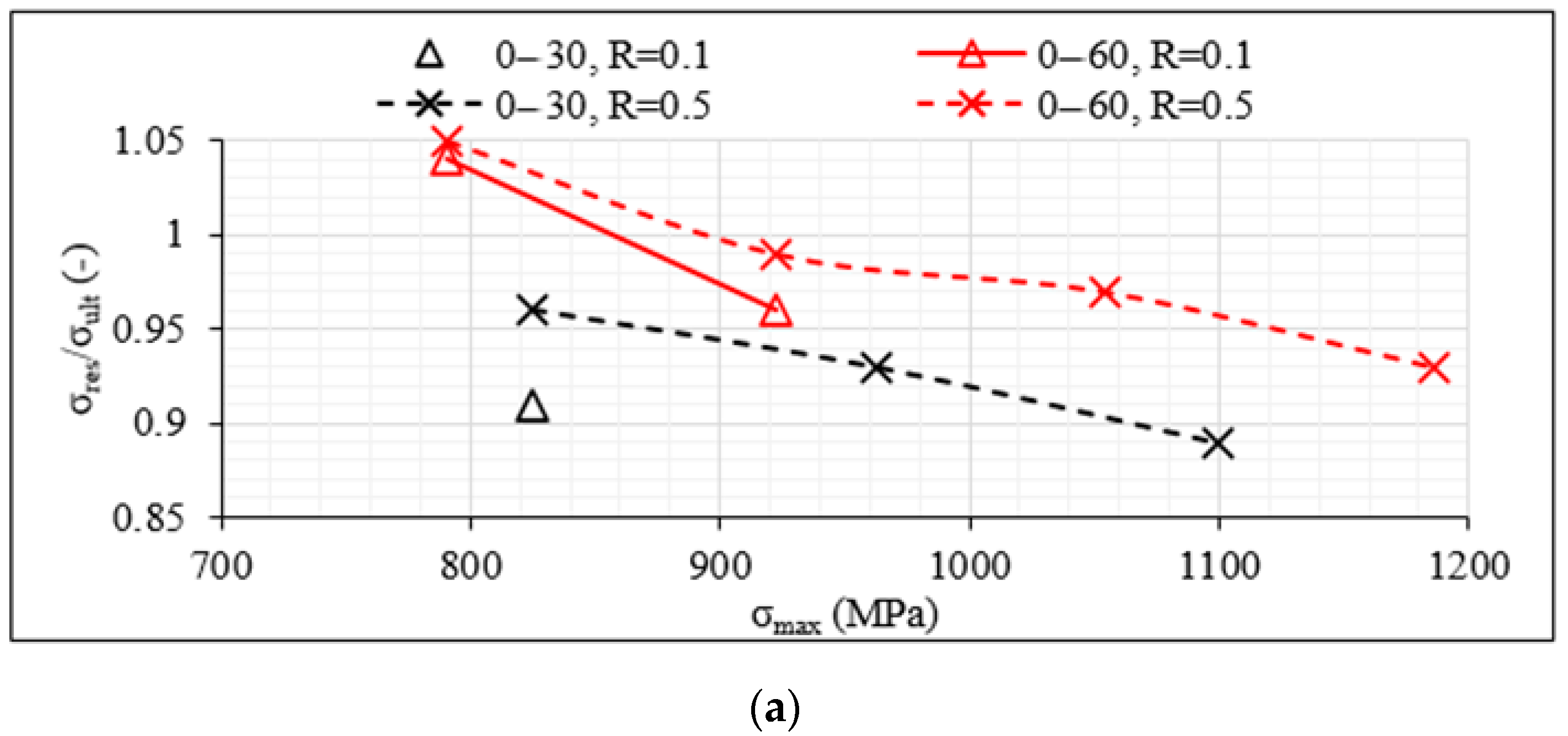
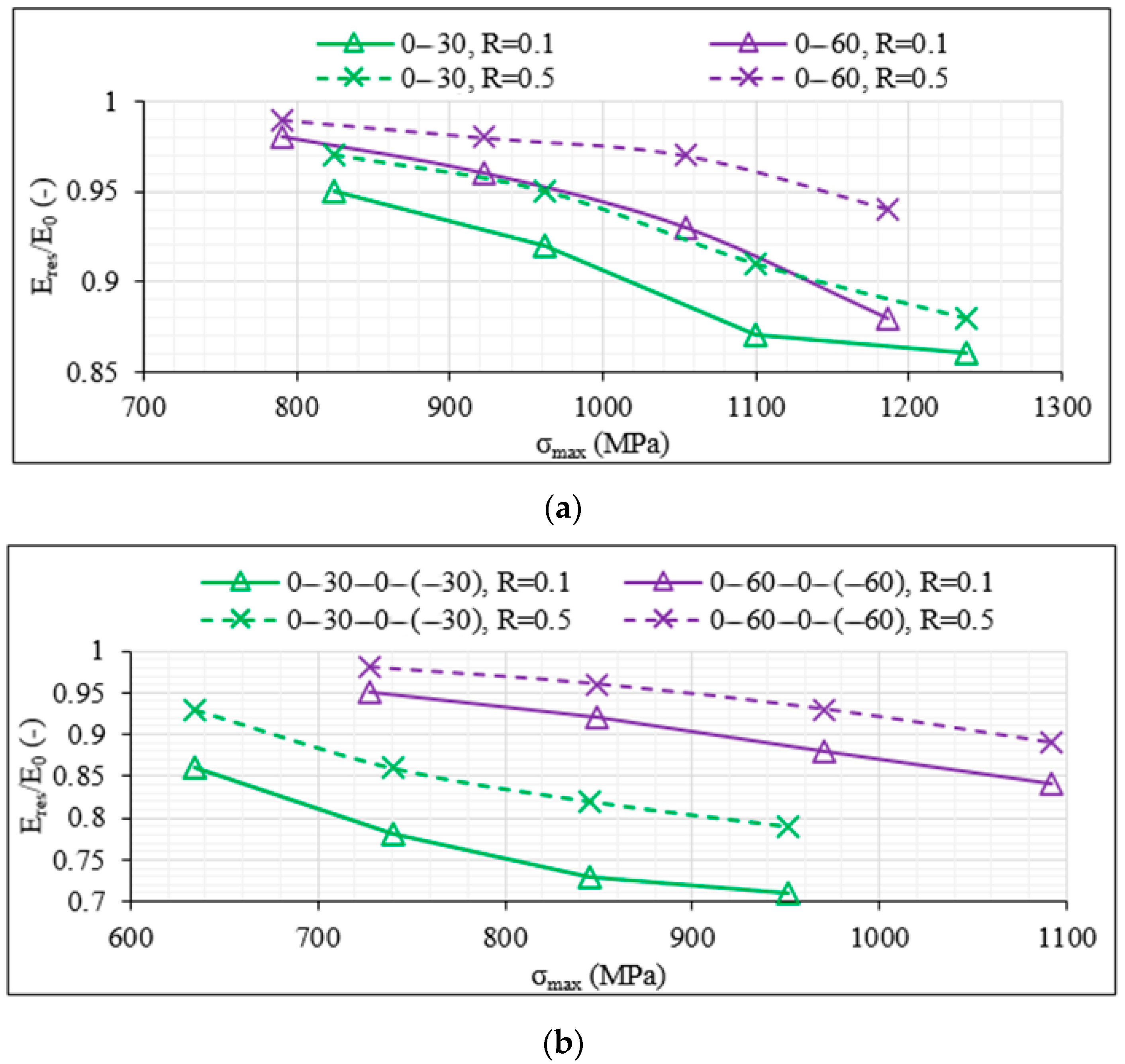
3.2. Residual Strength Measurements
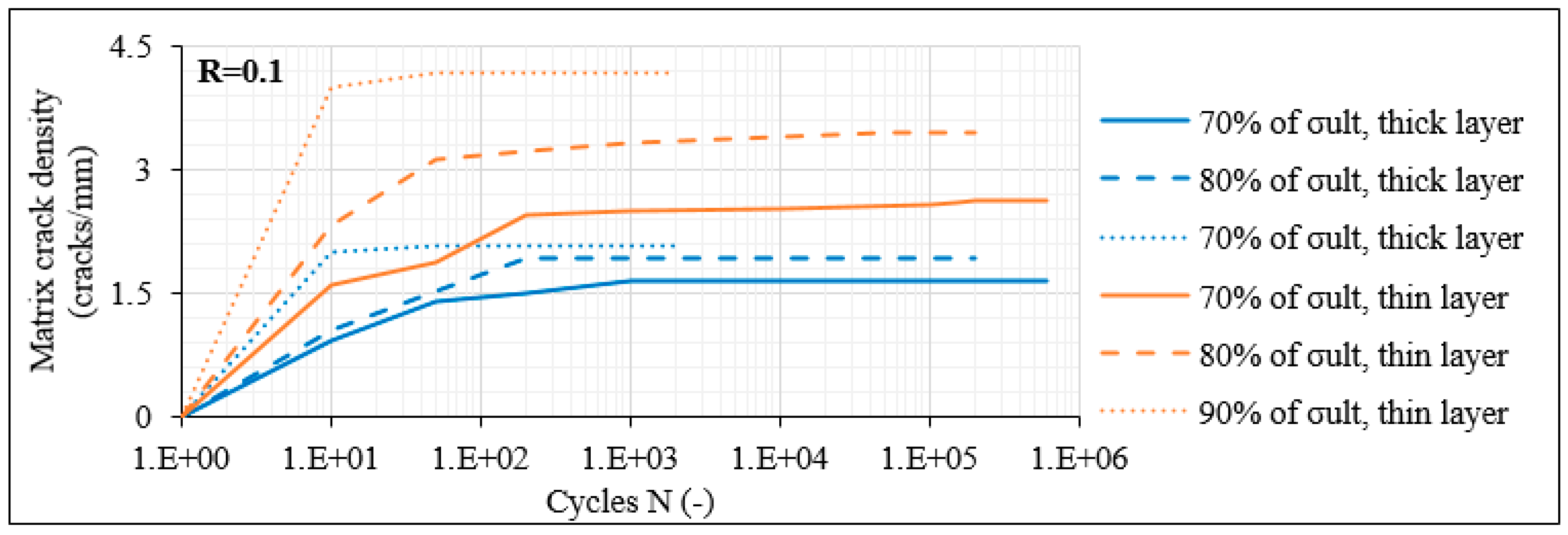
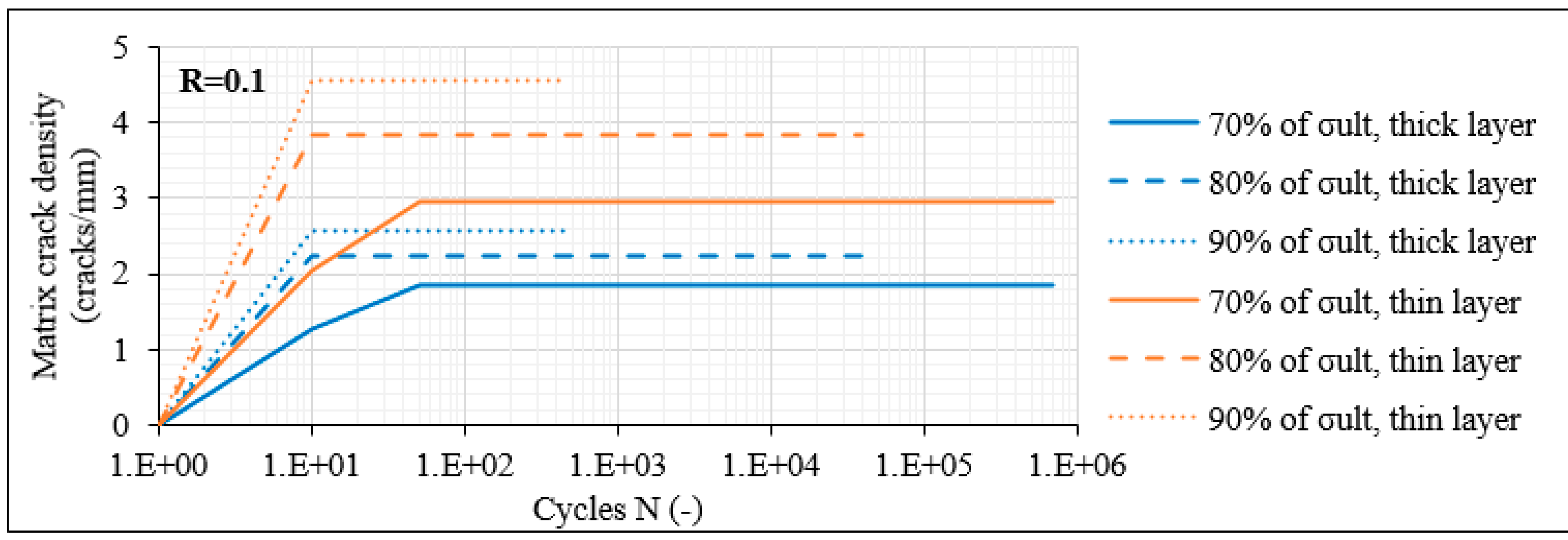
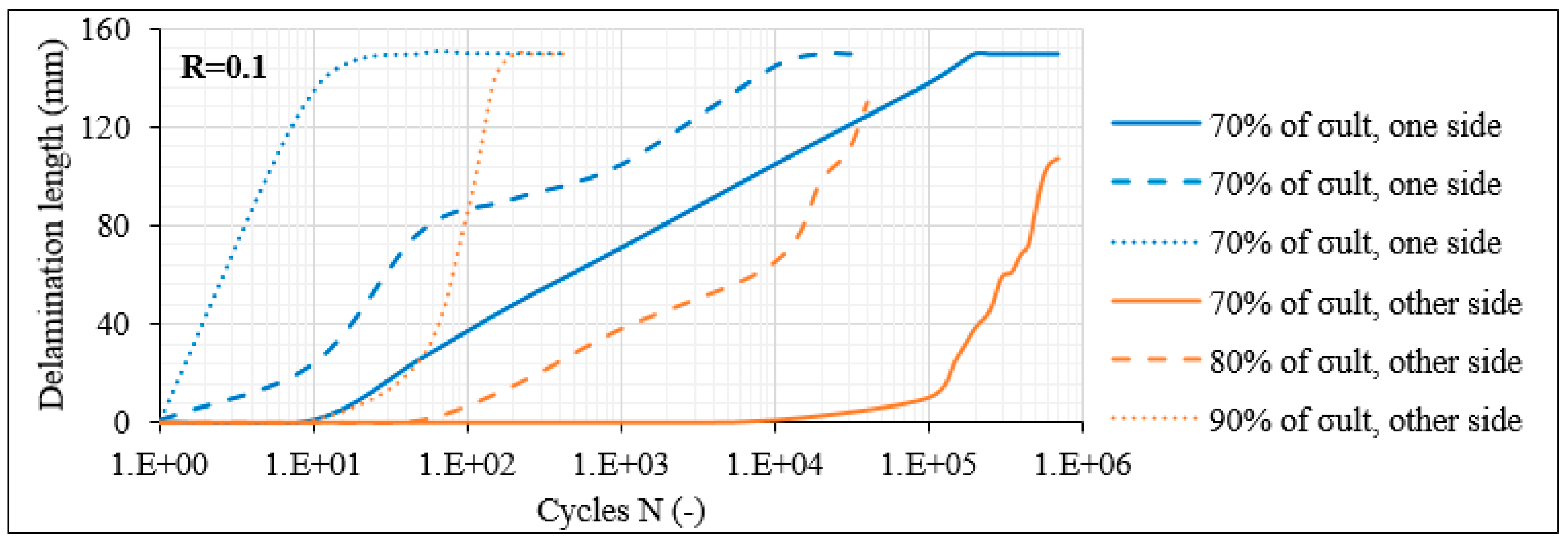
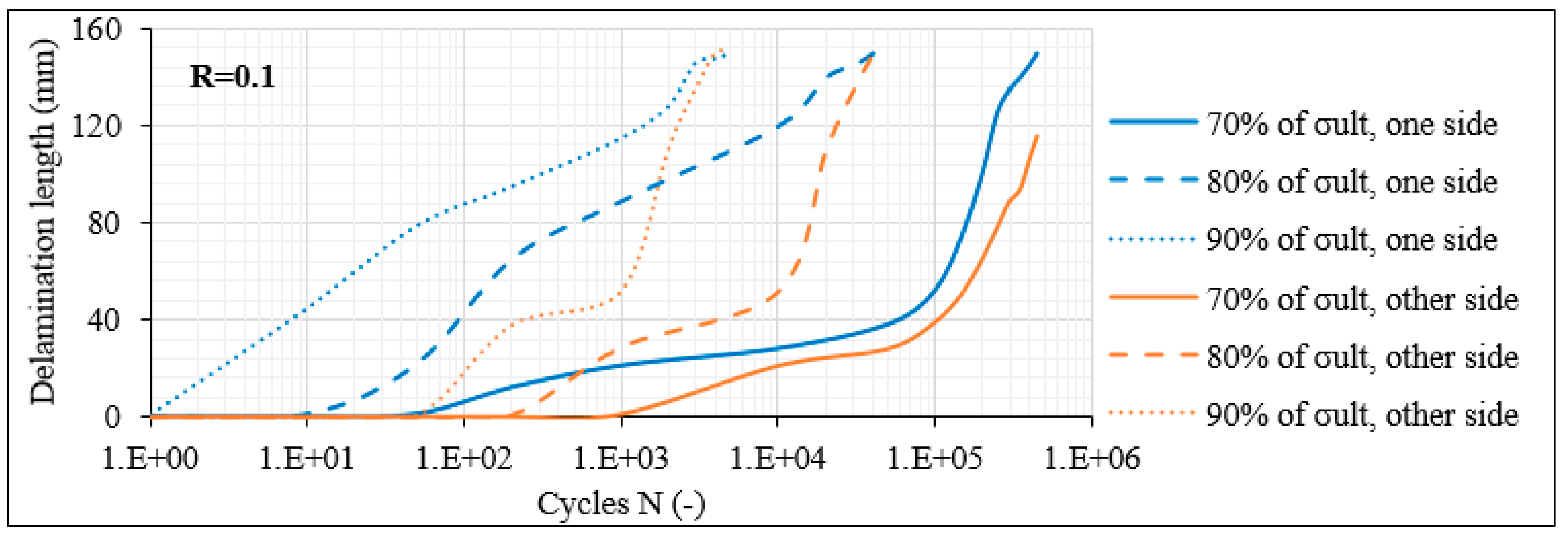
3.3. Investigation of Damage Accumulation
3.3.1. Damage Accumulation in Laminates with 60° Layers
3.3.2. Damage Accumulation in Laminates with 30° Layers
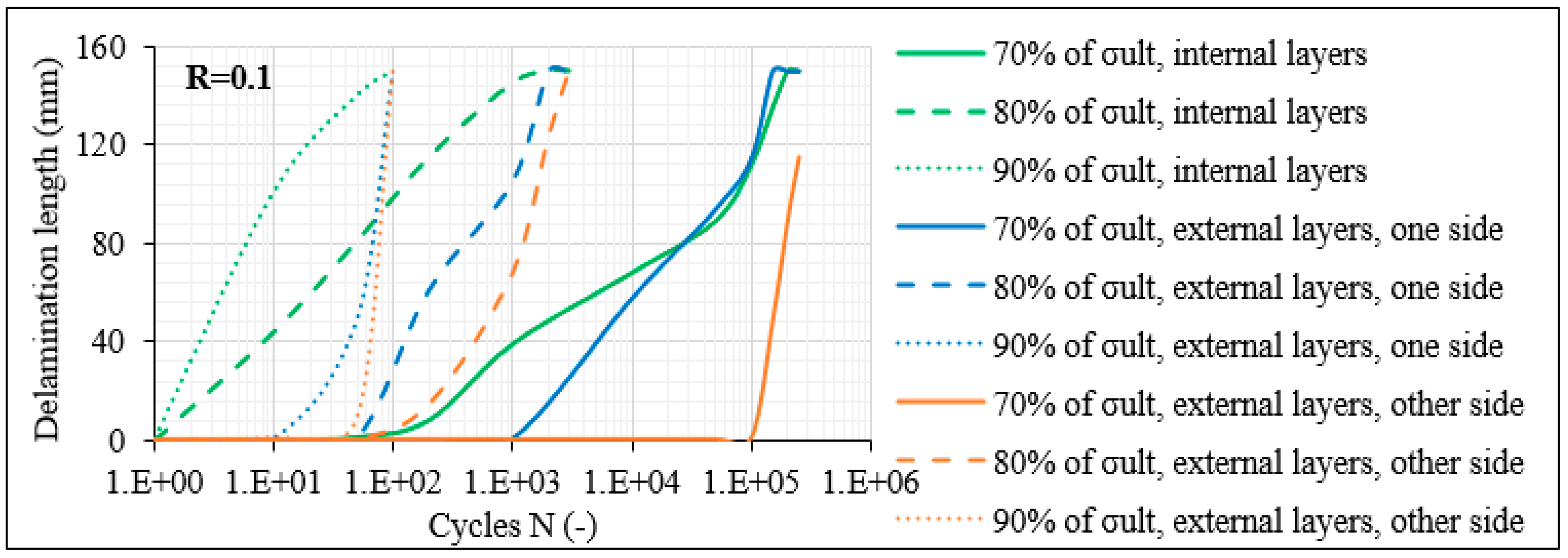
3.3.3. Edge Damage Microscopic Monitoring
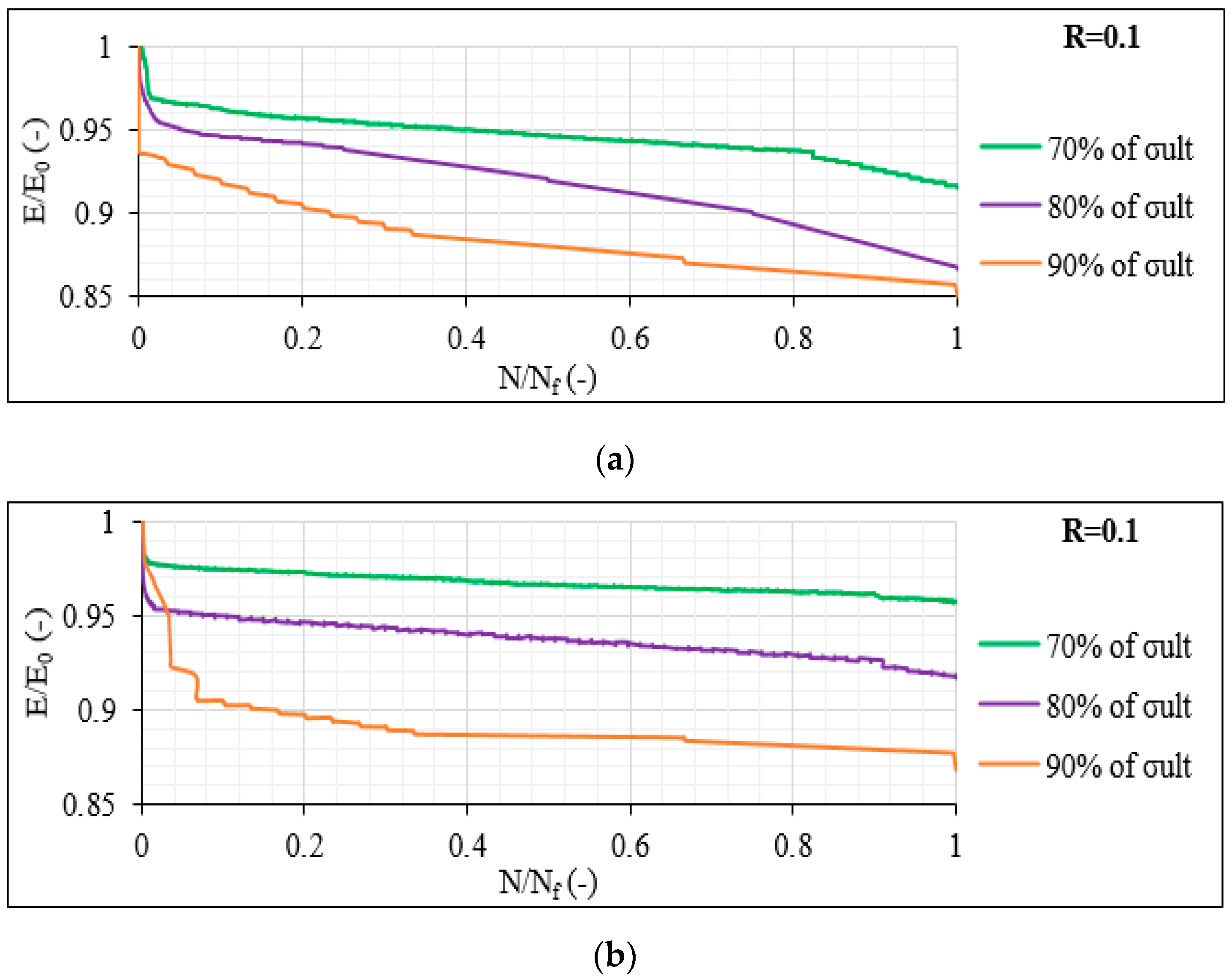
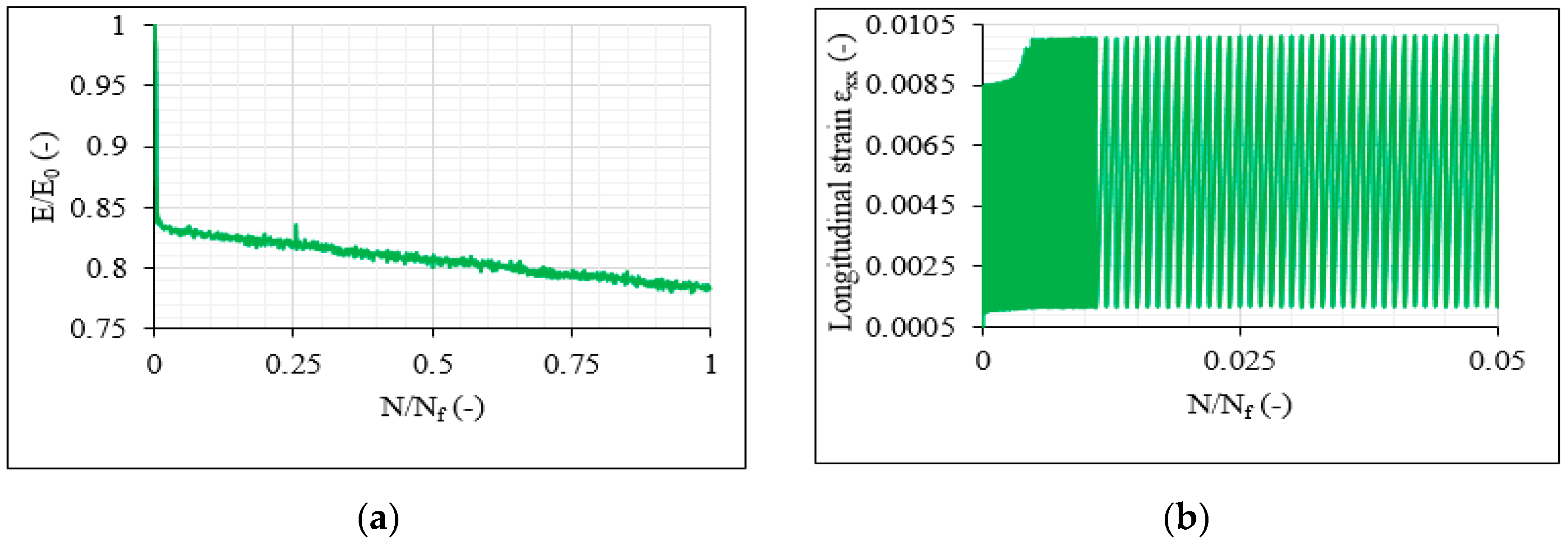
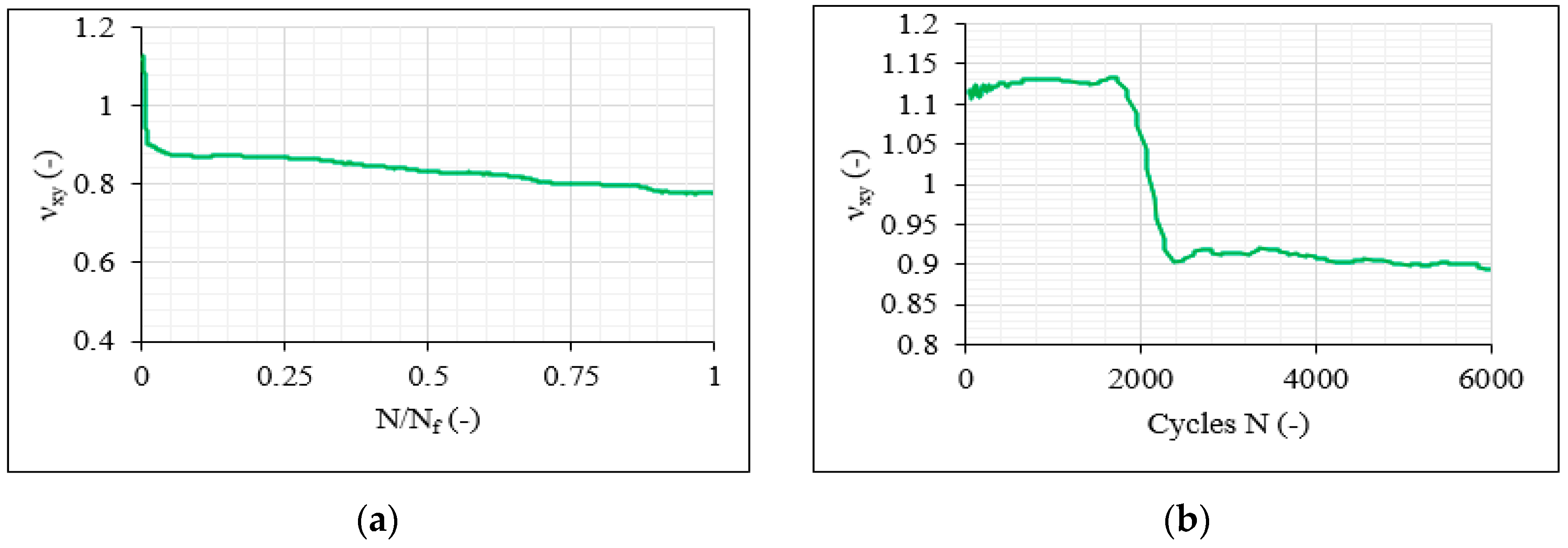
3.4. Stiffness Degradation and Poisson’s Ratio Measurements
4. Conclusions and Observations
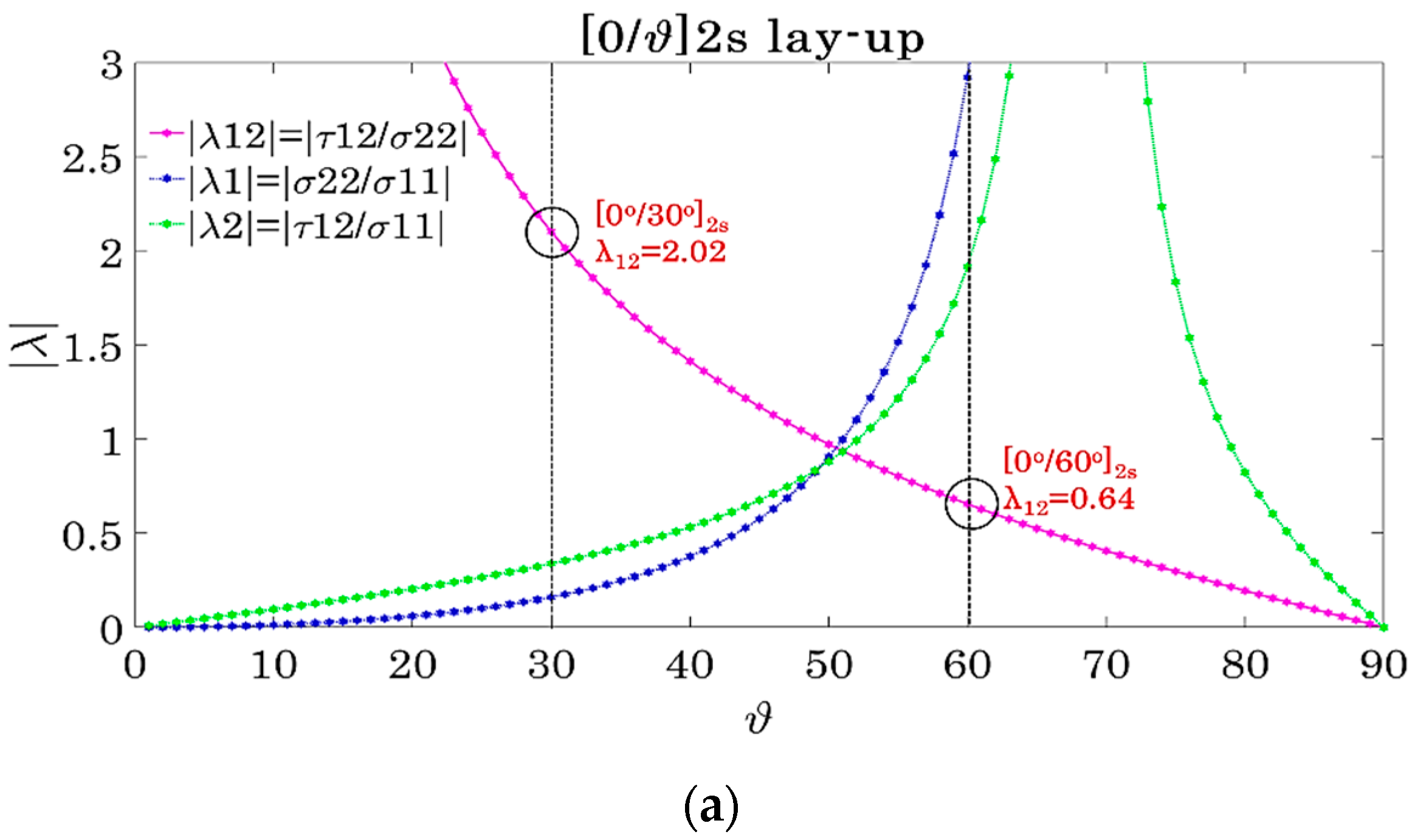
- The effect of multiaxiality, a comparison between balanced and unbalanced composite laminates and the impact of the number of off-axis layers on the tension–tension fatigue response were demonstrated in this work by testing angle-ply CFRP [0°/θ]2s, [0°/θ/0°/−θ]s and [0°/θ/−θ]2s laminates for two different off-axis angles, namely 30° and 60°.
- The mechanical response was initially studied in terms of S-Nf and residual strength data. The impact of shear was clearly indicated with laminates consisting of 30° off-axis plies leading to lower Nf and residual strength values.
- A high impact of the R-ratio was also revealed. An R-ratio equal to 0.5, corresponding to lower stress amplitude during fatigue loading, resulted always in higher fatigue life.
- One of the most interesting findings concerns the response of the unbalanced laminates when compared with the balanced lay-ups. Both in terms of S-Nf and residual strength data, a much better performance was observed for the first time for the unbalanced laminates having the same off-axis angle and being tested under the same fatigue conditions as the balanced ones.
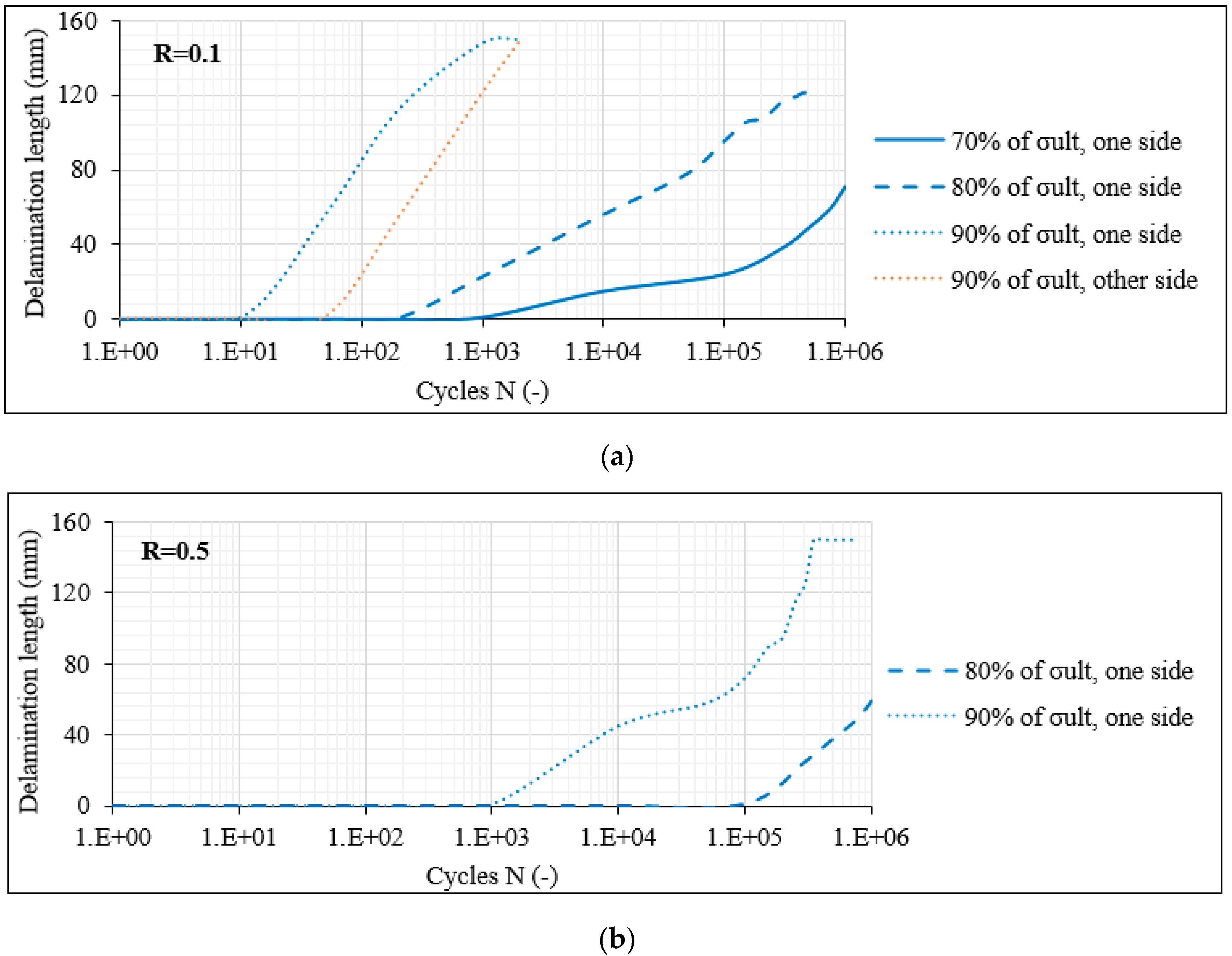
- All findings were confirmed by studying the progressive damage accumulation during fatigue. In all cases, matrix cracking was the initial damage mode appearing, leading to the interlaminar delaminations and final fibre breakage in laminates that did not survive the run-out of one million cycles. Nevertheless, important uncoverings were obtained when the shear-dominated laminates were compared with the laminates in which the transverse stresses dominate the stress state.
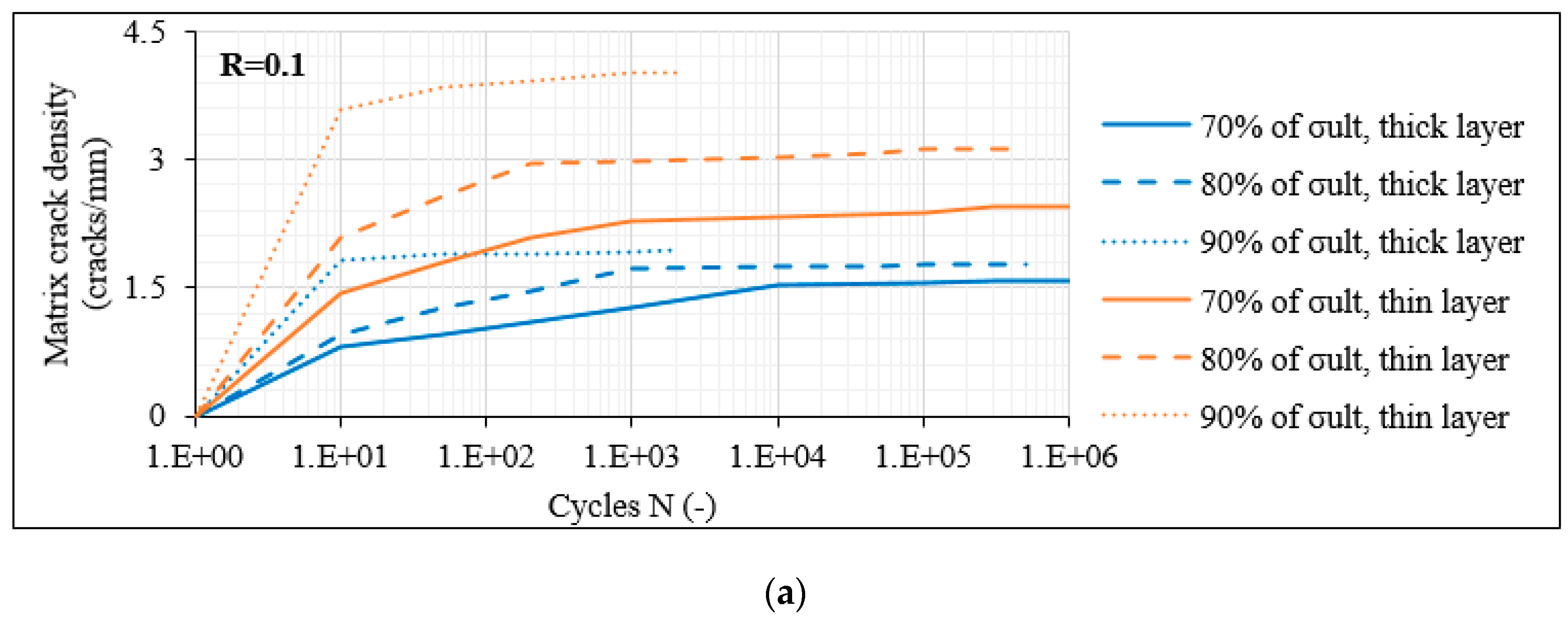
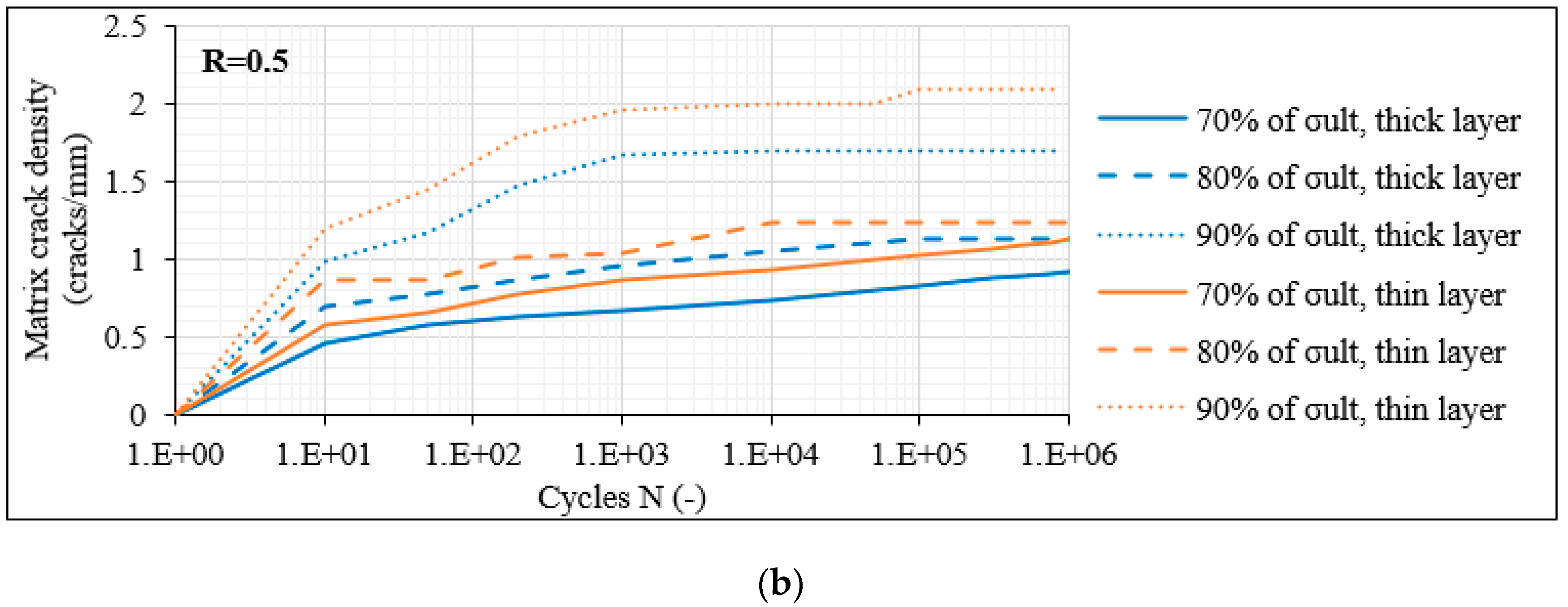
- Specifically, for the laminates with 60° off-axis plies, matrix cracks appeared in all off-axis layers during the very first fatigue cycles. Moreover, a saturation criterion applied, indicating that when the transverse stresses determine the damage accumulation, interlaminar delaminations during fatigue loading occur only after a certain saturation of the matrix cracks was reached.
- It was confirmed that the CDS was very similar both for the balanced and the unbalanced 8-ply laminates. However, it was reached quite earlier in the balanced lay-up, leading more quickly to the initiation and propagation of interlaminar delaminations for the same stress level.
- Significantly higher matrix crack densities were acquired though for the 12-ply laminates with an off-axis angle of 60°, showing a certain impact of the number of off-axis plies on the fatigue response.
- By contrast, the damage response was different in the shear-dominated laminates. In addition, in this case, matrix cracking was the initial damage mode appearing. However, initial matrix cracks only appeared in the middle thick layer in the 8-ply balanced and unbalanced lay-ups, and the onset of cracking was not consistently observed during the very first fatigue cycles. Only when the crack density reached a certain value in the middle thick layer, delaminations and matrix cracks in the thin off-axis layers initiated.
- The crack density limit, after which the delaminations started occurring in the laminate was quite smaller for the balanced laminates, indicating a significantly lower fracture toughness.
- The 12-ply shear-dominated laminates presented a somehow different damage response. In this case, the multiple interphases owing to the higher number of off-axis layers rapidly led to the local deterioration of the laminate at certain fractured areas. Nevertheless, the interphases acted also as obstacles for the development of damage along the total laminate length.
- The impact of the different parameters on the fatigue response was confirmed in all cases by applying both edge and midplane microscopy.
- Finally, stiffness degradation and Poisson’s ratio measurements validated the response of the material under the different conditions.
- Higher stiffness degradation was observed for increasing shear stresses and for the balanced lay-ups.
- The Poisson’s ratio seemed to be a satisfactory qualitative damage indicator, maintaining reducing trends during fatigue and correlating promisingly with the extent of damage.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Quaresimin, M. 50th anniversary article: Multiaxial fatigue testing of composites: From the pioneers to future directions. Strain 2015, 51, 16–29. [Google Scholar] [CrossRef]
- Hinton, M.; Kaddour, A.S.; Soden, P.D. Failure Criteria in Fibre Reinforced Polymer Composites: The World-Wide Failure Exercise, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Takeda, N.; Ogihara, S.; Kobayashi, A. Microscopic fatigue damage progress in CFRP cross-ply laminates. Composites 1995, 26, 859–867. [Google Scholar] [CrossRef]
- Kobayashi, S.; Takeda, N. Experimental and analytical characterization of transverse cracking behavior in carbon/bismaleimide cross-ply laminates under mechanical fatigue loading. Compos. Part B Eng. 2002, 33, 471–478. [Google Scholar] [CrossRef]
- Berthelot, J.M. Transverse cracking and delamination in cross-ply glass-fiber and carbon-fiber reinforced plastic laminates: Static and fatigue loading. Appl. Mech. Rev. 2003, 56, 111–147. [Google Scholar] [CrossRef]
- Bezazi, A.R.; El Mahi, A.; Berthelot, J.M.; Bezzazi, B. Flexural fatigue behavior of cross-ply laminates: An experimental approach. Strength Mater. 2003, 35, 149–161. [Google Scholar] [CrossRef]
- Silberschmidt, V.V. Matrix cracking in cross-ply laminates: Effect of randomness. Compos. Part A Appl. Sci. Manuf. 2005, 36, 129–135. [Google Scholar] [CrossRef]
- Van Paepegem, W.; De Baere, I.; Lamkanfi, E.; Degrieck, J. Monitoring quasi-static and cyclic fatigue damage in fibre-reinforced plastics by Poisson’s ratio evolution. Int. J. Fatigue 2010, 32, 184–196. [Google Scholar] [CrossRef] [Green Version]
- Al-Khudairi, O.; Hadavinia, H.; Waggott, A.; Lewis, E.; Little, C. Characterising mode I/mode II fatigue delamination growth in unidirectional fibre reinforced polymer laminates. Mater Des (1980–2015) 2015, 66, 93–102. [Google Scholar] [CrossRef] [Green Version]
- Yao, L.; Sun, Y.; Guo, L.; Jia, L.; Zhao, M. A validation of a modified Paris relation for fatigue delamination growth in unidirectional composite laminates. Compos. Part B Eng. 2018, 132, 97–106. [Google Scholar] [CrossRef]
- Kim, H.S.; Huang, S. S-N curve characterisation for composite materials and prediction of remaining fatigue life using damage function. J. Compos. Sci. 2021, 5, 76. [Google Scholar] [CrossRef]
- Plumtree, A.; Melo, M.; Dahl, J. Damage evolution in a [±45]2s CFRP laminate under block loading conditions. Int. J. Fatigue 2010, 32, 139–145. [Google Scholar] [CrossRef]
- Movahedi-Rad, A.V.; Keller, T.; Vassilopoulos, A.P. Fatigue damage in angle-ply GFRP laminates under tension-tension fatigue. Int. J. Fatigue 2018, 109, 60–69. [Google Scholar] [CrossRef]
- Reifsnider, K.L.; Talug, A. Analysis of fatigue damage in composite laminates. Int. J. Fatigue 1980, 2, 3–11. [Google Scholar] [CrossRef]
- Ramakrishnan, V.; Jayaraman, N. Mechanistically based fatigue-damage evolution model for brittle matrix fibre-reinforced composites. J. Mater. Sci. 1993, 28, 5592–5602. [Google Scholar] [CrossRef]
- Varvani-Farahani, A.; Shirazi, A. A fatigue damage model for (0/90) FRP composites based on stiffness degradation of 0 and 90 composite plies. J. Reinf. Plast. Comp. 2007, 26, 1319–1336. [Google Scholar] [CrossRef]
- Korkiakoski, S.; Brøndsted, P.; Sarlin, E.; Saarela, O. Influence of specimen type and reinforcement on measured tension–tension fatigue life of unidirectional GFRP laminates. Int. J. Fatigue 2016, 85, 114–129. [Google Scholar] [CrossRef] [Green Version]
- Roundi, W.; El Mahi, A.; El Gharad, A.; Rebiere, J.L. Acoustic emission monitoring of damage progression in glass/epoxy composites during static and fatigue tensile tests. Appl. Acoust. 2018, 132, 124–134. [Google Scholar] [CrossRef]
- Ye, L. On fatigue damage accumulation and material degradation in composite materials. Compos. Sci. Technol. 1989, 36, 339–350. [Google Scholar] [CrossRef]
- Tserpes, K.I.; Papanikos, P.; Labeas, G.; Pantelakis, S. Fatigue damage accumulation and residual strength assessment of CFRP laminates. Compos. Struct. 2004, 63, 219–230. [Google Scholar] [CrossRef]
- May, M.; Hallett, S.R. Damage initiation in polymer matrix composites under high-cycle fatigue loading—A question of definition or a material property? Int. J. Fatigue 2016, 87, 59–62. [Google Scholar] [CrossRef] [Green Version]
- El Kadi, H.; Ellyin, F. Effect of stress ratio on the fatigue of unidirectional glass fibre/epoxy composite laminae. Composites 1994, 25, 917–924. [Google Scholar] [CrossRef]
- Philippidis, T.P.; Vassilopoulos, A.P. Fatigue of composite laminates under off-axis loading. Int. J. Fatigue 1999, 21, 253–262. [Google Scholar] [CrossRef]
- Kawai, M.; Suda, H. Effects of non-negative mean stress on the off-axis fatigue behavior of unidirectional carbon/epoxy composites at room temperature. J. Compos. Mater. 2004, 38, 833–854. [Google Scholar] [CrossRef]
- Burhan, I.; Kim, H.S. S-N curve models for composite materials characterisation: An evaluative review. J. Compos. Sci. 2018, 2, 38. [Google Scholar] [CrossRef] [Green Version]
- Böhm, M.; Głowacka, K. Fatigue life estimation with mean stress effect compensation for lightweight structures—The case of GLARE 2 composite. Polymers 2020, 12, 251. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- May, M.; Pullin, R.; Eaton, M.; Featherston, C.; Hallett, S.R. An advanced model for initiation and propagation of damage under fatigue loading—Part II: Matrix cracking validation cases. Compos. Struct. 2011, 93, 2350–2357. [Google Scholar] [CrossRef]
- Quaresimin, M.; Carraro, P.A.; Mikkelsen, L.P.; Lucato, N.; Vivian, L.; Brøndsted, P.; Sørensen, B.F.; Varna, J.; Talreja, R. Reprint of: Damage evolution under cyclic multiaxial stress state: A comparative analysis between glass/epoxy laminates and tubes. Compos. Part B Eng. 2014, 65, 2–10. [Google Scholar] [CrossRef]
- Liu, D. Impact-induced delamination—A view of bending stiffness mismatching. J. Compos. Mater. 1988, 22, 674–692. [Google Scholar] [CrossRef]
- Ho, K.C.; Hwang, J.R.; Doong, J.L. Impact fatigue of short glass fiber reinforced polycarbonate. J. Reinf. Plast. Comp. 1997, 16, 903–925. [Google Scholar] [CrossRef]
- Baucom, J.N.; Zikry, M.A.; Rajendran, A.M. Low-velocity impact damage accumulation in woven S2-glass composite systems. Compos. Sci. Technol. 2006, 66, 1229–1238. [Google Scholar] [CrossRef]
- Azouaoui, K.; Azari, Z.; Pluvinage, G. Evaluation of impact fatigue damage in glass/epoxy composite laminate. Int. J. Fatigue 2010, 32, 443–452. [Google Scholar] [CrossRef]
- Lee, C.S.; Hwang, W.; Park, H.C.; Han, K.S. Failure of carbon/epoxy composite tubes under combined axial and torsional loading 1. Experimental results and prediction of biaxial strength by the use of neural networks. Compos. Sci. Technol. 1999, 59, 1779–1788. [Google Scholar] [CrossRef]
- Qi, D.; Cheng, G. Fatigue behavior of filament-wound glass fiber reinforced epoxy composite tubes under tension/torsion biaxial loading. Polym. Compos. 2007, 28, 116–123. [Google Scholar] [CrossRef]
- Quaresimin, M.; Carraro, P.A. Damage initiation and evolution in glass/epoxy tubes subjected to combined tension-torsion fatigue loading. Int. J. Fatigue 2014, 63, 25–35. [Google Scholar] [CrossRef]
- Susuki, I. Fatigue damage of composite laminate under biaxial loads. In Mechanical Behaviour of Materials VI; Elsevier: Amsterdam, The Netherlands, 1992; pp. 543–548. [Google Scholar]
- Makris, A.; Ramault, C.; Van Hemelrijck, D.; Zarouchas, D.; Lamkanfi, E.; Van Paepegem, W. An investigation of the mechanical behavior of carbon epoxy cross ply cruciform specimens under biaxial loading. Polym. Compos. 2010, 31, 1554–1561. [Google Scholar] [CrossRef]
- Satapathy, M.R.; Vinayak, B.G.; Jayaprakash, K.; Naik, N.K. Fatigue behavior of laminated composites with a circular hole under in-plane multiaxial loading. Mater. Des. 2013, 51, 347–356. [Google Scholar] [CrossRef]
- Quaresimin, M.; Carraro, P.A. On the investigation of the biaxial fatigue behaviour of unidirectional composites. Compos. Part B Eng. 2013, 54, 200–208. [Google Scholar] [CrossRef]
- Kalteremidou, K.A.; Hajikazemi, M.; Van Paepegem, W.; Van Hemelrijck, D.; Pyl, L. Effect of multiaxiality, stacking sequence and number of off-axis layers on the mechanical response and damage sequence of carbon/epoxy composite laminates under static loading. Compos. Sci. Technol. 2020, 190, 108044. [Google Scholar] [CrossRef]
- ASTM. D3039, Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials; ASTM: West Conshohocken, PA, USA, 2008. [Google Scholar]











| Property | Value (Average and Standard Error) | Unit |
|---|---|---|
| σ11,ult | 2272 ± 89 | MPa |
| σ22,ult | 53 ± 2 | MPa |
| τ12,ult | 52 ± 1 | MPa |
| E11 | 125.8 ± 3.9 | GPa |
| E22 | 9.4 ± 0.3 | GPa |
| G12 | 4.1 ± 0.1 | GPa |
| ν12 | 0.335 ± 0.014 | - |
| Fatigue Tests | Microscopic Inspection after (x) Cycles | |
| For Nf = 106 cycles | 10, 50, 200, 103, 104, 105, 3 × 105, 5 × 105, 7.5 × 105, 106 | |
| Condition | Cycle count | Microscopic inspection every (x) cycles |
| If Nf < 103 | 50-failure | 50 |
| If Nf < 104 | 103-failure | 103 |
| If Nf < 105 | 104-failure | 104 |
| If Nf < 106 | 5 × 104-failure | 5 × 104 |
| Parameter | Value | Unit |
|---|---|---|
| Lenses | 23 | mm |
| Subset size | 21 | pixels |
| Step size | 7 | pixels |
| Resolution (x × y) | 2085 × 896 | pixels |
| Sensitivity | 0.028 | mm/pixel |
| Pixel resolution (x/y) | 28/28 | μm/μm |
| Subset resolution (x/y) | 588/588 | μm/μm |
| Average speckle diameter | 100 | μm |
| Cycle Count | Image Taken Every (x) Cycles |
|---|---|
| 0–500 | 20 |
| 500–103 | 50 |
| 103–104 | 200 |
| 104-N | 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalteremidou, K.-A.; Van Hemelrijck, D.; Pyl, L. The Influence of Different Lay-Up Parameters on the Fatigue Response of Carbon/Epoxy Laminates under Internal Multiaxial Stress States. Materials 2021, 14, 7494. https://doi.org/10.3390/ma14247494
Kalteremidou K-A, Van Hemelrijck D, Pyl L. The Influence of Different Lay-Up Parameters on the Fatigue Response of Carbon/Epoxy Laminates under Internal Multiaxial Stress States. Materials. 2021; 14(24):7494. https://doi.org/10.3390/ma14247494
Chicago/Turabian StyleKalteremidou, Kalliopi-Artemi, Danny Van Hemelrijck, and Lincy Pyl. 2021. "The Influence of Different Lay-Up Parameters on the Fatigue Response of Carbon/Epoxy Laminates under Internal Multiaxial Stress States" Materials 14, no. 24: 7494. https://doi.org/10.3390/ma14247494
APA StyleKalteremidou, K.-A., Van Hemelrijck, D., & Pyl, L. (2021). The Influence of Different Lay-Up Parameters on the Fatigue Response of Carbon/Epoxy Laminates under Internal Multiaxial Stress States. Materials, 14(24), 7494. https://doi.org/10.3390/ma14247494






