Mode II Behavior of High-Strength Concrete under Monotonic, Cyclic and Fatigue Loading
Abstract
:1. Introduction
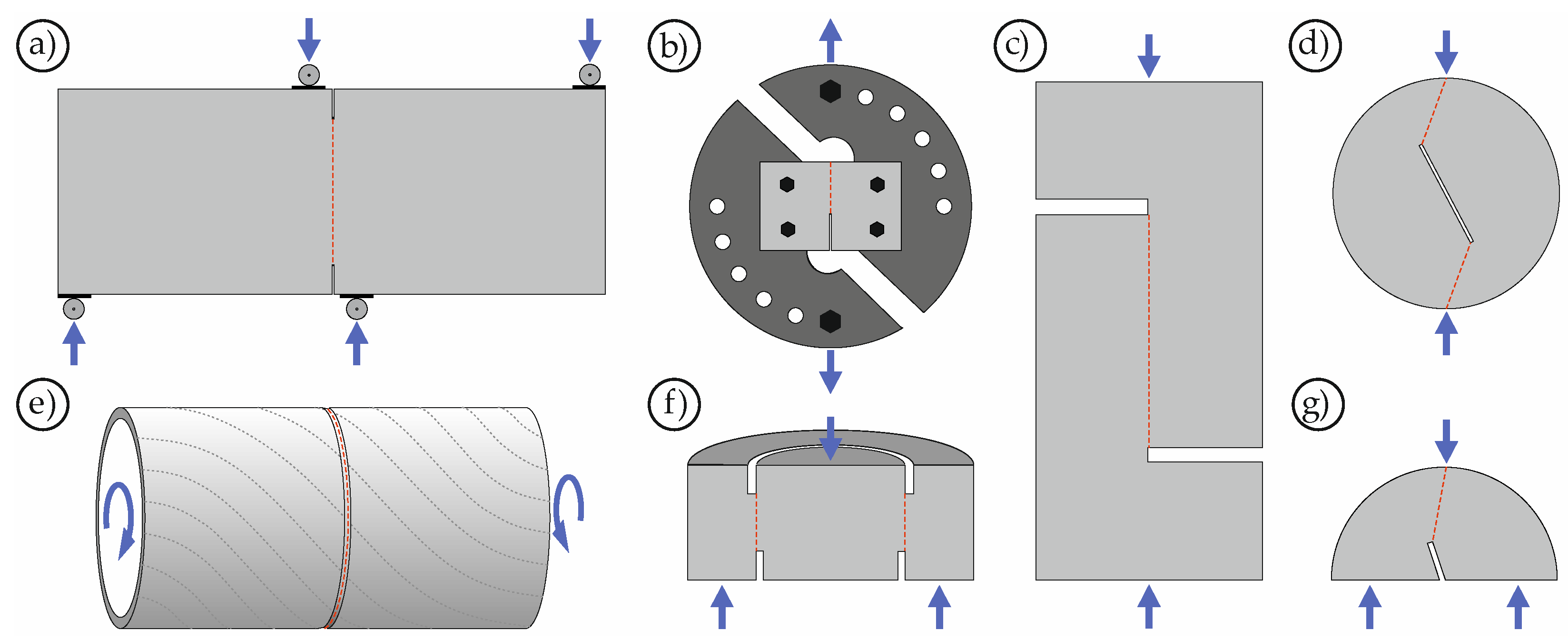
2. A Brief Overview of Shear Testing
3. Experimental Program
3.1. Material Properties
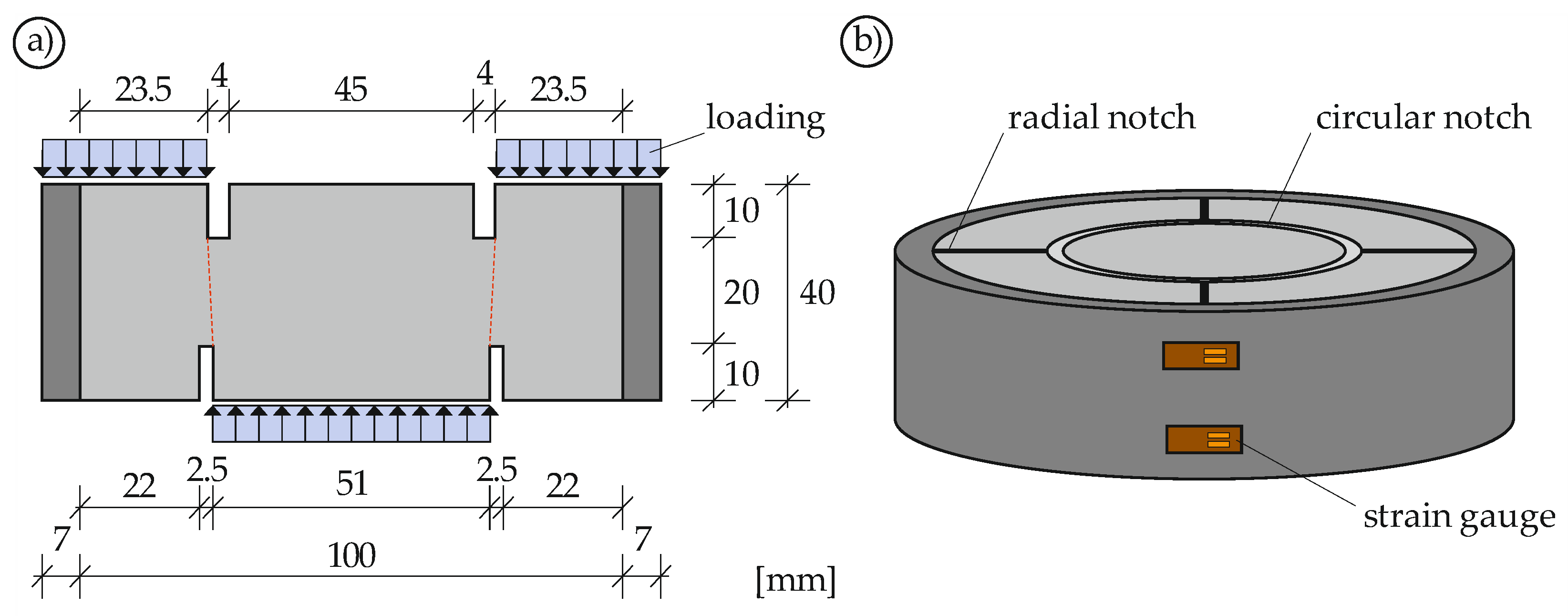
3.2. Specimen Geometry and Preparation
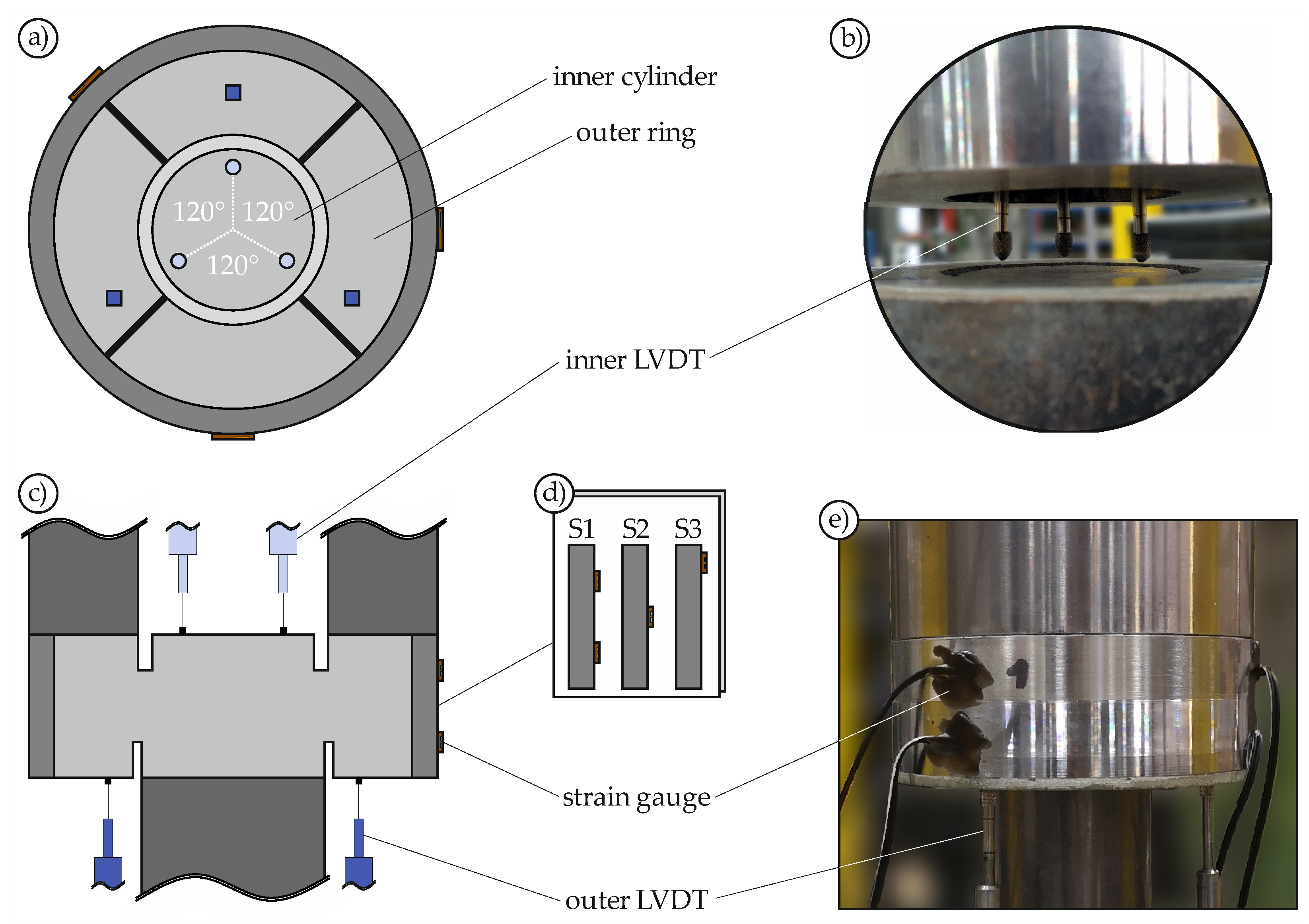
3.3. Test Setup, Instrumentation and Test Procedure
3.4. Loading Scenarios
4. Experimental Results and Discussion
4.1. Monotonic Behavior
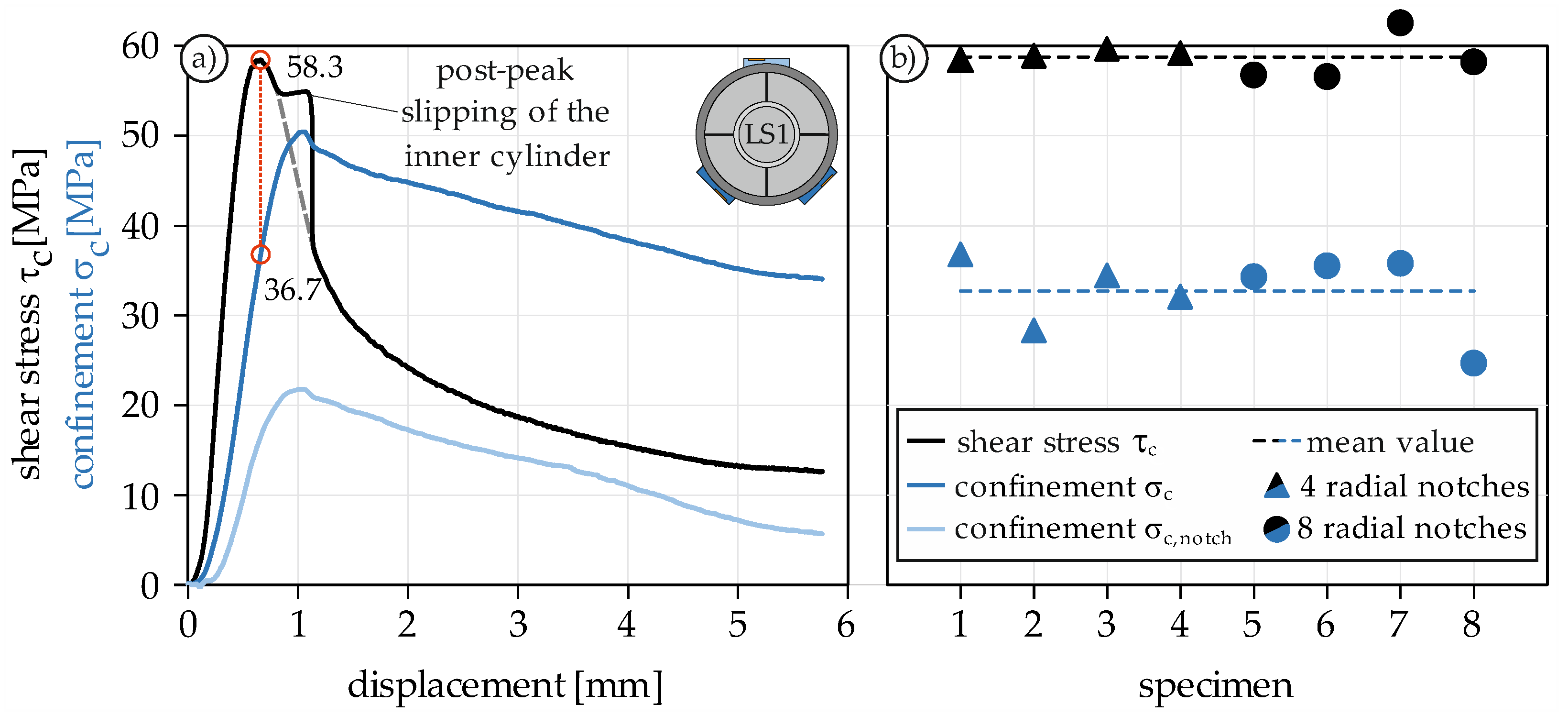
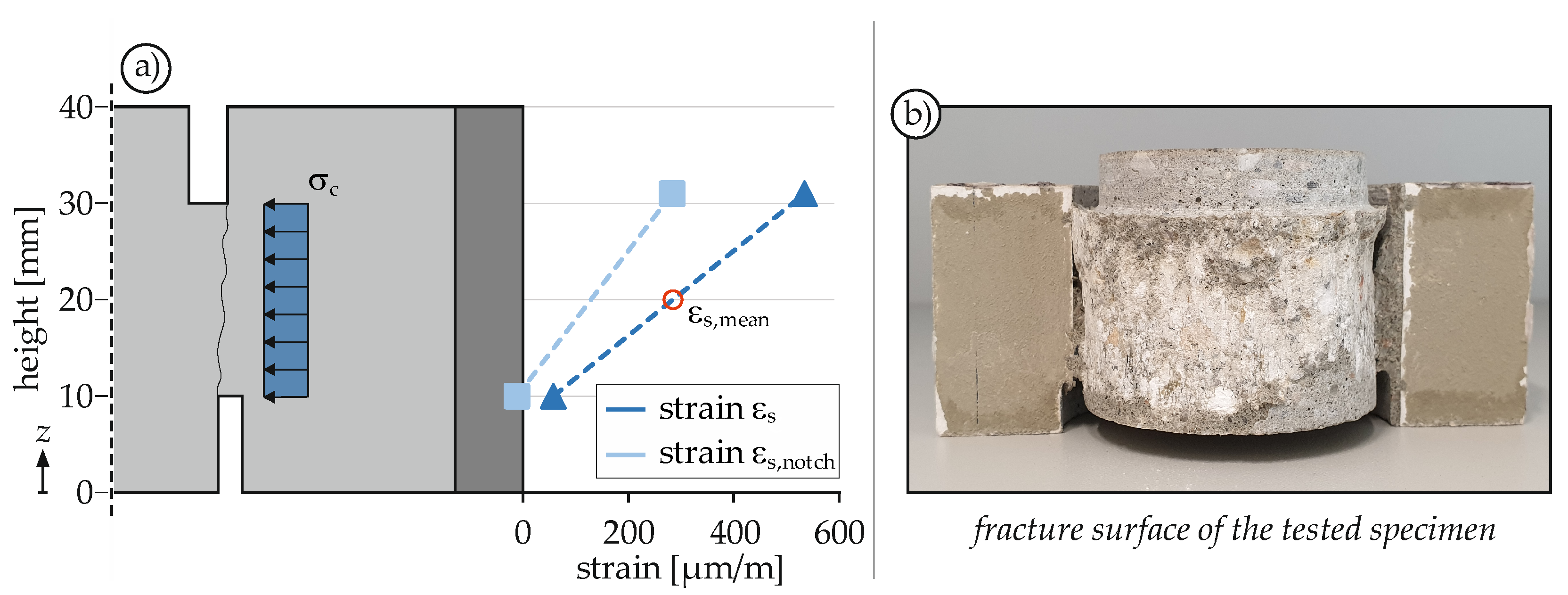
4.1.1. Calculation of the Confinement
4.1.2. Stress-Displacement Curve
4.1.3. Interaction of Shear Strength and Confinement
4.1.4. Fracture Behavior
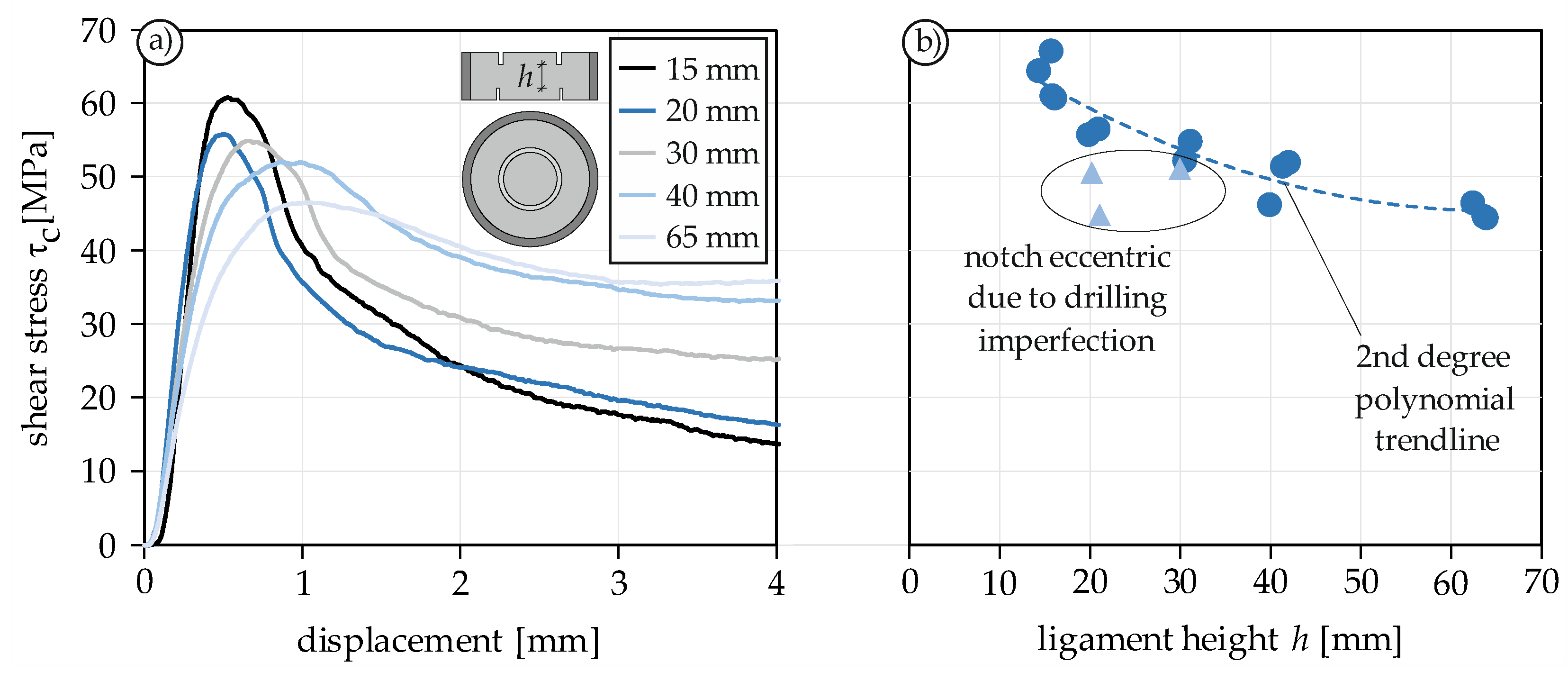
4.1.5. Size Effect
4.2. Post-Peak Cyclic Behavior
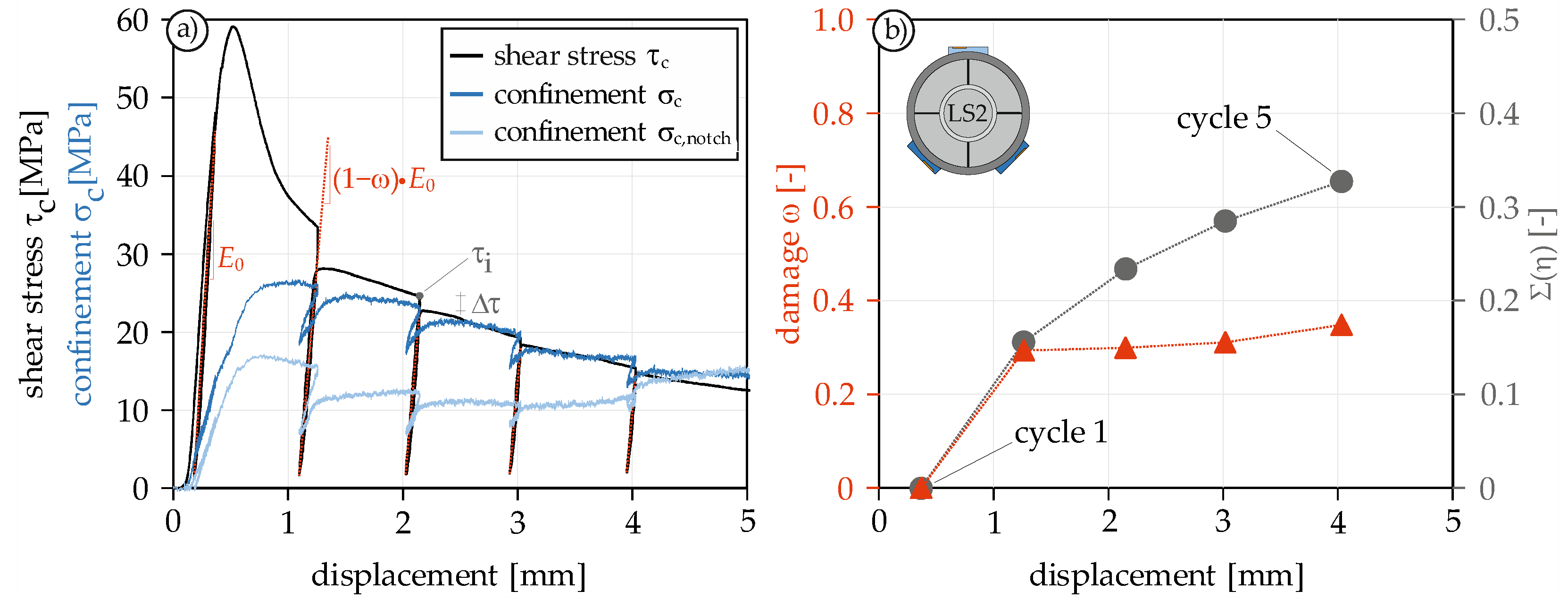
4.2.1. Stress-Displacement Curve
4.2.2. Evaluation of the Degradation Effects
4.3. Pre-Peak Cyclic Behavior
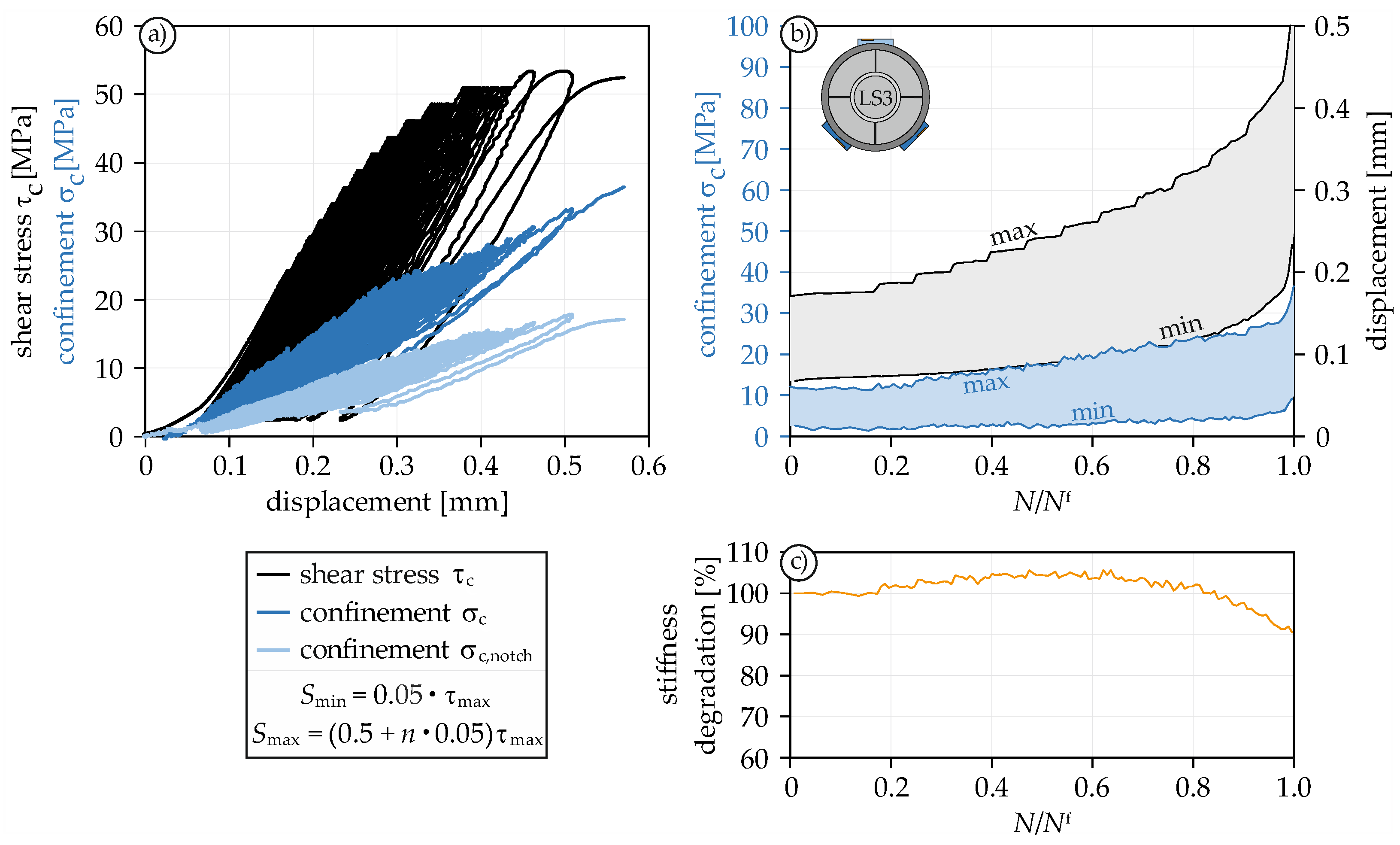
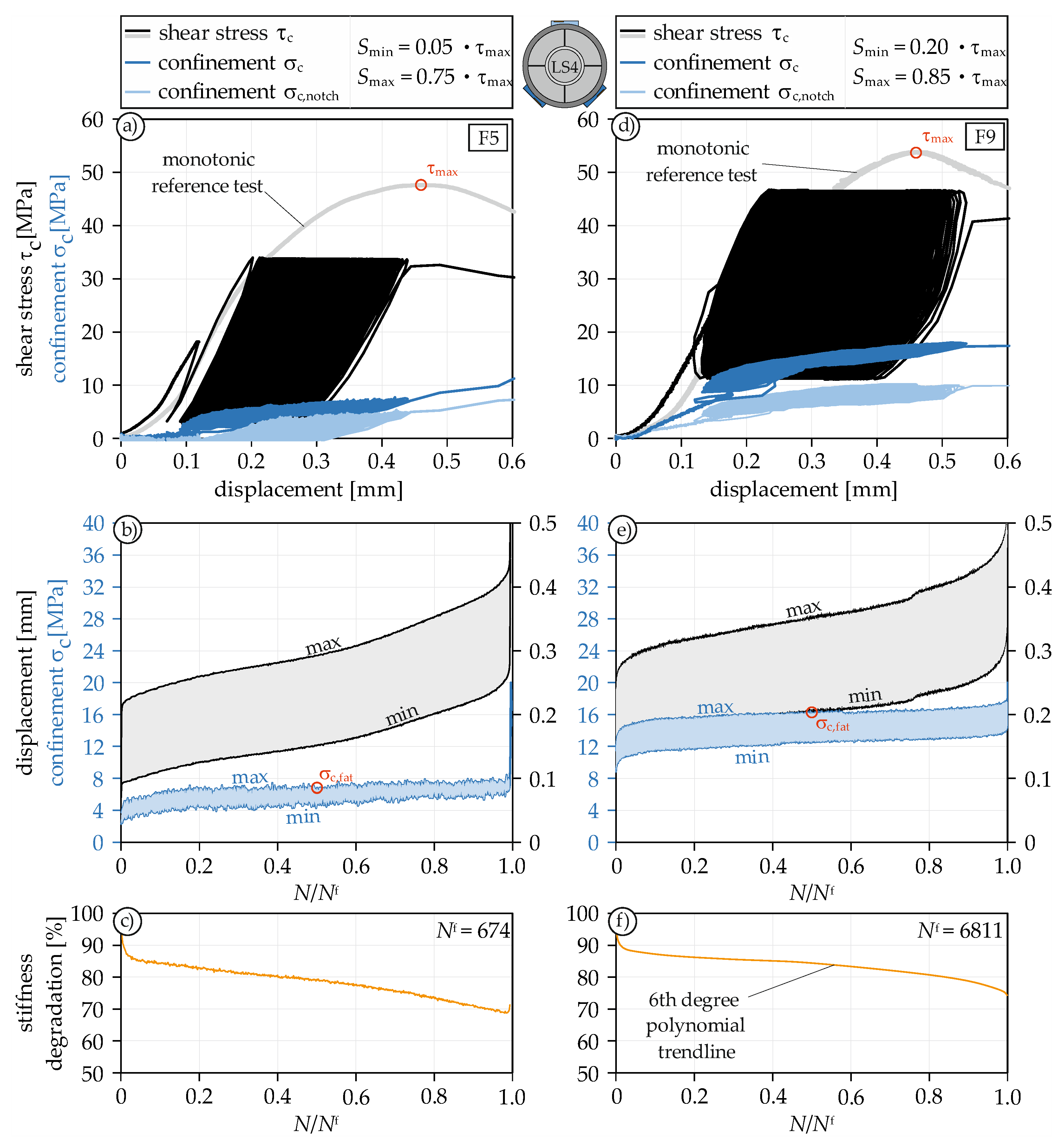
4.4. Fatigue Behavior under Constant Amplitudes
4.4.1. General
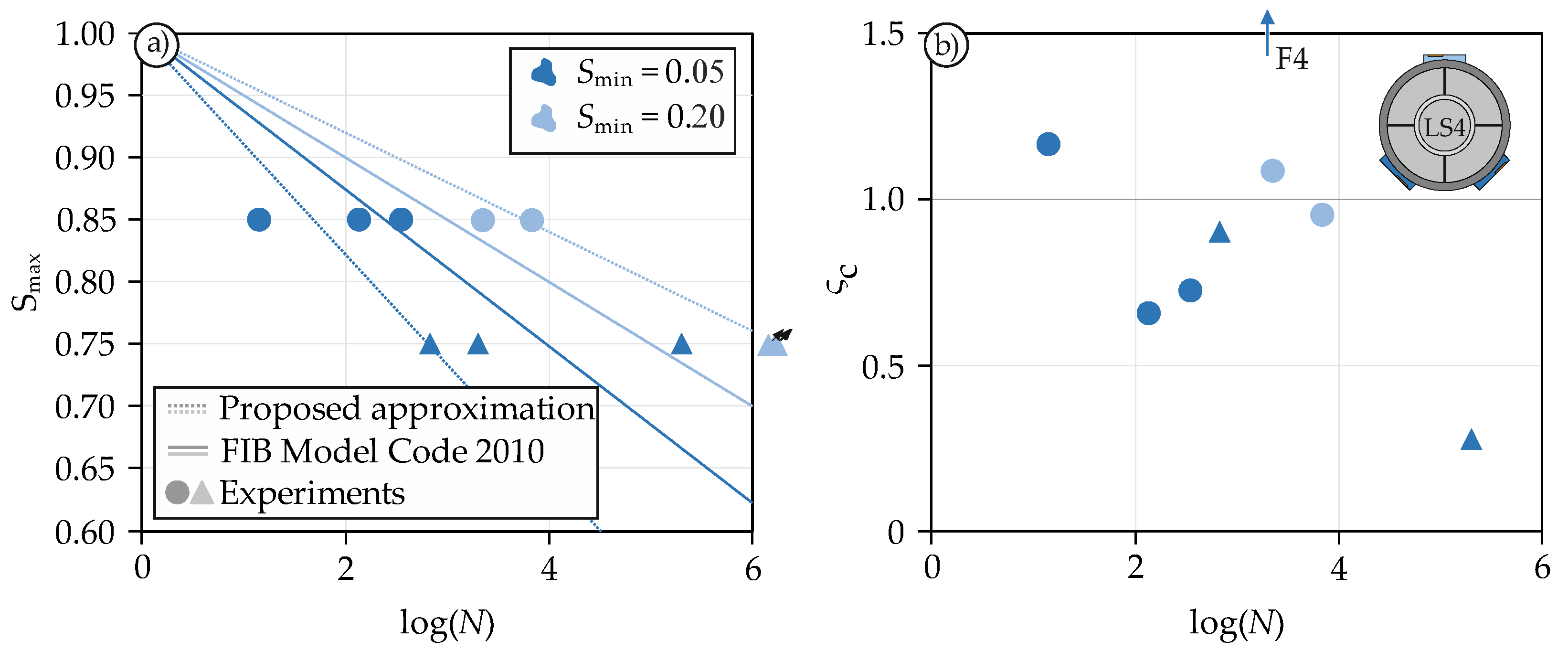
4.4.2. Interaction of Fatigue Life and Confinement
4.4.3. Limitation of the Test Method
5. Conclusions
- The presented PTST setup is applicable for introducing steady compressive shear loading in a very straightforward manner without causing secondary cracks.
- With the help of the steel ring strain measurements, it is possible to determine the simultaneously acting compressive stress and thus correlate it with the shear strength. In addition, this allows to determine the nonlinear stress distribution along the specimen height.
- Size effect, which describes the influence of the specimen height on shear strength, could be systematically investigated and quantified. A statement about the shear strength of concrete should always be related to the specimen size or conducted using a specimen geometry that is not influenced by size effect.
- Low-cycle shear tests can be used for a systematic investigation of the loading and unloading behavior, even if the parameter ω is not suitable for defining the actual damage under compressive shear loading, due to the confinement, which compresses the shear surfaces even after the maximum shear strength is exceeded.
- By means of pre-peak cyclic tests, it could be shown that stiffness degradation is initiated at about 80% of the fatigue life, indicating that the development of the fracture zone starts rather late.
- The presented test setup provides the possibility to apply a controlled fatigue shear loading with simultaneously constant, measurable fatigue compressive loading.
- The results of the fatigue tests indicate that the variation of the upper/lower load in shear fatigue tests has a greater influence on the fatigue life than the variation of the upper/lower load in compression fatigue tests.
- The scattering of the results can be attributed to the confinement, which was not controllable and thus varied in each test.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, F.; Zhou, J. Fatigue Strain and Damage Analysis of Concrete in Reinforced Concrete Beams under Constant Amplitude Fatigue Loading. Shock. Vib. 2016, 2016, 1–7. [Google Scholar] [CrossRef]
- Huang, B.-T.; Li, Q.-H.; Xu, S.-L. Fatigue Deformation Model of Plain and Fiber-Reinforced Concrete Based on Weibull Function. J. Struct. Eng. 2019, 145, 04018234. [Google Scholar] [CrossRef]
- Pfanner, D. Zur Degradation von Stahlbetonbauteilen Unter Ermüdungsbeanspruchung. Ph.D. Thesis, Ruhr-Universität Bochum, Bochum, Germany, 2002. [Google Scholar]
- Pfister, T.; Petryna, Y.S.; Stangenberg, F. Damage Modelling of Reinforced Concrete under Multi-Axial Fatigue Loading; Meschke, G., de Borst, R., Mang, H., Bicanic, N., Eds.; EURO-C: Mayrhofen, Austria; Taylor & Francis: London, UK, 2006; pp. 421–429. [Google Scholar]
- Desmorat, R.; Ragueneau, F.; Pham, H. Continuum damage mechanics for hysteresis and fatigue of quasi-brittle materials and structures. Int. J. Numer. Anal. Methods Géoméch. 2007, 31, 307–329. [Google Scholar] [CrossRef]
- Alliche, A. Damage model for fatigue loading of concrete. Int. J. Fatigue 2004, 26, 915–921. [Google Scholar] [CrossRef]
- Zhaodong, D.; Jie, L. A physically motivated model for fatigue damage of concrete. Int. J. Damage Mech. 2018, 27, 1192–1212. [Google Scholar] [CrossRef]
- Baktheer, A.; Becks, H. Fracture mechanics based interpretation of the load sequence effect in the flexural fatigue behavior of concrete using digital image correlation. Constr. Build. Mater. 2021, 307, 124817. [Google Scholar] [CrossRef]
- Baktheer, A.; Chudoba, R. Experimental and theoretical evidence for the load sequence effect in the compressive fatigue behavior of concrete. Mater. Struct. 2021, 54, 1–23. [Google Scholar] [CrossRef]
- Deutscher, M.; Tran, N.L.; Scheerer, S. Experimental Investigations on the Temperature Increase of Ultra-High Performance Concrete under Fatigue Loading. Appl. Sci. 2019, 9, 4087. [Google Scholar] [CrossRef] [Green Version]
- Tomann, C.; Oneschkow, N. Influence of moisture content in the microstructure on the fatigue deterioration of high-strength concrete. Struct. Concr. 2019, 20, 1204–1211. [Google Scholar] [CrossRef]
- Kirane, K.; Bažant, Z.P. Microplane damage model for fatigue of quasibrittle materials: Sub-critical crack growth, lifetime and residual strength. Int. J. Fatigue 2015, 70, 93–105. [Google Scholar] [CrossRef]
- Baktheer, A.; Aguilar, M.; Chudoba, R. Microplane fatigue model MS1 for plain concrete under compression with damage evolution driven by cumulative inelastic shear strain. Int. J. Plast. 2021, 143, 102950. [Google Scholar] [CrossRef]
- Skarżyński, Ł.; Marzec, I.; Tejchman, J. Fracture evolution in concrete compressive fatigue experiments based on X-ray micro-CT images. Int. J. Fatigue 2019, 122, 256–272. [Google Scholar] [CrossRef]
- Xu, Y.; Yao, W.; Zhao, G.; Xia, K. Evaluation of the short core in compression (SCC) method for measuring mode II fracture toughness of rocks. Eng. Fract. Mech. 2020, 224, 106747. [Google Scholar] [CrossRef]
- Bridgman, P.W. Effects of High Shearing Stress Combined with High Hydrostatic Pressure. Phys. Rev. 1935, 48, 825–847. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics–Fundamentals and Applications, 4th ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Robertson, E.C. Experimental study of the strength of rocks. GSA Bull. 1955, 66, 1275–1314. [Google Scholar] [CrossRef]
- Byerlee, J.D. Frictional characteristics of granite under high confining pressure. J. Geophys. Res. Space Phys. 1967, 72, 3639–3648. [Google Scholar] [CrossRef]
- Jumikis, A.R. Rock Mechanics; Rockport, Trans Tech Publications: Beverly, MA, USA, 1979. [Google Scholar]
- Ingraffea, A.R. Mixed-Mode fracture initiation in Indiana limestone and westerly granite. In Proceedings of the 22nd U.S. Symposium on Rock Mechanics (USRMS), Cambridge, MA, USA, 29 June–2 July 1981. [Google Scholar]
- Luong, M.P. Fracture behaviour of concrete and rock under mode II and mode III shear loading. In International Conference on Recent Developments in the Fracture of Concrete and Rock; Shah, S.P., Swartz, S.E., Barr, B., Eds.; Elsevier Applied Science: Cardiff, Wales; London, UK, 1989; pp. 18–26. [Google Scholar]
- Stephansson, O.; Backers, T.; Rybacki, E. Shear Fracture Mechanics of Rocks and a New Testing Methid for K||c. In ISRM Regional Symposium EUROCK 2001; Särkkä, P., Eloranta, P., Eds.; CRC Press Balkema: Espoo, FL, USA, 2001; pp. 163–168. [Google Scholar]
- Backers, T.; Stephansson, O.; Rybacki, E. Rock fracture toughness testing in Mode II—punch-through shear test. Int. J. Rock Mech. Min. Sci. 2002, 39, 755–769. [Google Scholar] [CrossRef]
- Labuz, J.; Riedel, J.; Dai, S. Shear fracture in sandstone under plane-strain compression. Eng. Fract. Mech. 2006, 73, 820–828. [Google Scholar] [CrossRef]
- Ko, T.Y.; Kemeny, J. Determination of Mode II Stress Intensity Factor Using Short Beam Compression Test, 4th ed.; Leung, C.F., Zhou, Y.X., Eds.; Asian And International Rock Mechanics Symposium: Singapore, 2006. [Google Scholar]
- Lee, J.S. Time-Dependent Crack Growth in Brittle Rocks and Field Applications to Geologic Hazards. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 2007. [Google Scholar]
- Hasanpour, R.; Choupani, N. Rock fracture characterization using the modified Arcan test specimen. Int. J. Rock Mech. Min. Sci. 2009, 46, 346–354. [Google Scholar] [CrossRef]
- Zipkes, S. Die Scher- und Schubfestigkeit des Eisenbetons; Wilhelm Ernst & Sohn: Berlin, Germany, 1906. [Google Scholar]
- Bažant, Z.P.; Pfeiffer, P.A. Shear fracture tests of concrete. Mater. Struct. 1986, 19, 111–121. [Google Scholar] [CrossRef]
- Watkins, J. Fracture toughness test for soll-cement samples in mode II. Int. J. Fract. 1983, 23, R135–R138. [Google Scholar] [CrossRef]
- Jenq, Y.S.; Shah, S.P. Mixed-mode fracture of concrete. Int. J. Fract. 1988, 38, 123–142. [Google Scholar] [CrossRef]
- Keuser, W. Bruchmechanisches Verhalten von Beton unter Mixed-Mode Beanspruchung. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 1989. [Google Scholar]
- Jung, Y.; Park, E.; Kim, H. Determination of mode II toughness of granite by using SCC test. In ISRM International Symposium EUROCK; Ulusay, R., Aydan, Ö., Gerçek, H., Hindistan, M.A., Tuncay, E., Eds.; CRC Press: Cappadocia, Turkey; Boca Raton, FL, USA; London, UK; New York, NY, USA; Leiden, The Netherlands, 2016; pp. 271–276. [Google Scholar]
- Azar, H.F.; Choupani, N.; Afshin, H.; Moghadam, R.H. Effect of mineral admixtures on the mixed-mode (I/II) fracture characterization of cement mortar: CTS, CSTBD and SCB specimens. Eng. Fract. Mech. 2015, 134, 20–34. [Google Scholar] [CrossRef]
- Chang, S.-H.; Lee, C.-I.; Jeon, S. Measurement of rock fracture toughness under modes I and II and mixed-mode conditions by using disc-type specimens. Eng. Geol. 2002, 66, 79–97. [Google Scholar] [CrossRef]
- Classen, M.; Adam, V.; Hillebrand, M. Torsion Test Setup to Investigate Aggregate Interlock and Mixed Mode Fracture of Monolithic and 3D-Printed Concrete. In fib Symposium 2019; Derkowski, W., Gwozdziewicz, P., Hojdys, L., Krajewski, P., Pantak, M., Eds.; International Federation for Structural Concrete (fib): Krakow, Poland, 2019; pp. 521–528. [Google Scholar]
- Montenegro, O.I.; Sfer, D.; Lopez, C.M.; Carol, I. Experimental tests and numerical modeling to indentify the asymptotic shear-compression mode IIa of concrete fracture. In Proceedings of the FraMCoS-8, Toledo, Spain, 10–14 March 2013. [Google Scholar]
- Forquin, P.; Sallier, L. A Testing Technique to Characterise the Shear Behaviour of Concrete at High Strain-Rates. In Dynamic Behavior of Materials; Chalivendra, V., Song, B., Casem, D., Eds.; Springer: New York, NY, USA, 2013; Volume 1, pp. 531–536. [Google Scholar]
- Lin, Q.; Wang, S.; Pan, P.-Z.; Ji, W.-W.; Lu, Y. Fracture initiation under pure shear revisited: Remarks on the mode II fracture in quasi-brittle materials. Theor. Appl. Fract. Mech. 2020, 109, 102700. [Google Scholar] [CrossRef]
- Liu, H.-Z.; Lin, J.-S.; He, J.-D.; Xie, H.-Q. Dominant mode of planar fractures and the role of material properties. Eng. Fract. Mech. 2018, 195, 57–79. [Google Scholar] [CrossRef]
- Luong, M. Fracture testing of concrete and rock materials. Nucl. Eng. Des. 1992, 133, 83–95. [Google Scholar] [CrossRef]
- Luong, M.P. Tensile and shear strengths of concrete and rock. Eng. Fract. Mech. 1990, 35, 127–135. [Google Scholar] [CrossRef]
- Luong, M.P. Measuring Toughness Indices on Brittle Materials; Van Mier, J.G.M., Ed.; RILEM/ESIS International Symposium: Noordwijk, The Netherlands, 1991. [Google Scholar]
- Backers, T. Fracture Toughness Determination and Micromechanics of Rock under Mode I and Mode II Loading. Ph.D. Thesis, Universität Potsdam, Potsdam, Germany, 2004. [Google Scholar]
- Backers, T.; Dresen, G.; Rybacki, E.; Stephansson, O. New data on mode II fracture toughness of rock from the punchthrough shear test. Int. J. Rock Mech. Min. Sci. 2004, 41, 2–7. [Google Scholar] [CrossRef]
- Montenegro, O.I.; Carol, I.; Sfer, D. Characterization of Confined Mixed-Mode Fracture in Concrete; FraMCoS-6: Catania, Italy, 2007; pp. 257–261. [Google Scholar]
- Montenegro, O.I.; Sfer, D.; Carol, I. Characterization of Concrete in Mixed Mode Fracture Under Confined Conditions. In 13th International Conference on Experimental Mechanics; Gdoutos, E.E., Ed.; Springer: Alexandroupolis, Greece; Dordrecht, The Netherlands, 2007; pp. 197–198. [Google Scholar]
- Lukic, B.; Forquin, P. Experimental characterization of the punch through shear strength of an ultra-high performance concrete. Int. J. Impact Eng. 2016, 91, 34–45. [Google Scholar] [CrossRef]
- Coulomb, C.A. Essai sur une Application des Règles de Maximis & Minimis à Quelques Problèmes de Statique, Relatifs à L’architecture in: Mémoires fe Mathematique et de Physique, Présentés à l’Academie des Sciences par Divers Savans (Année 1773); De L’Imprimerie Royale: Paris, France, 1776; pp. 346–384. [Google Scholar]
- Melin, S. When does a crack grow under mode II conditions? Int. J. Fract. 1986, 30, 103–114. [Google Scholar] [CrossRef]
- Becks, H.; Aguilar, M.; Baktheer, A.; Chudoba, R.; Classen, M. Experimental and Numerical Investigations on the Fatigue Behavior of High-Strength Concrete under Combined Shear-Compression Loading; IABSE Symposium: Prague, Czech Republic, 2022. [Google Scholar]
- Forquin, P. Influence of Free Water and Strain-Rate on the Shear Behaviour of Concrete. Appl. Mech. Mater. 2011, 82, 148–153. [Google Scholar] [CrossRef]
- Forquin, P. Influence of strain-rate and confining pressure on the shear strength of concrete. In Dynamic Behavior of Materials; Proulx, T., Ed.; Springer: New York, NY, USA, 2011; Volume 1, pp. 29–35. [Google Scholar]
- Hanson, N.W. Precast-Prestressed Concrete Bridges 2. horizontal Shear Connections. J. PCA Res. Dev. Lab. 1960, 2, 38–58. [Google Scholar]
- Mu, B. Fatigue behavior of concrete subjected to biaxial loading in the compression region. Mater. Struct. 2005, 38, 289–298. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z. Handbook of Damage Mechanics; Springer: New York, NY, USA, 2015. [Google Scholar]
- Paulay, T.; Loeber, P.J. Shear Transfer By Aggregate Interlock. Mater. Sci. 1974, 42, 1–15. [Google Scholar] [CrossRef]
- Model Code 2010. Fib Model Code for Concrete Structures; Ernst & Sohn: Berlin, Germany, 2013. [Google Scholar]
- Aguilar, M.; Baktheer, A.; Chudoba, R. Numerical Investigation of Load Sequence Effect and Energy Dissipation in Concrete Due to Compressive Fatigue loading Using the New Microplane Fatigue Model MS1; Onate, E., Peric, D., Chiumenti, M., de Souza Neto, E., Eds.; COMPLAS: Barcelona, Spain, 2021. [Google Scholar]
- Classen, M. Shear Crack Propagation Theory (SCPT)–The mechanical solution to the riddle of shear in RC members without shear reinforcement. Eng. Struct. 2020, 210, 110207. [Google Scholar] [CrossRef]
- Ungermann, J.; Adam, V.; Classen, M. Fictitious Rough Crack Model (FRCM): A Smeared Crack Modelling Approach to Account for Aggregate Interlock and Mixed Mode Fracture of Plain Concrete. Materials 2020, 13, 2774. [Google Scholar] [CrossRef]

| Loading Scenario | Description | Purpose | Figure |
|---|---|---|---|
| LS1 | Monotonic loading | Studying the monotonic behavior and identifying the shear strength |  |
| LS2 | Cyclic loading | Providing detailed information on unloading and reloading in the post-peak regime | 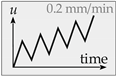 |
| LS3 | Cyclic step-wise increased loading | Providing detailed information on unloading and reloading in the pre-peak regime |  |
| LS4 | Fatigue loading with constant amplitudes | Characterizing the concrete fatigue behavior under constant amplitudes | 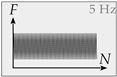 |
| Loading Scenario | LS1 | LS2 | LS3 | LS4.1 | LS4.2 | LS4.3 | LS4.4 |
|---|---|---|---|---|---|---|---|
| Smax | - | - | 0.5 + n ⋅ 0.05 | 0.85 | 0.75 | 0.85 | 0.75 |
| Smin | - | - | 0.05 | 0.05 | 0.05 | 0.20 | 0.20 |
| Repetitions | 8 + 17 | 2 | 2 (1) | 3 (1) | 3 (1) | 3 (1) | 3 (1) |
| Test | Loading Scenario | Smax | Smin | Number of Cycles Nf | Confinement Ratio ςc |
|---|---|---|---|---|---|
| F1 | LS4.1 | 0.85 | 0.05 | 350 | 0.73 |
| F2 | LS4.1 | 0.85 | 0.05 | 135 | 0.66 |
| F3 | LS4.1 | 0.85 | 0.05 | 14 | 1.17 |
| F4 | LS4.2 | 0.75 | 0.05 | 1998 | 2.78 |
| F5 | LS4.2 | 0.75 | 0.05 | 674 | 0.9 |
| F6 | LS4.2 | 0.75 | 0.05 | 201,740 | 0.28 |
| F7 | LS4.3 | 0.85 | 0.20 | 1 | - |
| F8 | LS4.3 | 0.85 | 0.20 | 2232 | 1.09 |
| F9 | LS4.3 | 0.85 | 0.20 | 6811 | 0.96 |
| F10 | LS4.4 | 0.75 | 0.20 | 1,669,000 | - |
| F11 | LS4.4 | 0.75 | 0.20 | 1,469,000 | - |
| F12 | LS4.4 | 0.75 | 0.20 | 1,739,359 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Becks, H.; Classen, M. Mode II Behavior of High-Strength Concrete under Monotonic, Cyclic and Fatigue Loading. Materials 2021, 14, 7675. https://doi.org/10.3390/ma14247675
Becks H, Classen M. Mode II Behavior of High-Strength Concrete under Monotonic, Cyclic and Fatigue Loading. Materials. 2021; 14(24):7675. https://doi.org/10.3390/ma14247675
Chicago/Turabian StyleBecks, Henrik, and Martin Classen. 2021. "Mode II Behavior of High-Strength Concrete under Monotonic, Cyclic and Fatigue Loading" Materials 14, no. 24: 7675. https://doi.org/10.3390/ma14247675
APA StyleBecks, H., & Classen, M. (2021). Mode II Behavior of High-Strength Concrete under Monotonic, Cyclic and Fatigue Loading. Materials, 14(24), 7675. https://doi.org/10.3390/ma14247675







