Enhancement of Gamma-ray Shielding Properties in Cobalt-Doped Heavy Metal Borate Glasses: The Role of Lanthanum Oxide Reinforcement
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fundamental Shielding Parameters
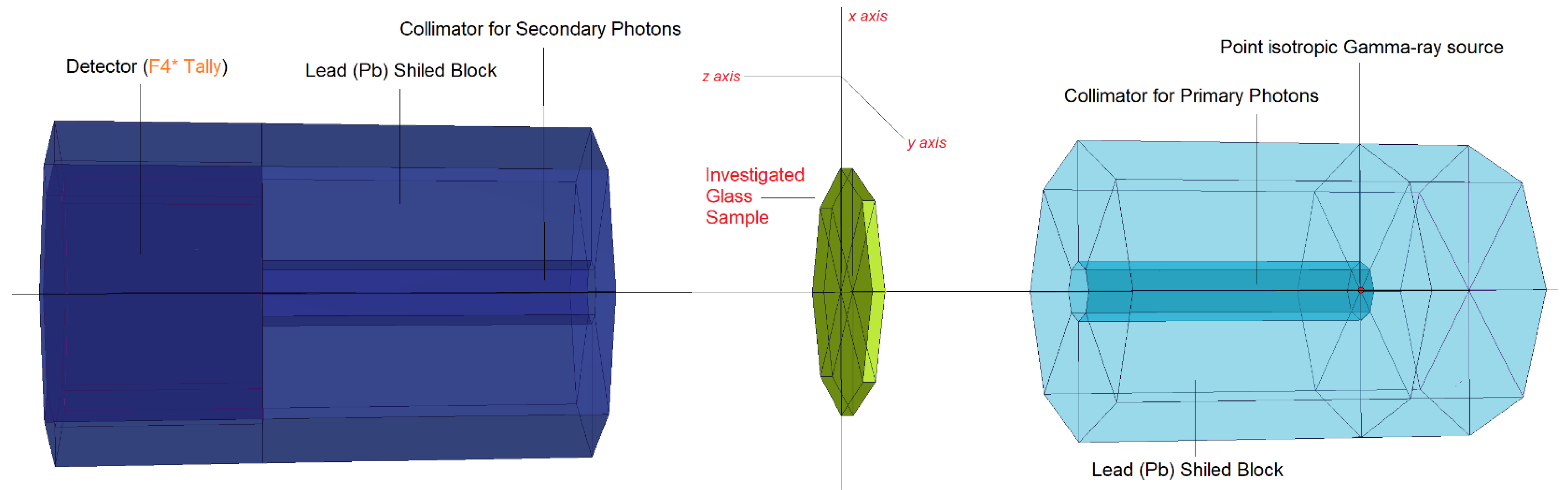
2.2. Monte Carlo Simulations and Theoretical Calculations of Gamma-ray Shielding Properties
- Card for a cell;
- Card for a surface;
- Source data.
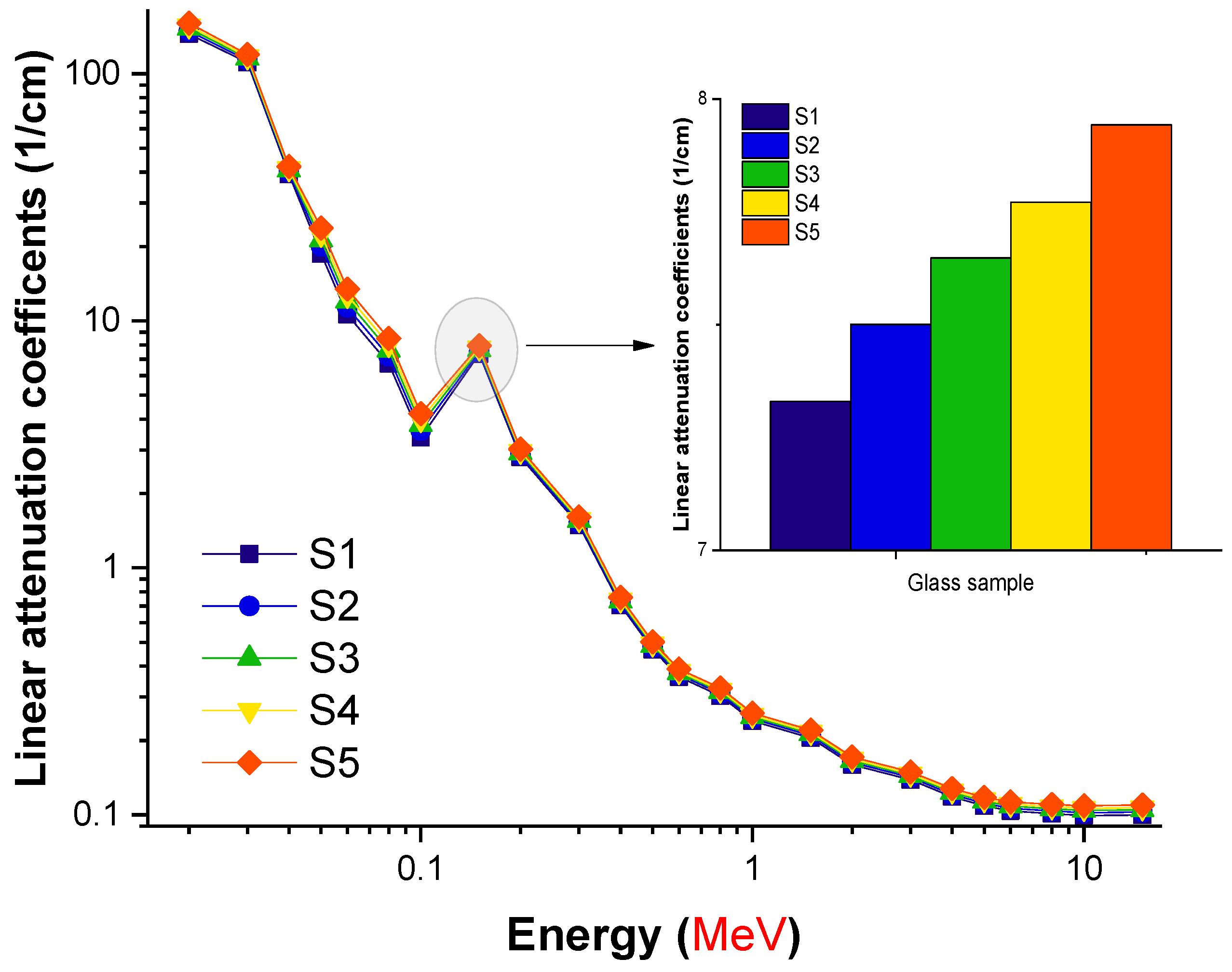
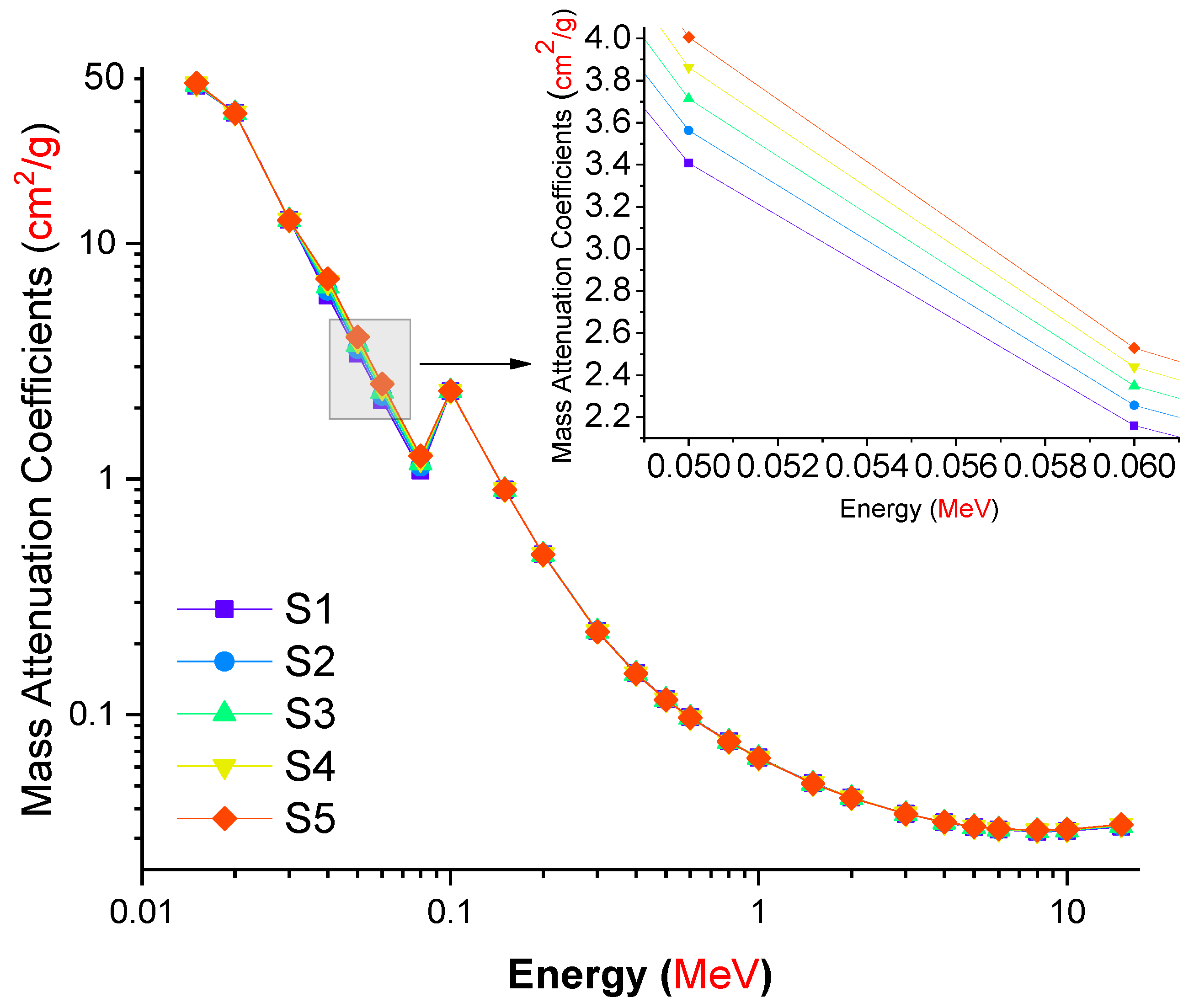
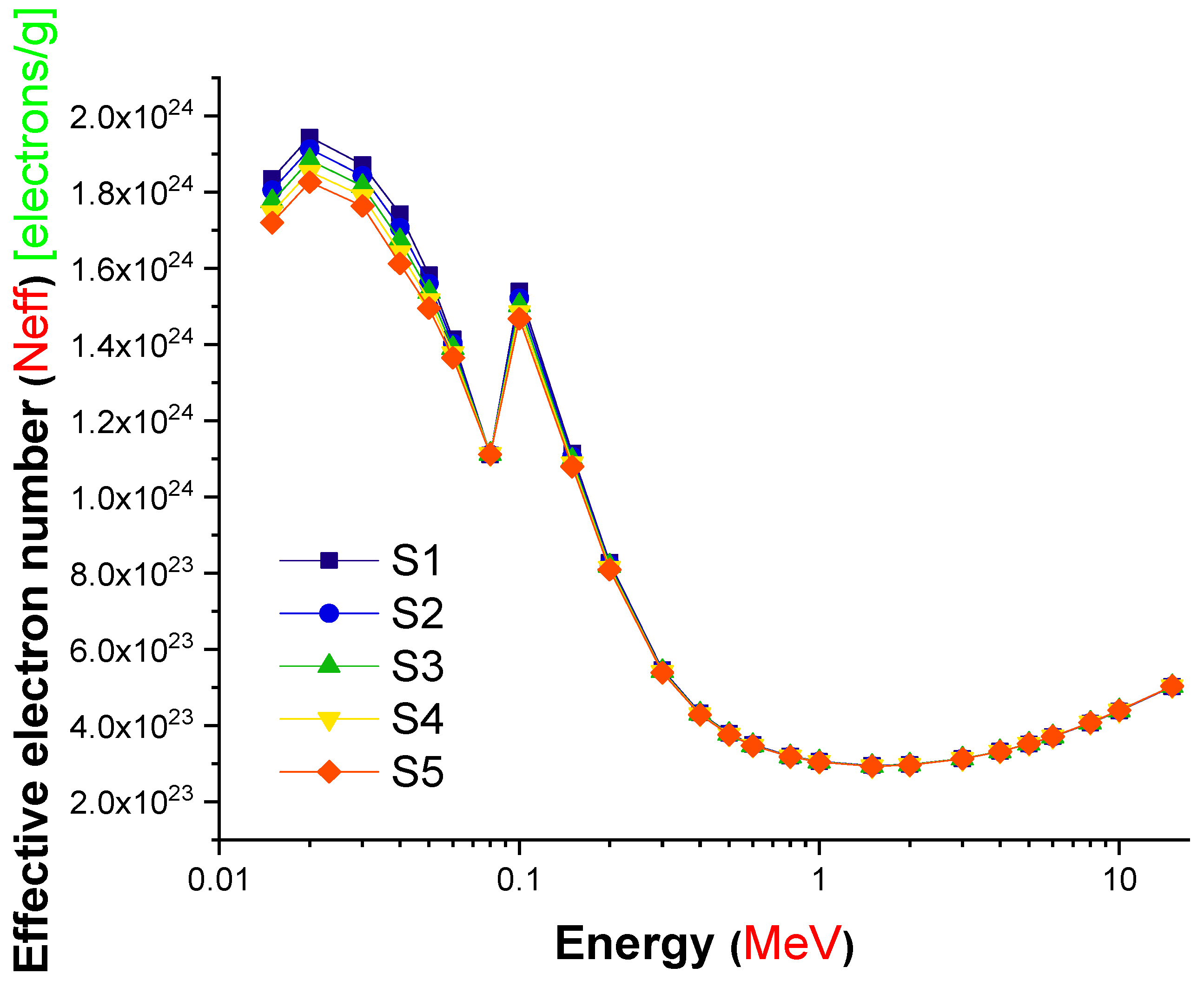
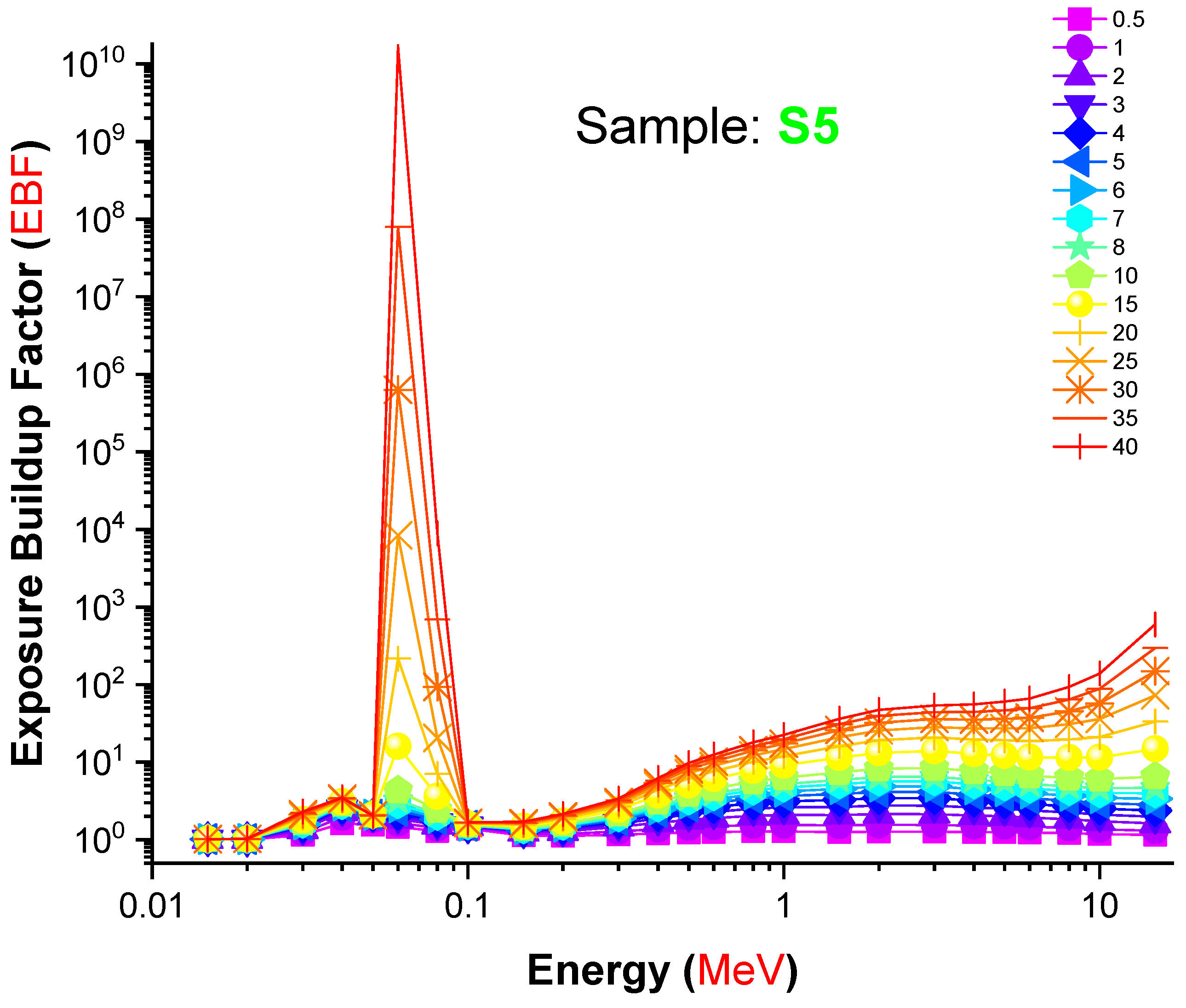
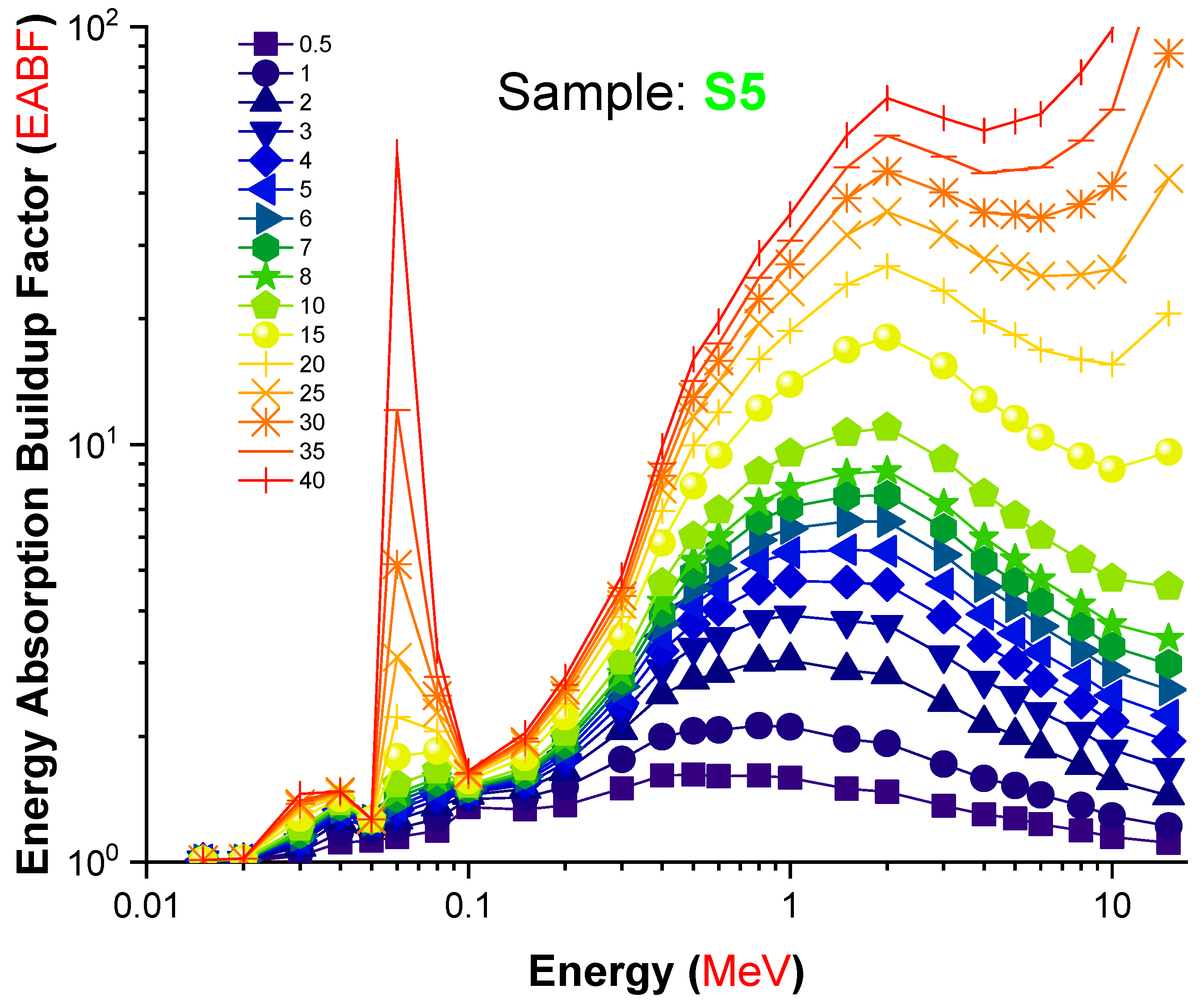
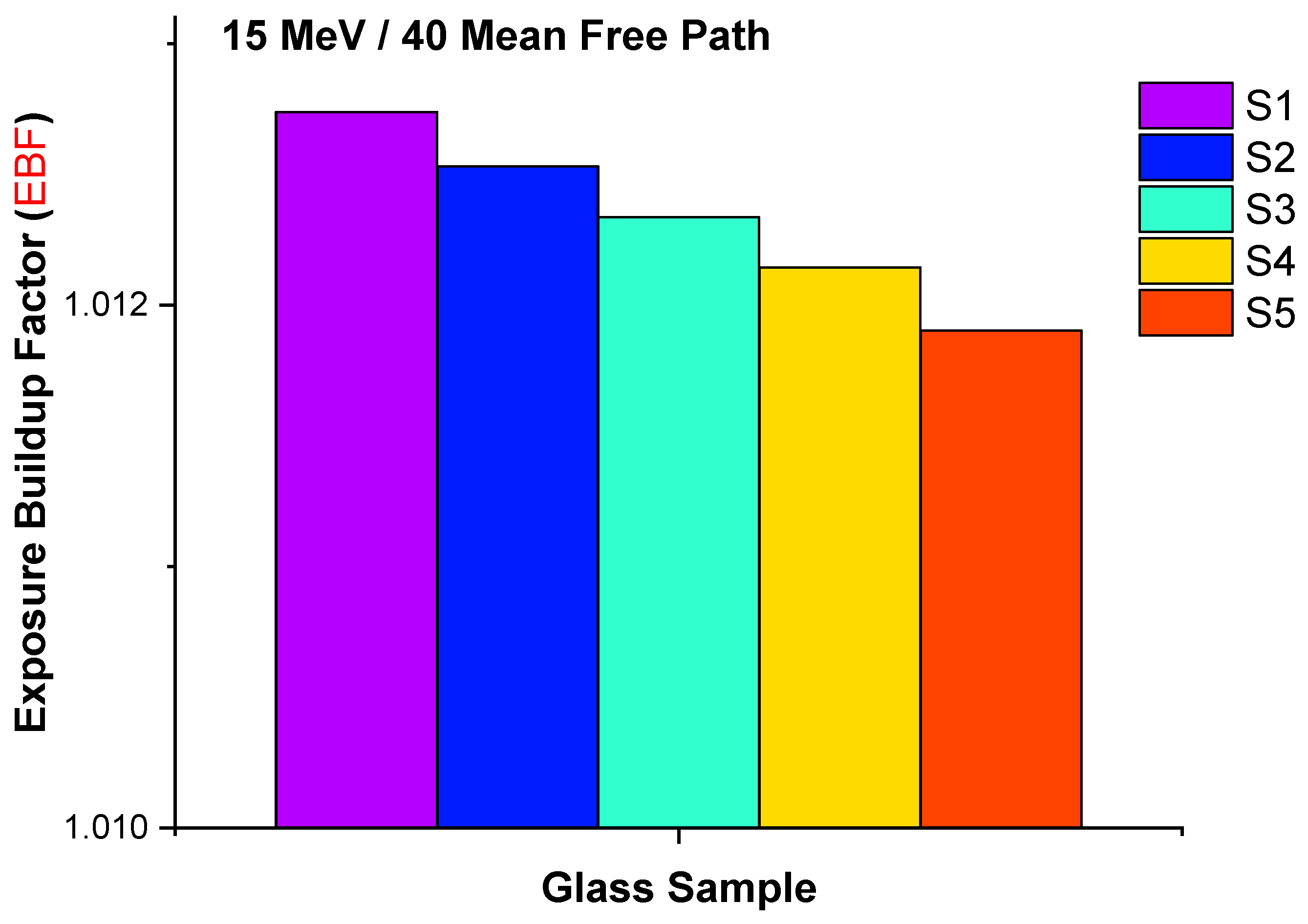
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harrell, C.R.; Djonov, V.; Fellabaum, C.; Volarevic, V. Risks of Using Sterilization by Gamma Radiation: The Other Side of the Coin. Int. J. Med. Sci. 2018, 15, 274. [Google Scholar] [CrossRef] [Green Version]
- Rammah, Y.S.; Kilic, G.; El-Mallawany, R.; Issever, U.G.; El-Agawany, F.I. Investigation of optical, physical, and gamma-ray shielding features of novel vanadyl boro-phosphate glasses. J. Non Cryst. Solids 2020, 533, 119905. [Google Scholar] [CrossRef]
- Rammah, Y.S.; Zakaly, H.M.H.; Issa, S.A.M.; Tekin, H.O.; Hessien, M.M.; Saudi, H.A.; Henaish, A.M.A. Fabrication, physical, structural, and optical investigation of cadmium lead-borate glasses doped with Nd3+ ions: An experimental study. J. Mater. Sci. Mater. Electron. 2021, 1–11. [Google Scholar] [CrossRef]
- Tekin, H.O.; Kassab, L.R.P.; Kilicoglu, O.; Magalhães, E.S.; Issa, S.A.M.; da Silva Mattos, G.R. Newly developed tellurium oxide glasses for nuclear shielding applications: An extended investigation. J. Non Cryst. Solids 2020, 528, 119763. [Google Scholar] [CrossRef]
- Olarinoye, I.O.; Rammah, Y.S.; Alraddadi, S.; Sriwunkum, C.; Abd El-Rehim, A.F.; Zahran, H.Y.; Al-Buriahi, M.S. The effects of La2O3 addition on mechanical and nuclear shielding properties for zinc borate glasses using Monte Carlo simulation. Ceram. Int. 2020, 46, 29191–29198. [Google Scholar] [CrossRef]
- Zakaly, H.M.; Abouhaswa, A.S.; Issa, S.A.M.; Mostafa, M.Y.A.; Pyshkina, M.; El-Mallawany, R. Optical and nuclear radiation shielding properties of zinc borate glasses doped with lanthanum oxide. J. Non Cryst. Solids 2020, 543, 120151. [Google Scholar] [CrossRef]
- Jun, J.H.; Jun, J.-H.; Wang, C.-H.; Won, D.-J.; Choi, D.-J. Structural and Electrical Properties of a La2O3 Thin Film as a Gate Dielectric. Artic. J. Korean Phys. Soc. 2002, 41, 998–1002. [Google Scholar]
- Abouhaswa, A.S.; Zakaly, H.M.H.; Issa, S.A.M.; Pyshkina, M.; El-Mallawany, R.; Mostafa, M.Y.A. Lead borate glasses and synergistic impact of lanthanum oxide additive: Optical and nuclear radiation shielding behaviors. J. Mater. Sci. Mater. Electron. 2020, 31, 14494–14501. [Google Scholar] [CrossRef]
- Gedam, R.S.; Ramteke, D.D. Electrical, dielectric and optical properties of La2O3 doped lithium borate glasses. J. Phys. Chem. Solids 2013, 74, 1039–1044. [Google Scholar] [CrossRef]
- Wong, H.; Yang, B.L.; Kakushima, K.; Ahmet, P.; Iwai, H. Effects of aluminum doping on lanthanum oxide gate dielectric films. Vacuum 2012, 86, 929–932. [Google Scholar] [CrossRef]
- Meza-Rocha, A.N.; Zaleta-Alejandre, E.; Cabañas-Moreno, J.G.; Gallardo-Hernández, S.; Rivera-Álvarez, Z.; Aguilar-Frutis, M.; Falcony, C. Characterization of Lanthanum-Aluminum Oxide Thin Films Deposited by Spray Pyrolysis. ECS J. Solid State Sci. Technol. 2014, 3, N1–N6. [Google Scholar] [CrossRef]
- Rammah, Y.S.; Abouhaswa, A.S.; Sayyed, M.I.; Tekin, H.O.; El-Mallawany, R. Structural, UV and shielding properties of ZBPC glasses. J. Non Cryst. Solids 2019, 509, 99–105. [Google Scholar] [CrossRef]
- Abul-Magd, A.A.; Abu-Khadra, A.S.; Abdel-Ghany, A.M. Influence of La2O3 on the structural, mechanical and optical features of cobalt doped heavy metal borate glasses. Ceram. Int. 2021, 47, 19886–19894. [Google Scholar] [CrossRef]
- Shultis, J.K.; Faw, R.E. Radiation shielding technology. Health Phys. 2005, 88, 297–322. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Medhat, M.E. Application of gamma-ray transmission method for study the properties of cultivated soil. Ann. Nucl. Energy 2012, 40, 53–59. [Google Scholar] [CrossRef]
- Sayyed, M.I.; Tekin, H.O.; Kılıcoglu, O.; Agar, O.; Zaid, M.H.M. Shielding features of concrete types containing sepiolite mineral: Comprehensive study on experimental, XCOM and MCNPX results. Results Phys. 2018, 11, 40–45. [Google Scholar] [CrossRef]
- Ilik, E.; Kilic, G.; Issever, U.G.; Issa, S.A.M.; Zakaly, H.M.H.; Tekin, H.O. Cerium (IV) oxide reinforced Lithium-Borotellurite glasses: A characterization study through physical, optical, structural and radiation shielding properties. Ceram. Int. 2022, 48, 1152–1165. [Google Scholar] [CrossRef]
- Tekin, H.O.; Ebru, E.; Guclu, A.; Manici, T.; Tekin, H.O.; Sayyed, M.I.; Altunsoy, E.E.; Manici, T. Shielding properties and effects of WO3 and PbO on mass attenuation coefficients by using MCNPX code. Artic. Dig. J. Nanomater. Biostructures 2017, 12, 861–867. [Google Scholar]
- Tekin, H.O.; Issa, S.A.M.; Kavaz, E.; Guclu, E.E.A. The direct effect of Er2O3 on bismuth barium telluro borate glasses for nuclear security applications. Mater. Res. Express 2019, 6, 115212. [Google Scholar] [CrossRef]
- Almatari, M.; Agar, O.; Altunsoy, E.E.; Kilicoglu, O.; Sayyed, M.I.; Tekin, H.O. Photon and neutron shielding characteristics of samarium doped lead alumino borate glasses containing barium, lithium and zinc oxides determined at medical diagnostic energies. Results Phys. 2019, 12, 2123–2128. [Google Scholar] [CrossRef]
- Agar, O.; Tekin, H.O.; Sayyed, M.I.; Korkmaz, M.E.; Culfa, O.; Ertugay, C. Experimental investigation of photon attenuation behaviors for concretes including natural perlite mineral. Results Phys. 2019, 12, 237–243. [Google Scholar] [CrossRef]
- El-Agawany, F.I.; Kavaz, E.; Perişanoğlu, U.; Al-Buriahi, M.; Rammah, Y.S. Sm2O3 effects on mass stopping power/projected range and nuclear shielding characteristics of TeO2–ZnO glass systems. Appl. Phys. A Mater. Sci. Process 2019, 125, 1–12. [Google Scholar] [CrossRef]
- Saudi, H.A.; Tekin, H.O.; Zakaly, H.M.H.; Issa, S.A.M.; Susoy, G.; Zhukovsky, M. The impact of samarium (III) oxide on structural, optical and radiation shielding properties of thallium-borate glasses: Experimental and numerical investigation. Opt. Mater. 2021, 114, 110948. [Google Scholar] [CrossRef]
- Akman, F.; Geçibesler, I.H.; Demirkol, I.; Çetin, A. Determination of effective atomic numbers and electron densities for some synthesized triazoles from the measured total mass attenuation coefficients at different energies. Can. J. Phys. 2019, 97, 86–92. [Google Scholar] [CrossRef]
- Obaid, S.S.; Sayyed, M.I.; Gaikwad, D.K.; Pawar, P.P. Attenuation coefficients and exposure buildup factor of some rocks for gamma ray shielding applications. Radiat. Phys. Chem. 2018, 148, 86–94. [Google Scholar] [CrossRef]
- Akman, F.; Kaçal, M.R.; Akman, F.; Soylu, M.S. Determination of effective atomic numbers and electron densities from mass attenuation coefficients for some selected complexes containing lanthanides. Can. J. Phys. 2017, 95, 1005–1011. [Google Scholar] [CrossRef] [Green Version]
- Kassab, L.R.P.; da Silva Mattos, G.R.; Issa, S.A.M.; Bilal, G.; Bordon, C.D.S.; Kilic, G.; Zakaly, H.M.H.; Tekin, H.O. Optical and physical behaviours of newly developed germanium-tellurium (GeTe) glasses: A comprehensive experimental and in-silico study with commercial glasses and ordinary shields. J. Mater. Sci. Mater. Electron. 2021, 32, 22953–22973. [Google Scholar] [CrossRef]
- Ekinci, N.; Kavaz, E.; Özdemir, Y. A study of the energy absorption and exposure buildup factors of some anti-inflammatory drugs. Appl. Radiat. Isot. 2014, 90, 265–273. [Google Scholar] [CrossRef]
- Ylldlz Yorgun, N. Gamma-ray shielding parameters of Li2B4O7 glasses: Undoped and doped with magnetite, siderite and Zinc-Borate minerals cases. Radiochim. Acta 2019, 107, 755–765. [Google Scholar] [CrossRef]
- Yorgun, N.Y.; Kavaz, E. Gamma photon protection properties of some cancer drugs for medical applications. Results Phys. 2019, 13. [Google Scholar] [CrossRef]
- Mostafa, A.M.A.; Issa, S.A.M.; Zakaly, H.M.H.; Zaid, M.H.M.; Tekin, H.O.; Matori, K.A.; Sidek, H.A.A.; Elsaman, R. The influence of heavy elements on the ionizing radiation shielding efficiency and elastic properties of some tellurite glasses: Theoretical investigation. Results Phys. 2020, 19, 103496. [Google Scholar] [CrossRef]
- Sathiyaraj, P.; Samuel, E.J.J.; Valeriano, C.C.S.; Kurudirek, M. Effective atomic number and buildup factor calculations for metal nano particle doped polymer gel. Vacuum 2017, 143, 138–149. [Google Scholar] [CrossRef]
- Sharaf, J.M.; Saleh, H. Gamma-ray energy buildup factor calculations and shielding effects of some Jordanian building structures. Radiat. Phys. Chem. 2015, 110, 87–95. [Google Scholar] [CrossRef]
- Kavaz, E.; Perişanoğlu, U.; Ekinci, N.; Özdemır, Y. Determination of energy absorption and exposure buildup factors by using G-P fitting approximation for radioprotective agents. Int. J. Radiat. Biol. 2016, 92, 380–387. [Google Scholar] [CrossRef]
- RSICC Computer Code Collection, MCNPX User’s Manual Version 2.4.0. MonteCarlo N-Particle Transport Code System for Multiple and High Energy Applications. 2002. Available online: https://www.google.com/search?q=RSICC+Computer+Code+Collection%2C+MCNPX+User%27s+Manual+Version+2.4.0.+MonteCarlo+N-Particle+Transport+Code+System+for+Multiple+and+High+Energy+Applications%2C (accessed on 31 December 2020).
- Uosif, M.A.M.; Mostafa, A.M.A.; Issa, S.A.M.; Tekin, H.O.; Alrowaili, Z.A.; Kilicoglu, O. Structural, mechanical and radiation shielding properties of newly developed tungsten lithium borate glasses: An experimental study. J. Non Cryst. Solids 2020, 532, 119882. [Google Scholar] [CrossRef]
- Issa, S.A.M.; Ahmad, M.; Tekin, H.O.; Saddeek, Y.B.; Sayyed, M.I. Effect of Bi2O3 content on mechanical and nuclear radiation shielding properties of Bi2O3-MoO3-B2O3-SiO2-Na2O-Fe2O3 glass system. Results Phys. 2019, 13, 102165. [Google Scholar] [CrossRef]
- Kavaz, E.; Ekinci, N.; Tekin, H.O.; Sayyed, M.I.; Aygün, B.; Perişanoğlu, U. Estimation of gamma radiation shielding qualification of newly developed glasses by using WinXCOM and MCNPX code. Prog. Nucl. Energy 2019, 115, 12–20. [Google Scholar] [CrossRef]
- Şakar, E.; Özpolat, Ö.F.; Alım, B.; Sayyed, M.I.; Kurudirek, M. Phy-X/PSD: Development of a user friendly online software for calculation of parameters relevant to radiation shielding and dosimetry. Radiat. Phys. Chem. 2020, 166, 108496. [Google Scholar] [CrossRef]
- Aktas, B.; Yalcin, S.; Dogru, K.; Uzunoglu, Z.; Yilmaz, D. Structural and radiation shielding properties of chromium oxide doped borosilicate glass. Radiat. Phys. Chem. 2019, 156, 144–149. [Google Scholar] [CrossRef]
- Yalcin, S.; Aktas, B.; Yilmaz, D. Radiation shielding properties of Cerium oxide and Erbium oxide doped obsidian glass. Radiat. Phys. Chem. 2019, 160, 83–88. [Google Scholar] [CrossRef]
- Mhareb, M.H.A.; Alajerami, Y.S.M.; Sayyed, M.I.; Dwaikat, N.; Alqahtani, M.; Alshahri, F.; Saleh, N.; Alonizan, N.; Ghrib, T.; Al-Dhafar, S.I. Radiation shielding, structural, physical, and optical properties for a series of borosilicate glass. J. Non Cryst. Solids 2020, 550, 120360. [Google Scholar] [CrossRef]
- Almuqrin, A.H.; Kumar, A.; Jecong, J.F.M.; Al-Harbi, N.; Hannachi, E.; Sayyed, M.I. Li2O-K2O-B2O3-PbO glass system: Optical and gamma-ray shielding investigations. Optik 2021, 247, 167792. [Google Scholar] [CrossRef]
- Al-Harbi, F.F.; Prabhu, N.S.; Sayyed, M.I.; Almuqrin, A.H.; Kumar, A.; Kamath, S.D. Evaluation of structural and gamma ray shielding competence of Li2O-K2O-B2O3-HMO (HMO = SrO/TeO2/PbO/Bi2O3) glass system. Optik 2021, 248, 168074. [Google Scholar] [CrossRef]
- Singh, S.; Kaur, R.; Rani, S.; Sidhu, B.S. Physical, structural and nuclear radiation shielding behaviour of xBaO-(0.30-x)MgO-0.10Na2O-0.10Al2O3-0.50B2O3 glass matrix. Mater. Chem. Phys. 2022, 276, 125415. [Google Scholar] [CrossRef]
- Bashter, I.I. Calculation of radiation attenuation coefficients for shielding concretes. Ann. Nucl. Energy 1997, 24, 1389–1401. [Google Scholar] [CrossRef]
- Bashter, I.I.; Makarious, A.S.; Abdo, E.S. Investigation of hematite-serpentine and ilmenite-limonite concretes for reactor radiation shielding. Ann. Nucl. Energy 1996, 23, 65–71. [Google Scholar] [CrossRef]
- ALMisned, G.; Akman, F.; Abushanab, W.S.; Tekin, H.O.; Kaçal, M.R.; Issa, S.A.M.; Polat, H.; Oltulu, M.; Ene, A.; Zakaly, H.M.H. Novel Cu/Zn Reinforced Polymer Composites: Experimental Characterization for Radiation Protection Efficiency (RPE) and Shielding Properties for Alpha, Proton, Neutron, and Gamma Radiations. Polymers 2021, 13, 3157. [Google Scholar] [CrossRef] [PubMed]
- Sayyed, M.I.; Akman, F.; Geçibesler, I.H.; Tekin, H.O. Measurement of mass attenuation coefficients, effective atomic numbers, and electron densities for different parts of medicinal aromatic plants in low-energy region. Nucl. Sci. Tech. 2018, 29, 1–10. [Google Scholar] [CrossRef]
- Akman, F.; Sayyed, M.I.; Kaçal, M.R.; Tekin, H.O. Investigation of photon shielding performances of some selected alloys by experimental data, theoretical and MCNPX code in the energy range of 81 keV–1333 keV. J. Alloys Compd. 2019, 772, 516–524. [Google Scholar] [CrossRef]
- Kaçal, M.R.; Polat, H.; Oltulu, M.; Akman, F.; Agar, O.; Tekin, H.O. Gamma shielding and compressive strength analyses of polyester composites reinforced with zinc: An experiment, theoretical, and simulation based study. Appl. Phys. A Mater. Sci. Process. 2020, 126, 1–15. [Google Scholar] [CrossRef]
- Ilik, E.; Kavaz, E.; Kilic, G.; Issa, S.A.M.; Zakaly, H.M.H.; Tekin, H.O. A closer-look on Copper(II) oxide reinforced Calcium-Borate glasses: Fabrication and multiple experimental assessment on optical, structural, physical, and experimental neutron/gamma shielding properties. Ceram. Int. 2021, in press. [Google Scholar] [CrossRef]
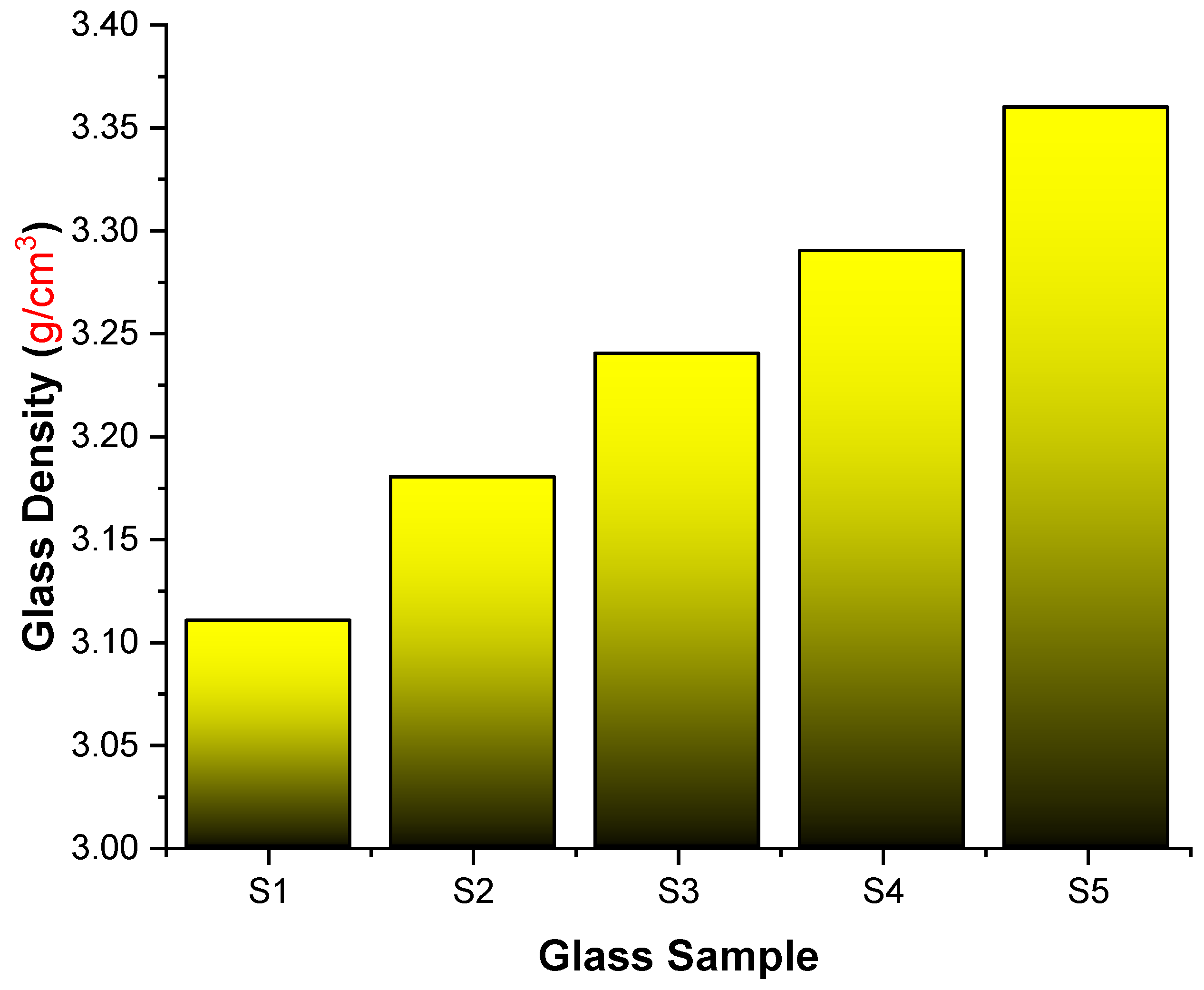
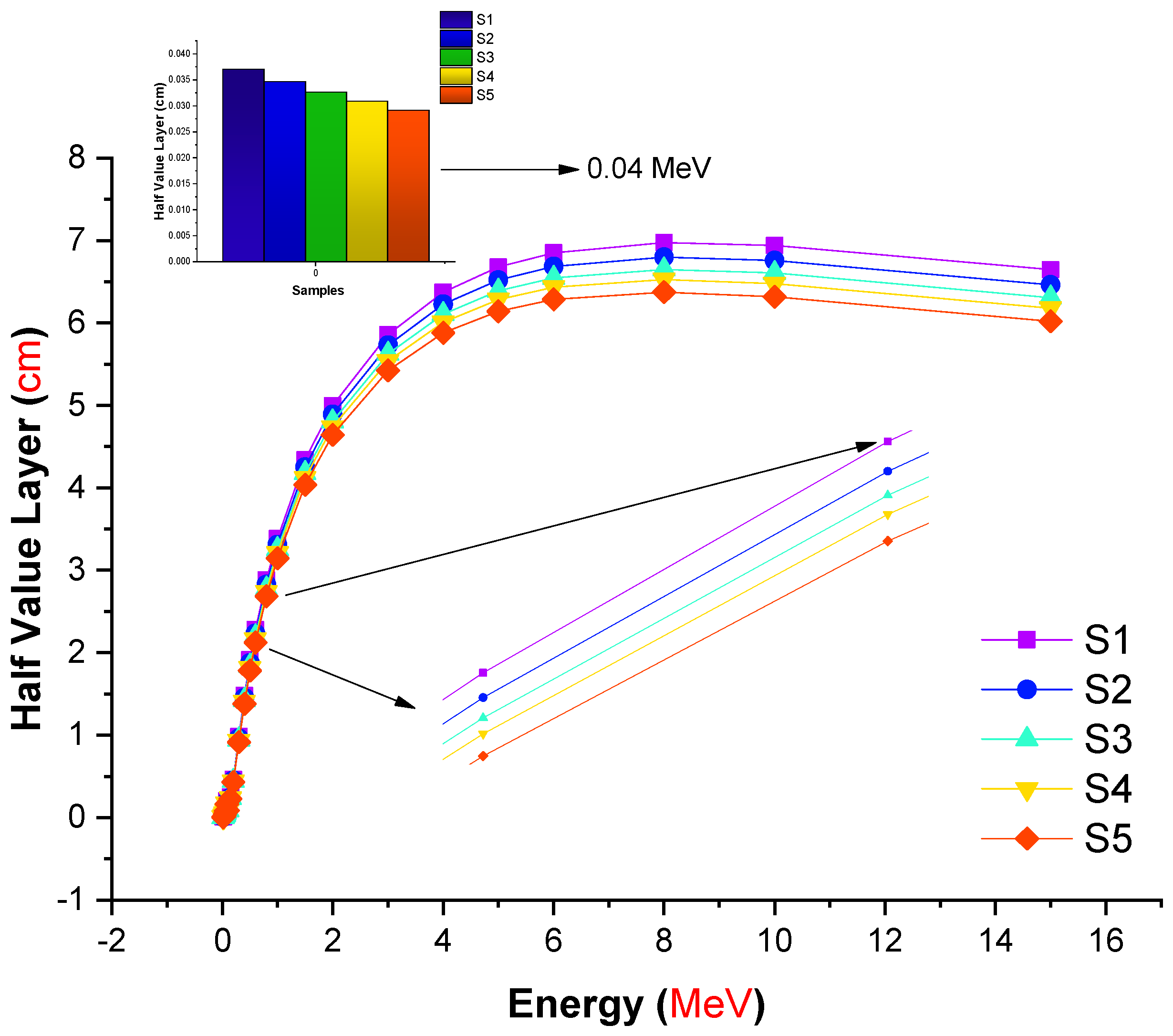
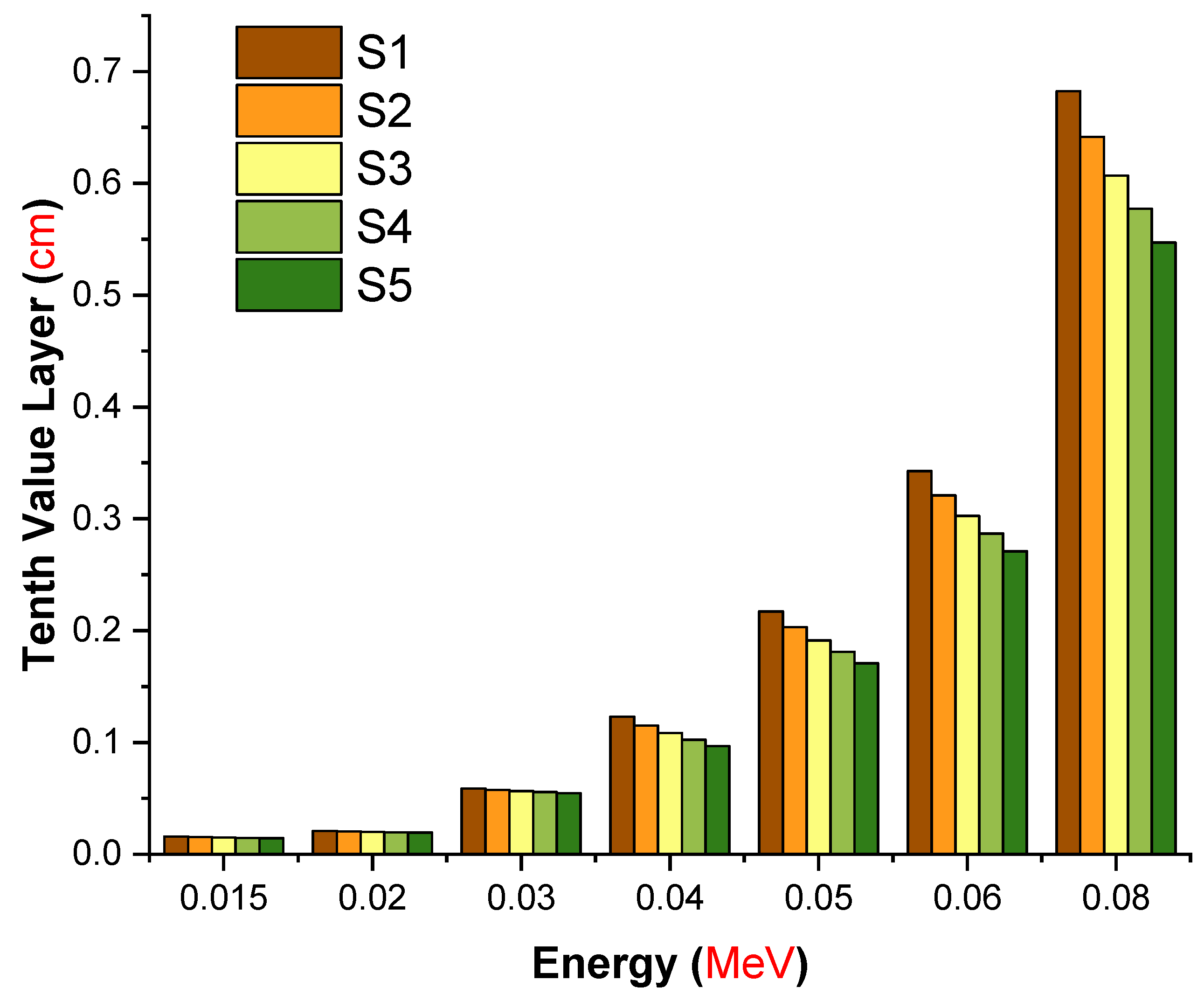
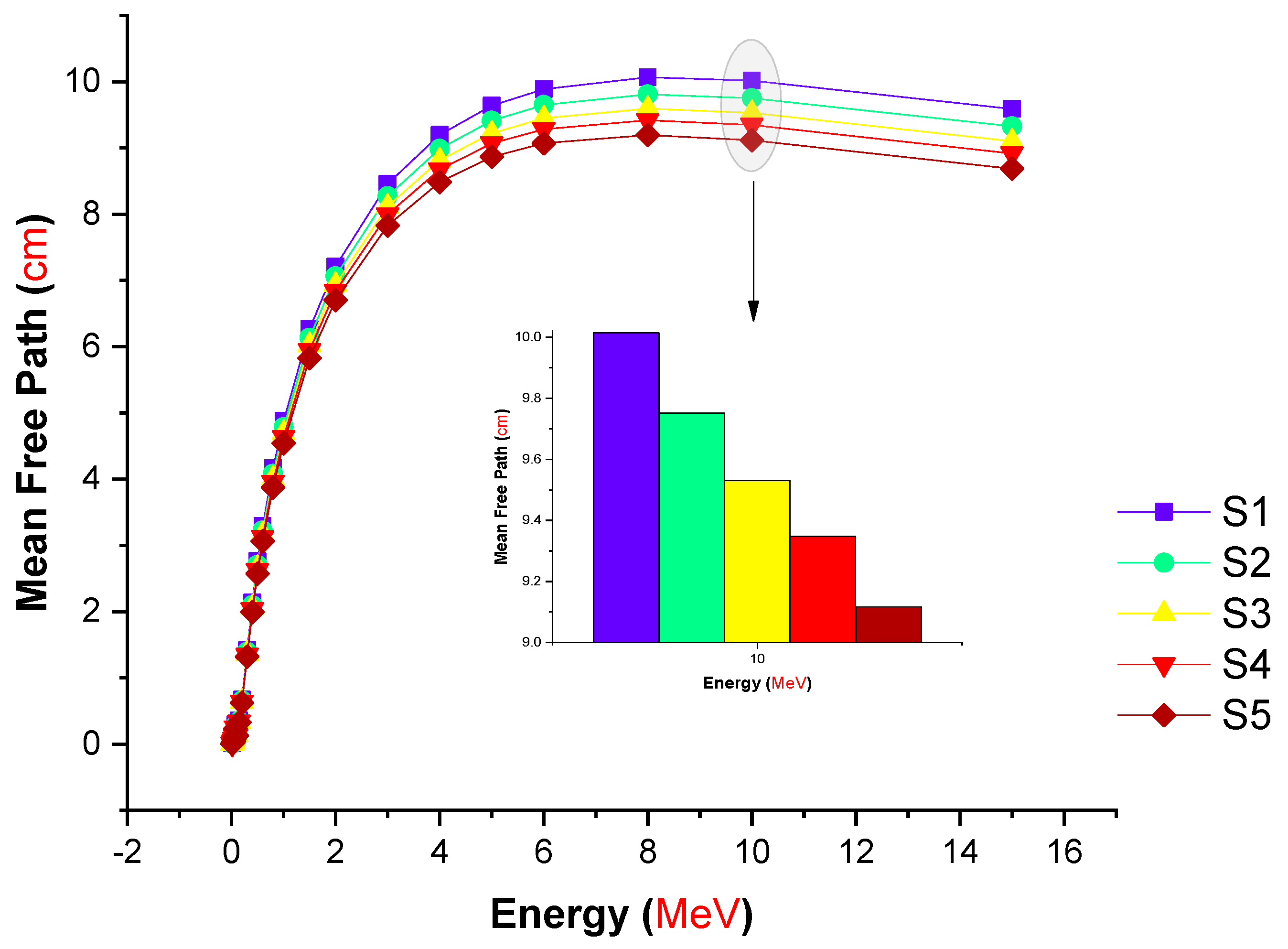
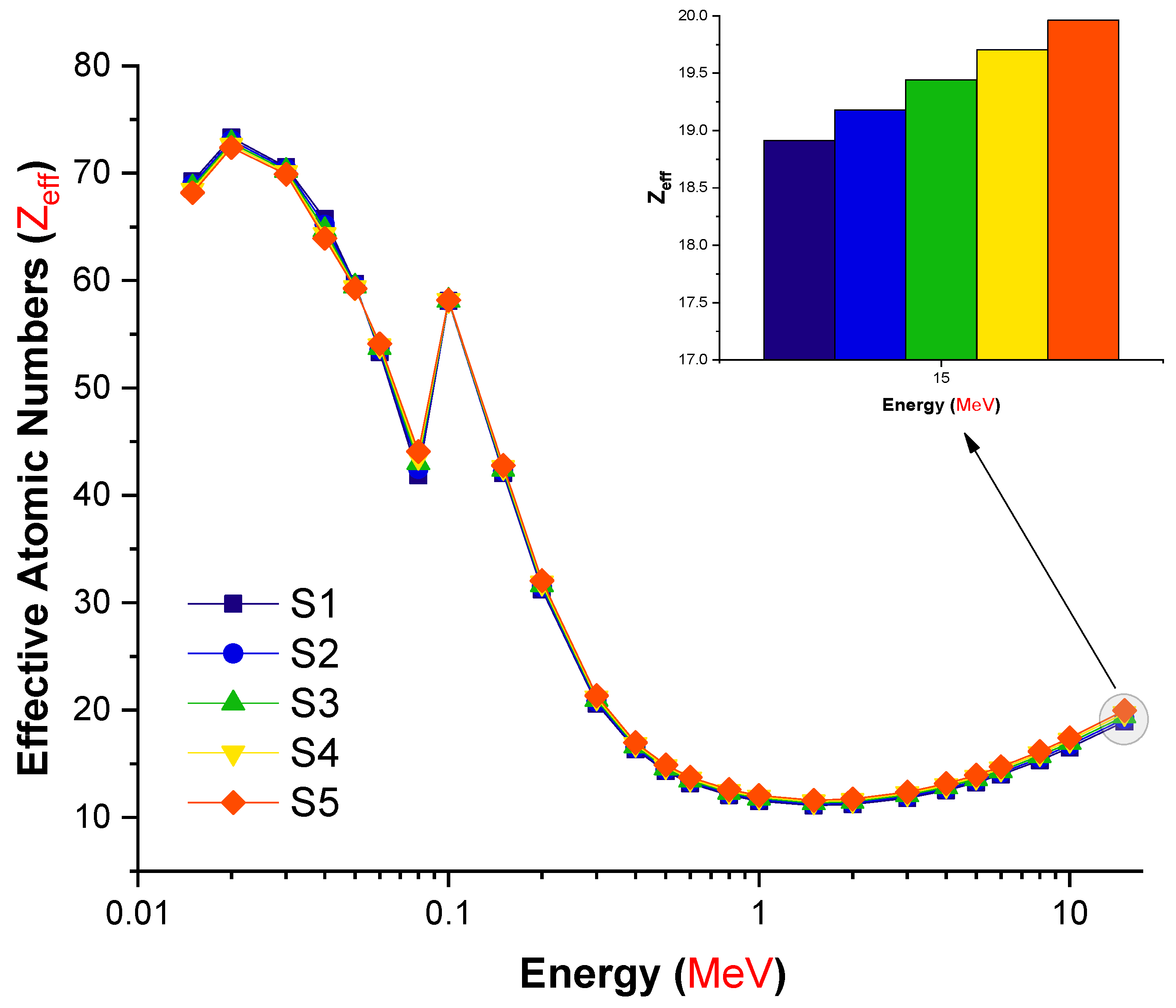
| Element | S1 | S2 | S3 | S4 | S5 | Density (g/cm3) |
|---|---|---|---|---|---|---|
| Co | 0.0018 | 0.0017 | 0.0017 | 0.0017 | 0.0017 | 3.11 |
| O | 0.4164 | 0.4112 | 0.4060 | 0.4010 | 0.3961 | 3.18 |
| B | 0.1732 | 0.1699 | 0.1667 | 0.1636 | 0.1606 | 3.24 |
| Pb | 0.4086 | 0.4035 | 0.3984 | 0.3935 | 0.3887 | 3.29 |
| La | 0.0137 | 0.0271 | 0.0402 | 0.0529 | 3.36 |
| Energy MeV | Cr2O3 Doped BS Glass | Obsidian Glass Doped with CeO2 | BaO-TiO2-SiO2-B2O3 Glass | Li2O-K2O-B2O3-PbO Glass | Li2O-K2O-B2O3-HMO (HMO = SrO/TeO2/PbO/Bi2O3) | xBaO-(0.30-x) MgO-0.10Na2O-0.10Al2O3-0.50B2O3 Glass | OC | HSC | ILC | S5 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.015 | 0.06999 | 0.01193 | 0.02506 | 0.01789 | 0.04208 | 0.01431 | 0.04339 | 0.01311 | 0.00819 | 0.00431 |
| 0.02 | 0.16263 | 0.02700 | 0.05557 | 0.02694 | 0.03728 | 0.03155 | 0.10046 | 0.02950 | 0.01844 | 0.00578 |
| 0.03 | 0.48514 | 0.08548 | 0.16504 | 0.07857 | 0.11118 | 0.09529 | 0.30814 | 0.09301 | 0.05865 | 0.01645 |
| 0.04 | 0.90467 | 0.18801 | 0.09281 | 0.16464 | 0.23530 | 0.03963 | 0.60803 | 0.20492 | 0.13169 | 0.02912 |
| 0.05 | 1.29146 | 0.33098 | 0.16032 | 0.28368 | 0.40383 | 0.07014 | 0.92174 | 0.36290 | 0.23959 | 0.05149 |
| 0.06 | 1.59083 | 0.45375 | 0.24766 | 0.42856 | 0.60044 | 0.11223 | 1.19271 | 0.55220 | 0.37682 | 0.08159 |
| 0.08 | 1.97435 | 0.78133 | 0.46435 | 0.75322 | 1.00373 | 0.23103 | 1.57142 | 0.94984 | 0.69461 | 0.16469 |
| 0.1 | 2.20245 | 1.06830 | 0.70521 | 0.42251 | 1.34681 | 0.39192 | 1.80291 | 1.29198 | 1.00007 | 0.08727 |
| 0.15 | 2.55314 | 1.54137 | 1.23868 | 0.90447 | 1.90600 | 0.88913 | 2.14202 | 1.84225 | 1.54005 | 0.22900 |
| 0.2 | 2.81264 | 1.81964 | 1.61220 | 1.37635 | 2.23682 | 1.36937 | 2.37485 | 2.16102 | 1.85716 | 0.43151 |
| 0.3 | 3.24638 | 2.18700 | 2.08431 | 2.09286 | 2.68077 | 2.07147 | 2.74889 | 2.58396 | 2.25913 | 0.91485 |
| 0.4 | 3.62308 | 2.46855 | 2.41137 | 2.58742 | 3.02579 | 2.53654 | 3.07150 | 2.91330 | 2.55906 | 1.38074 |
| 0.5 | 3.96650 | 2.71454 | 2.67917 | 2.96740 | 3.32676 | 2.89115 | 3.36401 | 3.20123 | 2.81693 | 1.78212 |
| 0.6 | 4.28767 | 2.94004 | 2.91751 | 3.28797 | 3.60324 | 3.18990 | 3.63650 | 3.46617 | 3.05218 | 2.12452 |
| 0.8 | 4.87972 | 3.35196 | 3.34302 | 3.83417 | 4.10858 | 3.70145 | 4.13916 | 3.95012 | 3.48116 | 2.68617 |
| 1 | 5.42603 | 3.73004 | 3.72850 | 4.31099 | 4.57193 | 4.15112 | 4.60294 | 4.39535 | 3.87447 | 3.14895 |
| 1.5 | 6.65908 | 4.57423 | 4.58515 | 5.33685 | 5.61216 | 5.11781 | 5.64834 | 5.38995 | 4.74804 | 4.03937 |
| 2 | 7.72495 | 5.28429 | 5.31191 | 6.17919 | 6.50486 | 5.89570 | 6.54876 | 6.22634 | 5.47198 | 4.64420 |
| 3 | 9.51059 | 6.41277 | 6.50536 | 7.52587 | 7.98139 | 7.08310 | 8.04572 | 7.56504 | 6.59537 | 5.42648 |
| 4 | 10.93855 | 7.25804 | 7.44252 | 8.55353 | 9.14832 | 7.93067 | 9.23181 | 8.57325 | 7.40447 | 5.88173 |
| 5 | 12.10378 | 7.89853 | 8.19022 | 9.35246 | 10.08779 | 8.54238 | 10.19199 | 9.33846 | 7.99386 | 6.14438 |
| 6 | 13.05219 | 8.38415 | 8.78821 | 9.97226 | 10.83892 | 8.98621 | 10.96492 | 9.92337 | 8.42200 | 6.28726 |
| 8 | 14.47857 | 9.03085 | 9.66371 | 10.83906 | 11.95002 | 9.53598 | 12.10822 | 10.71325 | 8.95527 | 6.37191 |
| 10 | 15.45685 | 9.40454 | 10.23140 | 11.36501 | 12.68374 | 9.80251 | 12.87456 | 11.17529 | 9.22487 | 6.31923 |
| 15 | 16.81245 | 9.76914 | 10.95281 | 11.93931 | 13.65135 | 9.93753 | 13.89992 | 11.63975 | 9.40269 | 6.01955 |
| S1 | S2 | S3 | S4 | S5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Energy (MeV) | Phy-X/PSD | MCNPX | Phy-X/PSD | MCNPX | Phy-X/PSD | MCNPX | Phy-X/PSD | MCNPX | Phy-X/PSD | MCNPX |
| 0.015 | 46.550 | 47.795 | 46.884 | 47.985 | 47.210 | 47.324 | 47.528 | 18.128 | 47.838 | 48.120 |
| 0.02 | 35.757 | 36.124 | 35.732 | 36.251 | 35.708 | 35.802 | 35.684 | 36.123 | 35.661 | 35.684 |
| 0.03 | 12.598 | 13.058 | 12.582 | 13.124 | 12.567 | 12.615 | 12.553 | 12.625 | 12.539 | 12.541 |
| 0.04 | 6.014 | 6.125 | 6.291 | 6.325 | 6.562 | 6.594 | 6.826 | 6.914 | 7.084 | 7.106 |
| 0.05 | 3.407 | 3.512 | 3.563 | 3.592 | 3.714 | 3.728 | 3.862 | 3.895 | 4.006 | 4.108 |
| 0.06 | 2.160 | 2.174 | 2.256 | 2.271 | 2.349 | 2.351 | 2.440 | 2.459 | 2.528 | 2.529 |
| 0.08 | 1.085 | 1.108 | 1.129 | 1.156 | 1.171 | 1.180 | 1.212 | 1.135 | 1.253 | 1.256 |
| 0.1 | 2.357 | 2.412 | 2.359 | 2.415 | 2.360 | 2.417 | 2.362 | 2.401 | 2.364 | 2.403 |
| 0.15 | 0.902 | 0.921 | 0.902 | 0.923 | 0.901 | 0.925 | 0.901 | 0.927 | 0.901 | 0.931 |
| 0.2 | 0.480 | 0.497 | 0.479 | 0.499 | 0.479 | 0.501 | 0.478 | 0.503 | 0.478 | 0.509 |
| 0.3 | 0.227 | 0.233 | 0.226 | 0.235 | 0.226 | 0.237 | 0.226 | 0.238 | 0.225 | 0.241 |
| 0.4 | 0.150 | 0.159 | 0.150 | 0.161 | 0.150 | 0.163 | 0.150 | 0.165 | 0.149 | 0.168 |
| 0.5 | 0.116 | 0.124 | 0.116 | 0.126 | 0.116 | 0.127 | 0.116 | 0.129 | 0.116 | 0.131 |
| 0.6 | 0.098 | 0.109 | 0.097 | 0.110 | 0.097 | 0.112 | 0.097 | 0.115 | 0.097 | 0.117 |
| 0.8 | 0.077 | 0.081 | 0.077 | 0.082 | 0.077 | 0.083 | 0.077 | 0.085 | 0.077 | 0.089 |
| 1 | 0.066 | 0.070 | 0.066 | 0.072 | 0.066 | 0.073 | 0.066 | 0.074 | 0.066 | 0.076 |
| 1.5 | 0.051 | 0.054 | 0.051 | 0.056 | 0.051 | 0.058 | 0.051 | 0.060 | 0.051 | 0.062 |
| 2 | 0.045 | 0.047 | 0.045 | 0.047 | 0.044 | 0.049 | 0.044 | 0.051 | 0.044 | 0.053 |
| 3 | 0.038 | 0.040 | 0.038 | 0.041 | 0.038 | 0.042 | 0.038 | 0.043 | 0.038 | 0.045 |
| 4 | 0.035 | 0.038 | 0.035 | 0.039 | 0.035 | 0.041 | 0.035 | 0.042 | 0.035 | 0.043 |
| 5 | 0.033 | 0.035 | 0.033 | 0.035 | 0.033 | 0.035 | 0.034 | 0.035 | 0.034 | 0.036 |
| 6 | 0.033 | 0.034 | 0.033 | 0.034 | 0.033 | 0.035 | 0.033 | 0.036 | 0.033 | 0.037 |
| 8 | 0.032 | 0.034 | 0.032 | 0.035 | 0.032 | 0.036 | 0.032 | 0.037 | 0.032 | 0.037 |
| 10 | 0.032 | 0.031 | 0.032 | 0.032 | 0.032 | 0.033 | 0.033 | 0.033 | 0.033 | 0.035 |
| 15 | 0.034 | 0.036 | 0.034 | 0.036 | 0.034 | 0.037 | 0.034 | 0.038 | 0.034 | 0.039 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
ALMisned, G.; Elshami, W.; Issa, S.A.M.; Susoy, G.; Zakaly, H.M.H.; Algethami, M.; Rammah, Y.S.; Ene, A.; Al-Ghamdi, S.A.; Ibraheem, A.A.; et al. Enhancement of Gamma-ray Shielding Properties in Cobalt-Doped Heavy Metal Borate Glasses: The Role of Lanthanum Oxide Reinforcement. Materials 2021, 14, 7703. https://doi.org/10.3390/ma14247703
ALMisned G, Elshami W, Issa SAM, Susoy G, Zakaly HMH, Algethami M, Rammah YS, Ene A, Al-Ghamdi SA, Ibraheem AA, et al. Enhancement of Gamma-ray Shielding Properties in Cobalt-Doped Heavy Metal Borate Glasses: The Role of Lanthanum Oxide Reinforcement. Materials. 2021; 14(24):7703. https://doi.org/10.3390/ma14247703
Chicago/Turabian StyleALMisned, Ghada, Wiam Elshami, Shams A. M. Issa, Gulfem Susoy, Hesham M. H. Zakaly, Merfat Algethami, Y. S. Rammah, Antoaneta Ene, S. A. Al-Ghamdi, Awad A. Ibraheem, and et al. 2021. "Enhancement of Gamma-ray Shielding Properties in Cobalt-Doped Heavy Metal Borate Glasses: The Role of Lanthanum Oxide Reinforcement" Materials 14, no. 24: 7703. https://doi.org/10.3390/ma14247703
APA StyleALMisned, G., Elshami, W., Issa, S. A. M., Susoy, G., Zakaly, H. M. H., Algethami, M., Rammah, Y. S., Ene, A., Al-Ghamdi, S. A., Ibraheem, A. A., & Tekin, H. O. (2021). Enhancement of Gamma-ray Shielding Properties in Cobalt-Doped Heavy Metal Borate Glasses: The Role of Lanthanum Oxide Reinforcement. Materials, 14(24), 7703. https://doi.org/10.3390/ma14247703











