A Novel Implementation of the LDEM in the Ansys LS-DYNA Finite Element Code
Abstract
:1. Introduction
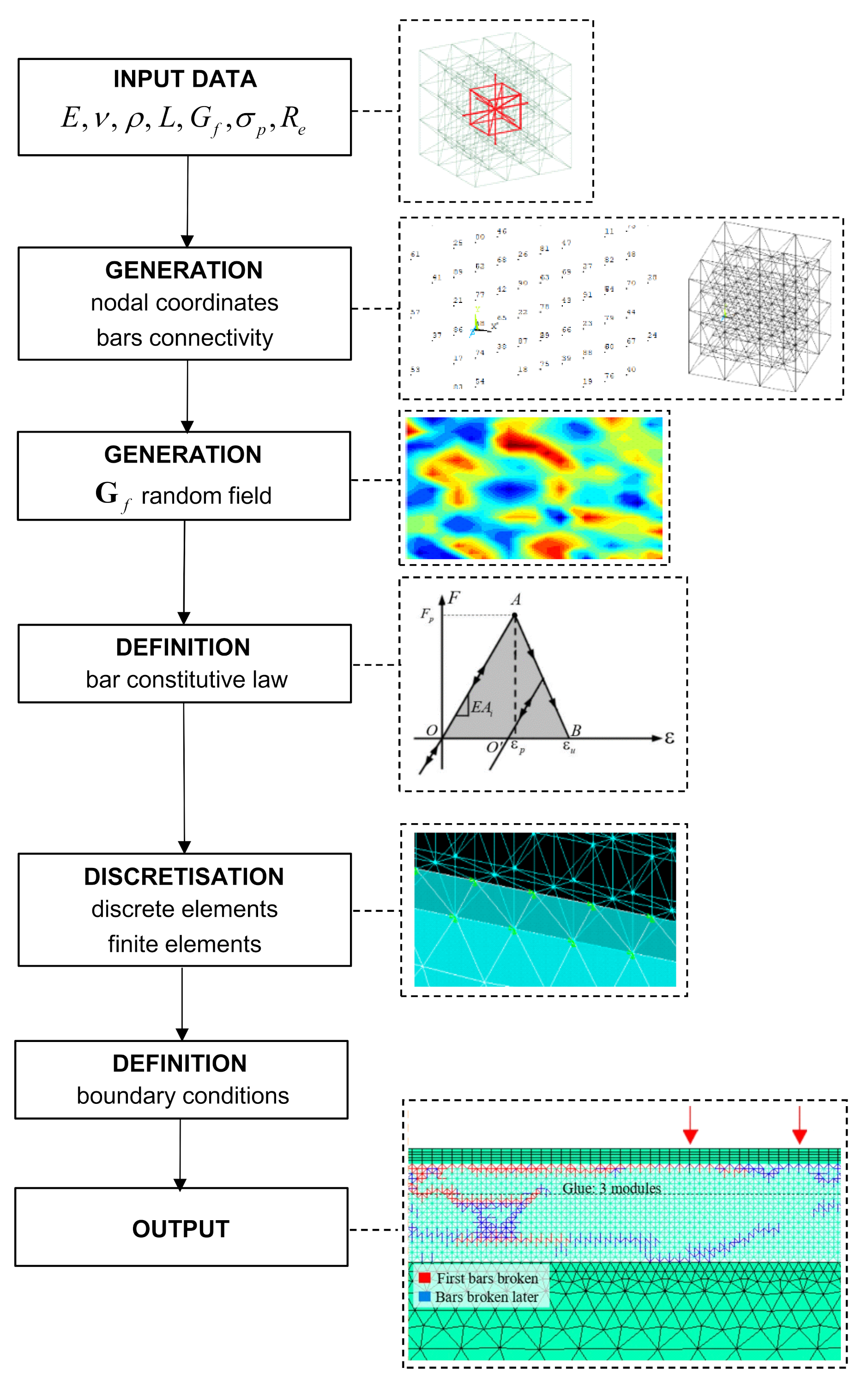
2. Lattice Discrete Element Method Description
3. LDEM Implementation in Ansys LS-DYNA
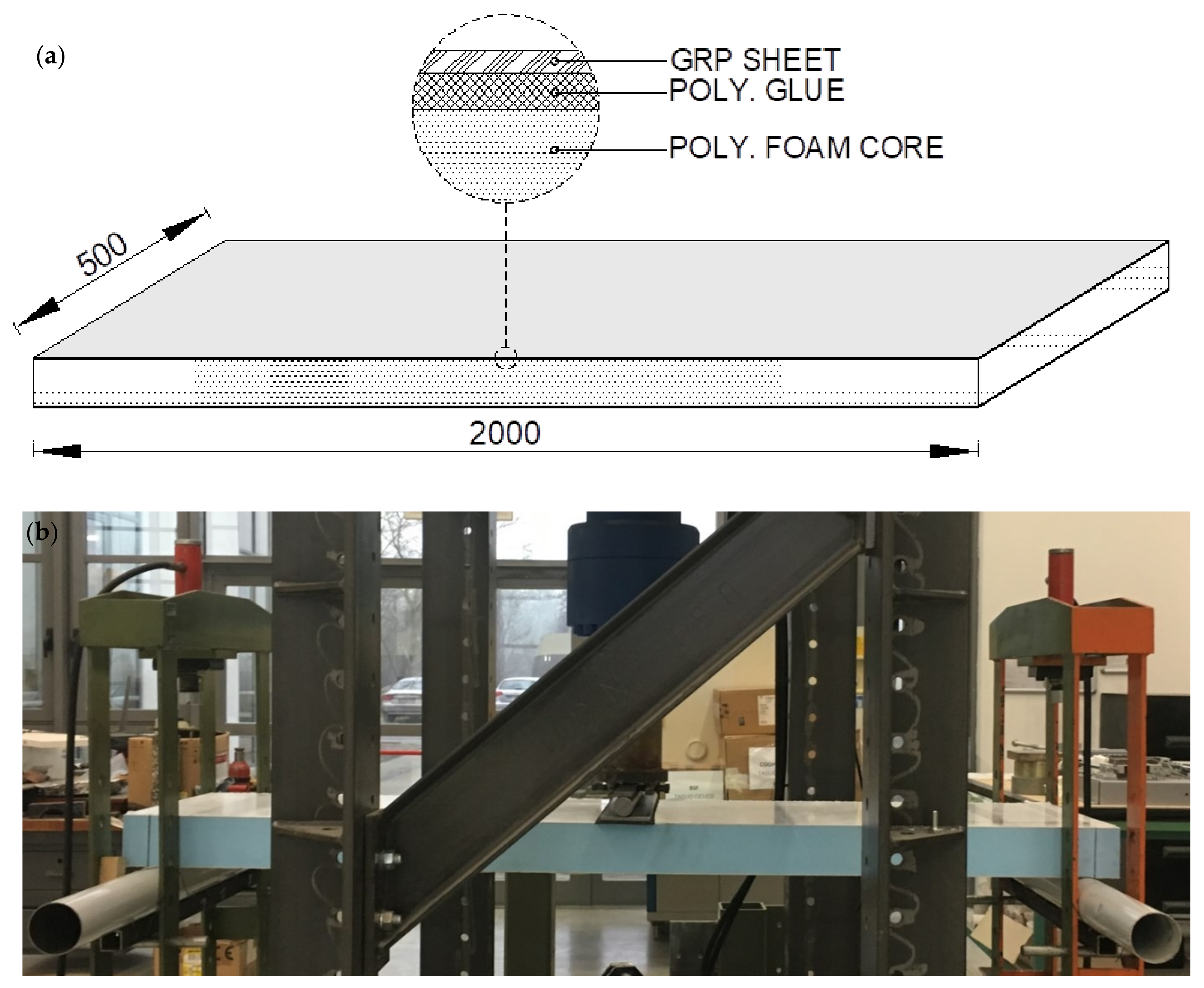
4. Experimental Campaign Examined
4.1. Testing Apparatus
4.2. Specimen Geometry and Material Properties
4.3. Experimental Results
5. Simulations by LDEM-DYNA
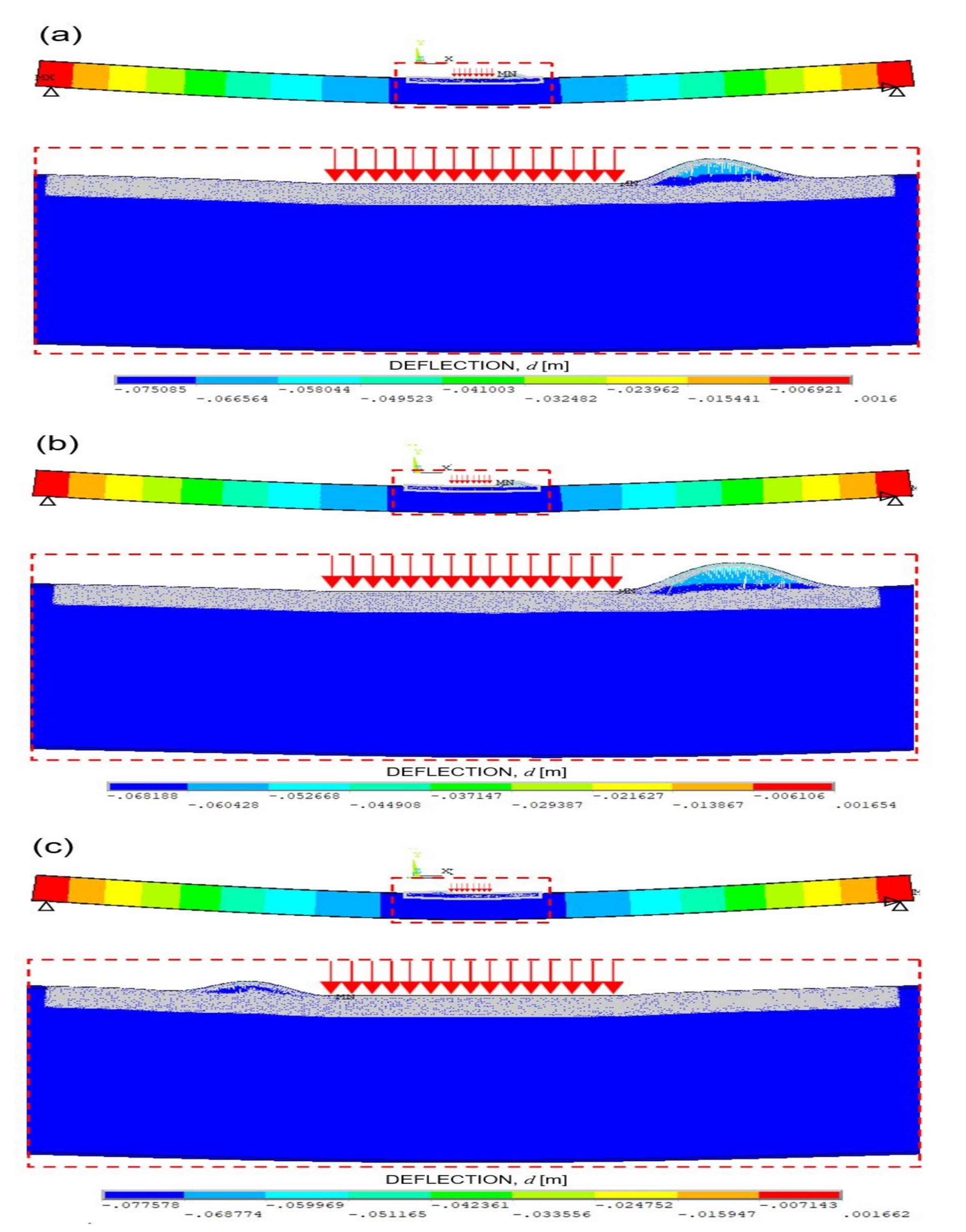
5.1. Three-Point Bending Testing
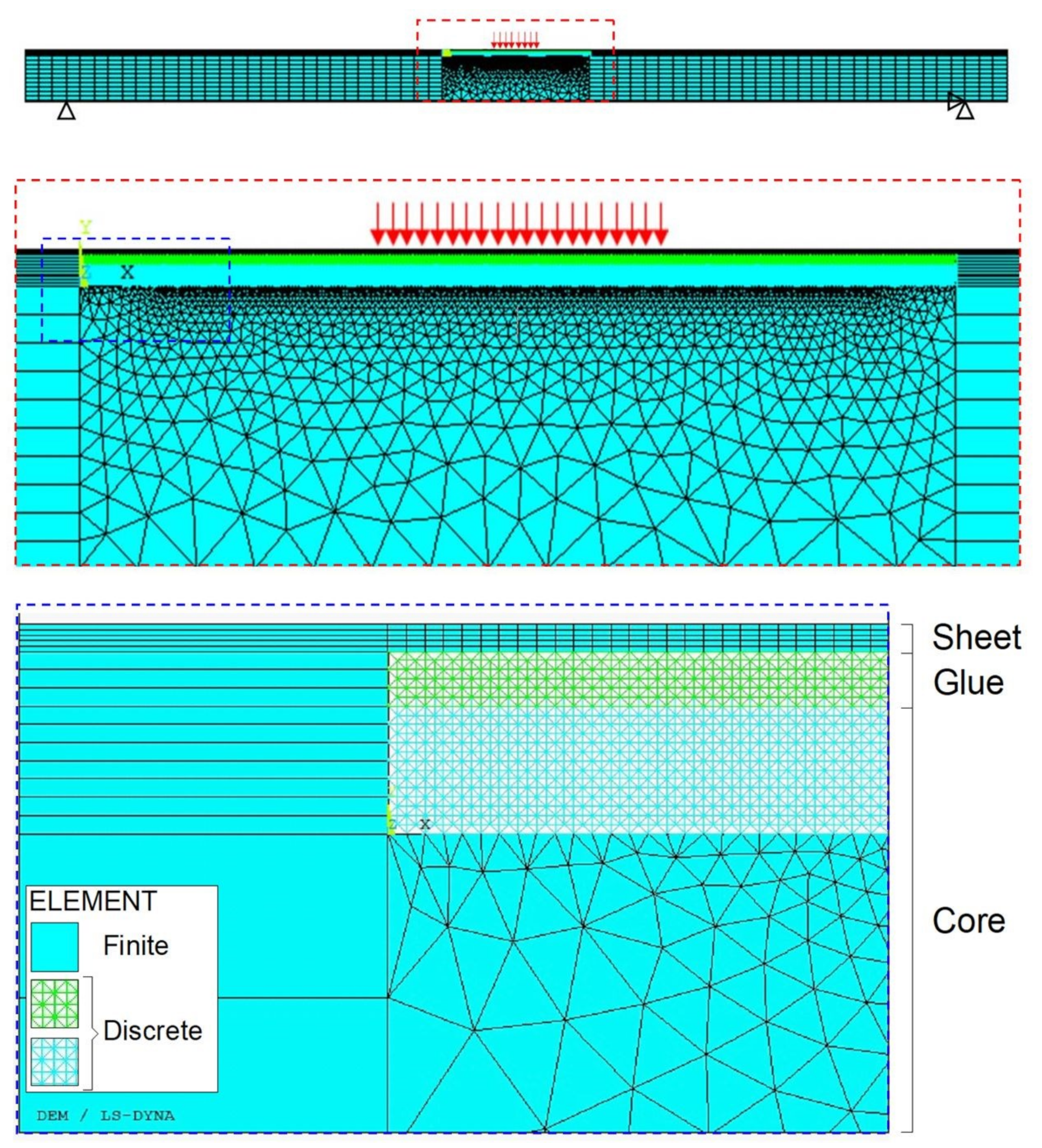
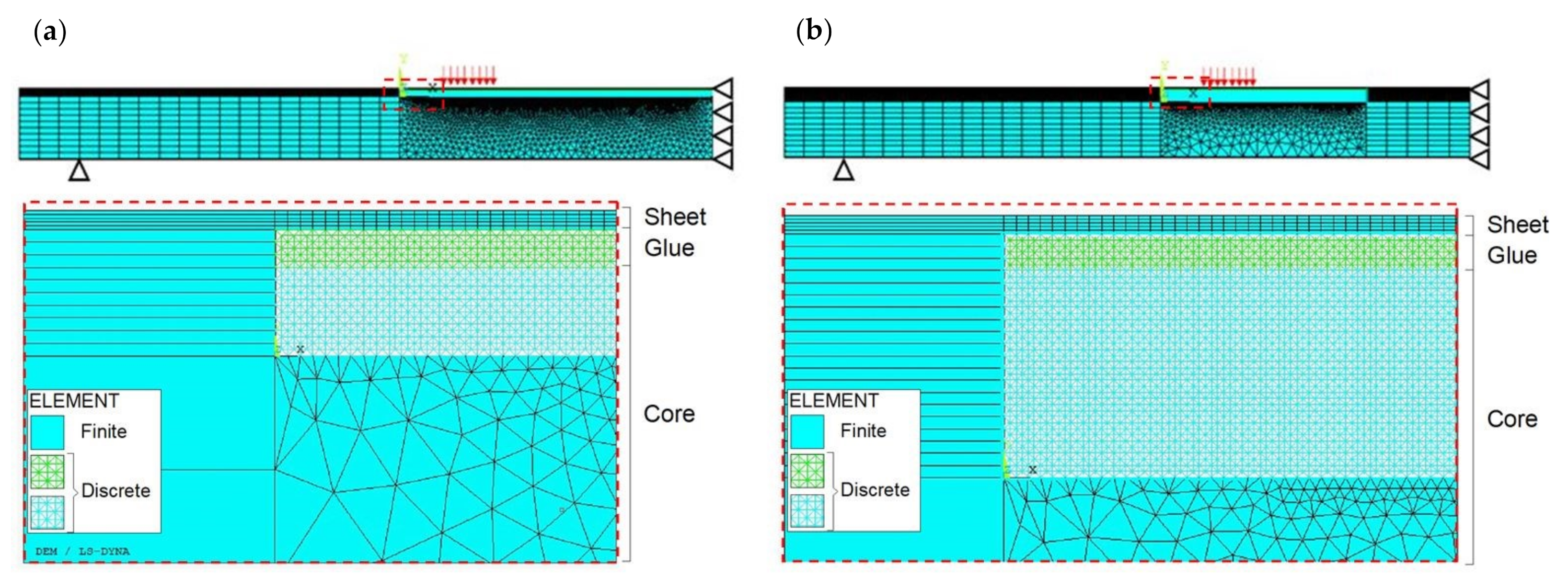
5.1.1. Numerical Model Description
- (a)
- In the central region of the specimen (covering a length equal to 300 mm):
- -
- the sheets (up and down layers) are modelled by means of FEs (SOLID164);
- -
- only the upper layer of the glue is modelled, by means of DEs;
- -
- the core is modelled by means of both DEs and FEs (SOLID164).
Perfect adhesion is assumed between the above layers; - (b)
- Outside the central region of the specimen, only the sheets and the core are modelled:
- -
- the sheets (up and down layers) are modelled by means of FEs (SOLID164);
- -
- the core is modelled by means of FEs (SOLID164).
Perfect adhesion is assumed between the above layers.
5.1.2. Calibration of the Numerical Model
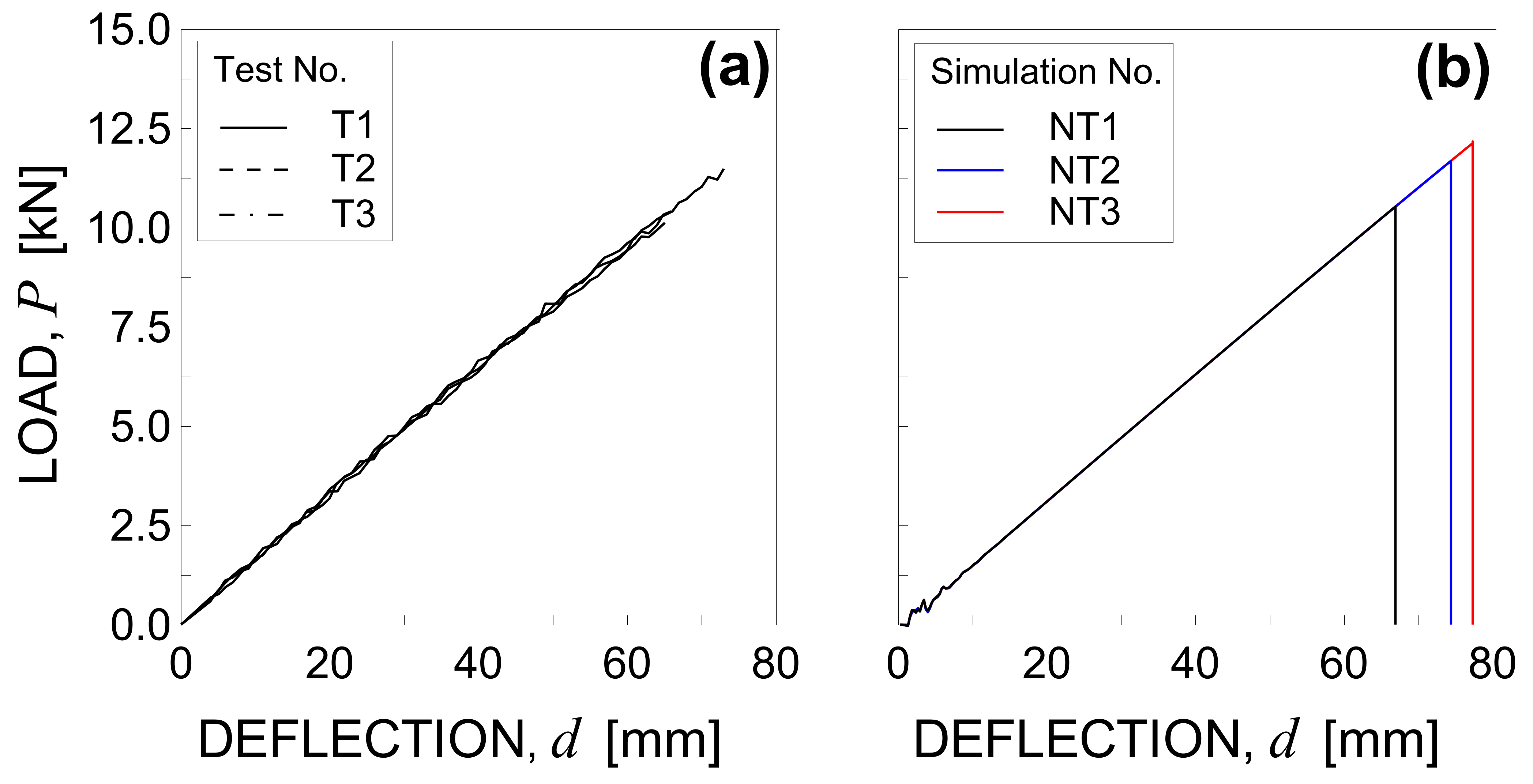
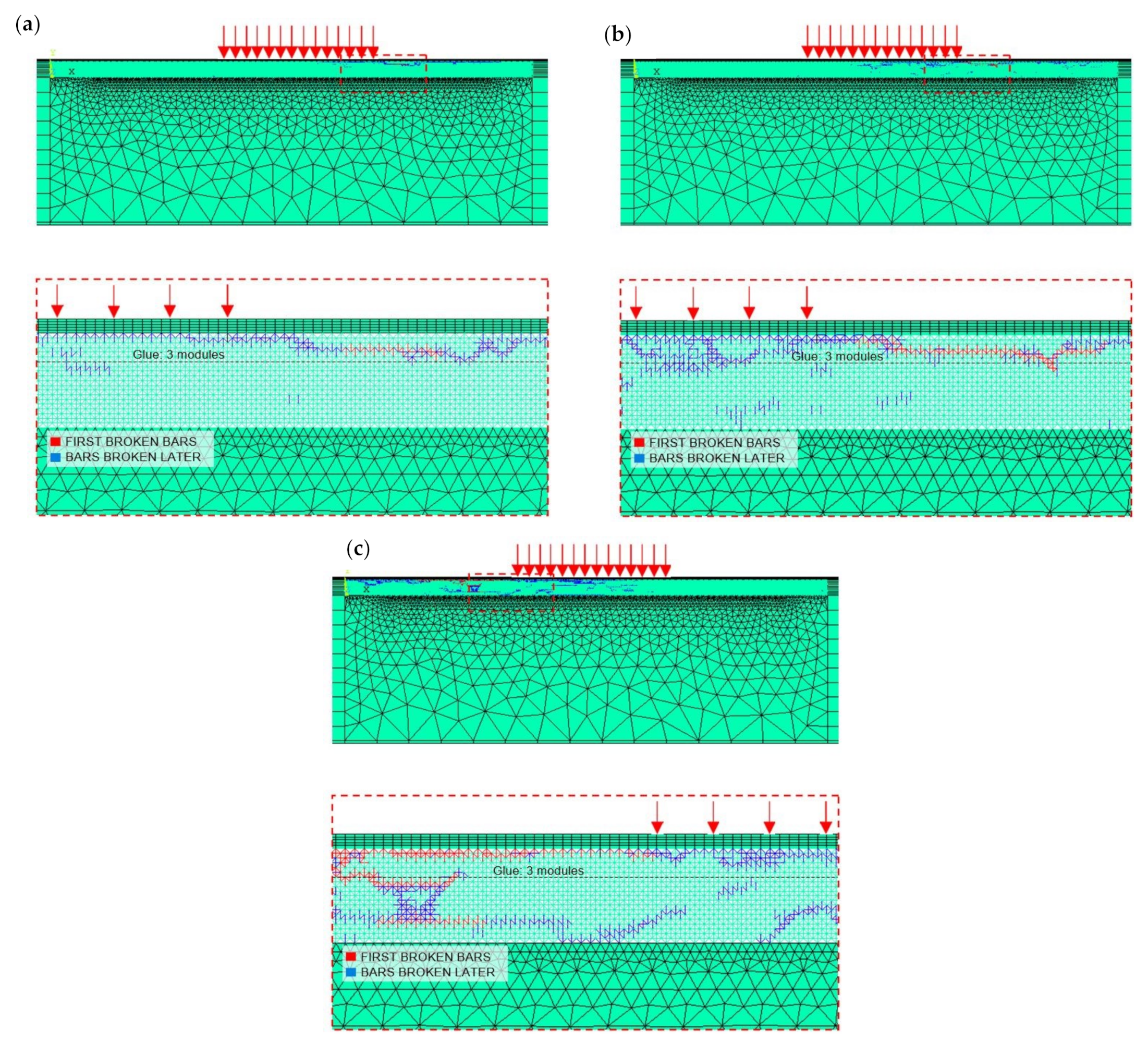
5.1.3. Results and Discussion
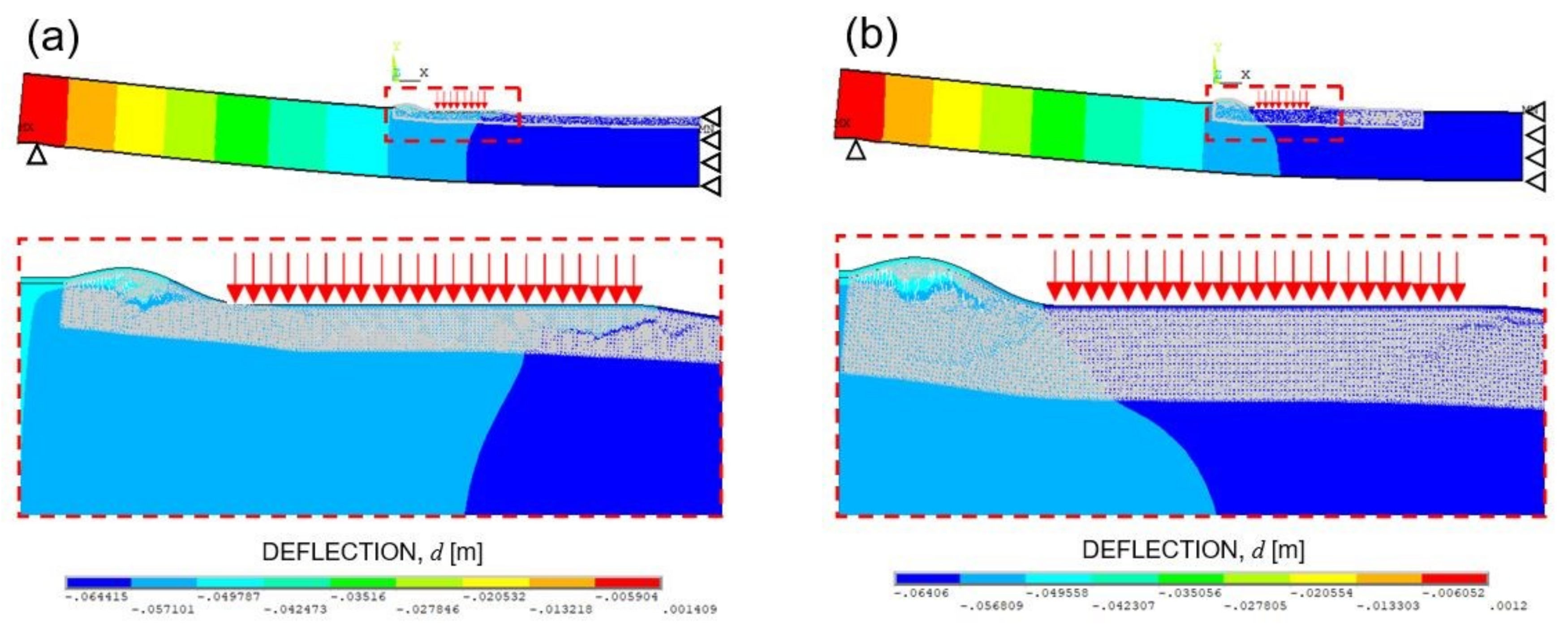
5.2. Four-Point Bending Testing
5.2.1. Numerical Model Description
- (i)
- A region on the right-hand side, covering a length equal to 450 mm, where:
- -
- the sheets (up and down layers) are modelled by means of FEs (SOLID164);
- -
- only the upper layer of the glue is modelled, by means of DEs;
- -
- the core is modelled by means of both DEs and FEs (SOLID164).
- Perfect adhesion is assumed between the above layers.
- (ii)
- A region on the left-hand side (outside the above one), where only the sheets and the core are modelled:
- -
- the sheets (up and down layers) are modelled by means of FEs (SOLID164);
- -
- the core is modelled by means of FEs (SOLID164).
- Perfect adhesion is assumed between the above layers.
- (i)
- In the central region (covering a length equal to 300 mm):
- -
- the sheets (up and down layers) are modelled by means of FEs (SOLID164);
- -
- only the upper layer of the glue is modelled by means of DEs;
- -
- the core is modelled by means of both DEs and FEs (SOLID164).
- Perfect adhesion is assumed between the above layers.
- (ii)
- Outside the central region, only the sheets and the core are modelled:
- -
- the sheets (up and down layers) are modelled by means of FEs (SOLID164);
- -
- the core is modelled by means of FEs (SOLID164).
- Perfect adhesion is assumed between the above layers.
5.2.2. Calibration of the Numerical Model
5.2.3. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| cross-sectional area of diagonal bar elements | |
| cross-sectional area of longitudinal bar elements | |
| equivalent fracture area of the i-th bar element | |
| damping matrix | |
| velocity wave | |
| equivalent length of the material | |
| Young’s modulus | |
| internal nodal forces | |
| fracture energy | |
| fracture energy field | |
| fracture toughness | |
| lengths of diagonal bar elements | |
| length of the i-th bar element | |
| lengths of longitudinal bar elements | |
| mass of the basic cubic modulus | |
| mass matrix | |
| external nodal forces | |
| critical crack length | |
| structure characteristic size | |
| stress brittleness number | |
| nodal velocity | |
| nodal acceleration | |
| maximum time-interval for integration | |
| critical strain | |
| ultimate strain | |
| Poisson ratio | |
| mass density | |
| material strength (tensile strength) |
References
- Chawla, K.K. Composite Materials; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; ISBN 978-3-030-28982-9. [Google Scholar] [CrossRef]
- Rajak, D.K.; Pagar, D.D.; Menezes, P.L.; Linul, E. Fiber-Reinforced Polymer Composites: Manufacturing, Properties, and Applications. Polymers 2019, 11, 1667. [Google Scholar] [CrossRef] [Green Version]
- Vantadori, S.; Carpinteri, A.; Guo, L.-P.; Ronchei, C.; Zanichelli, A. Synergy assessment of hybrid reinforcements in concrete. Compos. Part B Eng. 2018, 147, 197–206. [Google Scholar] [CrossRef]
- Zanichelli, A.; Carpinteri, A.; Fortese, G.; Ronchei, C.; Scorza, D.; Vantadori, S. Contribution of date-palm fibres reinforcement to mortar fracture toughness. Procedia Struct. Integr. 2018, 13, 542–547. [Google Scholar] [CrossRef]
- Gwon, S.; Kim, S.; Ahn, E.; Kim, C.; Shin, M. Strength and toughness of hybrid steel and glass fiber-reinforced sulfur polymer composites. Constr. Build. Mater. 2019, 228, 116812. [Google Scholar] [CrossRef]
- Vantadori, S.; Carpinteri, A.; Zanichelli, A. Lightweight construction materials: Mortar reinforced with date-palm mesh fibres. Theor. Appl. Fract. Mech. 2019, 100, 39–45. [Google Scholar] [CrossRef]
- Dumansky, A.; Alimov, M.; Bolinches, A.S. Analysis of nonlinear time-dependent properties of carbon fiber reinforced plastic under off-axis loading. Mater. Today Proc. 2021, 38, 1631–1635. [Google Scholar] [CrossRef]
- Shafei, B.; Kazemian, M.; Dopko, M.; Najimi, M. State-of-the-art review of capabilities and limitations of polymer and glass fibers used for fiber-reinforced concrete. Materials 2021, 14, 409. [Google Scholar] [CrossRef]
- Vantadori, S.; Carpinteri, A.; Głowacka, K.; Greco, F.; Osiecki, T.; Ronchei, C.; Zanichelli, A. Fracture toughness characterisation of a glass fibre-reinforced plastic composite. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 3–13. [Google Scholar] [CrossRef]
- Skorokhod, V.V. Layered composites: Structural classification, thermophysical and mechanical properties. Powder Metall. Met. Ceram. 2003, 42, 437–446. [Google Scholar] [CrossRef]
- Guan, N.; Hu, C.; Guan, L.; Zhang, W.; Yun, H.; Hu, X. A process optimization and performance study of environmentally friendly waste newspaper/polypropylene film layered composites. Materials 2020, 13, 413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mohammadabadi, M.; Yadama, V.; Dolan, J.D. Evaluation of wood composite sandwich panels as a promising renewable building material. Materials 2021, 14, 2083. [Google Scholar] [CrossRef]
- Wiener, J.; Kaineder, H.; Kolednik, O.; Arbeiter, F. Optimization of mechanical properties and damage tolerance in polymer-mineral multilayer composites. Materials 2021, 14, 725. [Google Scholar] [CrossRef]
- Słonina, M.; Dziurka, D.; Smardzewski, J. Experimental Research and Numerical Analysis of the Elastic Properties of Paper Cell Cores before and after Impregnation. Materials 2020, 13, 2058. [Google Scholar] [CrossRef]
- Njuguna, J. Lightweight Composite Structures in Transport; Woodhead Publishing: Sawston, UK, 2016; ISBN 9781782423256. [Google Scholar]
- Costa, J.P.M.; Legrand, V.; Fréour, S.; Jacquemin, F. Towards the prediction of sandwich composites durability in severe condition of temperature: A new numerical model describing the influence of material water content during a fire scenario. Materials 2020, 13, 5420. [Google Scholar] [CrossRef] [PubMed]
- Garbowski, T.; Gajewski, T. Determination of transverse shear stiffness of sandwich panels with a corrugated core by numerical homogenization. Materials 2021, 14, 1976. [Google Scholar] [CrossRef]
- May-Pat, A.; Avilés, F.; Aguilar, J.O. Mechanical properties of sandwich panels with perforated foam cores. J. Sandw. Struct. Mater. 2011, 13, 427–444. [Google Scholar] [CrossRef]
- Boccaccio, A.; Casavola, C.; Lamberti, L.; Pappalettere, C. Structural Response of Polyethylene Foam-Based Sandwich Panels Subjected to Edgewise Compression. Materials 2013, 6, 4545–4564. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Ren, J.; Du, S.; Wang, X.; Wei, Z.; Zhang, Q.; Zhou, Y.; Yang, Z.; Lu, T.J. Bending Response of 3D-Printed Titanium Alloy Sandwich Panels with Corrugated Channel Cores. Materials 2021, 14, 556. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Torsional and Transversal Stiffness of Orthotropic Sandwich Panels. Materials 2020, 13, 5016. [Google Scholar] [CrossRef]
- Rizov, V.; Shipsha, A.; Zenkert, D. Indentation study of foam core sandwich composite panels. Compos. Struct. 2005, 69, 95–102. [Google Scholar] [CrossRef]
- Ahmad, N.; Ranganath, R.; Ghosal, A. Modeling of the coupled dynamics of damping particles filled in the cells of a honeycomb sandwich plate and experimental validation. J. Vib. Control 2019, 25, 1706–1719. [Google Scholar] [CrossRef]
- Bunyawanichakul, P.; Castanié, B.; Barrau, J.-J. Non-linear finite element analysis of inserts in composite sandwich structures. Compos. Part B Eng. 2008, 39, 1077–1092. [Google Scholar] [CrossRef]
- Styles, M.; Compston, P.; Kalyanasundaram, S. Finite element modelling of core thickness effects in aluminium foam/composite sandwich structures under flexural loading. Compos. Struct. 2008, 86, 227–232. [Google Scholar] [CrossRef]
- Needleman, A. A continuum model for void nucleation by inclusion debonding. J. Appl. Mech. 1987, 54, 525–531. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Zha, X.; Wana, C.; Fan, Y.; Ye, J. Discrete element modeling of metal skinned sandwich composite panel subjected to uniform load. Comput. Mater. Sci. 2013, 69, 73–80. [Google Scholar] [CrossRef]
- Riera, J.D. Local Effects in Impact Problems on Concrete Structures. In Proceedings of the Conference on Structural Analysis and Design of Nuclear Power Plants, Porto Alegre, Brazil, 3–5 October 1984; pp. 57–79. [Google Scholar]
- ANSYS LS-DYNA User’s Guide (v14.0); ANSYS, Inc.: Canonsburg, PA, USA, 2011.
- Rios, J.D.; Riera, J.D. Size effects in the analysis of reinforced concrete structures. Eng. Struct. 2004, 26, 1115–1125. [Google Scholar] [CrossRef]
- Miguel, L.F.; Riera, J.D.; Iturrioz, I. Influence of size on the constitutive equations of concrete or rock dowels. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1857–1881. [Google Scholar] [CrossRef]
- Iturrioz, I.; Miguel, L.F.; Riera, J.D. Dynamic fracture analysis of concrete or rock plates by means of the Discrete Element Method. Lat. Am. J. Solids Struct. 2009, 6, 229–245. [Google Scholar]
- Iturrioz, I.; Lacidogna, G.; Carpinteri, A. Experimental analysis and truss-like discrete element model simulation of concrete specimens under uniaxial compression. Eng. Fract. Mech. 2013, 110, 81–98. [Google Scholar] [CrossRef]
- Kosteski, L.E.; Riera, J.D.; Iturrioz, I.; Singh, R.K.; Kant, T. Analysis of reinforced concrete plates subjected to impact employing the truss-like discrete element method. Fatigue Fract. Eng. Mater. Struct. 2014, 38, 276–289. [Google Scholar] [CrossRef]
- Birck, G.; Iturrioz, I.; Lacidogna, G.; Carpinteri, A. Damage process in heterogeneous materials analyzed by a lattice model simulation. Eng. Fail. Anal. 2016, 70, 157–176. [Google Scholar] [CrossRef]
- Colpo, A.B.; Kosteski, L.E.; Iturrioz, I. The size effect in quasi-brittle materials: Experimental and numerical analysis. Int. J. Damage Mech. 2016, 26, 395–416. [Google Scholar] [CrossRef]
- Birck, G.; Rinaldi, A.; Iturrioz, I. The fracture process in quasi-brittle materials simulated using a lattice dynamical model. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 2709–2724. [Google Scholar] [CrossRef]
- Iturrioz, I.; Birck, G.; Riera, J.D. Numerical DEM simulation of the evolution of damage and AE preceding failure of structural components. Eng. Fract. Mech. 2019, 210, 247–256. [Google Scholar] [CrossRef]
- Vantadori, S.; Carpinteri, A.; Iturrioz, I. Effectiveness of a lattice discrete element model to simulate mechanical wave shielding by using barriers into the ground. Eng. Fail. Anal. 2020, 110, 104360. [Google Scholar] [CrossRef]
- Vu, G.; Iskhakov, T.; Timothy, J.J.; Schulte-Schrepping, C.; Breitenbücher, R.; Meschke, G. Cementitious composites with high compaction potential: Modeling and calibration. Materials 2020, 13, 4989. [Google Scholar] [CrossRef] [PubMed]
- Hillerborg, A. A Model for Fracture Analysis; Division of Building Materials, LTH, Lund University: Lund, Sweden, 1978; ISSN 0348-7911. [Google Scholar]
- Silva, G.S.; Kosteski, L.; Iturrioz, I. Analysis of the failure process by using the Lattice Discrete Element Method in the Abaqus environment. Theor. Appl. Fract. Mech. 2020, 107, 102563. [Google Scholar] [CrossRef]
- Kosteski, L. Application of the Lattice Discrete Elements Method in the Study of Structural Collapse. Ph.D. Thesis, Federal University of Rio Grande do Sul, Porto Alegre, Brazil, 2012. [Google Scholar]
- Dalguer, A.; Irikura, K.; Riera, D.; Chiu, C. The importance of the dynamic source effects on strong ground motion during the 1999 Chi-Chi, Taiwan, earthquake: Brief interpretation of the damage distribution on buildings. Bull. Seismol. Soc. Am. 2001, 91, 1112–1127. [Google Scholar] [CrossRef] [Green Version]
- Kosteski, L.E.; Iturrioz, I.; Batista, R.G.; Cisilino, A.P. The truss-like discrete element method in fracture and damage mechanics. Eng. Comput. 2011, 6, 765–787. [Google Scholar] [CrossRef]
- Bathe, K.J.; Bolourchi, S. Large displacement analysis of three-dimensional beam structures. Int. J. Numer. Methods Eng. 1979, 14, 961–986. [Google Scholar] [CrossRef]
- Bathe, J. Finite Element Procedures; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1996; ISBN 978-0-9790049-5-7. [Google Scholar]
- Jivkov, A.P.; Yates, J.R. Elastic behaviour of a regular lattice for meso-scale modelling of solids. Int. J. Solids Struct. 2012, 49, 3089–3099. [Google Scholar] [CrossRef]
- Riera, J.D.; Rocha, M. A note on velocity of crack propagation in tensile fracture. Rev. Bras. De Ciências Mecânicas 1991, 7, 217–240. [Google Scholar] [CrossRef]
- Kosteski, L.E.; Iturrioz, I.; Lacidogna, G.; Carpinteri, A. Size effect in heterogeneous materials analyzed through a lattice discrete element method approach. Eng. Fract. Mech. 2020, 232, 107041. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics. Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2005; ISBN 9781315370293. [Google Scholar] [CrossRef]
- Soares, F.S. Modelagem de Fenômenos de Fadiga em Materiais Quase Frágeis Heterogêneos Utilizando Uma Versão Do Método de Elementos Discretos Formados Por Barras. Ph.D. Thesis, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil, 2019. [Google Scholar]
- Carpinteri, A. Static and energetic fracture parameters for rocks and concretes. Mater. Struct. 1981, 14, 151–162. [Google Scholar] [CrossRef]
- Shinozuka, M.; Deodatis, G. Simulation of stochastic processes by spectral representation. Appl. Mech. Rev. 1991, 44, 191–204. [Google Scholar] [CrossRef]
- Puglia, V.B.; Kosteski, L.E.; Riera, J.D.; Iturrioz, I. Random field generation of the material properties in the lattice discrete element method. J. Strain Anal. 2019, 54, 236–246. [Google Scholar] [CrossRef]
- Kosteski, L.E.; Iturrioz, I.; Cisilino, A.P.; Barrios D’Ambra, R.; Pettarin, V.; Fasce, L.; Frontini, P. A lattice discrete element method to model the falling-weight impact test of PMMA specimens. Int. J. Impact. Eng. 2016, 87, 120–131. [Google Scholar] [CrossRef]
- ASTM International. ASTM C393/C393M-20; Standard Test Method for Core Shear Properties of Sandwich Constructions by Beam Flexure; ASTM International: West Conshohocken, PA, USA, 2020. [Google Scholar] [CrossRef]
- ASTM International. ASTM D7249/D7249M-20; Standard Test Method for Facesheet Properties of Sandwich Constructions by Long Beam Flexure; ASTM International: West Conshohocken, PA, USA, 2020. [Google Scholar] [CrossRef]
- ASTM International. ASTM D7250/D7250M-20; Standard Practice for Determining Sandwich Beam Flexural and Shear Stiffness; ASTM International: West Conshohocken, PA, USA, 2020. [Google Scholar] [CrossRef]
- Bordin Colpo, A. Aplicação do Método dos Elementos Discretos na Simulação do Processo de Dano em Materiais. Ph.D. Thesis, Escola de Engenharia da Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil, 2021. [Google Scholar]
- Daniel, I.M.; Gdoutos, E.E.; Wang, K.A.; Abot, J.L. Failure Modes of Composite Sandwich Beams. Int. J. Damage Mech. 2002, 11, 309–334. [Google Scholar] [CrossRef]
- Lim, W.W.; Hatano, Y.; Mizumachi, H. Fracture toughness of adhesive joints. I. Relationship between strain energy release rates in three different fracture modes and adhesive strengths. J. Appl. Polym. Sci. 1994, 52, 967–973. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zanichelli, A.; Colpo, A.; Friedrich, L.; Iturrioz, I.; Carpinteri, A.; Vantadori, S. A Novel Implementation of the LDEM in the Ansys LS-DYNA Finite Element Code. Materials 2021, 14, 7792. https://doi.org/10.3390/ma14247792
Zanichelli A, Colpo A, Friedrich L, Iturrioz I, Carpinteri A, Vantadori S. A Novel Implementation of the LDEM in the Ansys LS-DYNA Finite Element Code. Materials. 2021; 14(24):7792. https://doi.org/10.3390/ma14247792
Chicago/Turabian StyleZanichelli, Andrea, Angélica Colpo, Leandro Friedrich, Ignacio Iturrioz, Andrea Carpinteri, and Sabrina Vantadori. 2021. "A Novel Implementation of the LDEM in the Ansys LS-DYNA Finite Element Code" Materials 14, no. 24: 7792. https://doi.org/10.3390/ma14247792
APA StyleZanichelli, A., Colpo, A., Friedrich, L., Iturrioz, I., Carpinteri, A., & Vantadori, S. (2021). A Novel Implementation of the LDEM in the Ansys LS-DYNA Finite Element Code. Materials, 14(24), 7792. https://doi.org/10.3390/ma14247792







