Non-Symmetrical Direct Extrusion—Analytical Modelling, Numerical Simulation and Experiment
Abstract
:1. Introduction
2. Theoretical Analysis
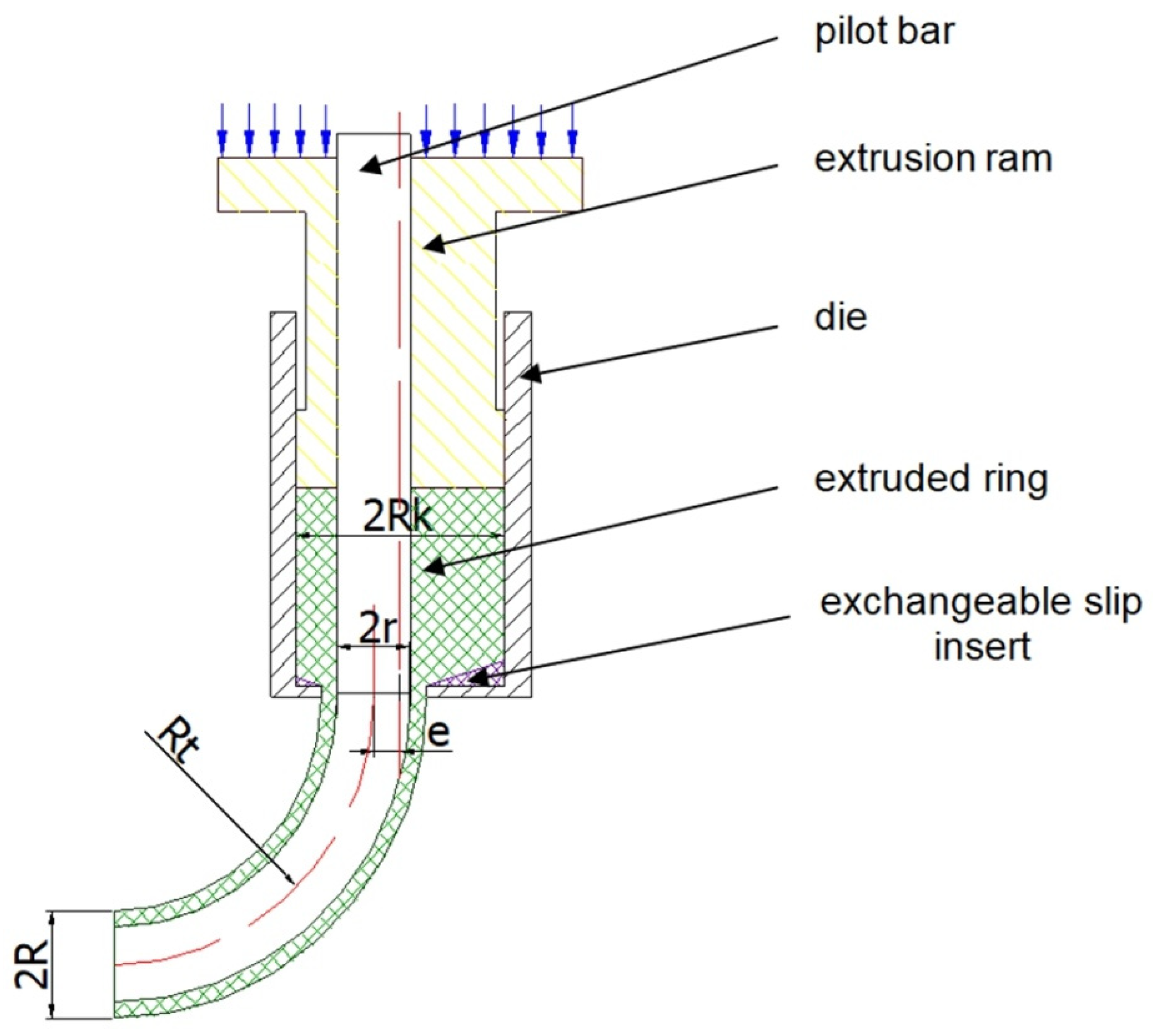
2.1. Eccentric Direct Extrusion Process
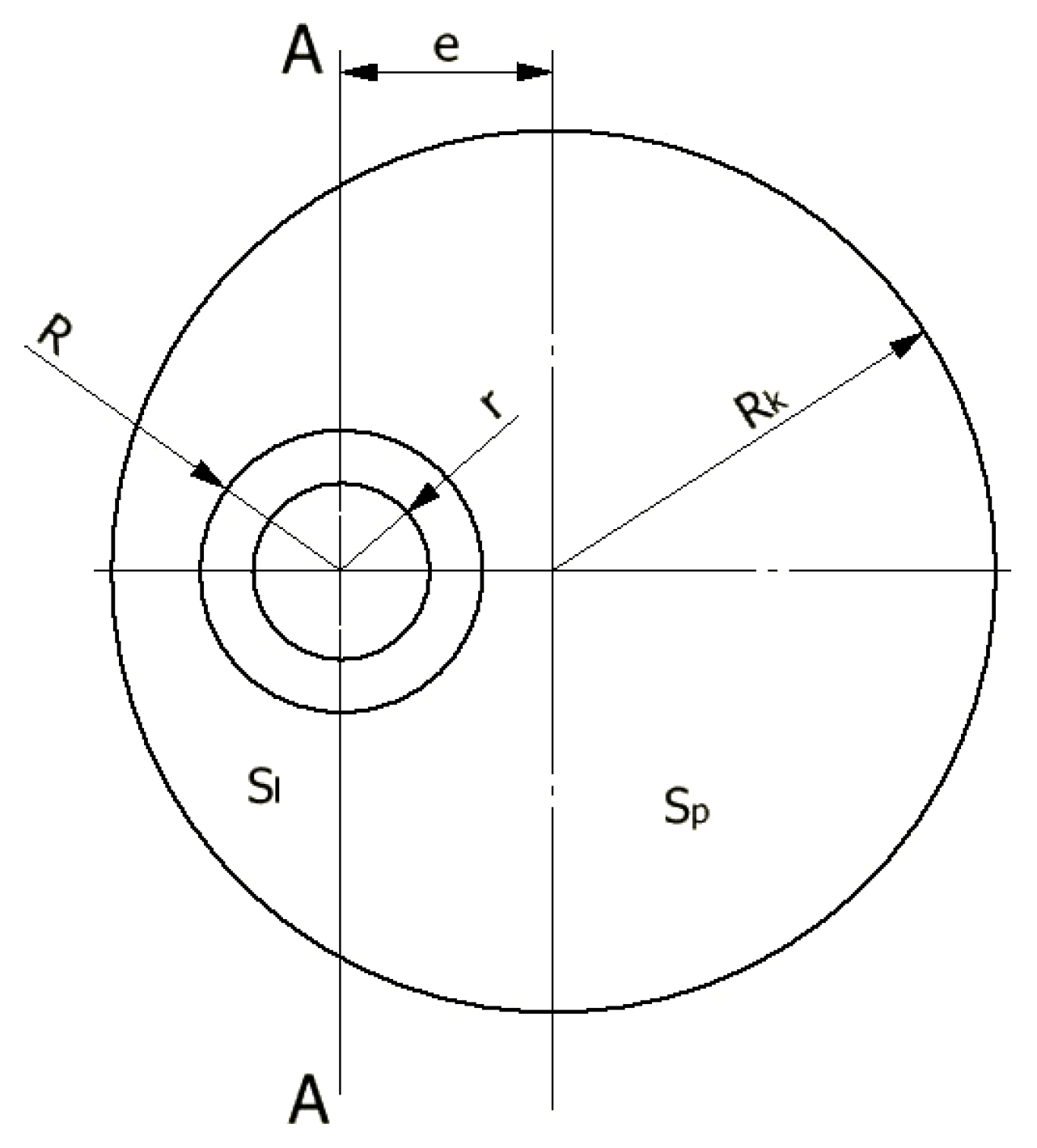
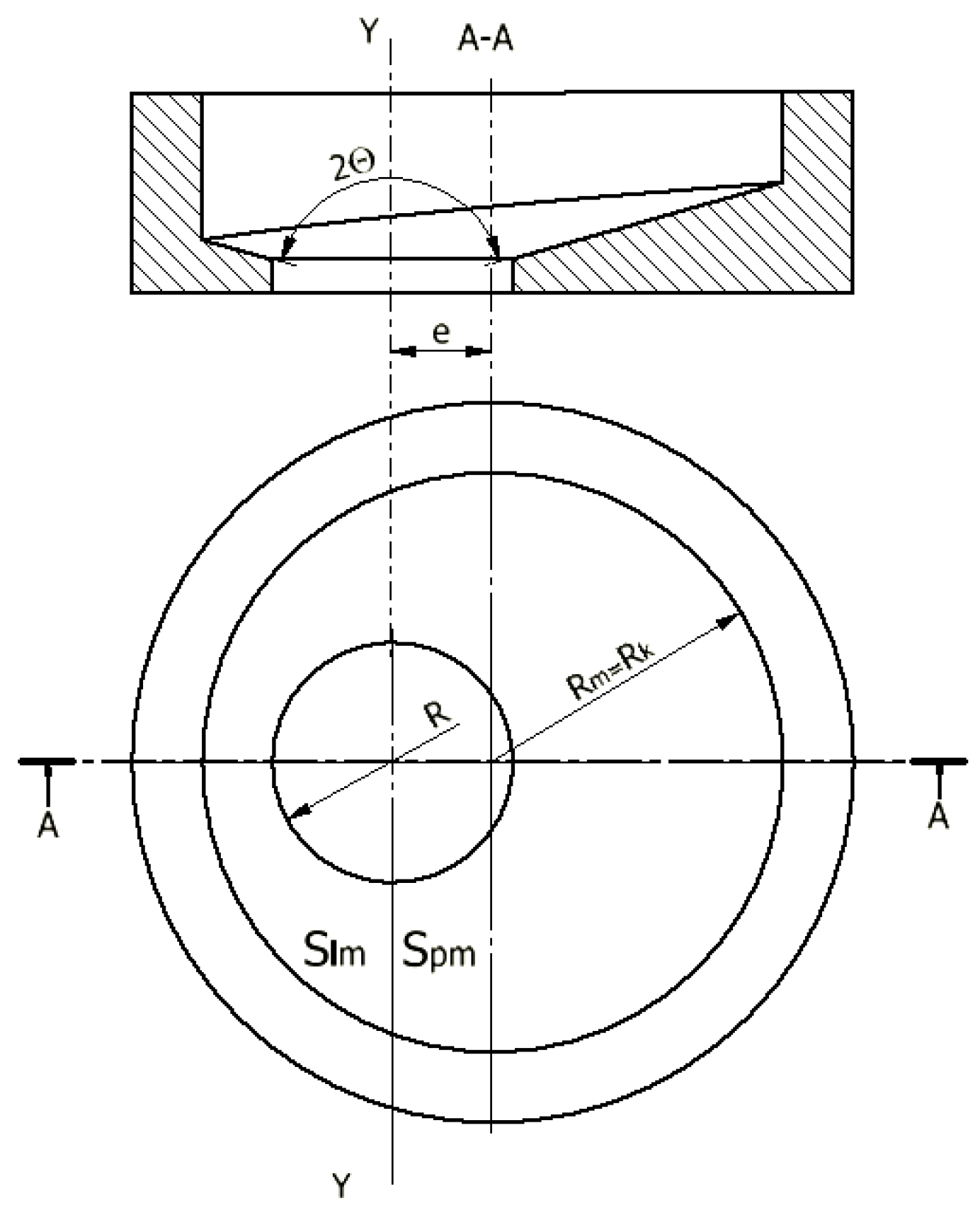
2.2. Formation of the Hollow Torus Profile
2.3. Volume of Material Flowing within the Gap
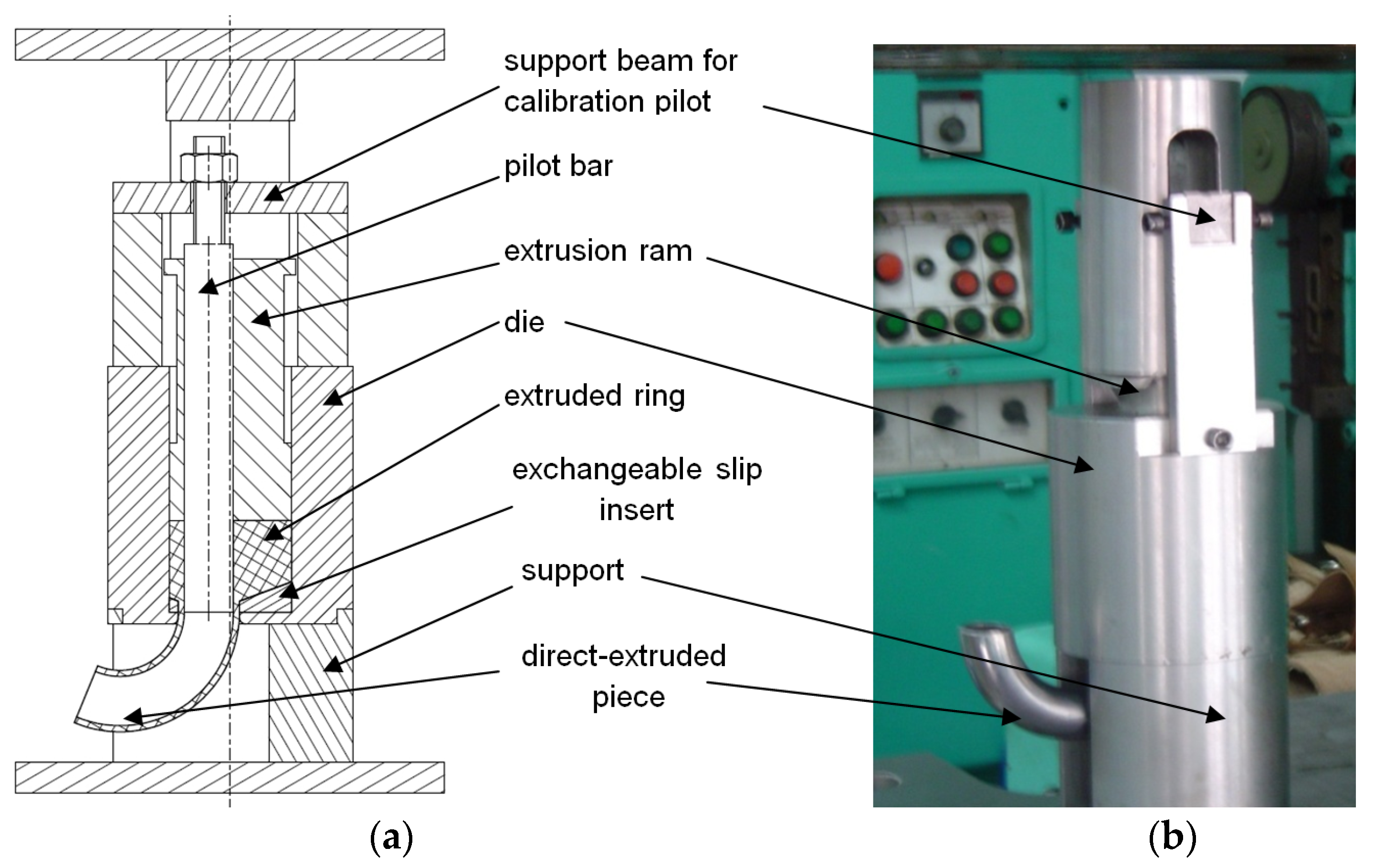
3. Experimental Apparatus and Methods
4. Experimental Results
4.1. Extrusion Process
4.2. Microstructural Examination
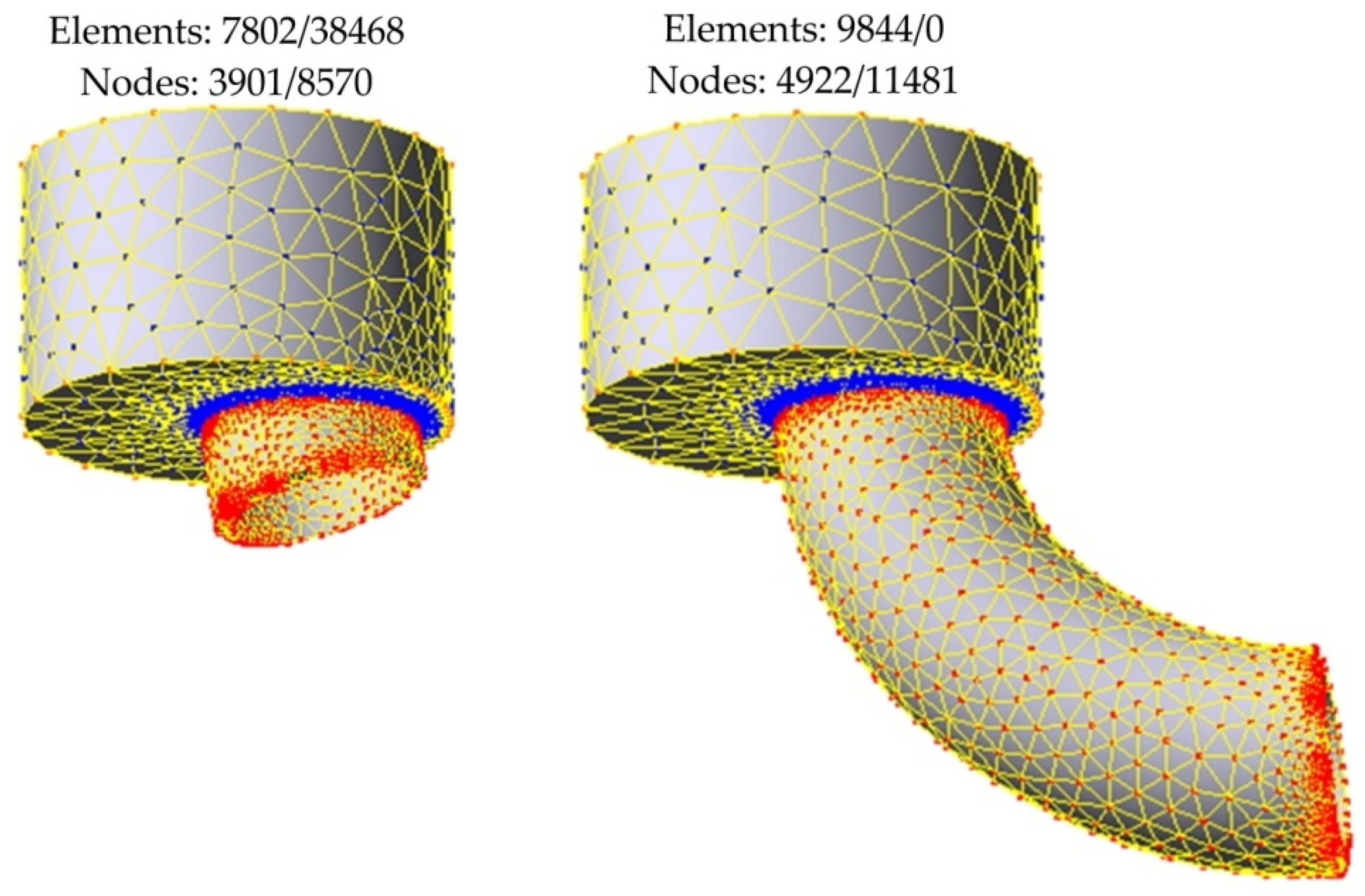
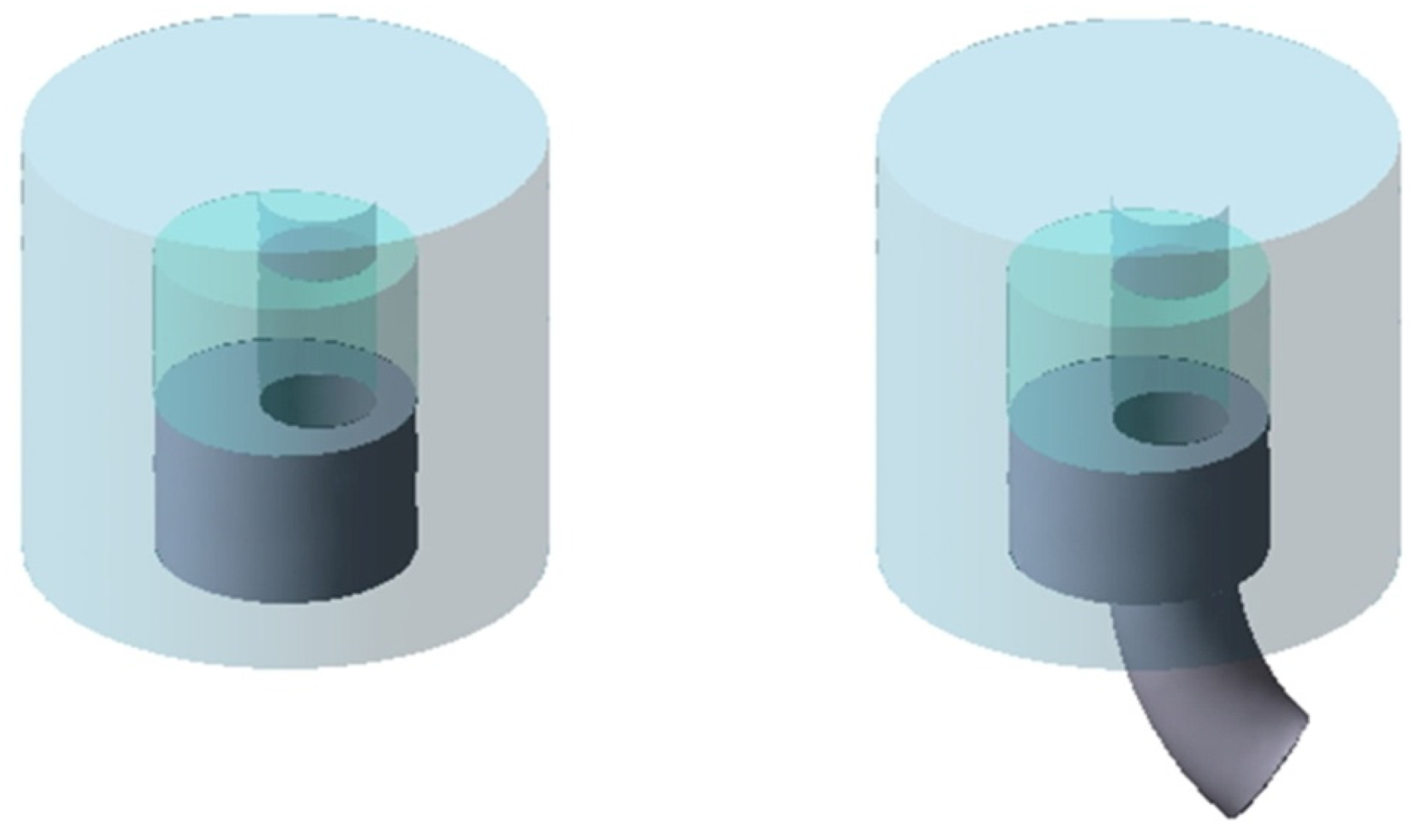
5. Numerical Modelling of Manufacture of Hollow Torus Pieces
6. Numerical Results and Discussion
6.1. Analysis of the Velocity and Flow Lines of the Lead Charge
6.2. Analysis of the State of Stress
7. Conclusions
- The obtained die stampings have uniform wall thicknesses and cross-sectional shapes around their circumference. They are characterised by good surface quality and favourable mechanical properties resulting from forming without damaging the metal structure. It ensures better operational properties of the elements obtained;
- The investigated technological process of forming the hollow toric elements makes it possible to obtain the desired arbitrary curvature of the torus axis in one operation, and does not require additional technological finishing;
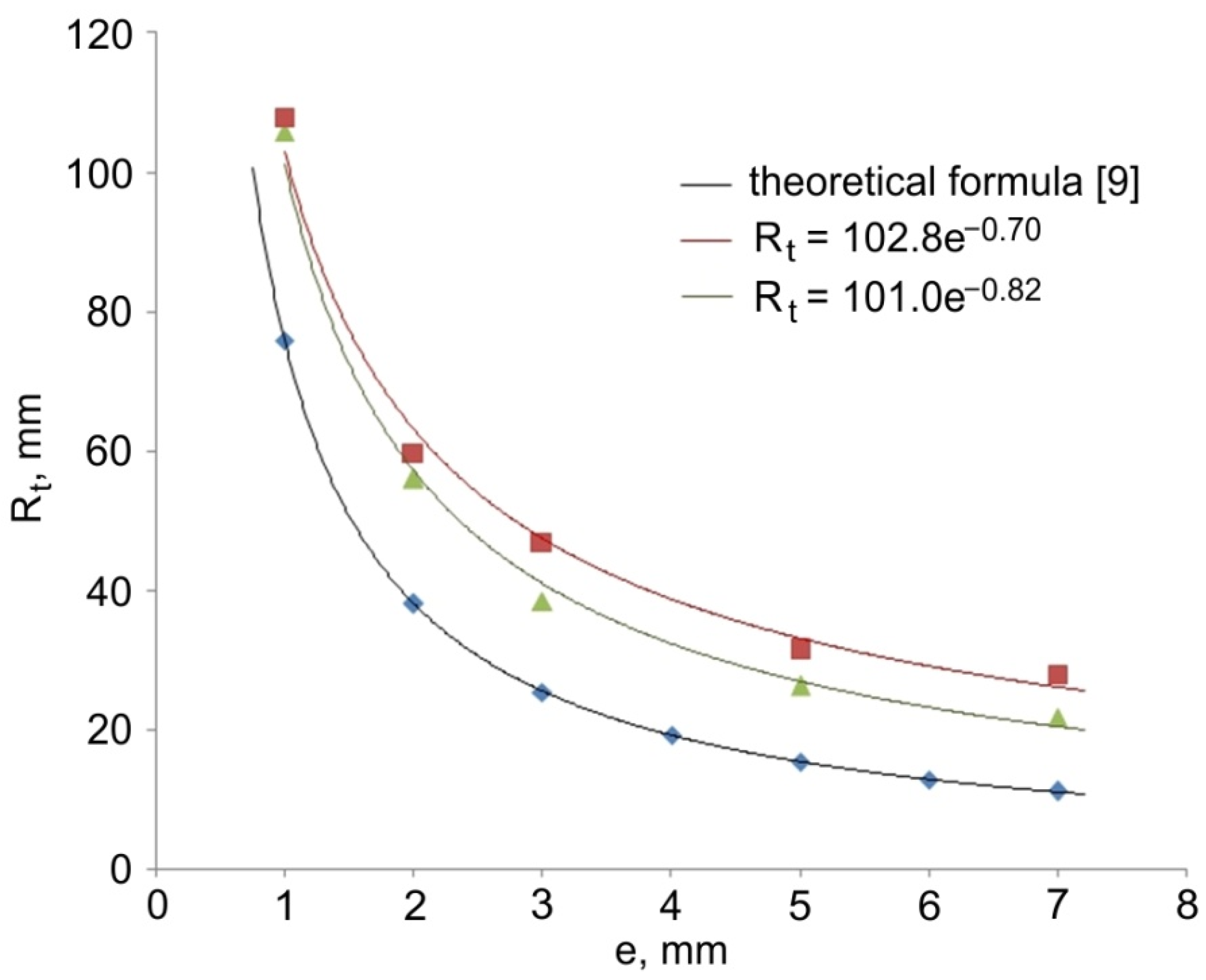
- The value of the radius Rt of the elements formed by the direct extrusion method from a specific stock is inversely proportional to the value of the eccentric e. The height of the material does not directly affect the radius of the torus Rt. The proposed method of extrusion uses the phenomenon of a uniform flow of material with a different volume in relation to the symmetry plane of the calibrating pin in the die;
- In the case of using a die with a conical bottom with an angle close to the stabilization zone of the material flow, the extrusion force decreases. The derived geometrical relationships shows that the angle Θ of the cone of die bottom has no direct impact on the radius Rt of the torus curvature;
- By slide out of the calibrating mandrel below the plane of the die bottom, it is possible to experimentally increase the radius Rt of the extruded piece in relation to the analytically determined value of this radius;
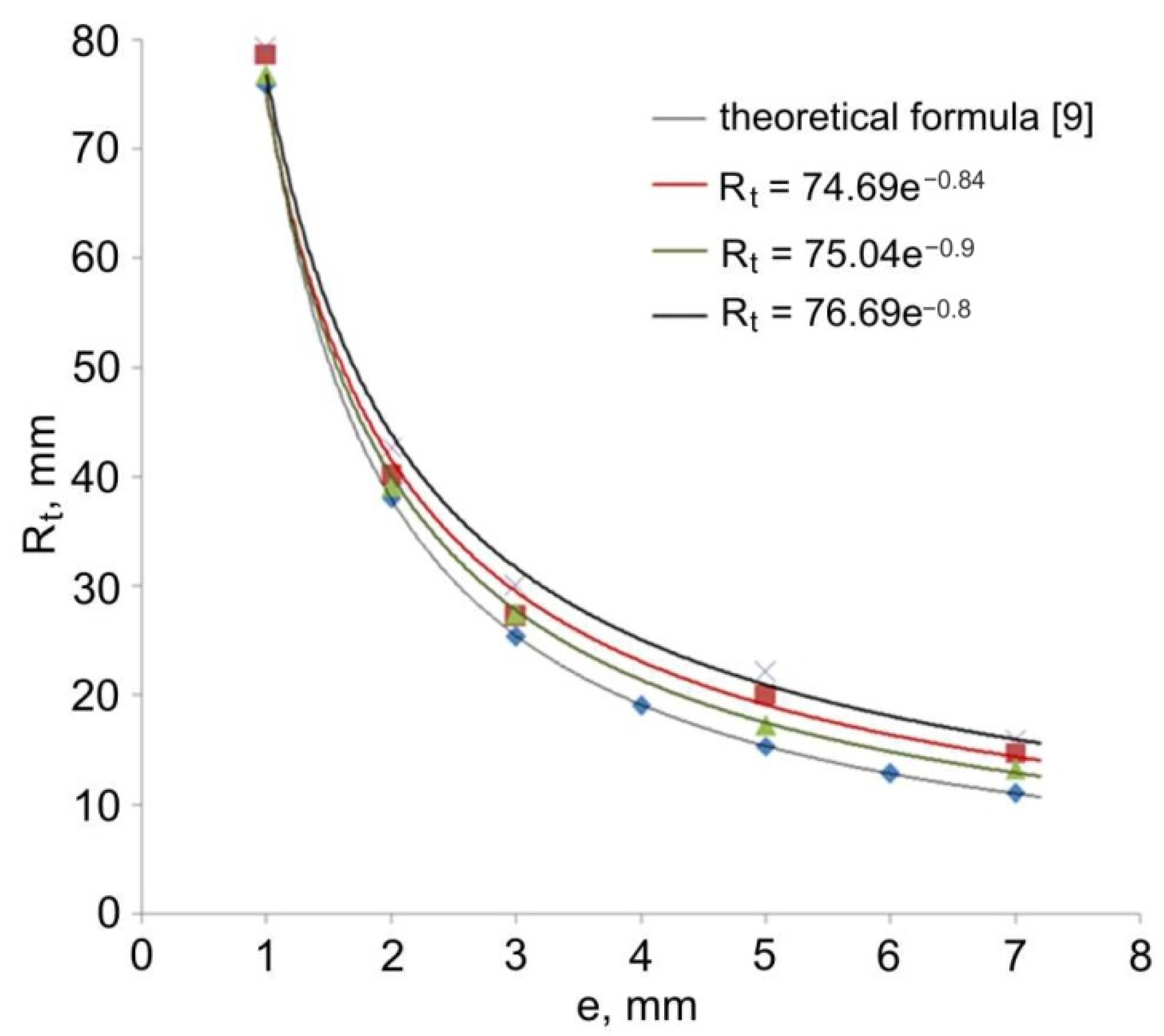
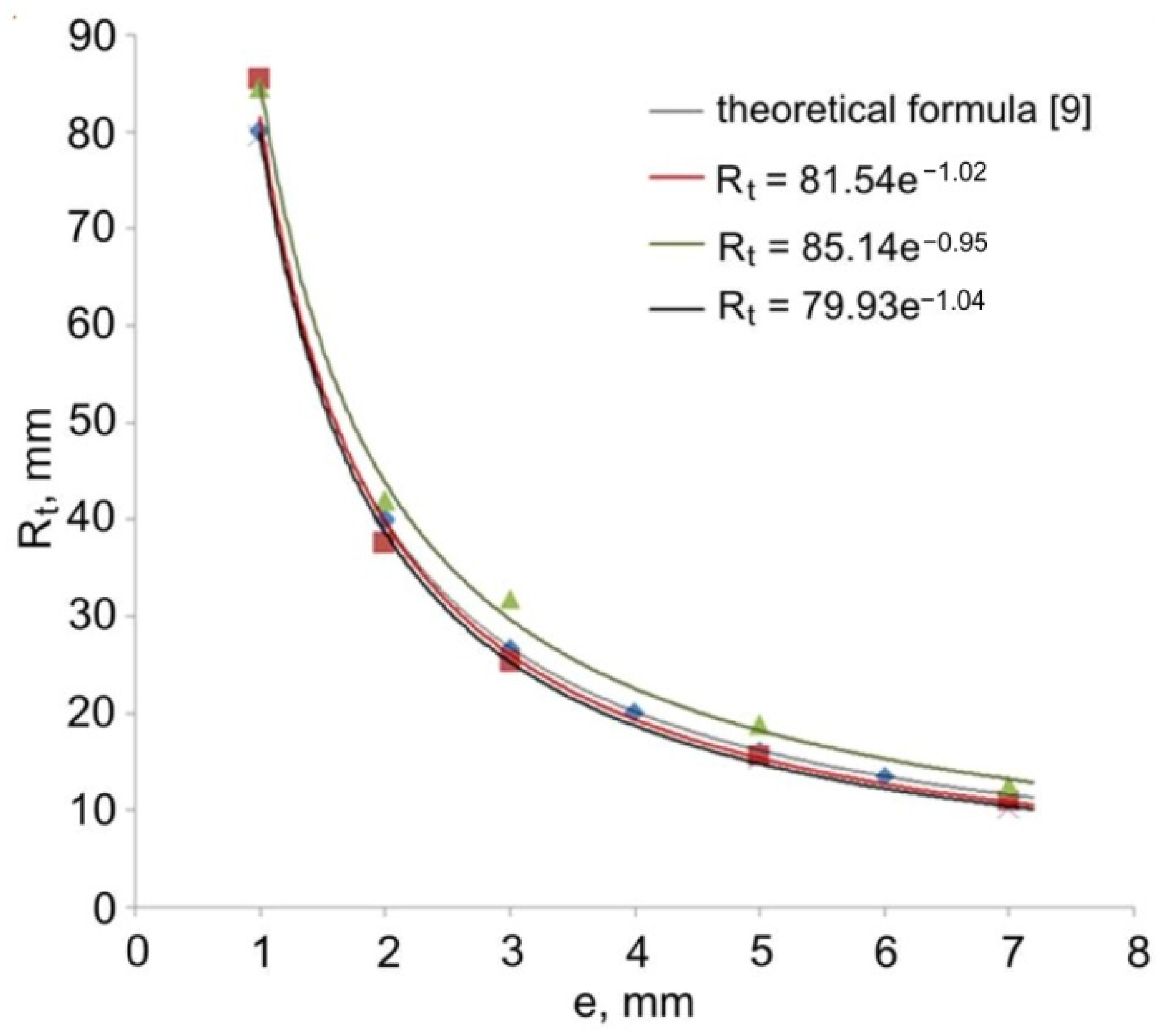
- Along with the decreasing coefficient of friction between the extruded material and the die, the radius of the curvature of the extruded part Rt increases in relation to the calculated theoretical formula [9];
- A significant increase in the eccentric displacement of the calibration gap in the die may affect the proper flow of the workpiece material;
- The proposed design of the tooling for direct extrusion with an eccentric die opening shows a satisfactory durability, can be easily adapted in order to obtain a large range of dimensions of extruded elements, and enables simple operation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oczoś, K.E.; Kawalec, A. Kształtowanie Metali Lekkich; Wydawnictwo Naukowe PWN: Warszawa, Polska, 2012. [Google Scholar]
- Tekkaya, A.E.; Khalifa, N.B.; Grzancic, G.; Hölker, R. Forming of Lightweight Metal Components: Need for New Technologies. Procedia Eng. 2014, 81, 28–37. [Google Scholar] [CrossRef] [Green Version]
- Workie, F.; Tesfaye, A. Analytical and Numerical Analysis of Extrusion Force, Stress and Strain Development During Extrusion Al6063-SiC Composite. Compos. Mater. 2021, 5, 1–16. [Google Scholar] [CrossRef]
- Kleiner, M.; Geiger, M.; Klaus, A. Manufacturing of Lightweight Components by Metal Forming. CIRP Ann. 2003, 52, 521–542. [Google Scholar] [CrossRef]
- Prakash, M.; Cleary, P.W. Modelling highly deformable metal extrusion using SPH. Comp. Part. Mech. 2015, 2, 19–38. [Google Scholar] [CrossRef] [Green Version]
- Qamar, S.Z.; Pervez, T.; Chekotu, J.C. Die Defects and Die Corrections in Metal Extrusion. Metals 2018, 8, 380. [Google Scholar] [CrossRef] [Green Version]
- Hatzenbichler, T.; Buchmayr, B.; Umgeher, A. A numerical sensitivity study to determine the main influence parameters on the back-end defect. J. Mater. Process. Technol. 2007, 182, 73–78. [Google Scholar] [CrossRef]
- Nouri, M.; Semnani, H.M.; Emadoddin, E.; Kim, H.S. Investigation of direct extrusion channel effects on twist extrusion using experimental and finite element analysis. Measurement 2018, 127, 115–123. [Google Scholar] [CrossRef]
- Raknes, C.A.; Welo, T.; Paulsen, F. Dimensional accuracy of aluminium extrusions in mechanical calibration. AIP Conf. Proc. 2018, 1960, 160024. [Google Scholar] [CrossRef] [Green Version]
- Tiernan, P.; Hillery, M.T.; Draganescu, B.; Gheorghe, M. Modelling of cold extrusion with experimental verification. J. Mater. Process. Technol. 2005, 168, 360–366. [Google Scholar] [CrossRef]
- Nagpal, V.; Altan, T. Analysis of the Three-Dimensional Metal Flow in Extrusion of Shapes and the Use of Dual Stream Function. In Proceedings of the 3rd North American Metalworking Research Conference, Pittsburgh, PA, USA, 13–18 February 1975; pp. 26–40. [Google Scholar]
- Basily, B.B.; Sansome, D.H. Some theoretical considerations for the direct drawing of section rod from round bar. Int. J. Mech. Sci. 1976, 18, 201–208. [Google Scholar] [CrossRef]
- Yang, D.Y.; Lee, C.H. Analysis of three-dimensional extrusion of sections through curved dies by conformal transformation. Int. J. Mech. Sci. 1978, 20, 541–552. [Google Scholar] [CrossRef]
- Prakash, R.; Khan, Q.M. An analysis of plastic flow through polygonal converging dies with generalized boundaries of the zone of plastic deformation. Int. J. Mach. Tool Des. Res. 1979, 19, 1–19. [Google Scholar] [CrossRef]
- Boer, C.R.; Schneider, W.R.; Eliasson, B.; Avitzur, B. An Upper Bound Approach for the Direct Drawing of Square Section Rod from Round Bar. In Proceedings of the 20th International Machine Tool, Design and Research Conference, Birmingham, UK, 10–14 September 1979; pp. 149–156. [Google Scholar] [CrossRef]
- Gunasekera, J.S.; Gegel, H.L.; Malas, J.C.; Doraivelu, S.M.; Morgan, J.T.; Altan, T. Computer-Aided Process Modelling of Hot Forging and Extrusion of Aluminum Alloys. CIRP Ann. 1982, 31, 131–135. [Google Scholar] [CrossRef]
- Kiuchi, M.; Kishi, H.; Ishikawa, M. Study on Non-Symmetric Extrusion and Drawing. In Proceedings of the Twenty-Second International Machine Tool Design and Research Conference; Davies, B.J., Ed.; Springer: Cham, Switzerland, 1982. [Google Scholar] [CrossRef]
- Piwnik, J. Mechanika Plastycznego Płynięcia w Zagadnieniach Wyciskania Metali; Wyższa Szkoła Ekonomiczna w Białymstoku: Białystok, Poland, 2010. [Google Scholar]
- Kowalik, M.; Trzepieciński, T. Numerical and Experimental Estimation of Forces During Longitudinal Rolling Process of Shaft Formation. Arab. J. Sci. Eng. 2014, 39, 1251–1260. [Google Scholar] [CrossRef]
- Brzózka, K.; Żurowski, W.; Górka, B. Structure of friction products and the surface of tribological system elements. Nukleonika 2013, 58, 99–103. [Google Scholar]
- Abrinia, K.; Ghorbani, M. Theoretical and Experimental Analyses for the Forward Extrusion of Nonsymmetric Sections. Mater. Manuf. Process. 2012, 27, 420–429. [Google Scholar] [CrossRef]
- Chitkara, N.R.; Celik, K.F. A generalised CAD/CAM solution to the three-dimensional off-centric extrusion of shaped sections: Analysis. Int. J. Mech. Sci. 2000, 42, 273–294. [Google Scholar] [CrossRef]
- Chitkara, N.R.; Celik, K.F. Off-centric extrusion of circular rods through streamlined dies, CAD/CAM applications, analysis and some experiments. Int. J. Mech. Sci. 2000, 42, 295–320. [Google Scholar] [CrossRef]
- Celik, K.F.; Chitkara, N.R. Extrusion of non-symmetric U- and I-shaped sections through ruled-surface dies: Numerical simulations and some experiments. Int. J. Mech. Sci. 2002, 44, 217–246. [Google Scholar] [CrossRef]
- Abrinia, K.; Farahmand, P.; Parchami-Sarghin, M. Formulation of a new generalized kinematically admissible velocity field with a variable axial component for the forward extrusion of shaped sections. Int. J. Adv. Manuf. Technol. 2014, 70, 1427–1435. [Google Scholar] [CrossRef]
- Libura, W.; Rękas, A. Numerical Modelling in Designing Aluminium Extrusion. In Aluminium Alloys—New Trends in Fabrication and Applications; Ahmad, Z., Ed.; IntechOpen: Rijeka, Croatia, 2012; Chapter 6. [Google Scholar] [CrossRef] [Green Version]
- Qamar, S.Z. FEM study of extrusion complexity and dead metal zone. Arch. Mater. Sci. Eng. 2009, 36, 110–117. [Google Scholar]
- Zhou, W.; Lin, J.; Dean, T.A.; Wang, L. A novel application of sideways extrusion to produce curved aluminium profiles: Feasibility study. Procedia Eng. 2017, 207, 2304–2309. [Google Scholar] [CrossRef]
- Yu, J.; Lin, J.; Dean, T.A. Development of novel differential velocity sideway extrusion techniques to fabricate lightweight curved structural components. Procedia Manuf. 2020, 50, 125–128. [Google Scholar] [CrossRef]
- Zhou, W.; Lin, J.; Dean, T.A.; Wang, L. Analysis and modelling of a novel process for extruding curved metal alloy profiles. Int. J. Mech. Sci. 2018, 138–139, 524–536. [Google Scholar] [CrossRef]
- Chen, F.K.; Chuang, W.C.; Torng, S. Finite element analysis of multi-hole extrusion of aluminum-alloy tubes. J. Mater. Process. Technol. 2008, 201, 150–155. [Google Scholar] [CrossRef]
- Min, F.; Zhu, G.; Yue, B.; Wang, Z.; Yang, Z.; Zhai, X. Influence of exit velocity distribution on self-bending extrusion. Eng. Res. Express 2020, 2, 015033. [Google Scholar] [CrossRef]
- Takahashi, Y.; Kihara, S.; Yamaji, K.; Shiraishi, M. Effects of Die Dimensions for Curvature Extrusion of Curved Rectangular Bars. Mater. Trans. 2015, 56, 844–849. [Google Scholar] [CrossRef] [Green Version]
- Pater, Z. Lead as a model material to simulate of hot metal forming processes. Plast. Work. 2003, 14, 41–48. [Google Scholar]
- Zhou, W.; Shao, Z.; Yu, J.; Lin, J. Advances and Trends in Forming Curved Extrusion Profiles. Materials 2021, 14, 1603. [Google Scholar] [CrossRef] [PubMed]
- Huida, Z. Metallurgy for Physicists and Engineers: Fundamentals, Applications, and Calculations; Taylor & Francis Group: Boca Raton, FL, USA, 2020. [Google Scholar]
- Klocke, F. Manufacturing Processes 4. Forming; Spinger: Heidelberg, Germany, 2013. [Google Scholar]
- Ershov, A.A.; Kotov, V.V.; Loginov, Y.N. Capabilities of QForm-extrusion based on an example of the extrusion of complex shapes. Metallurgist 2012, 55, 695–701. [Google Scholar] [CrossRef]
- Biba, N.; Stebunov, S.; Lishny, A. Simulation of Material Flow Coupled with Die Analysis in Complex Shape Extrusion. Key Eng. Mater. 2013, 585, 85–92. [Google Scholar] [CrossRef]
- Stebunov, S.; Lishnij, A.; Biba, N.; Bellotti, S.; Fazzini, P.B. Development and Industrial Verification of QForm-Extrusion Program for Simulation of Profile Extrusion. Available online: https://qform3d.com/files_com/2009Development%20and%20industrial%20verification%20of%20QForm-Extrusion%20program.pdf (accessed on 27 August 2021).
- Biba, N.; Stebunov, S.; Lishny, A. Automated Extrusion Die Design Integrated with Simulation of Material Flow. Available online: https://qform3d.com/files_com/Nikolay%20Biba%2C%20Sergey%20Stebunov%2C%20Andrey%20Lishny%20-%20Automated%20Extrusion%20Die%20Design%20Integrated%20with%20Simulation.pdf (accessed on 27 August 2021).
- Faizov, S.; Sarafanov, A.; Erdakov, I.; Gromov, D.; Svistun, A.; Glebov, L.; Bykov, V.; Bryk, A.; Radionova, L. On the Direct Extrusion of Solder Wire from 52In-48Sn Alloy. Machines 2021, 9, 93. [Google Scholar] [CrossRef]
- Lu, D.; Flewitt, P.E.J. Raman measurements of stress in films and coatings. In Spectroscopic Properties of Inorganic and Organometallic Compounds; Royal Society of Chemistry: London, UK, 2014; Volume 45, pp. 141–177. [Google Scholar] [CrossRef]
- Salvati, E.; Korsunsky, A.M. An analysis of macro-and micro-scale residual stresses of Type I, II and III using FIB-DIC micro-ring-core milling and crystal plasticity FE modelling. Int. J. Plast. 2017, 98, 123–138. [Google Scholar] [CrossRef]









| Yield Stress Re, MPa | Ultimate Tensile Stress Rm, MPa | Elongation A5, % | Young’s Modulus E, MPa | Poisson’s Ratio ν |
|---|---|---|---|---|
| 5 | 20 | 50 | 0.16×105 | 0.44 |
| Eccentric e, mm | Number of Experiment | Radius of the Toric Part of the Pipe Rt, mm |
|---|---|---|
| 1 | 1 | 78.7 |
| 2 | 76.8 | |
| 3 | 79.2 | |
| 2 | 1 | 40.1 |
| 2 | 39.1 | |
| 3 | 42.7 | |
| 3 | 1 | 27.2 |
| 2 | 27.5 | |
| 3 | 30.0 | |
| 5 | 1 | 20.1 |
| 2 | 17.3 | |
| 3 | 22.1 | |
| 7 | 1 | 14.7 |
| 2 | 13.3 | |
| 3 | 15.9 |
| Eccentric e, mm | Number of Experiment | Radius of the Toric Part of the Pipe Rt, mm |
|---|---|---|
| 1 | 1 | 85.4 |
| 2 | 84.5 | |
| 3 | 79.6 | |
| 2 | 1 | 37.6 |
| 2 | 42.0 | |
| 3 | 38.7 | |
| 3 | 1 | 25.4 |
| 2 | 31.9 | |
| 3 | 25.5 | |
| 5 | 1 | 15.8 |
| 2 | 18.9 | |
| 3 | 15.3 | |
| 7 | 1 | 11.1 |
| 2 | 12.6 | |
| 3 | 10.2 |
| Eccentric e, mm | Radius of the Toric Part of the Pipe Rt, mm (Friction Coefficient 0.2) | Radius of the Toric Part of the Pipe Rt, mm (Friction Coefficient 0.5) |
|---|---|---|
| 1 | 107.9 | 105.8 |
| 2 | 59.7 | 55.9 |
| 3 | 46.9 | 38.3 |
| 5 | 31.3 | 26.2 |
| 7 | 27.8 | 21.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kowalik, M.; Paszta, P.; Trzepieciński, T.; Kukiełka, L. Non-Symmetrical Direct Extrusion—Analytical Modelling, Numerical Simulation and Experiment. Materials 2021, 14, 7856. https://doi.org/10.3390/ma14247856
Kowalik M, Paszta P, Trzepieciński T, Kukiełka L. Non-Symmetrical Direct Extrusion—Analytical Modelling, Numerical Simulation and Experiment. Materials. 2021; 14(24):7856. https://doi.org/10.3390/ma14247856
Chicago/Turabian StyleKowalik, Marek, Piotr Paszta, Tomasz Trzepieciński, and Leon Kukiełka. 2021. "Non-Symmetrical Direct Extrusion—Analytical Modelling, Numerical Simulation and Experiment" Materials 14, no. 24: 7856. https://doi.org/10.3390/ma14247856
APA StyleKowalik, M., Paszta, P., Trzepieciński, T., & Kukiełka, L. (2021). Non-Symmetrical Direct Extrusion—Analytical Modelling, Numerical Simulation and Experiment. Materials, 14(24), 7856. https://doi.org/10.3390/ma14247856








