A First-Principles Study of the Cu-Containing β″ Precipitates in Al-Mg-Si-Cu Alloy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Atomic Model
2.2. Computational Details
3. Results and Discussion
3.1. Structure Stability
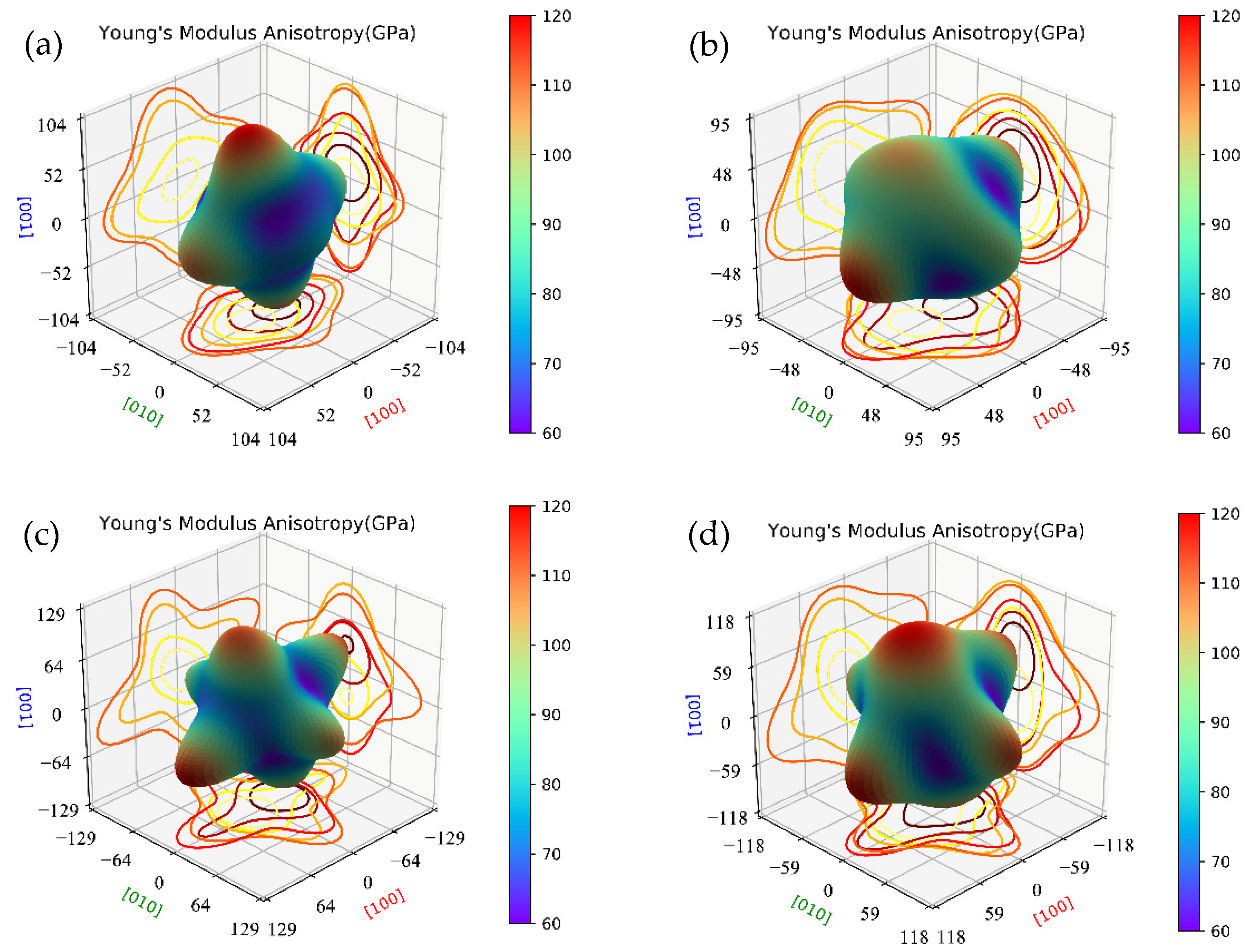
3.2. Elastic Properties
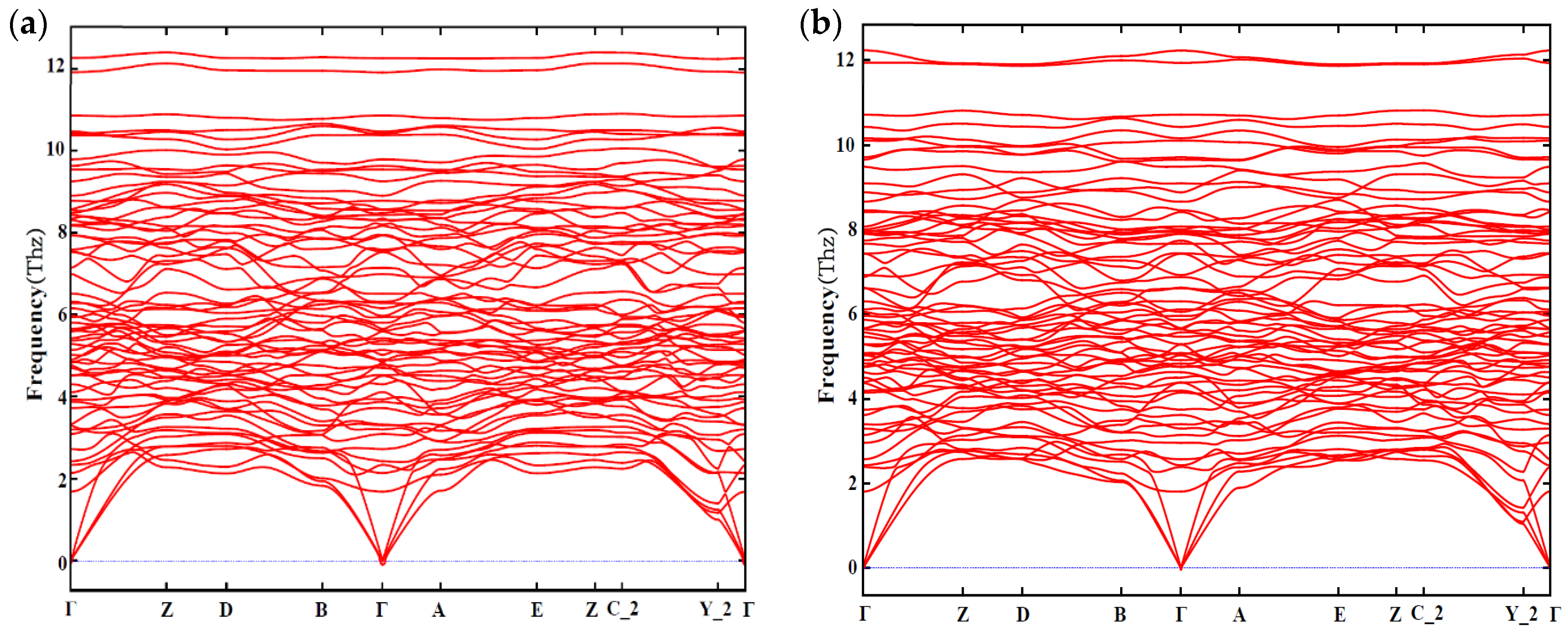
3.3. Phonon Spectra
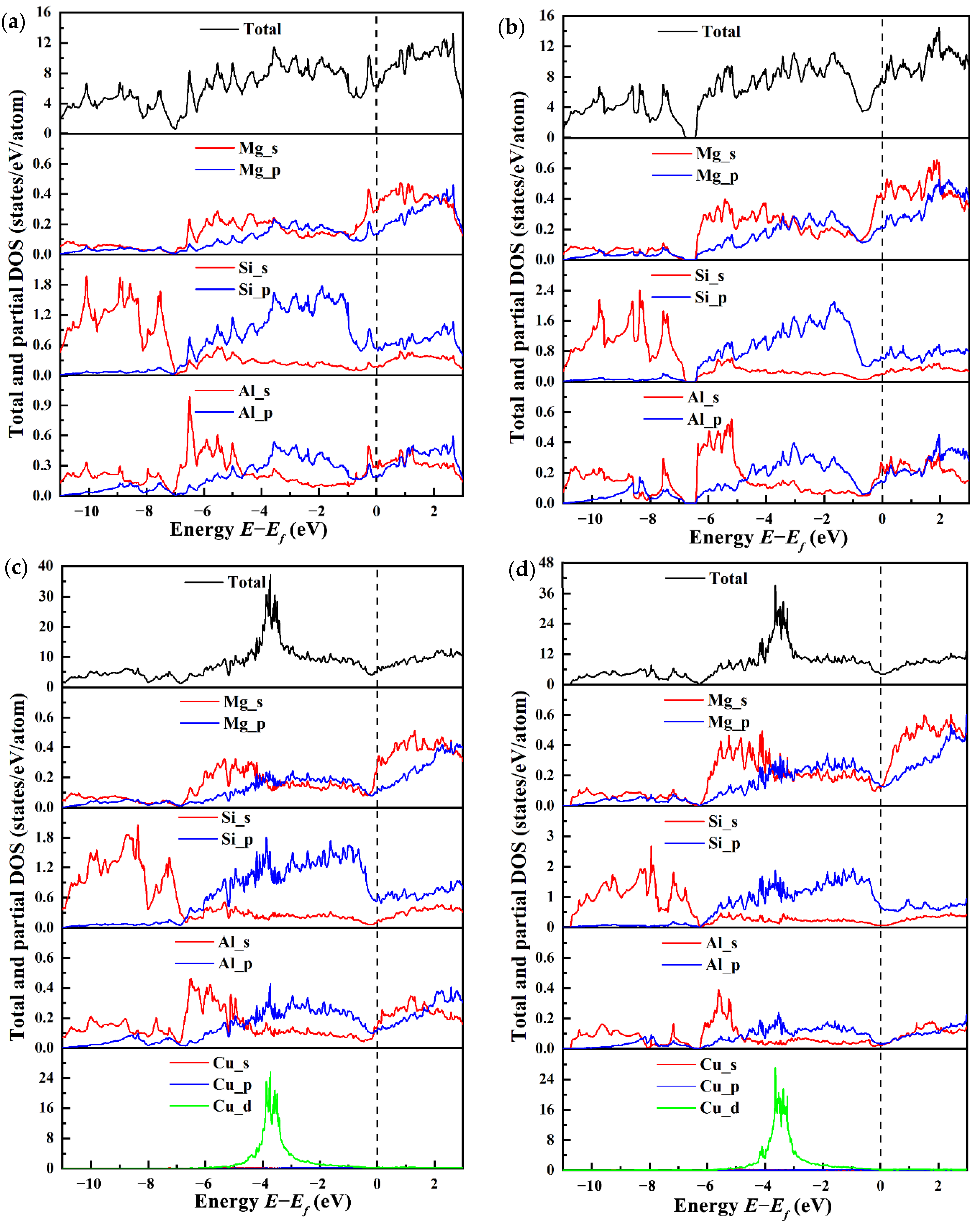
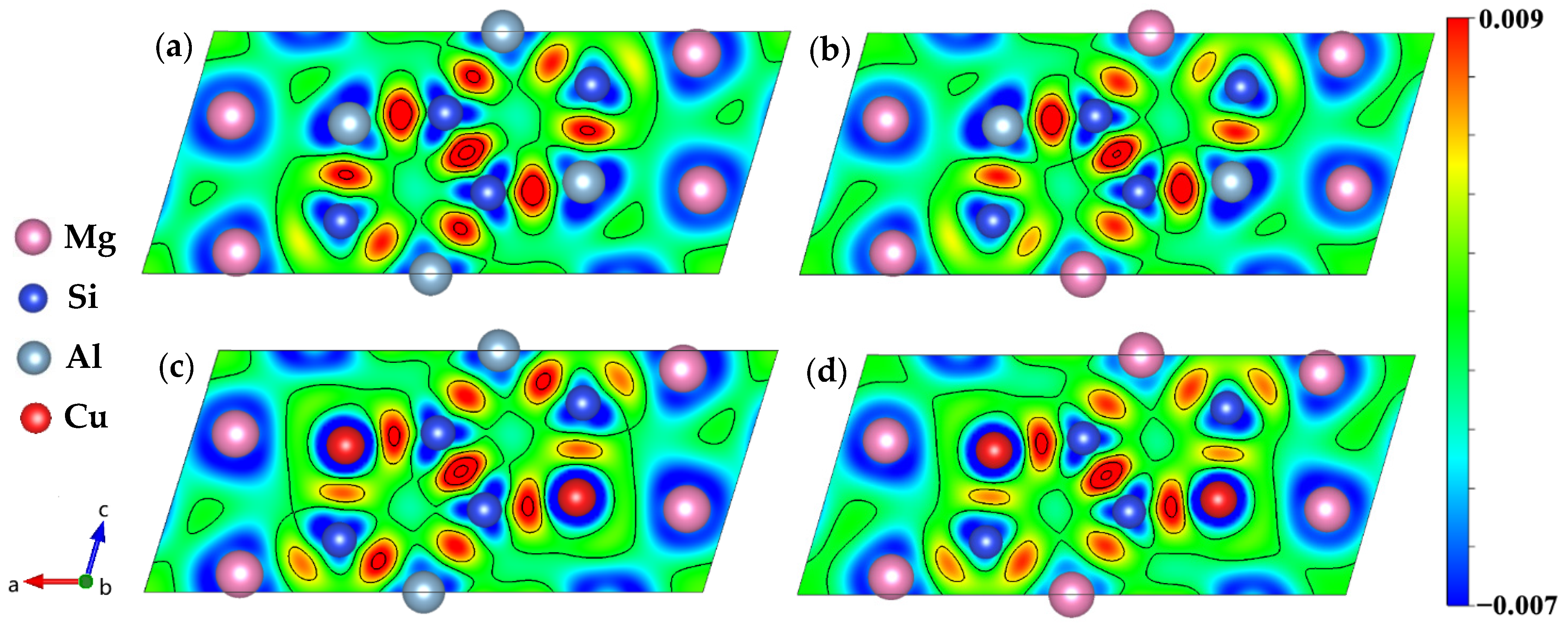
3.4. Electronic Structure
4. Conclusions
- (1)
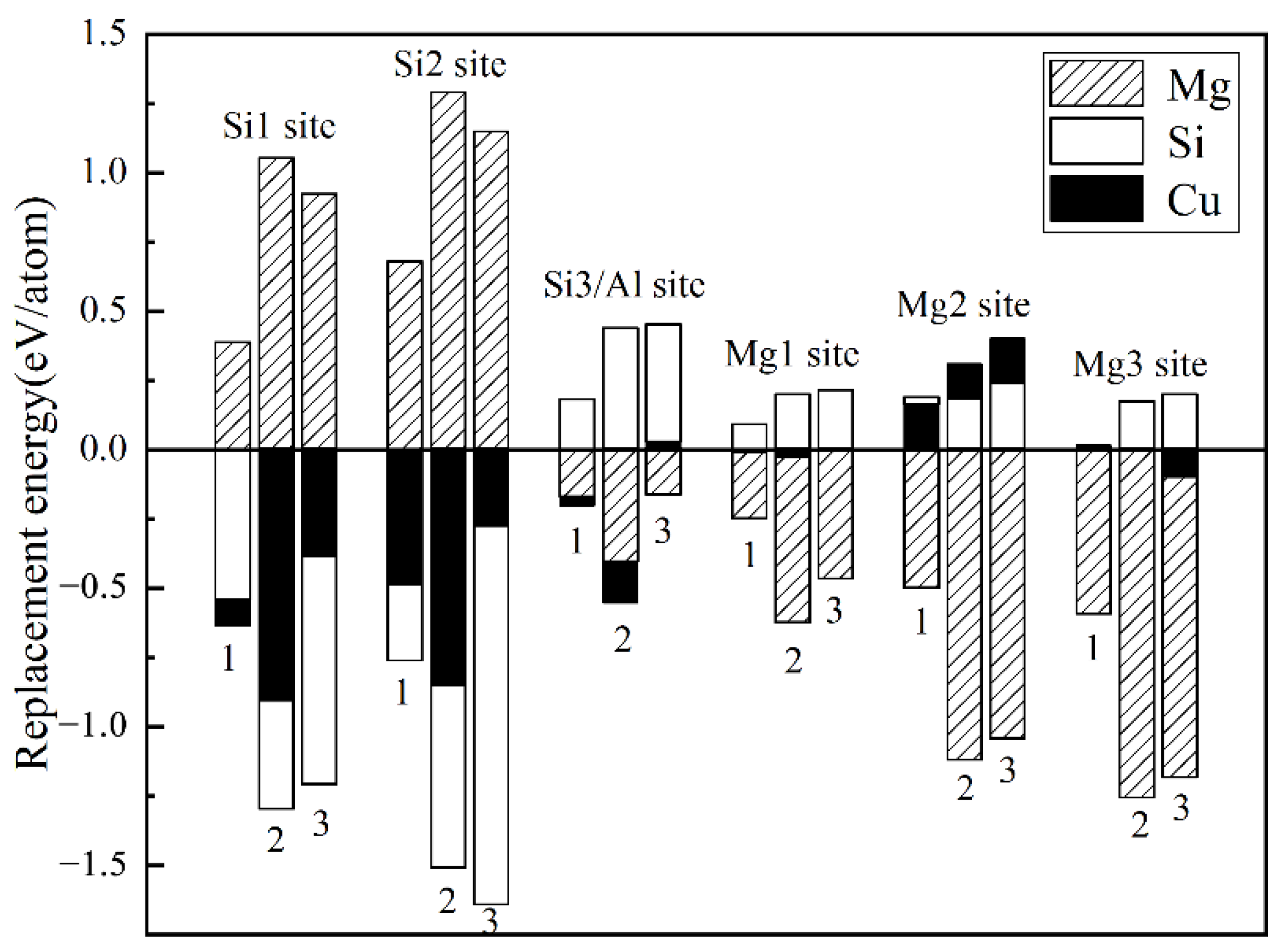
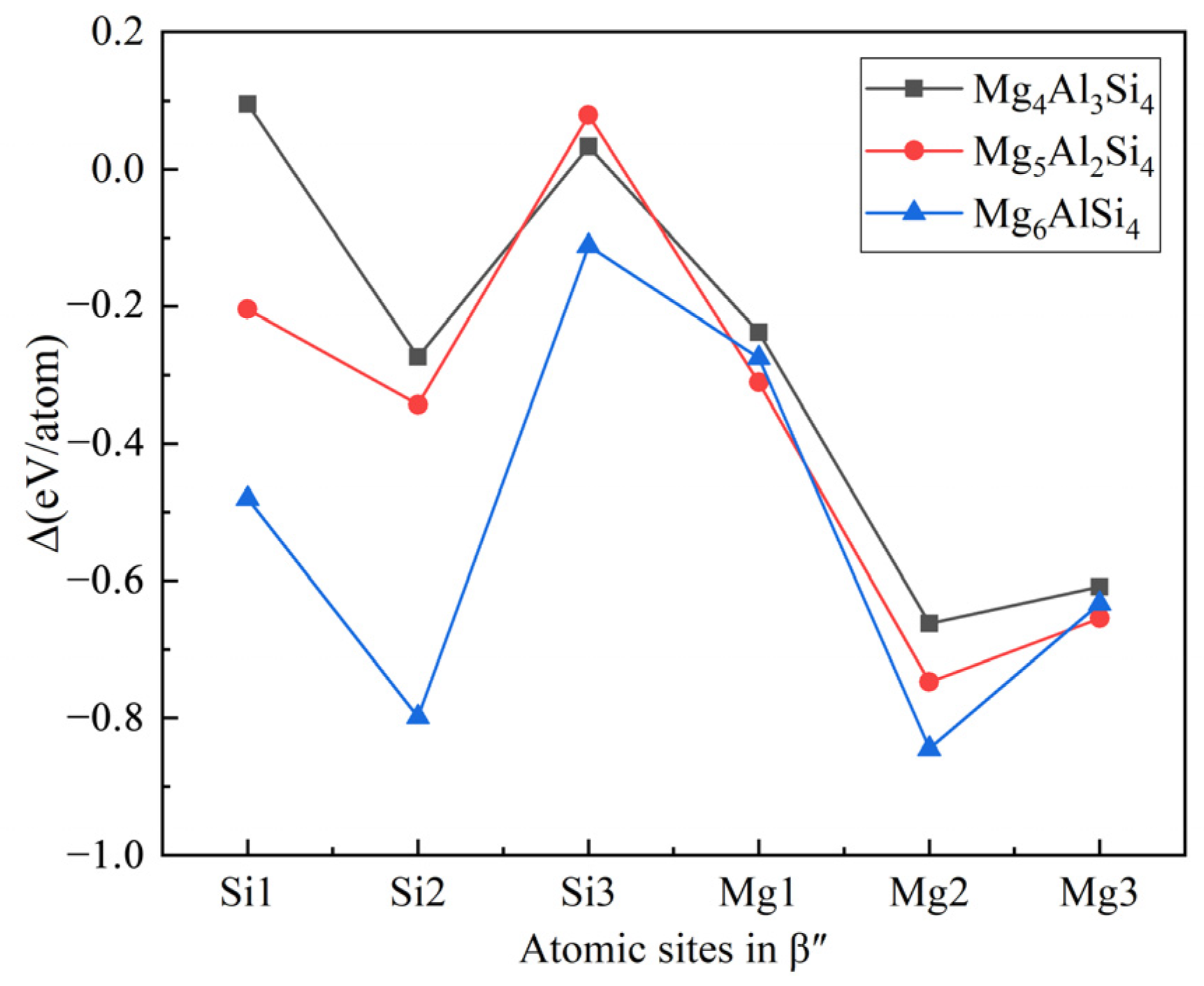
- The calculation of the formation enthalpies of 33 Cu-containing β″ phases shows that the replacement order of Cu atoms in β″ phases can be summarized as one Si3/Al site → two Si3/Al sites → two Si3/Al sites and one Mg1 site.
- (2)
- The Cu atoms strongly favor occupying one of each pair of Si3/Al sites and the most stable Cu-containing β″ phases were expected to have a stoichiometry of Mg4+xAl2−xCuSi4 (x = 0, 1). In addition, taking into account the change of Cu content in β″ phases, the stoichiometry of Mg4Al3−xCuxSi4 (1 ≤ x ≤ 3) may precipitate.
- (3)
- The calculated mechanical properties show that all calculated β″ phases are mechanically stable. The incorporation of Cu atoms improves the values of bulk modulus (B), shear modulus (G), and Young’s modulus (E) of β″, respectively, and all β″ phases calculated show ductile behavior. Furthermore, the calculation of the phonon spectra shows that Mg4+xAl2−xCuSi4 (x = 0, 1) are dynamically stable.
- (4)
- The electronic structure results shows that the Cu atom will join the Si network, and the bond between the Si atom and the Cu atom has the covalent property. The incorporation of Cu atom increases the electron interaction between the Mg2 and the Si3 atom, which may be one of the reasons why the incorporation of Cu atom increases the stability of the β″ phase structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Li, H.; Katgerman, L.; Du, Q.; Zhang, J.; Zhuang, L. Recent advances in hot tearing during casting of aluminium alloys. Prog. Mater. Sci. 2021, 117, 100741. [Google Scholar] [CrossRef]
- Abouarkoub, A.; Thompson, G.E.; Zhou, X.; Hashimoto, T.; Scamans, G. The influence of prolonged natural aging on the subsequent artificial aging response of the AA6111 automotive alloy. Met. Mater. Trans. A 2015, 46, 4380–4393. [Google Scholar] [CrossRef]
- Zhang, D.-L.; Wang, J.; Kong, Y.; Zou, Y.; Du, Y. First-principles investigation on stability and electronic structure of Sc-doped θ′/Al interface in Al-Cu alloys. Trans. Nonferrous Met. Soc. China 2021, 31, 3342–3355. [Google Scholar] [CrossRef]
- Chakrabarti, D.; Laughlin, E.D. Phase relations and precipitation in Al–Mg–Si alloys with Cu additions. Prog. Mater. Sci. 2004, 49, 389–410. [Google Scholar] [CrossRef]
- Gupta, A.; Lloyd, D.; Court, S. Precipitation hardening in Al–Mg–Si alloys with and without excess Si. Mater. Sci. Eng. A 2001, 316, 11–17. [Google Scholar] [CrossRef]
- Safyari, M.; Moshtaghi, M.; Hojo, T.; Akiyama, E. Mechanisms of hydrogen embrittlement in high-strength aluminum alloys containing coherent or incoherent dispersoids. Corros. Sci. 2021, 194, 109895. [Google Scholar] [CrossRef]
- Ardell, A.J. Precipitation hardening. Met. Mater. Trans. A 1985, 16, 2131–2165. [Google Scholar] [CrossRef]
- Polmear, I. In Aluminium alloys—A century of age hardening. Mater. Forum 2004, 28, 1–14. [Google Scholar]
- Van Huis, M.; Chen, J.; Sluiter, M.; Zandbergen, H. Phase stability and structural features of matrix-embedded hardening precipitates in Al–Mg–Si alloys in the early stages of evolution. Acta Mater. 2007, 55, 2183–2199. [Google Scholar] [CrossRef]
- Edwards, G.; Stiller, K.; Dunlop, G.; Couper, M. The precipitation sequence in Al–Mg–Si alloys. Acta Mater. 1998, 46, 3893–3904. [Google Scholar] [CrossRef]
- Guinier, A. Structure of age-hardened aluminium-copper alloys. Nat. Cell Biol. 1938, 142, 569–570. [Google Scholar] [CrossRef]
- Preston, G.D. Structure of age-hardened aluminium-copper alloys. Nat. Cell Biol. 1938, 142, 570. [Google Scholar] [CrossRef]
- Matsuda, K.; Ikeno, S.; Terayama, K.; Matsui, H.; Sato, T.; Uetani, Y. Comparison of precipitates between excess Si-type and balanced-type Al-Mg-Si alloys during continuous heating. Met. Mater. Trans. A 2005, 36, 2007–2012. [Google Scholar] [CrossRef]
- Miao, W.F.; Laughlin, D.E. Effects of Cu content and preaging on precipitation characteristics in aluminum alloy 6022. Met. Mater. Trans. A 2000, 31, 361–371. [Google Scholar] [CrossRef]
- Marioara, C.D.; Nordmark, H.; Andersen, S.J.; Holmestad, R. Post-β″ phases and their influence on microstructure and hardness in 6xxx Al-Mg-Si alloys. J. Mater. Sci. 2006, 41, 471–478. [Google Scholar] [CrossRef]
- Esmaeili, S.; Lloyd, D.; Poole, W. A yield strength model for the Al-Mg-Si-Cu alloy AA6111. Acta Mater. 2003, 51, 2243–2257. [Google Scholar] [CrossRef]
- Zandbergen, H.W.; Andersen, S.J.; Jansen, J. Structure determination of Mg5Si6 particles in Al by dynamic electron diffraction studies. Science 1997, 277, 1221–1225. [Google Scholar] [CrossRef]
- Andersen, S.J.; Zandbergen, H.; Jansen, J.; Træholt, C.; Tundal, U.; Reiso, O. The crystal structure of the β″ phase in Al–Mg–Si alloys. Acta Mater. 1998, 46, 3283–3298. [Google Scholar] [CrossRef]
- Hasting, H.S.; Frøseth, A.G.; Andersen, S.J.; Vissers, R.; Walmsley, J.C.; Marioara, C.D.; Danoix, F.; Lefebvre, W.; Holmestad, R. Composition of β″ precipitates in Al–Mg–Si alloys by atom probe tomography and first principles calculations. J. Appl. Phys. 2009, 106, 123527. [Google Scholar] [CrossRef]
- Pogatscher, S.; Antrekowitsch, H.; Leitner, H.; Sologubenko, A.; Uggowitzer, P. Influence of the thermal route on the peak-aged microstructures in an Al–Mg–Si aluminum alloy. Scr. Mater. 2013, 68, 158–161. [Google Scholar] [CrossRef]
- Ehlers, F.J. Ab initio interface configuration determination for β″ in Al–Mg–Si: Beyond the constraint of a preserved precipitate stoichiometry. Comput. Mater. Sci. 2014, 81, 617–629. [Google Scholar] [CrossRef] [Green Version]
- Ninive, P.H.; Strandlie, A.; Gulbrandsen-Dahl, S.; Lefebvre, W.; Marioara, C.D.; Andersen, S.J.; Friis, J.; Holmestad, R.; Løvvik, O.M. Detailed atomistic insight into the β″ phase in Al–Mg–Si alloys. Acta Mater. 2014, 69, 126–134. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Q.; Liu, H.; Yi, D.; Yin, D.; Chen, Y.; Zhang, Y.; Wang, B. Effect of Cu content on precipitation and age-hardening behavior in Al-Mg-Si-xCu alloys. J. Alloys Compd. 2017, 695, 1005–1013. [Google Scholar] [CrossRef]
- Man, J.; Jing, L.; Jie, S.G. The effects of Cu addition on the microstructure and thermal stability of an Al–Mg–Si alloy. J. Alloys Compd. 2007, 437, 146–150. [Google Scholar] [CrossRef]
- Ding, L.; Jia, Z.; Liu, Y.; Weng, Y.; Liu, Q. The influence of Cu addition and pre-straining on the natural aging and bake hardening response of Al-Mg-Si alloys. J. Alloys Compd. 2016, 688, 362–367. [Google Scholar] [CrossRef]
- Saito, T.; Marioara, C.D.; Andersen, S.J.; Lefebvre, W.; Holmestad, R. Aberration-corrected HAADF-STEM investigations of precipitate structures in Al–Mg–Si alloys with low Cu additions. Philos. Mag. 2014, 94, 520–531. [Google Scholar] [CrossRef] [Green Version]
- Saito, T.; Mørtsell, E.A.; Wenner, S.; Marioara, C.D.; Andersen, S.J.; Friis, J.; Matsuda, K.; Holmestad, R. Atomic structures of precipitates in Al-Mg-Si alloys with small additions of other elements. Adv. Eng. Mater. 2018, 20, 18. [Google Scholar] [CrossRef] [Green Version]
- Murayama, M.; Hono, K.; Miao, W.F.; Laughlin, D.E. The effect of Cu additions on the precipitation kinetics in an Al-Mg-Si alloy with excess Si. Met. Mater. Trans. A 2001, 32, 239–246. [Google Scholar] [CrossRef]
- Jia, Z.; Ding, L.; Cao, L.; Sanders, R.; Li, S.; Liu, Q. The influence of composition on the clustering and precipitation behavior of Al-Mg-Si-Cu alloys. Met. Mater. Trans. A 2016, 48, 459–473. [Google Scholar] [CrossRef]
- Zandbergen, M.; Cerezo, A.; Smith, G. Study of precipitation in Al–Mg–Si Alloys by atom probe tomography II. Influence of Cu additions. Acta Mater. 2015, 101, 149–158. [Google Scholar] [CrossRef]
- Bobel, A.; Kim, K.; Wolverton, C.; Walker, M.; Olson, G.B. Equilibrium composition variation of Q-phase precipitates in aluminum alloys. Acta Mater. 2017, 138, 150–160. [Google Scholar] [CrossRef]
- Ehlers, F.J.H.; Wenner, S.; Andersen, S.J.; Marioara, C.D.; Lefebvre, W.; Boothroyd, C.B.; Holmestad, R. Phase stabilization principle and precipitate-host lattice influences for Al–Mg–Si–Cu alloy precipitates. J. Mater. Sci. 2014, 49, 6413–6426. [Google Scholar] [CrossRef] [Green Version]
- Torsæter, M.; Ehlers, F.; Marioara, C.; Andersen, S.J.; Holmestad, R. Applying precipitate–host lattice coherency for compositional determination of precipitates in Al–Mg–Si–Cu alloys. Philos. Mag. 2012, 92, 3833–3856. [Google Scholar] [CrossRef]
- Marioara, C.D.; Andersen, S.J.; Stene, T.N.; Hasting, H.; Walmsley, J.; van Helvoort, A.T.J.; Holmestad, R. The effect of Cu on precipitation in Al–Mg–Si alloys. Philos. Mag. 2007, 87, 3385–3413. [Google Scholar] [CrossRef]
- Weng, Y.; Jia, Z.; Ding, L.; Liu, M.; Wu, X.; Liu, Q. Combined effect of pre-aging and Ag/Cu addition on the natural aging and bake hardening in Al-Mg-Si alloys. Prog. Nat. Sci. 2018, 28, 363–370. [Google Scholar] [CrossRef]
- Li, K.; Beche, A.; Song, M.; Sha, G.; Lu, X.; Zhang, K.; Du, Y.; Ringer, S.; Schryvers, D. Atomistic structure of Cu-containing β″ precipitates in an Al–Mg–Si–Cu alloy. Scr. Mater. 2014, 75, 86–89. [Google Scholar] [CrossRef]
- Sunde, J.K.; Marioara, C.D.; Holmestad, R. The effect of low Cu additions on precipitate crystal structures in overaged Al-Mg-Si(-Cu) alloys. Mater. Charact. 2020, 160, 110087. [Google Scholar] [CrossRef]
- Saito, T.; Ehlers, F.J.; Lefebvre, W.; Hernandez-Maldonado, D.; Bjørge, R.; Marioara, C.D.; Andersen, S.J.; Mørtsell, E.A.; Holmestad, R. Cu atoms suppress misfit dislocations at the β″/Al interface in Al–Mg–Si alloys. Scr. Mater. 2016, 110, 6–9. [Google Scholar] [CrossRef] [Green Version]
- Dong, L.; Chu, S.; Hu, B.; Zeng, X.; Chen, B. Atomic-scale investigation into precipitated phase thickening in Al-Si-Mg-Cu alloy. J. Alloys Compd. 2018, 766, 973–978. [Google Scholar] [CrossRef]
- Wolverton, C. Crystal structure and stability of complex precipitate phases in Al–Cu–Mg–(Si) and Al–Zn–Mg alloys. Acta Mater. 2001, 49, 3129–3142. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, 1133–1138. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Shang, S.-L.; Wang, Y.; Kim, D.; Liu, Z.-K. First-principles thermodynamics from phonon and Debye model: Application to Ni and Ni3Al. Comput. Mater. Sci. 2010, 47, 1040–1048. [Google Scholar] [CrossRef]
- Wang, J.; Shang, S.-L.; Wang, Y.; Mei, Z.-G.; Liang, Y.; Du, Y.; Liu, Z.-K. First-principles calculations of binary Al compounds: Enthalpies of formation and elastic properties. Calphad 2011, 35, 562–573. [Google Scholar] [CrossRef]
- Saito, T.; Ehlers, F.; Lefebvre, W.; Hernandez-Maldonado, D.; Bjørge, R.; Marioara, C.D.; Andersen, S.J.; Holmestad, R. HAADF-STEM and DFT investigations of the Zn-containing β″ phase in Al–Mg–Si alloys. Acta Mater. 2014, 78, 245–253. [Google Scholar] [CrossRef] [Green Version]
- Van Huis, M.; Chen, J.; Zandbergen, H.; Sluiter, M. Phase stability and structural relations of nanometer-sized, matrix-embedded precipitate phases in Al–Mg–Si alloys in the late stages of evolution. Acta Mater. 2006, 54, 2945–2955. [Google Scholar] [CrossRef]
- Mehl, M.J.; Osburn, J.E.; Papaconstantopoulos, D.A.; Klein, B.M. Structural properties of ordered high-melting-temperature intermetallic alloys from first-principles total-energy calculations. Phys. Rev. B 1990, 41, 10311–10323. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Du, Y.; Tao, X.; Ouyang, Y.; Zhang, L.; Chen, Q.; Engström, A. First-principles generated mechanical property database for multi-component Al alloys: Focusing on Al-rich corner. J. Min. Met. Sect. B Met. 2017, 53, 1–7. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Wu, Z.-J.; Zhao, E.-J.; Xiang, H.-P.; Hao, X.-F.; Liu, X.-J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Wang, D.; Amsler, M.; Hegde, V.I.; Saal, J.E.; Issa, A.; Zhou, B.-C.; Zeng, X.; Wolverton, C. Crystal structure, energetics, and phase stability of strengthening precipitates in Mg alloys: A first-principles study. Acta Mater. 2018, 158, 65–78. [Google Scholar] [CrossRef]
- Ravi, C. First-principles study of crystal structure and stability of Al–Mg–Si–(Cu) precipitates. Acta Mater. 2004, 52, 4213–4227. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.-K.; Chen, L.-Q.; Wolverton, C. First-principles calculations of β″-Mg5Si6/α-Al interfaces. Acta Mater. 2007, 55, 5934–5947. [Google Scholar] [CrossRef]
- Zhao, D.; Zhou, L.; Kong, Y.; Wang, A.; Wang, J.; Peng, Y.; Du, Y.; Ouyang, Y.; Zhang, W. Structure and thermodynamics of the key precipitated phases in the Al–Mg–Si alloys from first-principles calculations. J. Mater. Sci. 2011, 46, 7839–7849. [Google Scholar] [CrossRef]
- Grimvall, G.; Magyari-Köpe, B.; Ozolins, V.; Persson, K.A. Lattice instabilities in metallic elements. Rev. Mod. Phys. 2012, 84, 945–986. [Google Scholar] [CrossRef] [Green Version]
- Jain, A.C.P.; Marchand, D.; Glensk, A.; Ceriotti, M.; Curtin, W.A. Machine learning for metallurgy III: A neural network potential for Al-Mg-Si. Phys. Rev. Mater. 2021, 5, 053805. [Google Scholar] [CrossRef]
- Kobayashi, R.; Giofré, D.; Junge, T.; Ceriotti, M.; Curtin, W.A. Neural network potential for Al-Mg-Si alloys. Phys. Rev. Mater. 2017, 1, 053604. [Google Scholar] [CrossRef]
- Guan, Y.; Zhang, H.; Li, W. First-principles study on alloying stability, electronic structure, and mechanical properties of Al-based intermetallics. Phys. B Condens. Matter 2011, 406, 1149–1153. [Google Scholar] [CrossRef]
- Pugh, S. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Ravindran, P.; Fast, L.; Korzhavyi, P.; Johansson, B.; Wills, J.; Eriksson, O. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2. J. Appl. Phys. 1998, 84, 4891–4904. [Google Scholar] [CrossRef]
- Greaves, G.N.; Greer, A.L.; Lakes, R.S.; Rouxel, T. Poisson’s ratio and modern materials. Nat. Mater. 2011, 10, 823–837. [Google Scholar] [CrossRef]
- Ouyang, Y.; Liu, F.; Lu, T.; Tao, X.; Du, Y.; He, Y. First-principles investigation of the mechanical, electronic and thermophysical properties of Q-phase in Al–Mg–Si–Cu alloys. Comput. Mater. Sci. 2013, 67, 334–340. [Google Scholar] [CrossRef]
- Derlet, P.M.; Andersen, S.J.; Marioara, C.D.; Froseth, A.G. A first-principles study of the β″-phase in Al-Mg-Si alloys. J. Phys. Condens. Matter 2002, 14, 4011–4024. [Google Scholar] [CrossRef]
- Frøseth, A.G.; Høier, R.; Derlet, P.M.; Andersen, S.J.; Marioara, C.D. Bonding in MgSi and Al-Mg-Si compounds relevant to Al-Mg-Si alloys. Phys. Rev. B 2003, 67, 224106. [Google Scholar] [CrossRef] [Green Version]

 represents the Mg5Si6,
represents the Mg5Si6,  represents the Mg5Al2Si4,
represents the Mg5Al2Si4,  represents the Mg5AlCuSi4 where Cu atoms occupy a Si3 site,
represents the Mg5AlCuSi4 where Cu atoms occupy a Si3 site,  represents the Mg4Al2CuSi4 where Cu atoms occupy a Si3 site,
represents the Mg4Al2CuSi4 where Cu atoms occupy a Si3 site,  represents the Mg4AlCu2Si4 where Cu atoms occupy two Si3 sites, and
represents the Mg4AlCu2Si4 where Cu atoms occupy two Si3 sites, and  represents the Mg4Cu3Si4 where Cu atoms occupy a Mg1 site and two Si3 sites.
represents the Mg4Cu3Si4 where Cu atoms occupy a Mg1 site and two Si3 sites.
 represents the Mg5Si6,
represents the Mg5Si6,  represents the Mg5Al2Si4,
represents the Mg5Al2Si4,  represents the Mg5AlCuSi4 where Cu atoms occupy a Si3 site,
represents the Mg5AlCuSi4 where Cu atoms occupy a Si3 site,  represents the Mg4Al2CuSi4 where Cu atoms occupy a Si3 site,
represents the Mg4Al2CuSi4 where Cu atoms occupy a Si3 site,  represents the Mg4AlCu2Si4 where Cu atoms occupy two Si3 sites, and
represents the Mg4AlCu2Si4 where Cu atoms occupy two Si3 sites, and  represents the Mg4Cu3Si4 where Cu atoms occupy a Mg1 site and two Si3 sites.
represents the Mg4Cu3Si4 where Cu atoms occupy a Mg1 site and two Si3 sites.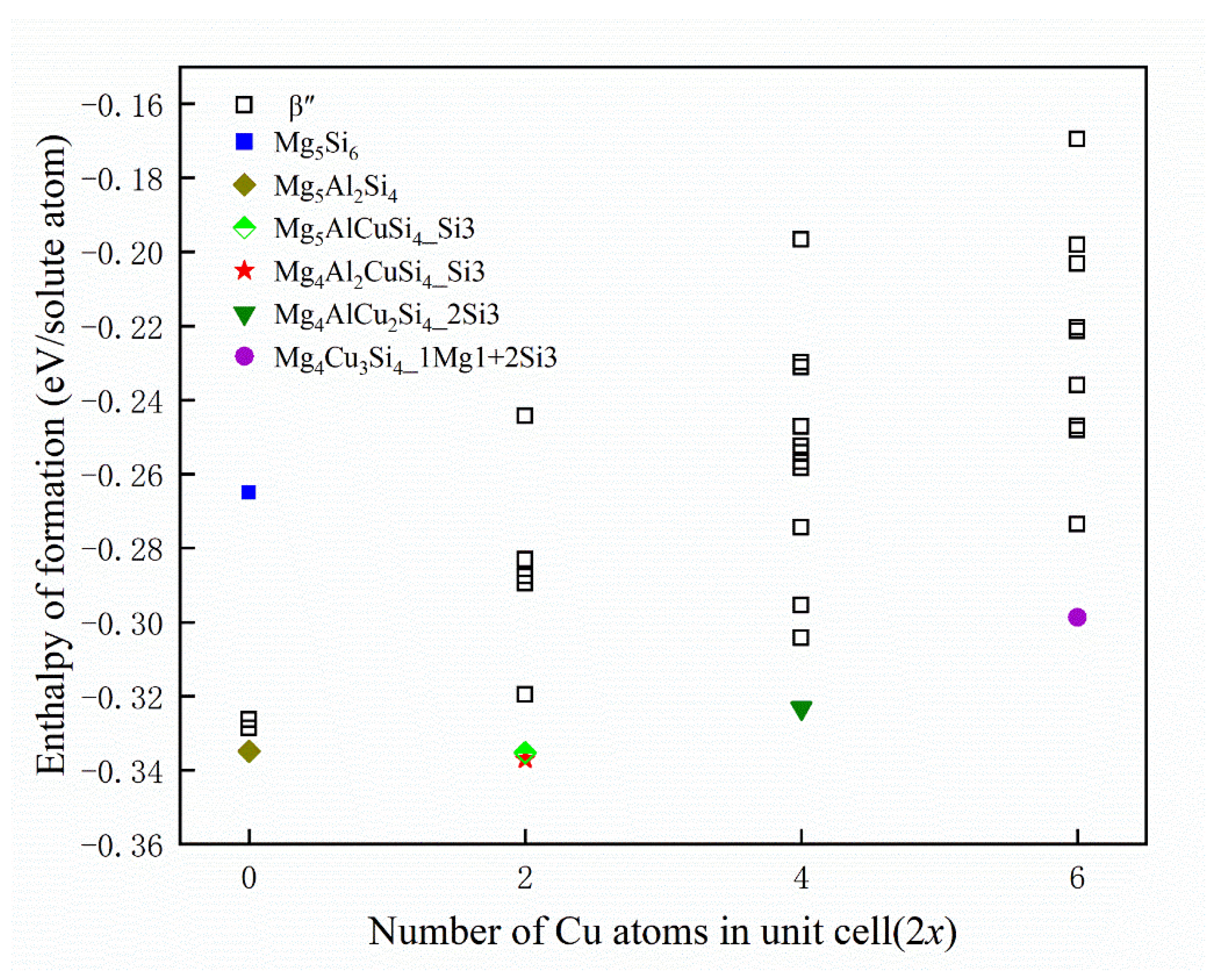
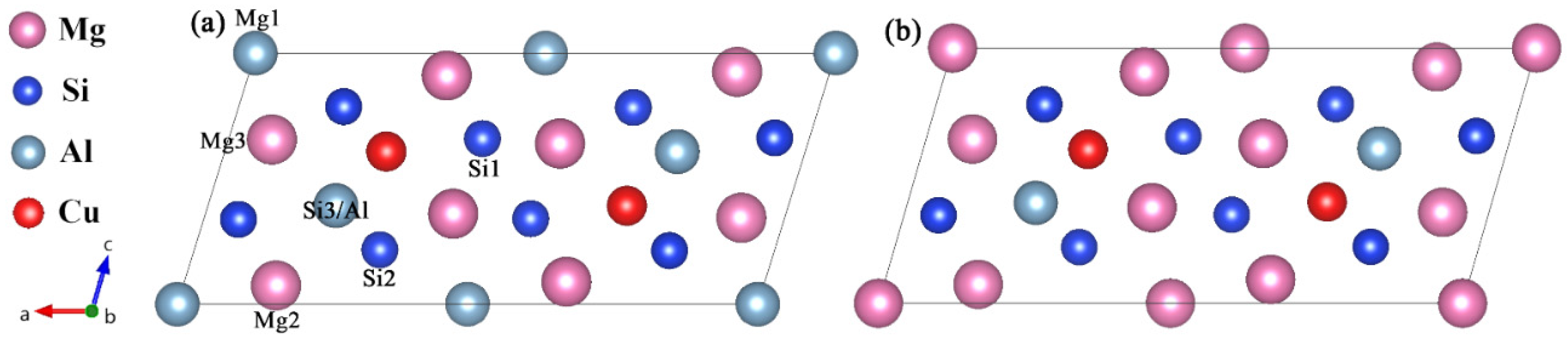
| Site | Occupation | x | y | z |
|---|---|---|---|---|
| Mg1 | 2a | 0 | 0 | 0 |
| Mg2 | 4i | 0.3419 | 0 | 0.099 |
| Mg3 | 4i | 0.4225 | 0 | 0.659 |
| Si1 | 4i | 0.0501 | 0 | 0.678 |
| Si2 | 4i | 0.1876 | 0 | 0.225 |
| Si3/Al | 4i | 0.2213 | 0 | 0.618 |
| Configurations | a (Å) | b (Å) | c (Å) | β (°) | Ref. |
|---|---|---|---|---|---|
| Mg5Si6 | 15.12 | 4.04 | 6.99 | 110.6 | |
| Mg5Si6 (exp.) | 15.16 ± 0.02 | 4.05 | 6.74 ± 0.02 | 105.3 ± 0.5 | [17] |
| Mg5Si6 (GGA) | 15.11 | 4.080 | 6.932 | 110.4 | [21] |
| Mg5Si6 (GGA) | 15.13 | 4.05 | 6.96 | 110 | [58] |
| Mg5Si6 (GGA) | 15.12 | 4.084 | 6.928 | 110.5 | [59] |
| Mg5Si6 (GGA) | 15.14 | 4.05 | 6.94 | 110 | [60] |
| Mg4Al3Si4 | 15.05 | 4.16 | 6.59 | 106.6 | |
| Mg4Al3Si4 (GGA) | 15.11 | 4.131 | 6.615 | 106.6 | [21] |
| Mg5Al2Si4 | 15.36 | 4.05 | 6.79 | 105.7 | |
| Mg5Al2Si4 (GGA) | 15.32 | 4.075 | 6.778 | 105.9 | [21] |
| Mg5Al2Si4 (GGA) | 15.50 | 4.05 | 6.74 | 106 | [19] |
| Mg6AlSi4 | 15.63 | 4.06 | 6.82 | 105.9 | |
| Mg6AlSi4 (GGA) | 15.59 | 4.069 | 6.830 | 106.1 | [21] |
| Mg4Al2CuSi4 | 14.78 | 4.02 | 6.69 | 107.3 | |
| Mg5AlCuSi4 | 15.08 | 3.95 | 6.86 | 106.2 | |
| Mg4AlCu2Si4 | 14.46 | 4.03 | 6.68 | 109.2 | |
| Mg4Cu3Si4 | 14.17 | 4.11 | 6.37 | 107.5 |
| Configurations | Cu Occupied Sites | xMg/(xMg + xSi) | xCu | ΔEβ″ (eV/Solute Atom) |
|---|---|---|---|---|
| Mg5Si6 | - | 0.45 | 0.00 | −0.2650 |
| Mg5Si6 [21] | - | 0.45 | 0.00 | −0.2665 |
| Mg4Al3Si4 | - | 0.50 | 0.00 | −0.3264 |
| Mg5Al2Si4 | - | 0.56 | 0.00 | −0.3348 |
| Mg5Al2Si4 [21] | - | 0.56 | 0.00 | −0.3456 |
| Mg6AlSi4 | - | 0.60 | 0.00 | −0.3286 |
| Mg6AlSi4 [21] | - | 0.60 | 0.00 | −0.3380 |
| Mg4Al3CuSi3 | 1 Si1 | 0.57 | 0.09 | −0.2896 |
| Mg4Al2CuSi4 | 1 Si3/Al | 0.50 | 0.09 | −0.3370 |
| Mg4Al2CuSi4 | 1 Mg1 | 0.50 | 0.09 | −0.3196 |
| Mg4Al3Cu2Si2 | 2 Si1 | 0.67 | 0.18 | −0.2525 |
| Mg4AlCu2Si4 | 2 Si3/Al | 0.50 | 0.18 | −0.3232 |
| Mg4Al2Cu2Si3 | 1 Si1 and 1 Si3 | 0.57 | 0.18 | −0.2567 |
| Mg4Al2Cu2Si3 | 1 Si1 and 1 Mg1 | 0.57 | 0.18 | −0.2583 |
| Mg4AlCu2Si4 | 1 Si3/Al and 1 Mg1 | 0.50 | 0.18 | −0.3043 |
| Mg4Al2Cu3Si2 | 2 Si1 and 1 Si3/Al | 0.67 | 0.27 | −0.2205 |
| Mg4AlCu3Si3 | 1 Si1 and 2 Si3/Al | 0.57 | 0.27 | −0.2737 |
| Mg4Al2Cu3Si2 | 2 Si1/Al and 1 Mg1 | 0.67 | 0.27 | −0.2215 |
| Mg4Cu3Si4 | 2 Si3/Al and 1 Mg1 | 0.50 | 0.27 | −0.2988 |
| Mg4AlCu3Si3 | 1 Si1 and 1 Si3/Al and 1 Mg1 | 0.57 | 0.27 | −0.2482 |
| Mg5Al2CuSi3 | 1 Si1 | 0.63 | 0.09 | −0.2831 |
| Mg5AlCuSi4 | 1 Si3/Al | 0.56 | 0.09 | −0.3352 |
| Mg5Al2Cu2Si2 | 2 Si1 | 0.71 | 0.18 | −0.2298 |
| Mg5Cu2Si4 | 2 Si3/Al | 0.56 | 0.18 | −0.2955 |
| Mg5AlCu2Si3 | 1 Si1 and 1 Si3 | 0.63 | 0.18 | −0.2542 |
| Mg5AlCu3Si2 | 2 Si1 and 1 Si3 | 0.71 | 0.27 | −0.2033 |
| Mg5Cu3Si3 | 1 Si1 and 2 Si3 | 0.63 | 0.27 | −0.2471 |
| Mg6AlCuSi3 | 1 Si1 | 0.67 | 0.09 | −0.2444 |
| Mg6CuSi4 | 1 Si3/Al | 0.60 | 0.09 | −0.2876 |
| Mg6AlCu2Si2 | 2 Si1 | 0.75 | 0.18 | −0.1967 |
| Mg6Cu2Si3 | 1 Si1 and 1 Si3 | 0.67 | 0.18 | −0.2311 |
| Mg5AlCu2Si3 | 1 Si1 and 1 Mg1 | 0.63 | 0.18 | −0.2472 |
| Mg5Cu2Si4 | 1 Si3/Al and 1 Mg1 | 0.56 | 0.18 | −0.2744 |
| Mg5AlCu3Si2 | 2 Si1 and 1 Mg1 | 0.71 | 0.27 | −0.1981 |
| Mg6Cu3Si2 | 2 Si1 and 1 Si3 | 0.75 | 0.27 | −0.1696 |
| Mg5Cu3Si3 | 1 Si1 and 1 Si3 and 1 Mg1 | 0.63 | 0.27 | −0.2361 |
| Configuration | C11 | C12 | C13 | C15 | C22 | C23 | C25 | C33 | C35 | C44 | C46 | C55 | C66 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mg5Si6 | 110 | 42 | 42 | −3 | 103 | 49 | 4 | 94 | 11 | 19 | 5 | 17 | 25 |
| Mg5Si6 [62] | 106 | 49 | 50 | −11 | 90 | 46 | 6 | 88 | 9 | 17 | 1 | 33 | 30 |
| Mg5Si6 [63] | 98 | 50 | 48 | 8 | 84 | 46 | 6 | 88 | 5.4 | 22 | −10 | 29 | 51 |
| Mg4Al3Si4 | 119 | 52 | 35 | −3 | 99 | 47 | 3 | 122 | 10 | 19 | −1 | 29 | 20 |
| Mg4Al3Si4 [62] | 114 | 46 | 48 | −4 | 104 | 49 | 6 | 104 | 7 | 21 | 0 | 34 | 23 |
| Mg4Al3Si4 [63] | 107 | 47 | 48 | 9 | 97 | 48 | 6 | 97 | 9 | 26 | 6 | 36 | 46 |
| Mg5Al2Si4 | 111 | 38 | 44 | −4 | 102 | 46 | 3 | 106 | 7 | 25 | 4 | 31 | 25 |
| Mg5Al2Si4 [62] | 108 | 42 | 48 | −3 | 95 | 46 | 5 | 100 | 3 | 23 | 4 | 33 | 27 |
| Mg5Al2Si4 [63] | 107 | 40 | 46 | −13 | 95 | 43 | 4 | 99 | 12 | 27 | 5 | 36 | 49 |
| Mg6AlSi4 | 121 | 28 | 40 | −5 | 125 | 28 | 2 | 117 | 6 | 28 | 4 | 35 | 21 |
| Mg4Al2CuSi4 | 136 | 44 | 48 | −13 | 133 | 43 | 9 | 130 | 14 | 25 | 3 | 35 | 23 |
| Mg5AlCuSi4 | 127 | 41 | 46 | −9 | 128 | 32 | 5 | 131 | 6 | 31 | 4 | 38 | 22 |
| Mg4AlCu2Si4 | 128 | 44 | 70 | −3 | 136 | 53 | 6 | 103 | 10 | 28 | 7 | 32 | 22 |
| Mg4Cu3Si4 | 128 | 47 | 75 | 7 | 153 | 43 | 3 | 115 | −6 | 20 | 3 | 51 | 26 |
| Configurations | B (GPa) | G (GPa) | E (GPa) | B/G | ν |
|---|---|---|---|---|---|
| Mg5Si6 | 62 | 22 | 60 | 2.77 | 0.34 |
| Mg5Si6 [63] | 62 | - | - | - | - |
| Mg4Al3Si4 | 67 | 26 | 69 | 2.57 | 0.33 |
| Mg4Al3Si4 [63] | 64 | - | - | - | - |
| Mg5Al2Si4 | 63 | 28 | 74 | 2.23 | 0.30 |
| Mg5Al2Si4 [63] | 61 | - | - | - | - |
| Mg6AlSi4 | 62 | 33 | 84 | 1.87 | 0.27 |
| Mg4Al2CuSi4 | 72 | 32 | 84 | 2.26 | 0.31 |
| Mg5AlCuSi4 | 69 | 34 | 88 | 2.01 | 0.29 |
| Mg4AlCu2Si4 | 76 | 28 | 74 | 2.73 | 0.34 |
| Mg4Cu3Si4 | 81 | 32 | 84 | 2.54 | 0.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, S.; Wang, J.; Zhang, D.; Wu, Q.; Kong, Y.; Du, Y. A First-Principles Study of the Cu-Containing β″ Precipitates in Al-Mg-Si-Cu Alloy. Materials 2021, 14, 7879. https://doi.org/10.3390/ma14247879
He S, Wang J, Zhang D, Wu Q, Kong Y, Du Y. A First-Principles Study of the Cu-Containing β″ Precipitates in Al-Mg-Si-Cu Alloy. Materials. 2021; 14(24):7879. https://doi.org/10.3390/ma14247879
Chicago/Turabian StyleHe, Shaozhi, Jiong Wang, Donglan Zhang, Qing Wu, Yi Kong, and Yong Du. 2021. "A First-Principles Study of the Cu-Containing β″ Precipitates in Al-Mg-Si-Cu Alloy" Materials 14, no. 24: 7879. https://doi.org/10.3390/ma14247879
APA StyleHe, S., Wang, J., Zhang, D., Wu, Q., Kong, Y., & Du, Y. (2021). A First-Principles Study of the Cu-Containing β″ Precipitates in Al-Mg-Si-Cu Alloy. Materials, 14(24), 7879. https://doi.org/10.3390/ma14247879






