Transferability of Molecular Potentials for 2D Molybdenum Disulphide
Abstract
1. Introduction
2. Computational Methodology
2.1. Ab Initio Calculations
2.2. Molecular Calculations
Molecular Potentials
- SW2013 [13]: the Stillinger–Weber (SW) potential fitted to an experimentally obtained phonon spectrum along the -M direction for bulk 2H-MoS.
- SW2015 [14]: the Stillinger–Weber (SW) potential derived from the valence force-field model.
- SW2016 [46]: the Stillinger–Weber (SW) potential fitted to lattice parameters, distance between two chalcogen atoms and elastic constants for SL 1H-MoS obtained from DFT calculations.
- REBO [48]: the reactive many-body potential (REBO) fitted to structure and energetics of Mo molecules, three-dimensional Mo crystals, two-dimensional Mo structures, small S molecules and binary Mo-S crystal structures.
- SNAP [49]: the machine-learning-based spectral neighbour analysis potential (SNAP) fitted to total energies and interatomic forces in SL 1H-MoS obtained from first-principles density functional theory (DFT) calculations.
- ReaxFF [50]: the reactive force-field (ReaxFF) parameters fitted to a training set of geometries, energies, and charges derived from DFT calculations for both clusters and periodic MoS systems.
3. Results
3.1. Structural and Mechanical Properties
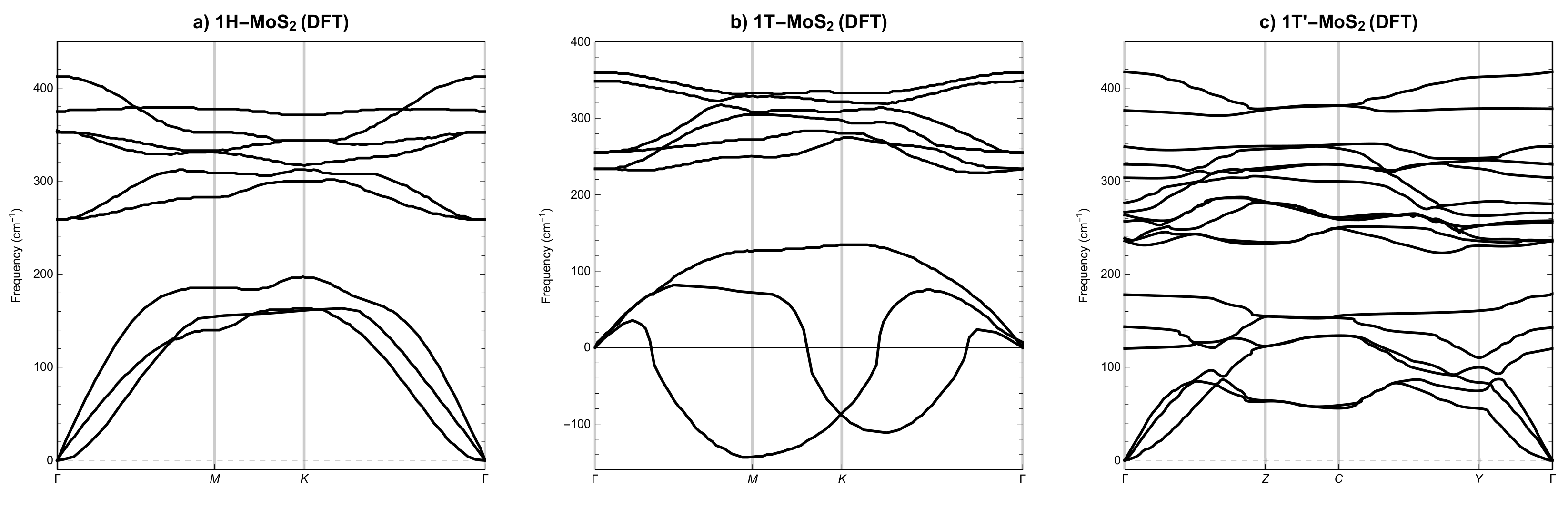
3.2. Phonon Spectra
4. Conclusions
- The transferability of analysed molecular potentials leaves much to be desired.
- Three potentials: SW2016, SW2017 and REBO demonstrate the best quantitative performance.
- None of the above three potentials correctly reproduces the dynamical stability of all SL MoS phases.
- Only the REBO potential distinguishes three different 2D molybdenum disulphide allotropes.
- Two potentials, ReaxFF and SNAP, demonstrate significantly lower quantitative efficiency.
- It seems that the low transferability of the analysed potentials is a result of the improper fitting of their parameters.
- To increase the transferability of potentials, the number of configurations to be taken into account in the parameter optimisation process should be significantly increased.
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| G6-TMD | Group 6 transition metal dichalcogenide |
| SL MoS | single-layer molybdenum disulphide |
| MS | molecular statics |
| DFT | density functional theory |
| DFPT | density functional perturbation theory |
| PP-PW | pseudopotential, plane-wave |
| XC | exchange-correlation |
| LDA | local density approximation |
| GGA | generalized gradient approximation |
| PBE | Perdew–Burke–Ernzerhof |
Appendix A
References
- Samadi, M.; Sarikhani, N.; Zirak, M.; Zhang, H.; Zhang, H.L.; Moshfegh, A.Z. Group 6 transition metal dichalcogenide nanomaterials: Synthesis, applications and future perspectives. Nanoscale Horiz. 2018, 3, 90–204. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.; Novoselov, K. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Manzeli, S.; Ovchinnikov, D.; Pasquier, D.; Yazyev, O.V.; Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2017, 2, 17033. [Google Scholar] [CrossRef]
- Maździarz, M.; Mrozek, A.; Kuś, W.; Burczyński, T. Anisotropic-Cyclicgraphene: A New Two-Dimensional Semiconducting Carbon Allotrope. Materials 2018, 11, 432. [Google Scholar] [CrossRef]
- Zhao, X.; Ning, S.; Fu, W.; Pennycook, S.J.; Loh, K.P. Differentiating Polymorphs in Molybdenum Disulfide via Electron Microscopy. Adv. Mater. 2018, 30, 1802397. [Google Scholar] [CrossRef]
- Esteban-Puyuelo, R.; Sarma, D.D.; Sanyal, B. Complexity of mixed allotropes of MoS2 unraveled by first-principles theory. Phys. Rev. B 2020, 102, 165412. [Google Scholar] [CrossRef]
- Tadmor, E.B.; Miller, R.E. Modeling Materials: Continuum, Atomistic and Multiscale Techniques; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Rowe, P.; Deringer, V.L.; Gasparotto, P.; Csányi, G.; Michaelides, A. An accurate and transferable machine learning potential for carbon. J. Chem. Phys. 2020, 153, 034702. [Google Scholar] [CrossRef]
- Mrozek, A. Basic mechanical properties of 2h and 1t single-layer molybdenum disulfide polymorphs. a short comparison of various atomic potentials. Int. J. Multiscale Comput. Eng. 2019, 17, 339–359. [Google Scholar] [CrossRef]
- Xiong, S.; Cao, G. Molecular dynamics simulations of mechanical properties of monolayer MoS2. Nanotechnology 2015, 26, 185705. [Google Scholar] [CrossRef]
- Xu, K.; Gabourie, A.J.; Hashemi, A.; Fan, Z.; Wei, N.; Farimani, A.B.; Komsa, H.P.; Krasheninnikov, A.V.; Pop, E.; Ala-Nissila, T. Thermal transport in MoS2 from molecular dynamics using different empirical potentials. Phys. Rev. B 2019, 99, 054303. [Google Scholar] [CrossRef]
- Wen, M.; Shirodkar, S.N.; Plecháč, P.; Kaxiras, E.; Elliott, R.S.; Tadmor, E.B. A force-matching Stillinger-Weber potential for MoS2: Parameterization and Fisher information theory based sensitivity analysis. J. Appl. Phys. 2017, 122, 244301. [Google Scholar] [CrossRef]
- Jiang, J.W.; Park, H.S.; Rabczuk, T. Molecular dynamics simulations of single-layer molybdenum disulphide (MoS2): Stillinger-Weber parametrization, mechanical properties, and thermal conductivity. J. Appl. Phys. 2013, 114, 064307. [Google Scholar] [CrossRef]
- Jiang, J.W. Parametrization of Stillinger–Weber potential based on valence force field model: Application to single-layer MoS2 and black phosphorus. Nanotechnology 2015, 26, 315706. [Google Scholar] [CrossRef] [PubMed]
- Mortazavi, B.; Ostadhossein, A.; Rabczuk, T.; van Duin, A. Mechanical response of all-MoS2 single-layer hetrostructures: A ReaxFF investigation. Phys. Chem. Chem. Phys. 2016, 18, 23695–23701. [Google Scholar] [CrossRef] [PubMed]
- Bao, H.; Huang, Y.; Yang, Z.; Sun, Y.; Bai, Y.; Miao, Y.; Chu, P.K.; Xu, K.; Ma, F. Molecular Dynamics Simulation of Nanocrack Propagation in Single-Layer MoS2 Nanosheets. J. Phys. Chem. C 2018, 122, 1351–1360. [Google Scholar] [CrossRef]
- Pang, H.; Li, M.; Gao, C.; Huang, H.; Zhuo, W.; Hu, J.; Wan, Y.; Luo, J.; Wang, W. Phase Transition of Single-Layer Molybdenum Disulfide Nanosheets under Mechanical Loading Based on Molecular Dynamics Simulations. Materials 2018, 11, 502. [Google Scholar] [CrossRef]
- Javeed Akhter, M.; Kuś, W.; Mrozek, A.; Burczyński, T. Mechanical Properties of Monolayer MoS2 with Randomly Distributed Defects. Materials 2020, 13, 1307. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Weber, T.A. Computer simulation of local order in condensed phases of silicon. Phys. Rev. B 1985, 31, 5262–5271. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Gonze, X.; Jollet, F.; Araujo, F.A.; Adams, D.; Amadon, B.; Applencourt, T.; Audouze, C.; Beuken, J.M.; Bieder, J.; Bokhanchuk, A.; et al. Recent developments in the ABINIT software package. Comput. Phys. Commun. 2016, 205, 106–131. [Google Scholar] [CrossRef]
- Gonze, X.; Amadon, B.; Antonius, G.; Arnardi, F.; Baguet, L.; Beuken, J.M.; Bieder, J.; Bottin, F.; Bouchet, J.; Bousquet, E.; et al. The ABINIT project: Impact, environment and recent developments. Comput. Phys. Commun. 2020, 248, 107042. [Google Scholar] [CrossRef]
- Hamann, D.R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef]
- van Setten, M.; Giantomassi, M.; Bousquet, E.; Verstraete, M.; Hamann, D.; Gonze, X.; Rignanese, G.M. The PseudoDojo: Training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 2018, 226, 39–54. [Google Scholar] [CrossRef]
- Bloch, F. Bemerkung zur Elektronentheorie des Ferromagnetismus und der elektrischen Leitfähigkeit. Zeitschrift für Physik 1929, 57, 545–555. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Lehtola, S.; Steigemann, C.; Oliveira, M.J.; Marques, M.A. Recent developments in LIBXC—A comprehensive library of functionals for density functional theory. SoftwareX 2018, 7, 1–5. [Google Scholar] [CrossRef]
- Calandra, M. Chemically exfoliated single-layer MoS2: Stability, lattice dynamics, and catalytic adsorption from first principles. Phys. Rev. B 2013, 88, 245428. [Google Scholar] [CrossRef]
- Maździarz, M.; Mościcki, T. Structural, mechanical, optical, thermodynamical and phonon properties of stable ReB2 polymorphs from density functional calculations. J. Alloys Compd. 2016, 657, 878–888. [Google Scholar] [CrossRef]
- Hamann, D.R.; Wu, X.; Rabe, K.M.; Vanderbilt, D. Metric tensor formulation of strain in density-functional perturbation theory. Phys. Rev. B 2005, 71, 035117. [Google Scholar] [CrossRef]
- Grimvall, G.; Magyari-Köpe, B.; Ozoliņš, V.; Persson, K.A. Lattice instabilities in metallic elements. Rev. Mod. Phys. 2012, 84, 945–986. [Google Scholar] [CrossRef]
- Maździarz, M. Comment on ‘The Computational 2D Materials Database: High-throughput modeling and discovery of atomically thin crystals’. 2D Mater. 2019, 6, 048001. [Google Scholar] [CrossRef]
- Maździarz, M.; Mościcki, T. New Zirconium Diboride Polymorphs–First-Principles Calculations. Materials 2020, 13, 3022. [Google Scholar] [CrossRef]
- Hinuma, Y.; Pizzi, G.; Kumagai, Y.; Oba, F.; Tanaka, I. Band structure diagram paths based on crystallography. Comput. Mater. Sci. 2017, 128, 140–184. [Google Scholar] [CrossRef]
- Řehák, P.; Černý, M.; Pokluda, J. Dynamic stability of fcc crystals under isotropic loading from first principles. J. Phys. Condens. Matter 2012, 24, 215403. [Google Scholar] [CrossRef]
- Maździarz, M.; Young, T.D.; Dłuzewski, P.; Wejrzanowski, T.; Kurzydłowski, K.J. Computer modelling of nanoindentation in the limits of a coupled molecular–statics and elastic scheme. J. Comput. Theor. Nanosci. 2010, 7, 1172–1181. [Google Scholar] [CrossRef]
- Maździarz, M.; Young, T.D.; Jurczak, G. A study of the affect of prerelaxation on the nanoindentation process of crystalline copper. Arch. Mech. 2011, 63, 533. [Google Scholar]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Maździarz, M.; Gajewski, M. Estimation of Isotropic Hyperelasticity Constitutive Models to Approximate the Atomistic Simulation Data for Aluminium and Tungsten Monocrystals. Comput. Model. Eng. Sci. 2015, 105, 123–150. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Carreras, A.; Togo, A.; Tanaka, I. DynaPhoPy: A code for extracting phonon quasiparticles from molecular dynamics simulations. Comput. Phys. Commun. 2017, 221, 221–234. [Google Scholar] [CrossRef]
- Kandemir, A.; Yapicioglu, H.; Kinaci, A.; Çağın, T.; Sevik, C. Thermal transport properties of MoS2 and MoSe2 monolayers. Nanotechnology 2016, 27, 055703. [Google Scholar] [CrossRef]
- Tadmor, E.B.; Elliott, R.S.; Sethna, J.P.; Miller, R.E.; Becker, C.A. The potential of atomistic simulations and the Knowledgebase of Interatomic Models. JOM 2011, 63, 17. [Google Scholar] [CrossRef]
- Liang, T.; Phillpot, S.R.; Sinnott, S.B. Parametrization of a reactive many-body potential for Mo–S systems. Phys. Rev. B 2012, 79, 245110, Erratum in 2012, 85, 199903. [Google Scholar] [CrossRef]
- Gu, X.; Zhao, C. Thermal conductivity of single-layer MoS2(1−x)Se2x alloys from molecular dynamics simulations with a machine-learning-based interatomic potential. Comput. Mater. Sci. 2019, 165, 74–81. [Google Scholar] [CrossRef]
- Ostadhossein, A.; Rahnamoun, A.; Wang, Y.; Zhao, P.; Zhang, S.; Crespi, V.H.; van Duin, A.C.T. ReaxFF Reactive Force-Field Study of Molybdenum Disulfide (MoS2). J. Phys. Chem. Lett. 2017, 8, 631–640. [Google Scholar] [CrossRef]
- Antunes, F.P.N.; Vaiss, V.S.; Tavares, S.R.; Capaz, R.B.; Leitão, A.A. Van der Waals interactions and the properties of graphite and 2H-, 3R- and 1T-MoS2: A comparative study. Comput. Mater. Sci. 2018, 152, 146–150. [Google Scholar] [CrossRef]
- Råsander, M.; Moram, M.A. On the accuracy of commonly used density functional approximations in determining the elastic constants of insulators and semiconductors. J. Chem. Phys. 2015, 143. [Google Scholar] [CrossRef] [PubMed]
- Maździarz, M.; Mrozek, A.; Kuś, W.; Burczyński, T. First-principles study of new X-graphene and Y-graphene polymorphs generated by the two stage strategy. Mater. Chem. Phys. 2017, 202, 7–14. [Google Scholar] [CrossRef]
- Stokes, H.T.; Hatch, D.M. FINDSYM: Program for identifying the space-group symmetry of a crystal. J. Appl. Crystallogr. 2005, 38, 237–238. [Google Scholar] [CrossRef]
- Duerloo, K.A.; Li, Y.; Reed, E. Structural phase transitions in two-dimensional Mo- and W-dichalcogenide monolayers. Nat. Commun. 2014, 5, 4214. [Google Scholar] [CrossRef]
- Hu, T.; Li, R.; Dong, J. A new (2 × 1) dimerized structure of monolayer 1T-molybdenum disulfide, studied from first principles calculations. J. Chem. Phys. 2013, 139, 174702. [Google Scholar] [CrossRef]
- Hung, N.T.; Nugraha, A.R.T.; Saito, R. Two-dimensional MoS2 electromechanical actuators. J. Phys. D Appl. Phys. 2018, 51, 075306. [Google Scholar] [CrossRef]
- Luo, X.; Zhao, Y.; Zhang, J.; Xiong, Q.; Quek, S.Y. Anomalous frequency trends in MoS2 thin films attributed to surface effects. Phys. Rev. B 2013, 88, 075320. [Google Scholar] [CrossRef]
- Tornatzky, H.; Gillen, R.; Uchiyama, H.; Maultzsch, J. Phonon dispersion in MoS2. Phys. Rev. B 2019, 99, 144309. [Google Scholar] [CrossRef]
- Singh, A.; Shirodkar, S.N.; Waghmare, U.V. 1H and 1T polymorphs, structural transitions and anomalous properties of (Mo,W)(S,Se)2 monolayers: First-principles analysis. 2D Mater. 2015, 2, 035013. [Google Scholar] [CrossRef]
- Soni, H.; Jha, P.K. Ab-initio study of dynamical properties of two dimensional MoS2 under strain. AIP Adv. 2015, 5, 107103. [Google Scholar] [CrossRef]
- Molina-Sánchez, A.; Wirtz, L. Phonons in single-layer and few-layer MoS2 and WS2. Phys. Rev. B 2011, 84, 155413. [Google Scholar] [CrossRef]
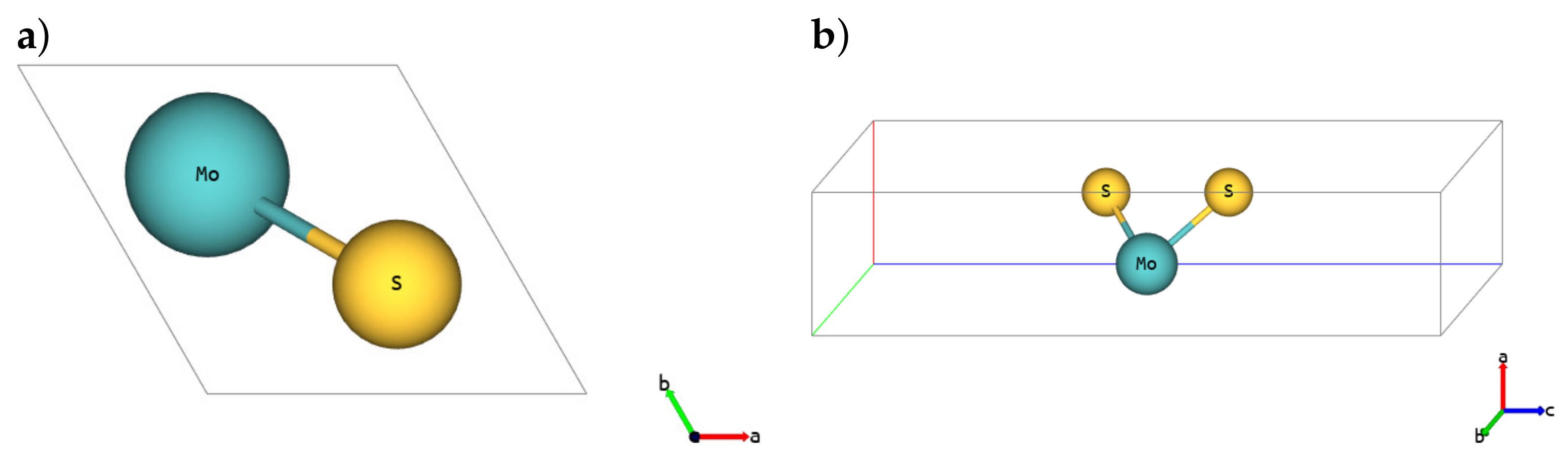
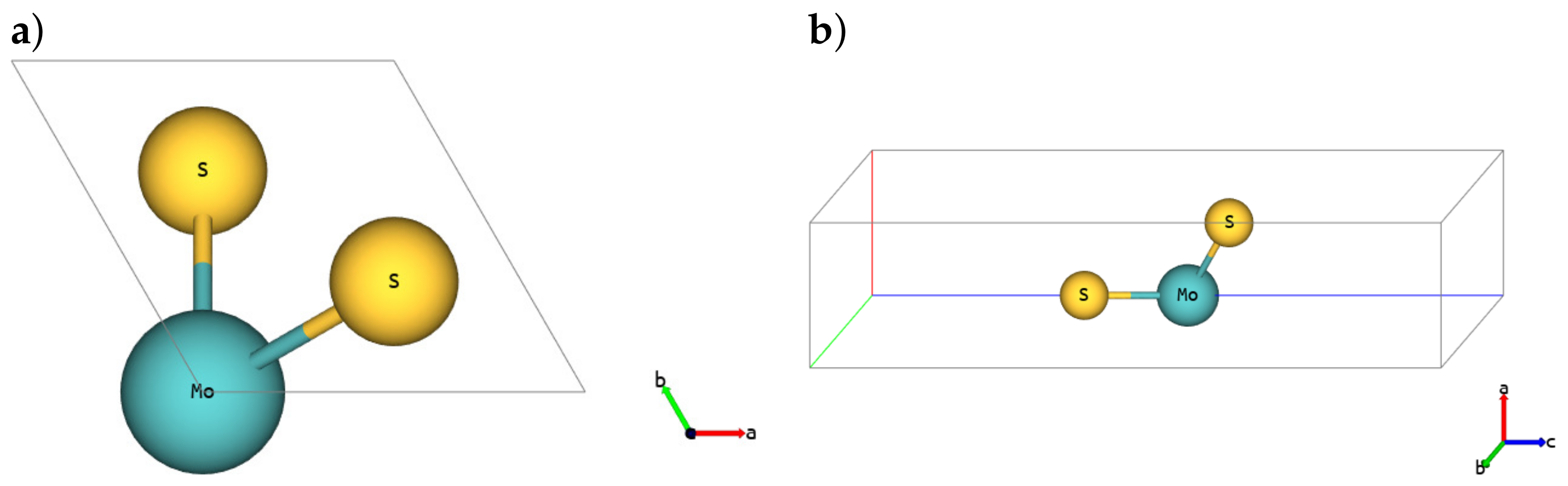
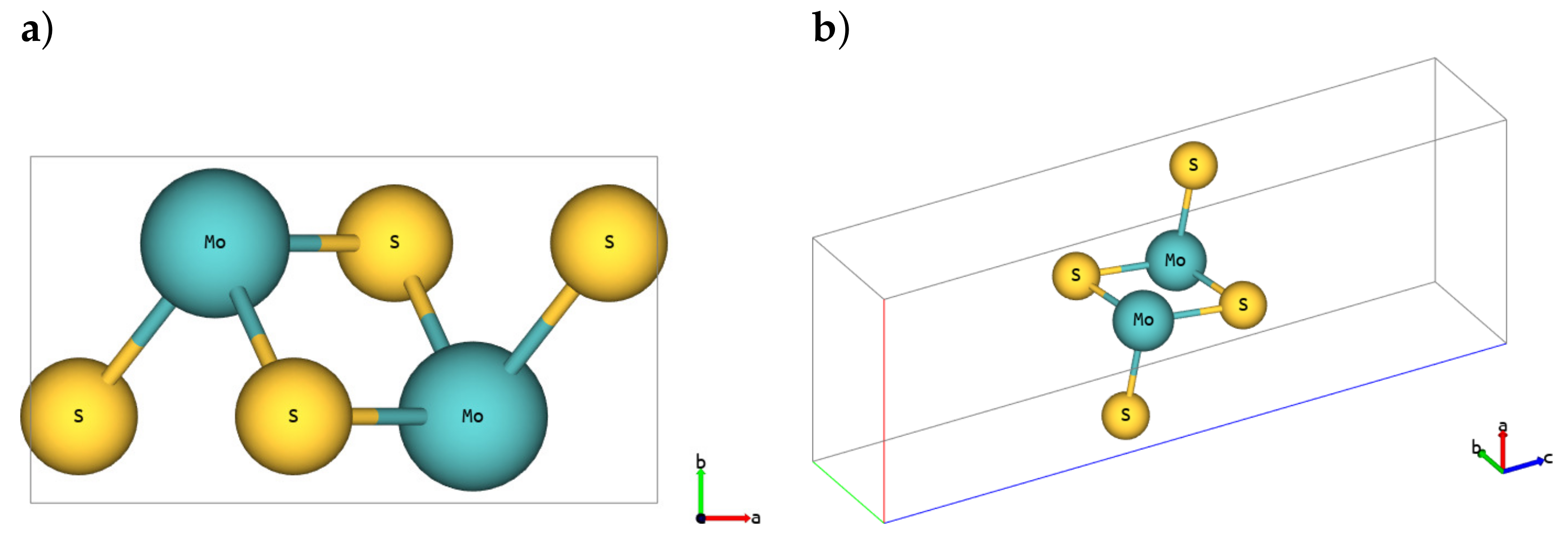
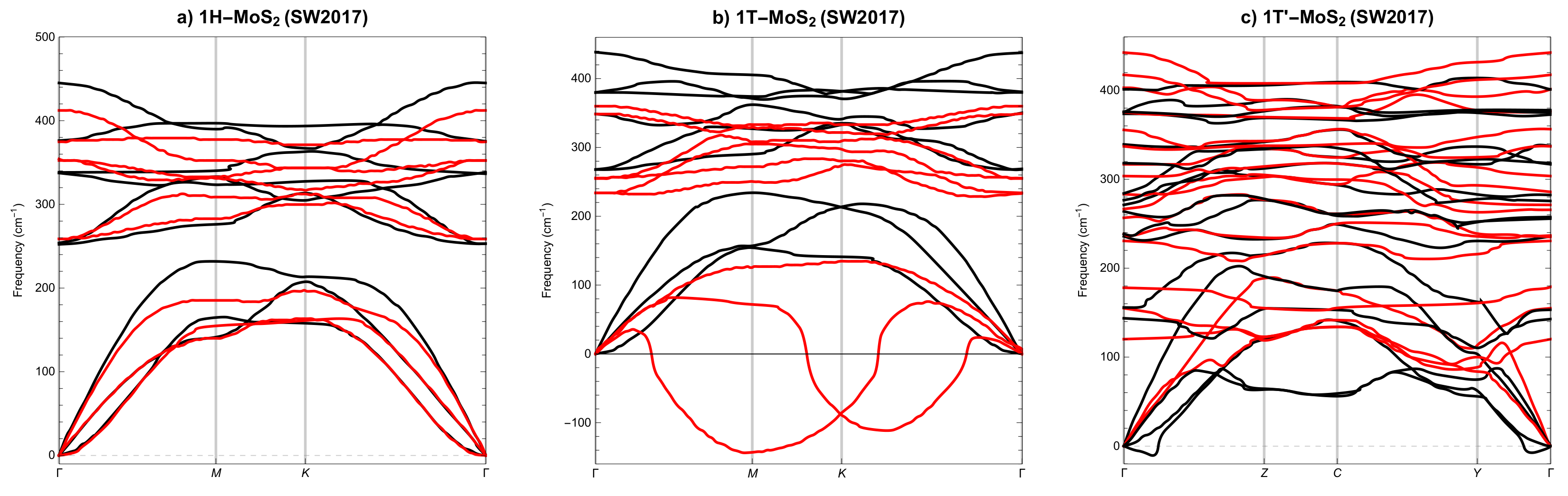
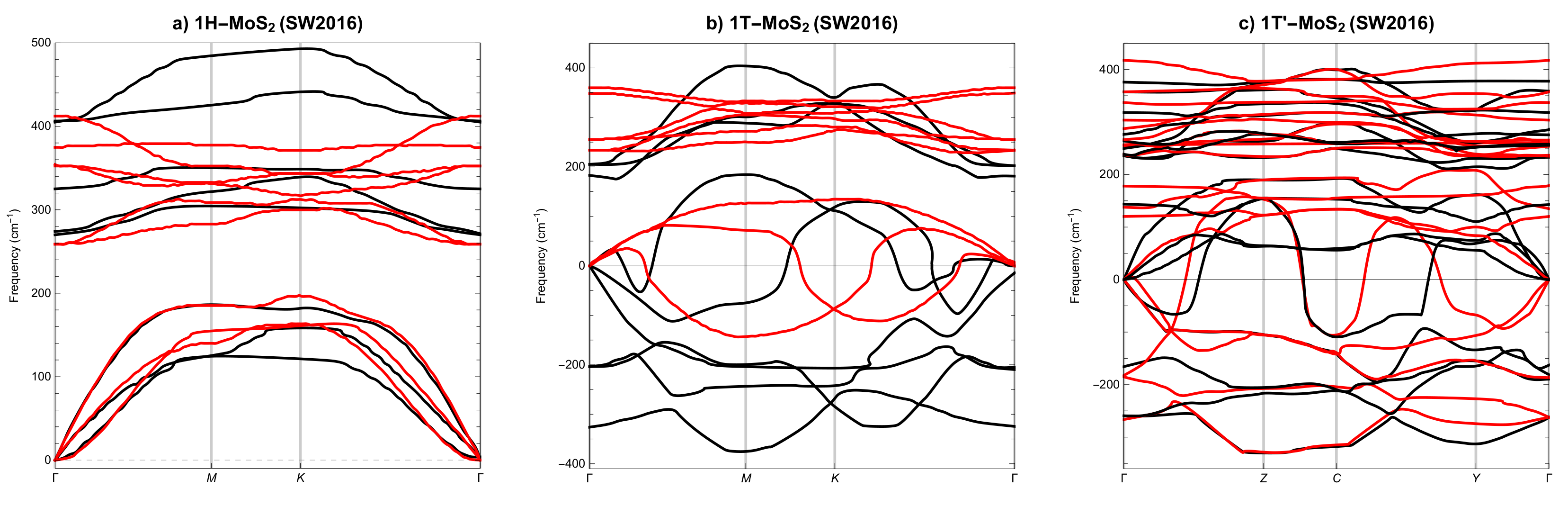
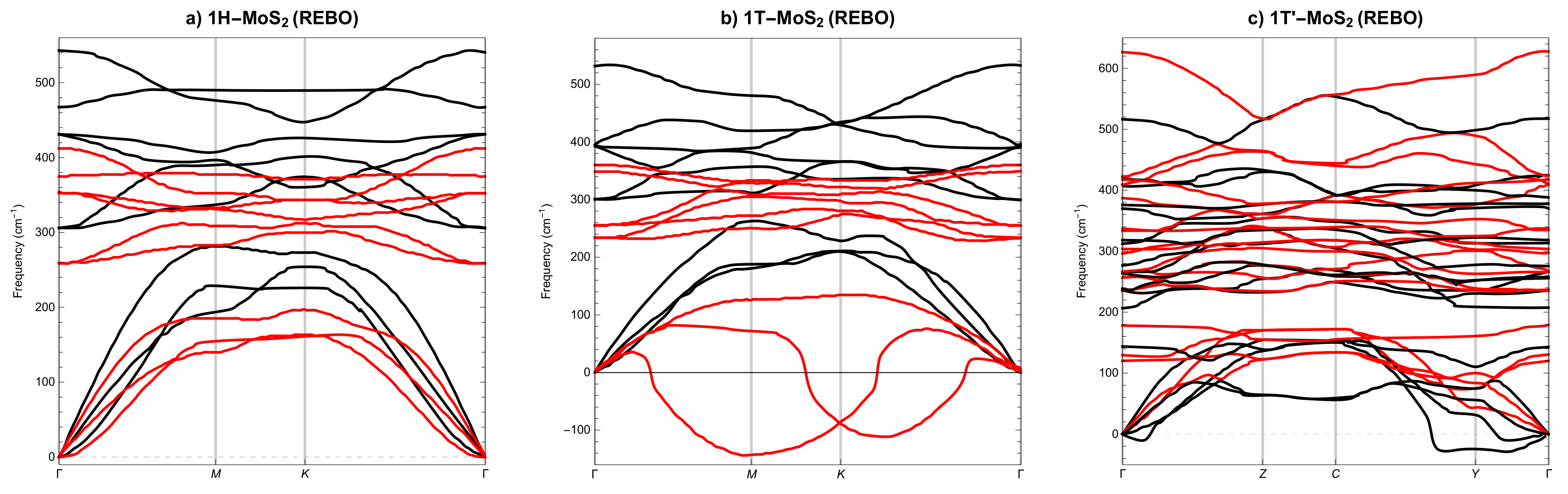
| Polymorph | 1H | 1T | 1T′ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Source | Present | Exp. | DFT | Present | Exp. | DFT | Present | Exp. | DFT |
| a | 3.165 | 3.157 a | 3.183 b | 3.194 | 3.179 b | 5.751 | 5.717 b | ||
| b | 3.165 | 3.157 a | 3.183 b | 3.194 | 3.176 b | 3.177 | 3.179 b | ||
| 5.64 | 5.35 a | 5.52 | 5.56 | ||||||
| 2.403 | 2.38 a | 2.43 a | 2.422 | 2.430 c | 2.415 ‡ | ||||
| 3.120 | 3.116 a | 3.11 a | 3.142 | 3.184 c | 3.364 | ||||
| 126.5 | 127.2 d | 84.1 | 103.8 d | 68.1 | 94.0 d | ||||
| 126.5 | 127.2 d | 84.1 | 103.8 d | 78.9 | 119.2 d | ||||
| 28.5 | 25.8 d | 5.0 | −2.5 d | 18.2 | 17.2 d | ||||
| 49.0 | 51.0 d | 39.6 | 52.8 d | 43.2 | 37.5 d | ||||
| 155.0 | 89.1 | 90.9 | |||||||
| 98.0 | 79.1 | 56.1 | |||||||
| 98.0 | 79.1 | 86.4 | |||||||
| Method | DFT | SW2013 | SW2015 | SW2016 | SW2017 | REBO | SNAP | ReaxFF |
|---|---|---|---|---|---|---|---|---|
| a | 3.165 | 3.062 | 3.117 | 3.174 | 3.196 | 3.168 | 3.139 | 3.186 |
| b | 3.165 | 3.062 | 3.117 | 3.174 | 3.196 | 3.168 | 3.139 | 3.186 |
| 5.64 | 3.00 | 0.62 | 1.84 | 5.11 | 7.16 | 2.28 | 5.05 | |
| 2.403 | 2.399 | 2.382 | 2.515 | 2.441 | 2.445 | 2.392 | 2.431 | |
| 3.120 | 4.223 | 4.257 | 4.032 | 3.194 | 3.242 | 3.124 | 3.183 | |
| 126.5 | 103.9 | 45.8 | 90.0 | 118.9 | 154.4 | 140.3 | 237.3 | |
| 126.5 | 103.9 | 45.8 | 90.0 | 118.9 | 154.4 | 140.3 | 262.4 | |
| 28.5 | 33.4 | 8.0 | 30.1 | 40.9 | 45.8 | 35.7 | 121.2 | |
| 49.0 | 35.2 | 18.9 | 30.0 | 39.0 | 54.3 | 52.3 | 71.2 | |
| 155.0 | 137.3 | 53.8 | 120.1 | 159.8 | 200.2 | 176.0 | 370.4 | |
| 98.0 | 70.5 | 37.8 | 59.9 | 78.0 | 108.6 | 104.6 | 129.3 | |
| 98.0 | 70.4 | 37.8 | 60.0 | 78.0 | 108.6 | 104.6 | 142.4 | |
| MAPE | 19.797 | 48.204 | 25.342 | 11.263 | 16.602 | 11.886 | 66.398 |
| Method | DFT | SW2013 | SW2015 | SW2016 | SW2017 | REBO | SNAP | ReaxFF |
|---|---|---|---|---|---|---|---|---|
| a | 3.194 | 3.062 * | 3.117 * | 3.174 * | 3.307 | 3.194 | 3.072 | 3.162 |
| b | 3.194 | 3.062 * | 3.117 * | 3.174 * | 3.307 | 3.194 | 3.072 | 3.162 |
| 5.52 | 3.00 | 0.62 | 1.84 | 4.96 | 7.05 | 2.31 | 4.84 | |
| 2.422 | 2.399 | 2.382 | 2.515 | 2.42 | 2.445 | 2.476 | 2.433 | |
| 3.142 | 4.223 | 4.257 | 4.032 | 2.973 | 3.211 | 3.454 | 3.203 | |
| 84.1 | 103.9 | 45.8 | 91.7 | 121.8 | 118.2 | 437.1 | 173.3 | |
| 84.1 | 103.9 | 45.8 | 91.7 | 121.8 | 118.2 | 437.1 | 32.1 | |
| 5.0 | 33.4 | 8.0 | 28.4 | 28.6 | 32.4 | 6.1 | 83.8 | |
| 39.6 | 35.2 | 18.9 | 31.7 | 46.6 | 42.9 | 215.5 | 9.4 | |
| 89.1 | 137.3 | 53.8 | 120.1 | 150.4 | 150.6 | 443.2 | 147.8 | |
| 79.1 | 70.5 | 37.8 | 63.3 | 93.2 | 85.8 | 431.0 | 57.6 | |
| 79.2 | 70.4 | 37.8 | 63.4 | 93.2 | 85.8 | 431.0 | 18.8 | |
| MAPE | 65.962 | 39.849 | 56.735 | 58.860 | 62.843 | 222.509 | 167.192 |
| Method | DFT | SW2013 | SW2015 | SW2016 | SW2017 | REBO | SNAP | ReaxFF |
|---|---|---|---|---|---|---|---|---|
| a | 5.751 | 4.944 | 5.757 | 5.263 | 5.728 † | 5.563 | 5.321 † | 5.609 |
| b | 3.177 | 3.062 | 3.148 | 3.172 | 3.307 † | 3.245 | 3.072 † | 3.209 |
| 5.56 | 3.02 | 0.55 | 1.87 | 4.96 | 6.93 | 2.31 | 4.83 | |
| ‡ | 2.415 | 2.399 | 2.406 | 2.504 | 2.42 | 2.468 | 2.476 | 2.490 |
| 3.364 | 4.641 | 5.173 | 4.142 | 2.973 | 3.781 | 3.454 | 3.399 | |
| 68.1 | 1.1 | 0.0 | 60.4 | 121.8 | 56.8 | 437.1 | 120.1 | |
| 78.9 | 100.5 | 37.6 | 94.6 | 121.8 | 113.0 | 437.1 | 255.7 | |
| 18.2 | 1.1 | 0.0 | 20.3 | 28.6 | 23.1 | 6.1 | 68.1 | |
| 43.2 | 27.1 | 0.0 | 26.9 | 46.6 | 70.5 | 215.5 | 6.4 | |
| 90.9 | 100.5 | 37.6 | 88.4 | 150.4 | 121.3 | 443.2 | 194.3 | |
| 56.1 | 1.1 | 0.0 | 66.6 | 93.2 | 48.5 | 431.0 | 181.5 | |
| 86.4 | 54.2 | 0.0 | 53.8 | 93.2 | 141.0 | 431.0 | 12.8 | |
| MAPE | 42.070 | 63.020 | 20.110 | 30.399 | 25.395 | 249.177 | 91.913 | |
| ∑MAPE | 127.830 | 151.074 | 102.187 | 100.522 | 104.840 | 483.573 | 325.504 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maździarz, M. Transferability of Molecular Potentials for 2D Molybdenum Disulphide. Materials 2021, 14, 519. https://doi.org/10.3390/ma14030519
Maździarz M. Transferability of Molecular Potentials for 2D Molybdenum Disulphide. Materials. 2021; 14(3):519. https://doi.org/10.3390/ma14030519
Chicago/Turabian StyleMaździarz, Marcin. 2021. "Transferability of Molecular Potentials for 2D Molybdenum Disulphide" Materials 14, no. 3: 519. https://doi.org/10.3390/ma14030519
APA StyleMaździarz, M. (2021). Transferability of Molecular Potentials for 2D Molybdenum Disulphide. Materials, 14(3), 519. https://doi.org/10.3390/ma14030519





