First-Principles Studies for Electronic Structure and Optical Properties of p-Type Calcium Doped α-Ga2O3
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
3.1. Geometrical Structures
3.2. Electronic Structure
3.2.1. Electron Charge Density
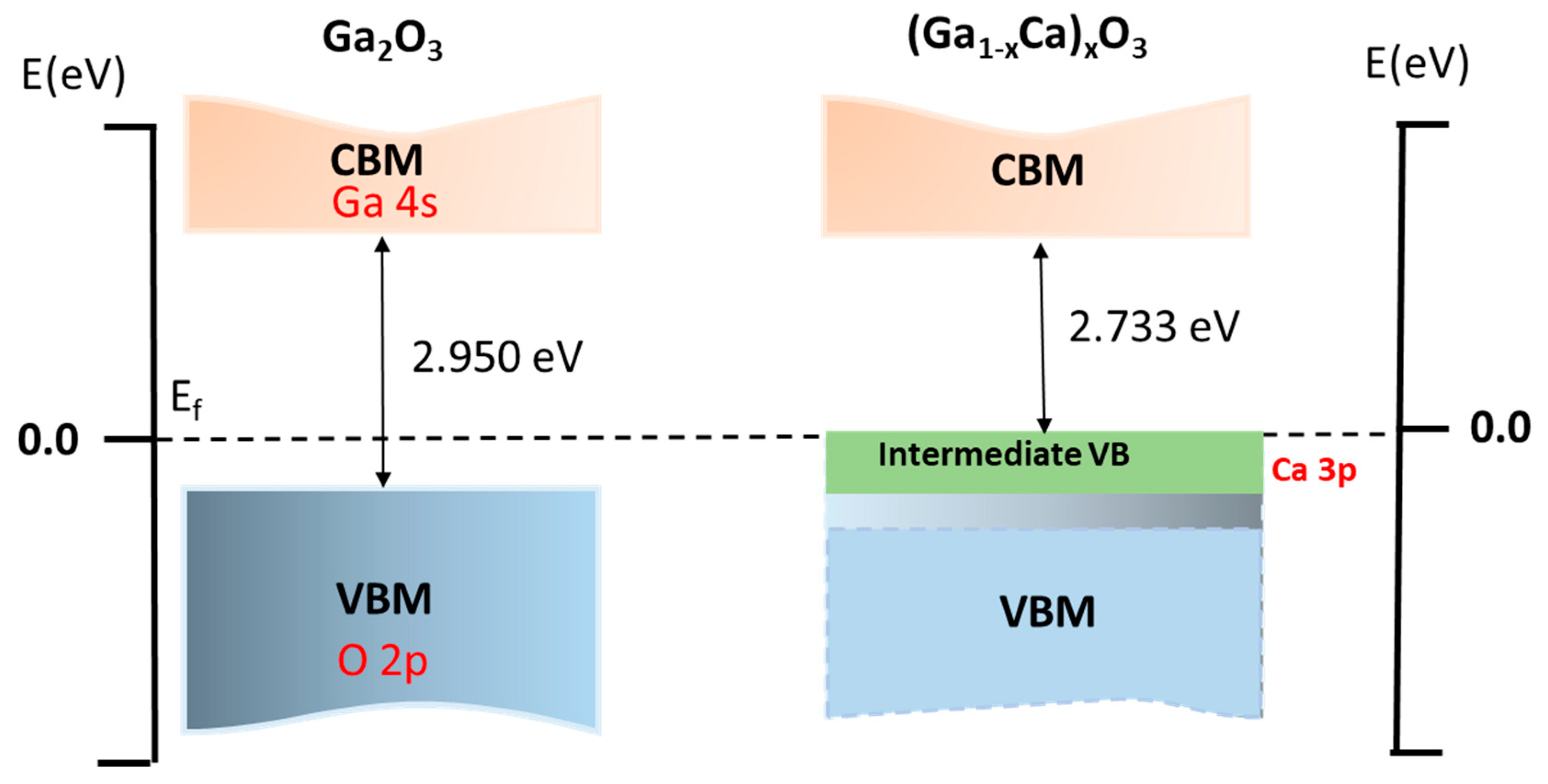
3.2.2. Band Structure and Density of States
3.3. Optical Properties
3.3.1. Theoretical Description and Optical Properties
3.3.2. Dielectric Function
3.3.3. Absorption and Reflectivity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dang, G.T.; Kawaharamura, T.; Furuta, M.; Allen, M.W. Mist-CVD Grown Sn-Doped αα -Ga2O3 MESFETs. IEEE Trans. Electron Devices 2015, 62, 3640–3644. [Google Scholar] [CrossRef]
- Oda, M.; Tokuda, R.; Kambara, H.; Tanikawa, T.; Sasaki, T.; Hitora, T. Schottky barrier diodes of corundum-structured gallium oxide showing on-resistance of 0.1 mΩ·cm2grown by MIST EPITAXY®. Appl. Phys. Express 2016, 9, 021101. [Google Scholar] [CrossRef]
- Chen, X.; Xuanhu, C.; Zhou, D.; Yang, S.; Ren, F.-F.; Lu, H.; Tang, K.; Gu, S.; Zhang, R.; Zheng, Y.; et al. Solar-Blind Photodetector with High Avalanche Gains and Bias-Tunable Detecting Functionality Based on Metastable Phase α-Ga2O3/ZnO Isotype Heterostructures. ACS Appl. Mater. Interfaces 2017, 9, 36997–37005. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Xu, Q.; Li, M.; Shen, S.; Wang, X.; Wang, Y.; Feng, Z.; Shi, J.; Han, H.; Li, C. Photocatalytic Overall Water Splitting Promoted by an α-β phase Junction on Ga2O3. Angew. Chem. 2012, 124, 13266–13269. [Google Scholar] [CrossRef]
- Fujita, S.; Oda, M.; Kaneko, K.; Hitora, T. Evolution of corundum-structured III-oxide semiconductors: Growth, properties, and devices. Jpn. J. Appl. Phys. 2016, 55, 1202A3. [Google Scholar] [CrossRef]
- Furthmüller, J.; Bechstedt, F. Quasiparticle bands and spectra of Ga2O3 polymorphs. Phys. Rev. B 2016, 93, 115204. [Google Scholar] [CrossRef]
- He, H.; Orlando, R.; Blanco, M.A.; Pandey, R.; Amzallag, E.; Baraille, I.; Rérat, M. First-principles study of the structural, electronic, and optical properties ofGa2O3in its monoclinic and hexagonal phases. Phys. Rev. B 2006, 74, 1–8. [Google Scholar] [CrossRef]
- Patrick, L.; Choyke, W.J.; Hamilton, D.R. Luminescence of4HSiC, and Location of Conduction-Band Minima in SiC Polytypes. Phys. Rev. 1965, 137, A1515–A1520. [Google Scholar] [CrossRef]
- De Paula, W.J.; Tavares, P.L.; Pereira, D.D.C.; Tavares, G.M.; Silva, F.L.; Almeida, P.S.; Braga, H.A.C. A review on gallium nitride switching power devices and applications. In Proceedings of the 2017 Brazilian Power Electronics Conference (COBEP), Juiz de Fora, Brazil, 19–22 November 2017; pp. 1–7. [Google Scholar]
- Sabino, F.P.; Cai, X.; Wei, S.-H.; Janotti, A. Bismuth-doped Ga2O3 as a candidate for p-type transparent conducting material. arXiv 2019, arXiv:1906.00840. [Google Scholar]
- Tadjer, M.J.; Lyons, J.L.; Nepal, N.; Freitas, J.A.; Koehler, A.D.; Foster, G.M. Editors’ Choice—Review—Theory and Characterization of Doping and Defects in β-Ga2O3. ECS J. Solid State Sci. Technol. 2019, 8, Q3187–Q3194. [Google Scholar] [CrossRef]
- Higashiwaki, M.; Kuramata, A.; Murakami, H.; Kumagai, Y. State-of-the-art technologies of gallium oxide power devices. J. Phys. D: Appl. Phys. 2017, 50, 333002. [Google Scholar] [CrossRef]
- Varley, J.B.; Weber, J.R.; Janotti, A.; Van De Walle, C.G. Oxygen vacancies and donor impurities in β-Ga2O3. Appl. Phys. Lett. 2010, 97, 142106. [Google Scholar] [CrossRef]
- Du, X.; Li, Z.; Luan, C.; Wang, W.; Wang, M.; Feng, X.; Xiao, H.; Ma, J. Preparation and characterization of Sn-doped β-Ga2O3 homoepitaxial films by MOCVD. J. Mater. Sci. 2015, 50, 3252–3257. [Google Scholar] [CrossRef]
- Lovejoy, T.C.; Chen, R.; Zheng, X.; Villora, E.G.; Shimamura, K.; Yoshikawa, H.; Yamashita, Y.; Ueda, S.; Kobayashi, K.F.; Dunham, S.T.; et al. Band bending and surface defects in β-Ga2O3. Appl. Phys. Lett. 2012, 100, 181602. [Google Scholar] [CrossRef]
- Fitzpatrick, T.; Munby, I. Knowledge of word associations. In Dimensions of Vocabulary Knowledge; Palgrave Macmillan: Basingstoke, UK, 2013; pp. 92–105. [Google Scholar]
- Tang, C.; Sun, J.; Lin, N.; Jia, Z.; Mu, W.; Tao, X.; Zhao, X. Electronic structure and optical property of metal-doped Ga2O3: A first principles study. RSC Adv. 2016, 6, 78322–78334. [Google Scholar] [CrossRef]
- Dong, L.; Yu, J.; Zhang, Y.; Jia, R. Elements (Si, Sn, and Mg) doped α-Ga2O3: First-principles investigations and predictions. Comput. Mater. Sci. 2019, 156, 273–279. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Zhang, L.; Yan, J.; Zhang, Y.; Li, T.; Ding, X. First-principles study on electronic structure and optical properties of N-doped P-type β-Ga2O3. Sci. China Ser. G Phys. Mech. Astron. 2011, 55, 19–24. [Google Scholar] [CrossRef]
- Smith, J.; Jones, S.; White, L. Rapid Communication. Gastroenterol 1977, 72, 193. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Pfrommer, B.G.; Côté, M.; Louie, S.G.; Cohen, M.L. Relaxation of Crystals with the Quasi-Newton Method. J. Comput. Phys. 1997, 131, 233–240. [Google Scholar] [CrossRef]
- Liu, X.; Stoffel, R.; Dronskowski, R. Syntheses, Crystal Structures, and Vibrational Properties of Two Lead Azide Halides PbN 3 X. (X = Cl, Br). Z. Anorg. Allg. Chem. 2020, 646, 1525–1530. [Google Scholar] [CrossRef]
- Fischer, T.H.; Almlof, J. General Methods for geometry and wave function optimization. J. Phys. Chem. 1992, 96, 9768–9774. [Google Scholar] [CrossRef]
- Marezio, M.; Remeika, J.P. Bond Lengths in the α-Ga2O3 Structure and the High-Pressure Phase of Ga2−xFexO3. J. Chem. Phys. 1967, 46, 1862–1865. [Google Scholar] [CrossRef]
- Yamaguchi, K. First principles study on electronic structure of β-Ga2O3. Solid State Commun. 2004, 131, 739–744. [Google Scholar] [CrossRef]
- Shinohara, D.; Fujita, S. Heteroepitaxy of Corundum-Structured α-Ga2O3Thin Films on α-Al2O3Substrates by Ultrasonic Mist Chemical Vapor Deposition. Jpn. J. Appl. Phys. 2008, 47, 7311–7313. [Google Scholar] [CrossRef]
- Shaukat, A.; Saeed, Y.; Nazir, S.; Ikram, N.; Tanveer, M. Ab initio study of structural, electronic and optical properties of Ca1−xSrxS compounds. Phys. B: Condens. Matter 2009, 404, 3964–3972. [Google Scholar] [CrossRef]
- Feng, J.; Xiao, B.; Xing, J.; Zhou, C.; Du, Y.; Zhou, R. Optical properties of new photovoltaic materials: AgCuO2 and Ag2Cu2O3. Solid State Commun. 2009, 149, 1569–1573. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, Y.; Dong, L.; Jia, R. First-principles calculations of electronic and optical properties of aluminum-doped β-Ga2O3 with intrinsic defects. Results Phys. 2017, 7, 1582–1589. [Google Scholar] [CrossRef]
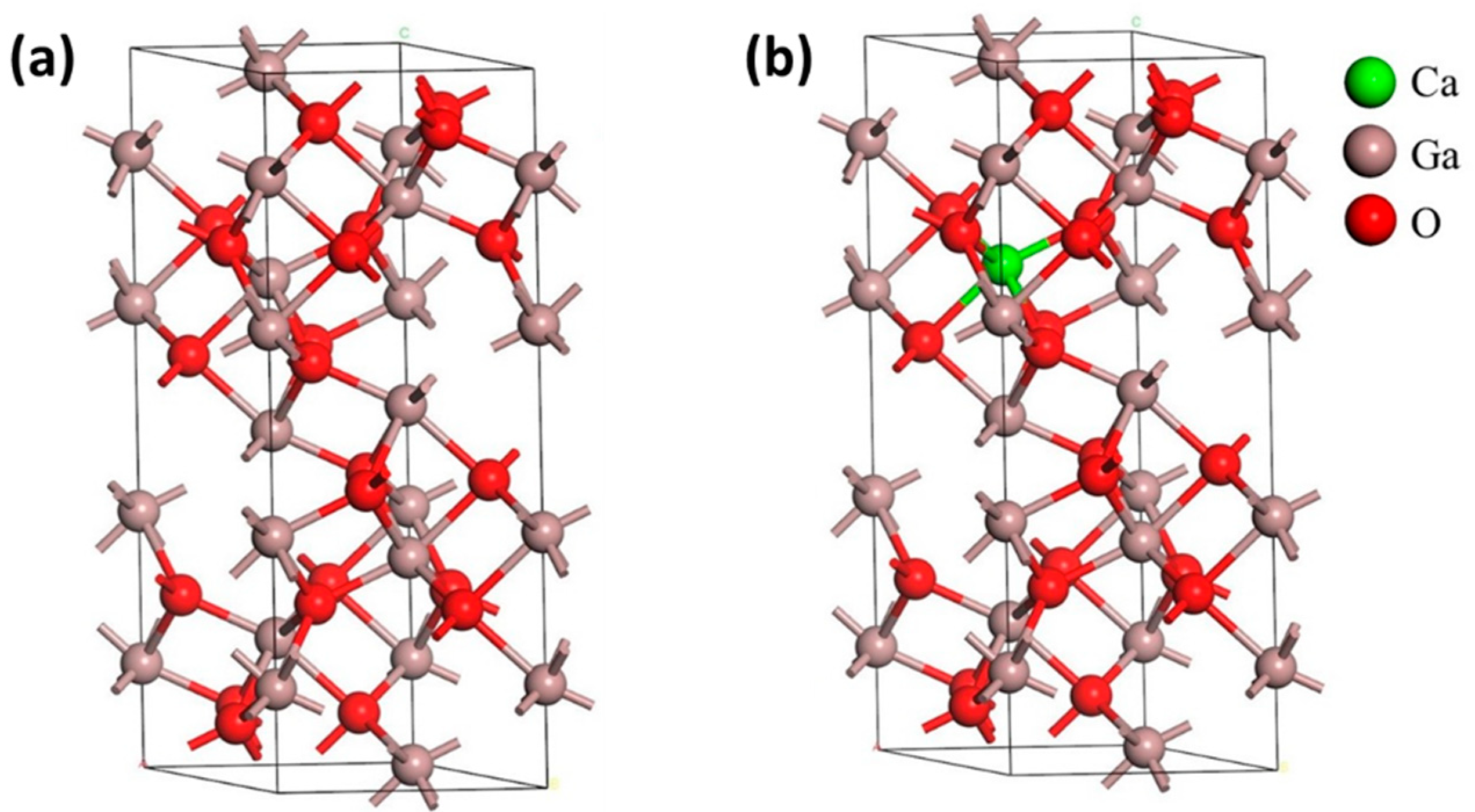
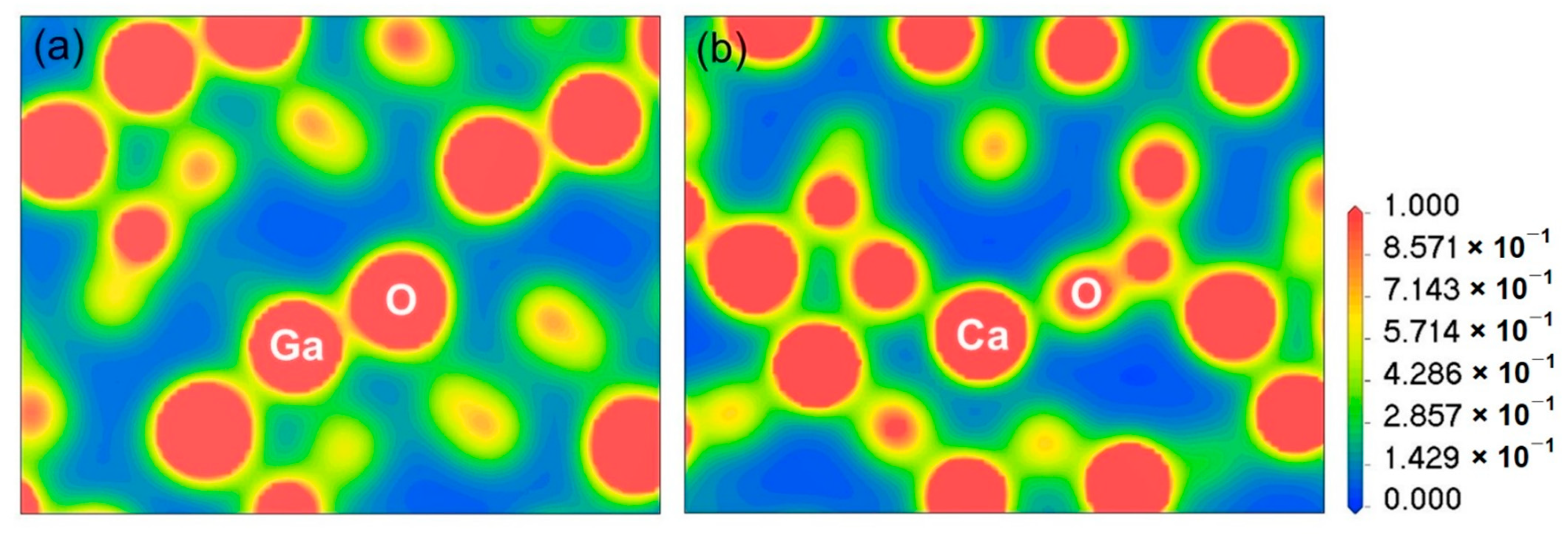
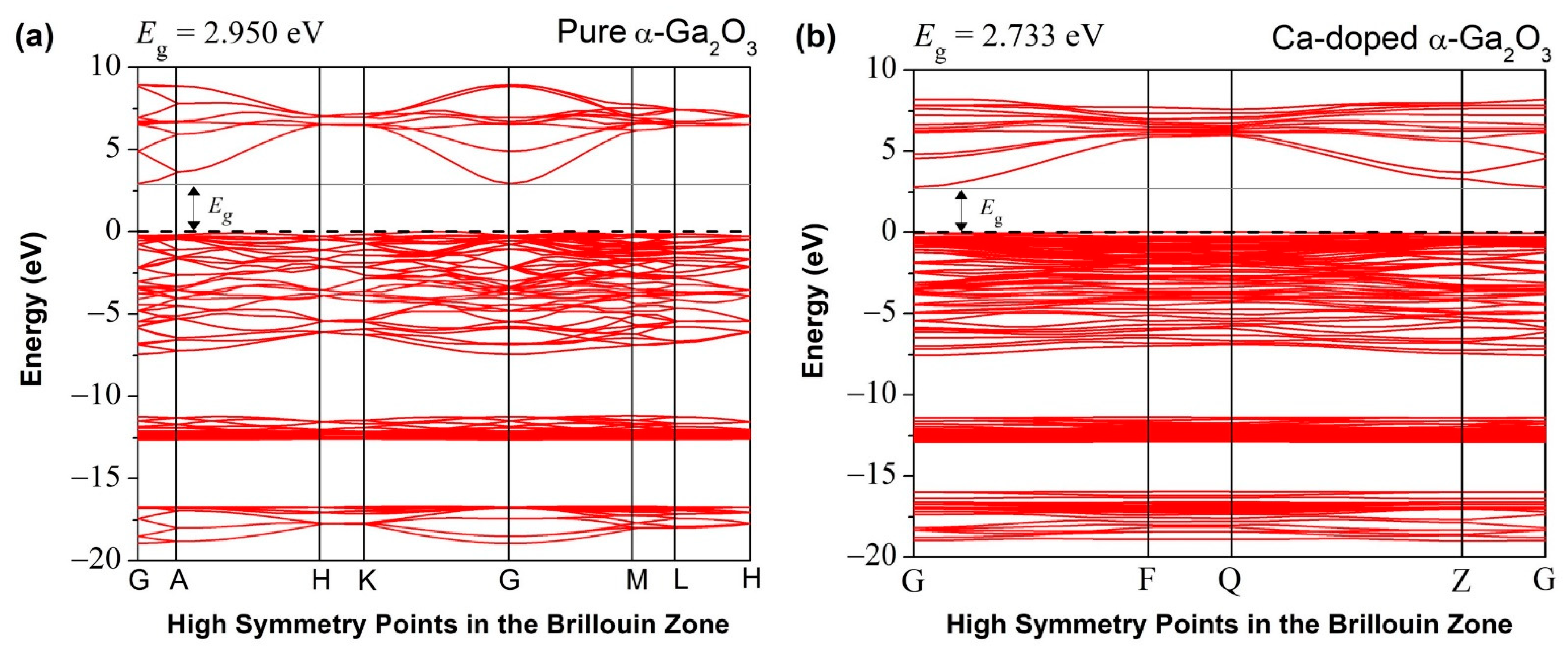
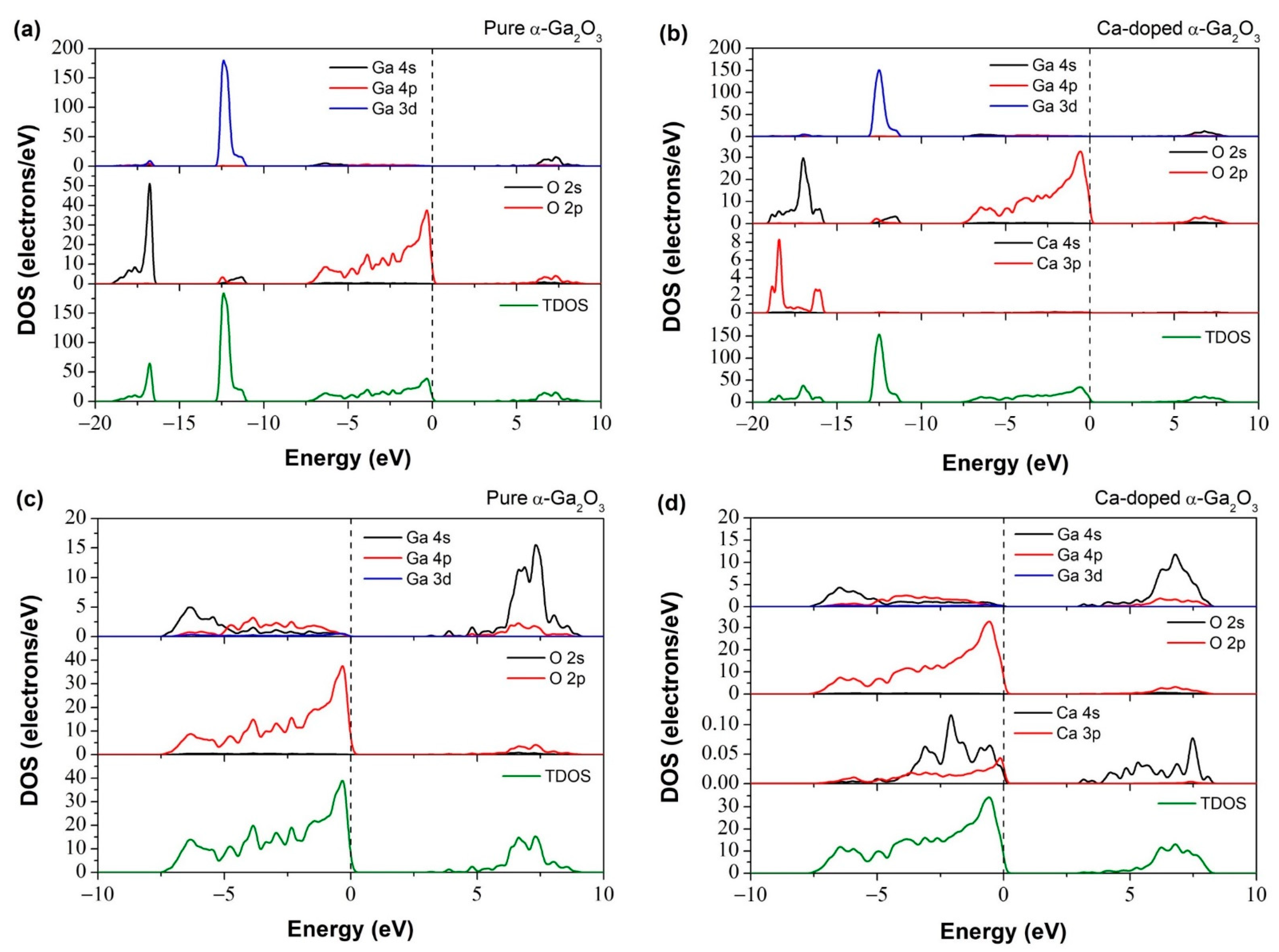


| Phase | a (Å) | b (Å) | c (Å) | V (Å3) | |
|---|---|---|---|---|---|
| Pure Ga2O3 | LDA-CAPZ | 4.965 (−0.36%) | 4.965 (−0.36%) | 13.338 (−0.71%) | 284.747 (−1.42%) |
| GGA-PBE | 5.074 (1.83%) | 5.074 (1.83%) | 13.664 (1.72%) | 304.656 (5.47%) | |
| GGA-PBEsol | 5.028 (0.90%) | 5.028 (0.90%) | 13.511 (0.58%) | 295.807 (2.41%) | |
| GGA-PBE (CASTEP) [6] | 5.07 | 5.07 | 13.67 | 304.309 | |
| Expt. [26] | 4.983 | 4.983 | 13.433 | 288.859 | |
| Ca-Doped Ga2O3 | LDA-CAPZ | 5.010 (0.54%) | 5.010 (0.54%) | 13.520 (0.647%) | 293.889 (1.74%) |
| Type of Bond Length | Pure α-Ga2O3 | Ca-doped α-Ga2O3 |
|---|---|---|
| Ga–O (Å) | 1.989 | 1.993 |
| O–O (Å) | 2.762 | 2.741 |
| Ca–O (Å) | – | 2.253 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mondal, A.K.; Mohamed, M.A.; Ping, L.K.; Mohamad Taib, M.F.; Samat, M.H.; Mohammad Haniff, M.A.S.; Bahru, R. First-Principles Studies for Electronic Structure and Optical Properties of p-Type Calcium Doped α-Ga2O3. Materials 2021, 14, 604. https://doi.org/10.3390/ma14030604
Mondal AK, Mohamed MA, Ping LK, Mohamad Taib MF, Samat MH, Mohammad Haniff MAS, Bahru R. First-Principles Studies for Electronic Structure and Optical Properties of p-Type Calcium Doped α-Ga2O3. Materials. 2021; 14(3):604. https://doi.org/10.3390/ma14030604
Chicago/Turabian StyleMondal, Abhay Kumar, Mohd Ambri Mohamed, Loh Kean Ping, Mohamad Fariz Mohamad Taib, Mohd Hazrie Samat, Muhammad Aniq Shazni Mohammad Haniff, and Raihana Bahru. 2021. "First-Principles Studies for Electronic Structure and Optical Properties of p-Type Calcium Doped α-Ga2O3" Materials 14, no. 3: 604. https://doi.org/10.3390/ma14030604
APA StyleMondal, A. K., Mohamed, M. A., Ping, L. K., Mohamad Taib, M. F., Samat, M. H., Mohammad Haniff, M. A. S., & Bahru, R. (2021). First-Principles Studies for Electronic Structure and Optical Properties of p-Type Calcium Doped α-Ga2O3. Materials, 14(3), 604. https://doi.org/10.3390/ma14030604





