Simultaneous Measurement of Temperature and Refractive Index Using High Temperature Resistant Pure Quartz Grating Based on Femtosecond Laser and HF Etching
Abstract
1. Introduction
2. Materials and Methods
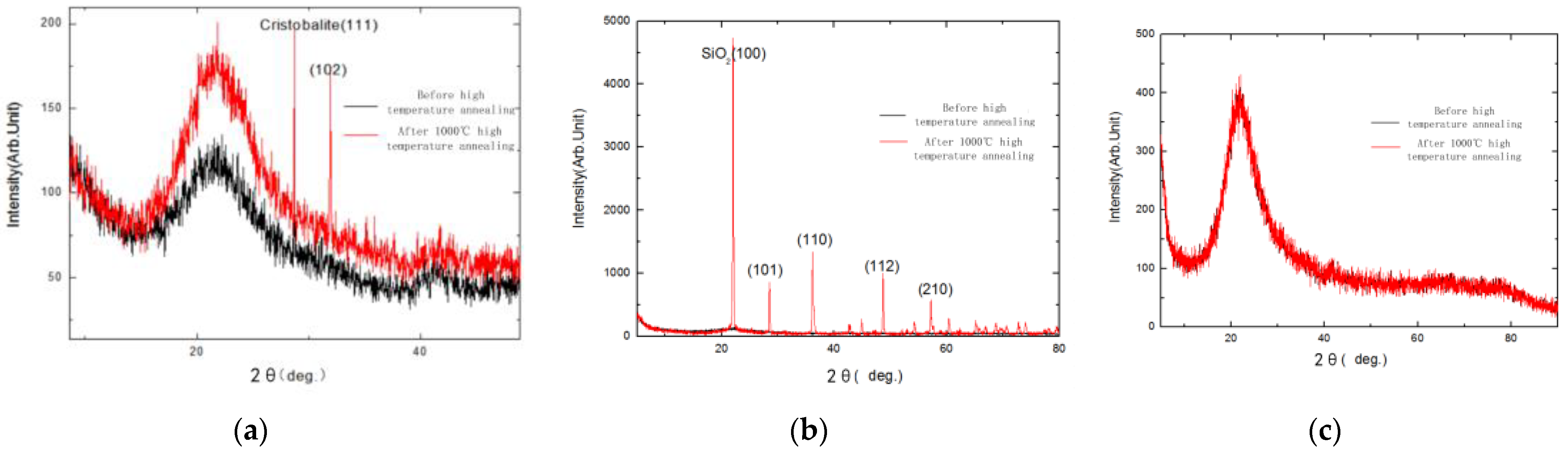
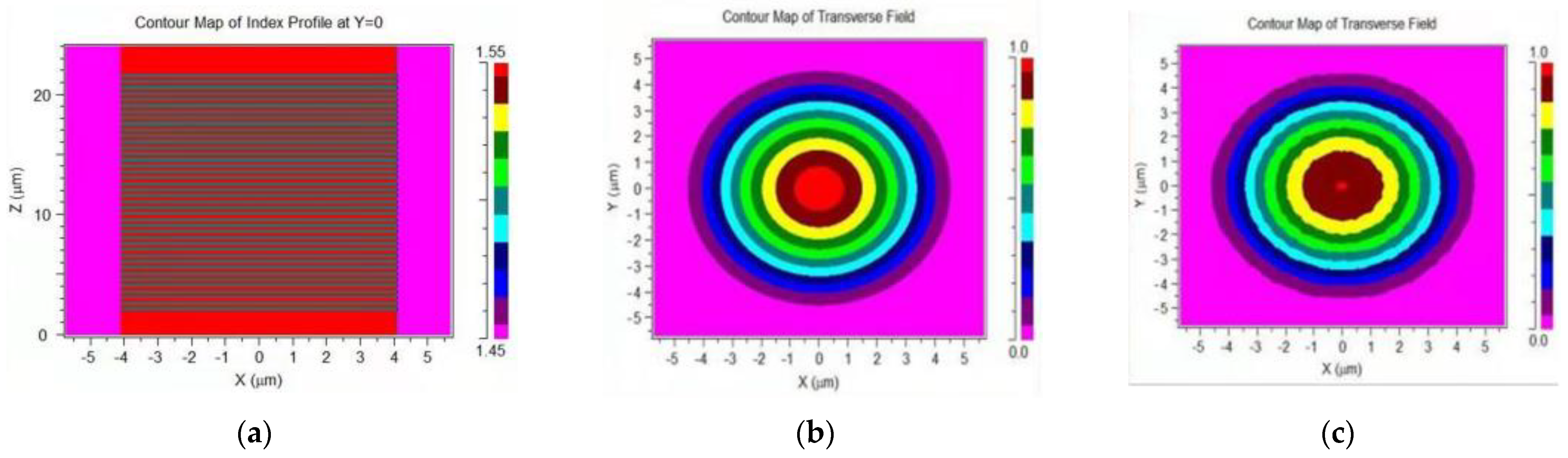
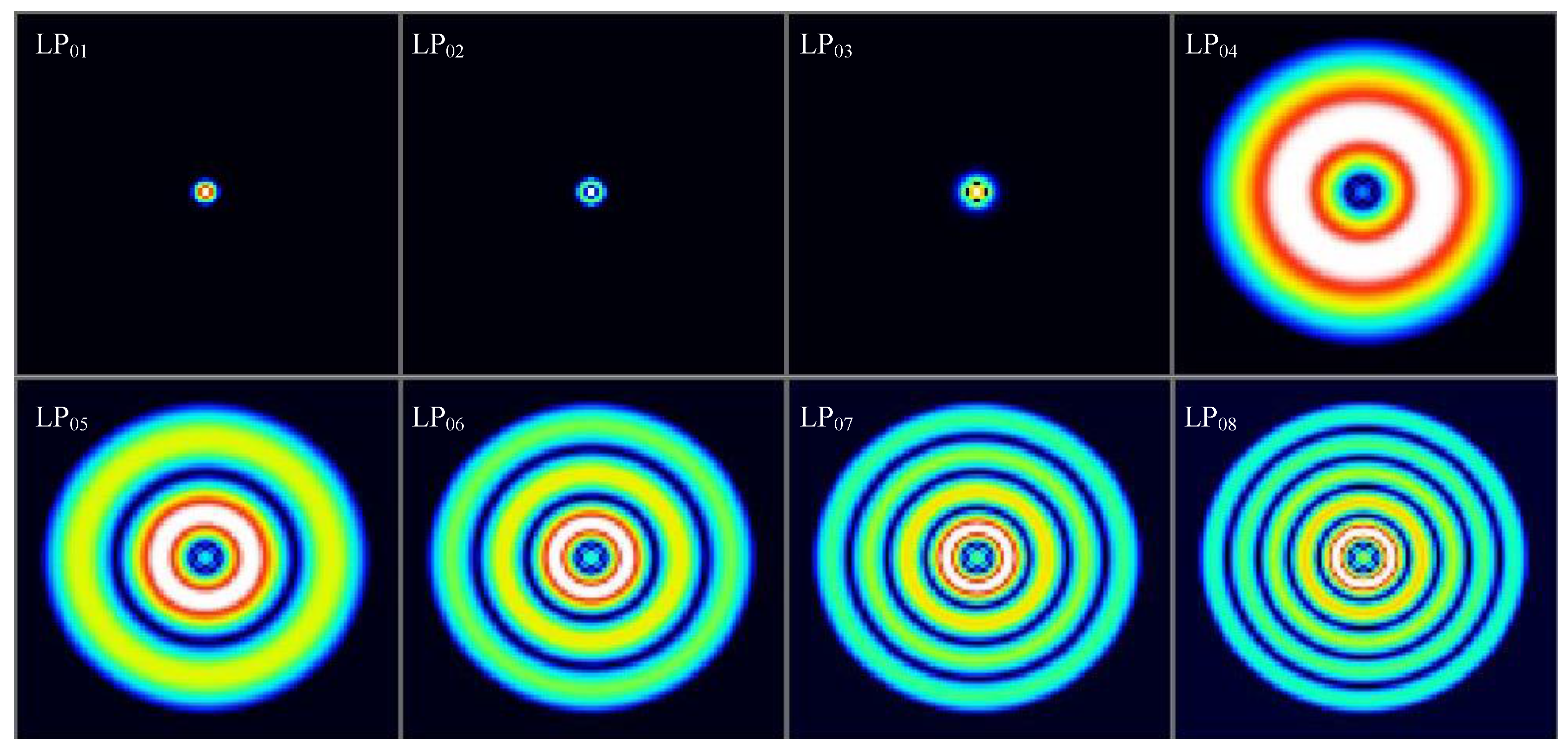
2.1. Material Selection and Analysis
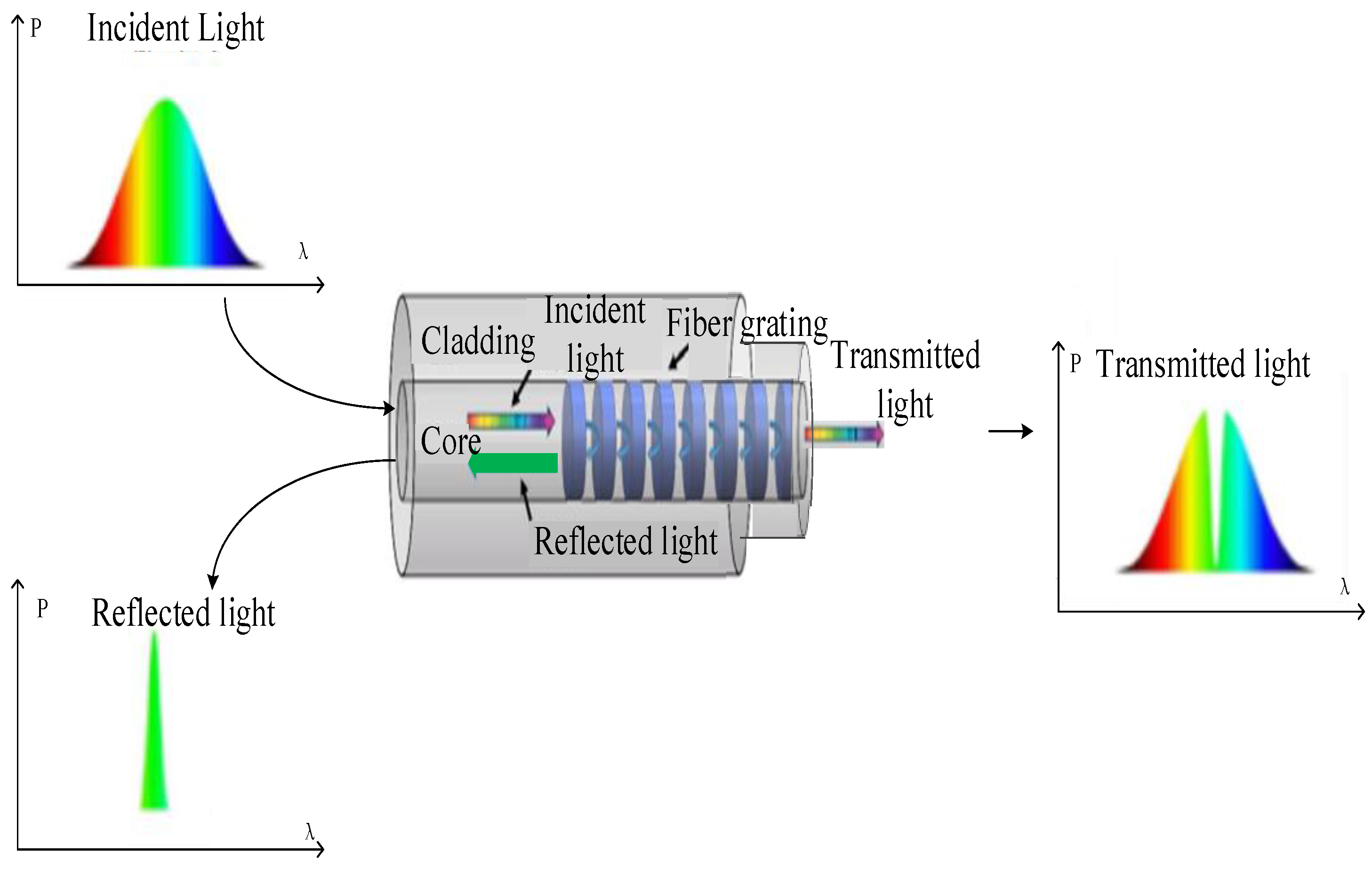
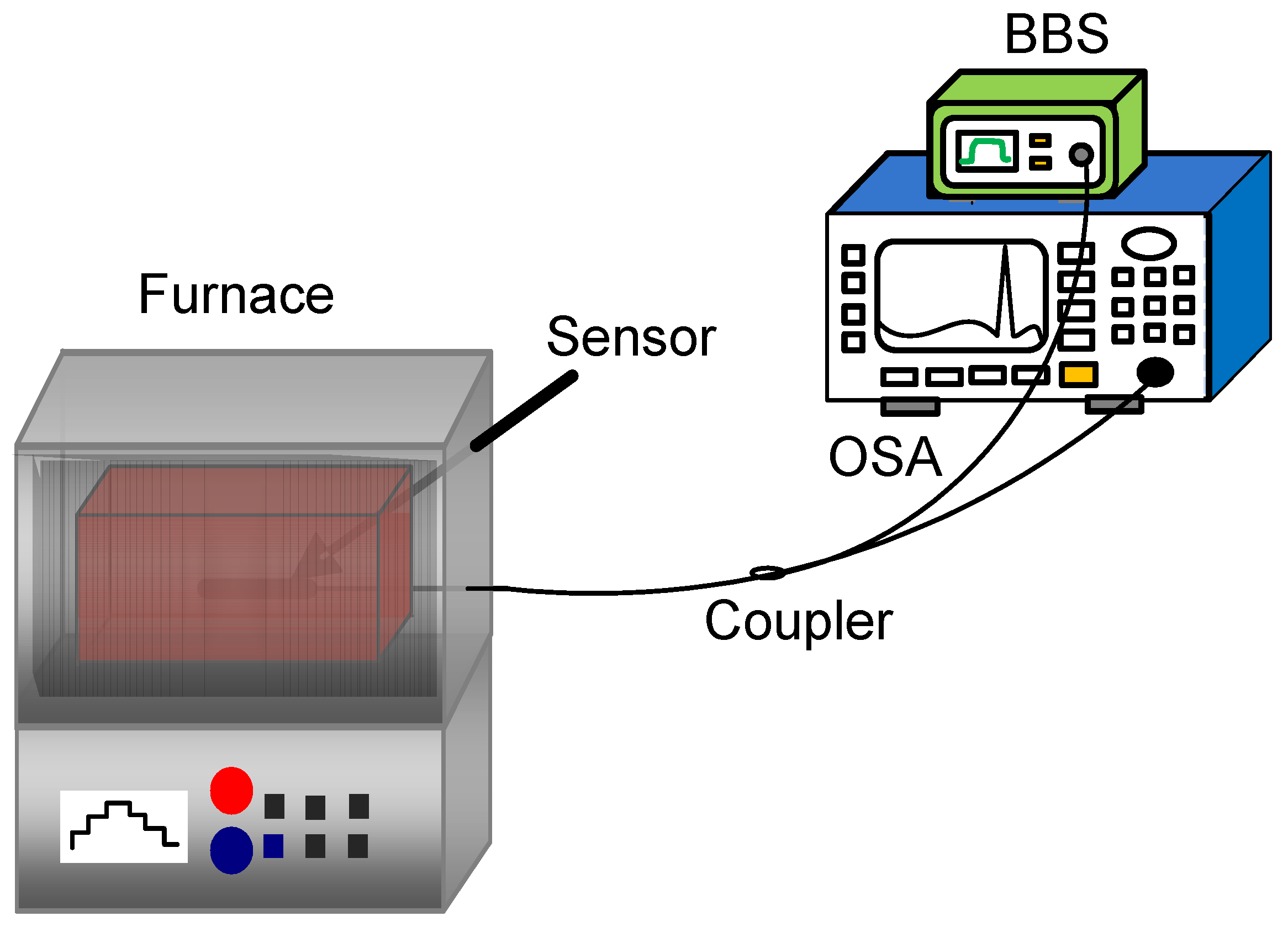
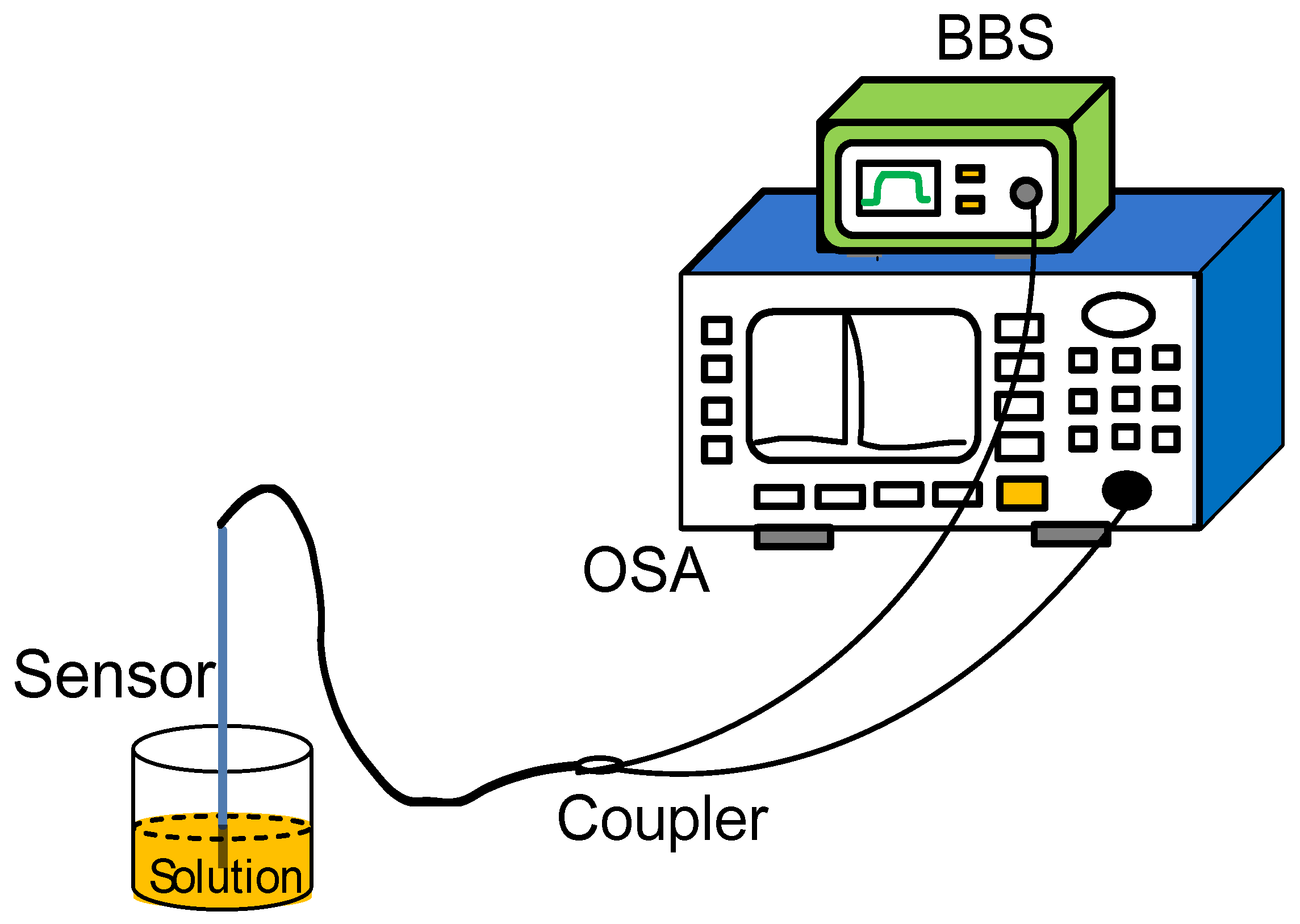
2.2. Measurement Method of Temperature Wavelength Sensor
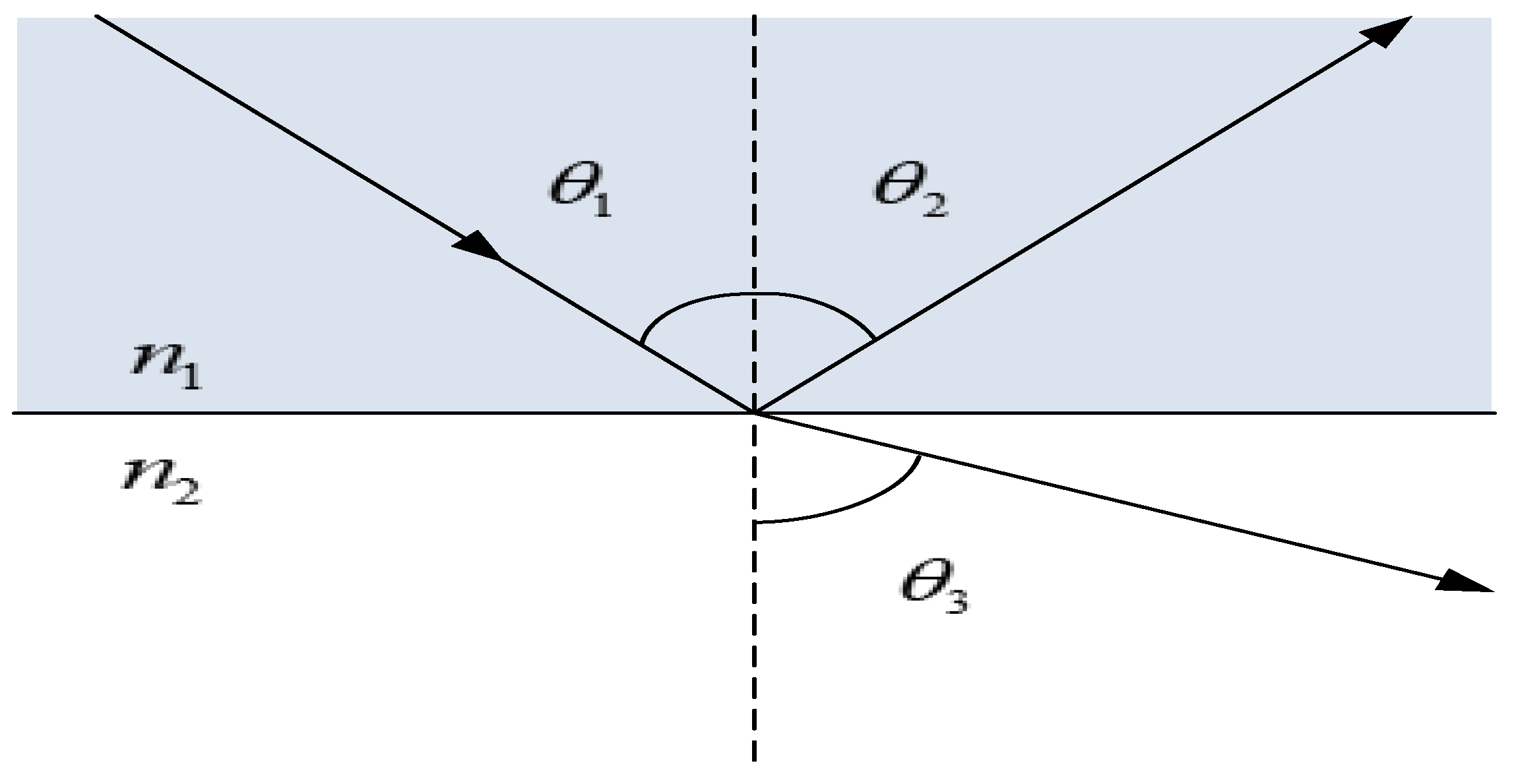
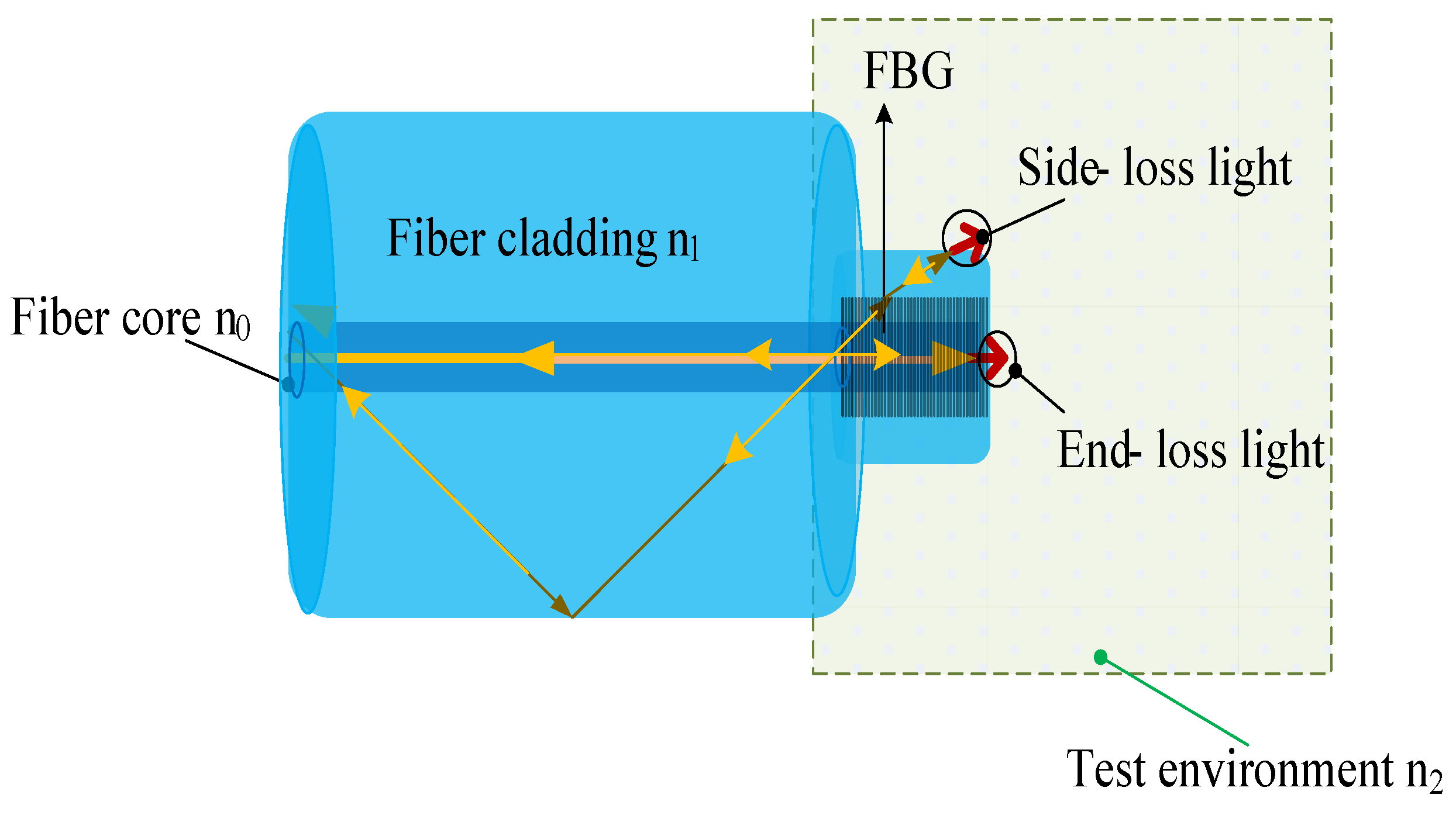
2.3. Measuring Method of Refractive Index Intensity Type Sensor
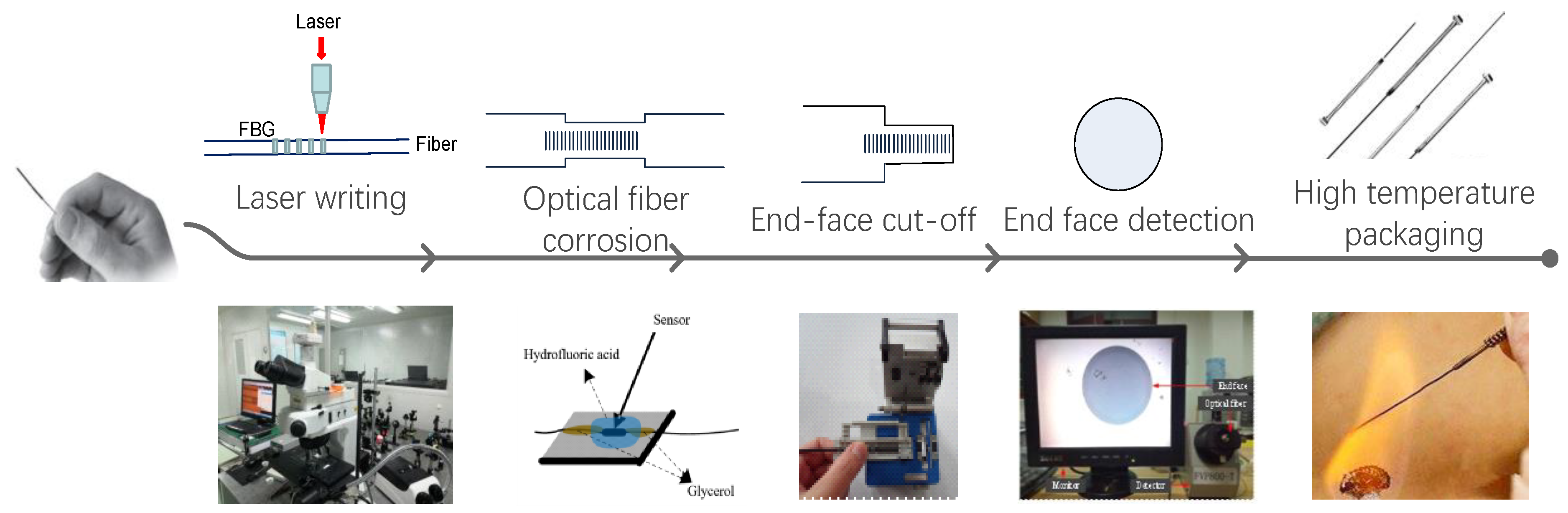
3. Production and Packaging
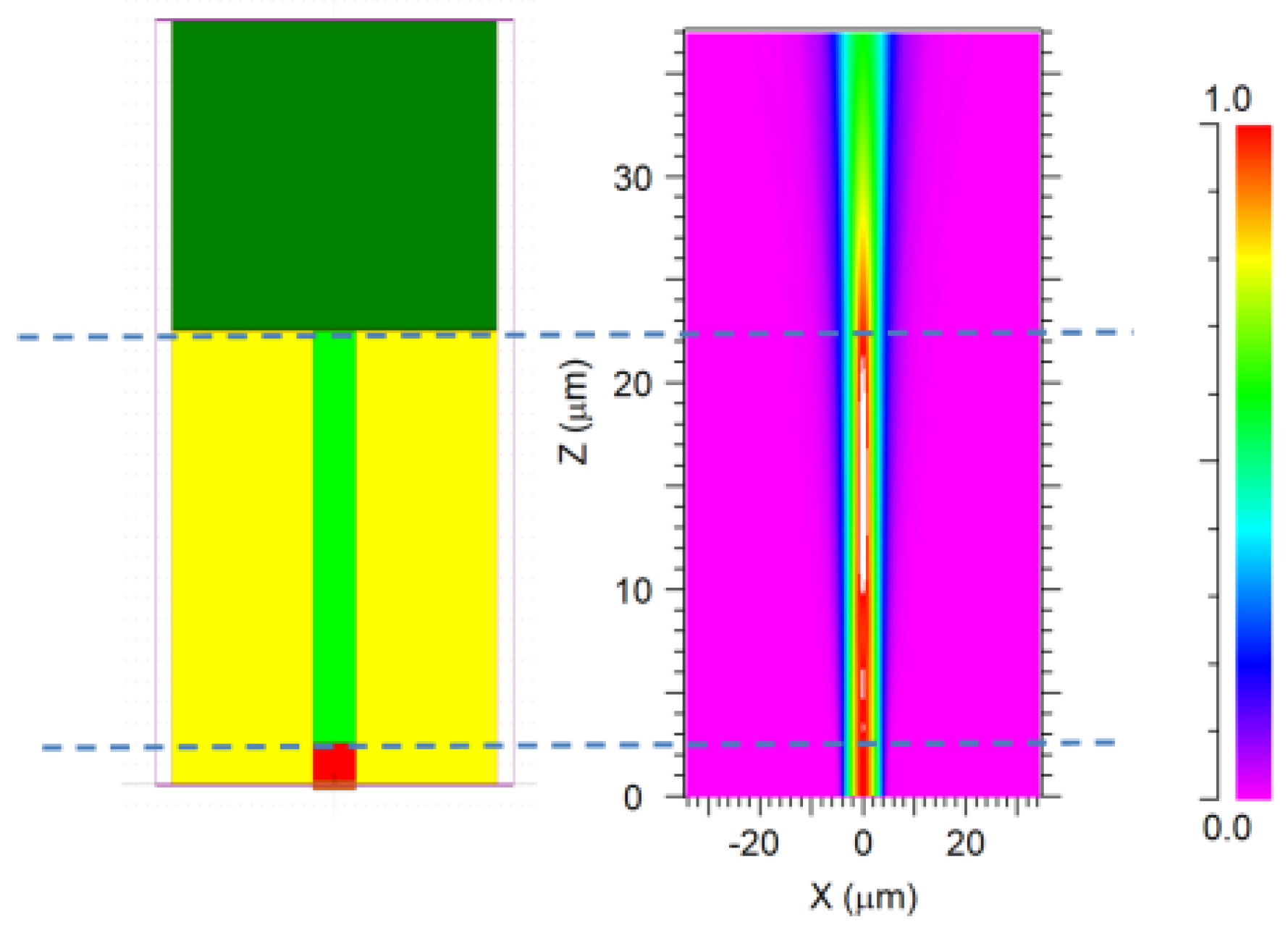
3.1. Laser Writing
3.2. Etching of the Sensor and End Face Cutting
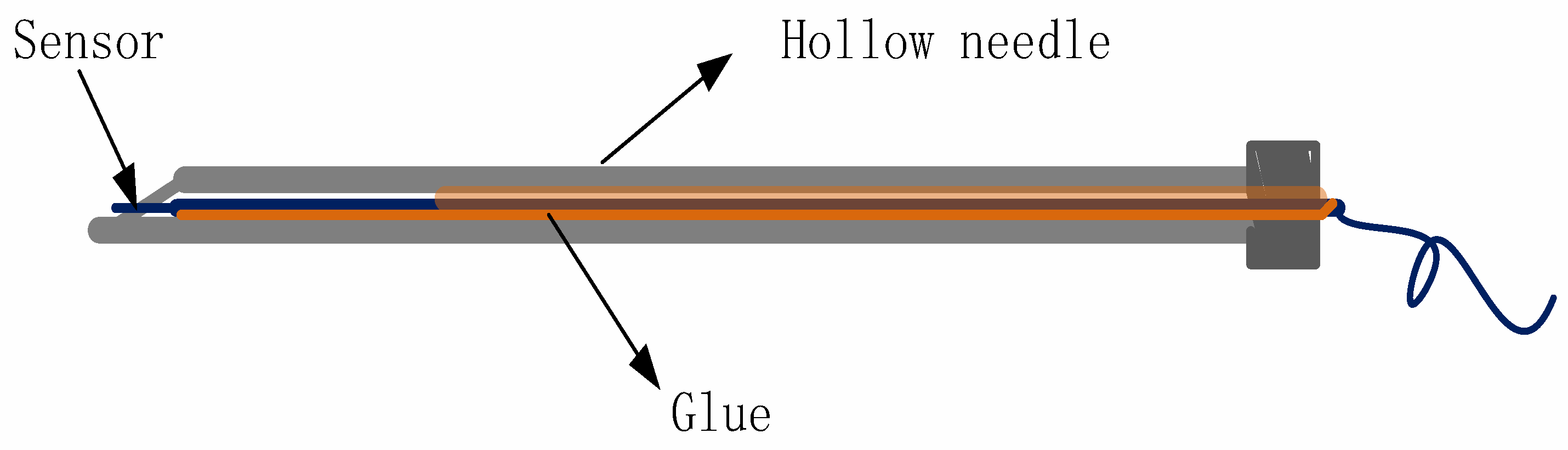
3.3. Fixing of Sensor Probe
4. Results
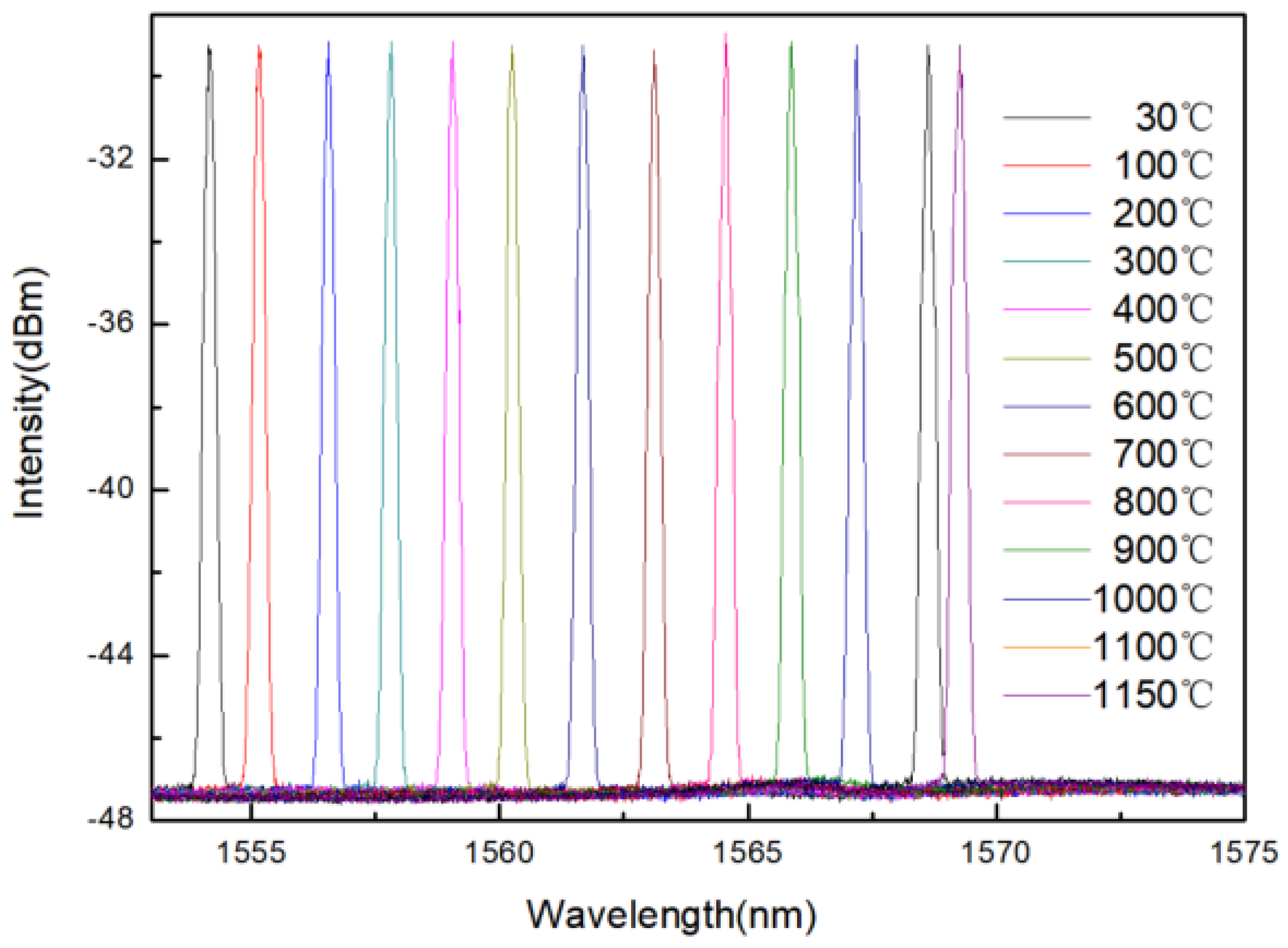
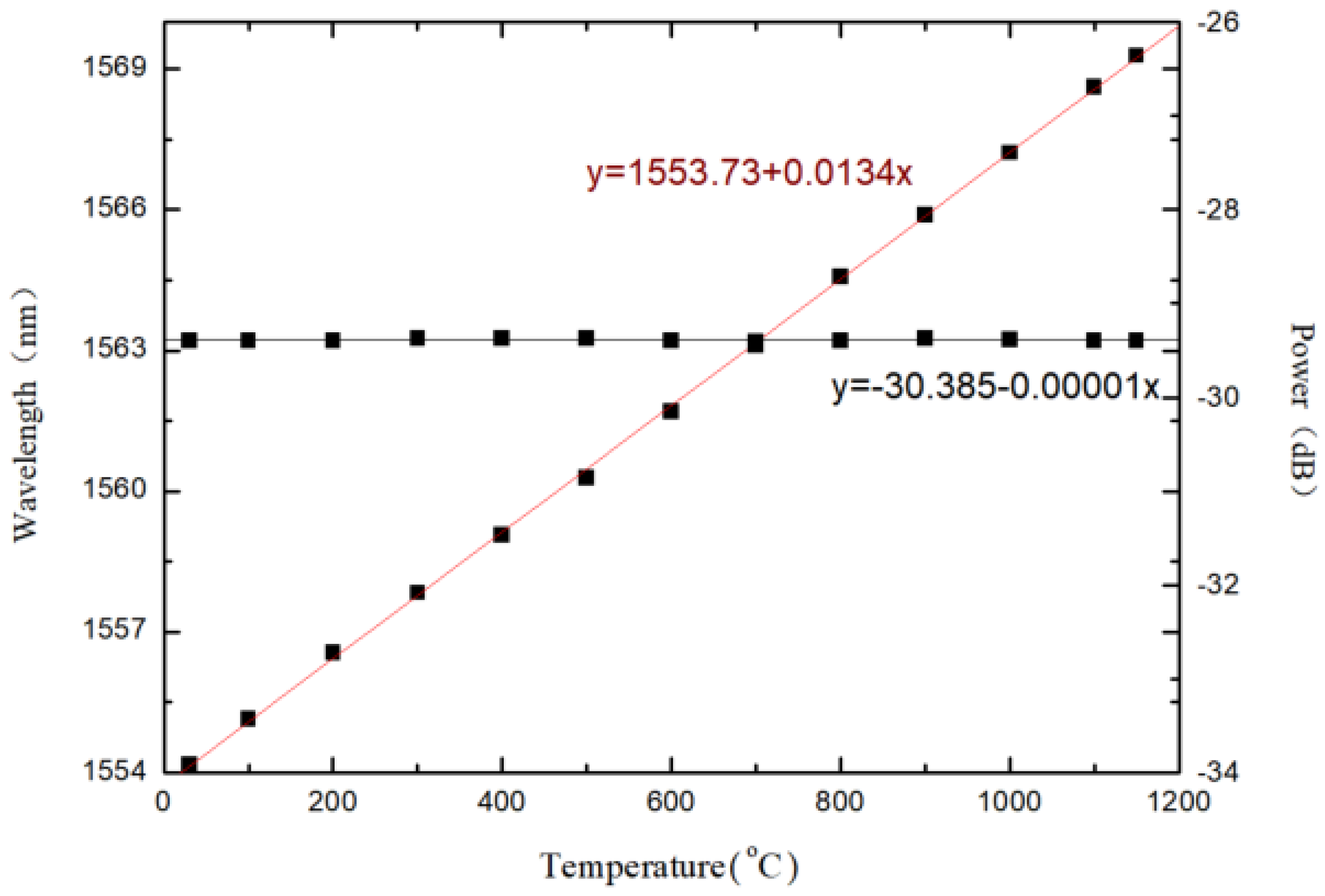
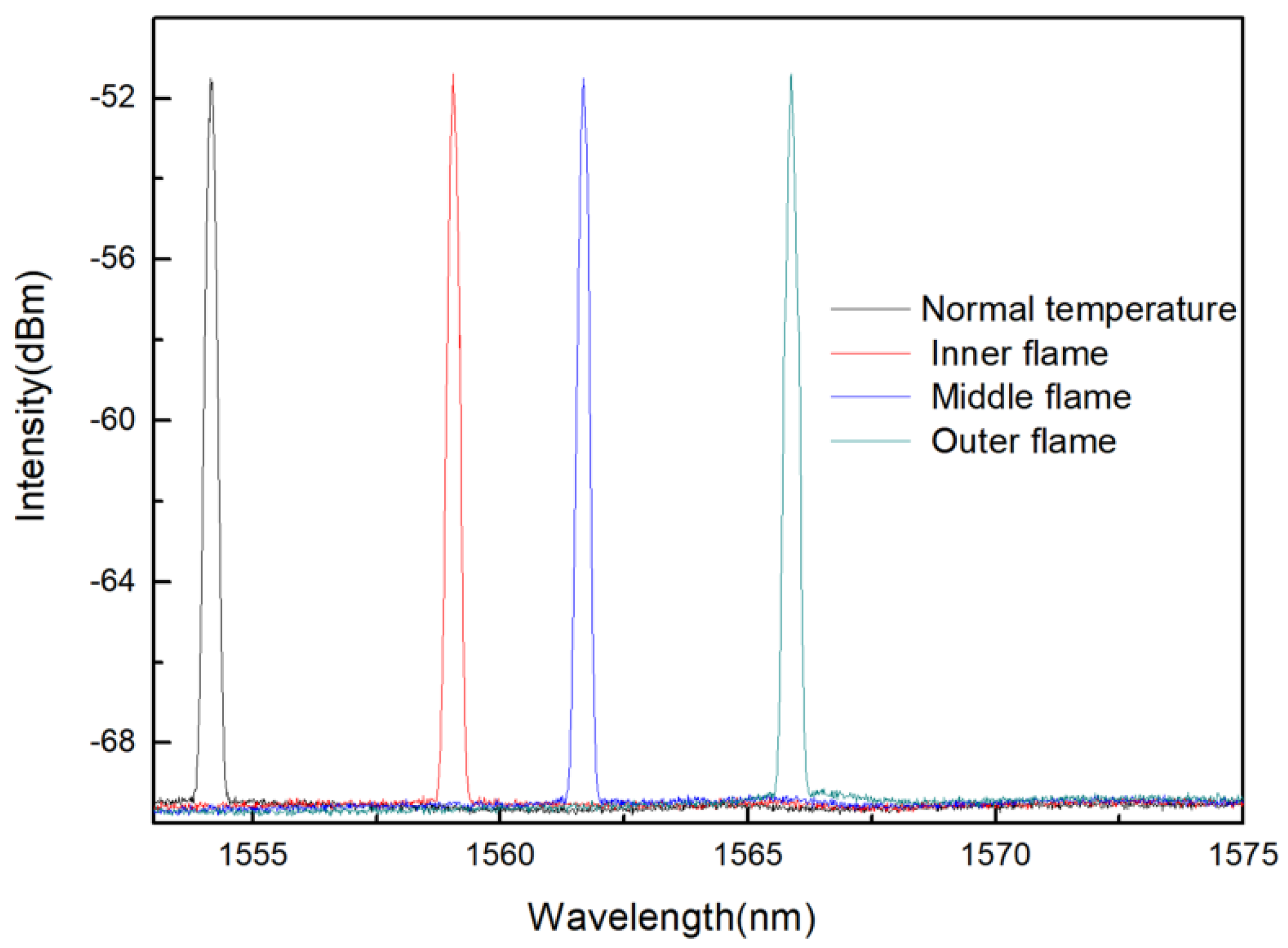
4.1. Temperature Measurement
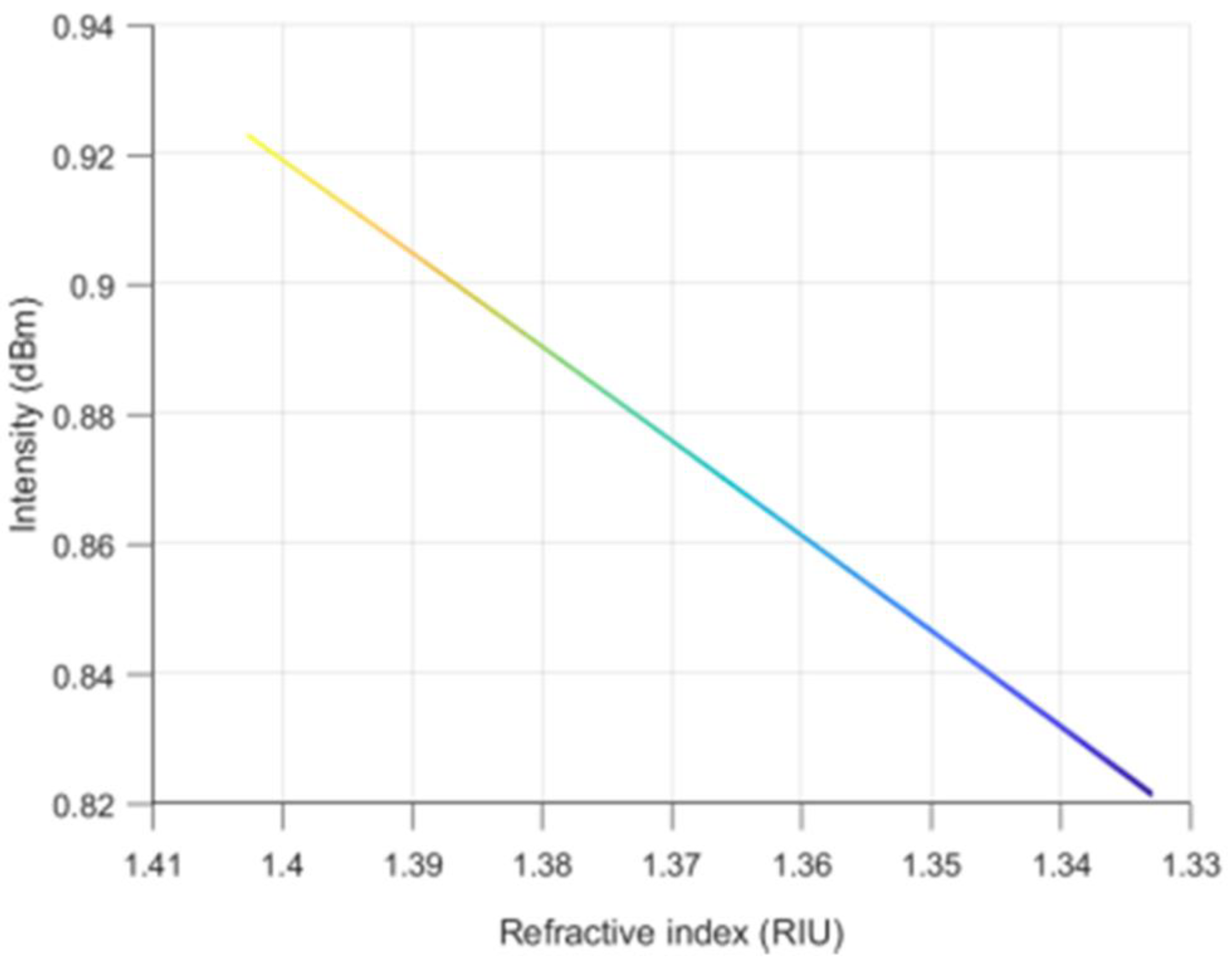
4.2. Refractive Index Measurement
5. Discussion
5.1. Temperature Response Characteristics of Sensor Wavelength
5.2. Refractive Index Response Characteristics of Sensor Intensity
5.3. Two-Parameter Simultaneous Measurement Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X. To Explore the Hollow Needle Acupuncture Treatment the Clinical Curative Effect of Chronic Lumbocrural Pain. Guide China Med. 2014. [Google Scholar] [CrossRef]
- Zhao, H.; Li, Y.J.; Liu, R.J.; Zhao, F.Y.; Hu, Y.Q. Synthesis Method for Silica Needle-Shaped Nano-Hollow Structure. Mater. Lett. 2008, 62, 3401–3403. [Google Scholar] [CrossRef]
- Richard, C.H.; Stephen, J.M.; Patrick, O.; Tracy, S.H. Lateral Canthopexy Using the Hollow Needle Technique. Plast. Reconstr. Surg. 2006, 117, 1289–1291. [Google Scholar]
- Zhang, W.W.; Gao, S.M.; Chen, D.H. Preparation of Ce3+ Doped Bi2O3 Hollow Needle-Shape with Enhanced Visible-Light Photocatalytic Activity. J. Rare Earths 2019, 37, 726–731. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Stephen, A.C.; Sreejith, K. Finite Element Analysis of Hollow out-of-Plane HfO2 Microneedles for Transdermal Drug Delivery Applications. Biomed. Microdevices 2018, 20, 19. [Google Scholar] [CrossRef]
- Ji, S.Y.; Li, R.; Cai, Z.; Pan, D.; Yang, L.; Hu, Y.L.; Li, J.W.; Wu, D.; Chu, J.R. Holographic Femtosecond Laser Integration of Microtube Arrays inside a Hollow Needle as a Lab-in-a-Needle Device. Opt. Lett. 2019, 44, 5073–5076. [Google Scholar] [CrossRef] [PubMed]
- Du, G.S.; Hathout, R.M.; Nasr, M.; Nejadnik, M.R.; Tu, J.; Koning, R.I.; Koster, A.J.; Slütter, B.; Kros, A.; Jiskoot, W.; et al. Intradermal Vaccination with Hollow Microneedles: A Comparative Study of Various Protein Antigen and Adjuvant Encapsulated Nanoparticles. J. Control. Release 2017, 266, 109–118. [Google Scholar] [CrossRef]
- Chen, L.; Dong, L.; She, L.; Zhang, H.Z.; Wang, X.D.; Yan, Z.C.; Wu, W.; Yang, L. Treatment of Chronic Subdural Hematoma by Novel YL-1 Hollow Needle Aspiration Drainage System (697 Cases Report). Neurol. Sci. 2017, 38, 109–113. [Google Scholar] [CrossRef] [PubMed]
- Yang, J. Dacheng of Acupuncture and Moxibustion; People’s Medical Publishing House: Beijing, China, 1988. [Google Scholar]
- Gomes, A.D.; Becker, M.; Dellith, J.; Zibaii, M.I.; Latifi, H.; Rothhardt, M.; Bartelt, H.; Frazão, O. Multimode Fabry−Perot Interferometer Probe Based on Vernier Effect for Enhanced Temperature Sensing. Sensors 2019, 19, 453. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.Z.; Zhao, N.; Lin, Q.J.; Wu, Z.R.; Tian, B.; Shi, P.; Yang, P.; Jiang, Z.D. The influence of key characteristic parameters on performance of optical fiber Fabry–Perot temperature sensor. AIP Adv. 2020, 10, 085119. [Google Scholar] [CrossRef]
- Tian, Z.B.; Scott, S.H.; Hans, P.L. Refractive Index Sensor Based on an Abrupt Taper Michelson Interferometer in a Single-Mode Fiber. Opt. Lett. 2008, 33, 1105–1107. [Google Scholar] [CrossRef]
- Ahsani, V. Tapered Fiber-Optic Mach-Zehnder Interferometer for Ultra-High Sensitivity Measurement of Refractive Index. Sensors 2019, 19, 1652. [Google Scholar] [CrossRef]
- Fan, X.; Wang, Q.; Zhou, M.; Liu, F.; Shen, H.; Wei, Z.; Wang, F.; Tan, C.; Meng, H. Humidity Sensor Based on a Graphene Oxide-Coated Few-Mode Fiber Mach-Zehnder Interferometer. Opt. Express 2020, 28, 24682–24692. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Wang, S.W.; Fu, X.H.; Fu, G.W.; Jin, W.; Bi, W.H. Refractive index insensitive temperature sensor based on waist-enlarged few mode fiber bitapers. Optoelectron. Lett. 2017, 13, 25–28. [Google Scholar] [CrossRef]
- Woyessa, G.; Fasano, A.; Stefani, A.; Markos, C.; Nielsen, K.; Rasmussen, H.K.; Bang, O. Single mode step-index polymer optical fiber for humidity insensitive high temperature fiber Bragg grating sensors. Opt. Express 2016, 24, 1253. [Google Scholar] [CrossRef] [PubMed]
- Fasano, A.; Woyessa, G.; Stajanca, P.; Markos, C.; Stefani, A.; Nielsen, K.; Rasmussen, H.K.; Krebber, K.; Bang, O. Fabrication and characterization of polycarbonate microstructured polymer optical fibers fo rhigh-temperature-resistant fiber Bragg grating strain sensors. Opt. Mater. Express 2016, 6, 649–659. [Google Scholar] [CrossRef]
- Ganziy, D.; Rose, B.; Bang, O. Performance of low-cost few-mode fiber Bragg grating sensor systems: Polarization sensitivity and linearity of temperature and strain response. Appl. Opt. 2016, 55, 6156–6161. [Google Scholar] [CrossRef] [PubMed]
- Li, T.L.; Tan, Y.G.; Xue, H.; Zheng, K.; Zhou, Z.D. Diaphragm Based Fiber Bragg Grating Acceleration Sensor with Temperature Compensation. Sensors 2017, 17, 218. [Google Scholar] [CrossRef] [PubMed]
- Hill, K.O.; Fujii, Y.; Johnson, D.C.; Kawasaki, B.S. Photosensitivity in optical fiber waveguides: Application to reflection filter fabrication. Appl. Phys. Lett. 1978, 32, 647–649. [Google Scholar] [CrossRef]
- Dong, L.; Cruz, J.L.; Reekie, L.; Xu, M.G.; Payne, D.N. Enhance Photosensitivity in Tin-Codoped Germanosilicate Optical Fibers. IEEE Photonics Technol. Lett. 1995, 7, 1048–1050. [Google Scholar] [CrossRef][Green Version]
- Rathje, J.; Kristensen, M.; Pedersenj, E. Continuous anneal method for characterizing the thermal stability of ultraviolet Bragg gratings. J. Appl. Phys. 2000, 88, 1050–1055. [Google Scholar] [CrossRef]
- Meltz, G.; Morey, W.W.; Glenn, W.H. Formation of Bragg gratings in optical fibers by a transverse holographic method. Opt. Lett. 1989, 14, 823–825. [Google Scholar] [CrossRef] [PubMed]
- Douay, M.; Xiew, W.X.; Taunay, T.; Bernage, P.; Niay, P.; Cordier, P.; Poumellec, B.; Dong, L.; Bayon, J.F.; Poignant, H.; et al. Densification involved in the UV-based photo sensitivity of silica glasses and optical fiber. J. Lightwave Technol. 1997, 15, 1329–1342. [Google Scholar] [CrossRef]
- Miao, Y.P.; Liu, B.; Zhao, Q.D. Refractive index sensor based on measuring the transmission power of tilted fiber Bragg grating. Opt. Fiber Technol. 2009, 15, 233–236. [Google Scholar] [CrossRef]
- He, J.; Wang, Y.P.; Liao, C.R.; Wang, C.; Liu, S.; Yang, K.M.; Wang, Y.; Yuan, X.C.; Wang, G.P.; Zhang, W.N. Negative-Index Gratings Formed by Femtosecond Laser Overexposure and Thermal Regeneration. Sci. Rep. 2016, 6, 23379. [Google Scholar] [CrossRef] [PubMed]
- Lowder, T.L.; Smith, K.H.; Ipson, B.L.; Hawkins, A.R.; Selfridge, R.H.; Schultz, S.M. High-Temperature Sensing Using Surface Relief Fiber Bragg Gratings. IEEE Photonics Technol. Lett. 2005, 17, 1926–1928. [Google Scholar] [CrossRef]
- Mamidi, V.R.; Kamineni, S.; Ravinuthala, L.N.S.P.; Martha, M.; Madhuvarasu, S.S.; Thumu, V.R. High-temperature measurement using fiber Bragg grating sensor accompanied by a low-cost detection system. J. Appl. Remote Sens. 2015, 9, 094098. [Google Scholar] [CrossRef]
- Ding, X.D.; Zhang, Y.M.; Song, Y.M.; Yang, R.T.; Zhu, L.Q. Response Characteristics of Pure-Quartz-Core Fiber Bragg Grating Under High Temperature Strain. Chin. J. Lasers 2017, 11, 175–181. [Google Scholar]
- Qian, Y.; Zhao, Y.; Wu, Q.L.; Yang, Y. Review of salinity measurement technology based on optical fiber sensor. Sens. Actuators B Chem. 2018, 260, 86–105. [Google Scholar] [CrossRef]
- Lee, B.H.; Kim, Y.H.; Park, K.S.; Eom, J.B.; Kim, M.J.; Rho, B.S.; Choi, H.Y. Interferometric fiber optic sensors. Sensors 2012, 12, 2467–2486. [Google Scholar] [CrossRef]
- Zhang, A.Q.; Wu, Y.; Yao, B.C.; Gong, Y. Optimization Study on Graphene-Coated Microfiber Bragg Grating Structures for Ammonia Gas Sensing. Photonic Sens. 2015, 5, 84–90. [Google Scholar] [CrossRef]
- Ran, Y.; Liu, T.; Liang, L.; Peng, X.; Guan, B.-O. Bragg grating in micro-scaled optical fiber for cardiac biomarker sensing. In Proceedings of the Optical Fibers and Sensors for Medical Diagnostics and Treatment Applications XVIII, San Francisco, CA, USA, 27 January–1 February 2018. [Google Scholar]
- Kobryń, J.; Zieba, T.; Sowa, S.K.; Musial, W. Influence of Acetylated Annealed Starch on the Release of β-Escin from the Anionic and Non-Ionic Hydrophilic Gels. Pharmaceutics 2020, 12, 84. [Google Scholar]
- Luo, B.B.; Wu, S.X.; Zou, W.G.; Zhang, Z.H.; Zhao, M.F.; Shi, S.H.; Liu, Y.; Xi, X.F.; Zeng, Z.; Liang, W.W.; et al. Label-Free Immunoassay for Porcine Circovirus Type 2 Based on Excessively Tilted Fiber Grating Modified with Staphylococcal Protein A. Biosens. Bioelectron. 2016, 86, 1054–1060. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.M. Development and Genetic Diagnosis of Nano-Optical Fiber DNA Biosensor; University of Electronic Science and Technology of China: Chengdu, China, 2010. [Google Scholar]
- Zheng, S.J.; Zhu, Y.N.; Krishnaswamy, S. Fiber Humidity Sensors with High Sensitivity and Selectivity Based on Interior Nanofilm-Coated Photonic Crystal Fiber Long-Period Gratings. Sens. Actuators B Chem. 2013, 176, 264–274. [Google Scholar] [CrossRef]
- Sohn, K.R. Liquid Sensors Using Refractive Intensity at the End-Face of a Glass Fiber Connected to Fiber-Bragg Grating. Sens. Actuators A Phys. 2010, 158, 193–197. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, S.; Zhao, J.; Li, H.; Bai, H.; Miaoet, C. Multipoint refractive index and temperature fiber optic sensor based on cascaded no core fiber-fiber Bragg grating structures. Opt. Eng. 2017, 56, 027102. [Google Scholar] [CrossRef]
- Zhang, W.; Tuerdahong, N.; Zhu, L.Q.; Dong, M.L.; Lou, X.P. Temperature and Refractive Index Measurement Using an Optical Fiber Sensor Featuring PCF-FP and FBG Inscribed by Femtosecond Laser. Optik 2019, 194, 163095. [Google Scholar] [CrossRef]
- Wu, Y.; Li, H.; Yan, G.; Meng, F.Y.; Zhu, L.Q. Simultaneous Measurement of Refractive Index and Temperature Based on Asymmetrical Fabry-Perot Interferometer. Microw. Opt. Technol. Lett. 2019, 61, 2190–2195. [Google Scholar] [CrossRef]
- Personick, S.D. Fiber Optics; Springer: New York, NY, USA, 1985; pp. 6–41. [Google Scholar]
- Zhao, N.; Lin, Q.J.; Jiang, Z.D.; Yao, K.; Tian, B.; Fang, X.D.; Shi, P.; Zhang, Z.K. High Temperature High Sensitivity Multipoint Sensing System Based on Three Cascade Mach−Zehnder Interferometers. Sensors 2018, 18, 2688. [Google Scholar] [CrossRef]










| FBG Type | Materials | Hydrogen Carrier | Anneal | Modulation Mode | Reflectivity | Temperature |
|---|---|---|---|---|---|---|
| Common FBG | Glass fiber | Yes | No | Refractive index modulation | 80% | <400 °C |
| Regenerative FBG | Glass fiber | Yes | No | Refractive index modulation | 20% | <1000 °C |
| Femtosecond pure silica FBG | Pure silica fiber | No | Yes | Physical destruction | 70% | >1000 °C |
| Sensor Number | Mach Number [Ma] | Reference Temperature [tg0/°C] | Temperature to be Calibrated [ti/°C] | Temperature Difference [Δti/°C] | Extended Uncertainty [U(Δti)/°C (k = 2)] |
|---|---|---|---|---|---|
| Xjtuipe-lbsfs | 0.198 | 890.2 | 889.7 | 0.5 | 17 |
| 0.202 | 1100.8 | 1100.3 | 0.5 | 19 |
| Measuring Position | Normal Temperature | Inner Flame | Middle Flame | Outer Flame |
|---|---|---|---|---|
| Wavelength (nm) | 1554.14 | 1559.52 | 1562.64 | 1565.56 |
| Temperature (°C) | 30.6 | 432.1 | 664.9 | 882.8 |
| Liquid Sample | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Intensity (dBm) | −48.870 | −48.747 | −48.281 | −46.467 | −46.403 | −45.682 |
| Measured refractive index (RIU) | 1.398 | 1.3955 | 1.386 | 1.349 | 1.3477 | 1.333 |
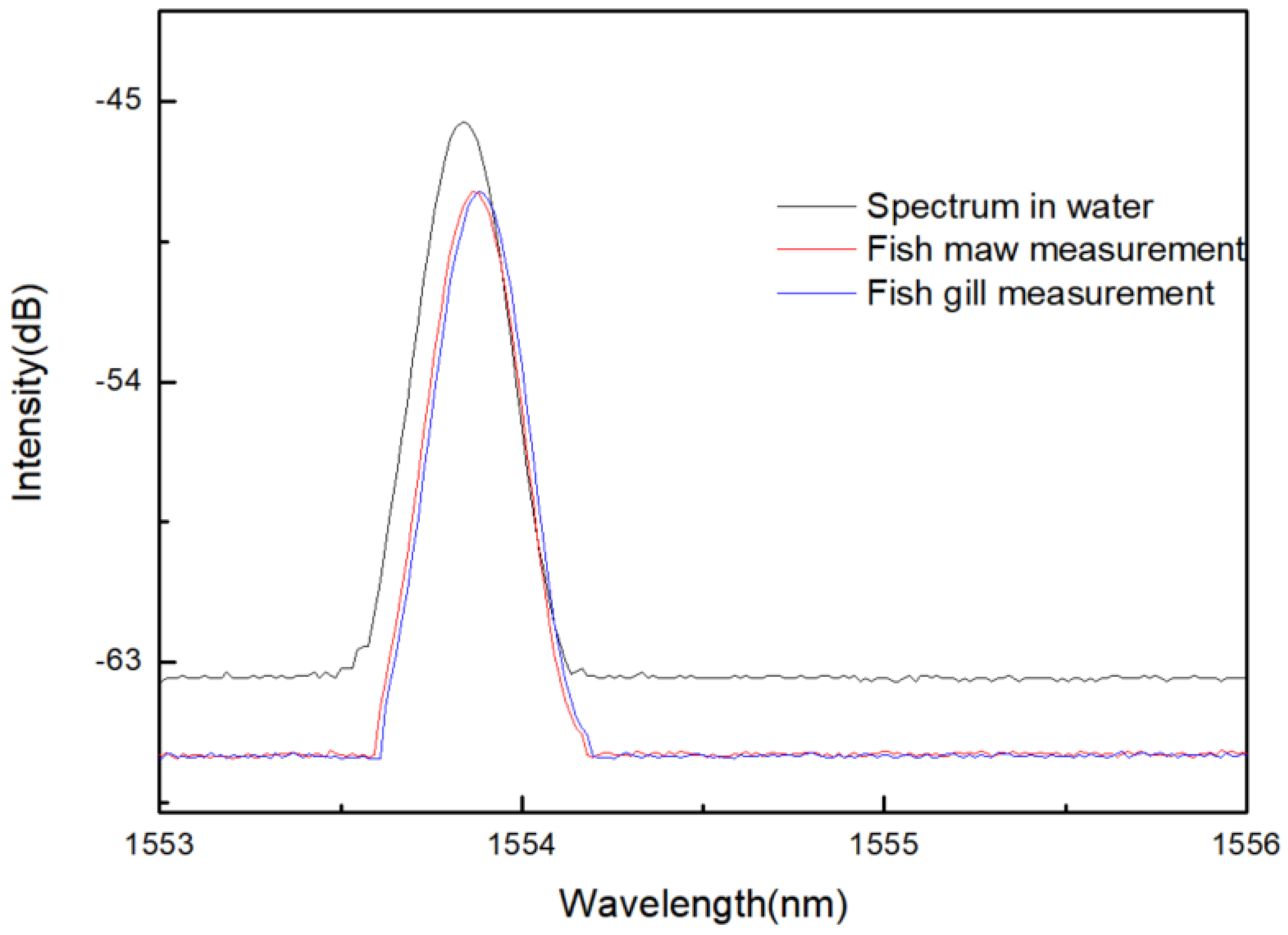
| Measuring Position | Spectrum in Water | Fish Maw Measurement | Fish Gill Measurement |
|---|---|---|---|
| Wavelength (nm) | 1553.84 | 1553.86 | 1553.90 |
| Intensity (dBm) | −45.682 | −47.938 | −48.331 |
| Temperature (°C) | 8 | 10 | 12 |
| refractive index (RIU) | 1.333 | 1.379 | 1.387 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, N.; Lin, Q.; Yao, K.; Zhang, F.; Tian, B.; Chen, F.; Jiang, Z. Simultaneous Measurement of Temperature and Refractive Index Using High Temperature Resistant Pure Quartz Grating Based on Femtosecond Laser and HF Etching. Materials 2021, 14, 1028. https://doi.org/10.3390/ma14041028
Zhao N, Lin Q, Yao K, Zhang F, Tian B, Chen F, Jiang Z. Simultaneous Measurement of Temperature and Refractive Index Using High Temperature Resistant Pure Quartz Grating Based on Femtosecond Laser and HF Etching. Materials. 2021; 14(4):1028. https://doi.org/10.3390/ma14041028
Chicago/Turabian StyleZhao, Na, Qijing Lin, Kun Yao, Fuzheng Zhang, Bian Tian, Feng Chen, and Zhuangde Jiang. 2021. "Simultaneous Measurement of Temperature and Refractive Index Using High Temperature Resistant Pure Quartz Grating Based on Femtosecond Laser and HF Etching" Materials 14, no. 4: 1028. https://doi.org/10.3390/ma14041028
APA StyleZhao, N., Lin, Q., Yao, K., Zhang, F., Tian, B., Chen, F., & Jiang, Z. (2021). Simultaneous Measurement of Temperature and Refractive Index Using High Temperature Resistant Pure Quartz Grating Based on Femtosecond Laser and HF Etching. Materials, 14(4), 1028. https://doi.org/10.3390/ma14041028









