Finite Element Modeling of Bond Behavior of FRP and Steel Plates
Abstract
:1. Introduction
2. Literature Review
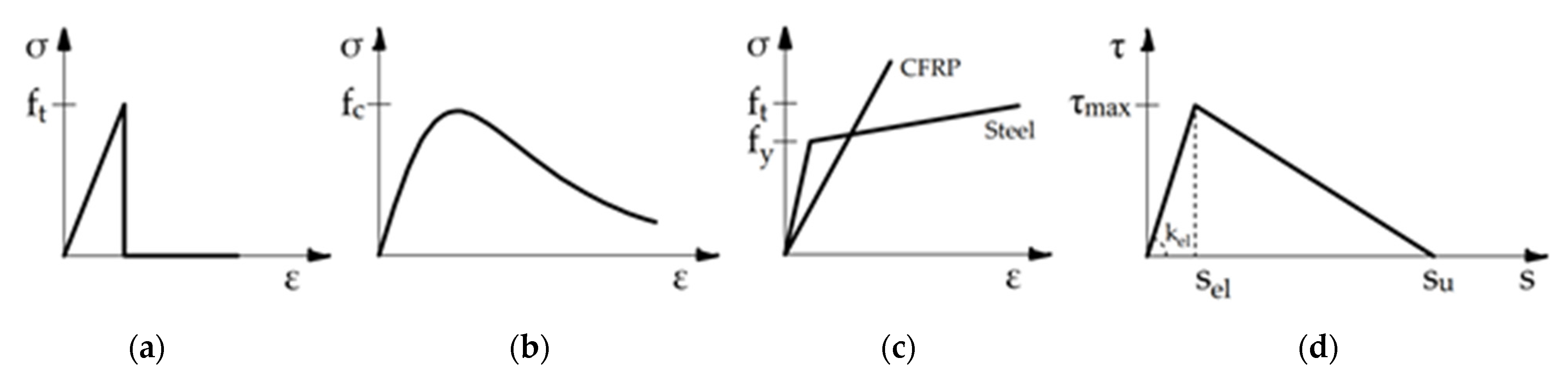
3. Modeling Approaches for Bonded Interface
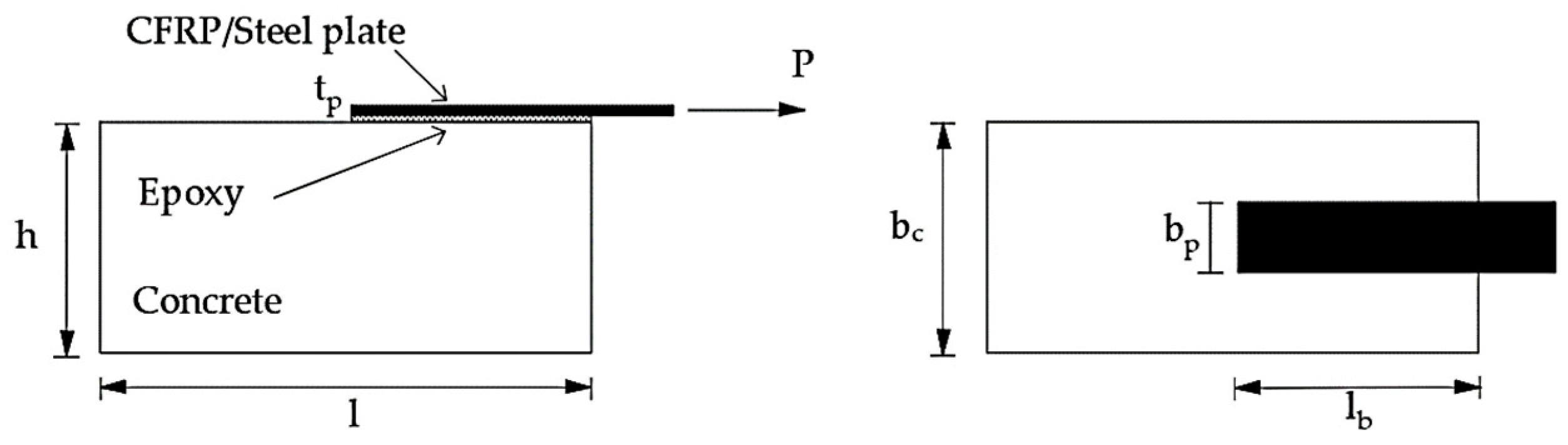
4. The FE 3D model
4.1. 3D FE Model with Nonlinear Interface Elements (IE Approach)
4.2. 3D FE Model with Adhesive Layer (AL Approach)
5. Analysis of Bond Behavior by Means of FE Models
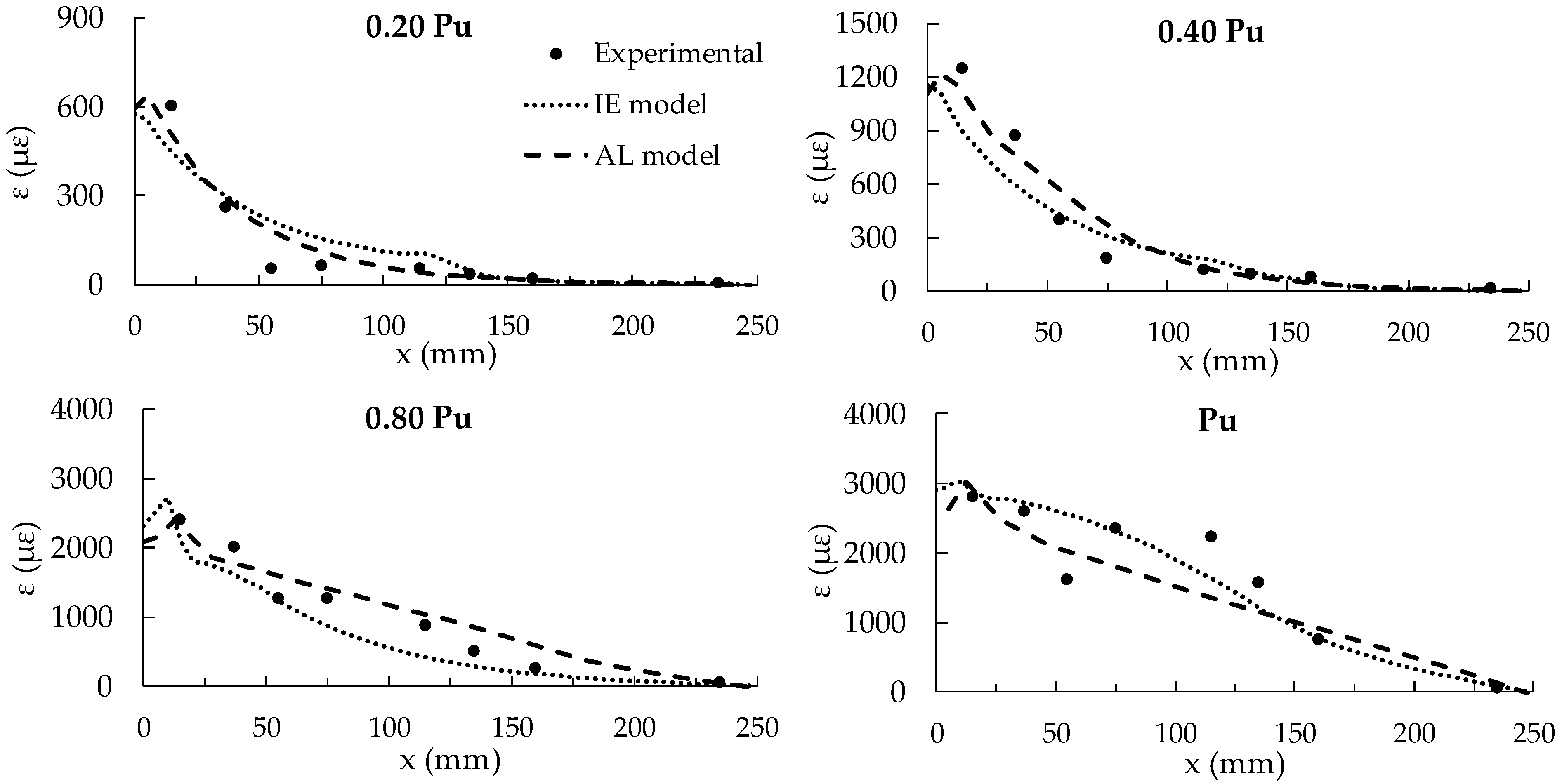
5.1. Validation of the FE Models by Means of Comparisons with Experimental Results
- the tensile strength and the elastic modulus of concrete have been evaluated from the compression strength according to formulations provided by Eurocode 2 [37];
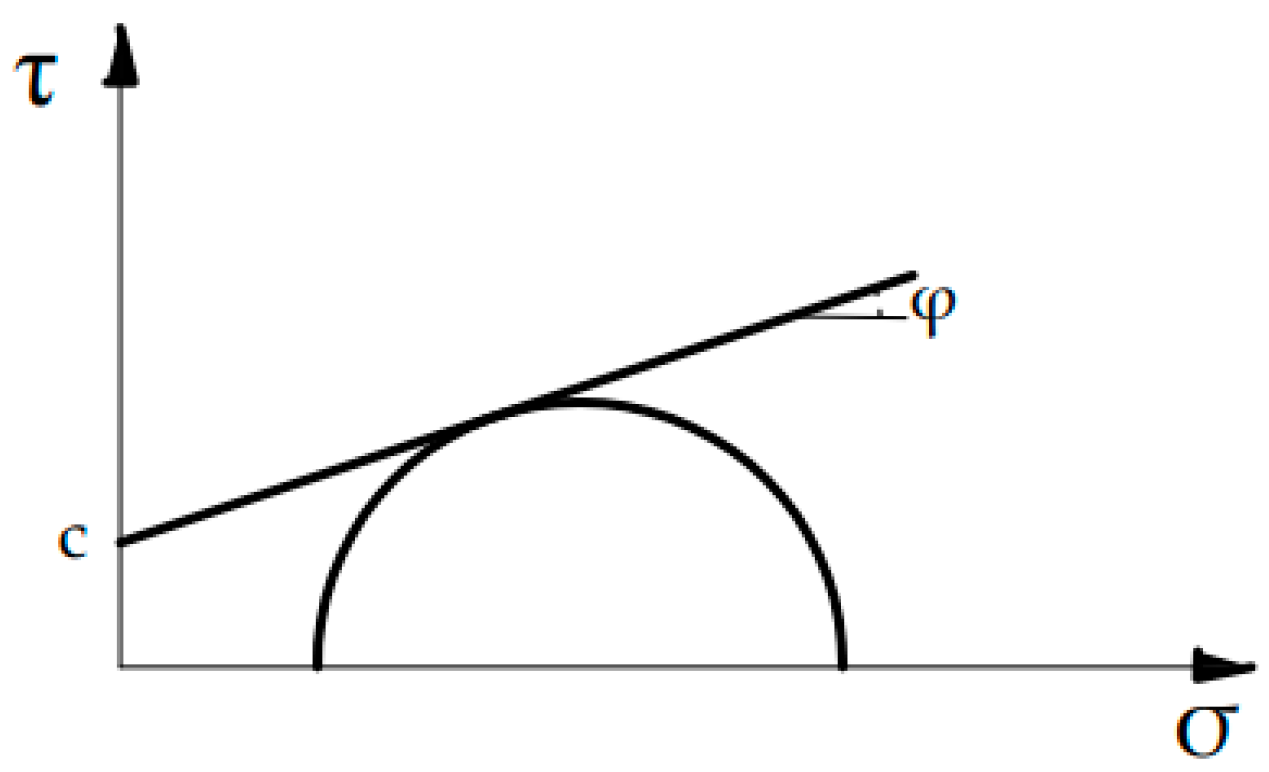
- the value of the cohesion, c, of the Mohr Coulomb criterion is assumed 1.8 and 2.6 MPa for the two concretes with fcm = 38 MPa and 58 MPa, respectively, while the friction angle, ϕ, is assumed 31° as provided by Lelović et al. [36] for both of them;
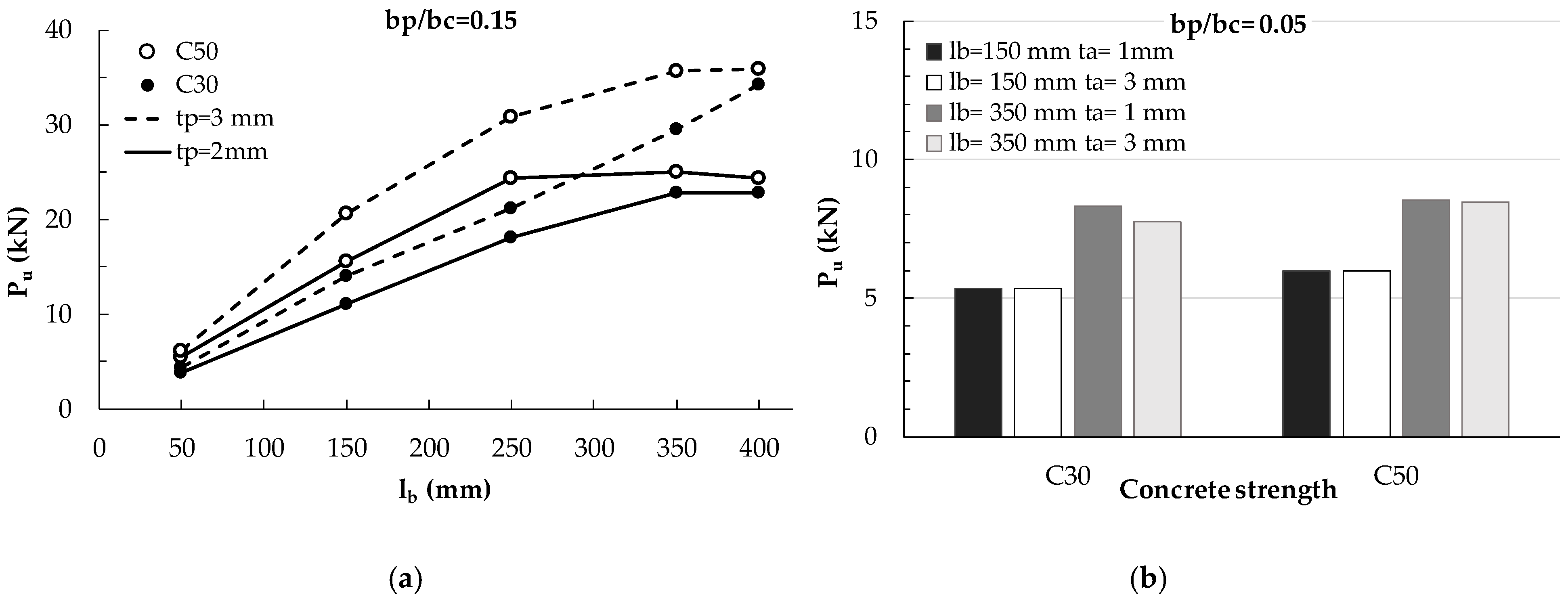
- the adhesive thickness was assumed 1 mm and 3 mm and the shear modulus Ga was calibrated basing on the experimental distribution of the strain along the strengthening plate. It resulted equal to 0.18 GPa and, however, it was also verified that it provides a low influence on the ultimate load.
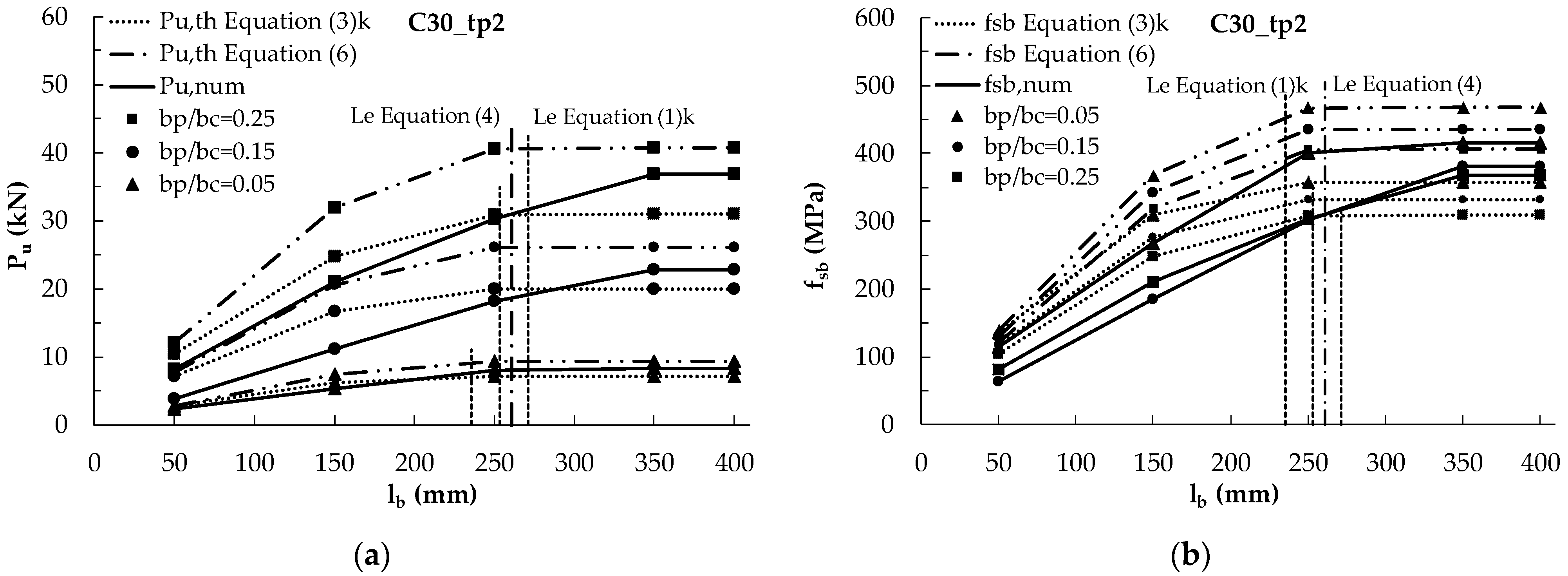
5.2. Analysis of Bond Behavior by Means of Parametric Analyses
6. Conclusions
- The two 3D FE models investigated, i.e., the AL approach that simulates the adhesive with its own thickness and the IE approach that adopts interface elements characterized by shear stress-slip relationships calibrated using experimental tests, give comparable results in terms of effective length and ultimate debonding load; the AL approach has the advantage that allows developing parametric analyses by changing the only properties of materials without necessity of reviewing the bond laws. However, the evaluation of the slips provided by the AL approach is not reliable, because the slips at the concrete-adhesive and the plate adhesive-interface are not computed, while, in the IE approach, they are directly included in bond laws experimentally calibrated.
- The effect of the mesh size on the results provided by the FE model was examined by calibrating the most suitable choice according to the dimension of the strengthening plate (smaller size mesh for smaller plate width), the sensitivity of the results in terms of ultimate load with the mesh size, and the computational effort. A further reduction of the mesh utilized in the analysis should give, indeed, a variation of the results of approximately 2%, but the calculation time would increase significantly.
- The numerical analyses confirm that the bond behavior of externally bonded steel plates is governed by the same parameters influencing that of the FRP plates; in particular, the main parameters are concrete strength, plate axial stiffness, and plate-to-concrete width ratio, but their role depends also on the effective length, which is shorter for higher strength concrete and longer for higher plate stiffness, which is the case of steel plates. The thickness of the adhesive has a little influence on the debonding load.
- About the effect of the axial stiffness of the plate, for bonded lengths lower than the effective ones, the debonding loads seem to be low sensitive to this parameter, while for longer bonded length, they start depending more significantly on the axial stiffness since the latter one influences the effective length too and, thus, the possibility of having bonded length lower or higher than the effective length.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mazzotti, C.; Ferracuti, B.; Savoia, M. An experimental study on FRP-concrete delamination. Proc. FraMCoS-5 2004, 1, 795–802. [Google Scholar]
- Ceroni, F.; Pecce, M.R. Statistical Analysis of Debonding Load in Concrete Elements Externally Strengthened with CFRP Materials. Adv. Struct. Eng. 2012, 15, 155–168. [Google Scholar] [CrossRef]
- Biscaia, H.C.; Chastre, C.; Silva, M. Nonlinear numerical analysis of the debonding failure process of FRP-to-concrete interfaces. Compos. Part B Eng. 2013, 50, 210–223. [Google Scholar] [CrossRef]
- Zhang, P.; Lei, D.; Ren, Q.; He, J.; Shen, H.; Yang, Z. Experimental and numerical investigation of debonding process of the FRP plate–concrete interface. Constr. Build. Mater. 2020, 235, 117457. [Google Scholar] [CrossRef]
- Oh, B.H.; Cho, J.-Y.; Park, D.G. Failure Behavior and Separation Criterion for Strengthened Concrete Members with Steel Plates. J. Struct. Eng. 2003, 129, 1191–1198. [Google Scholar] [CrossRef]
- Täljsten, B. Defining anchor lengths of steel and CFRP plates bonded to concrete. Int. J. Adhes. Adhes. 1997, 17, 319–327. [Google Scholar] [CrossRef]
- Ziraba, Y.N.; Baluch, M.H.; Basunbul, I.A.; Azad, A.K.; Al-Sulaimani, G.J.; Sharif, A.M. Combined experimental-numerical approach to characterization of steel-glue-concrete interface. Mater. Struct. 1995, 28, 518–525. [Google Scholar] [CrossRef]
- MIDAS FEA NX, Verision 2020, Nonlinear and Detail Analysis System. Midas Information Technology Co. Ltd.: Seohyenon-dong, Korea, 2020.
- Woo, S.-K.; Lee, Y. Experimental study on interfacial behavior of CFRP-bonded concrete. KSCE J. Civ. Eng. 2010, 14, 385–393. [Google Scholar] [CrossRef]
- Li, Y.-Q.; Esmaeeli, E.; Chen, J.-F.; Sha, W.; Soutsos, M. Single shear pull-off test of FRP-to-concrete and mortar bond. In Proceedings of the 14th International Symposium on Fiber Reinforced Polymers for reinforced concrete Structures (FRPRCS-14), Belfast, UK, 4–7 June 2019. [Google Scholar]
- Yao, J.; Teng, J.; Chen, J. Experimental study on FRP-to-concrete bonded joints. Compos. Part B: Eng. 2005, 36, 99–113. [Google Scholar] [CrossRef]
- Leung, C.K.; Klenke, M.; Tung, W.K.; Luk, H.C. Determination of Nonlinear Softening Behavior at FRP Composite/Concrete Interface. J. Eng. Mech. 2006, 132, 498–508. [Google Scholar] [CrossRef]
- Chen, J.F.; Yang, Z.J.; Holt, G.D. FRP or steel plate-to-concrete bonded joints: Effect of test methods on experimental bond strength. Steel Compos. Struct. 2001, 1, 231–244. [Google Scholar] [CrossRef]
- Sharma, S.; Ali, M.M.; Goldar, D.; Sikdar, P. Plate–concrete interfacial bond strength of FRP and metallic plated concrete specimens. Compos. Part B: Eng. 2006, 37, 54–63. [Google Scholar] [CrossRef]
- Täljsten, B. Strengthening of Beams by Plate Bonding. J. Mater. Civ. Eng. 1997, 9, 206–212. [Google Scholar] [CrossRef]
- Chen, J.F.; Teng, J.G. Anchorage Strength Models for FRP and Steel Plates bonded to concrete. J. Struct. Eng. 2001, 127, 784–791. [Google Scholar] [CrossRef]
- Dai, J.; Sato, Y.; Ueda, T. Improving the load transfer and effective bond length for FRP composites bonded to concrete. Pro. Jpn. Concr. Inst. 2002, 24, 1423–1428. [Google Scholar]
- Dai, J.; Ueda, T.; Sato, Y. Development of the Nonlinear Bond Stress–Slip Model of Fiber Reinforced Plastics Sheet–Concrete Interfaces with a Simple Method. J. Compos. Constr. 2005, 9, 52–62. [Google Scholar] [CrossRef] [Green Version]
- Neubauer, U.; Rostásy, F.S. Design aspects of concrete structures strengthened with externally bonded CFRP-plates. In Proceedings of the Seventh Intenational Conference Structural Faults and Repair, Edinburgh, UK, 8 July 1997. [Google Scholar]
- Täljsten, B. Strengthening of concrete prisms using the plate-bonding technique. Int. J. Fract. 1996, 82, 253–266. [Google Scholar] [CrossRef]
- Yuan, H.; Wu, Z.; Yoshizawa, H. Theoretical solutions on interfacial stress transfer of externally bonded steel/composite laminates. Doboku Gakkai Ronbunshu 2001, 2001, 27–39. [Google Scholar] [CrossRef] [Green Version]
- Holzenkämpfer, P. Ingenieurmodelle Des Verbundes Geklebter Bewehrung Für Betonbauteile; Institut für Baustoffe, Massivbau und Brandschutz (IBMB): Niedersachsen, Germany, 1994. [Google Scholar]
- Teng, J.G.; Smith, S.; Yao, J.; Chen, J. Intermediate crack-induced debonding in RC beams and slabs. Constr. Build. Mater. 2003, 17, 447–462. [Google Scholar] [CrossRef]
- Brosens, K.; Gemert, D.V. Anchorage design for externally bonded carbon fiber polymer laminates. In Proceedings of the 4th International Symposium on Fiber Reinforced Polymer Reinforcement for Reinforced Concrete Structures, Farmington Hills, MI, USA, 31 October–5 November 1999. [Google Scholar]
- Ueda, T.; Dai, J.; Sato, Y. A Nonlinear bond stress-slip relationship for FRP sheet-concrete interface. In Proceedings of the International Symposium on Latest Achievement of Technology and Research on Retrofitting Concrete Structures, Kyoto, Japan, 14 July 2003. [Google Scholar]
- López-González, J.C.; Gomez, J.A.F.; González-Valle, E. Effect of Adhesive Thickness and Concrete Strength on FRP-Concrete Bonds. J. Compos. Constr. 2012, 16, 705–711. [Google Scholar] [CrossRef] [Green Version]
- Fib CEB-FIP Externally Applied FRP Reinforcement for Concrete Structures; Fib: Lausanne, Switzerland, 2019.
- Faella, C.; Martinelli, E.; Nigro, E. Interface behaviour in FRP plates bonded to concrete: Experimental tests and theoretical analyses. In Proceedings of the Advanced Materials for Construction of Bridges, Buildings, and Other Structures III, Davos, Switzerland, 7–12 September 2003. [Google Scholar]
- Ceroni, F.; de Felice, G.; Grande, E.; Malena, M.; Mazzotti, C.; Murgo, F.; Sacco, E.; Valluzzi, M.R. Analytical and numerical modeling of composite-to-brick bond. Mater. Struct. 2014, 47, 1987–2003. [Google Scholar] [CrossRef]
- Coronado, C.A.; Lopez, M.M. Numerical Modeling of Concrete-FRP Debonding Using a Crack Band Approach. J. Compos. Constr. 2010, 14, 11–21. [Google Scholar] [CrossRef]
- Chen, T.-L.; Tao, W.; Zhu, W.; Zhou, M. Numerical simulation of the debonding process in pull-out tests of near-surface mounted FRP rod in concrete. Eng. Comput. 2019, 37, 1109–1130. [Google Scholar] [CrossRef]
- Sena-Cruz, J.; Barros, J. Modeling of bond between near-surface mounted CFRP laminate strips and concrete. Comput. Struct. 2004, 82, 1513–1521. [Google Scholar] [CrossRef] [Green Version]
- Ceroni, F.; Ianniciello, M.; Pecce, M.R. Bond behavior of FRP carbon plates externally bonded over steel and concrete elements: Experimental outcomes and numerical investigations. Compos. Part B Eng. 2016, 92, 434–446. [Google Scholar] [CrossRef]
- Ceroni, F.; Garofano, A.; Pecce, M.; Pecce, M.R. Bond tests on tuff elements externally bonded with FRP materials. Mater. Struct. 2014, 48, 2093–2110. [Google Scholar] [CrossRef]
- Thorenfeldt, E.; Tomaszewicz, A.; Jensen, J. Mechanical Properties of High-strength Concrete and Application in Design. In Proceedings of the International Conference on Behaviour of Offshore Structures (BOSS ‘88), Trondheim, Norway, 21–24 June 1988. [Google Scholar]
- Lelović, S.; Vasović, D.; Stojić, D. Determination of the Mohr–Coulomb Material Parameters for Concrete under Indirect Tensile Test. Teh. Vjesn.-Tech. Gaz. 2019, 26, 412–419. [Google Scholar]
- European Committee. EN 1992-1-1 Eurocode 2: Design of Concrete Structures; European Committee: London, UK, 2004. [Google Scholar]


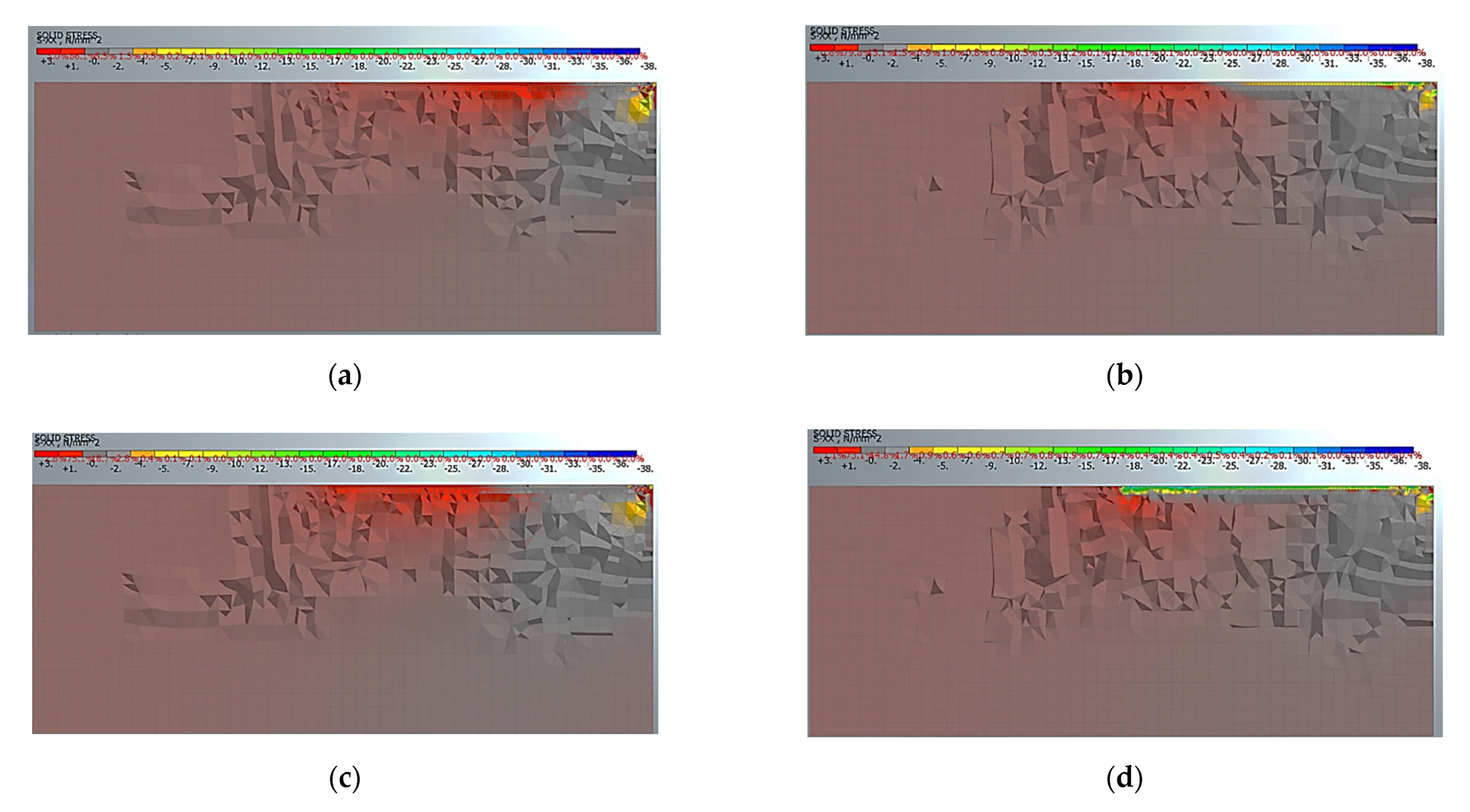




| Materials | fcm (MPa) | fy (MPa) | c (MPa) | ϕ (°) | ft (MPa) | E (MPa) | t (mm) |
|---|---|---|---|---|---|---|---|
| Concrete C30 | 38.0 | - | 1.8 | 31 | 2.9 | 33,000 | 200 |
| Concrete C50 | 58.0 | - | 2.6 | 31 | 4.1 | 37,000 | 200 |
| Adhesive | 80.3 | - | - | - | - | 500 | 1.0; 3.0 |
| CFRP | − | - | - | - | 2850.0 | 152,200 | 1.4 |
| Steel | 275.0 | 275.0 | - | - | 430.0 | 210,000 | 2.0; 3.0 |
| Specimen | C30_1.4_50_250 | C30_1.4_50_250 | |
|---|---|---|---|
| fc (MPa) | 30 | 50 | |
| tp (mm) | 1.4 | 1.4 | |
| Ep (MPa) | 152,200 | 152,200 | |
| bp (mm) | 50 | 50 | |
| lb (mm) | 250 | 250 | |
| Pu,exp (kN) | 28 | 34 | |
| Pu,th (kN) | Equation (3)m | 32.5 | 37.4 |
| Equation (6) | 27.3 | 32.2 | |
| Pu,num (kN) | AL | 27.9 | 35.8 |
| IE | 30.9 | 34.1 | |
| Pu,exp/Pu,th (-) | Equation (3)m | 0.86 | 0.91 |
| Equation (6) | 1.03 | 1.06 | |
| Pu,exp/Pu,num (-) | AL | 1 | 0.95 |
| IE | 0.91 | 1 | |
| Pu,numAL/Pu,th (-) | Equation (3)m | 0.86 | 0.96 |
| Equation (6) | 1.02 | 1.11 | |
| Specimen | fcm (MPa) | tp (mm) | Eptp (kN/mm) | bp (mm) | lb (mm) | bp/bc (-) | Pu,th (kN) | Pu,num (kN) AL FE | Pu,num/Pu,th (-) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equation (3)m | Equation (3)k | Equation (6) | Equation (3)m | Equation (3)k | Equation (6) | ||||||||
| C30_2_10_50 | 38 | 2 | 420 | 10 | 50 | 0.05 | 5.6 | 2.7 | 2.8 | 2.3 | 0.41 | 0.85 | 0.83 |
| C30_2_10_150 | 38 | 2 | 420 | 10 | 150 | 0.05 | 10.5 | 6.2 | 7.3 | 5.4 | 0.51 | 0.87 | 0.73 |
| C30_2_10_250 | 38 | 2 | 420 | 10 | 250 | 0.05 | 10.5 | 7.1 | 9.3 | 8.0 | 0.76 | 1.12 | 0.86 |
| C30_2_10_350 | 38 | 2 | 420 | 10 | 350 | 0.05 | 10.5 | 7.1 | 9.4 | 8.3 | 0.79 | 1.16 | 0.89 |
| C30_2_10_400 | 38 | 2 | 420 | 10 | 400 | 0.05 | 10.5 | 7.1 | 9.4 | 8.3 | 0.79 | 1.16 | 0.89 |
| C30_2_30_50 | 38 | 2 | 420 | 30 | 50 | 0.15 | 14.8 | 7.1 | 7.7 | 3.8 | 0.26 | 0.54 | 0.49 |
| C30_2_30_150 | 38 | 2 | 420 | 30 | 150 | 0.15 | 28.9 | 16.6 | 20.5 | 11.1 | 0.38 | 0.67 | 0.54 |
| C30_2_30_250 | 38 | 2 | 420 | 30 | 250 | 0.15 | 29.3 | 19.9 | 26.1 | 18.1 | 0.62 | 0.91 | 0.69 |
| C30_2_30_350 | 38 | 2 | 420 | 30 | 350 | 0.15 | 29.3 | 19.9 | 26.1 | 22.9 | 0.78 | 1.15 | 0.87 |
| C30_2_30_400 | 38 | 2 | 420 | 30 | 400 | 0.15 | 29.3 | 19.9 | 26.1 | 22.9 | 0.78 | 1.15 | 0.87 |
| C30_2_50_50 | 38 | 2 | 420 | 50 | 50 | 0.25 | 21.7 | 10.4 | 12.0 | 8.1 | 0.37 | 0.78 | 0.67 |
| C30_2_50_150 | 38 | 2 | 420 | 50 | 150 | 0.25 | 44.2 | 24.8 | 31.9 | 21.0 | 0.47 | 0.85 | 0.66 |
| C30_2_50_250 | 38 | 2 | 420 | 50 | 250 | 0.25 | 45.6 | 30.8 | 40.6 | 30.3 | 0.66 | 0.98 | 0.75 |
| C30_2_50_350 | 38 | 2 | 420 | 50 | 350 | 0.25 | 45.6 | 31.0 | 40.6 | 36.8 | 0.81 | 1.19 | 0.91 |
| C30_2_50_400 | 38 | 2 | 420 | 50 | 400 | 0.25 | 45.6 | 31.0 | 40.6 | 36.8 | 0.81 | 1.19 | 0.91 |
| C30_3_10_50 | 38 | 3 | 630 | 10 | 50 | 0.05 | 5.8 | 2.8 | 2.8 | 2.5 | 0.43 | 0.90 | 0.90 |
| C30_3_10_150 | 38 | 3 | 630 | 10 | 150 | 0.05 | 12.2 | 6.7 | 7.7 | 4.5 | 0.37 | 0.67 | 0.58 |
| C30_3_10_250 | 38 | 3 | 630 | 10 | 250 | 0.05 | 12.9 | 8.6 | 10.8 | 8.4 | 0.66 | 0.98 | 0.78 |
| C30_3_10_350 | 38 | 3 | 630 | 10 | 350 | 0.05 | 12.9 | 8.7 | 11.5 | 9.9 | 0.77 | 1.13 | 0.86 |
| C30_3_10_400 | 38 | 3 | 630 | 10 | 400 | 0.05 | 12.9 | 8.7 | 11.5 | 10.3 | 0.80 | 1.17 | 0.90 |
| C30_3_30_50 | 38 | 3 | 630 | 30 | 50 | 0.15 | 15.3 | 7.2 | 7.8 | 4.4 | 0.29 | 0.61 | 0.57 |
| C30_3_30_150 | 38 | 3 | 630 | 30 | 150 | 0.15 | 33.2 | 17.9 | 21.5 | 14.0 | 0.42 | 0.78 | 0.65 |
| C30_3_30_250 | 38 | 3 | 630 | 30 | 250 | 0.15 | 35.9 | 23.5 | 30.2 | 21.2 | 0.59 | 0.90 | 0.70 |
| C30_3_30_350 | 38 | 3 | 630 | 30 | 350 | 0.15 | 35.9 | 24.4 | 32.0 | 29.5 | 0.82 | 1.21 | 0.92 |
| C30_3_30_400 | 38 | 3 | 630 | 30 | 400 | 0.15 | 35.9 | 24.4 | 32.0 | 34.2 | 0.95 | 1.40 | 1.07 |
| C30_3_50_50 | 38 | 3 | 630 | 50 | 50 | 0.25 | 22.3 | 10.6 | 12.1 | 8.1 | 0.36 | 0.77 | 0.67 |
| C30_3_50_150 | 38 | 3 | 630 | 50 | 150 | 0.25 | 50.0 | 26.5 | 33.4 | 20.7 | 0.41 | 0.78 | 0.62 |
| C30_3_50_250 | 38 | 3 | 630 | 50 | 250 | 0.25 | 55.8 | 35.6 | 46.9 | 26.7 | 0.48 | 0.75 | 0.57 |
| C30_3_50_350 | 38 | 3 | 630 | 50 | 350 | 0.25 | 55.8 | 38.0 | 49.8 | 43.7 | 0.78 | 1.15 | 0.88 |
| C30_3_50_400 | 38 | 3 | 630 | 50 | 400 | 0.25 | 55.8 | 38.0 | 49.8 | 50.0 | 0.90 | 1.32 | 1.00 |
| C50_2_10_150 | 58 | 2 | 420 | 10 | 150 | 0.05 | 12.1 | 7.6 | 8.8 | 6.0 | 0.50 | 0.79 | 0.68 |
| C50_2_10_350 | 58 | 2 | 420 | 10 | 350 | 0.05 | 12.1 | 8.2 | 10.4 | 8.5 | 0.71 | 1.04 | 0.82 |
| C50_2_30_50 | 58 | 2 | 420 | 30 | 50 | 0.15 | 19.1 | 9.2 | 9.5 | 5.5 | 0.29 | 0.60 | 0.58 |
| C50_2_30_150 | 58 | 2 | 420 | 30 | 150 | 0.15 | 33.7 | 20.6 | 24.5 | 15.6 | 0.46 | 0.76 | 0.64 |
| C50_2_30_250 | 58 | 2 | 420 | 30 | 250 | 0.15 | 33.7 | 22.9 | 29.1 | 24.4 | 0.72 | 1.06 | 0.84 |
| C50_2_30_350 | 58 | 2 | 420 | 30 | 350 | 0.15 | 33.7 | 22.9 | 29.1 | 25.0 | 0.74 | 1.09 | 0.86 |
| C50_2_30_400 | 58 | 2 | 420 | 30 | 400 | 0.15 | 33.7 | 22.9 | 29.1 | 24.4 | 0.72 | 1.06 | 0.84 |
| C50_3_30_50 | 58 | 3 | 630 | 30 | 50 | 0.15 | 19.8 | 9.5 | 9.6 | 6.1 | 0.31 | 0.65 | 0.64 |
| C50_3_30_150 | 58 | 3 | 630 | 30 | 150 | 0.15 | 40.2 | 22.6 | 26.0 | 20.6 | 0.51 | 0.91 | 0.79 |
| C50_3_30_250 | 58 | 3 | 630 | 30 | 250 | 0.15 | 41.3 | 28.0 | 34.8 | 30.9 | 0.75 | 1.10 | 0.89 |
| C50_3_30_350 | 58 | 3 | 630 | 30 | 350 | 0.15 | 41.3 | 28.1 | 35.6 | 35.7 | 0.86 | 1.27 | 1.00 |
| C50_3_30_400 | 58 | 3 | 630 | 30 | 400 | 0.15 | 41.3 | 28.1 | 35.6 | 35.9 | 0.87 | 1.28 | 1.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciampa, E.; Ceroni, F.; Pecce, M.R. Finite Element Modeling of Bond Behavior of FRP and Steel Plates. Materials 2021, 14, 757. https://doi.org/10.3390/ma14040757
Ciampa E, Ceroni F, Pecce MR. Finite Element Modeling of Bond Behavior of FRP and Steel Plates. Materials. 2021; 14(4):757. https://doi.org/10.3390/ma14040757
Chicago/Turabian StyleCiampa, Elena, Francesca Ceroni, and Maria Rosaria Pecce. 2021. "Finite Element Modeling of Bond Behavior of FRP and Steel Plates" Materials 14, no. 4: 757. https://doi.org/10.3390/ma14040757
APA StyleCiampa, E., Ceroni, F., & Pecce, M. R. (2021). Finite Element Modeling of Bond Behavior of FRP and Steel Plates. Materials, 14(4), 757. https://doi.org/10.3390/ma14040757








