Controllable Hierarchical Mechanical Metamaterials Guided by the Hinge Design
Abstract
1. Introduction
2. Methods
2.1. Geometry
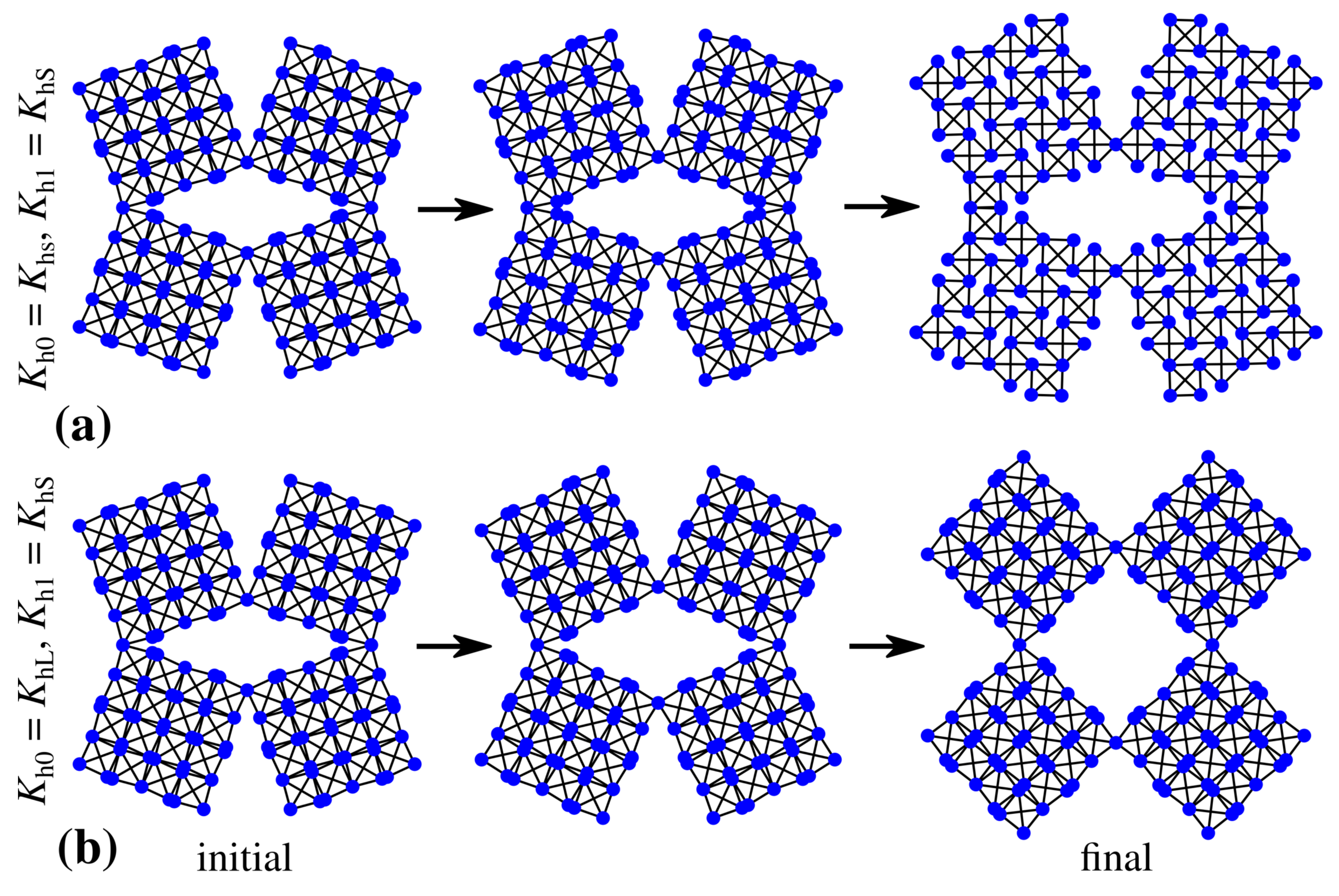
2.2. Deformation Process
2.3. Simulations and Parameters
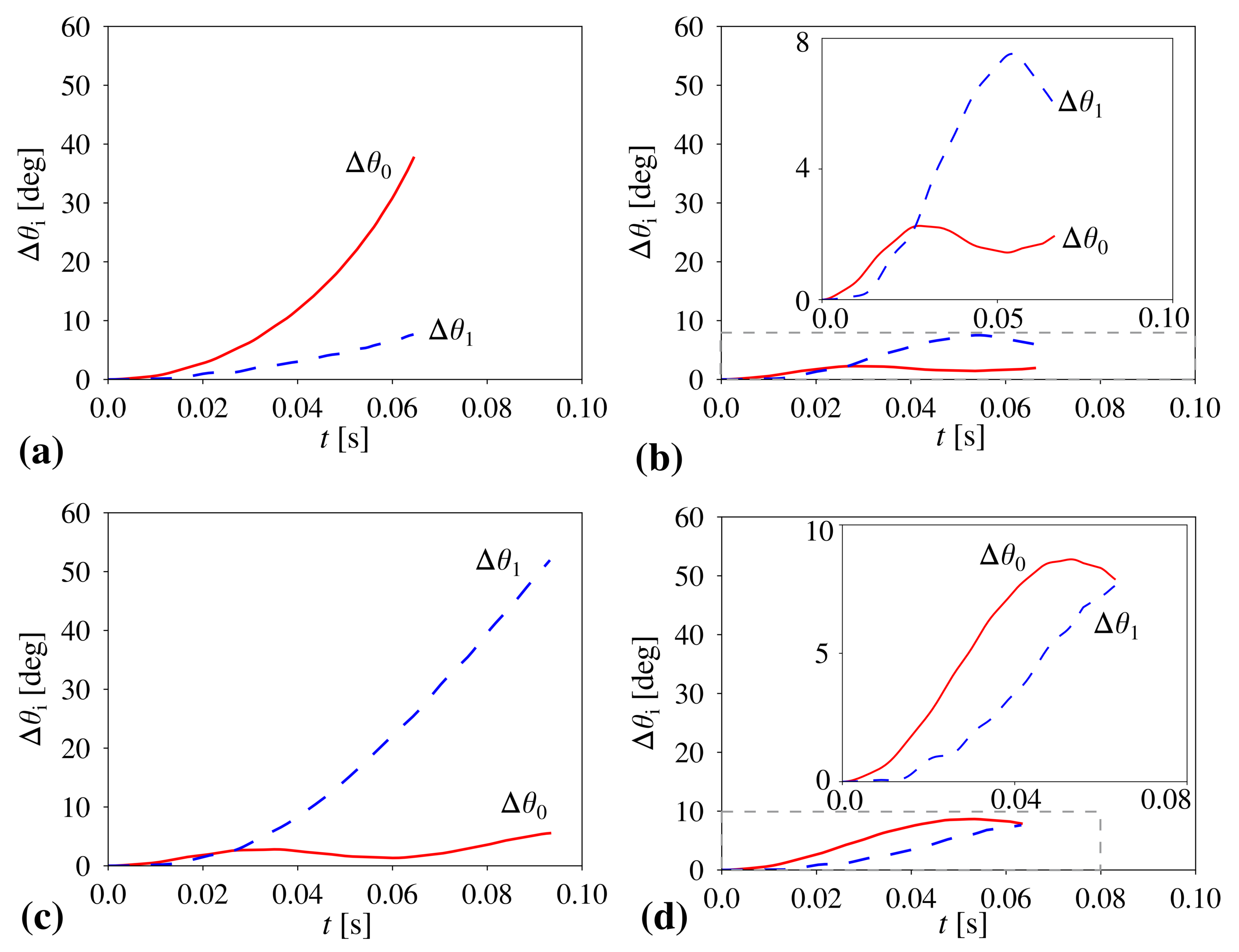
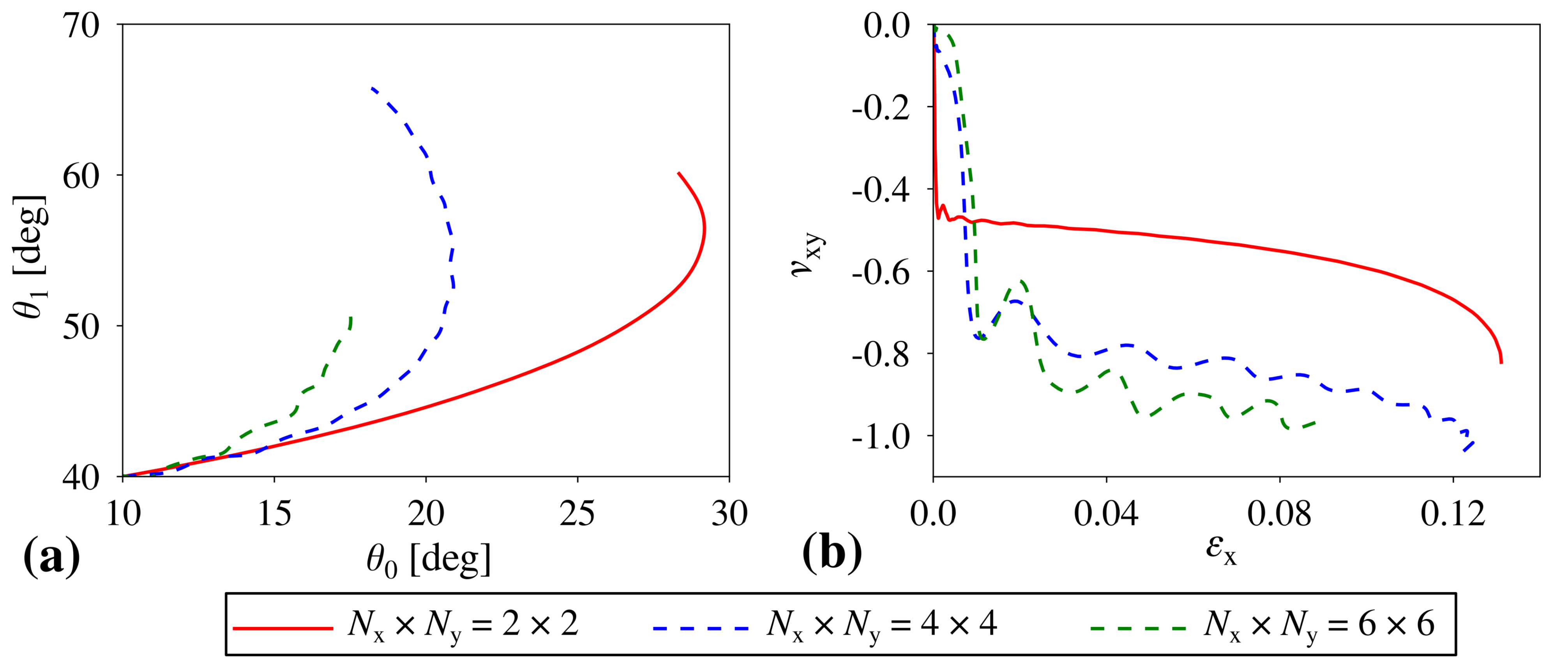
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J.; Rogers, S.C. Molecular Network Design. Nature 1991, 353, 124. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Mechanical meta-materials. Mater. Horiz. 2016, 3, 371–381. [Google Scholar] [CrossRef]
- Lim, T.-C. Mechanics of Metamaterials with Negative Parameters; Springer: Singapore, 2020. [Google Scholar]
- Evans, K.E.; Alderson, A. Auxetic Materials: Functional Materials and Structures from Lateral Thinking! Adv. Mater. 2000, 12, 617–628. [Google Scholar] [CrossRef]
- Scarpa, F.; Panayiotou, P.; Tomlinson, G. Numerical and experimental uniaxial loading on in-plane auxetic honeycombs. J. Strain Anal. Eng. 2000, 35, 383–388. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Two-dimensional isotropic system with a negative Poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Bertoldi, K.; Reis, P.M.; Willshaw, S.; Mullin, T. Negative Poisson’s Ratio Behavior Induced by an Elastic Instability. Adv. Mater. 2010, 22, 361–366. [Google Scholar] [CrossRef]
- Lim, T.-C. Analogies across auxetic models based on deformation mechanism. Phys. Status Solidi RRL 2017, 11, 1600440. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Idczak, E.; Wojciechowski, K.W. Computational Modelling of Structures with Non-Intuitive Behaviour. Materials 2017, 10, 1386. [Google Scholar] [CrossRef]
- Lim, T.-C. Auxeticity of Concentric Auxetic-Conventional Foam Rods with High Modulus Interface Adhesive. Materials 2018, 11, 223. [Google Scholar] [CrossRef]
- Xue, Y.; Gao, P.; Zhou, L.; Han, F. An Enhanced Three-Dimensional Auxetic Lattice Structure with Improved Property. Materials 2020, 13, 1008. [Google Scholar] [CrossRef]
- Strek, T.; Michalski, J.; Jopek, H. Computational Analysis of the Mechanical Impedance of the Sandwich Beam with Auxetic Metal Foam Core. Phys. Status Solidi B 2019, 256, 1800423. [Google Scholar] [CrossRef]
- Baughman, R.H.; Stafstrom, S.; Cui, C.; Dantas, S.O. Materials with negative compressibilities in one or more dimensions. Science 1998, 279, 1522–1524. [Google Scholar] [CrossRef] [PubMed]
- Lakes, R.; Wojciechowski, K.W. Negative compressibility, negative Poisson’s ratio, and stability. Phys. Status Solidi B 2008, 245, 545–551. [Google Scholar] [CrossRef]
- Nicolaou, Z.G.; Motter, A.E. Mechanical metamaterials with negative compressibility transitions. Nat. Mater. 2012, 11, 608–613. [Google Scholar] [CrossRef] [PubMed]
- Dudek, K.K.; Attard, D.; Caruana-Gauci, R.; Wojciechowski, K.W.; Grima, J.N. Unimode metamaterials exhibiting negative linear compressibility and negative thermal expansion. Smart Mater. Struct. 2016, 25, 025009. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, L.; Zhang, H.; Liu, Q.; Ren, T. 3D cellular models with negative compressibility through the wine-rack-type mechanism. Phys. Status Solidi B 2016, 253, 1977–1993. [Google Scholar] [CrossRef]
- Qu, J.; Kadic, M.; Wegener, M. Poroelastic metamaterials with negative effective static compressibility. Appl. Phys. Lett. 2017, 110, 171901. [Google Scholar] [CrossRef]
- Lim, T.-C. 2D Structures Exhibiting Negative Area Compressibility. Phys. Status Solidi B 2017, 254, 1600682. [Google Scholar] [CrossRef]
- Dudek, K.K.; Attard, D.; Gatt, R.; Grima-Cornish, J.N.; Grima, J.N. The Multidirectional Auxeticity and Negative Linear Compressibility of a 3D Mechanical Metamaterial. Materials 2020, 13, 2193. [Google Scholar] [CrossRef]
- Lakes, R.S.; Drugan, W.J. Dramatically stiffer elastic composite materials due to a negative stiffness phase? J. Mech. Phys. Solids 2002, 50, 979–1009. [Google Scholar] [CrossRef]
- Florijn, B.; Coulais, C.; van Hecke, M. Programmable mechanical metamaterials. Phys. Rev. Lett. 2014, 113, 175–503. [Google Scholar] [CrossRef]
- Hewage, T.A.M.; Alderson, K.L.; Alderson, A.; Scarpa, F. Double-negative mechanical metamaterials displaying simultaneous negative stiffness and negative Poissons ratio properties. Adv. Mater. 2016, 28, 10323. [Google Scholar] [CrossRef]
- Soo Ha, C.; Lakes, R.S.; Plesha, M.E. Cubic negative stiffness lattice structure for energy absorption: Numerical and experimental studies. Int. J. Solids Struct. 2019, 178–179, 127–135. [Google Scholar]
- Dudek, K.K.; Gatt, R.; Dudek, M.R.; Grima, J.N. Negative and positive stiffness in auxetic magneto-mechanical metamaterials. Proc. R. Soc. A 2018, 474, 20180003. [Google Scholar] [CrossRef]
- Dudek, K.K.; Gatt, R.; Grima, J.N. 3D composite metamaterial with magnetic inclusions exhibiting negative stiffness and auxetic behaviour. Mater. Des. 2020, 187, 108403. [Google Scholar] [CrossRef]
- Kolken, H.M.A.; Janbaz, S.; Leeflang, S.M.A.; Lietaert, K.; Weinans, H.H.; Zadpoor, A.A. Rationally designed meta-implants: A combination of auxetic and conventional meta-biomaterials. Mater. Horiz. 2018, 5, 28–35. [Google Scholar] [CrossRef]
- Cummer, S.A.; Christensen, J.; Alú, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 2016, 1, 16001. [Google Scholar] [CrossRef]
- Tang, Y.; Ren, S.; Meng, H.; Xin, F.; Huang, L.; Chen, T.; Zhang, C.; Lu, T.J. Hybrid acoustic metamaterial as super absorber for broadband low-frequency sound. Sci. Rep. 2017, 7, 43340. [Google Scholar] [CrossRef] [PubMed]
- Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038. [Google Scholar] [CrossRef] [PubMed]
- Imbalzano, G.; Linforth, S.; Ngo, T.D.; Lee, P.V.S.; Tran, P. Blast resistance of auxetic and honeycomb sandwich panels: Comparisons and parametric designs. Compos. Struct. 2018, 183, 242–261. [Google Scholar] [CrossRef]
- Al-Rifaie, H.; Sumelka, W. The Development of a New Shock Absorbing Uniaxial Graded Auxetic Damper (UGAD). Materials 2019, 12, 2573. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, L.; Ma, Z.-D.; Wang, T. A negative Poisson’s ratio suspension jounce bumper. Mater. Des. 2016, 103, 90–99. [Google Scholar] [CrossRef]
- Grima, J.N.; Alderson, A.; Evans, K.E. Auxetic behaviour from rotating rigid units. Phys. Status Solidi B 2005, 242, 561–575. [Google Scholar] [CrossRef]
- Yasuda, H.; Yang, J. Reentrant Origami-Based Metamaterials with Negative Poisson’s Ratio and Bistability. Phys. Rev. Lett. 2015, 114, 185502. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, Y. 3D Printed Auxetic Mechanical Metamaterial with Chiral Cells and Re-entrant Cores. Sci. Rep. 2018, 8, 2397. [Google Scholar] [CrossRef]
- Wu, W.; Hu, W.; Qian, G.; Liao, H.; Xu, X.; Berto, F. Mechanical design and multifunctional applications of chiral mechanical metamaterials: A review. Mater. Des. 2019, 180, 107950. [Google Scholar] [CrossRef]
- Frenzel, T.; Köpfler, J.; Jung, E.; Kadic, M.; Wegener, M. Ultrasound experiments on acoustical activity in chiral mechanical metamaterials. Nat. Commun. 2019, 10, 3384. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Frenzel, T.; Guenneau, S.; Kadic, M.; Wegener, M. Mapping acoustical activity in 3D chiral mechanical metamaterials onto micropolar continuum elasticity. J. Mech. Phys. Solids 2020, 137, 103877. [Google Scholar] [CrossRef]
- Dudek, K.K. New type of rotation of chiral mechanical metamaterials. Smart Mater. Struct. 2020, 29, 115027. [Google Scholar] [CrossRef]
- Mizzi, L.; Spaggiari, A. Chiralisation of Euclidean polygonal tessellations for the design of new auxetic metamaterials. Mech. Mater. 2021, 153, 103698. [Google Scholar] [CrossRef]
- Lakes, R. Materials with structural hierarchy. Nature 1993, 361, 511–515. [Google Scholar] [CrossRef]
- Oftadeh, R.; Haghpanah, B.; Vella, D.; Boudaoud, A.; Vaziri, A. Optimal Fractal-Like Hierarchical Honeycombs. Phys. Rev. Lett. 2014, 113, 104301. [Google Scholar] [CrossRef] [PubMed]
- Gatt, R.; Mizzi, L.; Azzopardi, J.I.; Azzopardi, K.M.; Attard, D.; Casha, A.; Briffa, J.; Grima, J.N. Hierarchical Auxetic Mechanical Metamaterials. Sci. Rep. 2015, 5, 8395. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.; Shin, J.-H.; Costa, A.; Kim, T.A.; Kunin, V.; Li, J.; Lee, S.Y.; Yang, S.; Han, H.N.; Choi, I.-S.; et al. Engineering the shape and structure of materials by fractal cut. Proc. Natl. Acad. Sci. USA 2014, 111, 17390–17395. [Google Scholar] [CrossRef]
- Mousanezhad, D.; Babaee, S.; Ebrahimi, H.; Ghosh, R.; Hamouda, A.S.; Bertoldi, K.; Vaziri, A. Hierarchical honeycomb auxetic metamaterials. Sci. Rep. 2016, 5, 18306. [Google Scholar] [CrossRef]
- Kunin, V.; Yang, S.; Cho, Y.; Deymier, P.; Srolovitz, D.J. Static and dynamic elastic properties of fractal-cut materials. Extreme Mech. Lett. 2016, 6, 103–114. [Google Scholar] [CrossRef]
- Tang, Y.; Lin, G.; Han, L.; Qiu, S.; Yang, S.; Yin, J. Design of Hierarchically Cut Hinges for Highly Stretchable and Reconfigurable Metamaterials with Enhanced Strength. Adv. Mater. 2015, 27, 7181–7190. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Yin, J. Design of cut unit geometry in hierarchical kirigami-based auxetic metamaterials for high stretchability and compressibility. Extreme Mech. Lett. 2017, 12, 77–85. [Google Scholar] [CrossRef]
- Dudek, K.K.; Gatt, R.; Mizzi, L.; Dudek, M.R.; Attard, D.; Evans, K.E.; Grima, J.N. On the dynamics and control of mechanical properties of hierarchical rotating rigid unit auxetics. Sci. Rep. 2017, 7, 46529. [Google Scholar] [CrossRef] [PubMed]
- Billon, K.; Zampetakis, I.; Scarpa, F.; Ouisse, M.; Sadoulet-Reboul, E.; Collet, M.; Perriman, A.; Hetherington, A. Mechanics and band gaps in hierarchical auxetic rectangular perforated composite metamaterials. Compos. Struct. 2017, 160, 1042–1050. [Google Scholar] [CrossRef]
- Attard, D.; Farrugia, P.S.; Gatt, R.; Grima, J.N. Starchirals-A novel class of auxetic hierarchal structures. Int. J. Mech. Sci. 2020, 179, 105631. [Google Scholar] [CrossRef]
- An, N.; Domel, A.G.; Zhou, J.; Rafsanjani, A.; Bertoldi, K. Programmable Hierarchical Kirigami: Programmable Hierarchical Kirigami. Adv. Funct. Mater. 2020, 30, 2070039. [Google Scholar] [CrossRef]
- Berwind, M.F.; Kamas, A.; Eberl, C. A Hierarchical Programmable Mechanical Metamaterial Unit Cell Showing Metastable Shape Memory. Adv. Eng. Mater. 2018, 20, 1800771. [Google Scholar] [CrossRef]
- Mizzi, L.; Spaggiari, A. Lightweight mechanical metamaterials designed using hierarchical truss elements. Smart Mater. Struct. 2020, 29, 105036. [Google Scholar] [CrossRef]
- Burden, R.L.; Faires, J.D. Numerical Analysis 220; PWS Publishers: Boston, MA, USA, 1985. [Google Scholar]
- Dudek, K.K.; Wojciechowski, K.W.; Dudek, M.R.; Gatt, R.; Mizzi, L.; Grima, J.N. Potential of mechanical metamaterials to induce their own global rotational motion. Smart Mater. Struct. 2018, 27, 055007. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dudek, K.K.; Gatt, R.; Dudek, M.R.; Grima, J.N. Controllable Hierarchical Mechanical Metamaterials Guided by the Hinge Design. Materials 2021, 14, 758. https://doi.org/10.3390/ma14040758
Dudek KK, Gatt R, Dudek MR, Grima JN. Controllable Hierarchical Mechanical Metamaterials Guided by the Hinge Design. Materials. 2021; 14(4):758. https://doi.org/10.3390/ma14040758
Chicago/Turabian StyleDudek, Krzysztof K., Ruben Gatt, Miroslaw R. Dudek, and Joseph N. Grima. 2021. "Controllable Hierarchical Mechanical Metamaterials Guided by the Hinge Design" Materials 14, no. 4: 758. https://doi.org/10.3390/ma14040758
APA StyleDudek, K. K., Gatt, R., Dudek, M. R., & Grima, J. N. (2021). Controllable Hierarchical Mechanical Metamaterials Guided by the Hinge Design. Materials, 14(4), 758. https://doi.org/10.3390/ma14040758






