Gradual Degradation of InGaAs LEDs: Impact on Non-Radiative Lifetime and Extraction of Defect Characteristics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Details
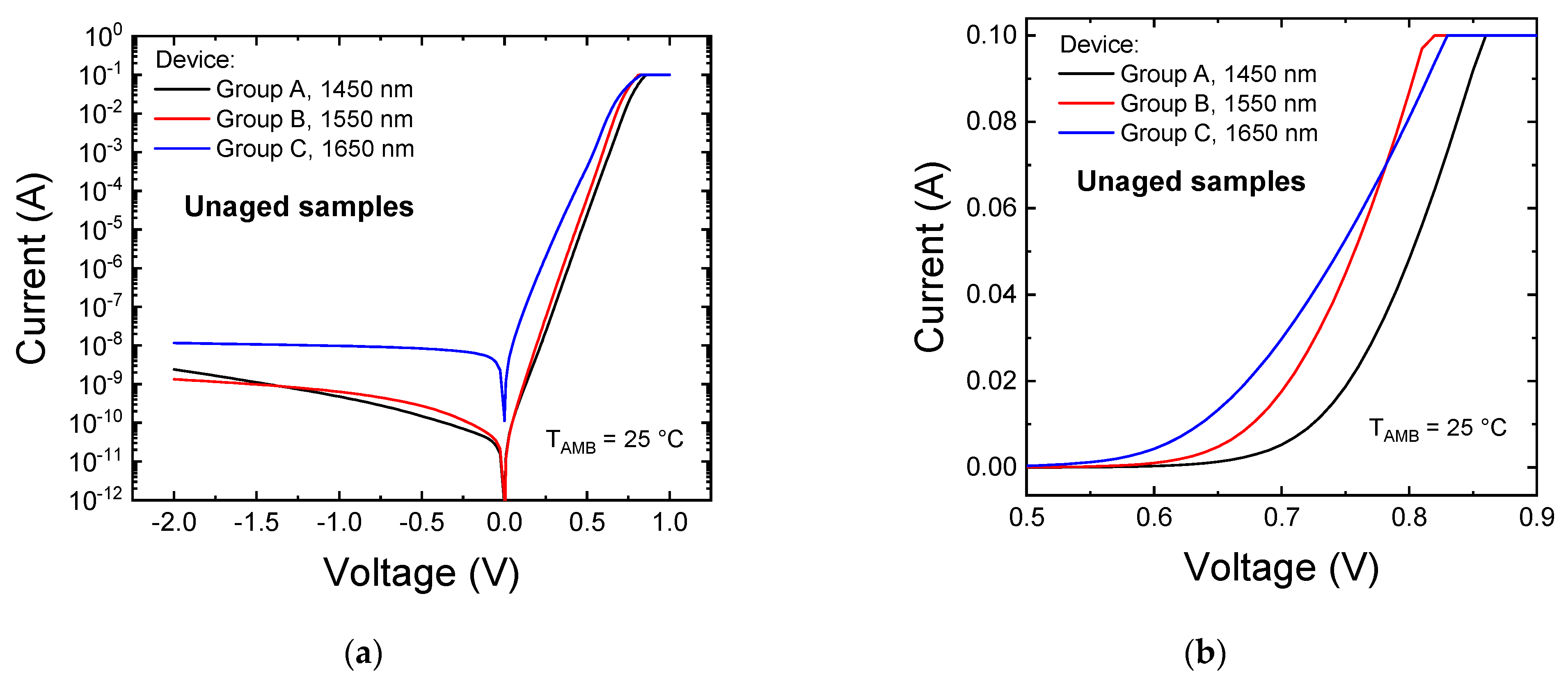
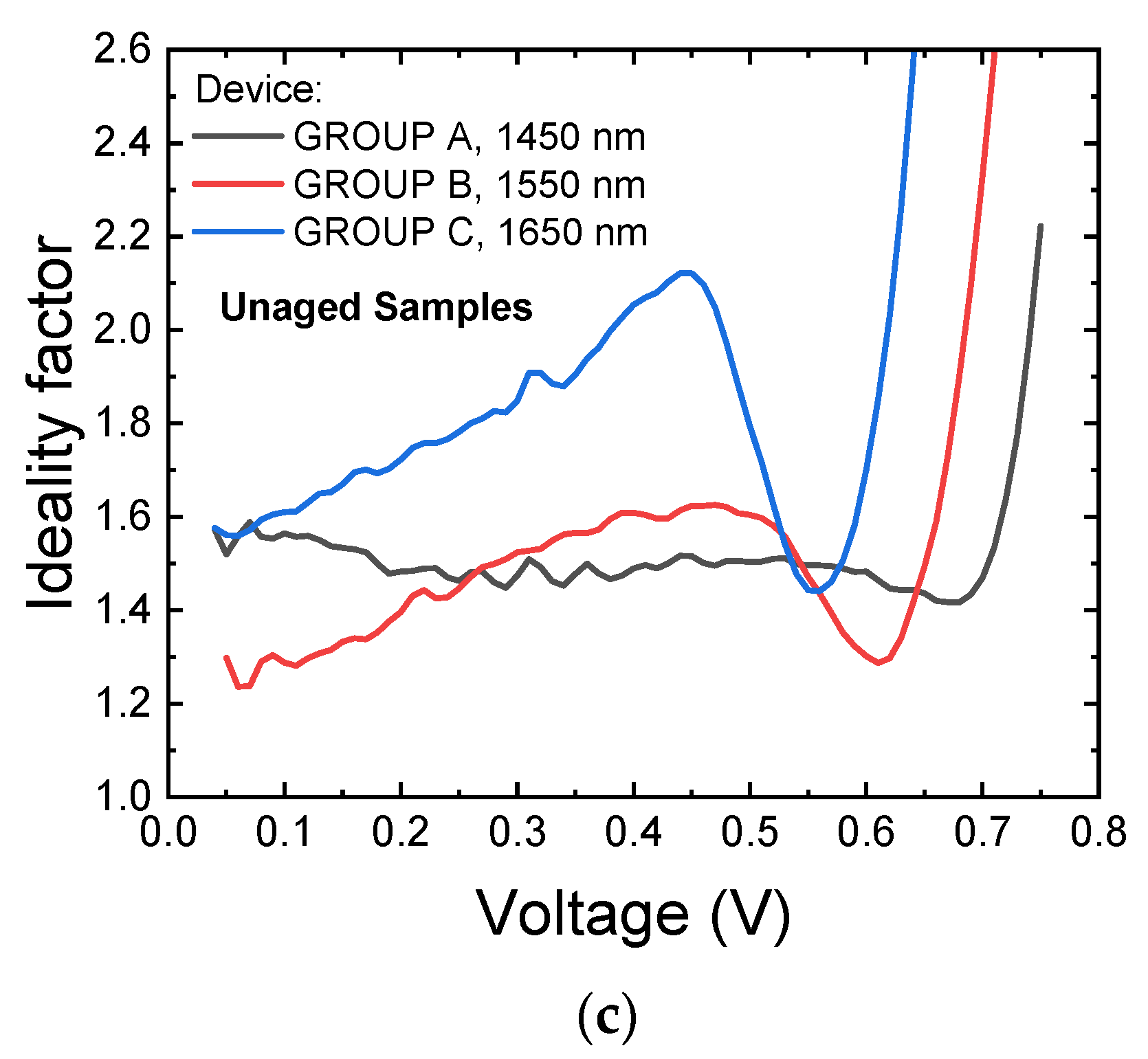
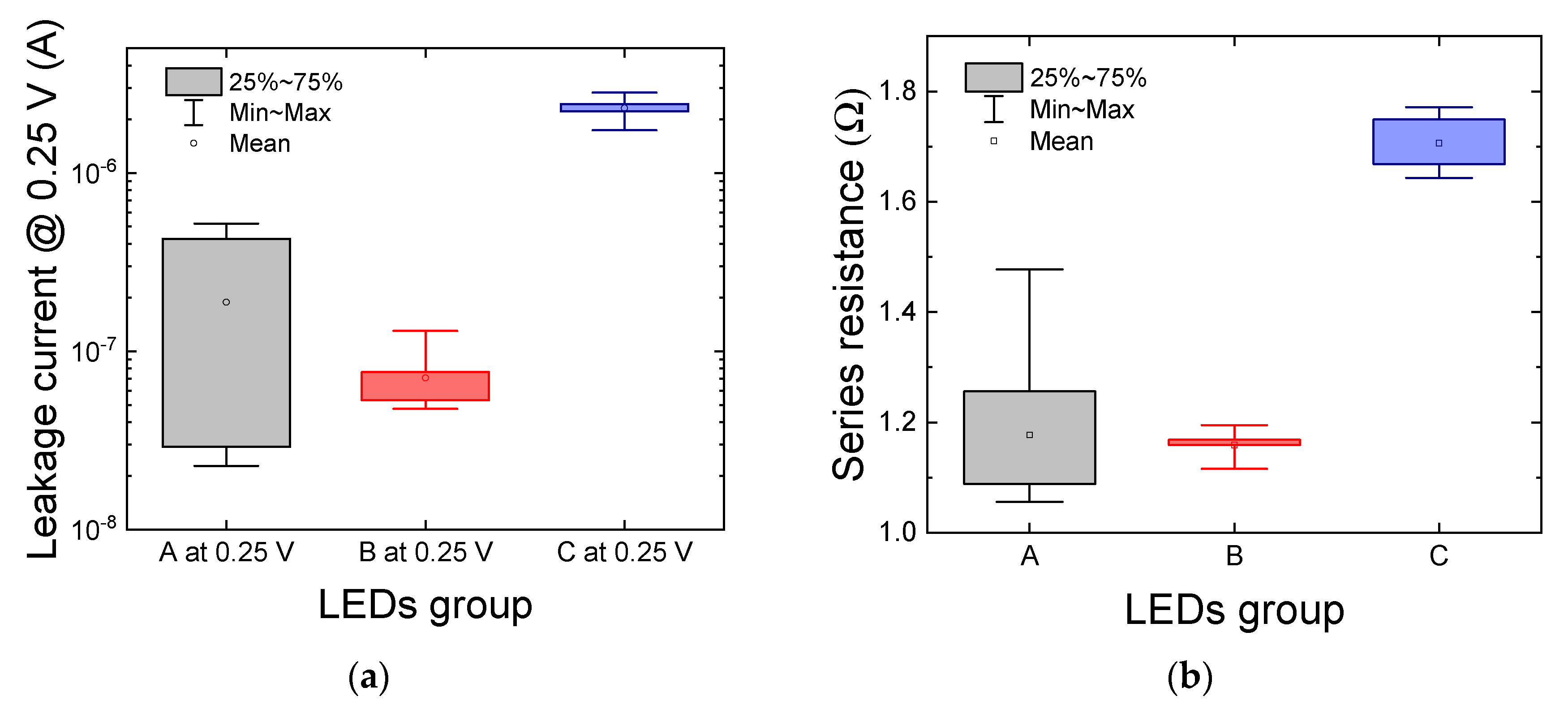
2.2. Preliminary Characterization: Electrical Characteristics
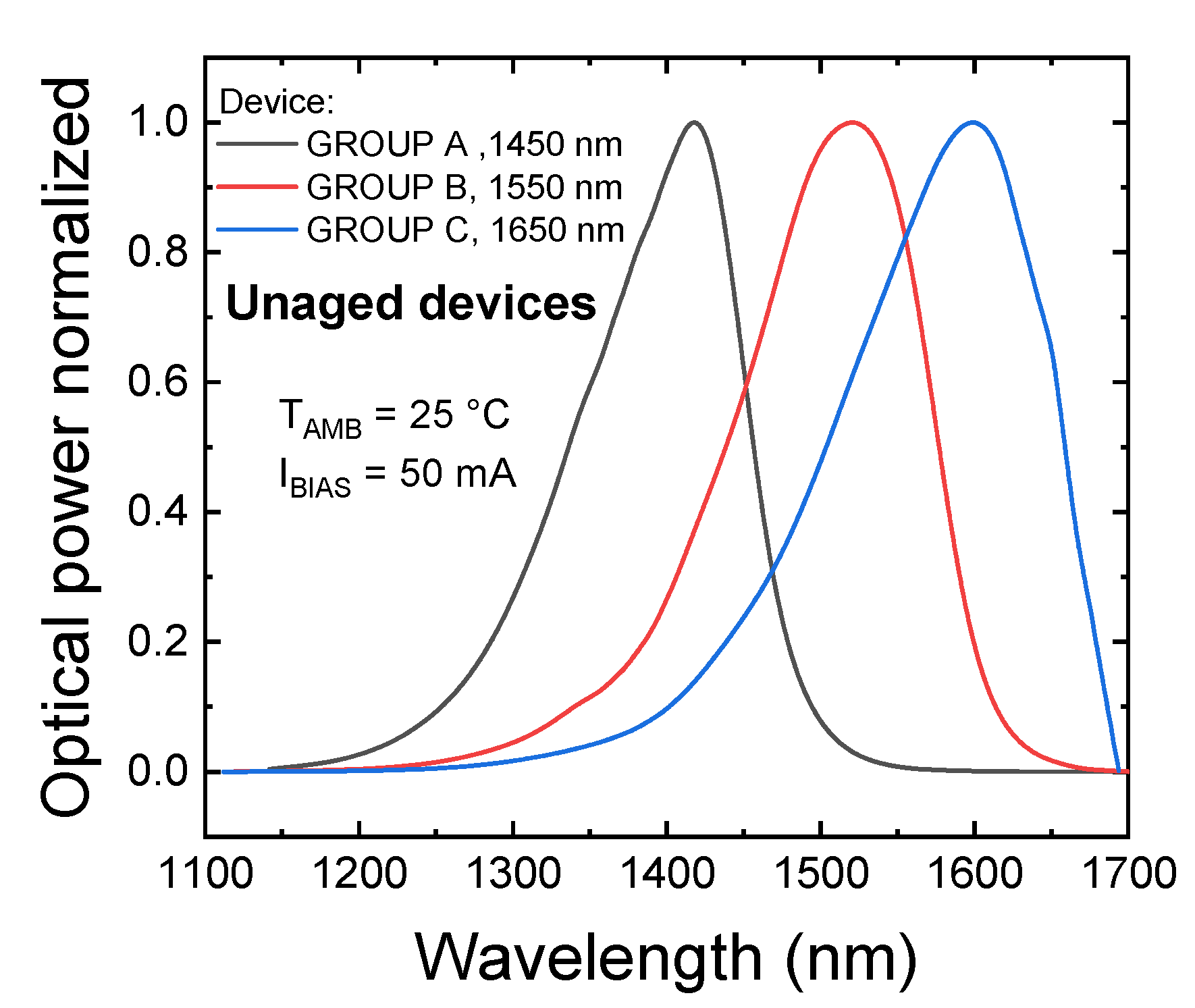
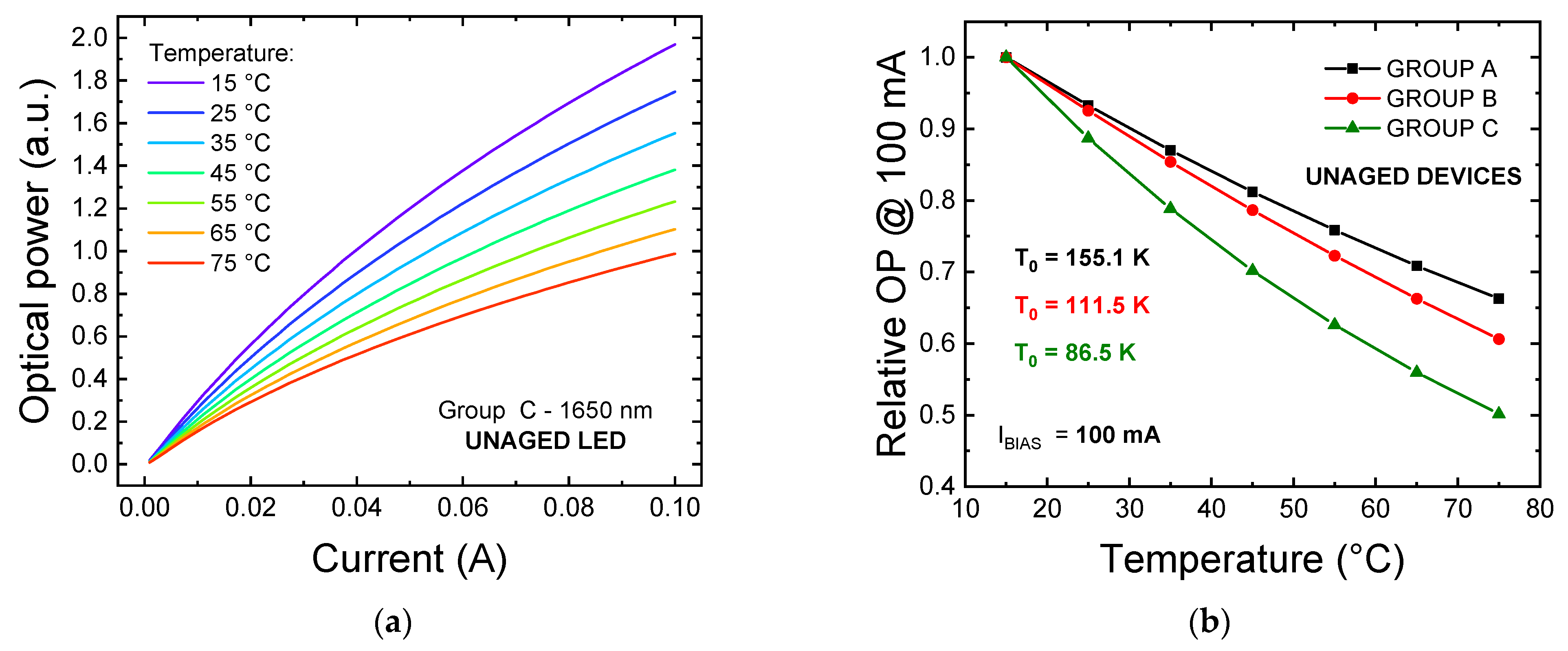
2.3. Preliminary Characterization: Optical Characteristics
3. Experiments Results and Discussion
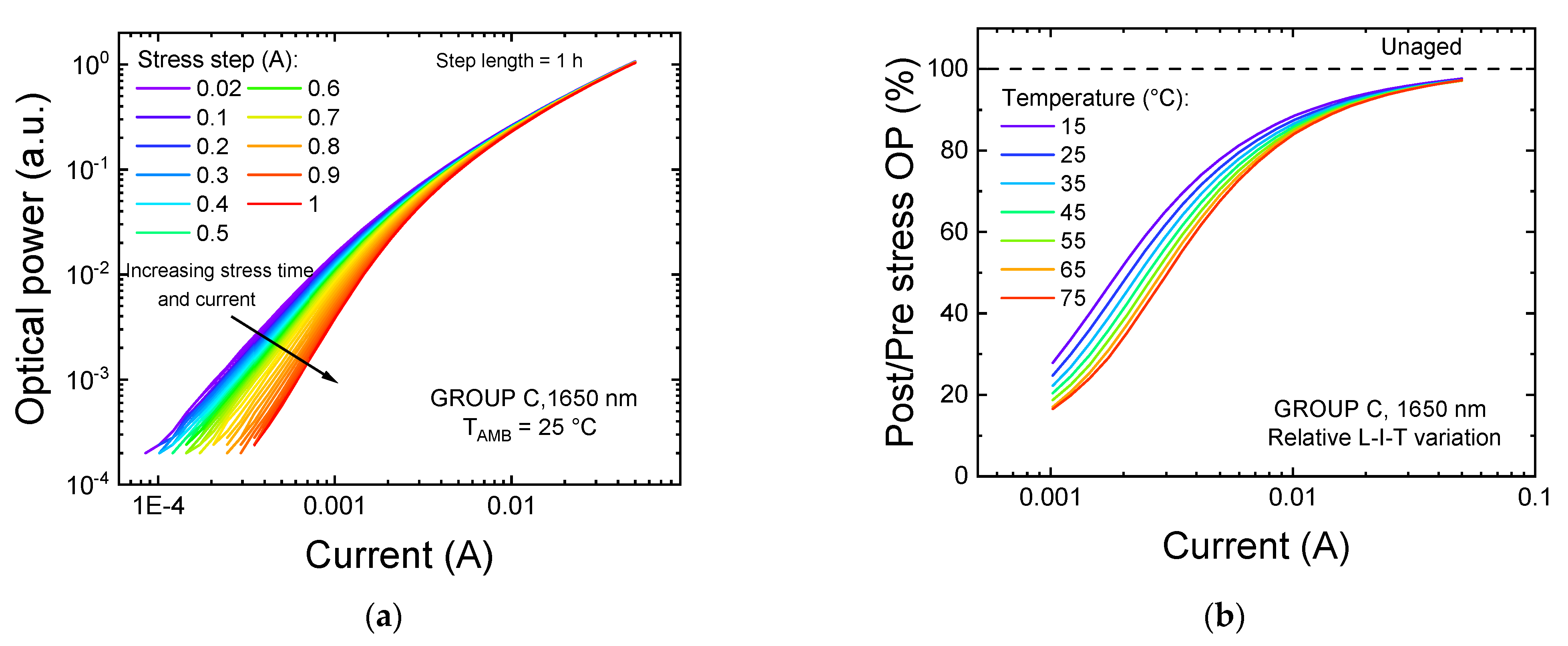
3.1. Current Step-Stress
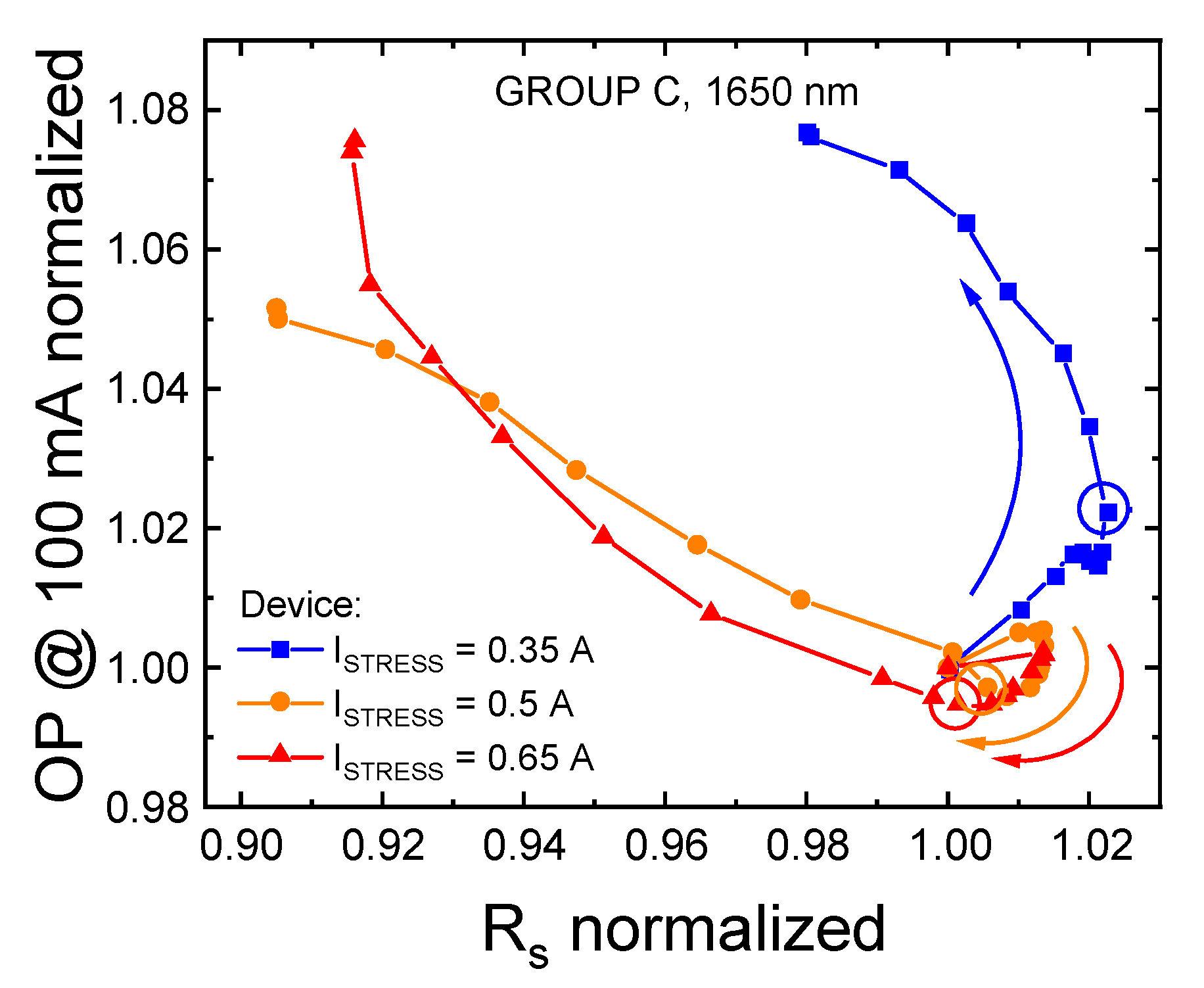
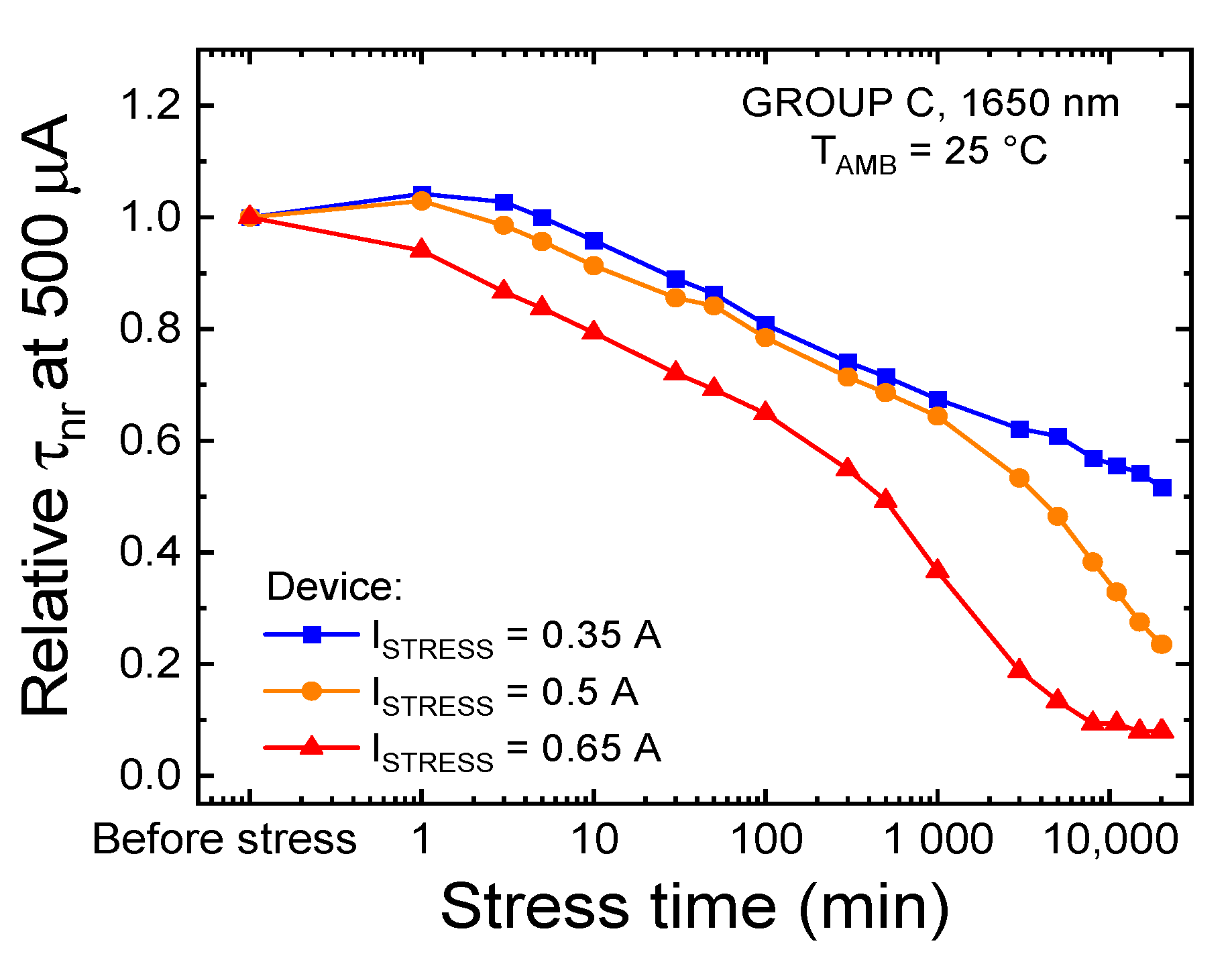
3.2. Constant-Current Stress
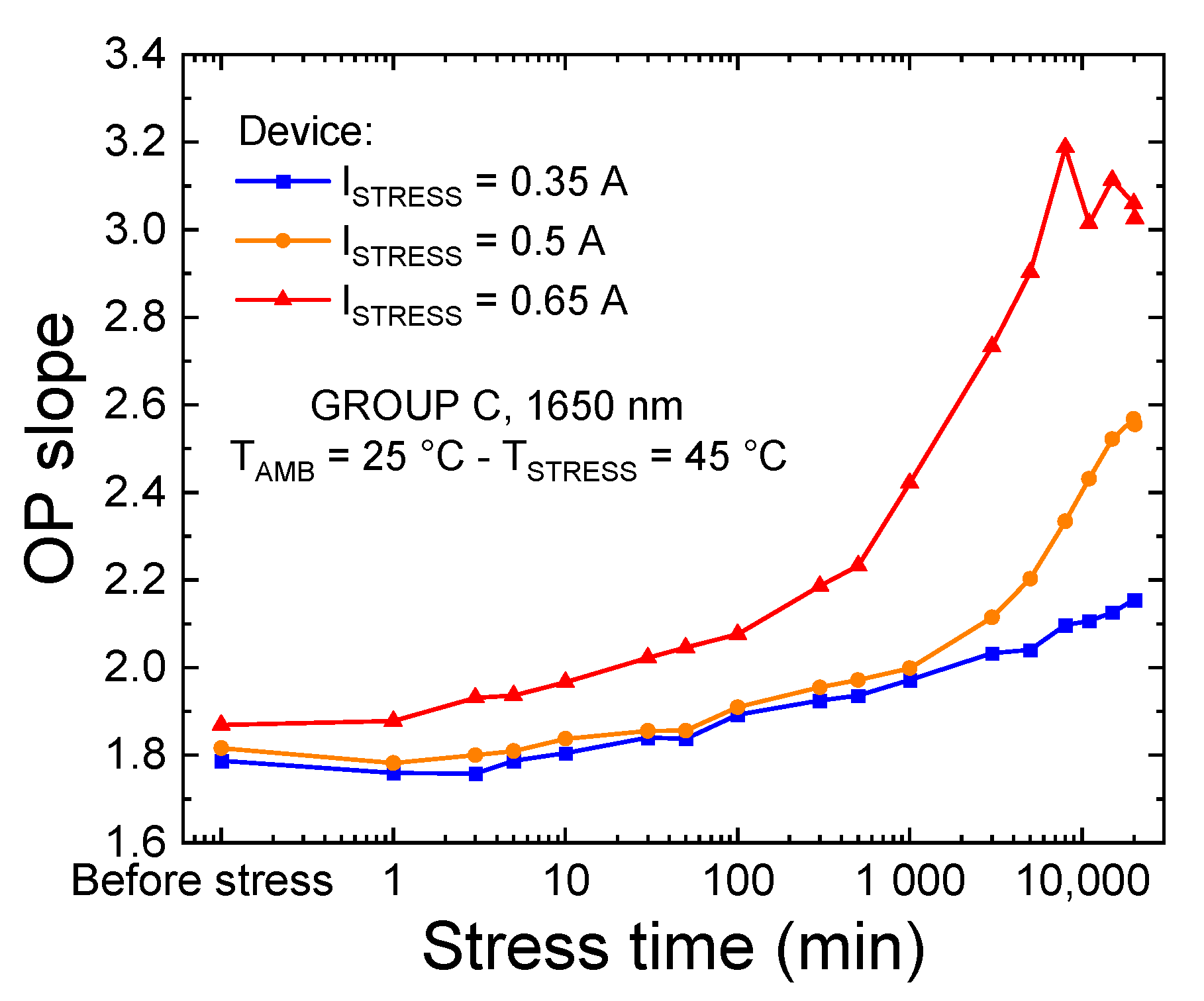
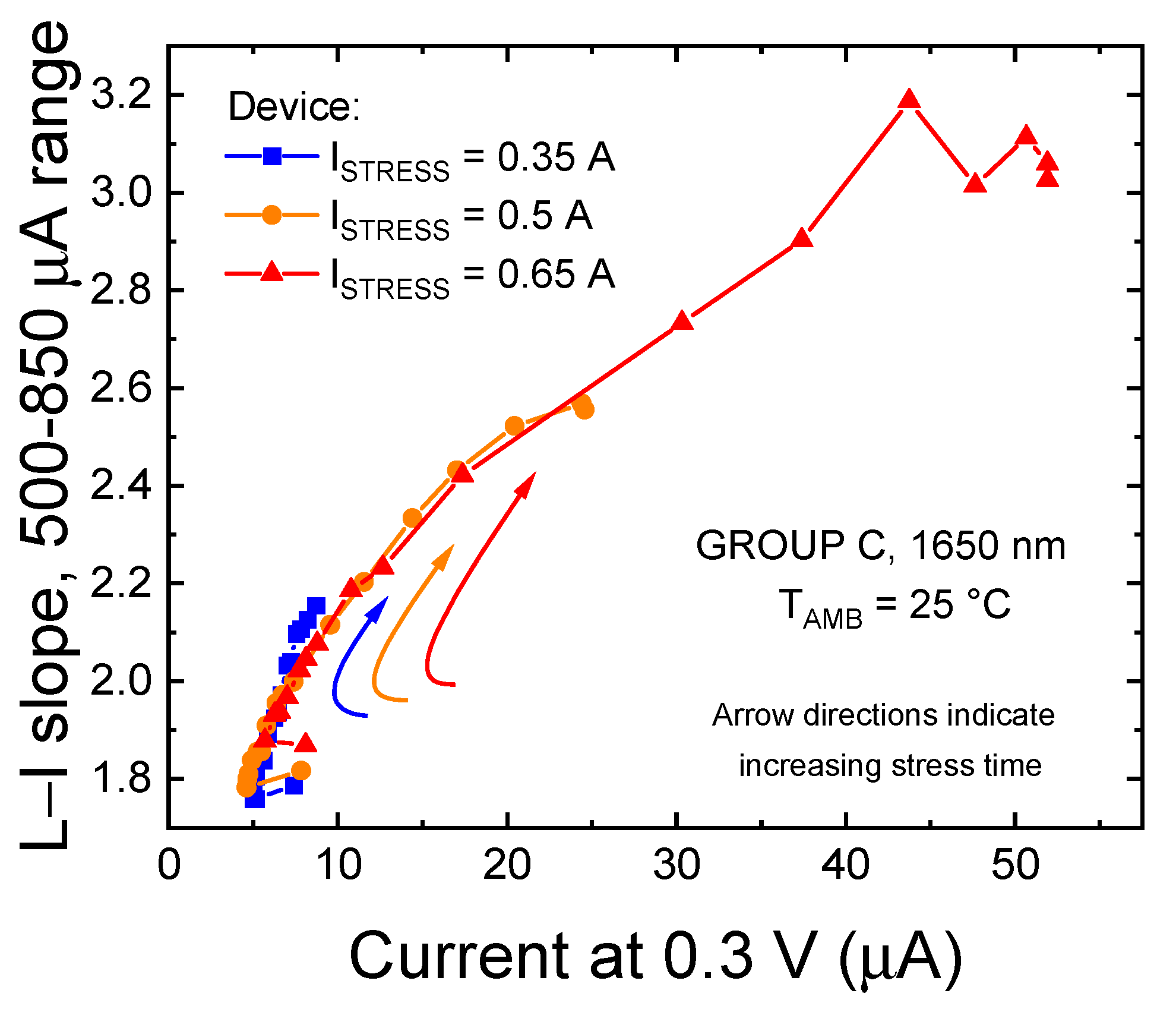
3.2.1. Variation in High-Current Regime
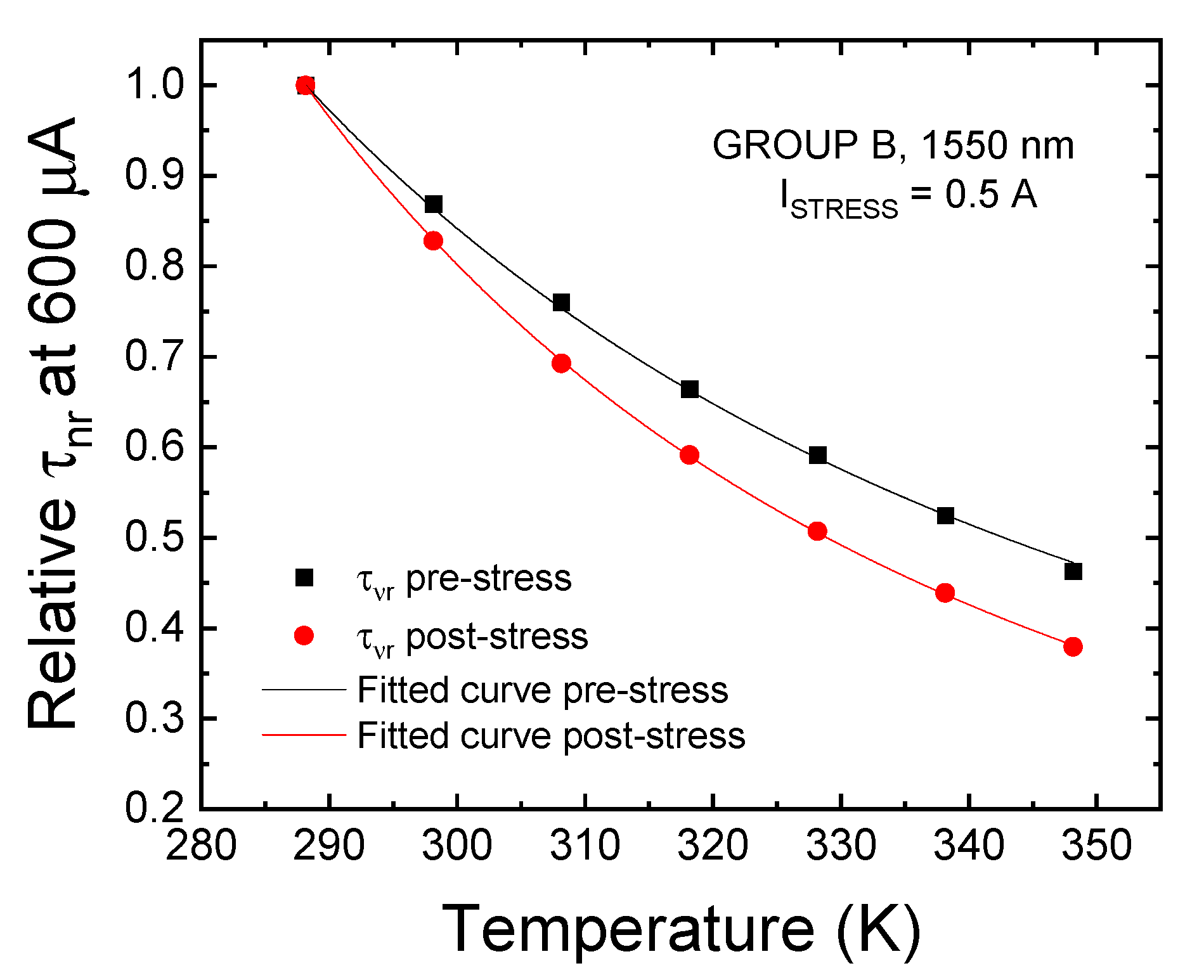
3.2.2. Trend of the Non-Radiative Lifetime
3.2.3. Emission in the Low-Bias Regime
3.2.4. Extrapolation of the Dominant Defect Parameters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Geisz, J.F.; Friedman, D.J.; Ward, J.S.; Duda, A.; Olavarria, W.J.; Moriarty, T.E.; Kiehl, J.T.; Romero, M.J.; Norman, A.G.; Jones, K.M. 40.8% efficient inverted triple-junction solar cell with two independently metamorphic junctions. Appl. Phys. Lett. 2008, 93, 123505. [Google Scholar] [CrossRef]
- García, I.; Geisz, J.F.; France, R.M.; Kang, J.; Wei, S.H.; Ochoa, M.; Friedman, D.J. Metamorphic Ga0.76In0.24As/GaAs0.75Sb 0.25 tunnel junctions grown on GaAs substrates. J. Appl. Phys. 2014, 116, 074508. [Google Scholar]
- Jiang, W.H.; Gao, X.J.; Fang, Y.Q.; Liu, J.H.; Zhou, Y.; Jiang, L.Q.; Chen, W.; Jin, G.; Zhang, J.; Pan, J.W. Miniaturized high-frequency sine wave gating InGaAs/InP single-photon detector. Rev. Sci. Instrum. 2018, 89, 123104. [Google Scholar] [CrossRef] [Green Version]
- Tångring, I.; Ni, H.Q.; Wu, B.P.; Wu, D.H.; Xiong, Y.H.; Huang, S.S.; Niu, Z.C.; Wang, S.M.; Lai, Z.H.; Larsson, A. 1.58 μm InGaAs quantum well laser on GaAs. Appl. Phys. Lett. 2007, 91, 221101. [Google Scholar]
- Mano, T.; Mitsuishi, K.; Ha, N.; Ohtake, A.; Castellano, A.; Sanguinetti, S.; Noda, T.; Sakuma, Y.; Kuroda, T.; Sakoda, K. Growth of metamorphic InGaAs on GaAs (111)A: Counteracting lattice mismatch by inserting a thin InAs interlayer. Cryst. Growth Des. 2016, 16, 5412–5417. [Google Scholar] [CrossRef]
- Molina, S.I.; Pacheco, F.J.; Araújo, D.; García, R.; Sacedón, A.; Calleja, E.; Yang, Z.; Kidd, P. Strain relief in linearly graded composition buffer layers: A design scheme to grow dislocation-free (<105 cm−2) and unstrained epilayers. Appl. Phys. Lett. 1994, 65, 2460–2462. [Google Scholar]
- Nguyen, H.Q.; Chang, E.Y.; Yu, H.W.; Trinh, H.D.; Dee, C.F.; Wong, Y.Y.; Hsu, C.H.; Tran, B.T.; Chung, C.C. Threading dislocation blocking in metamorphic InGaAs/GaAs for growing high-quality In0.5Ga0.5As and In0.3Ga0.7As on GaAs substrate by using metal organic chemical vapor deposition. Appl. Phys. Express 2012, 5, 055503. [Google Scholar] [CrossRef]
- Cordier, Y.; Zaknoune, M.; Trassaert, S.; Chauveau, J.M. Stacking of metamorphic InAlAs/InGaAs heterostructures on GaAs substrate. J. Appl. Phys. 2001, 90, 5774–5777. [Google Scholar] [CrossRef]
- Bernabé, S.; Wilmart, Q.; Hasharoni, K.; Hassan, K.; Thonnart, Y.; Tissier, P.; Désières, Y.; Olivier, S.; Tekin, T.; Szelag, B. Silicon photonics for terabit/s communication in data centers and exascale computers. Solid State Electron. 2020, 107928. [Google Scholar] [CrossRef]
- Royo, S.; Ballesta-Garcia, M. An overview of lidar imaging systems for autonomous vehicles. Appl. Sci. 2019, 9, 4093. [Google Scholar] [CrossRef] [Green Version]
- Liu, A.Y.; Peters, J.; Huang, X.; Jung, D.; Norman, J.; Lee, M.L.; Gossard, A.C.; Bowers, J.E. Electrically pumped continuous-wave 13 μm quantum-dot lasers epitaxially grown on on-axis (001) GaP/Si. Opt. Lett. 2017, 42, 338. [Google Scholar] [CrossRef]
- Buffolo, M.; Samparisi, F.; De Santi, C.; Jung, D.; Norman, J.; Bowers, J.E.; Herrick, R.W.; Meneghesso, G.; Zanoni, E.; Meneghini, M. Physical origin of the optical degradation of InAs quantum dot lasers. IEEE J. Quantum Electron. 2019, 55, 1–7. [Google Scholar] [CrossRef]
- Buffolo, M.; Samparisi, F.; Rovere, L.; De Santi, C.; Jung, D.; Norman, J.; Bowers, J.E.; Herrick, R.W.; Meneghesso, G.; Zanoni, E.; et al. Investigation of current-driven degradation of 1.3 μm quantum-dot lasers epitaxially grown on silicon. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–8. [Google Scholar] [CrossRef]
- Selvidge, J.; Norman, J.; Salmon, M.E.; Hughes, E.T.; Bowers, J.E.; Herrick, R.; Mukherjee, K. Non-radiative recombination at dislocations in InAs quantum dots grown on silicon. Appl. Phys. Lett. 2019, 115, 131102. [Google Scholar] [CrossRef]
- Jung, D.; Herrick, R.; Norman, J.; Turnlund, K.; Jan, C.; Feng, K.; Gossard, A.C.; Bowers, J.E. Impact of threading dislocation density on the lifetime of InAs quantum dot lasers on Si. Appl. Phys. Lett. 2018, 112, 153507. [Google Scholar] [CrossRef]
- Łozińska, A. The influence of quantum well and barrier thicknesses on photoluminescence spectra of InGaAs/AlInAs superlattices grown by LP-MOVPE. Opt. Appl. 2020, 50. [Google Scholar] [CrossRef]
- De Santi, C.; Buffolo, M.; Renso, N.; Neviani, A.; Meneghesso, G.; Zanoni, E.; Meneghini, M. Evidence for defect-assisted tunneling and recombination at extremely low current in InGaN/GaN-based LEDs. Appl. Phys. Express 2019, 12, 052007. [Google Scholar] [CrossRef]
- Kosa, A.; Stuchlikova, L.; Harmatha, L.; Kovac, J.; Sciana, B.; Dawidowski, W.; Tlaczala, M. DLTS study of InGaAs and GaAsN structures with different indium and nitrogen compositions. Mater. Sci. Semicond. Process. 2018, 74, 313–318. [Google Scholar] [CrossRef]
- Keppens, A.; Ryckaert, W.R.; Deconinck, G.; Hanselaer, P. High power light-emitting diode junction temperature determination from current-voltage characteristics. J. Appl. Phys. 2008, 104, 093104. [Google Scholar] [CrossRef]
- Houle, T.J.; Yong, J.C.L.; Marinelli, C.M.; Yu, S.; Rorison, J.M.; White, I.H.; White, J.K.; SpringThorpe, A.J.; Garrett, B. Characterization of the temperature sensitivity of gain and recombination mechanisms in 1.3-μm AlGaInAs MQW lasers. IEEE J. Quantum Electron. 2005, 41, 132–139. [Google Scholar] [CrossRef]
- Massé, N.F.; Adams, A.R.; Sweeney, S.J. Experimental determination of the band gap dependence of Auger recombination in InGaAs/InP multiple quantum well lasers at room temperature. Appl. Phys. Lett. 2007, 90, 161113. [Google Scholar] [CrossRef] [Green Version]
- De Santi, C.; Meneghini, M.; La Grassa, M.; Galler, B.; Zeisel, R.; Goano, M.; Dominici, S.; Mandurrino, M.; Bertazzi, F.; Robidas, D.; et al. Role of defects in the thermal droop of InGaN-based light emitting diodes. J. Appl. Phys. 2016, 119, 094501. [Google Scholar] [CrossRef]
- Meneghini, M.; Trevisanello, L.-R.; Meneghesso, G.; Zanoni, E. A review on the reliability of GaN-Based LEDs. IEEE Trans. Device Mater. Reliab. 2008, 8, 323–331. [Google Scholar] [CrossRef]
- Muller, R.S.; Kamins, T.I.; Chan, M. Device Electronics for Integrated Devices; John Wiley & Sons: Hoboken, NJ, USA, 2002; ISBN 978-0471593980. [Google Scholar]
- Liu, J.P.; Ryou, J.H.; Dupuis, R.D.; Han, J.; Shen, G.D.; Wang, H.B. Barrier effect on hole transport and carrier distribution in InGaNGaN multiple quantum well visible light-emitting diodes. Appl. Phys. Lett. 2008, 93, 021102. [Google Scholar] [CrossRef]
- Su, C.Y.; Tu, C.G.; Liu, W.H.; Lin, C.H.; Yao, Y.F.; Chen, H.T.; Wu, Y.R.; Kiang, Y.W.; Yang, C.C. Enhancing the hole-injection efficiency of a light-emitting diode by increasing mg doping in the p-AlGaN electron-blocking layer. IEEE Trans. Electron. Devices 2017, 64, 3226–3233. [Google Scholar] [CrossRef]
- Buffolo, M.; Davanzo, E.; De Santi, C.; Trivellin, N.; Meneghesso, G.; Zanoni, E.; Meneghini, M. Efficiency and catastrophic failure of high-power blue gan leds during extremely high temperature and current stress. IEEE Trans. Device Mater. Reliab. 2020, 20, 429–435. [Google Scholar] [CrossRef]
- Bochkareva, N.I.; Efremov, A.A.; Rebane, Y.T.; Gorbunov, R.I.; Klochkov, A.V.; Shreter, Y.G. Nonuniformity of carrier injection and the degradation of blue LEDs. Semiconductors 2006, 40, 118–123. [Google Scholar] [CrossRef]
- Cai, M.; Liang, Z.; Qin, Y.; Fan, J.; Ma, D.; Yang, D.; Zhang, G. Effects of silicone lens aging on degradation kinetics of light-emitting diode package in various accelerated testing. Opt. Mater. 2020, 107, 110071. [Google Scholar] [CrossRef]
- Yuan, J.H.; Chuang, T.H. Luminous efficiency of pd-doped ag-alloy wire bonded led package after reliability tests. Mater. Sci. Forum 2019, 960, 221–230. [Google Scholar] [CrossRef]
- Dai, Q.; Shan, Q.; Wang, J.; Chhajed, S.; Cho, J.; Schubert, E.F.; Crawford, M.H.; Koleske, D.D.; Kim, M.H.; Park, Y. Carrier recombination mechanisms and efficiency droop in GaInN/GaN light-emitting diodes. Appl. Phys. Lett. 2010, 97, 133507. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.S.; Han, D.P.; Kim, H.S.; Shim, J.I. Analysis of dominant carrier recombination mechanisms depending on injection current in InGaN green light emitting diodes. Appl. Phys. Lett. 2014, 104, 091110. [Google Scholar] [CrossRef]
- Auf der Maur, M.; Galler, B.; Pietzonka, I.; Strassburg, M.; Lugauer, H.; Di Carlo, A. Trap-assisted tunneling in InGaN/GaN single-quantum-well light-emitting diodes. Appl. Phys. Lett. 2014, 105, 133504. [Google Scholar] [CrossRef]
- Meneghini, M.; De Santi, C.; Tibaldi, A.; Vallone, M.; Bertazzi, F.; Meneghesso, G.; Zanoni, E.; Goano, M. Thermal droop in III-nitride based light-emitting diodes: Physical origin and perspectives. J. Appl. Phys. 2020, 127, 211102. [Google Scholar] [CrossRef]
- Renso, N.; Meneghini, M.; Buffolo, M.; De Santi, C.; Meneghesso, G.; Zanoni, E. Understanding the degradation processes of GaN based LEDs submitted to extremely high current density. Microelectron. Reliab. 2017, 76–77, 556–560. [Google Scholar] [CrossRef]
- Mandurrino, M.; Verzellesi, G.; Goano, M.; Vallone, M.; Bertazzi, F.; Ghione, G.; Meneghini, M.; Meneghesso, G.; Zanoni, E. Physics-based modeling and experimental implications of trap-assisted tunneling in InGaN/GaN light-emitting diodes. Phys. Status Solidi Appl. Mater. Sci. 2015, 212, 947–953. [Google Scholar] [CrossRef]


| Before Stress | After Stress | ||||
|---|---|---|---|---|---|
| Istress (A) | ΔE (eV) | Et (eV) | ΔE (eV) | Et (eV) | ΔEt 1 (meV) |
| Group A | |||||
| 0.5 | 0.119 | 0.547 | 0.108 | 0.536 | −10.6 |
| 0.65 | 0.108 | 0.536 | 0.118 | 0.546 | +10.3 |
| Group B | |||||
| 0.35 | 0.0826 | 0.483 | 0.122 | 0.522 | +39.3 |
| 0.5 | 0.099 | 0.5 | 0.128 | 0.528 | +28.24 |
| 0.65 | 0.097 | 0.497 | 0.127 | 0.527 | +29.7 |
| Group C | |||||
| 0.35 | 0.152 | 0.527 | 0.212 | 0.588 | +60.4 |
| 0.5 | 0.15 | 0.526 | 0.239 | 0.615 | +89.4 |
| 0.65 | 0.156 | 0.532 | 0.252 | 0.628 | +95.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buffolo, M.; Magri, A.; De Santi, C.; Meneghesso, G.; Zanoni, E.; Meneghini, M. Gradual Degradation of InGaAs LEDs: Impact on Non-Radiative Lifetime and Extraction of Defect Characteristics. Materials 2021, 14, 1114. https://doi.org/10.3390/ma14051114
Buffolo M, Magri A, De Santi C, Meneghesso G, Zanoni E, Meneghini M. Gradual Degradation of InGaAs LEDs: Impact on Non-Radiative Lifetime and Extraction of Defect Characteristics. Materials. 2021; 14(5):1114. https://doi.org/10.3390/ma14051114
Chicago/Turabian StyleBuffolo, Matteo, Alessandro Magri, Carlo De Santi, Gaudenzio Meneghesso, Enrico Zanoni, and Matteo Meneghini. 2021. "Gradual Degradation of InGaAs LEDs: Impact on Non-Radiative Lifetime and Extraction of Defect Characteristics" Materials 14, no. 5: 1114. https://doi.org/10.3390/ma14051114
APA StyleBuffolo, M., Magri, A., De Santi, C., Meneghesso, G., Zanoni, E., & Meneghini, M. (2021). Gradual Degradation of InGaAs LEDs: Impact on Non-Radiative Lifetime and Extraction of Defect Characteristics. Materials, 14(5), 1114. https://doi.org/10.3390/ma14051114









