Enhancement of Hard Magnetic Properties in Fraktal-Like Nano and Mesoscopic Grains
Abstract
:1. Introduction
2. Simulation Procedure
- Select a random i-th node for further analysis and choose a random number r1 ∊ [0,1).
- If r1 < Pcl (i.e., cluster analysis probability), find a cluster around selected node and change cluster directions by θ angle, otherwise only the direction of the selected node is changed. In order to simulate multiphase ferromagnetic systems, it is necessary to use the disorder-based cluster MC method (which we described in [21]) with the adding probability equal to:where is the direct exchange coupling energy between the spins attributed to nodes i and j, is the local configuration entropy of anisotropy (calculated in the defined sphere around the i-th node) and α is the factor responsible for strengthening and weakening of the entropy impact on the adding probability (can be randomly selected from a selected range).
- Calculate the difference of the system energy ΔE before and after the change in step 2. The energy is calculated based on the 3D Heisenberg model:where Jij is the exchange parameter, Si is the spin vector on site i, Ki is the anisotropy constant (per site), is the versor of the easy magnetization axis, is the versor of the spin, g is the Lande factor, µB is the Bohr magneton, µ0 is the vacuum permeability, Hi is the magnetic field on site i, D is the dipolar constant, eij is the directional versor between the i-th and j-th nodes and rij is the distance between them.
- Choose a random number r2 ∊ [0,1) and if r2 > restore all changes made in step 2, otherwise accept the new configuration.
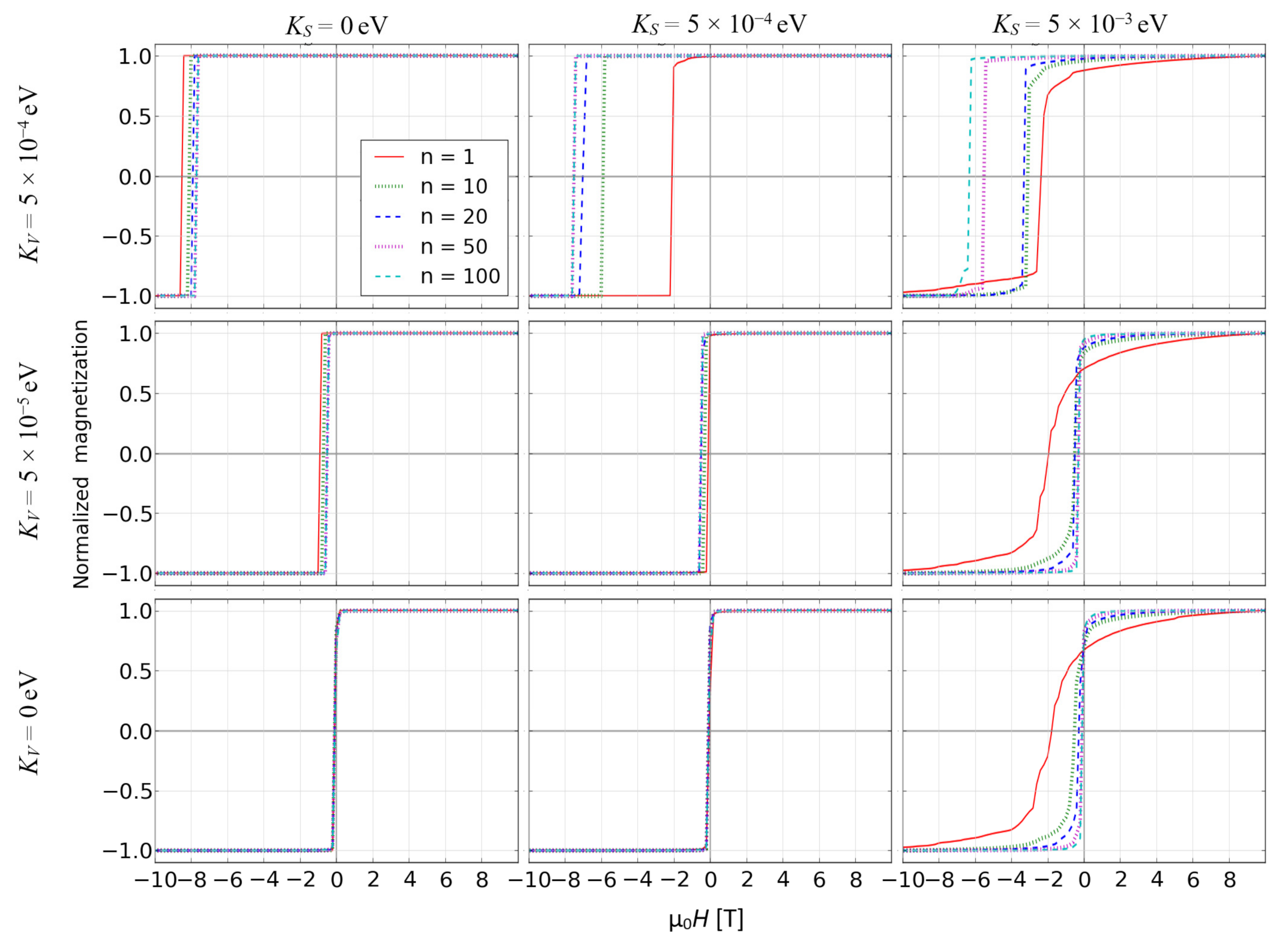
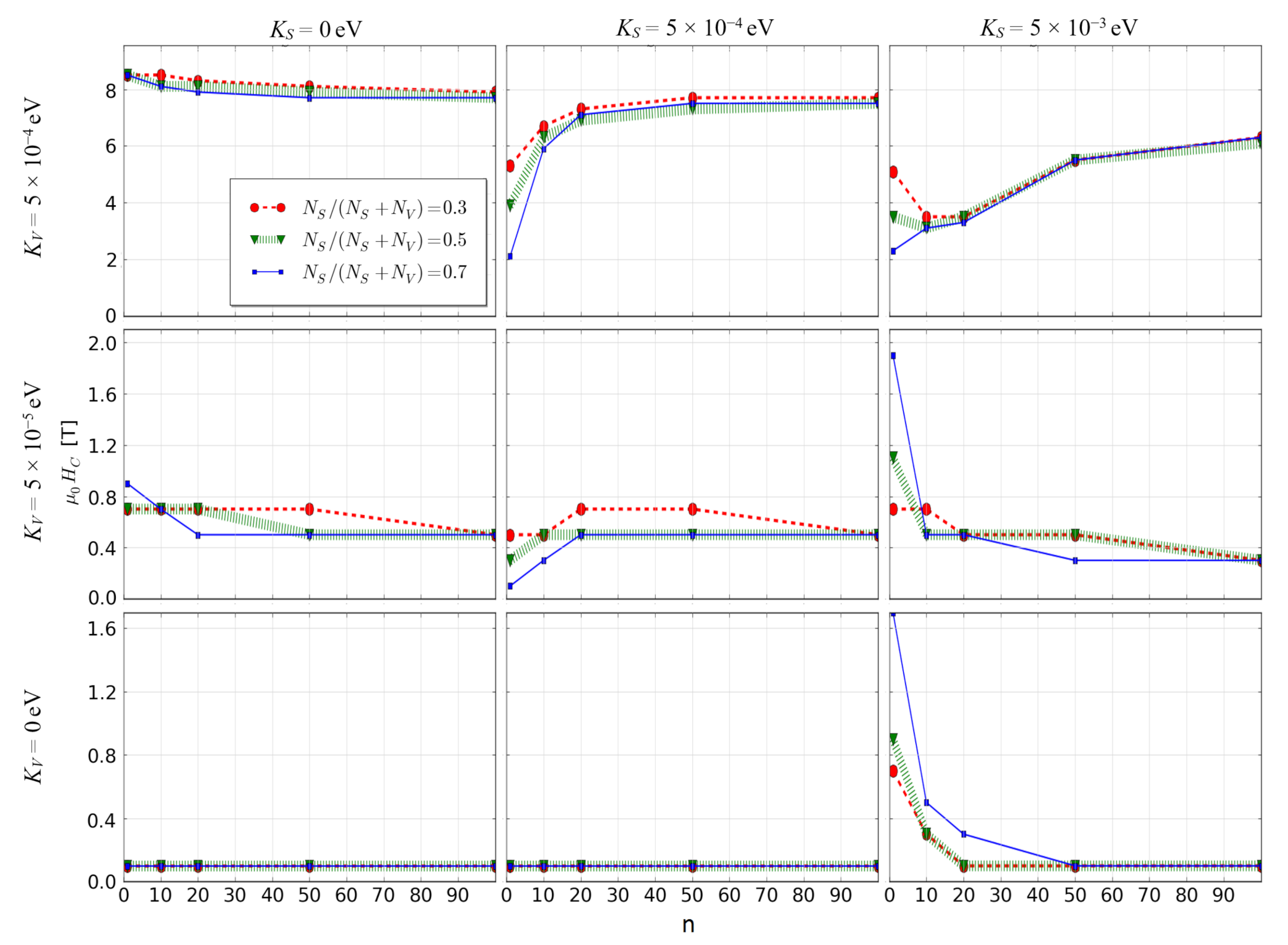
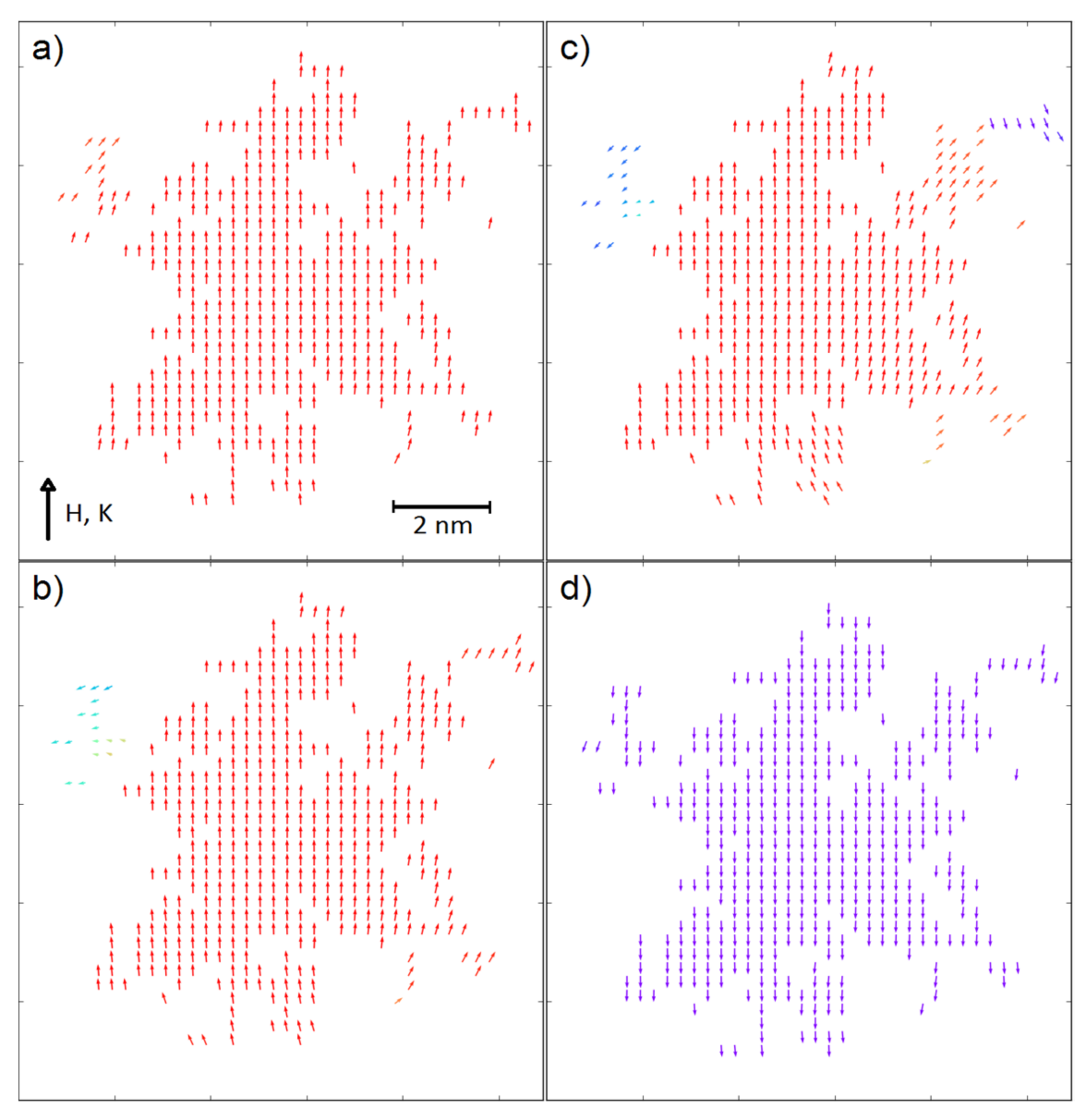
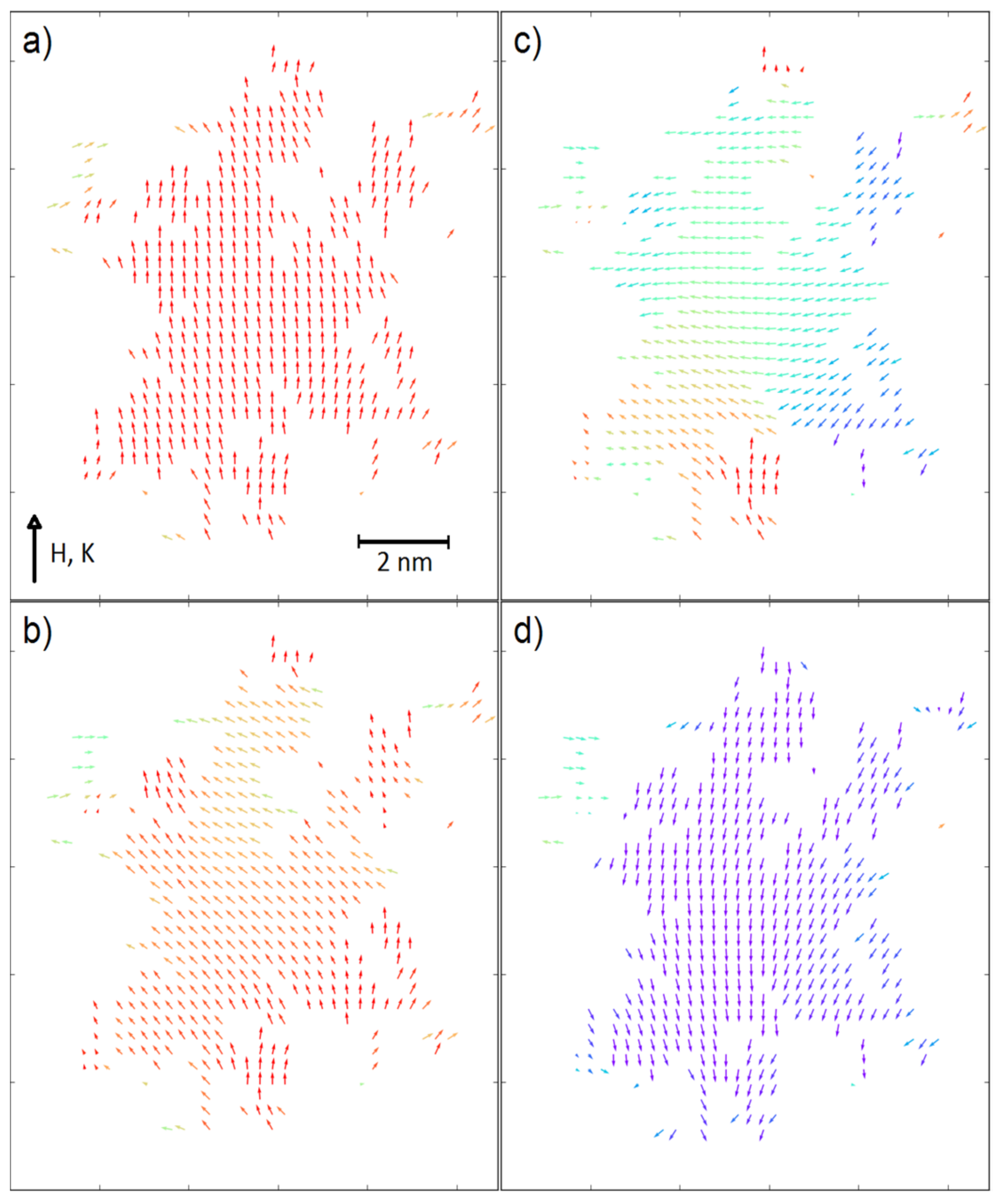
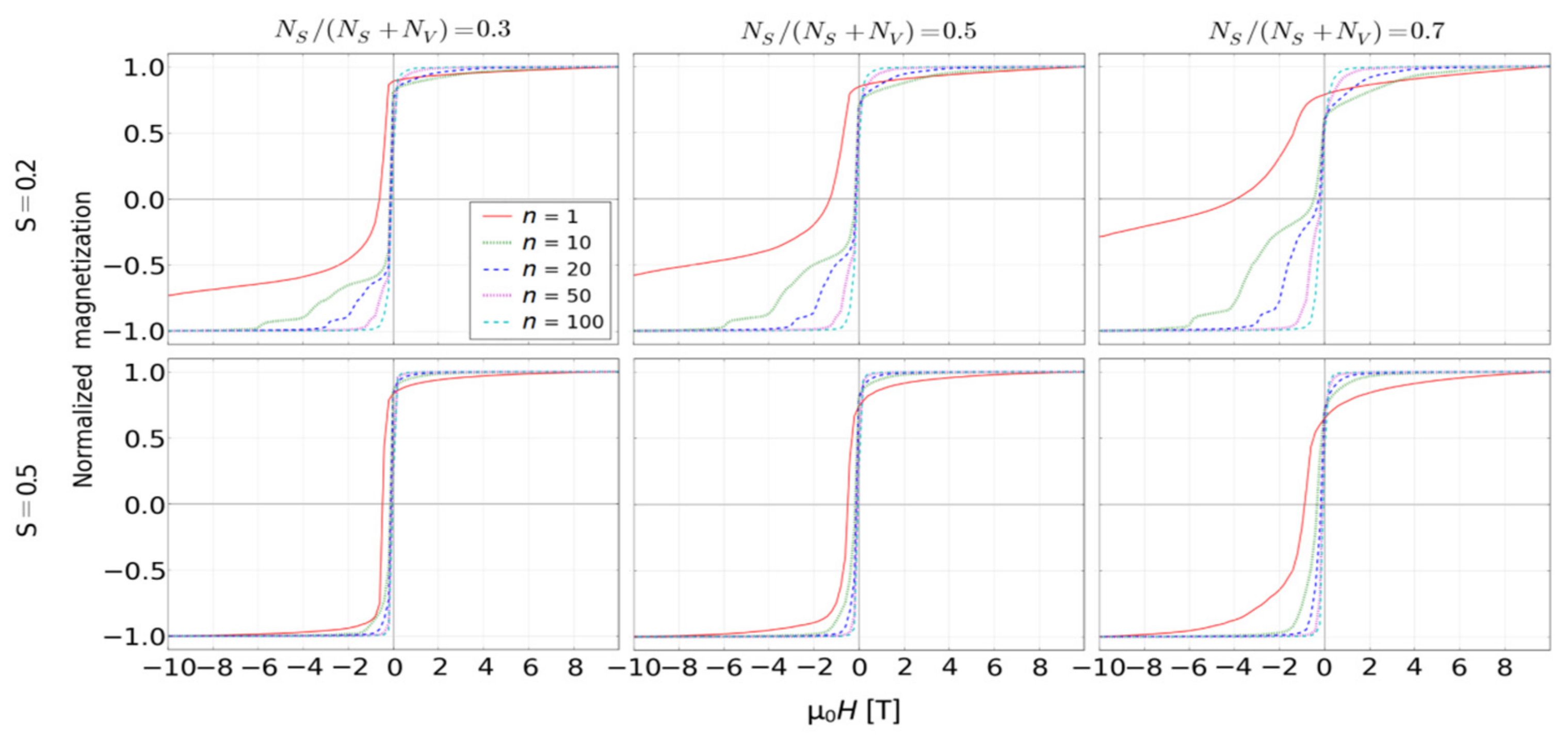
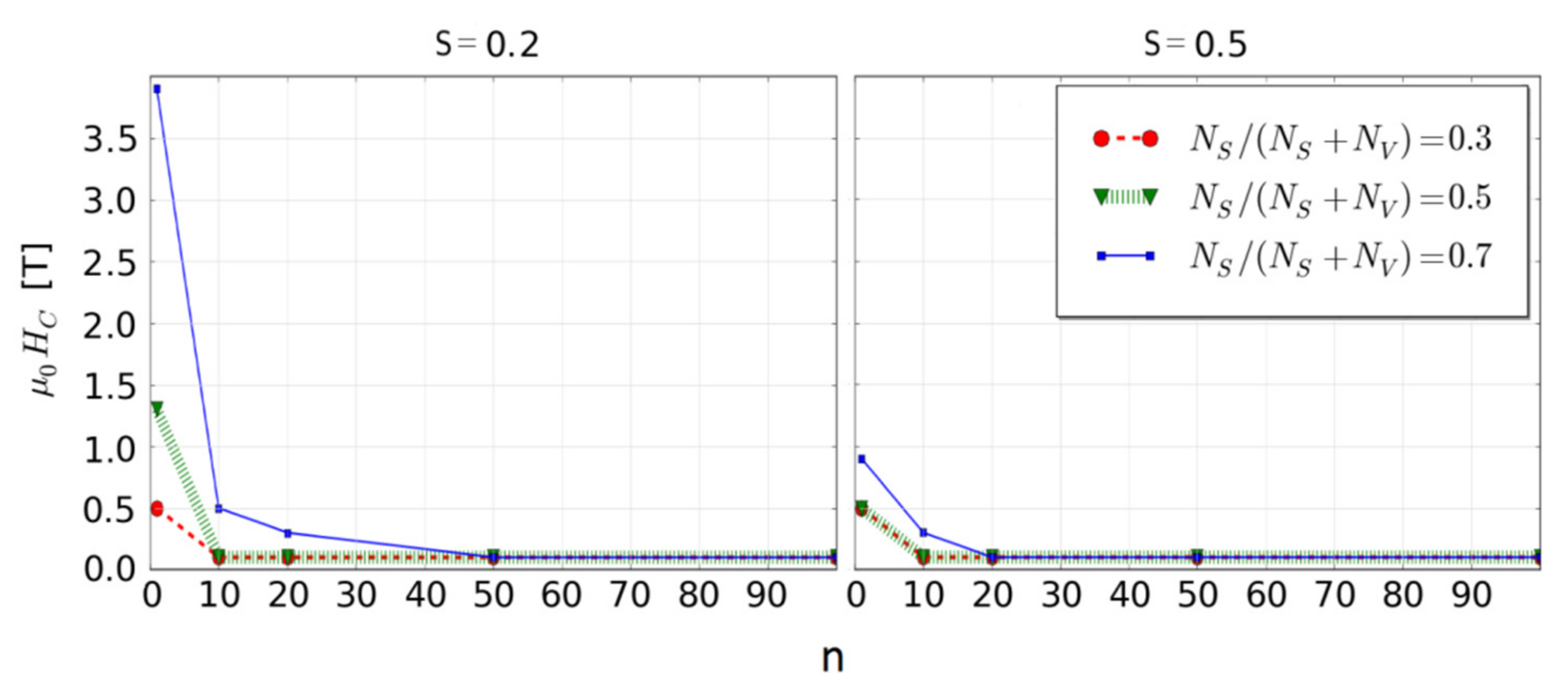
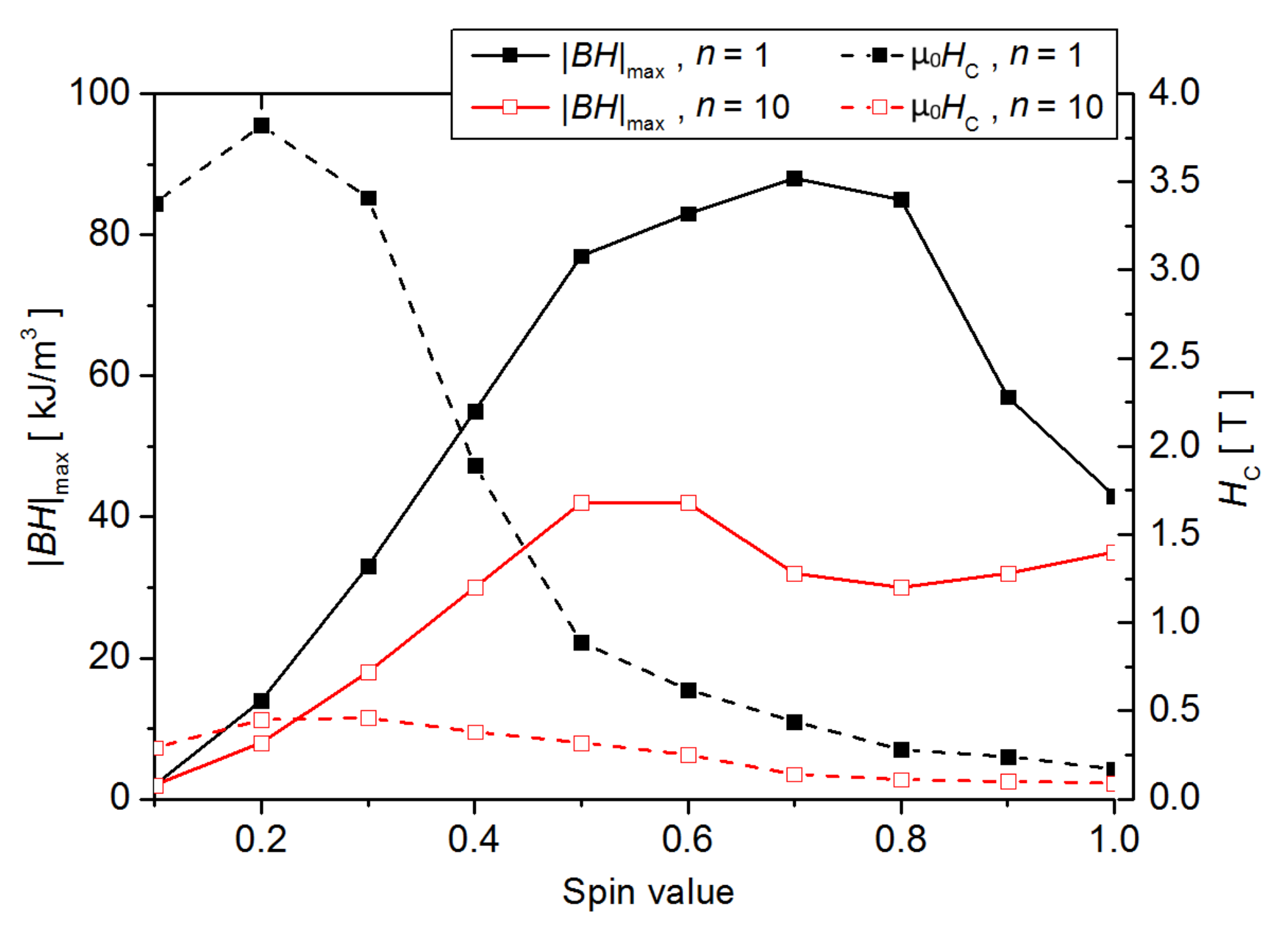
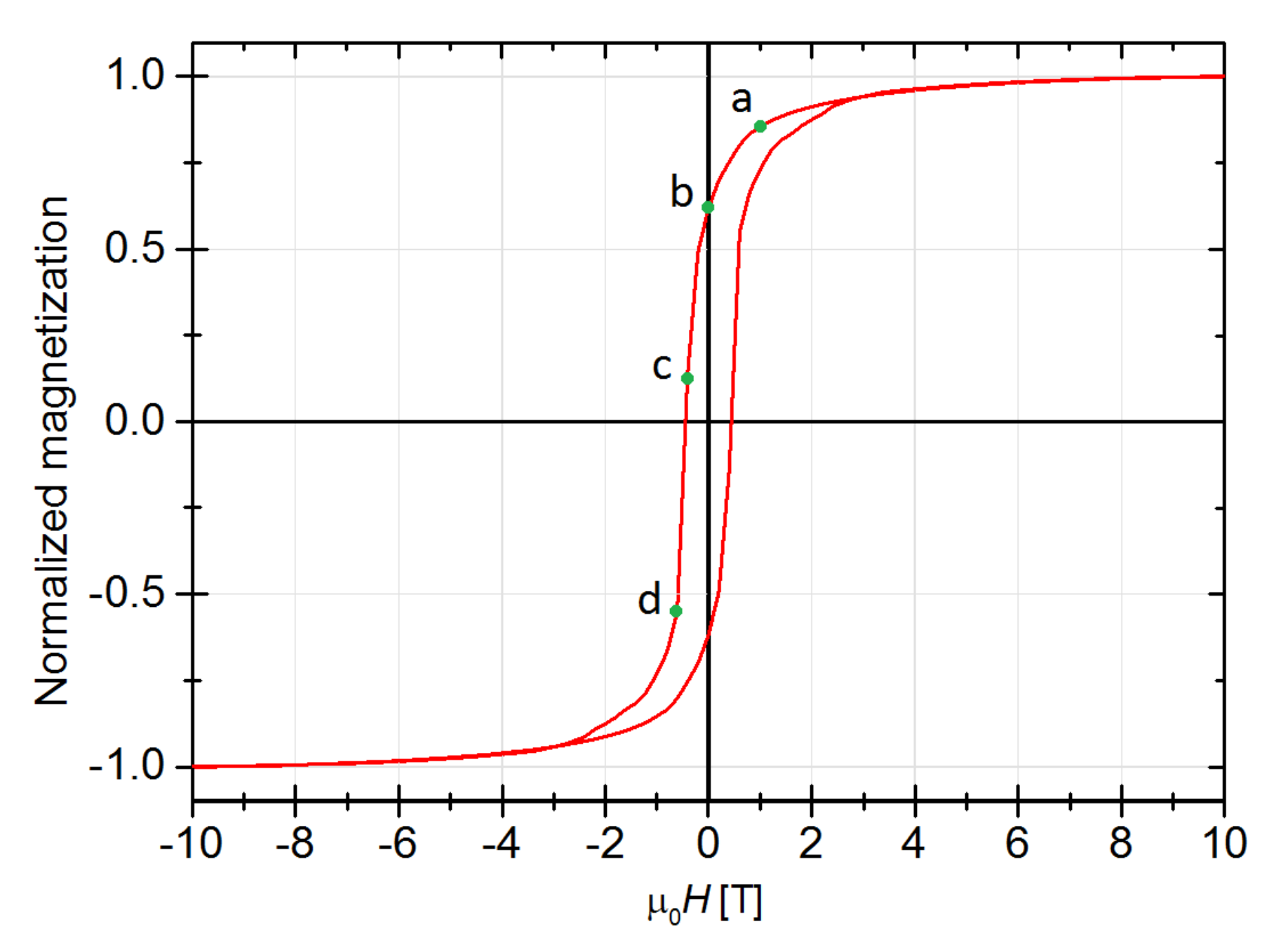
3. Results and Discussion
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- McHenry, M.E.; Willard, M.A.; Laughlin, D.E. Amorphous and nanocrystalline materials for applications as soft magnets. Prog. Mater. Sci. 1999, 44, 291. [Google Scholar] [CrossRef]
- Herzer, G.; Varga, L.L. Structure and coactivity of nanocrystalline Fe-Si-B-Nb-Cu alloys. J. Magn. Magn. Mater. 2000, 215/216, 506–512. [Google Scholar]
- Luborsky, F.E. Permanent Magnets in Use Today. J. Appl. Phys. 1966, 37, 1091–1094. [Google Scholar] [CrossRef] [Green Version]
- Sagawa, M.; Fujimura, S.; Yamamoto, H.; Matsuura, Y.; Hiraga, K. Permanent magnet materials based on the rare earth-iron-boron tetragonal compounds. IEEE Trans. Magn. 1984, 20, 1584–1589. [Google Scholar] [CrossRef] [Green Version]
- Croat, J.J.; Herbst, J.F.; Lee, R.W.; Pinkerton, F.E. Pr-Fe and Nd-Fe based materials: A new class of high performance permanent magnets. J. Appl. Phys. 1984, 55, 2078–2081. [Google Scholar] [CrossRef]
- Gutfleisch, O. Controlling the properties of high energy density permanent magnetic materials by different processing routes. J. Phys. D Appl. Phys. 2000, 33, 157–172. [Google Scholar] [CrossRef]
- Coey, J.M.D. Perspective and Prospects for Rare Earth Permanent Magnets. Engineering 2020, 6, 119–131. [Google Scholar] [CrossRef]
- Ziółkowski, G.; Randrianantoandro, N.; Chrobak, A.; Klimontko, J.; Kędziołka-Gaweł, M.; Haneczok, G. Influence of Transition and Rare Earth Elements on Magnetic Properties of Fe-Nb-B-M (M = Ni, Ag, Gd, Tb) Bulk Nanocrystalline Alloys. Acta Phys. Pol. A 2012, 121, 1266–1269. [Google Scholar] [CrossRef]
- Rao, A.S. Alnico permanent magnets an overview. In Proceedings of the Electrical/Electronics Insulation Conference, Chicago, IL, USA, 4–7 October 1993. [Google Scholar] [CrossRef]
- Zhou, L.; Tang, W.T.; Ke, L.; Guo, W.; Poplawsky, J.D.; Anderson, I.E.; Kramer, M.J. Microstructural and magnetic property evolution with different heat-treatment conditions in an alnico alloy. Acta Mater. 2017, 133, 73–80. [Google Scholar] [CrossRef] [Green Version]
- Coey, J.M.D. Permanent magnets: Plugging the gap. Scr. Mater. 2012, 67, 524–529. [Google Scholar] [CrossRef]
- Yuan, X.H.; Zhao, G.P.; Yue, M.; Ye, L.N.; Xia, J.; Zhang, X.C.; Chang, J. 3D and 1D calculation of hysteresis loops and energy products for anisotropic nanocomposite films with perpendicular anisotropy. J. Magn. Magn. Mater. 2013, 343, 245–250. [Google Scholar] [CrossRef]
- Pellicelli, R.; Solzi, M.; Pernechele, C.; Ghidini, M. Continuum micromagnetic modeling of antiferromagnetically exchange-coupled multilayers. Phys. Rev. B 2011, 83, 054434. [Google Scholar] [CrossRef]
- Pellicelli, R.; Solzi, M.; Neu, V.; Häfner, K.; Pernechele, C.; Ghidini, M. Characterization and modeling of the demagnetization processes in exchange-coupled SmCo5/Fe/SmCo5 trilayers. Phys. Rev. B 2010, 81, 184430. [Google Scholar] [CrossRef]
- Sadovnikov, A.V.; Grachev, A.A.; Gubanov, V.A.; Odintsov, S.A.; Martyshkin, A.A.; Sheshukova, S.E.; Sharaevskii, Y.P.; Nikitov, S.A. Spin-wave intermodal coupling in the interconnection of magnonic units. Appl. Phys. Lett. 2018, 112, 142402. [Google Scholar] [CrossRef]
- Komogortseva, S.V.; Iskhakova, R.S.; Felk, V.A. Fractal Dimension Effect on the Magnetization Curves of Exchange-Coupled Clusters of Magnetic Nanoparticles. J. Exp. Theor. Phys. 2019, 128, 754–760. [Google Scholar] [CrossRef]
- Zou, G.; Xiong, K.; Jiang, C.; Li, H.; Li, T.; Du, J.; Qian, Y. Fe3O4 Nanocrystals with Novel Fractal. J. Phys. Chem. B 2005, 109, 18356–18360. [Google Scholar] [CrossRef]
- Ziółkowski, G.; Chrobak, A. Magnetization processes of irregular dendrite structures-A Monte Carlo study. Phys. B 2020, 577, 411745. [Google Scholar] [CrossRef]
- Chrobak, A.; Zółkowski, G.; Randrianantoandro, N.; Klimontko, J.; Chrobak, D.; Prusik, K.; Rak, J. Ultra-high coercivity of (Fe86−xNbxB14)0.88Tb0.12 bulk nanocrystalline magnets. Acta Mater. 2015, 98, 318–326. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087. [Google Scholar] [CrossRef] [Green Version]
- Chrobak, A.; Ziółkowski, G.; Granek, K.; Chrobak, D. Disorder-based cluster Monte Carlo algorithm and its application in simulations of magnetization processes. Comput. Phys. Commun. 2019, 238, 157–164. [Google Scholar] [CrossRef]
- Chrobak, A.; Ziółkowski, G.; Chrobak, D.; Chełkowska, G. From atomic level to large-scale Monte Carlo magnetic simulations. Materials 2020, 13, 3696. [Google Scholar] [CrossRef]
- Wolff, U. Collective Monte Carlo Updating for Spin Systems. Phys. Rev. Lett. 1989, 62, 361. [Google Scholar] [CrossRef]
- Witten, T.A.; Sander, L.M. Diffusion-Limited Aggregation: A Kinetic Critical Phenomenon. Phys. Rev. Lett. 1981, 47, 1400–1403. [Google Scholar] [CrossRef]
- Sander, L.M. Fractal growth processes. Nature 1986, 322, 789–793. [Google Scholar] [CrossRef] [Green Version]
- Witten, T.A.; Sander, L.M. Diffusion-limited aggregation. Phys. Rev. B 1983, 27, 5686. [Google Scholar] [CrossRef] [Green Version]
- Sander, L.M.; Cheng, Z.M.; Richter, R. Diffusion-limited aggregation in three dimensions. Phys. Rev. B 1983, 28, 6394–6396. [Google Scholar] [CrossRef]
- Bourke, P.D. Constrained Diffusion Limited Aggregation in 3 Dimensions. Comput. Graph. 2006, 30, 646–649. [Google Scholar] [CrossRef]
- Levi, A.; Kotrla, M. Theory and Simulation of Crystal Growth. J. Phys. Condens. Matter 1996, 9, 299–344. [Google Scholar] [CrossRef]
- Hadj-Achour, M.; Brutin, D. Fractal pattern formation in nanosuspension sessile droplets via evaporation-spreading on a glass substrate. J. Colloid Interface Sci. 2014, 1, 43–46. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Braun, H.G.; Meyer, E. Crystalline structures in ultrathin poly(ethylene oxide)/poly(methyl methacrylate) blend films. Polymer 2003, 44, 5015–5021. [Google Scholar] [CrossRef]
- Lad, K.; Maaroof, M.; Raval, K.G.; Pratap, A. Fractal Growth Kinetics during crystallization of amorphous Cu50Zr50. Prog. Cryst. Growth Charact. Mater. 2002, 45, 15–19. [Google Scholar] [CrossRef]
- Takayama, H.; Bohnen, K.P.; Fulde, P. Magnetic surface anisotropy of transition metals. Phys. Rev. B 1976, 14, 2287. [Google Scholar] [CrossRef]
- Gradmann, U. Magnetic surface anisotropies. J. Magn. Magn. Mater. 1986, 54–57, 733–736. [Google Scholar] [CrossRef]


| Parameter | Base Values | Scaling Rules |
|---|---|---|
| Scaling factor | from 1 to 100 | - |
| Distance between nodes | 0.28 nm | r’ = r × n |
| Dipolar constant | 2.15 × 10−7 eVnm3 | D’ = D |
| Anisotropy constant (surface) | from 0 eV to 5 × 10−3 eV | K’S = KS × n2 |
| Anisotropy constant (volume) | from 0 eV to 5 × 10−4 eV | K’V = KV × n3 |
| Spin | from 0.1 to 1 | S’ = S × n3 |
| Exchange integral parameter | 1.5 × 10−3 eV | J’ = J × n−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziółkowski, G.; Chrobak, D.; Chełkowska, G.; Zivotsky, O.; Chrobak, A. Enhancement of Hard Magnetic Properties in Fraktal-Like Nano and Mesoscopic Grains. Materials 2021, 14, 1443. https://doi.org/10.3390/ma14061443
Ziółkowski G, Chrobak D, Chełkowska G, Zivotsky O, Chrobak A. Enhancement of Hard Magnetic Properties in Fraktal-Like Nano and Mesoscopic Grains. Materials. 2021; 14(6):1443. https://doi.org/10.3390/ma14061443
Chicago/Turabian StyleZiółkowski, Grzegorz, Dariusz Chrobak, Grażyna Chełkowska, Ondrej Zivotsky, and Artur Chrobak. 2021. "Enhancement of Hard Magnetic Properties in Fraktal-Like Nano and Mesoscopic Grains" Materials 14, no. 6: 1443. https://doi.org/10.3390/ma14061443
APA StyleZiółkowski, G., Chrobak, D., Chełkowska, G., Zivotsky, O., & Chrobak, A. (2021). Enhancement of Hard Magnetic Properties in Fraktal-Like Nano and Mesoscopic Grains. Materials, 14(6), 1443. https://doi.org/10.3390/ma14061443






