Mechanical Vibration Damping and Compression Properties of a Lattice Structure
Abstract
:1. Introduction
2. Materials and Methods
2.1. Characteristics of Samples
2.2. Measurement Methodology
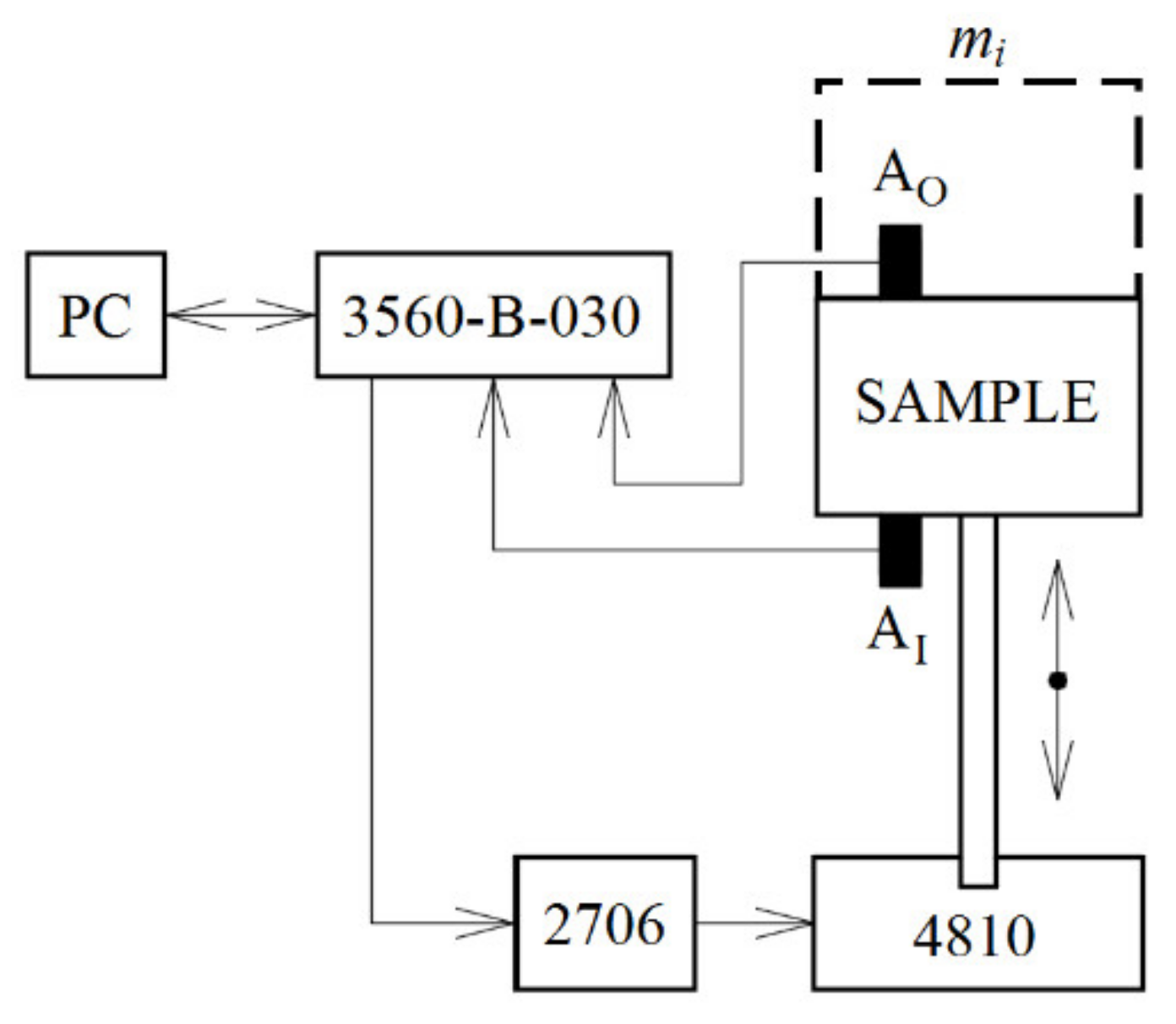
2.2.1. Mechanical Vibration Damping Testing
2.2.2. Compression Testing
3. Results and discussions
3.1. Frequency Dependencies of the Displacement Transmissibility
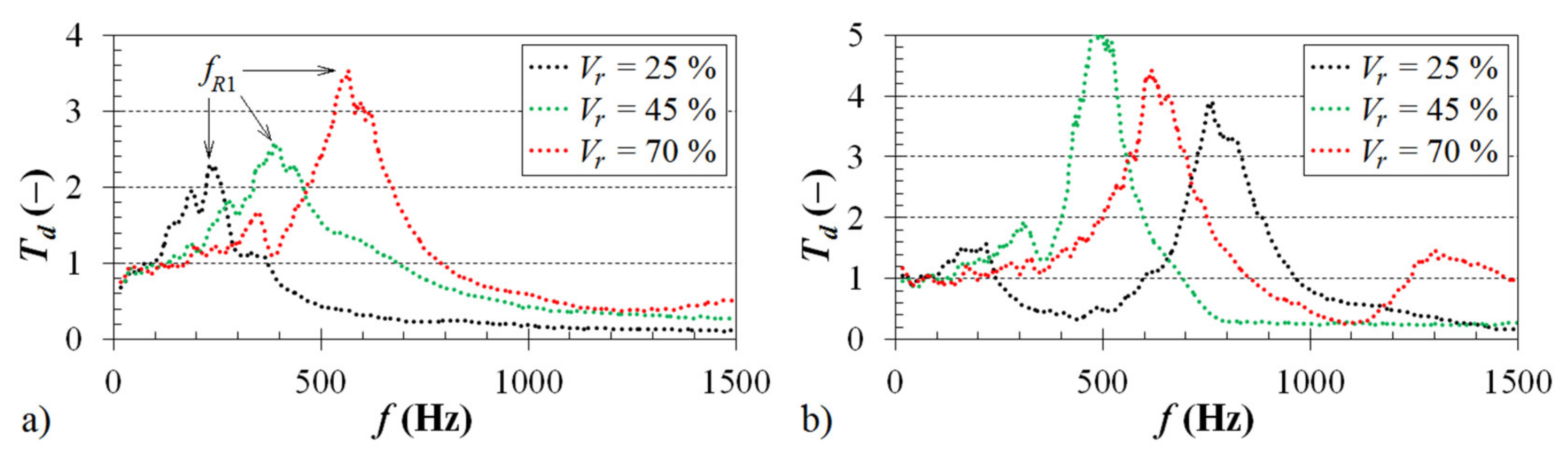
3.1.1. Effect of Volume Ratio
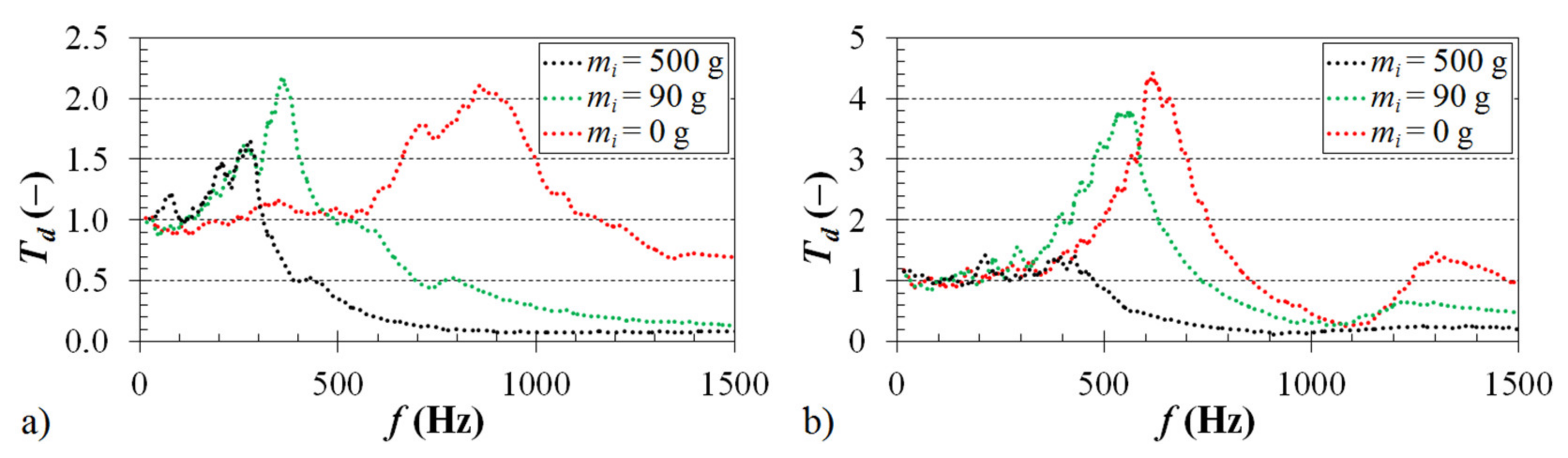
3.1.2. Effect of Inertial Mass
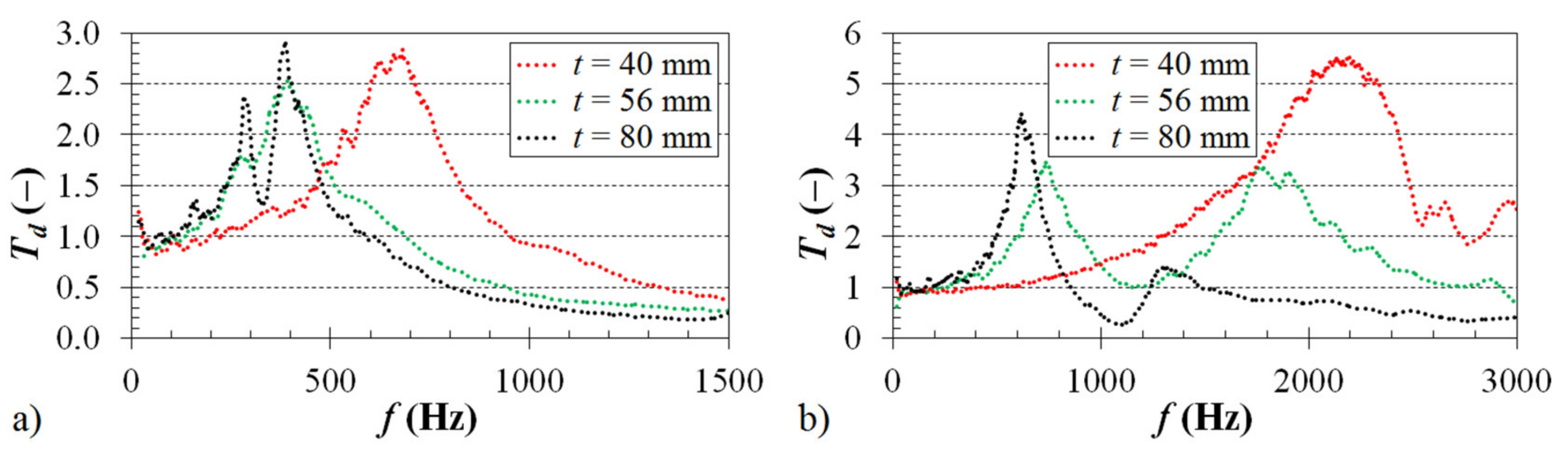
3.1.3. Effect of Material Thickness
3.1.4. Influence of Excitation Frequency
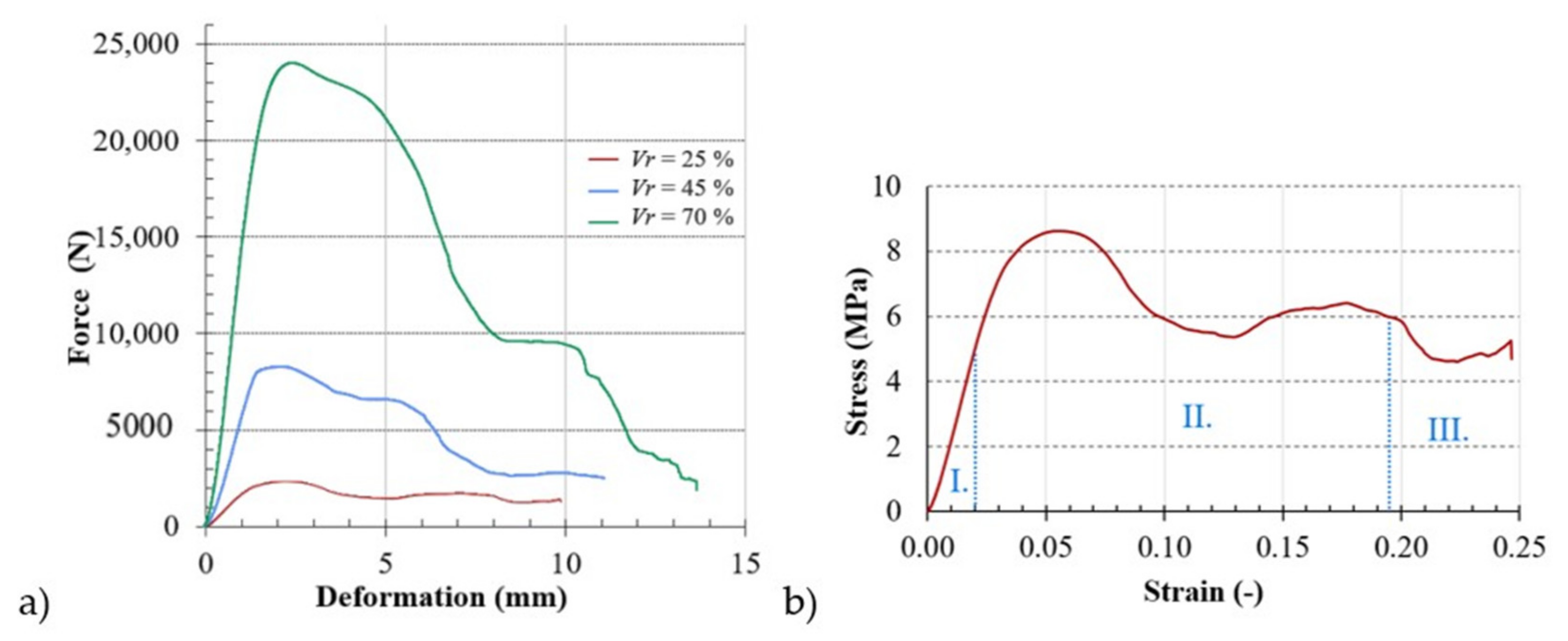
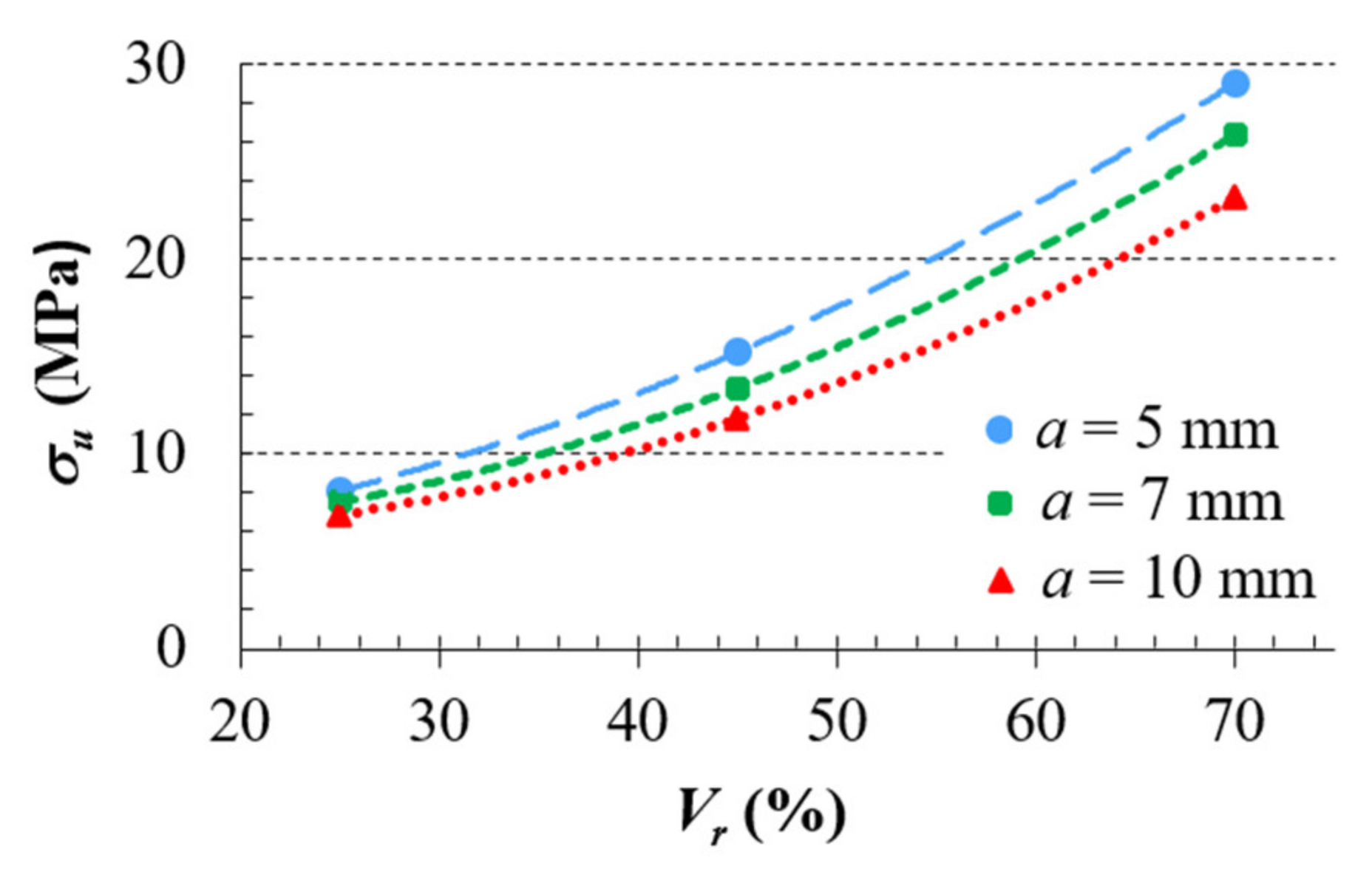
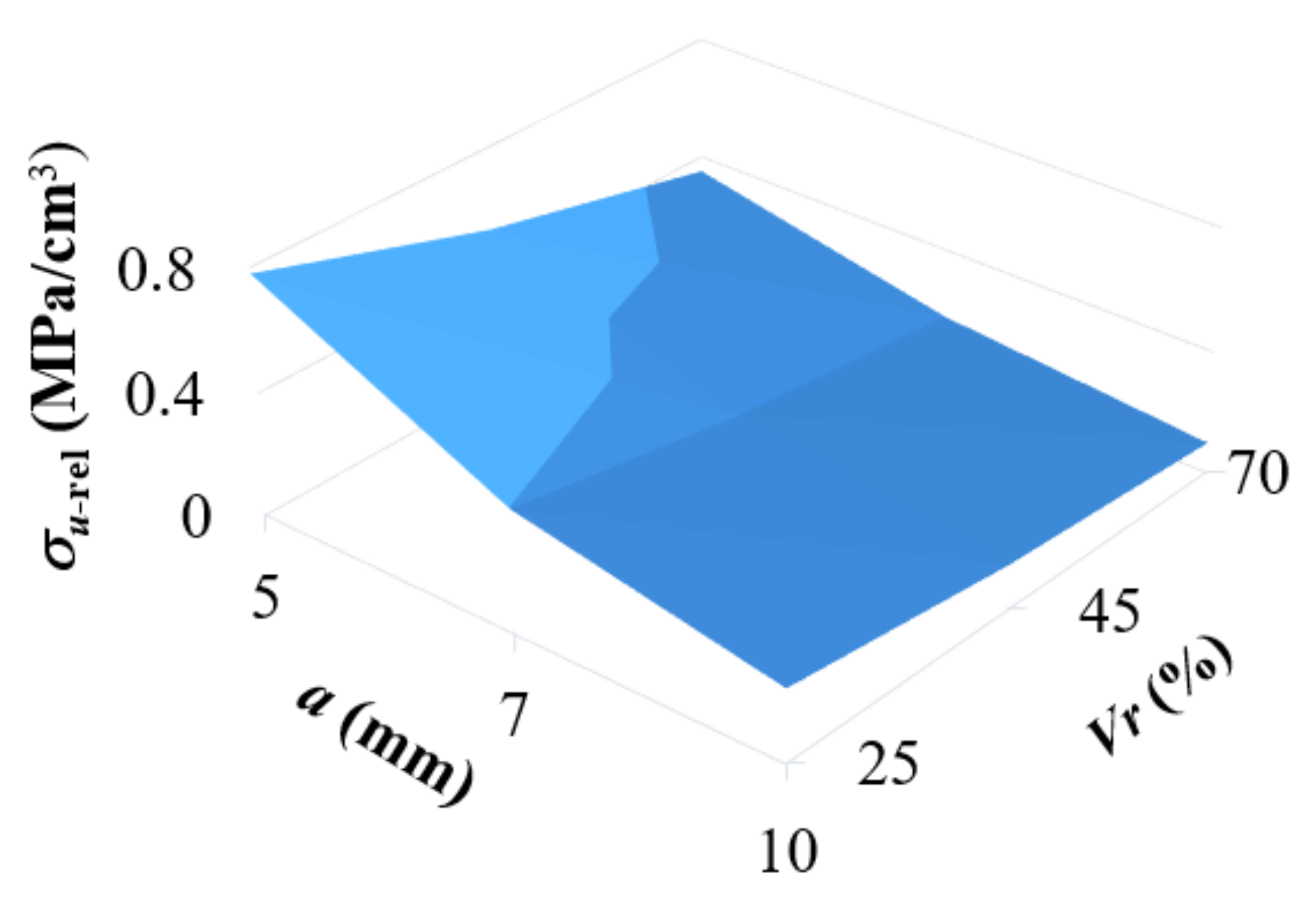
3.2. Compression Behavior of the ABS 3D-Printed Lattice Structure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mamalis, A.G.; Manolakos, D.E.; Szalay, A.; Pantazopoulos, G. Processing of High-Temperature Superconductors at High Strain Rates. In Processing of High-Temperature Superconductors at High Strain Rates; CRC Press: New York, NY, USA, 2019; Volume 4, p. 94. [Google Scholar]
- Hasanain, S.A.; Ahsan, M. Effect of strut length and orientation on elastic mechanical response of modified body-centered cubic lattice structures. Proc. Inst. Mech. Eng. L. 2019, 233, 2219–2233. [Google Scholar]
- Tahseen, A.; Mian, A. Developing and Equivalent Solid Material Model for BCC Lattice Cell Structures Involving Vertical and Horizontal Struts. J. Compos. Sci. 2020, 4, 1–12. [Google Scholar]
- Alwattar, T.A.; Mian, A. Development of an Elastic Material Model for BCC Lattice Cell Structures Using Finite Element Analysis and Neural Networks Approaches. J. Compos. Sci. 2019, 3, 33. [Google Scholar] [CrossRef] [Green Version]
- Iyibilgin, O.; Yigit, C. Experimental investigation of different cellular lattice structures manufactured by fused deposition modeling. In Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, USA, 12–14 August 2013; pp. 895–907. [Google Scholar]
- Fadeel, A.; Mian, A.; Al Rifaie, M.; Srinivasan, R. Effect of Vertical Strut Arrangements of Compression Characteristics of 3D Printed Polymer Lattice Structures: Experimental and Computational Study. J. Mater. Eng. Perform. 2019, 28, 709–716. [Google Scholar] [CrossRef]
- Gautam, R.; Idapalati, S. Compressive Properties of Additively Manufactured Functionally Graded Kagome Lattice Structure. Metals 2019, 9, 517. [Google Scholar] [CrossRef] [Green Version]
- Cantrell, J.T.; Rohde, S.; Damiani, D.; Gurnani, R.; DiSandro, L.; Anton, J.; Young, A.; Jerez, A.; Steinbach, D.; Kroese, C.; et al. Experimental characterization of the mechanical properties of 3D-printed ABS and polycarbonate parts. Rapid Prototyp. J. 2017, 23, 811–824. [Google Scholar] [CrossRef]
- Al Rifaie, M.; Lian, A.; Srinivasan, R. Compression behavior of three-dimensional printed polymer lattice structures. Proc. Inst. Mech. Eng. L. 2018, 233, 1574–1584. [Google Scholar] [CrossRef]
- Calise, G.J.; Saigal, A. Anisotropy and failure in octahedral lattice structure parts fabricated using the fdm technology. In Proceedings of the ASME 2017 International Mechanical Engineering Congress and Exposition, Tampa, FL, USA, 3–9 November 2017. [Google Scholar]
- Helou, M.; Vongbunyong, S.; Kara, S. Finite Element Analysis and Validation of Cellular Structures. Procedia CIRP 2016, 50, 94–99. [Google Scholar] [CrossRef] [Green Version]
- Bauer, J.; Hengsbach, S.; Tesari, I.; Schwaiger, R.; Kraft, O. High-strength cellular ceramic composites with 3D microarchitecture. Proc. Natl. Acad. Sci. USA 2014, 111, 2453–2458. [Google Scholar] [CrossRef] [Green Version]
- Messner, M.C. Optimal lattice-structured materials. J. Mech. Phys. Solids 2016, 96, 162–183. [Google Scholar] [CrossRef] [Green Version]
- Hou, A.; Gramoll, K. Compressive Strength of Composite Lattice Structures. J. Reinf. Plast. Comp. 2016, 17, 462–493. [Google Scholar] [CrossRef]
- Gawrońska, E.; Dyja, R. A Numerical Study of Geometry’s Impact on the Thermal and Mechanical Properties of Periodic Surface Structures. Materials 2021, 14, 427. [Google Scholar] [CrossRef] [PubMed]
- Mahshid, R.; Hansen, H.N.; Hojbjerre, K.L. Strength analysis and modeling of cellular lattice structures manufactured using selective laser melting for tooling applications. Mater. Des. 2016, 104, 276–283. [Google Scholar] [CrossRef] [Green Version]
- Utomo, M.S.; Whulanza, Y.; Lestari, E.P.; Erryani, A.; Kartika, I.; Alief, N.A. Determination of compressive strength of 3D polymeric lattice structure as template in powder metallurgy. IOP Conf. Ser. Mater. Sci. Eng. 2019, 541, 1–7. [Google Scholar] [CrossRef]
- Ozdemir, Z.; Hernandez-Nava, E.; Tyas, A.; Warren, J.A.; Fay, S.D.; Goodall, R.; Todd, I.; Askes, H. Energy absorption in lattice structures in dynamics: Experiments. Int. J. Impact Eng. 2016, 89, 49–61. [Google Scholar] [CrossRef] [Green Version]
- Azmi, M.S.; Ismail, R.; Hasan, R.; Alkahari, M.R. Vibration Analysis of Fused Deposition Modelling Printed Lattice Structure Bar for Application in Automated Device. Int. J. Eng. Technol. 2018, 7, 21–24. [Google Scholar] [CrossRef]
- Simssek, U.; Arslan, T.; Kavas, B.; Gayir, C.E.; Sendur, P. Parametric studies on vibration characteristics of triply periodic minimum surface sandwich lattice structures. Int. J. Adv. Manuf. Technol. 2020. [Google Scholar] [CrossRef]
- Tyburec, M.; Zeman, J.; Novak, J. Design modular 3D Printed reinforcement of wound composite bellow beams with semidefinite programming. Mater. Des. 2019, 183, 1–11. [Google Scholar] [CrossRef]
- Pantazopoulos, G.A. Pantazopoulos, G.A., 2019. A short review on fracture mechanisms of mechanical components operated under industrial process conditions: Fractographic analysis and selected prevention strategies. Metals 2019, 9, 148. [Google Scholar] [CrossRef] [Green Version]
- Rybachuk, M.; Alice Mauger, C.; Fiedler, T.; Öchsner, A. Anisotropic mechanical properties of fused deposition modeled parts fabricated by using Acrylonitrile Butadiene Styrene polymer. J. Polym. Eng. 2017, 37, 699–706. [Google Scholar] [CrossRef]
- Rao, S.S. Mechanical Vibrations, 5th ed.; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2011; pp. 281–287. [Google Scholar]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Lopes, V., Jr. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Latif, N.A.; Rus, A.Z.M. Vibration transmissibility study of high density solid waste biopolymer foam. In Proceedings of the International Conference on Mechanical Engineering Research, High Tatras, Slovakia, 28–31 May 2012; pp. 426–429. [Google Scholar]
- Kelly, S.G. Mechanical Vibrations: Theory and Applications, SI, 1st ed.; Cengage Learning: Stamford, CT, USA, 2012; pp. 228–233. [Google Scholar]
- Liu, K.; Liu, J. The damped dynamic vibration absorbers: Revisited and next result. J. Sound Vib. 2005, 284, 1181–1189. [Google Scholar] [CrossRef]
- Hadas, Z.; Ondrusek, C. Non-linear spring-less electromagnetic vibration energy havresting system. Eur. Phys. J. 2005, 224, 2881–2896. [Google Scholar]
- Stephen, N. On energy harvesting from ambient vibration. J. Sound Vib. 2006, 293, 409–425. [Google Scholar] [CrossRef] [Green Version]
- Liao, W.H.; Loai, C.Y. Harmonic analysis of a magnetorheological damper for vibration control. Smart Mater. Struct. 2002, 11, 288–296. [Google Scholar] [CrossRef]
- Lv, Q.; Yao, Z. Analysis of the effects of nonlinear viscous damping on vibration isolator. Nonlinear Dyn. 2015, 79, 2325–2332. [Google Scholar] [CrossRef]
- Ho, C.; Lang, Z.; Billings, S.A. The benefits of nonlinear cubic viscous damping of the force transmissibility of a Duffing-type vibration isolator. In Proceedings of the UKACC International Conference on Control, Cardiff, UK, 3–5 September 2012; pp. 479–484. [Google Scholar]
- Meštrović, R.; Dragovic, B. Modelling of the Loading Process at Seaside Link in Port: Case Study of Seaport Automobile Terminal. In Proceedings of the XXIII International Conference on “Material Handling, Constructions and Logistics”, Bar, Montenegro, 1–2 July 2019. [Google Scholar]
- ISO 844:2014 Standard. Rigid Cellular Plastics—Determination of Compression Properties; International Organization for Standardization (ISO): Geneva, Switzerland, 2014. [Google Scholar]
- Ozcelik, B.; Ozbay, A.; Demirbas, E. Influence of injection parameters and mold materials on mechanical properties of ABS in plastic injection molding. Int. Commun. Heat Mass Transf. 2010, 37, 1359–1365. [Google Scholar] [CrossRef]
- Kadkhodapour, J.; Montazerian, H.; Darabi, A.C.; Anaraki, A.P.; Ahmadi, S.M.; Zadpoor, A.A.; Schmauder, S. Failure mechanisms of additively manufactured porous biomaterials. J. Mech. Behav. Biomed. Mater. 2015, 50, 180–191. [Google Scholar] [CrossRef]
- Sudarmadji, N.; Tan, J.Y.; Leong, K.F.; Chua, C.K.; Loh, Y.T. Investigation of the mechanical properties and porosity relationships in selective laser-sintered polyhedral for functionally graded scaffolds. Acta Biomater. 2011, 7, 530–537. [Google Scholar] [CrossRef]
- Byrne, D.P.; Lacroix, D.; Planell, J.A.; Kelly, D.J.; Prendergast, P.J. Simulation of tissue differentiation in a scaffold as a function of porosity, Young’s modulus and dissolution rate: Application of mechanobiological models in tissue engineering. Biomaterials 2007, 28, 5544–5554. [Google Scholar] [CrossRef]
- Parthasarathy, J.; Starly, B.; Raman, S.; Christensen, A. Mechanical evaluation of porous titanium (Ti6Al4V) structures with electron beam melting (BEM). J. Mech. Behav. Biomed. Mater. 2010, 3, 249–259. [Google Scholar] [CrossRef]
- Maciejewski, I.; Meyer, L.; Krzyzynski, T. The vibration damping effectiveness of an active seat suspension system and its robustness to varying mass loading. J. Sound Vib. 2010, 329, 3898–3914. [Google Scholar] [CrossRef]
- Rezali, K.A.M.; Griffin, M.J. Transmission of vibration through gloves: Effects of material thickness. Ergonomics 2016, 59, 1026–1037. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X. Measurement and Modeling of Seating Dynamics to Predict Seat Transmissibility, 1st ed.; University of Southampton: Southampton, UK, 2014; pp. 25–34. [Google Scholar]
- Sadowski, T.; Samborski, S. Development of damage state in porous ceramics under compression. Comput. Mater. Sci. 2008, 43, 75–81. [Google Scholar] [CrossRef]
- Tkac, J.; Samborski, S.; Monkova, K.; Debski, H. Analysis of mechanical properties of a lattice structure produced with the additive technology. Compos. Struct. 2020, 242, 112138. [Google Scholar] [CrossRef]
- Li, Q.M.; Magkiriadis, I.; Harrigan, J.J. Compressive Strain at the Onset of Densification of Cellular Solids. J. Cell. Plast. 2006, 42, 371–392. [Google Scholar] [CrossRef]
- Arau’jo, H.; Leite, M.; Ribeiro, A.M.R.; Deus, A.M.; Reis, L.; Vaz, M.F. Investigating the contribution of geometry on the failure of cellular core structures obtained by additive manufacturing. Frat. Integrita Strutt. 2019, 49, 478–486. [Google Scholar]
- Mooney, B.; Kourousis, K. A Review of Factors Affecting the Mechanical Properties of Maraging Steel 300 Fabricated via Laser Powder Bed Fusion. Metals 2020, 10, 1273. [Google Scholar] [CrossRef]





| Property | Symbol | Unit | Value |
|---|---|---|---|
| Ultimate limit of strength | σu | MPa | 37 |
| Absolute extension | Δl | mm | 4.4 |
| Young’s modulus | E | MPa | 1920 |
| Yield strength | σY | MPa | 37 |
| Poisson’s constant | ν | - | 0.394 |
| Density | ρ | g/cm3 | 1.04 |
| a (mm) | Vr (%) | mi (g) | mi (g) | mi (g) |
|---|---|---|---|---|
| 0 | 90 | 500 | ||
| 5 | 25 | 848 ± 37 | 357 ± 13 | 266 ± 12 |
| 45 | 1835 ± 62 | 682 ± 25 | 269 ± 11 | |
| 70 | 2197 ± 73 | 775 ± 24 | 398 ± 14 | |
| 7 | 25 | 470 ± 21 | 226 ± 9 | 199 ± 8 |
| 45 | 587 ± 18 | 391 ± 12 | 205 ± 10 | |
| 70 | 721 ± 33 | 585 ± 22 | 330 ± 15 | |
| 10 | 25 | 221 ± 10 | 199 ± 9 | 183 ± 7 |
| 45 | 456 ± 14 | 381 ± 19 | 188 ± 8 | |
| 70 | 615 ± 24 | 551 ± 24 | 225 ± 9 |
| a | Vr | σY | σu | E |
|---|---|---|---|---|
| (mm) | (%) | (Mpa) | (Mpa) | (Mpa) |
| 5 | 25 | 5.0 ± 0.4 | 8.6 ± 0.4 | 253 ± 17 |
| 45 | 7.6 ± 0.4 | 15.2 ± 0.5 | 380 ± 20 | |
| 70 | 13.1 ± 0.6 | 29.0 ± 0.9 | 653 ± 32 | |
| 7 | 25 | 4.5 ± 0.3 | 7.5 ± 0.3 | 227 ± 13 |
| 45 | 6.9 ± 0.4 | 13.4 ± 0.5 | 348 ± 17 | |
| 70 | 12.4 ± 0.5 | 26.4 ± 0.7 | 619 ± 26 | |
| 10 | 25 | 4.3 ± 0.2 | 6.9 ± 0.3 | 213 ± 12 |
| 45 | 6.5 ± 0.4 | 11.8 ± 0.5 | 325 ± 20 | |
| 70 | 11.7 ± 0.5 | 23.1 ± 0.6 | 583 ± 36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monkova, K.; Vasina, M.; Zaludek, M.; Monka, P.P.; Tkac, J. Mechanical Vibration Damping and Compression Properties of a Lattice Structure. Materials 2021, 14, 1502. https://doi.org/10.3390/ma14061502
Monkova K, Vasina M, Zaludek M, Monka PP, Tkac J. Mechanical Vibration Damping and Compression Properties of a Lattice Structure. Materials. 2021; 14(6):1502. https://doi.org/10.3390/ma14061502
Chicago/Turabian StyleMonkova, Katarina, Martin Vasina, Milan Zaludek, Peter Pavol Monka, and Jozef Tkac. 2021. "Mechanical Vibration Damping and Compression Properties of a Lattice Structure" Materials 14, no. 6: 1502. https://doi.org/10.3390/ma14061502
APA StyleMonkova, K., Vasina, M., Zaludek, M., Monka, P. P., & Tkac, J. (2021). Mechanical Vibration Damping and Compression Properties of a Lattice Structure. Materials, 14(6), 1502. https://doi.org/10.3390/ma14061502









