Numerically Efficient Three-Dimensional Model for Non-Linear Finite Element Analysis of Reinforced Concrete Structures
Abstract
:1. Introduction
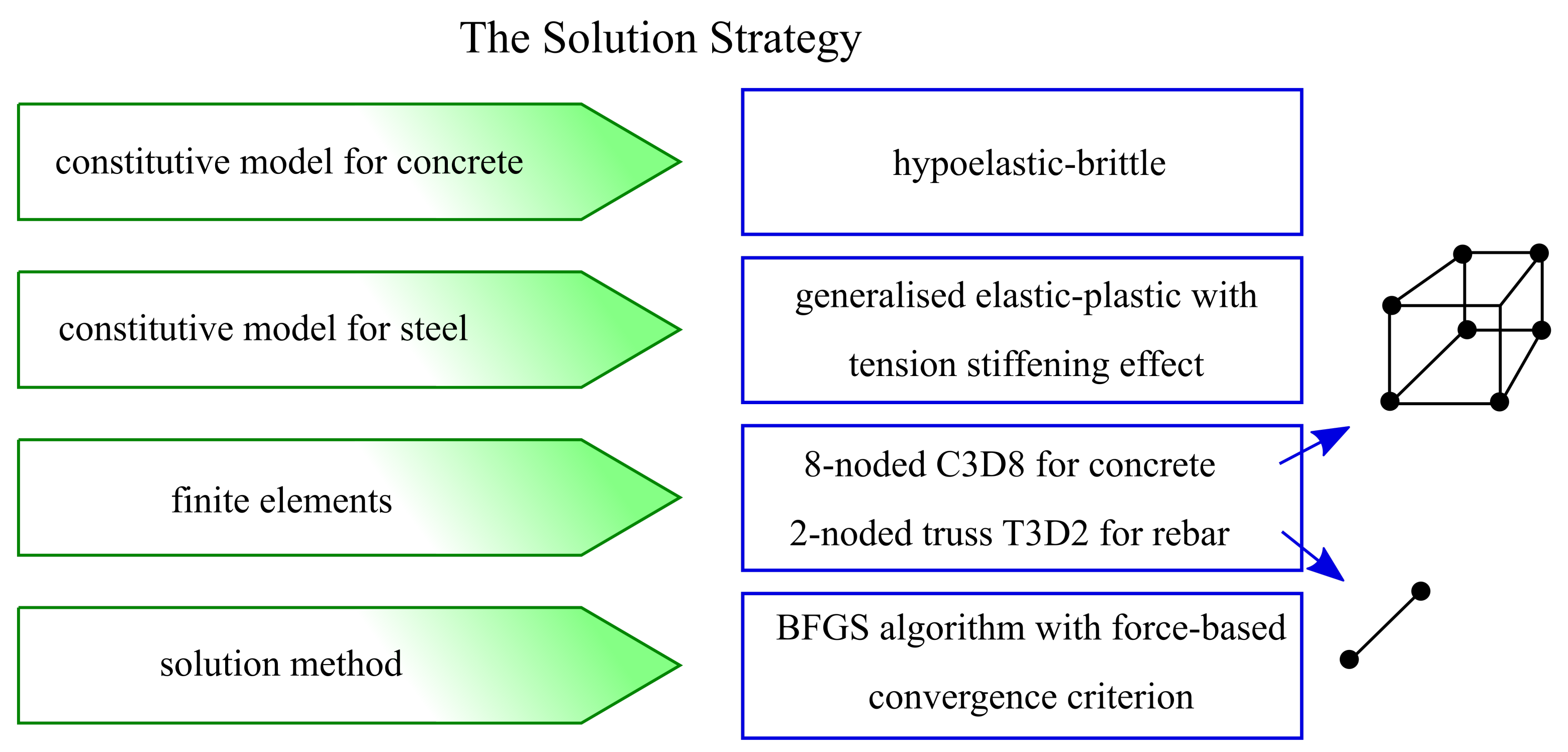
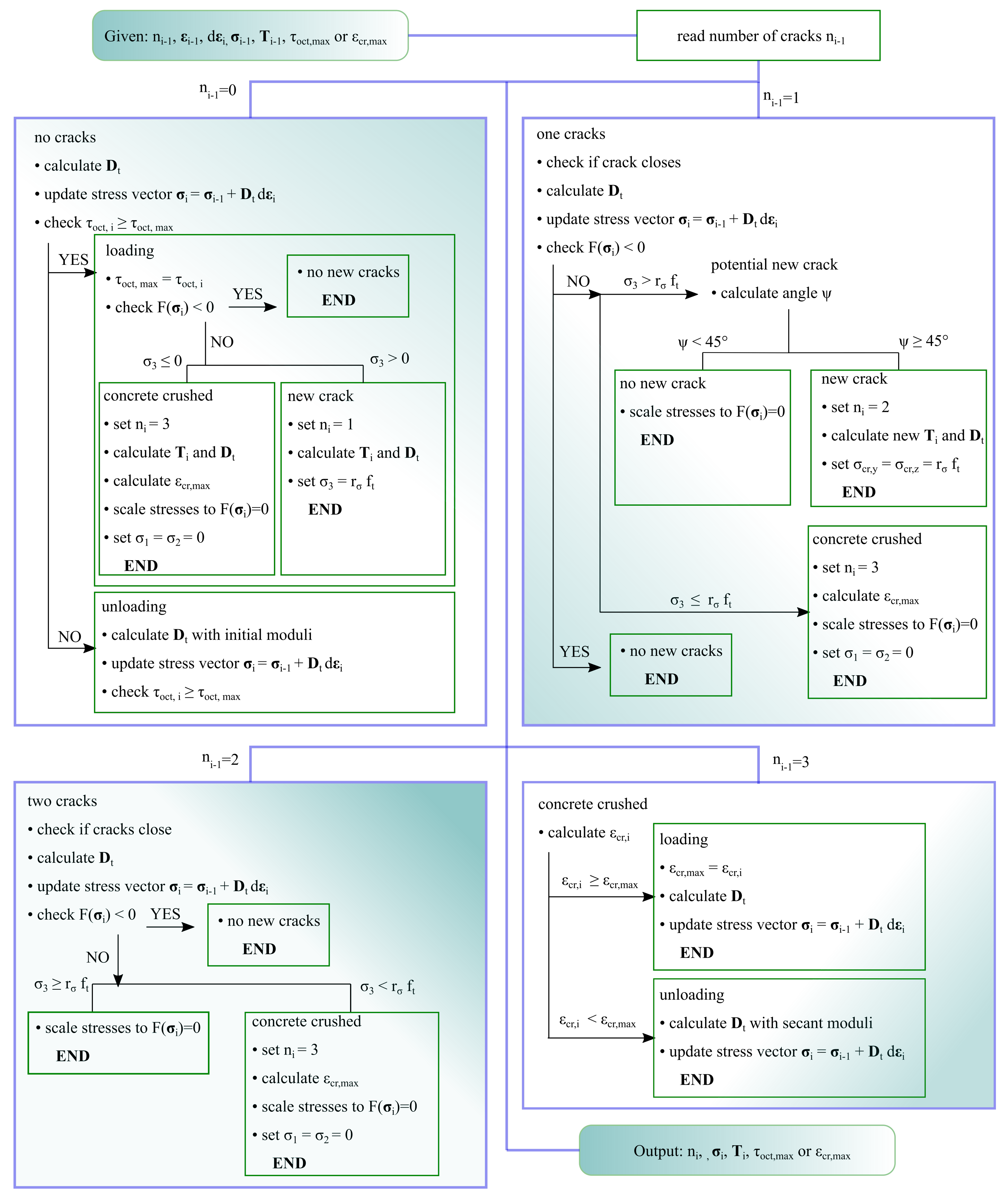
2. Proposed Solution Strategy
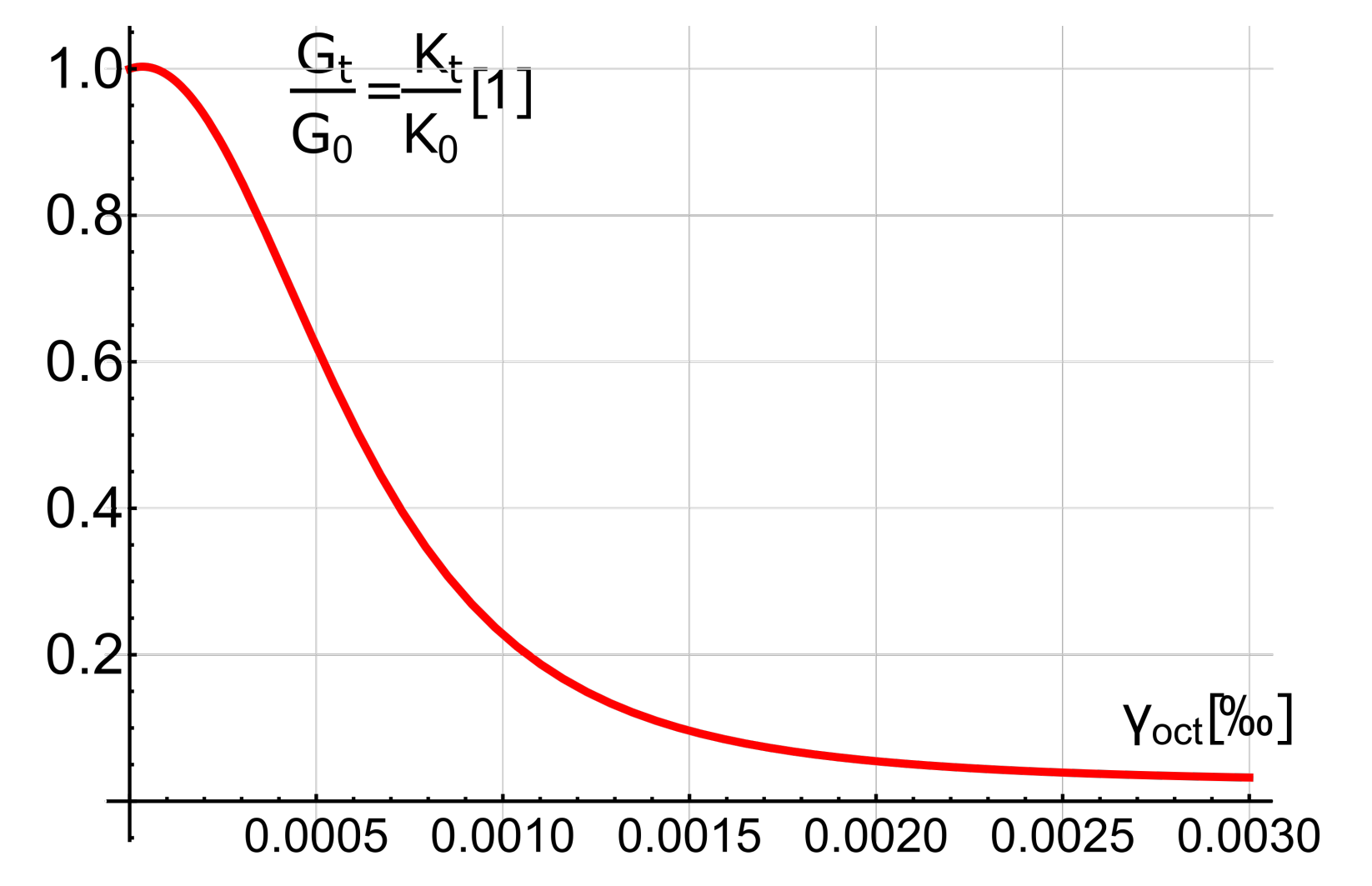
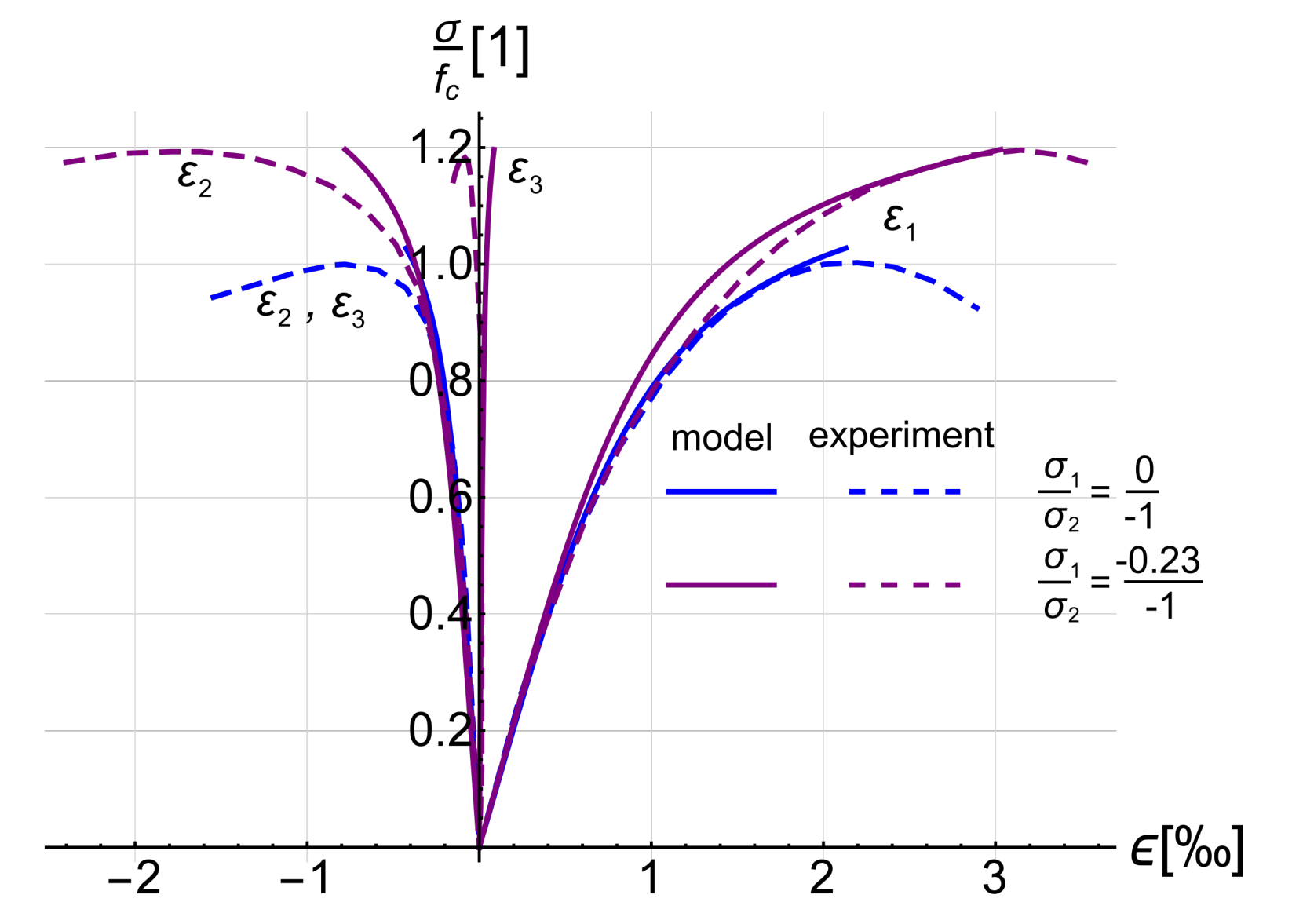
2.1. Constitutive Model of Concrete
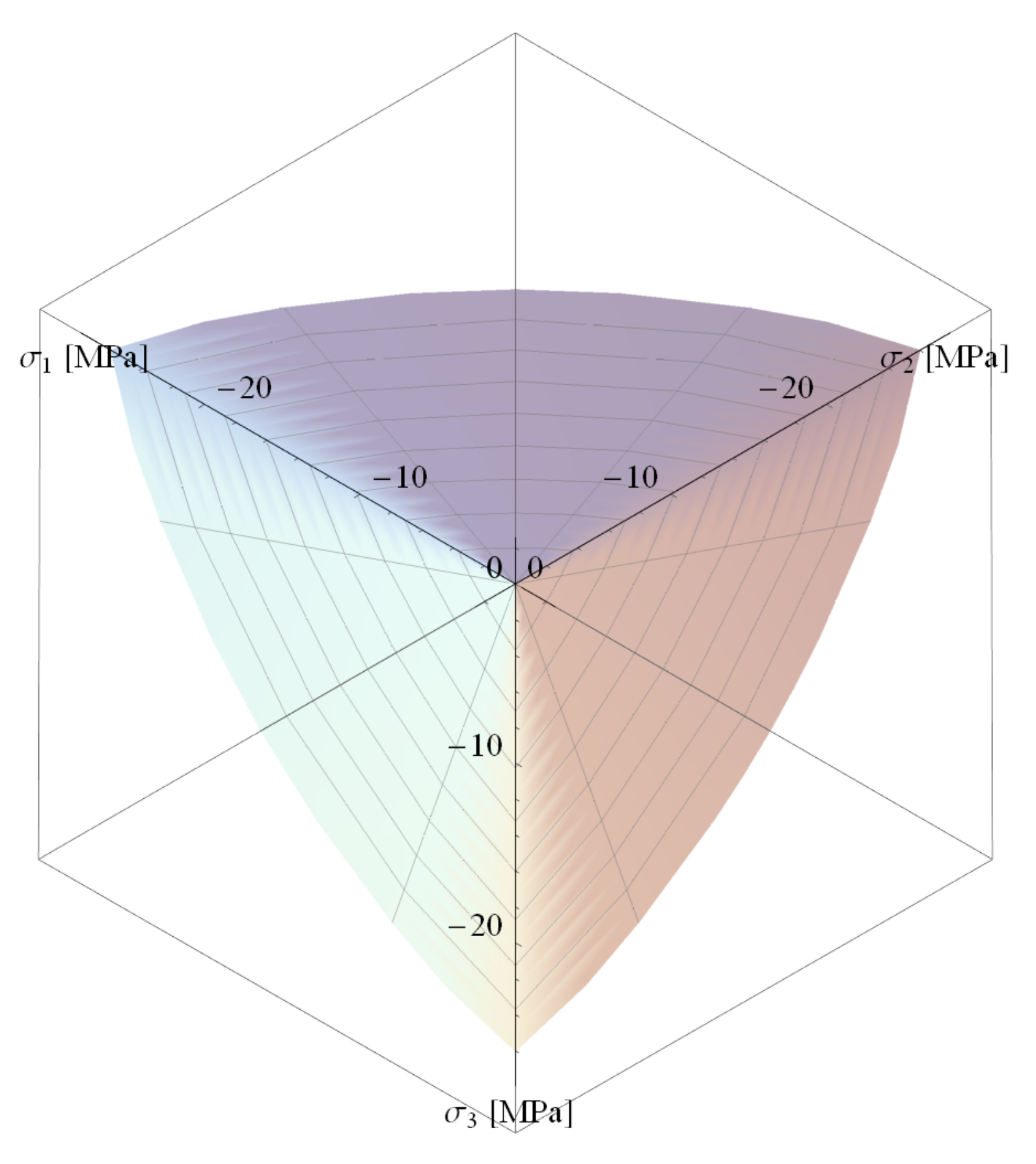
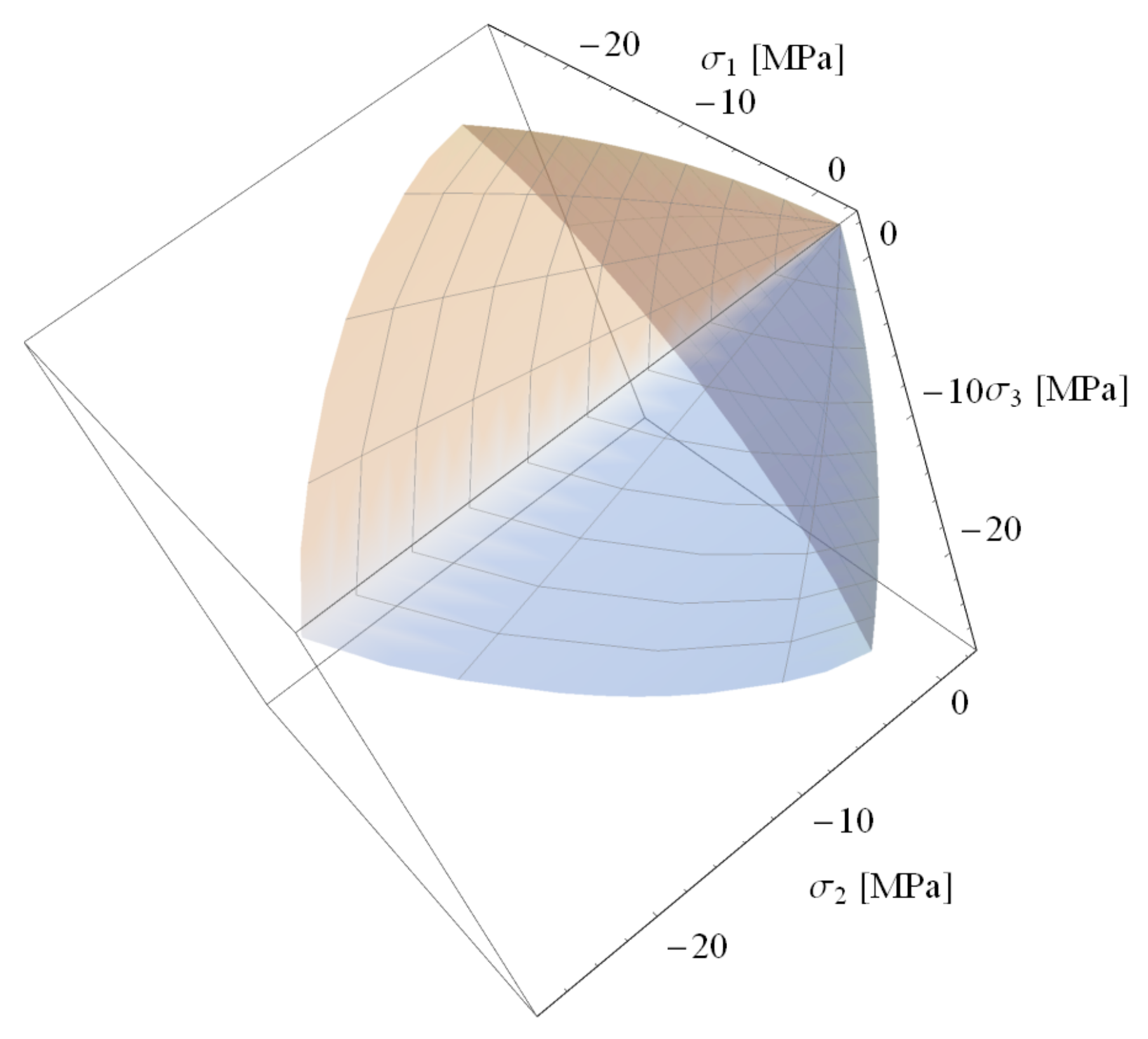
2.2. Ultimate Surface of Concrete
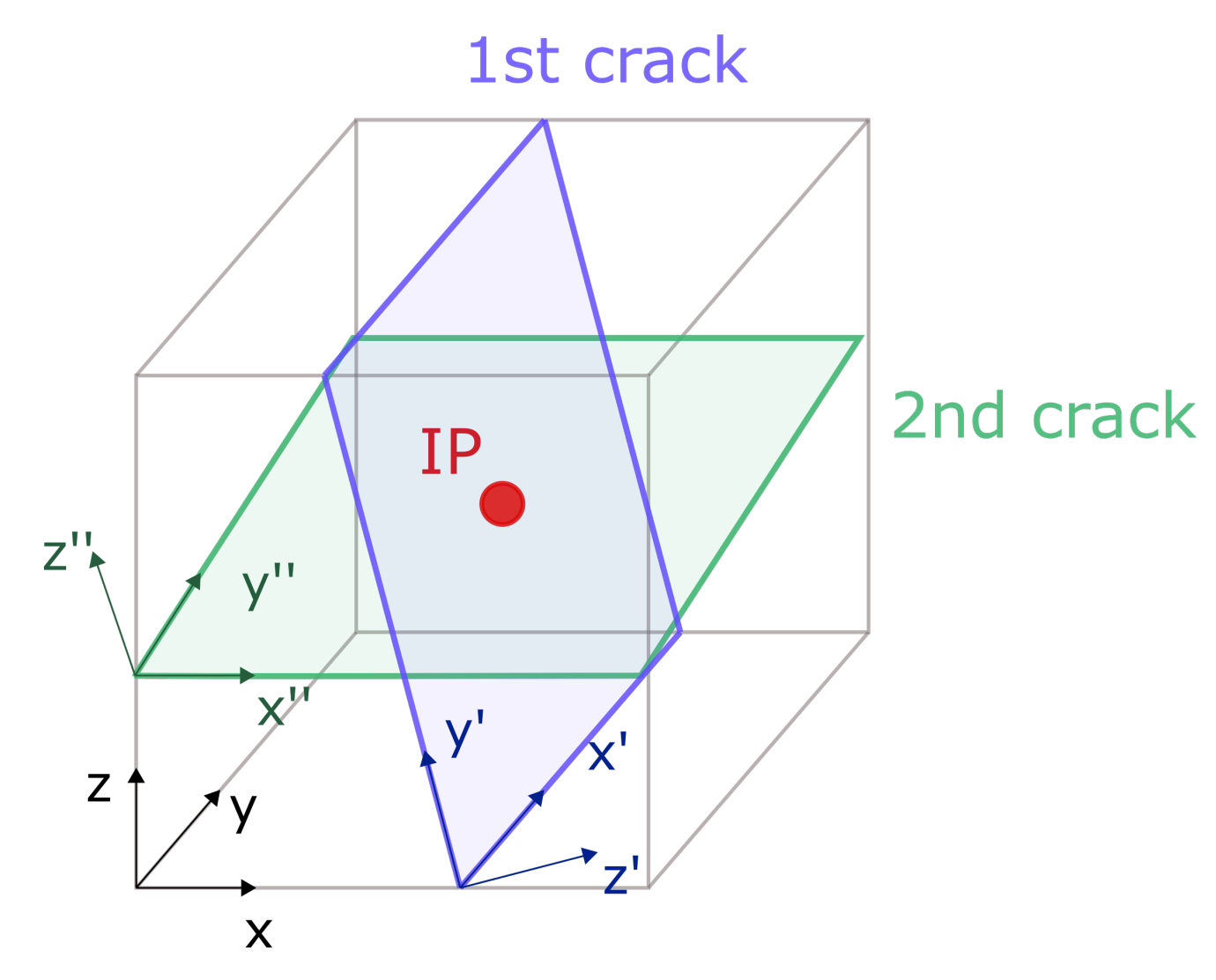
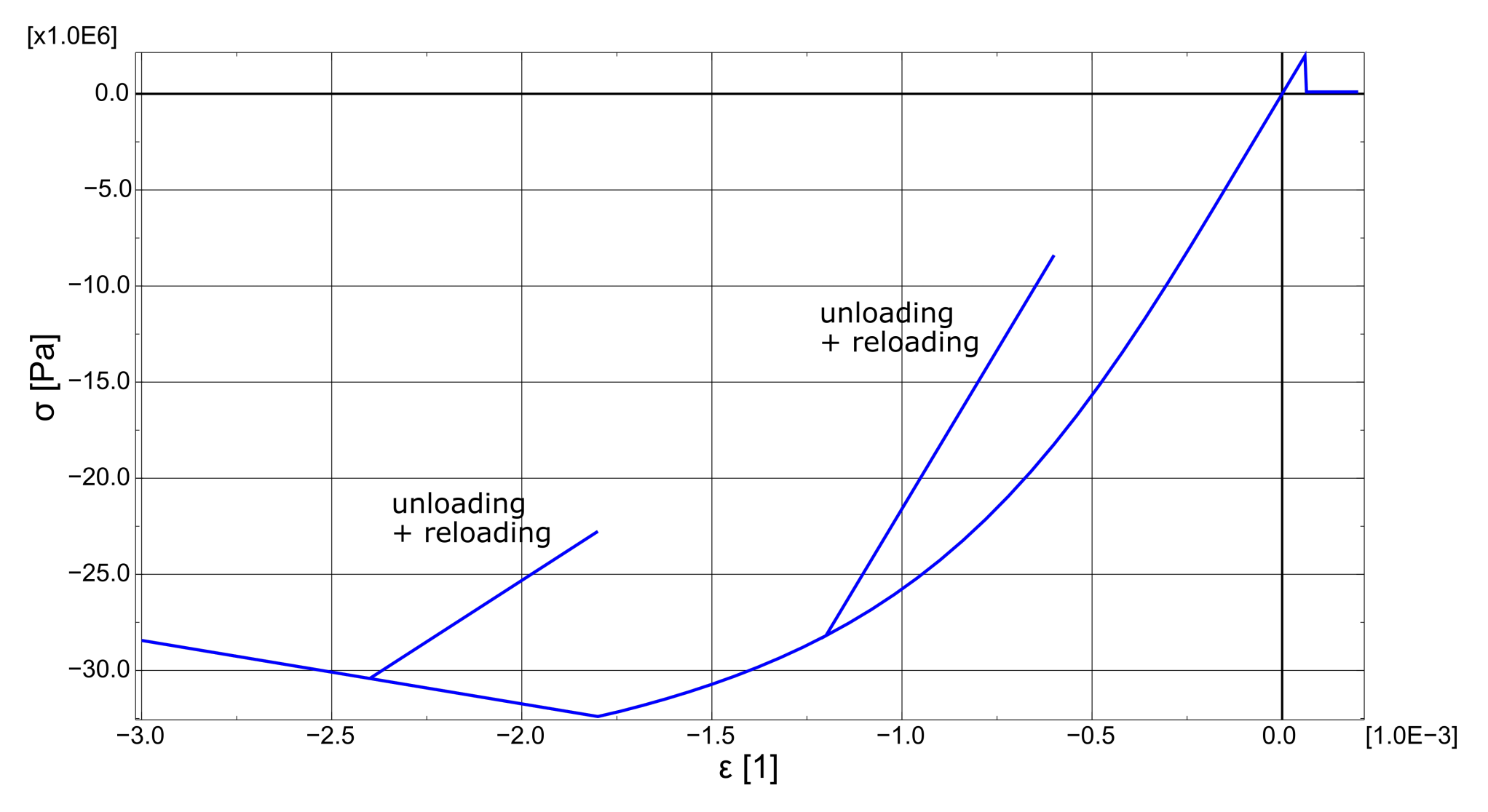
2.3. Smeared Crack Model and Crushing
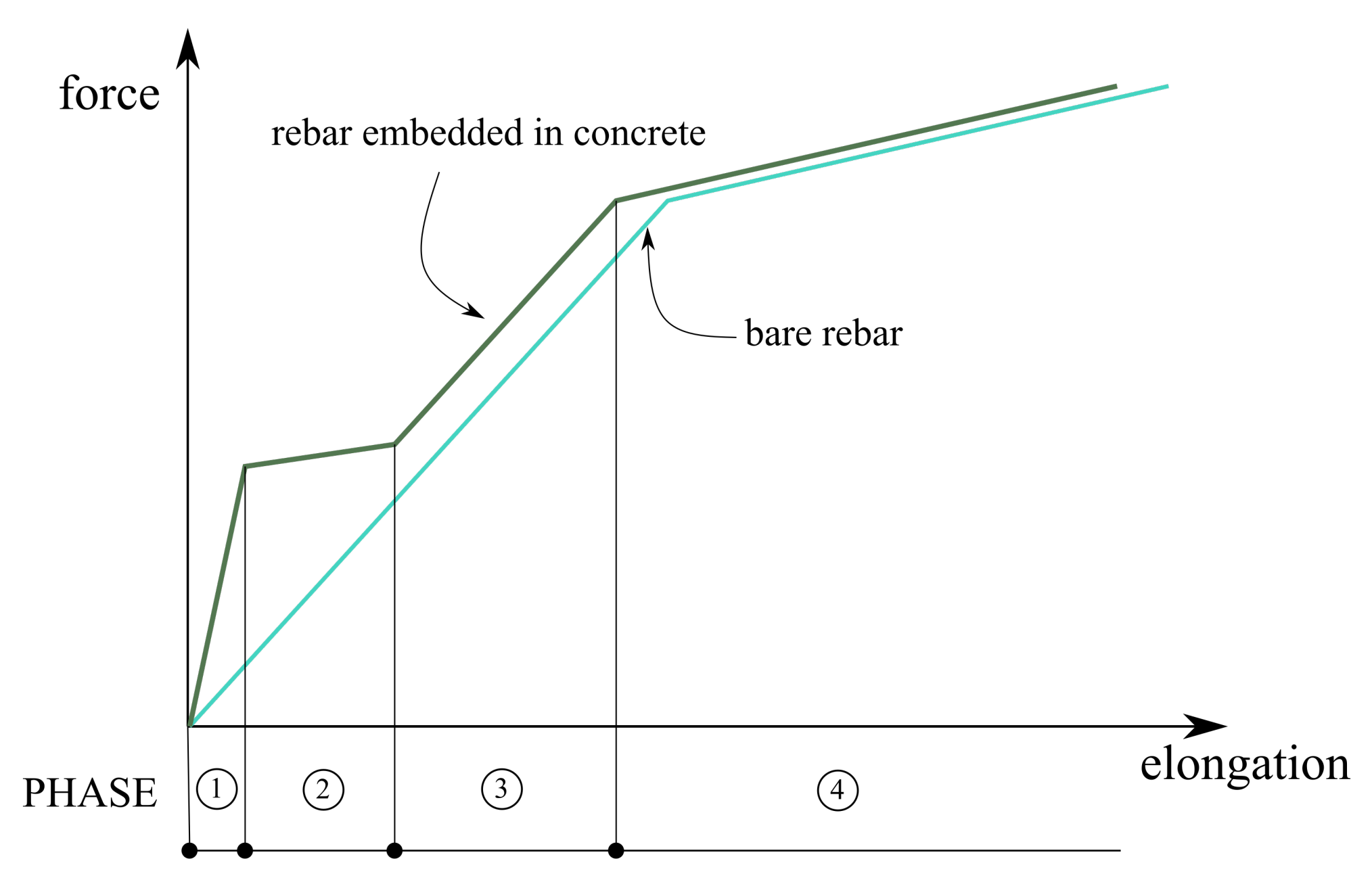
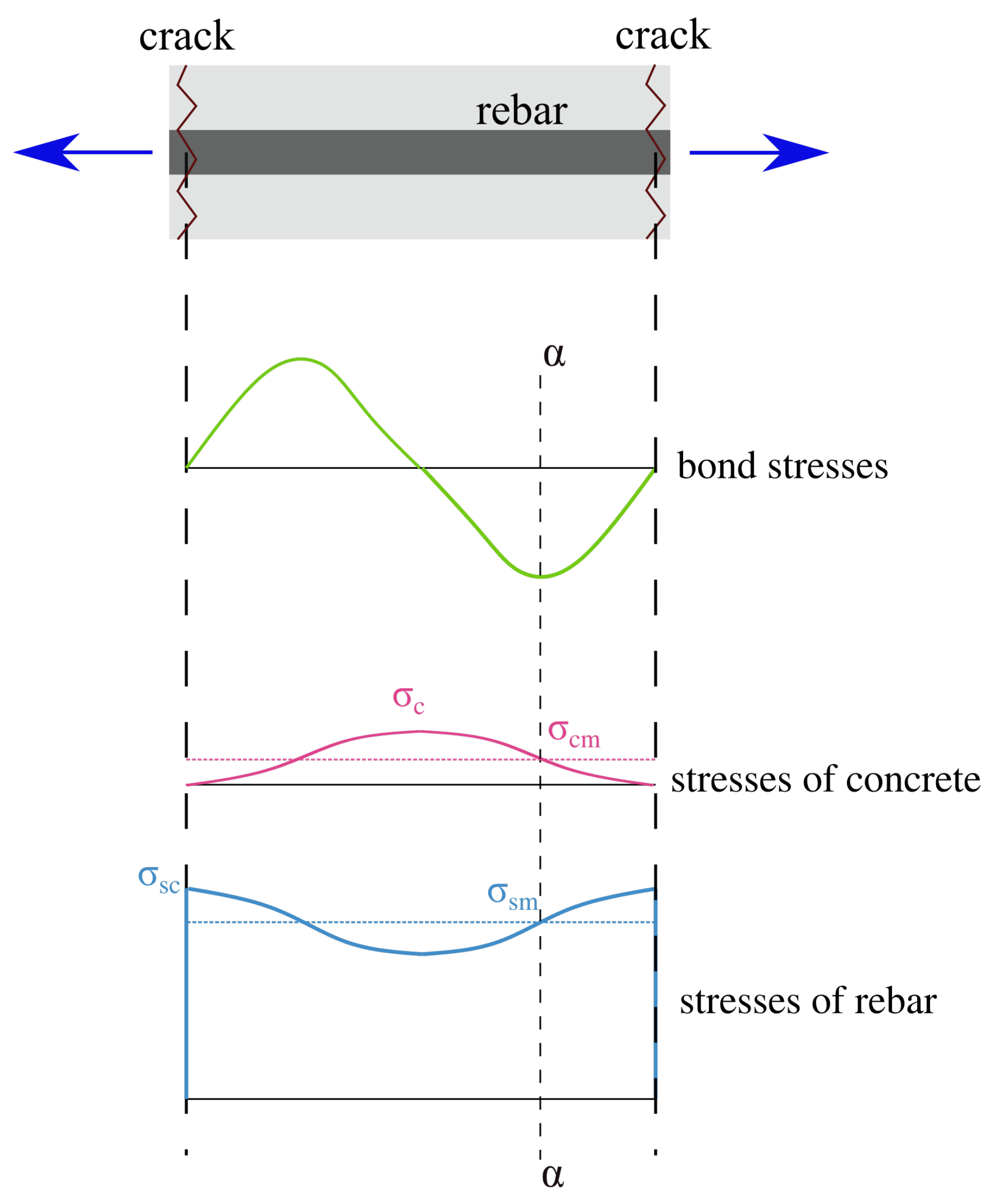
2.4. Generalised Constitutive Model of Steel
- Phase 1—elastic stage, in which concrete and steel behave in a linear manner and have equal strains;
- Phase 2—crack formation, which begins when stresses in concrete cover reach tensile strength;
- Phase 3—stabilised cracking; and
- Phase 4—yielding of steel, in which the TS effect vanishes due to the degradation of the bonding properties between reinforcing steel and concrete.
2.5. Implementation, Finite Elements, Solution Method, Convergence Criteria
- mesh size should be larger than approximately 1.5 the aggregate size (approximately 50 mm),
- mesh size should be smaller than typical crack spacing (approximately 150 mm).
3. Verification and Validation of the Proposed Strategy
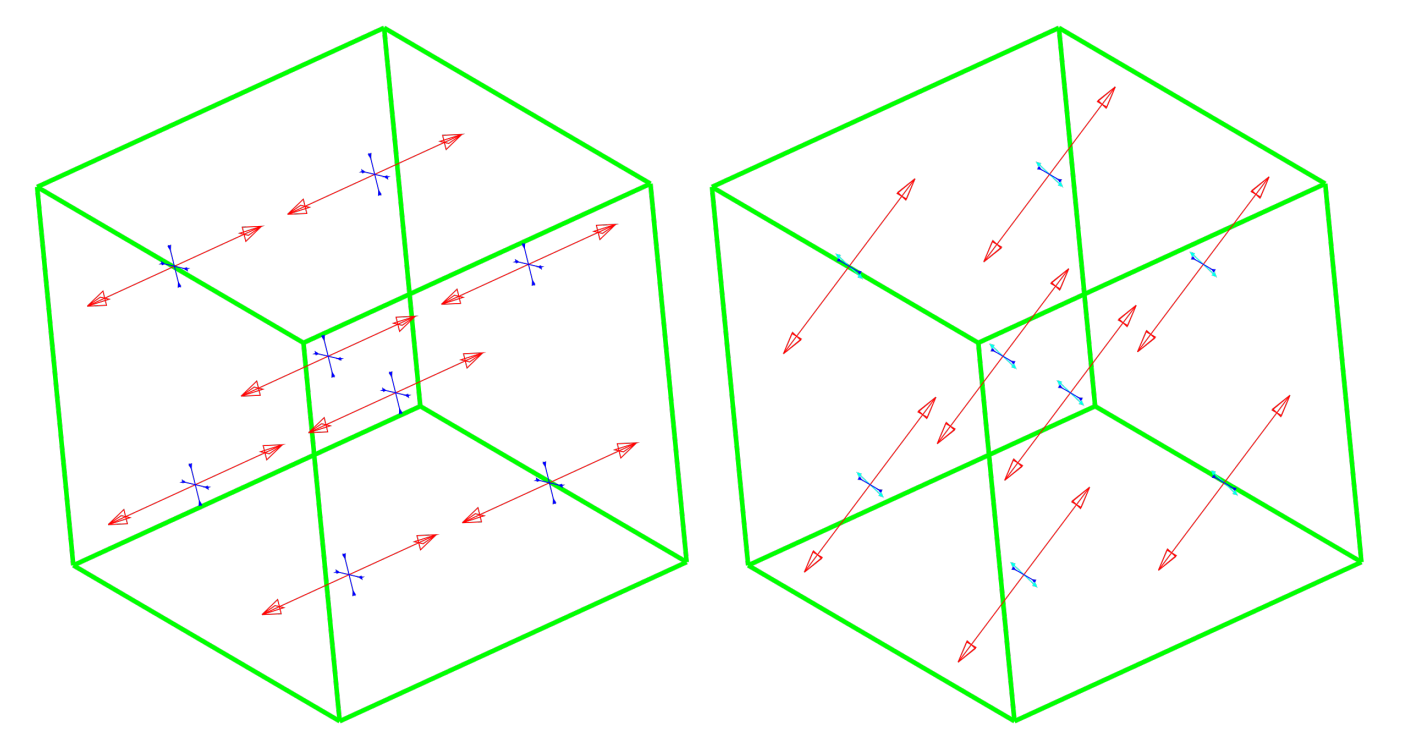
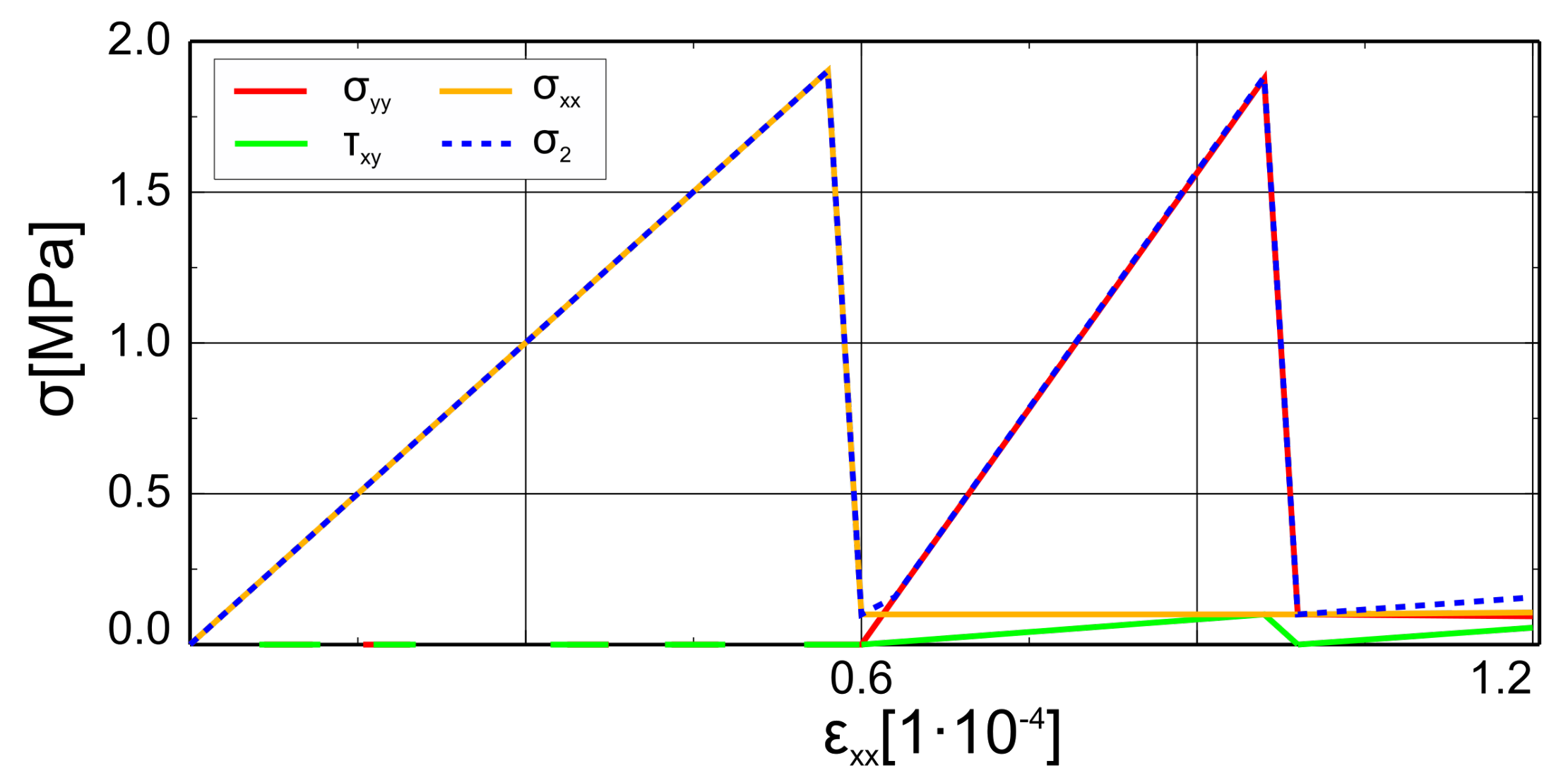
3.1. CS1 Numerical Willam’s Test
- phase 1—uniaxial tension up to the crack formation, components of the strain increments vector in the Cartesian coordinate system have the following ratio: ;
- phase 2—biaxial tension and shear, components of the strain increments vector in the Cartesian coordinate system have the following ratio: .
- during the test, the larger principal stress does not exceed the tensile strength;
- at the end of phase 2 all stresses tend to zero.
3.2. CS2 Beam in Bending
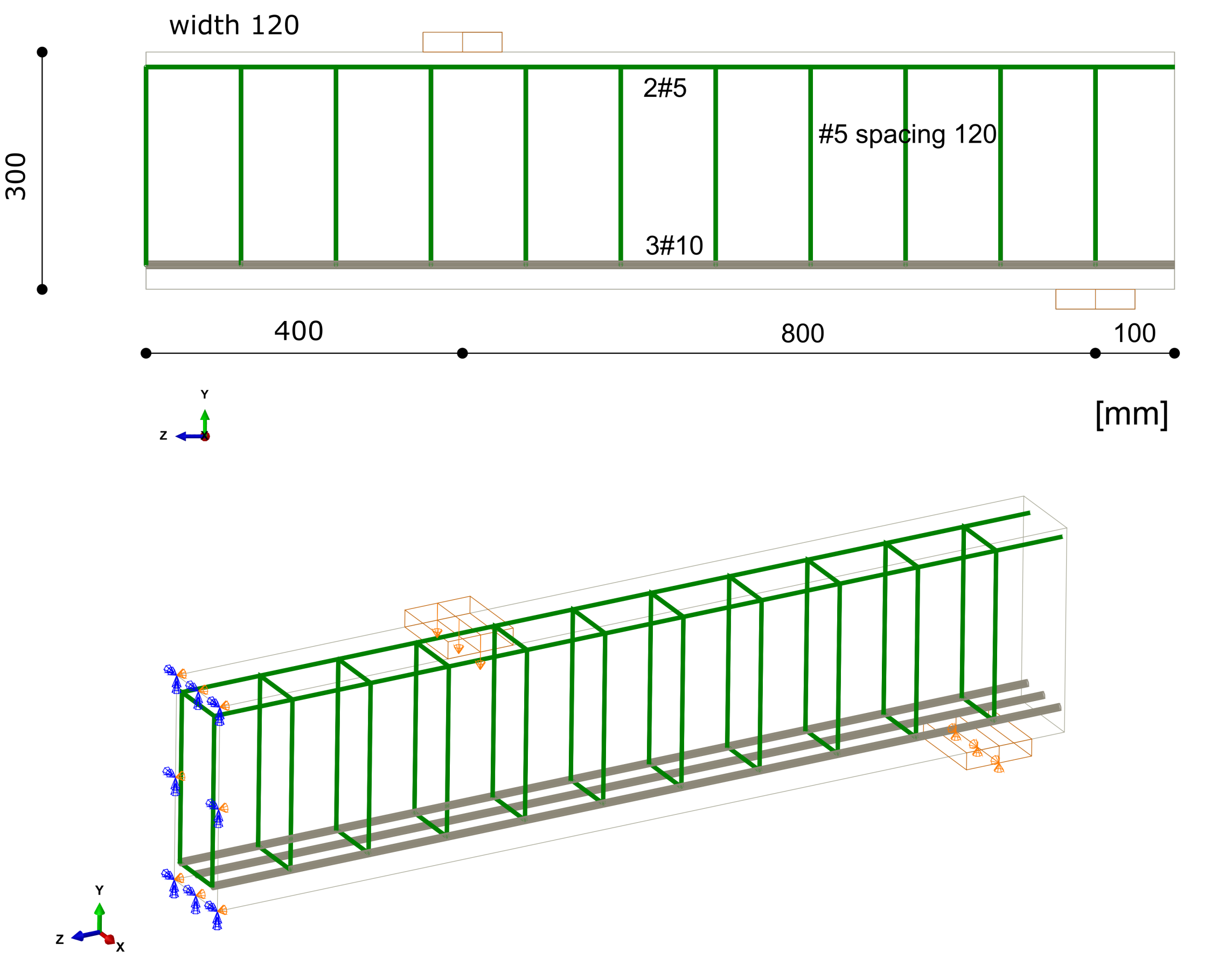
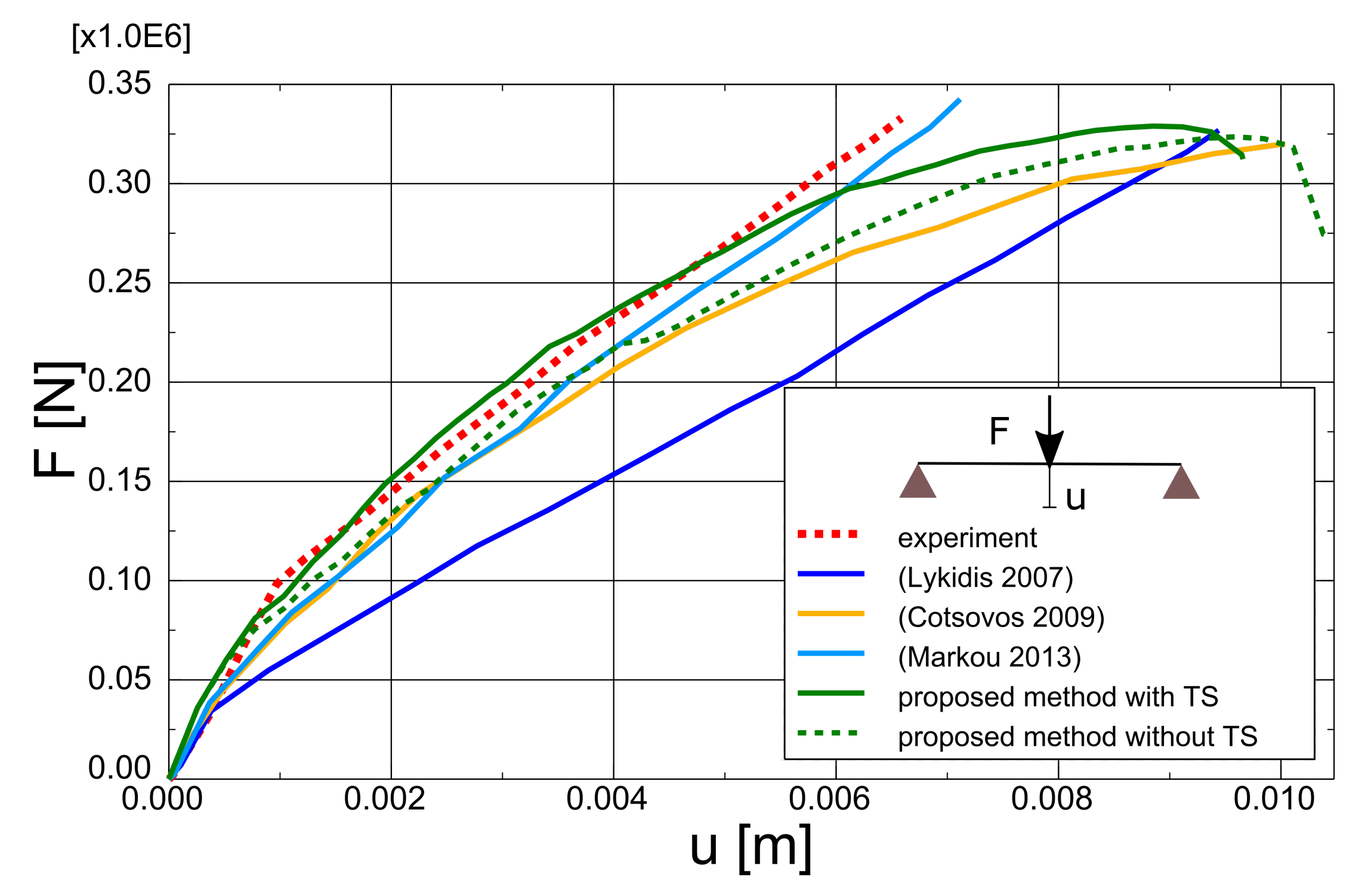
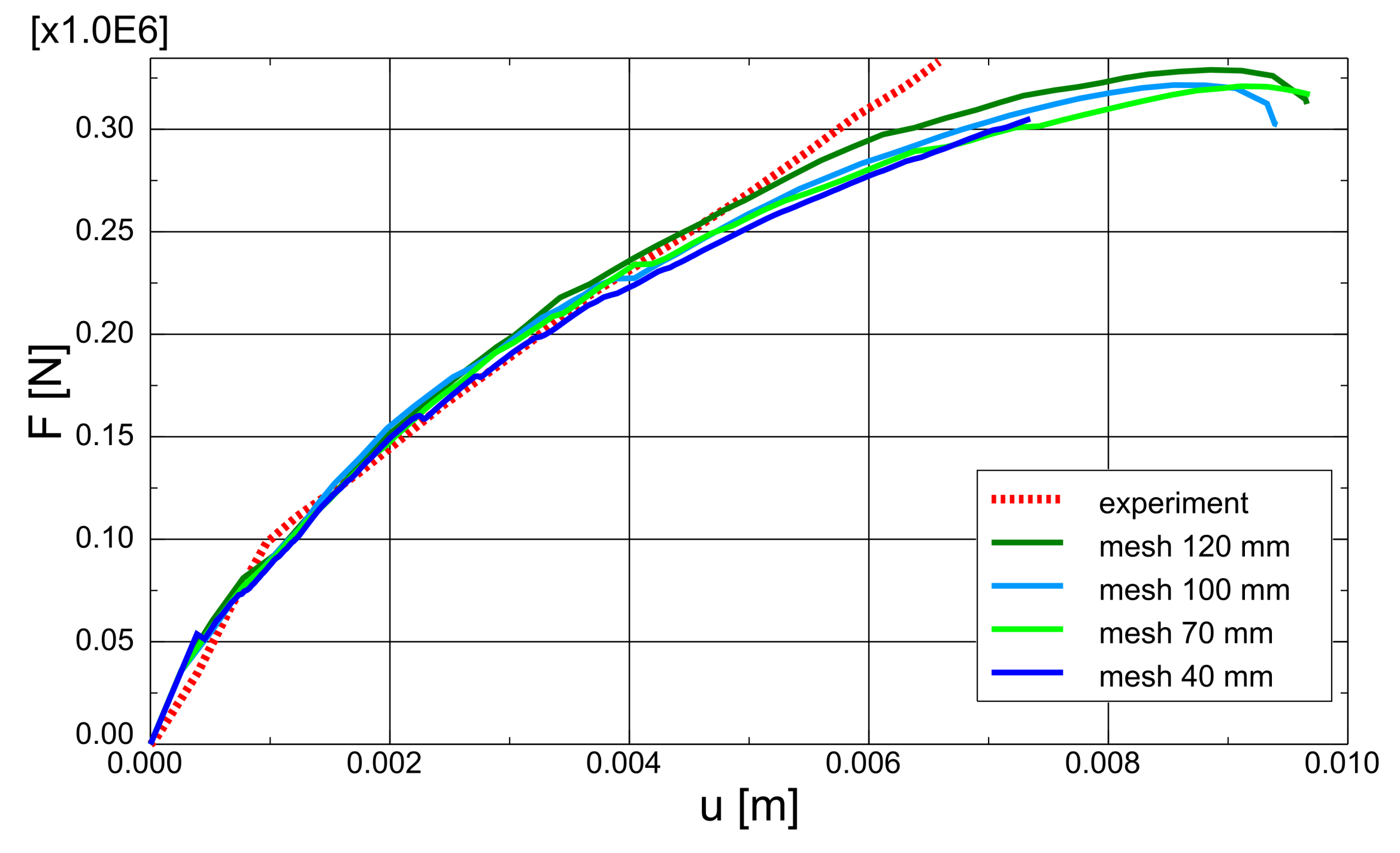
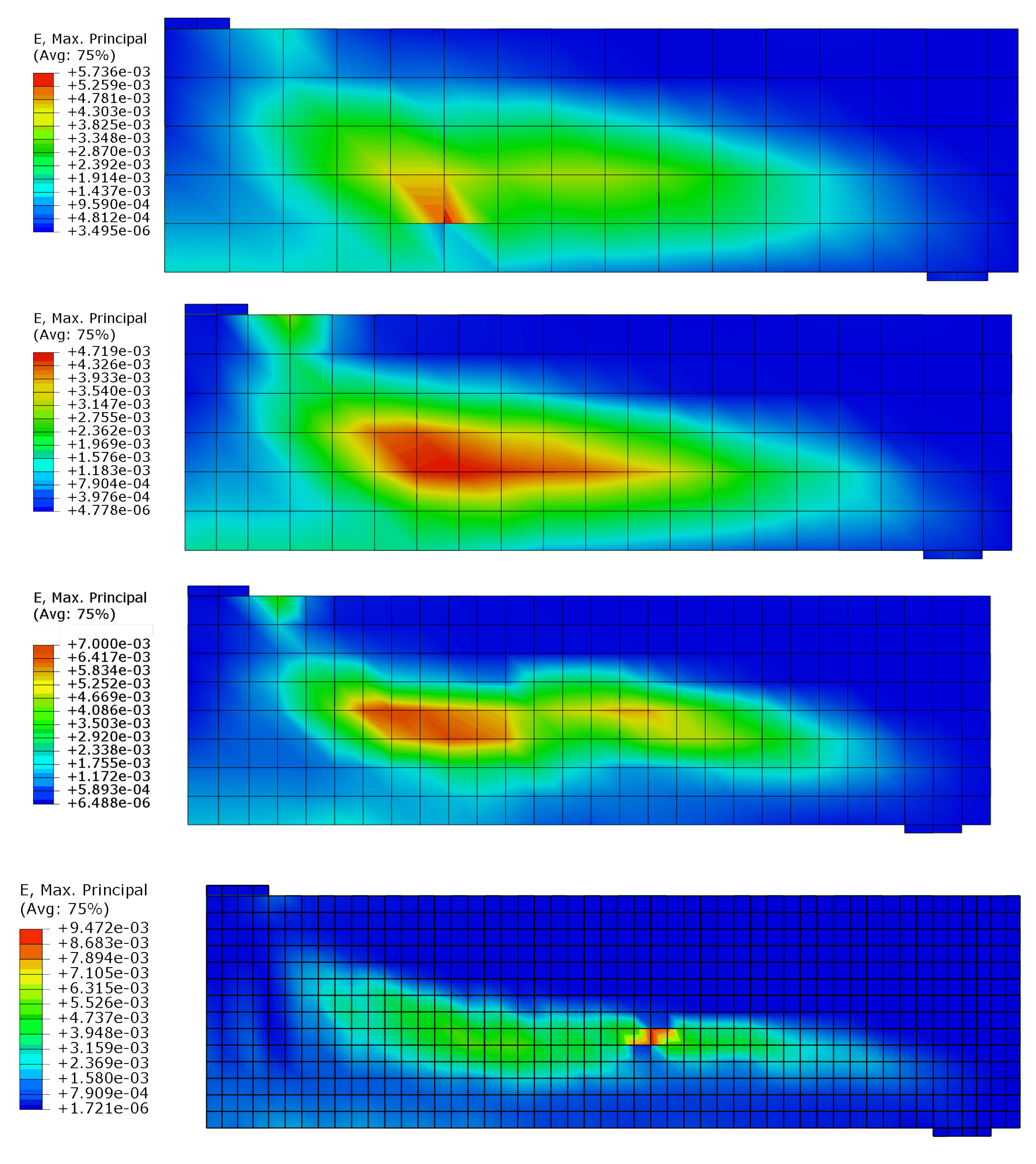
3.3. CS3 Beam without Stirrups in Shear
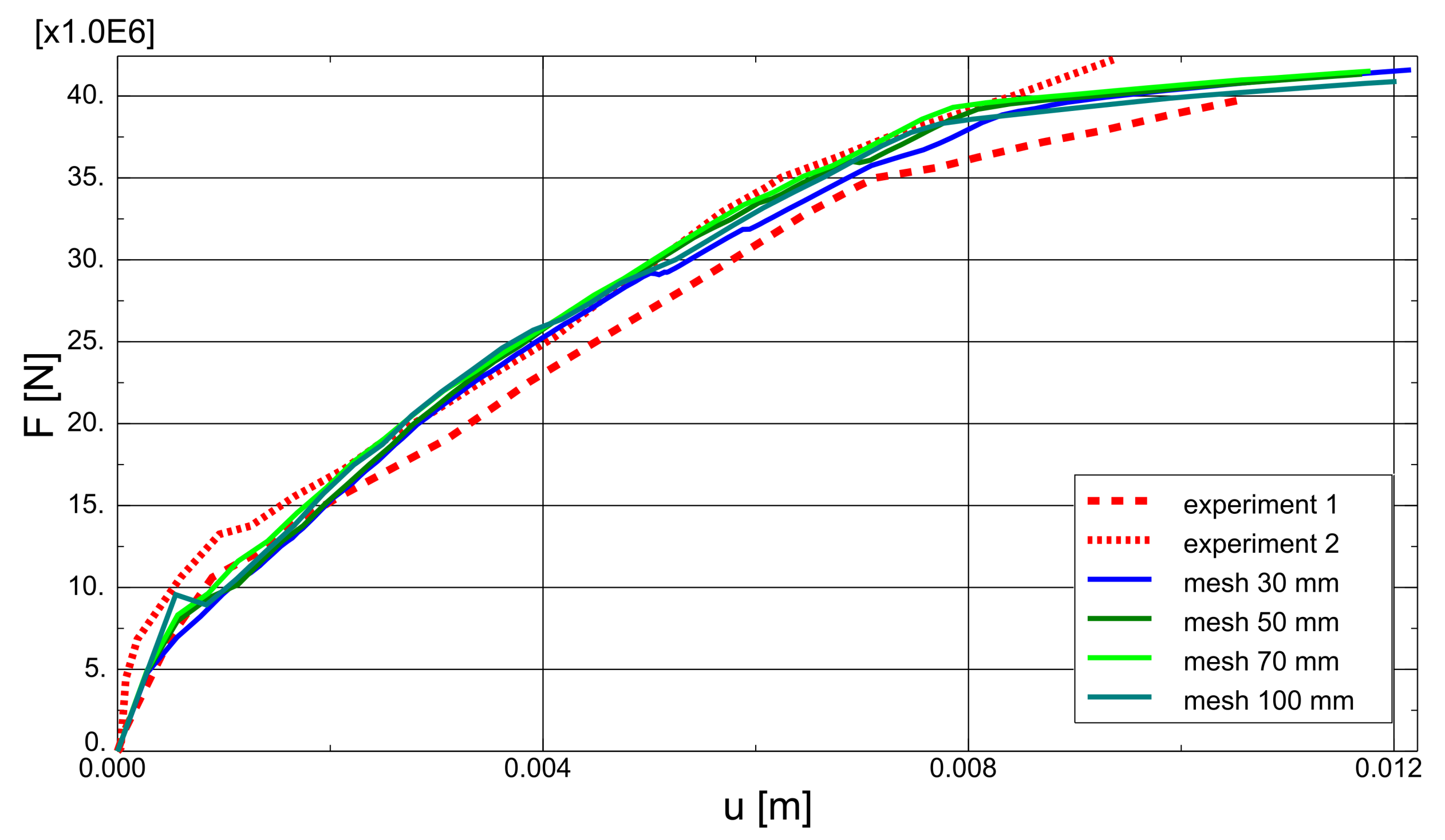
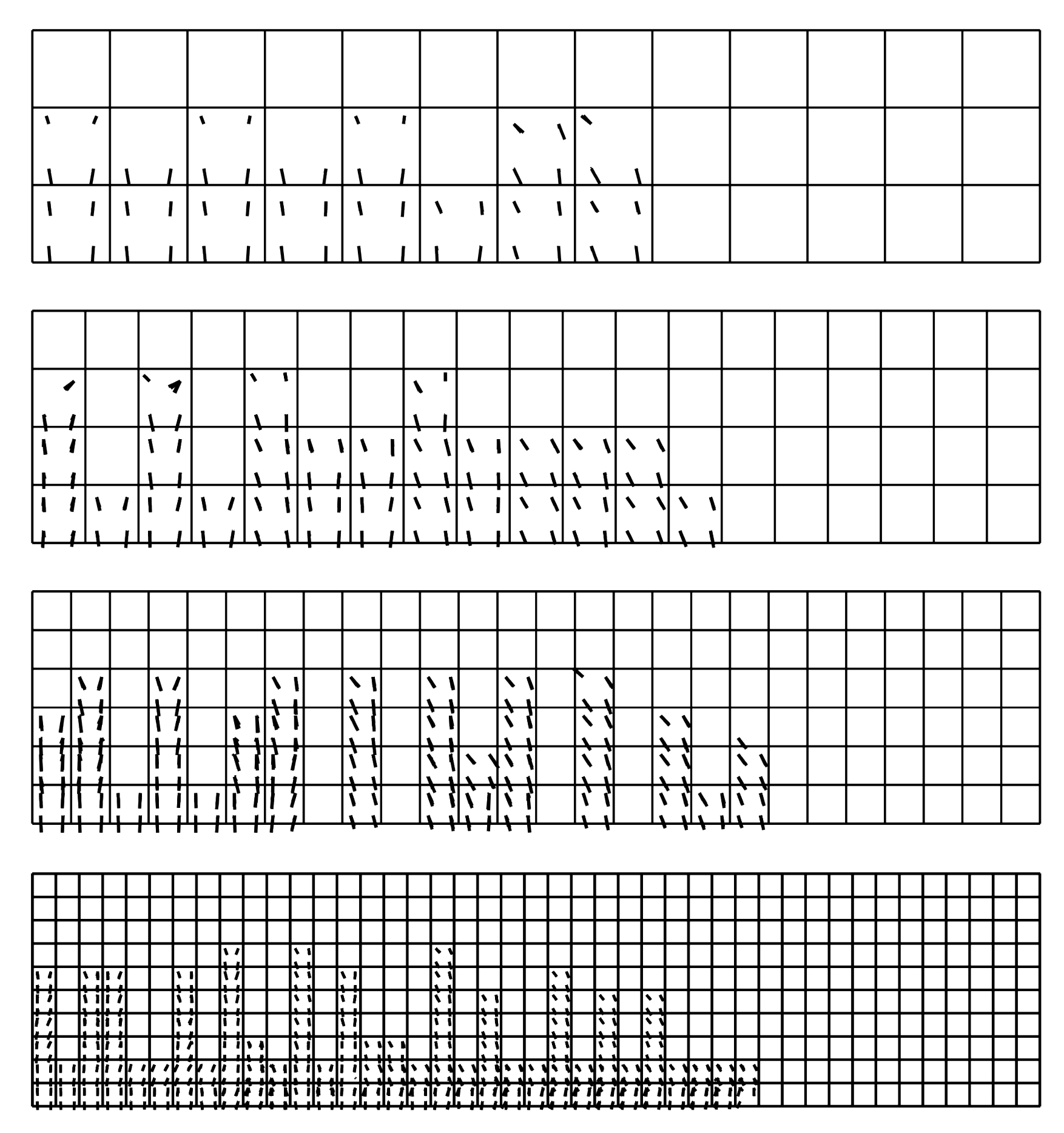
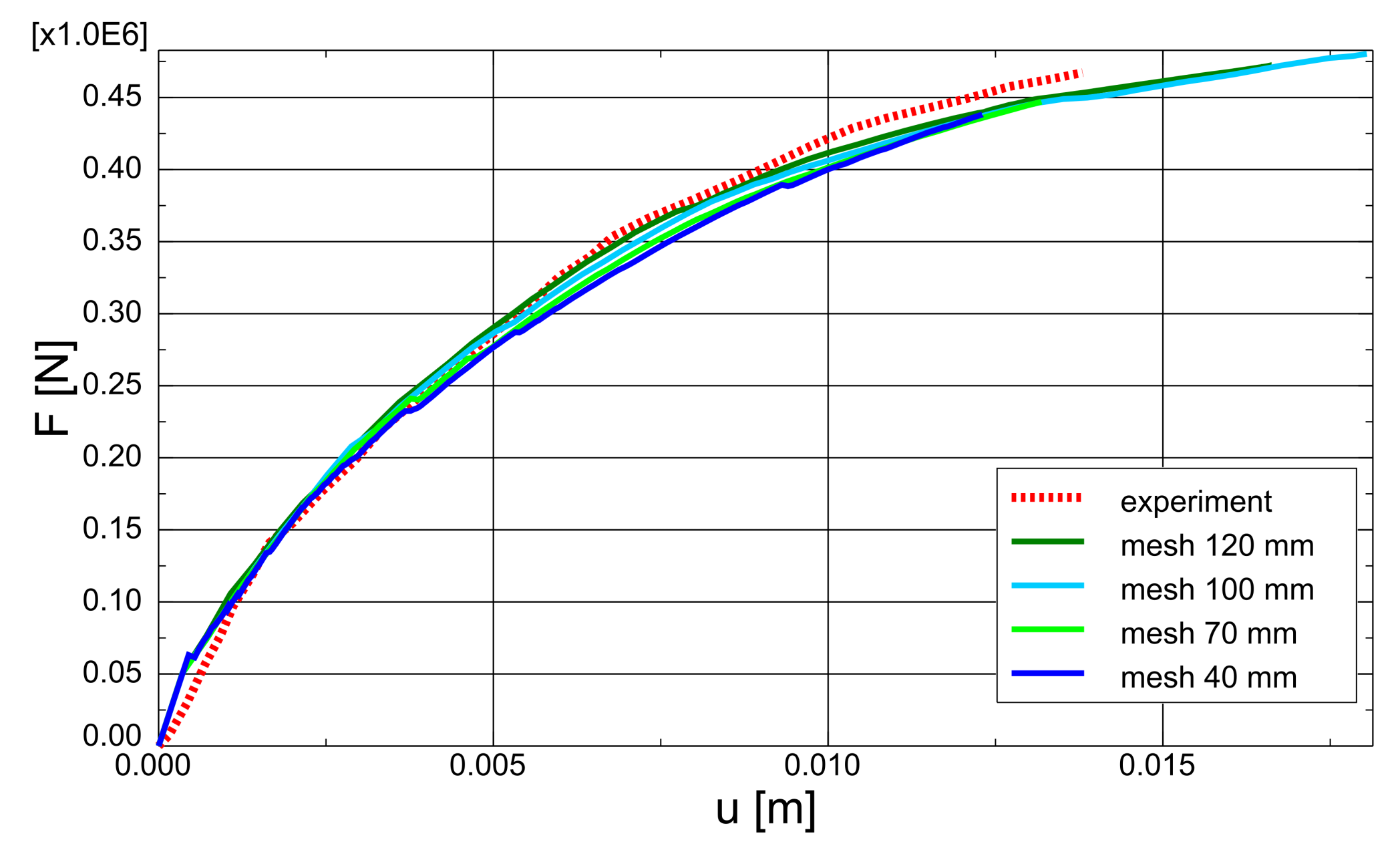
3.4. CS4 Beam with Stirrups in Shear
4. Discussion
5. Conclusions and Future Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Foster, S. (Ed.) fib Bulletin 45. Practitioners’ Guide to Finite Element Modelling of Reinforced Concrete Structures; fib Bulletins, fib; The International Federation for Structural Concrete: Lausanne, Switzerland, 2008. [Google Scholar] [CrossRef]
- Hendriks, M.A.; Roosen, M. RTD 1016–1:2020 Guidelines for Nonlinear Finite Element Analysis of Concrete Structures; Technical Report; Rijkswaterstaat Ministerie van Infrastructuur en Milieu: Copenhagen, Denmark, 2020. [Google Scholar]
- Waszczyszyn, Z.; Pabisek, E.; Pamin, J.; Radwańska, M. Nonlinear analysis of a RC cooling tower with geometrical imperfections and a technological cut-out. Eng. Struct. 2000, 22, 480–489. [Google Scholar] [CrossRef]
- Cervenka, V.; Cervenka, J.; Pukl, R. Design Resistance of Concrete Structures By Numerical Simulation. In Proceedings of the 8th International Conference AMCM 2014, Wrocław, Poland, 16–18 June 2014. [Google Scholar]
- Markou, G.; Mourlas, C.; Bark, H.; Papadrakakis, M. Simplified HYMOD non-linear simulations of a full-scale multistory retrofitted RC structure that undergoes multiple cyclic excitations—An infill RC wall retrofitting study. Eng. Struct. 2018, 176, 892–916. [Google Scholar] [CrossRef] [Green Version]
- Funari, M.F.; Spadea, S.; Fabbrocino, F.; Luciano, R. A moving interface finite element formulation to predict dynamic edge debonding in FRP-strengthened concrete beams in service conditions. Fibers 2020, 8, 42. [Google Scholar] [CrossRef]
- Ombres, L.; Verre, S. Experimental and Numerical Investigation on the Steel Reinforced Grout (SRG) Composite-to-Concrete Bond. J. Compos. Sci. 2020, 4, 182. [Google Scholar] [CrossRef]
- Valentina, G.; Poiani, M.; Clementi, F.; Pace, G.; Lenci, S. Influence of FE Modelling Approaches on Vulnerabilities of RC School Buildings and Proposal of a CFRP Retrofitting Intervention. Open Constr. Build. Technol. J. 2019, 13, 269–287. [Google Scholar] [CrossRef] [Green Version]
- Chalioris, C.E.; Kytinou, V.K.; Voutetaki, M.E.; Karayannis, C.G. Flexural damage diagnosis in reinforced concrete beams using a wireless admittance monitoring system—Tests and finite element analysis. Sensors 2021, 21, 679. [Google Scholar] [CrossRef]
- Kytinou, V.K.; Chalioris, C.E.; Karayannis, C.G.; Elenas, A. Effect of steel fibers on the hysteretic performance of concrete beams with steel reinforcement-tests and analysis. Materials 2020, 13, 2923. [Google Scholar] [CrossRef]
- Kotsovos, M.D.; Pavlovic, M.N.; Cotsovos, D.M. Characteristic features of concrete behaviour: Implications for the development of an engineering finite-element tool. Comput. Concr. 2008, 5, 243–260. [Google Scholar] [CrossRef]
- Chen, W.F.; Saleeb, A.F. Constitutive Equations for Engineering Materials; Elsevier Science Limited: Amsterdam, The Netherlands, 1994; p. 604. [Google Scholar]
- Vermeer, P.A.; De Borst, R. Non-Associated Plasticity for Soils, Concrete and Rock. HERON 1984, 29, 1984. [Google Scholar]
- Stolarski, A.; Cichorski, W.; Szcześniak, A. Non-classical model of dynamic behavior of concrete. Appl. Sci. 2019, 9, 2590. [Google Scholar] [CrossRef] [Green Version]
- Wosatko, A.; Winnicki, A.; Polak, M.A.; Pamin, J. Role of dilatancy angle in plasticity-based models of concrete. Arch. Civ. Mech. Eng. 2019, 19, 1268–1283. [Google Scholar] [CrossRef]
- Spiliopoulos, K.V.; Lykidis, G.C. An efficient three-dimensional solid finite element dynamic analysis of reinforced concrete structures. Earthq. Eng. Struct. Dyn. 2006, 35, 137–157. [Google Scholar] [CrossRef]
- Kotsovos, M.D.; Pavlovic, M.N. Structural Concrete: Finite-Element Analysis and Design; Thomas Telford Publishing: London, UK, 1995; p. 1. [Google Scholar]
- Markou, G.; Papadrakakis, M. Computationally efficient 3D finite element modeling of RC structures. Comput. Concr. 2013, 12, 443–498. [Google Scholar] [CrossRef]
- Markou, G. Numerical Investigation of a Full-Scale Rc Bridge Through 3D Detailed Nonlinear Limit-State Simulations. In Proceedings of the SEECCM III 3rd South-East European Conference on Computational Mechanics—An ECCOMAS and IACM Special Interest Conference, Kos Island, Greece, 12–14 June 2013; pp. 492–519. [Google Scholar] [CrossRef]
- Mourlas, C.; Papadrakakis, M.; Markou, G. A computationally efficient model for the cyclic behavior of reinforced concrete structural members. Eng. Struct. 2017, 141, 97–125. [Google Scholar] [CrossRef]
- Mourlas, C.; Markou, G.; Papadrakakis, M. Accurate and computationally efficient nonlinear static and dynamic analysis of reinforced concrete structures considering damage factors. Eng. Struct. 2019, 178, 258–285. [Google Scholar] [CrossRef]
- Engen, M.; Hendriks, M.A.; Øverli, J.A.; Åldstedt, E. Non-linear finite element analyses applicable for the design of large reinforced concrete structures. Eur. J. Environ. Civ. Eng. 2019, 23, 1381–1403. [Google Scholar] [CrossRef]
- Lewiński, P.M.; Wiȩch, P.P. Finite element model and test results for punching shear failure of RC slabs. Arch. Civ. Mech. Eng. 2020, 20, 36. [Google Scholar] [CrossRef] [Green Version]
- Häußler-Combe, U. Computational Methods for Reinforced Concrete Structures; John Wiley & Sons: Weinheim, Germany, 2014; p. 357. [Google Scholar] [CrossRef]
- Clark, L.A.; Speirs, D.M. Tension Stiffening in Reniforced Concrete Beams and Slabs Under Short-Term Load; Technical Report; Cement and Concrete Association: Buckinghamshire, UK, 1978. [Google Scholar]
- Jakubovskis, R.; Kaklauskas, G. Bond-stress and bar-strain profiles in RC tension members modelled via finite elements. Eng. Struct. 2019, 194, 138–146. [Google Scholar] [CrossRef]
- Dassault Systèmes. Manual Abaqus 6.14; Dassault Systèmes: Velizy-Villacoublay, France, 2014. [Google Scholar]
- Kupfer, H.B.; Gerstle, K.H. Behavior of Concrete under Biaxial Stresses. J. Eng. Mech. Div. 1973, 99, 853–866. [Google Scholar] [CrossRef]
- Bathe, K.J.; Walczak, J.; Welch, A.; Mistry, N. Nonlinear analysis of concrete structures. Comput. Struct. 1989, 32, 563–590. [Google Scholar] [CrossRef] [Green Version]
- EN 1992-1-1 Eurocode 2: Design of Concrete Structures. Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2005.
- fib Model Code for Concrete Structures 2010; Ernst&Sohn: Lausanne, Switzerland, 2013.
- Chernin, L.; Vilnay, M.; Cotsovos, D.M. Extended P-I diagram method. Eng. Struct. 2020, 224, 111217. [Google Scholar] [CrossRef]
- Kupfer, H.; Hilsdorf, H.K.; Rusch, H. Behaviour of Concrete under Biaxial Stresses. Am. Concr. Inst. J. 1969, 99, 656–666. [Google Scholar]
- Ottosen, N.S.; Ristinmaa, M. The Mechanics of Constitutive Modeling; Elsevier: Amsterdam, The Netherlands, 2005; p. 745. [Google Scholar] [CrossRef]
- Ottosen, N.S. A Failure Criterion for Concrete. J. Eng. Mech. Div. 1977, 103, 527–535. [Google Scholar] [CrossRef]
- Podgórski, J. Limit State Condition and the Dissipation Function for Isotropic Materials. Arch. Mech. 1983, 36, 323–342. [Google Scholar]
- Podgórski, J. General Failure Criterion for Isotropic Media. J. Eng. Mech. 1985, 111, 188–201. [Google Scholar] [CrossRef]
- Lewiński, P.M. Nieliniowa analiza osiowo-symetrycznych żelbetowych konstrukcji powłokowych i ich interakcja z podłożem. Pr. Nauk. Politech. Warsz. 1996, 131, 73–115. [Google Scholar]
- Podgórski, J. Criterion fo Angle Prediction for the Crack in Materials with Random Structure. Mech. Control 2011, 30, 229–233. Available online: https://journals.agh.edu.pl/mech/article/view/1587 (accessed on 3 February 2021).
- William, K.; Warnke, E. Constitutive model for the triaxial behaviour of concrete. Proc. Int. Assoc. Bridge Struct. Eng. ISMES Bergamo 1975, 19, 174. [Google Scholar]
- Lewiński, P.M.; Zygowska, M. Comparative study of two elasto-plastic work-hardening spatial models for concrete. MATEC Web Conf. 2018, 196, 01019. [Google Scholar] [CrossRef]
- Rashid, Y. Ultimate strength analysis of prestressed concrete pressure vessels. Nucl. Eng. Des. 1968, 7, 334–344. [Google Scholar] [CrossRef]
- Vidosa, F.G. Three-Dimensional Finite Element Analysis of Structural Concrete under Static Loading. Ph.D. Thesis, Imperial College London, London, UK, 1989. [Google Scholar]
- Kotsovos, M.D.; Spiliopoulos, K.V. Modelling of crack closure for finite-element analysis of structural concrete. Comput. Struct. 1998, 69, 383–398. [Google Scholar] [CrossRef]
- Gonzalez-Vidosa, F.; Kotsovos, M.D.; Pavlovic, M.N. On the numerical instability of the smeared-crack approach in the non-linear modelling of concrete structures. Commun. Appl. Numer. Methods 1988, 4, 799–806. [Google Scholar] [CrossRef]
- De Borst, R.; Nauta, P. Non-othogonal cracks in a smeared finite element model. Eng. Comput. 1985, 2, 35–46. [Google Scholar] [CrossRef] [Green Version]
- Wójcicki, P.; Winnicki, A. Numeryczny test rozcia̧gania ze ścinaniem według Willama dla modelu plastycznego betonu. Czas. Tech. Bud. 2011, 108, 193–210. [Google Scholar]
- ANSYS Inc. ANSYS Mechanical APDL Element Reference; ANSYS Inc.: Canonsburg, PA, USA, 2012. [Google Scholar]
- Červenka, J.; Červenka, V.; Laserna, S. On crack band model in finite element analysis of concrete fracture in engineering practice. Eng. Fract. Mech. 2018, 197, 27–47. [Google Scholar] [CrossRef]
- Truty, A. Elastıc-Plastıc Damage Model for Concrete; Technical Report; Zace Services Ltd.: Prverenges, Switzerland, 2016. [Google Scholar]
- Bernardi, P.; Cerioni, R.; Michelini, E.; Sirico, A. Numerical modeling of the cracking behavior of RC and SFRC shear-critical beams. Eng. Fract. Mech. 2016, 167, 151–166. [Google Scholar] [CrossRef]
- Kaklauskas, G.; Tamulenas, V.; Bado, M.F.; Bacinskas, D. Shrinkage-free tension stiffening law for various concrete grades. Constr. Build. Mater. 2018, 189, 736–744. [Google Scholar] [CrossRef]
- Lazzari, B.M.; Filho, A.C.; Lazzari, P.M.; Pacheco, A.R. Using element-embedded rebar model in ANSYS for the study of reinforced and prestressed concrete structures. Comput. Concr. 2017, 19, 347–356. [Google Scholar] [CrossRef]
- Nagtegaal, J.; Parks, D.; Rice, J. On numerically accurate finite element solutions in the fully plastic range. Comput. Methods Appl. Mech. Eng. 1974, 4, 153–177. [Google Scholar] [CrossRef]
- Markou, G.; Roeloffze, W. Finite element modelling of plain and reinforced concrete specimens with the Kotsovos and Pavlovic material model, smeared crack approach and fine meshes. Int. J. Damage Mech. 2021. [Google Scholar] [CrossRef]
- Matthies, H.; Strang, G. The solution of nonlinear finite element equations. Int. J. Numer. Methods Eng. 1979, 14, 1613–1626. [Google Scholar] [CrossRef]
- Bathe, K.J.; Cimento, A.P. Some practical procedures for the solution of nonlinear finite element equations. Comput. Methods Appl. Mech. Eng. 1980, 22, 59–85. [Google Scholar] [CrossRef] [Green Version]
- Kwasniewski, L.; Bojanowski, C. Principles of verification and validation. J. Struct. Fire Eng. 2015, 6, 29–40. [Google Scholar] [CrossRef]
- Roache, P. Verification and Validation in Computational Science and Engineering; Hermosa Publishers: Albuquerque, NW, USA, 1998. [Google Scholar]
- Dudziak, S. Non-Linear Analysis of Reinforced Concrete Shell Structures with the Finite Element Method Taking into Account the Tension Stiffening Effect. Ph.D. Thesis, Instytut Techniki Budowlanej (ITB), Warszawa, Poland, 2019. [Google Scholar]
- Willam, K.; Pramono, E.; Sture, S. Fundamental Issues of Smeared Crack Models BT—Fracture of Concrete and Rock; Springer: New York, NY, USA, 1989; pp. 142–157. [Google Scholar]
- Wosatko, A.; Szczecina, M.; Winnicki, A. Selected Concrete Models Studied Using Willam’s Test. Materials 2020, 13, 4756. [Google Scholar] [CrossRef] [PubMed]
- Álvares, M.S. Estudo de um Modelo de Dano Para o Concreto: Formulação, Identificação Paramétrica e Aplicação com Emprego do Método dos Elementos Finitos. Ph.D. Thesis, Universidade de Sao Paulo, Sao Paulo, Brazil, 1993. [Google Scholar]
- Gomes, W.J.D.S. Reliability analysis of reinforced concrete beams using finite element models. In Proceedings of the XXXVIII Iberian Latin American Congress on Computational Methods in Engineering, Santa Catarina, Brazil, 5–8 November 2017. [Google Scholar] [CrossRef]
- Mazars, J. A description of micro- and macroscale damage of concrete structures. Eng. Fract. Mech. 1986, 25, 729–737. [Google Scholar] [CrossRef]
- Bresler, B.; Scordelis, A. Shear strength of reinforced concrete beams. ACI Struct. J. 1963, 60, 51–74. [Google Scholar]
- Cotsovos, D.M.; Zeris, C.A.; Abbas, A.A. Finite Element Modelling of Structural Concrete. In Proceedings of the 2nd International Conference on Computational Methods in Structural Dynamics & Earthquake Engineering 2009, Rodos, Greece, 22–24 June 2009. [Google Scholar]
- Engen, M.; Hendriks, M.A.N.; Øverli, J.A.; Åldstedt, E. Solution strategy for non-linear finite element analyses of large reinforced concrete structures. Struct. Concr. 2015, 16, 389–397. [Google Scholar] [CrossRef]
- Vecchio, F.J.; Shim, W. Experimental and analytical reexamination of classic concrete beam tests. J. Struct. Eng. 2004, 130, 460–469. [Google Scholar] [CrossRef] [Green Version]
- Lykidis, G.C. Static and Dynamic Analysis of Reinforced Concrete Structures with 3D Finite Elements and the Smeared Crack Approach. Ph.D. Thesis, National Technical University of Athens, Athens, Greece, 2007. [Google Scholar]
- Bazant, Z.P.; Oh, B.H. Crack band theory for fracture of concrete. Matériaux Constr. 1983, 16, 155–177. [Google Scholar] [CrossRef] [Green Version]
- Wosatko, A.; Genikomsou, A.; Pamin, J.; Polak, M.A.; Winnicki, A. Examination of two regularized damage-plasticity models for concrete with regard to crack closing. Eng. Fract. Mech. 2018, 194, 190–211. [Google Scholar] [CrossRef]
- Lykidis, G.C.; Spiliopoulos, K.V. 3D solid finite-element analysis of cyclically loaded RC structures allowing embedded reinforcement slippage. J. Struct. Eng. 2008, 134, 629–638. [Google Scholar] [CrossRef]
- Dhondt, G. CalculiX CrunchiX USER’S MANUAL Version 2.17. Technical Report. Groebenzell, Germany, 2020. [Google Scholar]









| No | Parameter | CS1 | CS2 | CS3 | CS4 |
|---|---|---|---|---|---|
| Concrete model | |||||
| 1 | (GPa) | 28 | 29 | 28 | 28 |
| 2 | 0.2 | 0.2 | 0.2 | 0.2 | |
| 3 | [1] | 0.2 | 0.2 | 0.2 | 0.2 |
| 4 | [1] | −0.08 | −0.05 | −0.05 | −0.005 |
| 5 | (MPa) | 24.0 | 27.0 | 22.5 | 24.1 |
| 6 | (MPa) | 2.0 | 3.2 | 2.2 | 2.5 |
| Tension stiffening model | |||||
| 7 | (GPa) | - | 196 | 200 | 200 |
| 8 | (GPa) | - | 10 | 10 | 10 |
| 9 | (MPa) | - | 500 | 555 | 555 |
| 10 | [1] | - | 1.1 | 1.1 | 1.1 |
| 11 | [1] | - | 0.4 | 0.4 | 0.4 |
| 12 | [1] | - | 0.017 | 0.035 | 0.035 |
| CS | [kN] | [kN] | [1] | [mm] | [mm] | [1] |
|---|---|---|---|---|---|---|
| 2 | 41.0 | 40.9 | 0.998 | 10.0 | 12.0 | 1.200 |
| 3 | 330.0 | 329.0 | 0.988 | 6.6 | 8.9 | 1.348 |
| 4 | 467.3 | 471.2 | 1.008 | 13.8 | 16.6 | 1.203 |
| mean | 0.998 | 1.250 | ||||
| CoV | 0.008 | 0.057 |
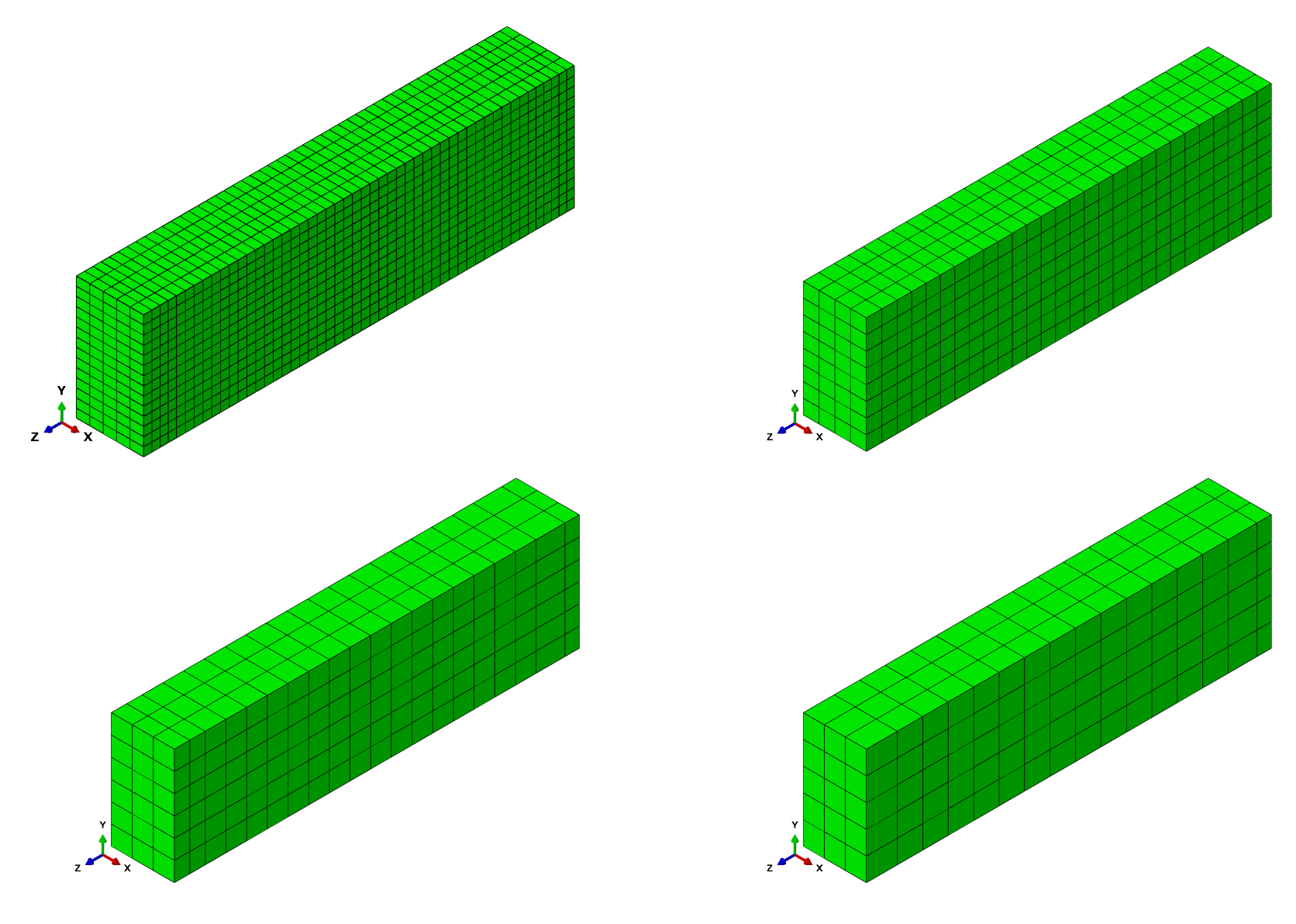
| Mesh | CS2 | CS3 | CS4 | |
|---|---|---|---|---|
| dimensions of model | ||||
| variables | coarse | 690 | 1572 | 1980 |
| medium | 1536 | 2160 | 2616 | |
| fine | 2451 | 4443 | 5085 | |
| very fine | 8781 | 14,730 | 16,818 | |
| equations | coarse | 420 | 1320 | 1320 |
| medium | 963 | 1848 | 1848 | |
| fine | 1755 | 4005 | 4005 | |
| very fine | 7440 | 13,950 | 13,950 | |
| calculation effort | ||||
| increments | coarse | 50 | 58 | 66 |
| medium | 50 | 57 | 55 | |
| fine | 70 | 82 | 87 | |
| very fine | 145 | 216 | 262 | |
| iterations | coarse | 129 | 676 | 691 |
| medium | 231 | 709 | 450 | |
| fine | 443 | 930 | 1046 | |
| very fine | 1389 | 2496 | 3214 | |
| calculation time [s] | coarse | 14 | 107 | 114 |
| medium | 28 | 204 | 57 | |
| fine | 70 | 361 | 276 | |
| very fine | 770 | 1660 | 2130 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dudziak, S. Numerically Efficient Three-Dimensional Model for Non-Linear Finite Element Analysis of Reinforced Concrete Structures. Materials 2021, 14, 1578. https://doi.org/10.3390/ma14071578
Dudziak S. Numerically Efficient Three-Dimensional Model for Non-Linear Finite Element Analysis of Reinforced Concrete Structures. Materials. 2021; 14(7):1578. https://doi.org/10.3390/ma14071578
Chicago/Turabian StyleDudziak, Sławomir. 2021. "Numerically Efficient Three-Dimensional Model for Non-Linear Finite Element Analysis of Reinforced Concrete Structures" Materials 14, no. 7: 1578. https://doi.org/10.3390/ma14071578






