Time-Dependent Reliability Analysis of Reinforced Concrete Beams Subjected to Uniform and Pitting Corrosion and Brittle Fracture
Abstract
:1. Introduction
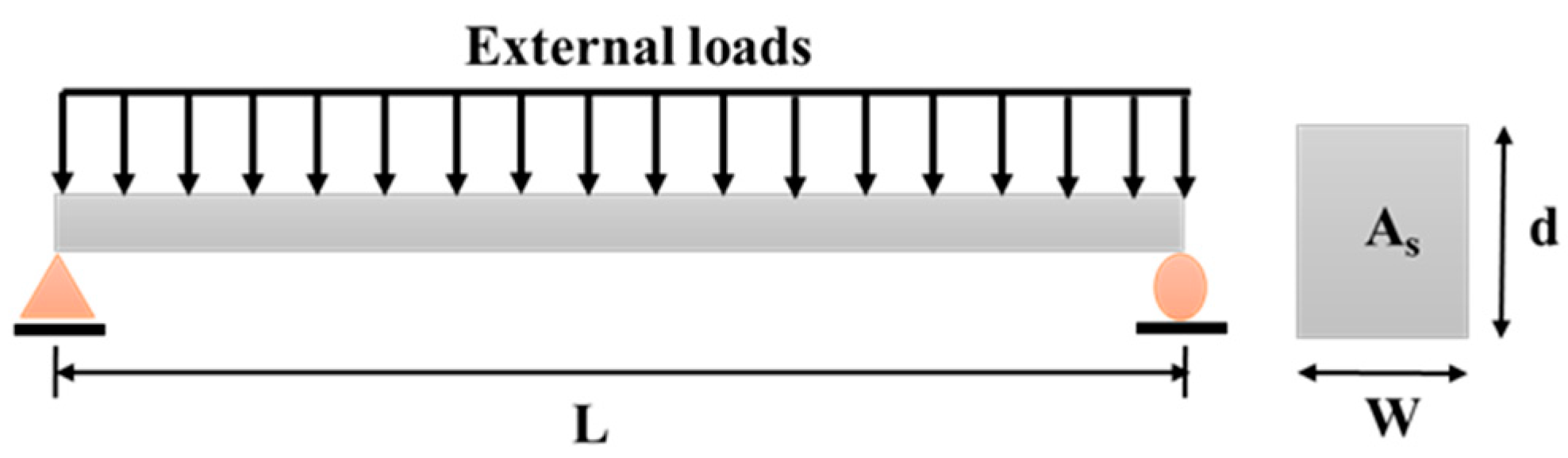
2. Mathematical Formulation of the Corroded Reinforced Concrete Beam
- (1)
- First, the time to corrosion initiation starts with corrosion activation on the steel bars, in which initiation begins when the received corrosive ions contact the bar’s surface.
- (2)
- Second, the time of the corrosion propagation; in this period, the corrosion defects/cracks are propagated and the cross-sectional areas of the reinforcing steel bars decreases, leading to bond strength reduction and subsequent structural performance degradation.
2.1. Limit State Function Formulation
2.2. Uniform Corrosion Model
2.3. Pitting Corrosion Model
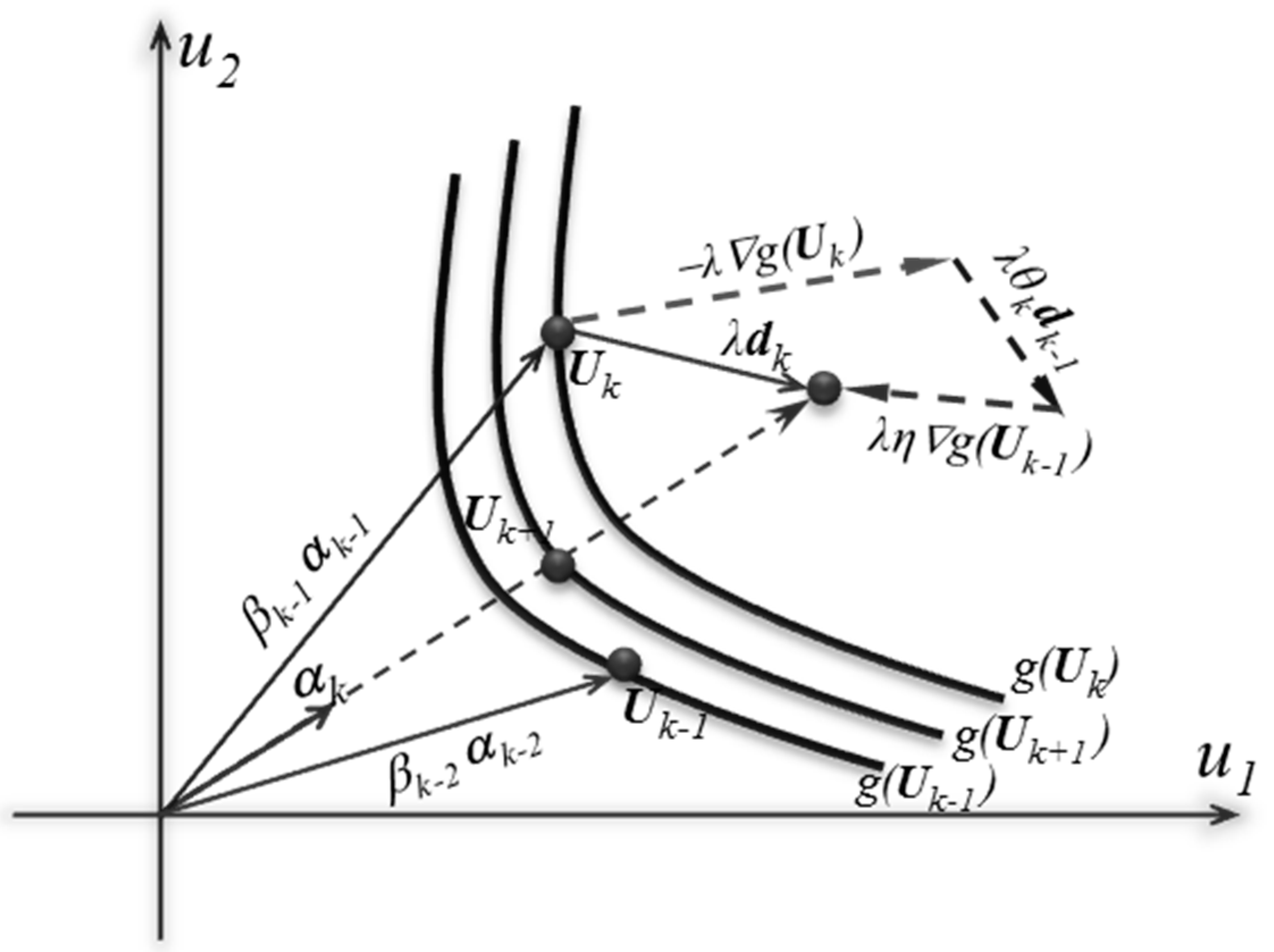
3. Proposed Reliability Approach
- 1.
- Establish the performance function and specify the basic random variables of the problem.
- 2.
- Set k = 0, d0 = 0 and and specify the convergence limit criteria, ε ( was adopted in this work).
- 3.
- Transfer the basic random variables from X space to U space.
- 4.
- Compute the values of and .
- 5.
- Determine at k = 0.
- 6.
- Compute the conjugate factors as and .
- 7.
- Compute using the three-term formulation as .
- 8.
- Compute the normalized conjugate sensitivity vector, i.e., .
- 9.
- Determine the results for the new iterations as and .
- 10.
- If , then k = k + 1 and go to Step 3; else, stop and print , , and .
4. Probabilistic Form of the Basic Random Variables for the Corroded RC Beam
5. Application, Results and Discussion
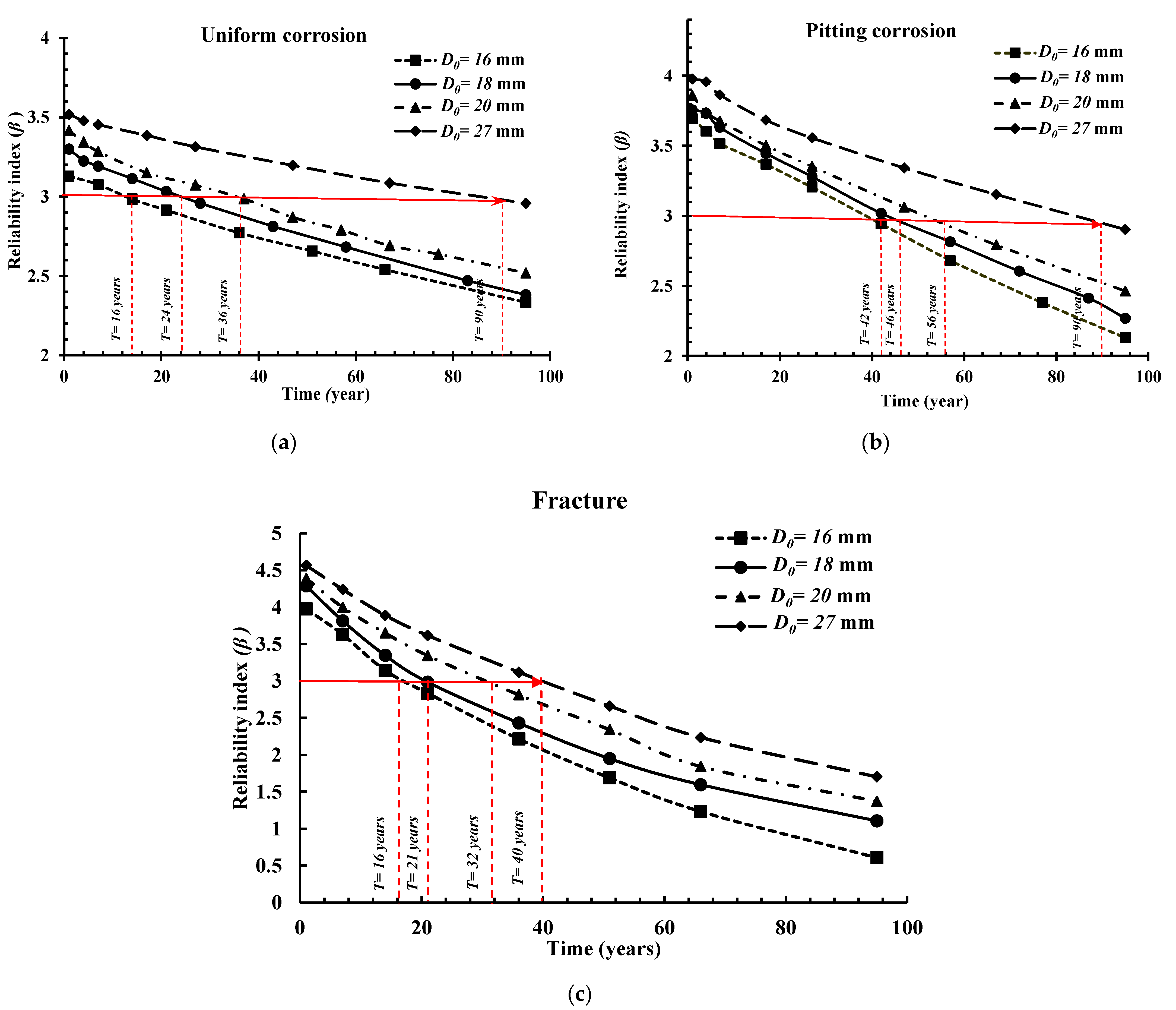
5.1. Effect of the Steel Bars Diameters (D0, mm)
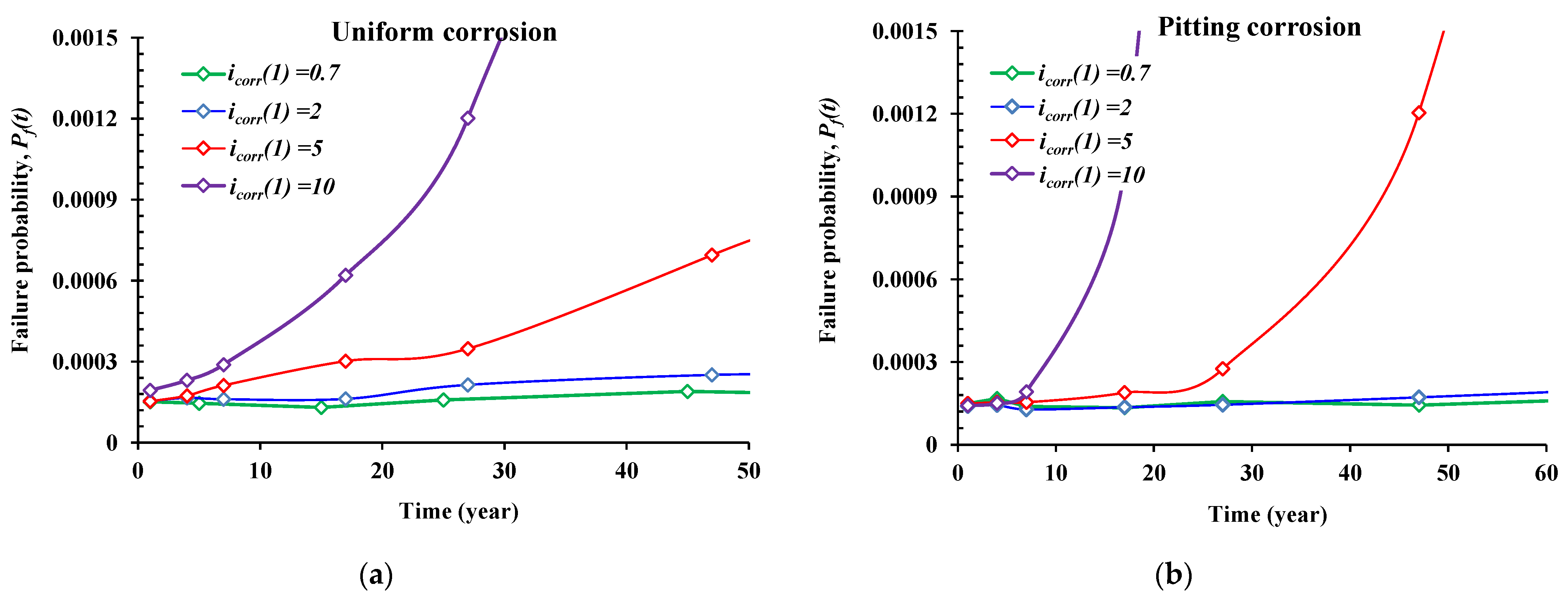
5.2. Effect of the Corrosion Imitation Time (icorr(1), μA/cm2)
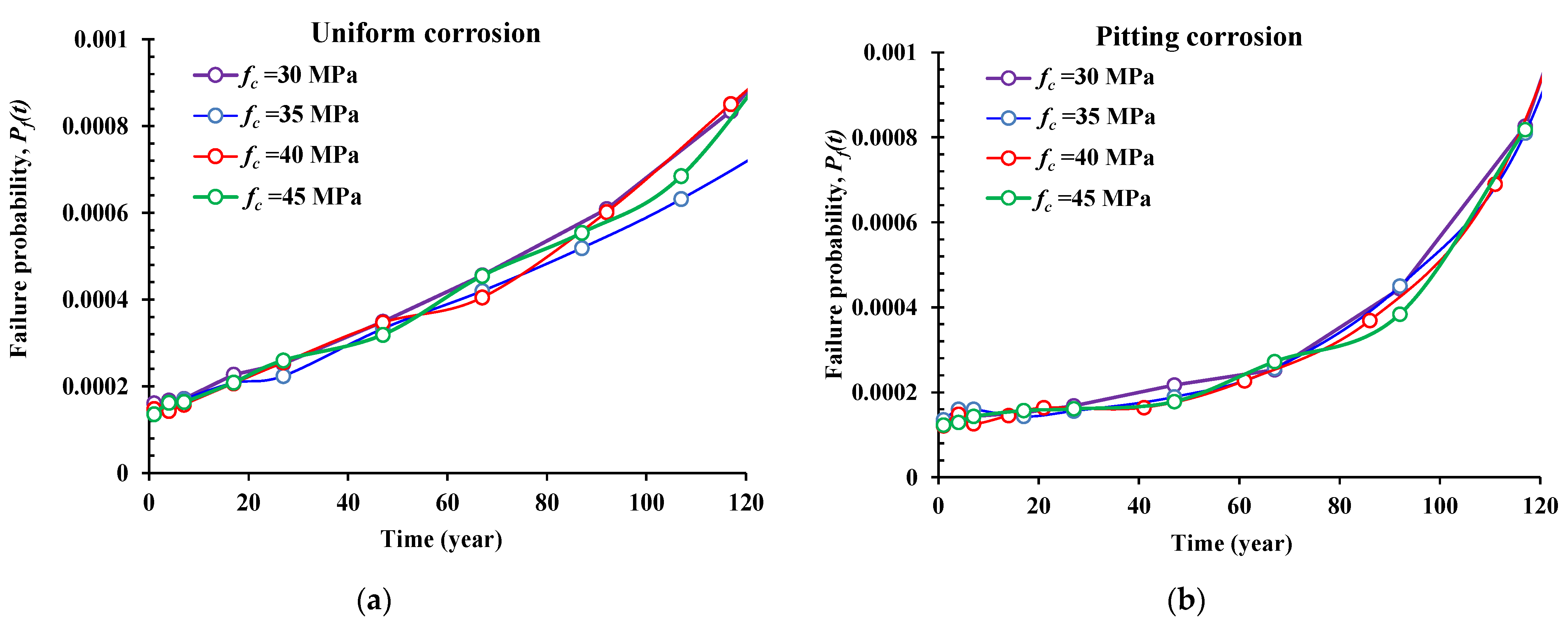
5.3. Effect of the Concrete Compressive Resistance (fc, MPa)
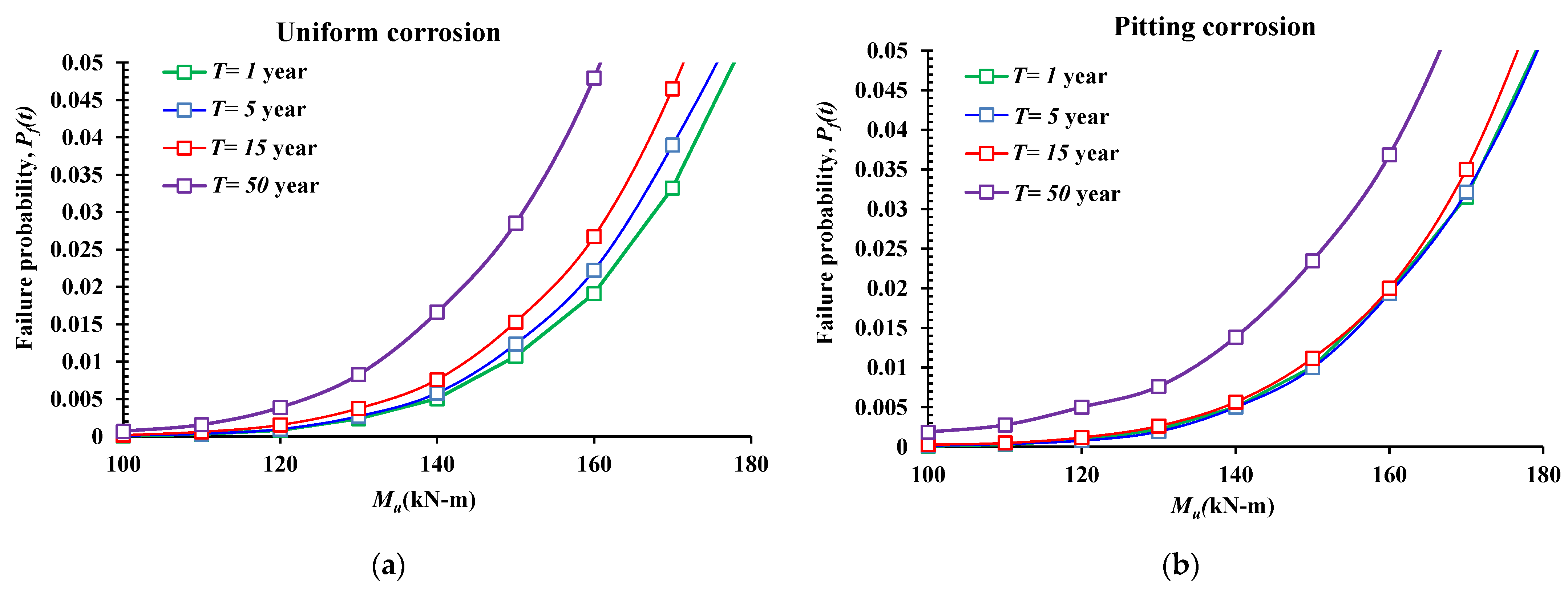
5.4. Effect of the Applied Moment (Mu, KN-m)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Javadian, A.; Smith, I.F.C.; Hebel, D.E. Application of sustainable bamboo-based composite reinforcement in structural-concrete beams: Design and evaluation. Materials 2020, 13, 696. [Google Scholar] [CrossRef] [Green Version]
- Mai, S.H.; Seghier, M.E.A.B.; Nguyen, P.L.; Jafari-Asl, J.; Thai, D.-K. A hybrid model for predicting the axial compression capacity of square concrete-filled steel tubular columns. Eng. Comput. 2020, 1–18. [Google Scholar] [CrossRef]
- Bai, C.; Nguyen, H.; Asteris, P.G.; Nguyen-Thoi, T.; Zhou, J. A refreshing view of soft computing models for predicting the deflection of reinforced concrete beams. Appl. Soft Comput. 2020, 97, 106831. [Google Scholar] [CrossRef]
- Sajedi, S.; Huang, Q. Probabilistic prediction model for average bond strength at steel–concrete interface considering corrosion effect. Eng. Struct. 2015, 99, 120–131. [Google Scholar] [CrossRef]
- Seghier, M.E.A.B.; Ouaer, H.; Ghriga, M.A.; Menad, N.A.; Thai, D.-K. Hybrid soft computational approaches for modeling the maximum ultimate bond strength between the corroded steel reinforcement and surrounding concrete. Neural Comput. Appl. 2020, 1–16. [Google Scholar] [CrossRef]
- Lee, H.-S.; Noguchi, T.; Tomosawa, F. Evaluation of the bond properties between concrete and reinforcement as a function of the degree of reinforcement corrosion. Cem. Concr. Res. 2002, 32, 1313–1318. [Google Scholar] [CrossRef]
- Ahmad, S. Reinforcement corrosion in concrete structures, its monitoring and service life prediction––A review. Cem. Concr. Compos. 2003, 25, 459–471. [Google Scholar] [CrossRef]
- Biondini, F.; Frangopol, D.M. Life-cycle performance of deteriorating structural systems under uncertainty. J. Struct. Eng. 2016, 142, F4016001. [Google Scholar] [CrossRef]
- Bertolini, L. Steel corrosion and service life of reinforced concrete structures. Struct. Infrastruct. Eng. 2008, 4, 123–137. [Google Scholar] [CrossRef]
- Ben Seghier, M.E.A.; Gao, X.-Z.; Jafari-Asl, J.; Thai, D.-K.; Ohadi, S.; Trung, N.-T. Modeling the nonlinear behavior of ACC for SCFST columns using experimental-data and a novel evolutionary-algorithm. Structures 2021, 30, 692–709. [Google Scholar] [CrossRef]
- Knudsen, A.; Jensen, F.M.; Klinghoffer, O.; Skovsgaard, T. Cost-effective enhancement of durability of concrete structures b intelligent use of stainless steel reinforcement. In Proceedings of the International Conference on Corrosion and Rehabilitation of Reinforced Concrete Structures, Orlando, FL, USA, 7–11 December 1998. [Google Scholar]
- Apostolopoulos, C.A.; Papadakis, V.G. Consequences of steel corrosion on the ductility properties of reinforcement bar. Constr. Build. Mater. 2008, 22, 2316–2324. [Google Scholar] [CrossRef]
- El, M.; Ben, A.; Keshtegar, B.; Fah, K.; Zayed, T.; Abbassi, R.; Thoi, N. Prediction of maximum pitting corrosion depth in oil and gas pipelines. Eng. Fail. Anal. 2020, 112, 104505. [Google Scholar] [CrossRef]
- Li, C.Q.; Yang, S.T.; Saafi, M. Numerical simulation of behavior of reinforced concrete structures considering corrosion effects on bonding. J. Struct. Eng. 2014, 140, 4014092. [Google Scholar] [CrossRef] [Green Version]
- Ben Seghier, M.E.A.; Keshtegar, B.; Taleb-Berrouane, M.; Abbassi, R.; Trung, N.-T. Advanced intelligence frameworks for predicting maximum pitting corrosion depth in oil and gas pipelines. Process Saf. Environ. Prot. 2021, 147, 818–833. [Google Scholar] [CrossRef]
- Bhargava, K.; Ghosh, A.K.; Mori, Y.; Ramanujam, S. Corrosion-induced bond strength degradation in reinforced concrete—Analytical and empirical models. Nucl. Eng. Des. 2007, 237, 1140–1157. [Google Scholar] [CrossRef]
- Zacchei, E.; Nogueira, C.G. 2D/3D Numerical Analyses of Corrosion Initiation in RC Structures Accounting Fluctuations of Chloride Ions by External Actions. KSCE J. Civ. Eng. 2021, 1–16. [Google Scholar] [CrossRef]
- Bagheri, M.; Hosseini, S.A.; Keshtegar, B.; Correia, J.A.F.O.; Trung, N.-T. Uncertain time-dependent reliability analysis of corroded RC structures applying three-term conjugate method. Eng. Fail. Anal. 2020, 115, 104599. [Google Scholar] [CrossRef]
- Miarnaeimi, F.; Azizyan, G.; Rashki, M. Reliability sensitivity analysis method based on subset simulation hybrid techniques. Appl. Math. Model. 2019, 75, 607–626. [Google Scholar] [CrossRef]
- Rashki, M. Structural reliability reformulation. Struct. Saf. 2021, 88, 102006. [Google Scholar] [CrossRef]
- Der Kiureghian, B.A.; Stefano, M. An Efficient Algorithm for Second-Order Reliability Analysis; University of California: Berkeley, CA, USA, 1992; Volume 117, pp. 2904–2923. [Google Scholar]
- Zhao, Y.; Ono, T. On the problems of the Fourth moment method. Struct. Saf. 2004, 26, 343–347. [Google Scholar] [CrossRef]
- Moarefzadeh, M.R.; Melchers, R.E. Directional importance sampling for ill-proportioned spaces. Struct. Saf. 1999, 21, 1–22. [Google Scholar] [CrossRef]
- Ben Seghier, M.A.; Bettayeb, M.; Correia, J.; De Jesus, A.; Calçada, R. Structural reliability of corroded pipeline using the so-called Separable Monte Carlo method. J. Strain Anal. Eng. Des. 2018, 53, 730–737. [Google Scholar] [CrossRef]
- Ben Seghier, M.A.; Keshtegar, B.; Correia, J.A.F.O.; Lesiuk, G.; Jesus, A.M.P. De Reliability analysis based on hybrid algorithm of M5 model tree and Monte Carlo simulation for corroded pipelines: Case of study X60 Steel grade pipes. Eng. Fail. Anal. 2019, 97, 793–803. [Google Scholar] [CrossRef]
- Zio, E. System Reliability and Risk Analysis. In The Monte Carlo Simulation Method for System Reliability and Risk Analysis; Springer: London, UK, 2013. [Google Scholar]
- Jafari-Asl, J.; Ben Seghier, M.E.A.; Ohadi, S.; Dong, Y.; Plevris, V. A Comparative Study on the Efficiency of Reliability Methods for the Probabilistic Analysis of Local Scour at a Bridge Pier in Clay-Sand-Mixed Sediments. Modelling 2021, 2, 63–77. [Google Scholar] [CrossRef]
- Jafari-Asl, J.; Ohadi, S.; Ben Seghier, M.E.A.; Trung, N.-T. Accurate Structural Reliability Analysis Using an Improved Line-Sampling-Method-Based Slime Mold Algorithm. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 4021015. [Google Scholar] [CrossRef]
- Low, B.K.; Tang, W.H. New FORM algorithm with example applications. In Proceedings of the 4th Asian-Pacific Symposium on Structural Reliability and Its Applications APSSAR’08, Hong Kong, China, 19–20 June 2008. [Google Scholar]
- Keshtegar, B.; Ben Seghier, M.E.A.; Zhu, S.-P.; Abbassi, R.; Trung, N.-T. Reliability analysis of corroded pipelines: Novel adaptive conjugate first order reliability method. J. Loss Prev. Process Ind. 2019, 62, 103986. [Google Scholar] [CrossRef]
- Bagheri, M.; Zhu, S.-P.; Seghier, M.E.; Keshtegar, B.; Trung , N.T. Hybrid intelligent method for fuzzy reliability analysis of corroded X100 steel pipelines. Eng. Comput. 2020, 1–15. [Google Scholar] [CrossRef]
- Meng, Z.; Pu, Y.; Zhou, H. Adaptive stability transformation method of chaos control for first order reliability method. Eng. Comput. 2017, 2, 1–13. [Google Scholar] [CrossRef]
- Keshtegar, B.; Meng, Z. A hybrid relaxed first-order reliability method for efficient structural reliability analysis. Struct. Saf. 2017, 66, 84–93. [Google Scholar] [CrossRef]
- Mangat, P.S.; Elgarf, M.S. Flexural strength of concrete beams with corroding reinforcement. Struct. J. 1999, 96, 149–158. [Google Scholar]
- Nepal, J. Modeling residual flexural strength of corroded reinforced concrete beams. ACI Struct. J. 2018, 115, 1625–1635. [Google Scholar]
- Azad, A.K.; Ahmad, S.; Al-Gohi, B.H.A. Flexural strength of corroded reinforced concrete beams. Mag. Concr. Res. 2010, 62, 405–414. [Google Scholar] [CrossRef]
- Stewart, M.G. Mechanical behaviour of pitting corrosion of flexural and shear reinforcement and its effect on structural reliability of corroding RC beams. Struct. Saf. 2009, 31, 19–30. [Google Scholar] [CrossRef]
- Torres-Acosta, A.A.; Navarro-Gutierrez, S.; Terán-Guillén, J. Residual flexure capacity of corroded reinforced concrete beams. Eng. Struct. 2007, 29, 1145–1152. [Google Scholar] [CrossRef]
- Stewart, M.G. Spatial variability of pitting corrosion and its influence on structural fragility and reliability of RC beams in flexure. Struct. Saf. 2004, 26, 453–470. [Google Scholar] [CrossRef]
- Darmawan, M.S. Pitting corrosion model for reinforced concrete structures in a chloride environment. Mag. Concr. Res. 2010, 62, 91–101. [Google Scholar] [CrossRef]
- Vu, K.; Stewart, M.G.; Mullard, J. Corrosion-induced cracking: Experimental data and predictive models. ACI Struct. J. 2005, 102, 719. [Google Scholar]
- Stewart, M.G.; Al-Harthy, A. Pitting corrosion and structural reliability of corroding RC structures: Experimental data and probabilistic analysis. Reliab. Eng. Syst. Saf. 2008, 93, 373–382. [Google Scholar] [CrossRef]
- Stewart, M.G.; Rosowsky, D.V. Time-dependent reliability of deteriorating reinforced concrete bridge decks. Struct. Saf. 1998, 20, 91–109. [Google Scholar] [CrossRef]
- Masoud, S.; Soudki, K.; Topper, T. Postrepair fatigue performance of FRP-repaired corroded RC beams: Experimental and analytical investigation. J. Compos. Constr. 2005, 9, 441–449. [Google Scholar] [CrossRef]
- Ben Seghier, M.E.A.; Carvalho, H.; Keshtegar, B.; Correia, J.A.F.O.; Berto, F. Novel hybridized adaptive neuro-fuzzy inference system models based particle swarm optimization and genetic algorithms for accurate prediction of stress intensity factor. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 2653–2667. [Google Scholar] [CrossRef]
- Sobieck, T.; Atadero, R.A.; Mahmoud, H.N. Fatigue crack propagation of notched steel rebar in RC beams repaired with externally bonded CFRP. J. Compos. Constr. 2015, 19, 4014076. [Google Scholar] [CrossRef]
- British Standards Institute BS 7910: 2005—Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures; British Standards Institute: London, UK, 2005; Volume 3.
- El Amine Ben Seghier, M.; Keshtegar, B.; Elahmoune, B. Reliability analysis of low, mid and high-grade strength corroded pipes based on plastic flow theory using adaptive nonlinear conjugate map. Eng. Fail. Anal. 2018, 90, 245–261. [Google Scholar] [CrossRef]
- Meng, Z.; Li, G.; Yang, D.; Zhan, L. A new directional stability transformation method of chaos control for first order reliability analysis. Struct. Multidiscip. Optim. 2017, 2, 601–612. [Google Scholar] [CrossRef]
- Yang, D.; Yi, P. Chaos control of performance measure approach for evaluation of probabilistic constraints. Struct. Multidiscip. Optim. 2009, 38, 83–92. [Google Scholar] [CrossRef]
- Hao, P.; Wang, Y.; Liu, X.; Wang, B.; Li, G.; Wang, L. An efficient adaptive-loop method for non-probabilistic reliability-based design optimization. Comput. Methods Appl. Mech. Eng. 2017, 324, 689–711. [Google Scholar] [CrossRef]
- Gong, J.-X.; Yi, P. A robust iterative algorithm for structural reliability analysis. Struct. Multidiscip. Optim. 2011, 43, 519–527. [Google Scholar] [CrossRef]
- Keshtegar, B.; Chakraborty, S. An efficient-robust structural reliability method by adaptive finite-step length based on Armijo line search. Reliab. Eng. Syst. Saf. 2018, 172, 195–206. [Google Scholar] [CrossRef]
- Roudak, M.A.; Karamloo, M. Establishment of non-negative constraint method as a robust and efficient first-order reliability method. Appl. Math. Model. 2019, 68, 281–305. [Google Scholar] [CrossRef]
- Keshtegar, B. Stability iterative method for structural reliability analysis. Nonlinear Dyn. 2016, 84, 2161–2174. [Google Scholar] [CrossRef]
- Keshtegar, B. Limited conjugate gradient method for structural reliability analysis. Eng. Comput. 2017, 33, 621–629. [Google Scholar] [CrossRef]
- Keshtegar, B.; Kolahchi, R. Reliability analysis-based conjugate map of beams reinforced by ZnO nanoparticles using sinusoidal shear deformation theory. Steel Compos. Struct. 2018, 28, 195–207. [Google Scholar]
- Keshtegar, B.; Zhu, S. Three-term conjugate approach for structural reliability analysis. Appl. Math. Model. 2019, 76, 428–442. [Google Scholar] [CrossRef]
- Teplý, B.; Vorechovska, D. Reinforcement corrosion: Limit states, reliability and modelling. J. Adv. Concr. Technol. 2012, 10, 353–362. [Google Scholar] [CrossRef]
- Vidal, T.; Castel, A.; François, R. Analyzing crack width to predict corrosion in reinforced concrete. Cem. Concr. Res. 2004, 34, 165–174. [Google Scholar] [CrossRef]
- Cairns, J.; Plizzari, G.A.; Du, Y.; Law, D.W.; Franzoni, C. Mechanical properties of corrosion-damaged reinforcement. ACI Mater. J. 2005, 102, 256. [Google Scholar]
- Bastidas-Arteaga, E.; Bressolette, P.; Chateauneuf, A.; Sánchez-Silva, M. Probabilistic lifetime assessment of RC structures under coupled corrosion–fatigue deterioration processes. Struct. Saf. 2009, 31, 84–96. [Google Scholar] [CrossRef] [Green Version]
- Tarighat, A.; Jalalifar, F. Assessing the performance of corroding RC bridge decks: A critical review of corrosion propagation models. Civ. Eng. Infrastruct. J. 2014, 47, 173–186. [Google Scholar]
- Du, Y.G.; Clark, L.A.; Chan, A.H.C. Residual capacity of corroded reinforcing bars. Mag. Concr. Res. 2005, 57, 135–147. [Google Scholar] [CrossRef]


| Variable | Description | Mean | CoV | Distribution |
|---|---|---|---|---|
| Concrete compressive resistance (MPa) | 30 | 0.18 | Normal | |
| Steel yield tension (MPa) | 400 | 0.11 | Log normal | |
| D0 | Bar diameter (mm) | 18 | 0.05 | Normal |
| Mn | Applied moment (kN-m) | 120 | 0.12 | Gumbel |
| b | Section width (mm) | 350 | 0.07 | Normal |
| d | Effective height (mm) | 500 | 0.07 | Log normal |
| C | concrete cover (mm) | 50 | 0.12 | Normal |
| η | Model coefficient | 1 | 0.1 | Normal |
| Yield empirical coefficient | 0.005 | 0.12 | Log normal | |
| K | Resistance ratio | 0.6 | 0.05 | Normal |
| Load coefficient | 1.05 | 0.1 | Normal | |
| R | The maximum to the average corrosion ratio | 6 | 0.2 | Gumbel |
| T | Corrosion initiation time (years) | variable | 0.35 | Log normal |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben Seghier, M.E.A.; Keshtegar, B.; Mahmoud, H. Time-Dependent Reliability Analysis of Reinforced Concrete Beams Subjected to Uniform and Pitting Corrosion and Brittle Fracture. Materials 2021, 14, 1820. https://doi.org/10.3390/ma14081820
Ben Seghier MEA, Keshtegar B, Mahmoud H. Time-Dependent Reliability Analysis of Reinforced Concrete Beams Subjected to Uniform and Pitting Corrosion and Brittle Fracture. Materials. 2021; 14(8):1820. https://doi.org/10.3390/ma14081820
Chicago/Turabian StyleBen Seghier, Mohamed El Amine, Behrooz Keshtegar, and Hussam Mahmoud. 2021. "Time-Dependent Reliability Analysis of Reinforced Concrete Beams Subjected to Uniform and Pitting Corrosion and Brittle Fracture" Materials 14, no. 8: 1820. https://doi.org/10.3390/ma14081820
APA StyleBen Seghier, M. E. A., Keshtegar, B., & Mahmoud, H. (2021). Time-Dependent Reliability Analysis of Reinforced Concrete Beams Subjected to Uniform and Pitting Corrosion and Brittle Fracture. Materials, 14(8), 1820. https://doi.org/10.3390/ma14081820







