Investigation of Microcrack Propagation and Energy Evolution in Brittle Rocks Based on the Voronoi Model
Abstract
:1. Introduction
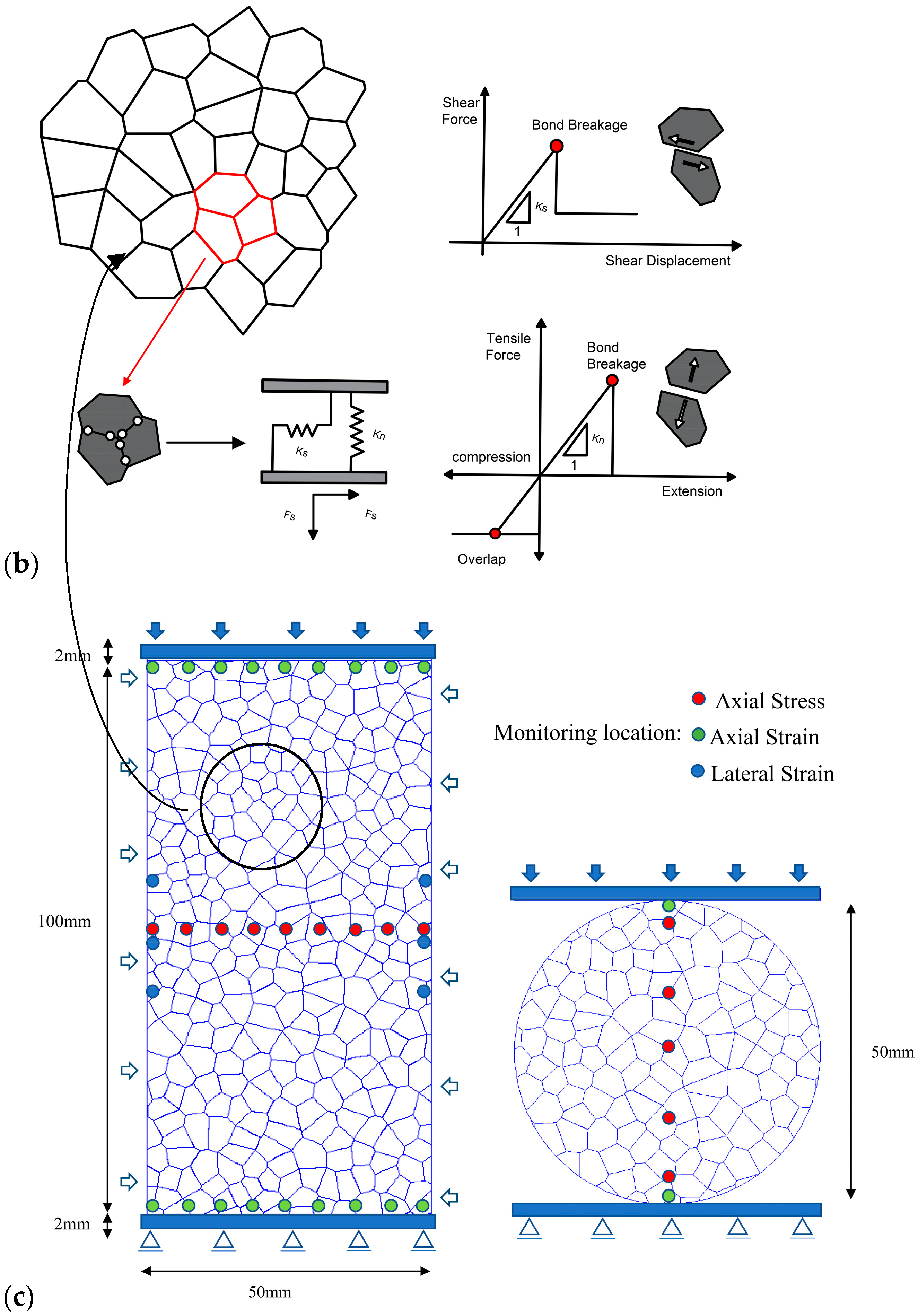
2. Numerical Modeling
2.1. Voronoi Model Mechanical Behavior
2.2. Modelling Characteristics
3. Microscopic Mechanical Properties of Voronoi Model
3.1. Micro-Properties Sensitivity Analysis
3.1.1. Micro Deformability Properties
- Young’s modulus of micro-block ()
- Contact normal stiffness () and shear stiffness ()
- Contact stiffness ratio (ks/kn)
3.1.2. Micro Strength Properties
- Contact-Cohesion () and Contact-Friction angle ()
- Contact-Tensile strength ()
3.1.3. Post-Peak Stress Parameters
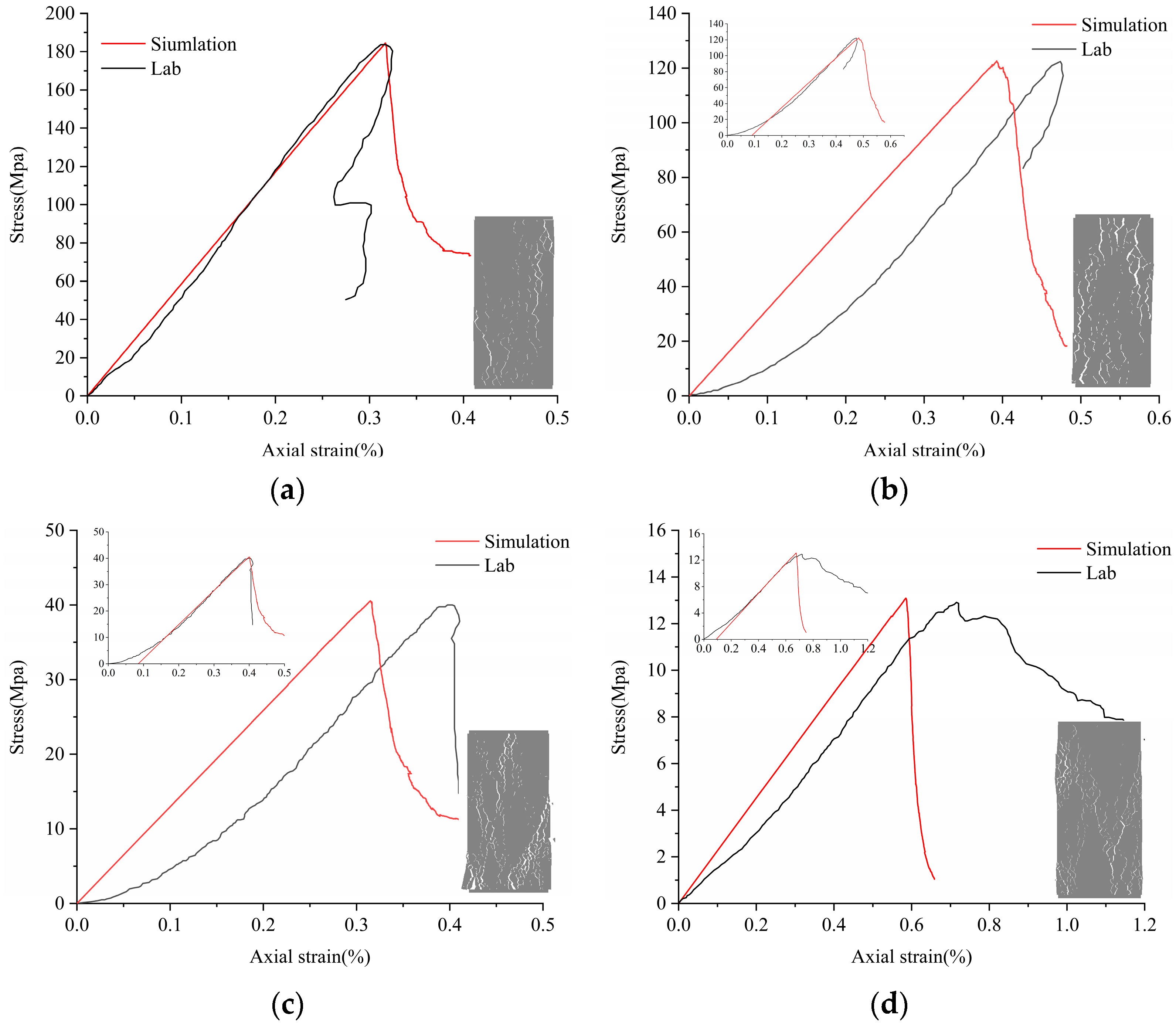
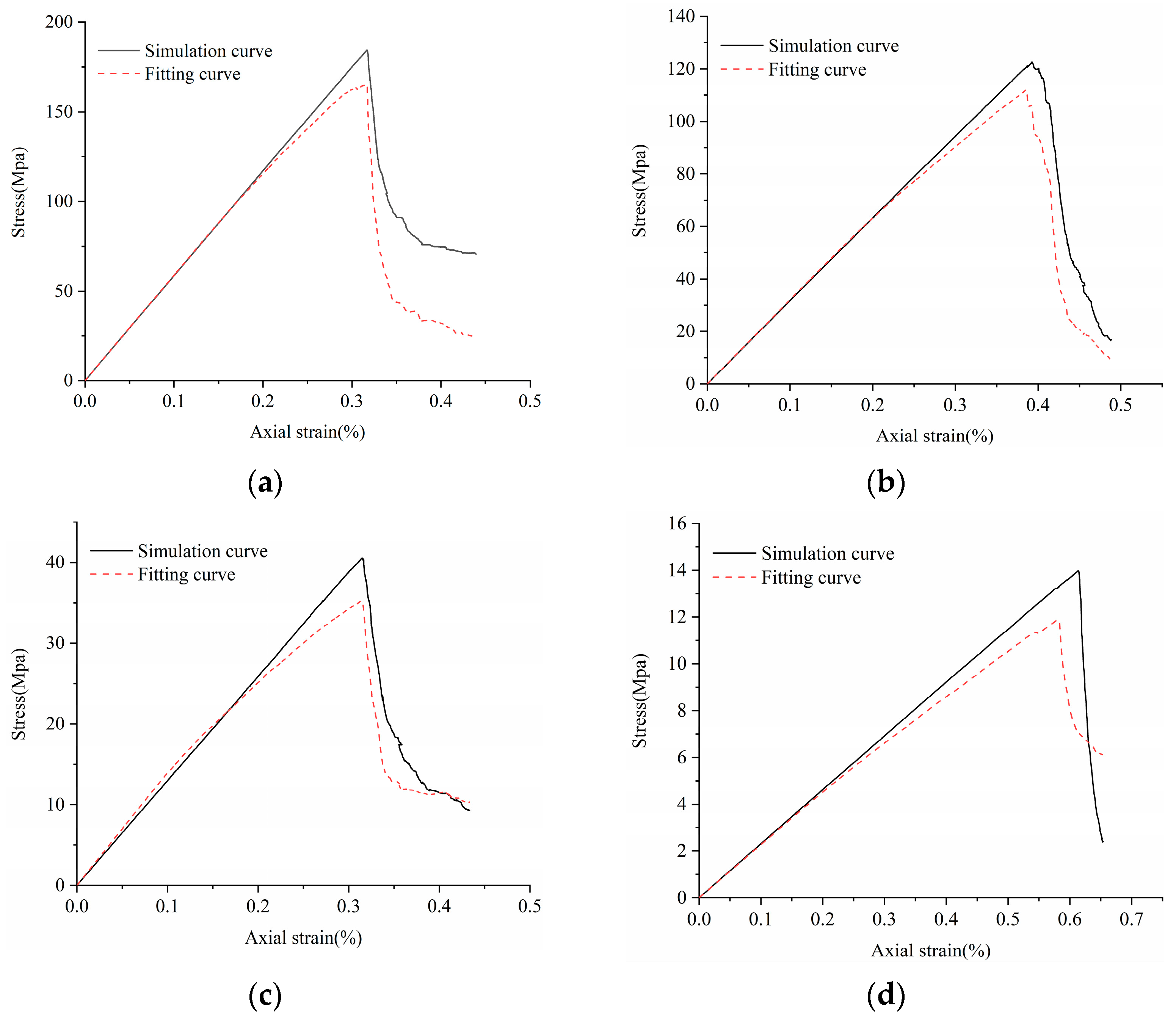
3.2. Calibration Procedure and Results Analysis
4. Micro-Crack Evolution in the Rock Fracture Process
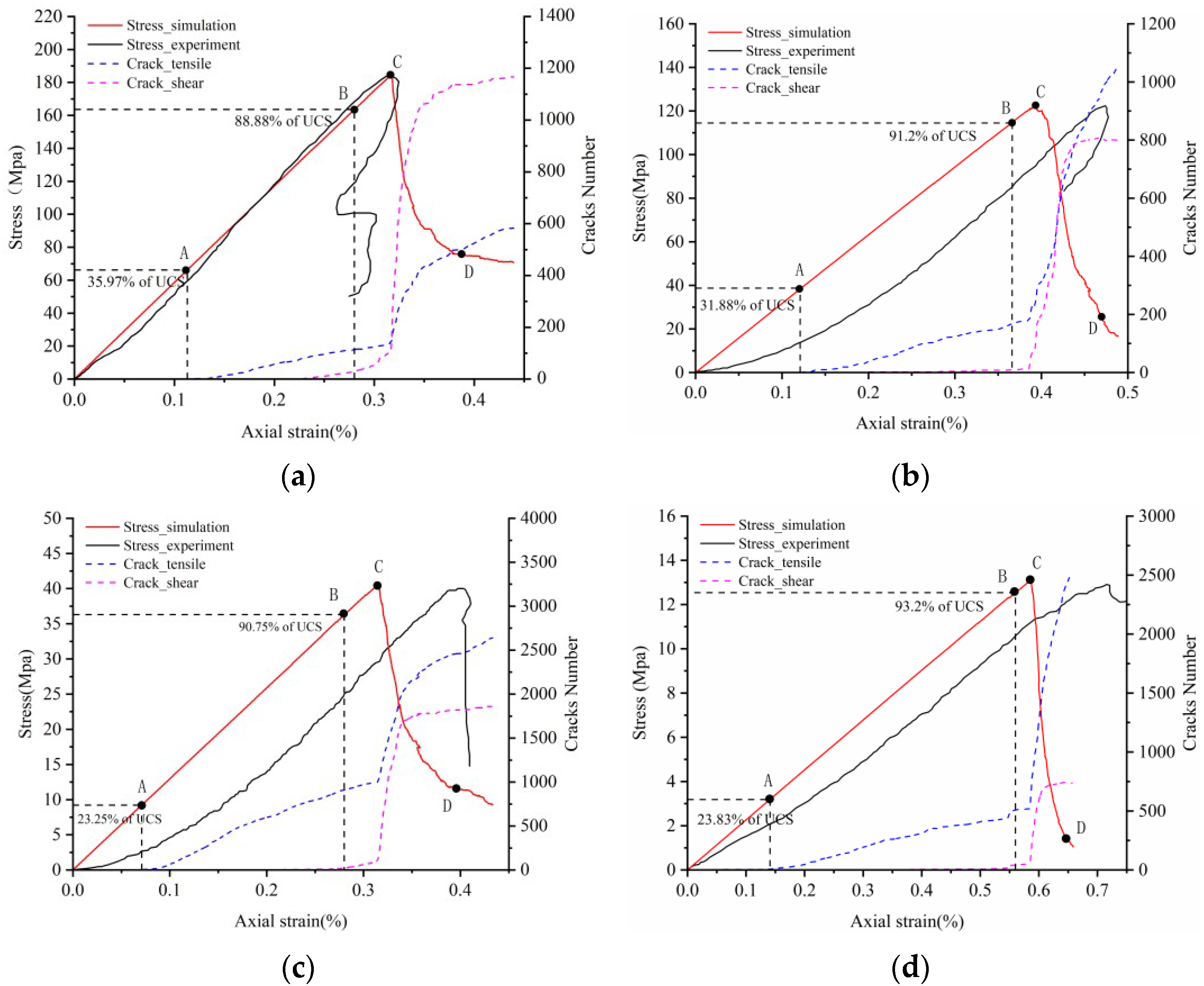
4.1. Strain–Stress Crack Analysis
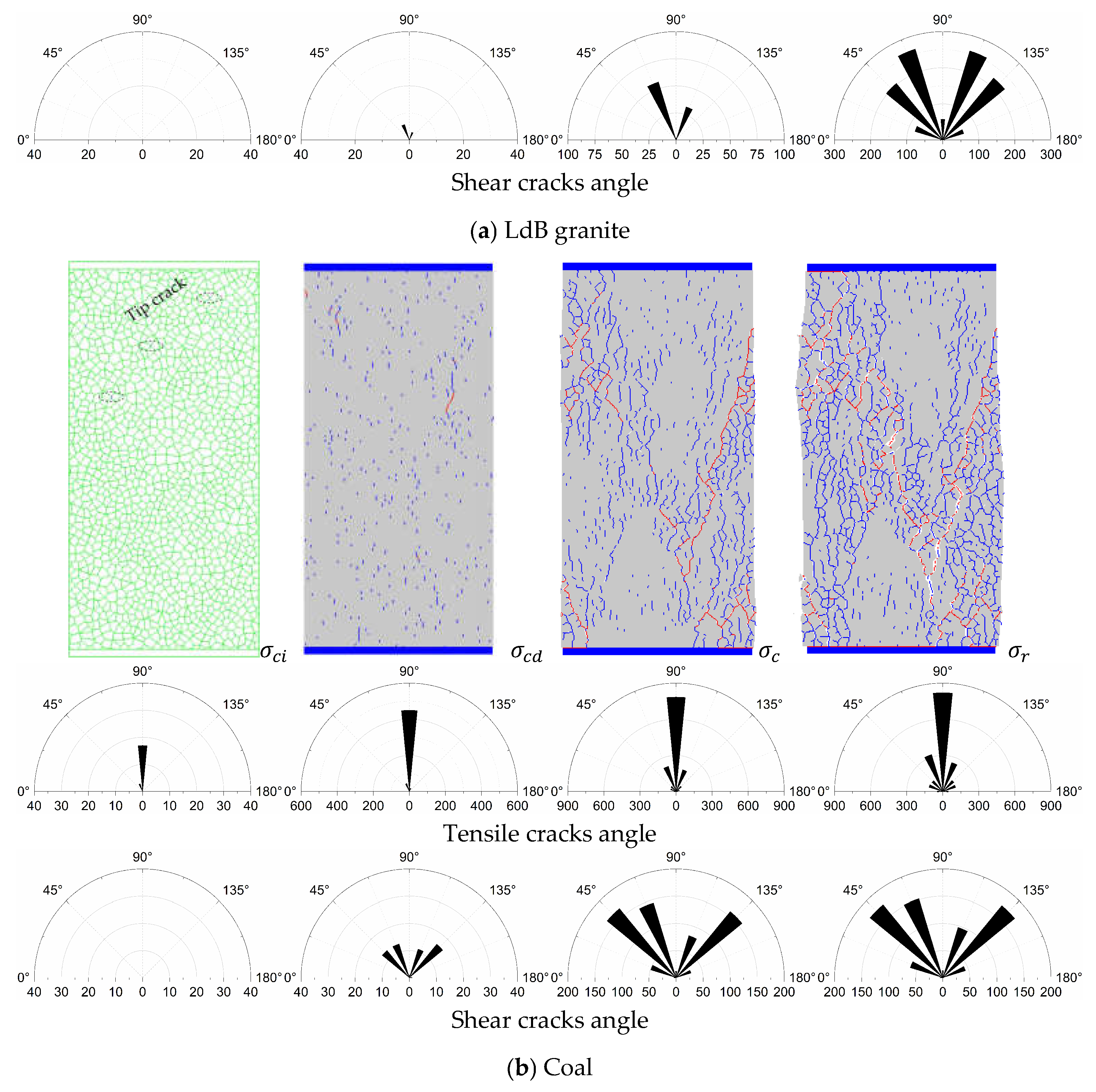
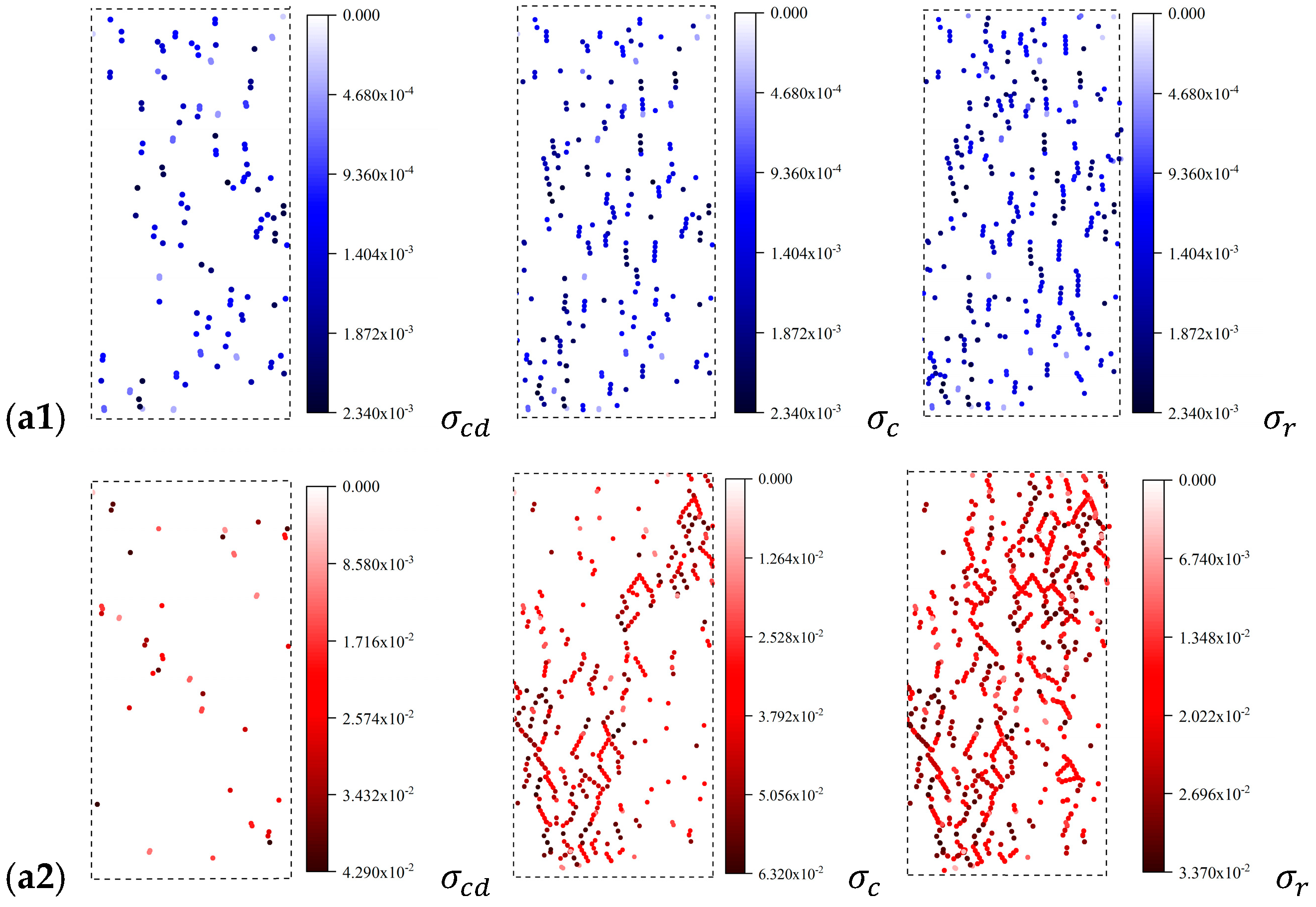
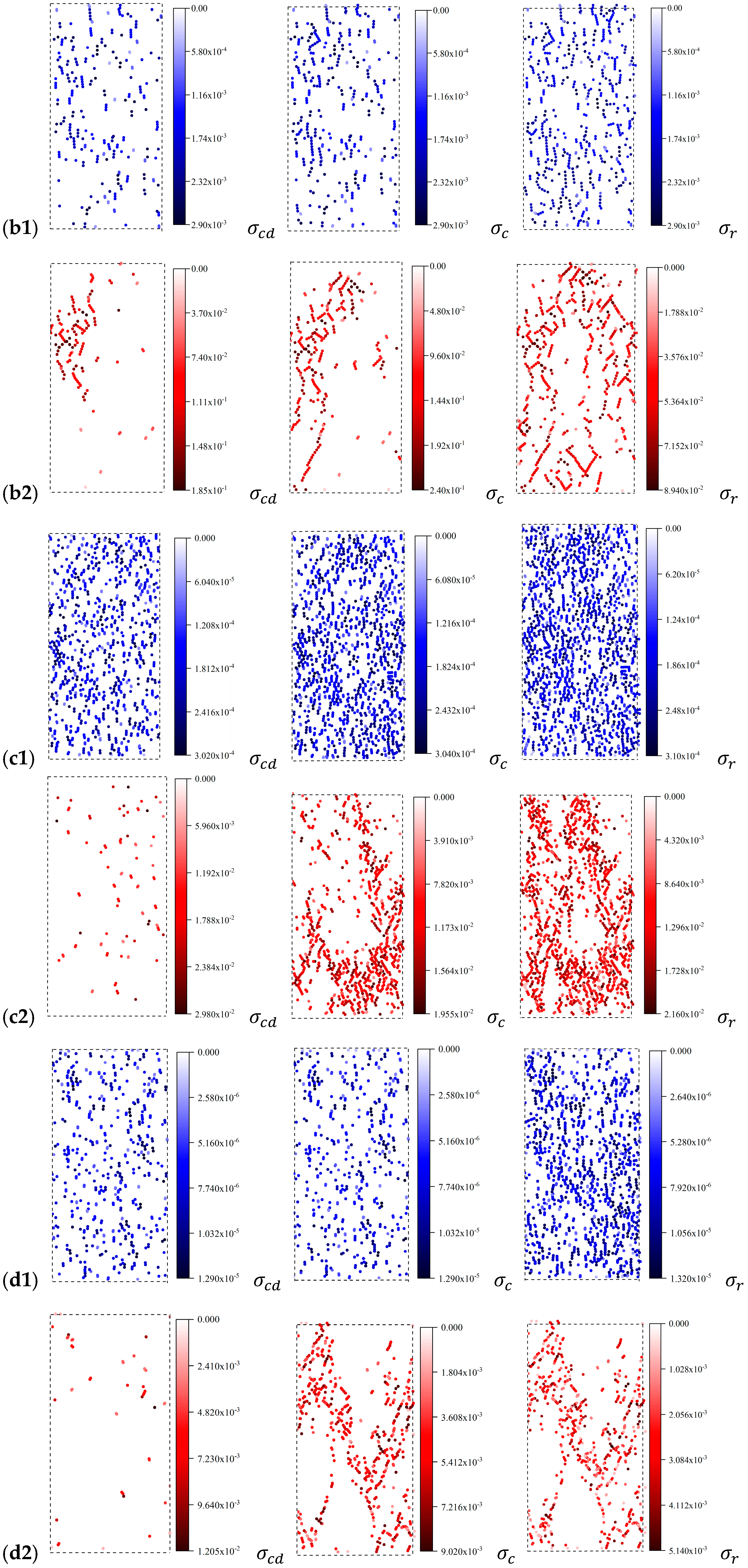
4.2. Crack Evolution Process and Crack Angle Analysis
4.3. AE Event Count
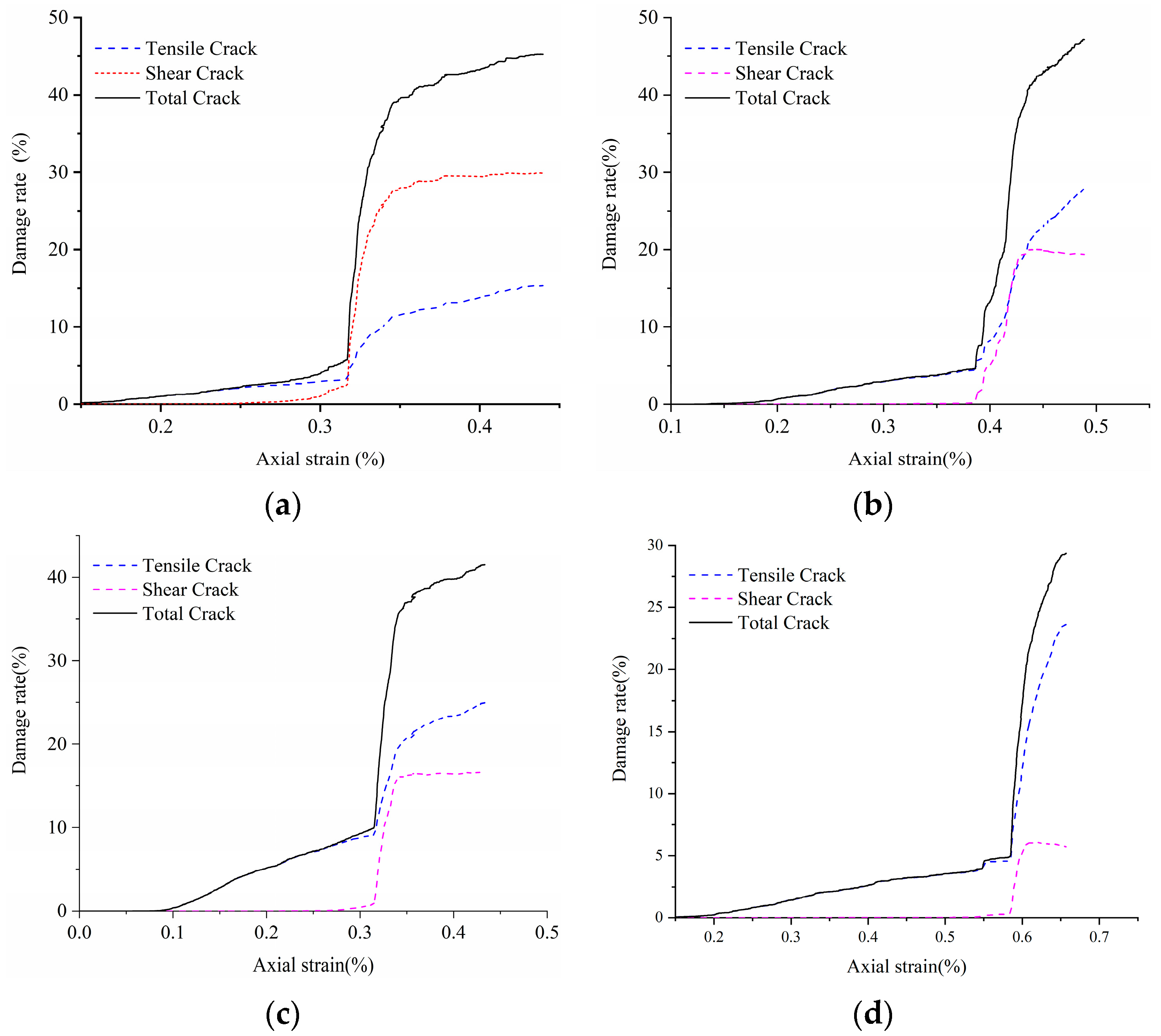
4.4. Crack Damage Analysis
4.5. Characteristics of Macroscopic Failure
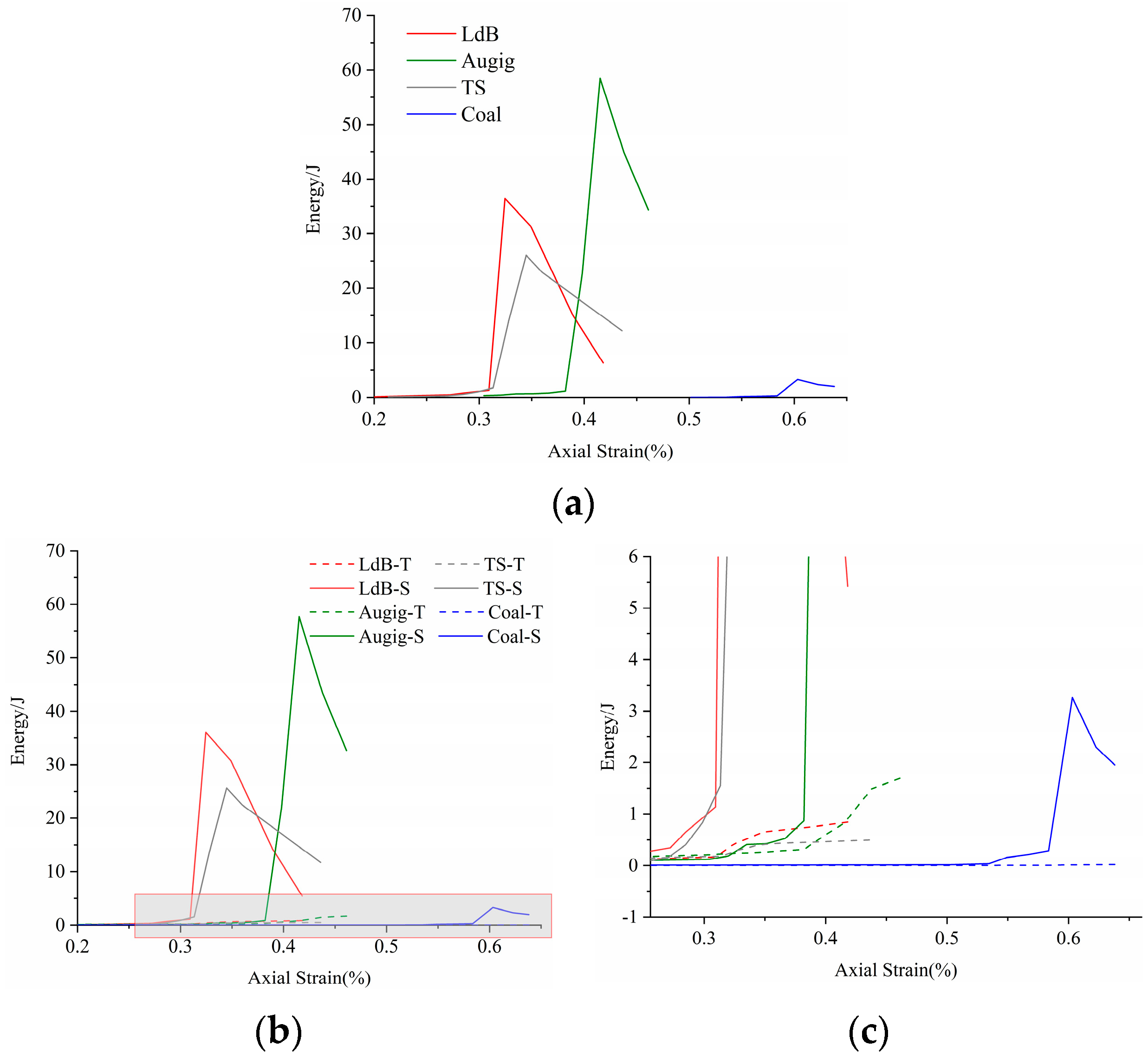
4.6. Energy Evolution Pattern
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Martini, C.D.; Read, R.S.; Martino, J.B. Observation of brittle failure around a circular test tunnel. Int. J. Rock Mech. Min. Sci. 1997, 34, 1065–1073. [Google Scholar] [CrossRef]
- Backblom, G.; Martin, C.D. Recent experiments in hard rocks to study the excavation response: Implications for the performance of a nuclear waste geological repository. Tunn. Undergr. Space Technol. 1999, 14, 377–394. [Google Scholar] [CrossRef]
- Brideau, M.-A.; Yan, M.; Stead, D. The role of tectonic damage and brittle rock fracture in the development of large rock slope failures. Geomorphology 2009, 103, 30–49. [Google Scholar] [CrossRef]
- Allegre, C.J.; Le Mouel, J.L.; Provost, A. Scaling rules in rock fracture and possible implications for earthquake prediction. Nature 1982, 297, 47–49. [Google Scholar] [CrossRef]
- Willis-Richards, J.; Watanabe, K.; Takahashi, H. Progress toward a stochastic rock mechanics model of engineered geothermal systems. J. Geophys. Res. 1996, 101, 17481–17496. [Google Scholar] [CrossRef]
- Kranz, R.L. Crack growth and development during creep of Barre granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 23–55. [Google Scholar] [CrossRef]
- Hallbauer, D.K.; Wagner, H.; Cook, N.G.W. Some observations concerning the microscopic and mechanical behaviour of quartzite specimens in stiff, triaxial compression tests. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1973, 10, 713–726. [Google Scholar] [CrossRef]
- Jing, L.; Hudson, J.A. Numerical methods in rock mechanics. Int. J. Rock Mech. Min. Sci. 2002, 39, 409–427. [Google Scholar] [CrossRef]
- Bittencourt, T.N.; Wawrzynek, P.A.; Ingraffea, A.R.; Sousa, J.L. Quasi-automatic simulation of crack propagation for 2D LEFM problems. Eng. Fract. Mech. 1996, 55, 321–334. [Google Scholar] [CrossRef]
- Reyes, O.; Einstein, H.H. Failure Mechanisms of Fractured Rock—A Fracture Coalescence Model. In Proceedings of the 7th ISRM Congress, Aachen, Germany, 16–20 September 1991. [Google Scholar]
- Li, H.; Wong, L.N.Y. Influence of flaw inclination angle and loading condition on crack initiation and propagation. Int. J. Solids Struct. 2012, 49, 2482–2499. [Google Scholar] [CrossRef] [Green Version]
- De Borst, R.; Sluys, L.J.; Muhlhaus, H.B.; Pamin, J. Fundamental issues in finite element analyses of localization of deformation. Eng. Comput. 1993, 10, 99–121. [Google Scholar] [CrossRef] [Green Version]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Moes, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Xie, Y.; Cao, P.; Liu, J.; Dong, L. Influence of crack surface friction on crack initiation and propagation: A numerical investigation based on extended finite element method. Comput. Geotech. 2016, 74, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Feng, X.T. Extended finite element simulation of crack propagation in fractured rock masses. Mater. Res. Innov. 2015, 15, s594–s596. [Google Scholar] [CrossRef]
- Zhuang, X.; Chun, J.; Zhu, H. A comparative study on unfilled and filled crack propagation for rock-like brittle material. Theor. Appl. Fract. Mech. 2014, 72, 110–120. [Google Scholar] [CrossRef]
- Won, J.; You, K.; Jeong, S.; Kim, S. Coupled effects in stability analysis of pile–slope systems. Comput. Geotech. 2005, 32, 304–315. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Morioka, H.; Minami, M.; Maejima, T.; Tasaka, Y.; Kurose, H. FLAC/PFC coupled numerical simulation of AE in large-scale underground excavations. Int. J. Rock Mech. Min. Sci. 2007, 44, 550–564. [Google Scholar] [CrossRef]
- Fu, J.-W.; Zhang, X.-Z.; Zhu, W.-S.; Chen, K.; Guan, J.-F. Simulating progressive failure in brittle jointed rock masses using a modified elastic-brittle model and the application. Eng. Fract. Mech. 2017, 178, 212–230. [Google Scholar] [CrossRef]
- Guo, S.; Qi, S.; Zou, Y.; Zheng, B. Numerical Studies on the Failure Process of Heterogeneous Brittle Rocks or Rock-Like Materials under Uniaxial Compression. Materials 2017, 10, 378. [Google Scholar] [CrossRef] [Green Version]
- Cundall, P.A. A computer model for simulating progressive large-scale movements in blocky rock systems. Proc. Int. Symp. Rock Fract. 1971, 1, 11–18. [Google Scholar]
- Cundall, P.A.; Hart, R.D. Numerical Modelling of Discontinua. Anal. Des. Methods 1993, 9, 231–243. [Google Scholar] [CrossRef]
- Itasca. PFC2D (Particle Flow Code in 2 Dimensions), Version 5.0; Itasca Consulting Group Inc: Minneapolis, MN, USA, 2014. [Google Scholar]
- Itasca. UDEC (Universal Distinct Element Code), Version 6.0; Itasca Consulting Group Inc: Minneapolis, MN, USA, 2014. [Google Scholar]
- Lee, C.; Cundall, P.A.; Potyondy, D.O. Modeling rock using bonded assemblies of circular particles. In Proceedings of the 2nd North American Rock Mechanics Symposium, Montreal, QC, Canada, 19–21 June 1996. [Google Scholar]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Gao, F.Q.; Stead, D. The application of a modified Voronoi logic to brittle fracture modelling at the laboratory and field scale. Int. J. Rock Mech. Min. Sci. 2014, 68, 1–14. [Google Scholar] [CrossRef]
- Lan, H.; Martin, C.D.; Hu, B. Effect of heterogeneity of brittle rock on micromechanical extensile behavior during compression loading. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Li, X.; Ju, M.; Yao, Q.; Zhou, J.; Chong, Z. Numerical Investigation of the Effect of the Location of Critical Rock Block Fracture on Crack Evolution in a Gob-side Filling Wall. Rock Mech. Rock Eng. 2016, 49, 1041–1058. [Google Scholar] [CrossRef]
- Lorig, L.J.; Cundall, P.A. Modeling of Reinforced Concrete Using the Distinct Element Method; Springer: New York, NY, USA, 1989. [Google Scholar]
- Koyama, T.; Jing, L. Effects of model scale and particle size on micro-mechanical properties and failure processes of rocks —A particle mechanics approach. Eng. Anal. Bound. Elem. 2007, 31, 458–472. [Google Scholar] [CrossRef]
- Zhang, X.P.; Wong, L.N.Y. Cracking Processes in Rock-Like Material Containing a Single Flaw Under Uniaxial Compression: A Numerical Study Based on Parallel Bonded-Particle Model Approach. Rock Mech. Rock Eng. 2012, 45, 711–737. [Google Scholar] [CrossRef]
- Kazerani, T.; Zhao, J. Micromechanical parameters in bonded particle method for modelling of brittle material failure. Int. J. Numer. Anal. Methods Geomech. 2010, 34, 1877–1895. [Google Scholar] [CrossRef]
- Cho, N.; Martin, C.D.; Sego, D.C. A clumped particle model for rock. Int. J. Rock Mech. Min. Sci. 2007, 44, 997–1010. [Google Scholar] [CrossRef]
- Diederichs, M.S. Instability of Hard Rockmasses, the Role of Tensile Damage and Relaxation; UWSpace: Waterloo, ON, Canada, 2000. [Google Scholar]
- Hoek, E.; Brown, E.T. Practical estimates of rock mass strength. Int. J. Rock Mech. Min. Sci. 1997, 34, 1165–1186. [Google Scholar] [CrossRef]
- Potyondy, D.O. A grain-based model for rock: Approaching the true microstructure. In Proceedings of the Bergmekanikk i Norden 2010—Rock Mechanics in the Nordic Countries (2010), Kongsberg, Norwey, 9–12 June 2010. [Google Scholar]
- Lisjak, A.; Grasselli, G. A review of discrete modeling techniques for fracturing processes in discontinuous rock masses. J. Rock Mech. Geotech. Eng. 2014, 6, 301–314. [Google Scholar] [CrossRef] [Green Version]
- Nikolić, M.; Karavelić, E.; Ibrahimbegovic, A.; Miščević, P. Lattice Element Models and Their Peculiarities. Arch. Comput. Methods Eng. 2018, 25, 753–784. [Google Scholar] [CrossRef] [Green Version]
- Rasmussen, L.L.; de Farias, M.M.; de Assis, A.P. Extended Rigid Body Spring Network method for the simulation of brittle rocks. Comput. Geotech. 2018, 99, 31–41. [Google Scholar] [CrossRef]
- Zhao, G.-F.; Hu, X.; Li, Q.; Lian, J.; Ma, G. On the four-dimensional lattice spring model for geomechanics. J. Rock Mech. Geotech. Eng. 2018, 10, 661–668. [Google Scholar] [CrossRef]
- Fabjan, T.; Ivars, D.M.; Vukadin, V. Numerical simulation of intact rock behavior via continuum and Voronoi tesselletion models—a sensitivity analysis. Acta Geotechnica Slovenica 2015, 12, 4–23. [Google Scholar]
- Stavrou, A.; Murphy, W. Quantifying the effects of scale and heterogeneity on the confined strength of micro-defected rocks. Int. J. Rock Mech. Min. Sci. 2018, 102, 131–143. [Google Scholar] [CrossRef] [Green Version]
- Ulusay, R. The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 2007–2014; Springer International Publishing: New York, NY, USA, 2014; pp. 47–48. [Google Scholar]
- Nicksiar, M.; Martin, C.D. Factors Affecting Crack Initiation in Low Porosity Crystalline Rocks. Rock Mech. Rock Eng. 2014, 47, 1165–1181. [Google Scholar] [CrossRef]
- Kazerani, T.; Zhao, J. A Microstructure-Based Model to Characterize Micromechanical Parameters Controlling Compressive and Tensile Failure in Crystallized Rock. Rock Mech. Rock Eng. 2014, 47, 435–452. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, X.; Liu, Q.; Yang, Y. A zero-thickness cohesive element-based numerical manifold method for rock mechanical behavior with micro-Voronoi grains. Eng. Anal. Bound. Elem. 2018, 96, 94–108. [Google Scholar] [CrossRef]
- Medhurst, T.P.; Brown, E.T. A study of the mechanical behaviour of coal for pillar design. Int. J. Rock Mech. Min. Sci. 1998, 35, 1087–1105. [Google Scholar] [CrossRef]
- Hoek, E. Hoek-Brown failure criterion-2002 edition. In Proceedings of the Fifth North American Rock Mechanics Symposium, Toronto, ON, Canada, 7–10 July 2002. [Google Scholar]
- Park, J.W.; Park, C.; Song, J.W.; Park, E.S.; Song, J.J. Polygonal grain-based distinct element modeling for mechanical behavior of brittle rock. Int. J. Numer. Anal. Methods Geomech. 2017. [Google Scholar] [CrossRef]
- Christianson, M.; Board, M.; Rigby, D. UDEC simulation of triaxial testing of lithophysal tuff. In Proceedings of the 41st U.S. Symposium on Rock Mechanics (USRMS), Golden Rocks, CO, USA, 17–21 June 2006. [Google Scholar]
- Eberhardt, E.; Stead, D.; Stimpson, B.; Read, R.S. Identifying crack initiation and propagation thresholds in brittle rock. Can. Geotech. J. 1998, 35, 222–233. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Tasaka, Y.; Maejima, T.; Morioka, H.; Minami, M. Generalized crack initiation and crack damage stress thresholds of brittle rock masses near underground excavations. Int. J. Rock Mech. Min. Sci. 2004, 41, 833–847. [Google Scholar] [CrossRef]
- Hoek, E.; Martin, C.D. Fracture initiation and propagation in intact rock—A review. J. Rock Mech. Geotech. Eng. 2014, 6, 287–300. [Google Scholar] [CrossRef] [Green Version]
- Xue, L.; Qin, S.; Sun, Q.; Wang, Y.; Lee, L.M.; Li, W. A Study on Crack Damage Stress Thresholds of Different Rock Types Based on Uniaxial Compression Tests. Rock Mech. Rock Eng. 2014, 47, 1183–1195. [Google Scholar] [CrossRef]
- Hoek, E.; Bieniawski, Z.T. Brittle fracture propagation in rock under compression. Int. J. Fract. 1965, 1, 137–155. [Google Scholar] [CrossRef]
- Yoon, J.S.; Zang, A.; Stephansson, O. Simulating fracture and friction of Aue granite under confined asymmetric compressive test using clumped particle model. Int. J. Rock Mech. Min. Sci. 2012, 49, 68–83. [Google Scholar] [CrossRef] [Green Version]
- Li, X.F.; Li, H.B.; Li, J.C.; Xia, X. Crack Initiation and Propagation Simulation for Polycrystalline-Based Brittle Rock UTILIZING Three Dimensional Distinct Element Method. In Rock Dynamics: From Research to Engeenering; Routledge: Oxfordshire, UK, 2016; pp. 341–348. [Google Scholar]
- Zhang, H.; Lu, C.-P.; Liu, B.; Liu, Y.; Zhang, N.; Wang, H.-Y. Numerical investigation on crack development and energy evolution of stressed coal-rock combination. Int. J. Rock Mech. Min. Sci. 2020, 133. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Stimpson, B. Quantifying progressive pre-peak brittle fracture damage in rock during uniaxial compression. Int. J. Rock Mech. Min. Sci. 1999, 36, 361–380. [Google Scholar] [CrossRef]
- Kachanov, L.M. Time of the Rupture Process under Creep Conditions. Nank S.S.R. Otd Tech. Nauk. 1958, 8, 26–31. [Google Scholar]
- Lemaitre, J.; Sermage, J.P.; Desmorat, R. A two scale damage concept applied to fatigue. Int. J. Fract. 1999, 97, 67–81. [Google Scholar] [CrossRef]






| Young’s Modulus | Voronoi Block Elastic Properties | |
|---|---|---|
| Poisson’s Ratio | ||
| Normal Stiffness | Voronoi contact elastic properties | |
| Shear Stiffness | ||
| Cohesion * | Voronoi contact strength properties | |
| Friction Angle * | ||
| Tensile Strength * |
| Hard Rock ⟶ Weak Rock | |||||
|---|---|---|---|---|---|
| Lithology | Loc du Bonnet [23] Granite | Augig [34,47] Granite | Transjuane [34,48] Sandstone | Coal [28,49] | |
| UCS (Mpa) | 183 | 122 | 40 | 13.33 | |
| Young’s Modulus (Gpa) | 63.2 | 25.8 | 12.5 | 2.4 | |
| Poisson’s ratio | 0.26 | 0.23 | 0.3 | 0.26 | |
| Cohesion (Mpa) | 30 | 21 | 8.5 | 1.22 | |
| Friction angle (°) | 59 | 53 | 41 | 21 | |
| Tensile strength (Mpa) | 9.3 | 8.8 | 2.8 | 0.39 | |
| Density (Kg/m3) | 2630 | 2600 | 2600 | 1450 | |
| Grain mean size (mm) | 4 | 4 | 2 | 2 | |
| Hard Rock ⟶ Weak Rock | |||||
|---|---|---|---|---|---|
| Lithology | Loc du Bonnet Granite | Augig Granite | Transjuane Sandstone | Coal | |
| Sample rock: | |||||
| UCS (Mpa) | 184.5 | 121.4 | 40.5 | 13.1 | |
| Young’s modulus (Gpa) Poisson’s ratio | 58.9 0.254 | 26.197 0.232 | 12.93 0.3 | 2.27 0.263 | |
| Tensile strength (Mpa) | 9.8 | 8.6 | 2.6 | 0.38 | |
| Contact: | |||||
| Normal stiffness (Gpa) | 67,500 | 22,432 | 15,000 | 4111.1 | |
| Shear stiffness (Gpa) Stiffness ratio | 40,500 0.6 | 13,459 0.6 | 8000 0.53 | 3288.9 0.8 | |
| Cohesion (Mpa) | 47 | 44 | 15 | 6.5 | |
| Friction angle (°) | 57.5 | 35 | 41 | 21 | |
| Tensile strength (Mpa) | 18 | 11.56 | 3.6 | 0.19 | |
| Residual Cohesion Residual Friction Angle Residual Tensile Strength | 0 30 0 | 0 10 0 | 0 5 0 | 0 4 0 | |
| Sample | E (Gpa) | V | UCS (Mpa) | BTS (Mpa) |
|---|---|---|---|---|
| Error (%) | Error (%) | Error (%) | Error (%) | |
| LdB Granite | 6.8 | 2.3 | 0.81 | 4.5 |
| Augig Granite | 1.54 | 0.86 | 0.49 | 2.6 |
| TS Sandstone | 3.44 | 0 | 1.2 | 1.3 |
| Coal | −5.41 | 1.1 | −0.17 | −1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Chen, Y.; Du, X.; Xiao, P.; Liao, S.; Azzam, R. Investigation of Microcrack Propagation and Energy Evolution in Brittle Rocks Based on the Voronoi Model. Materials 2021, 14, 2108. https://doi.org/10.3390/ma14092108
Liu G, Chen Y, Du X, Xiao P, Liao S, Azzam R. Investigation of Microcrack Propagation and Energy Evolution in Brittle Rocks Based on the Voronoi Model. Materials. 2021; 14(9):2108. https://doi.org/10.3390/ma14092108
Chicago/Turabian StyleLiu, Guanlin, Youliang Chen, Xi Du, Peng Xiao, Shaoming Liao, and Rafig Azzam. 2021. "Investigation of Microcrack Propagation and Energy Evolution in Brittle Rocks Based on the Voronoi Model" Materials 14, no. 9: 2108. https://doi.org/10.3390/ma14092108





