Bifunctional Metamaterials Using Spatial Phase Gradient Architectures: Generalized Reflection and Refraction Considerations
Abstract
:1. Introduction
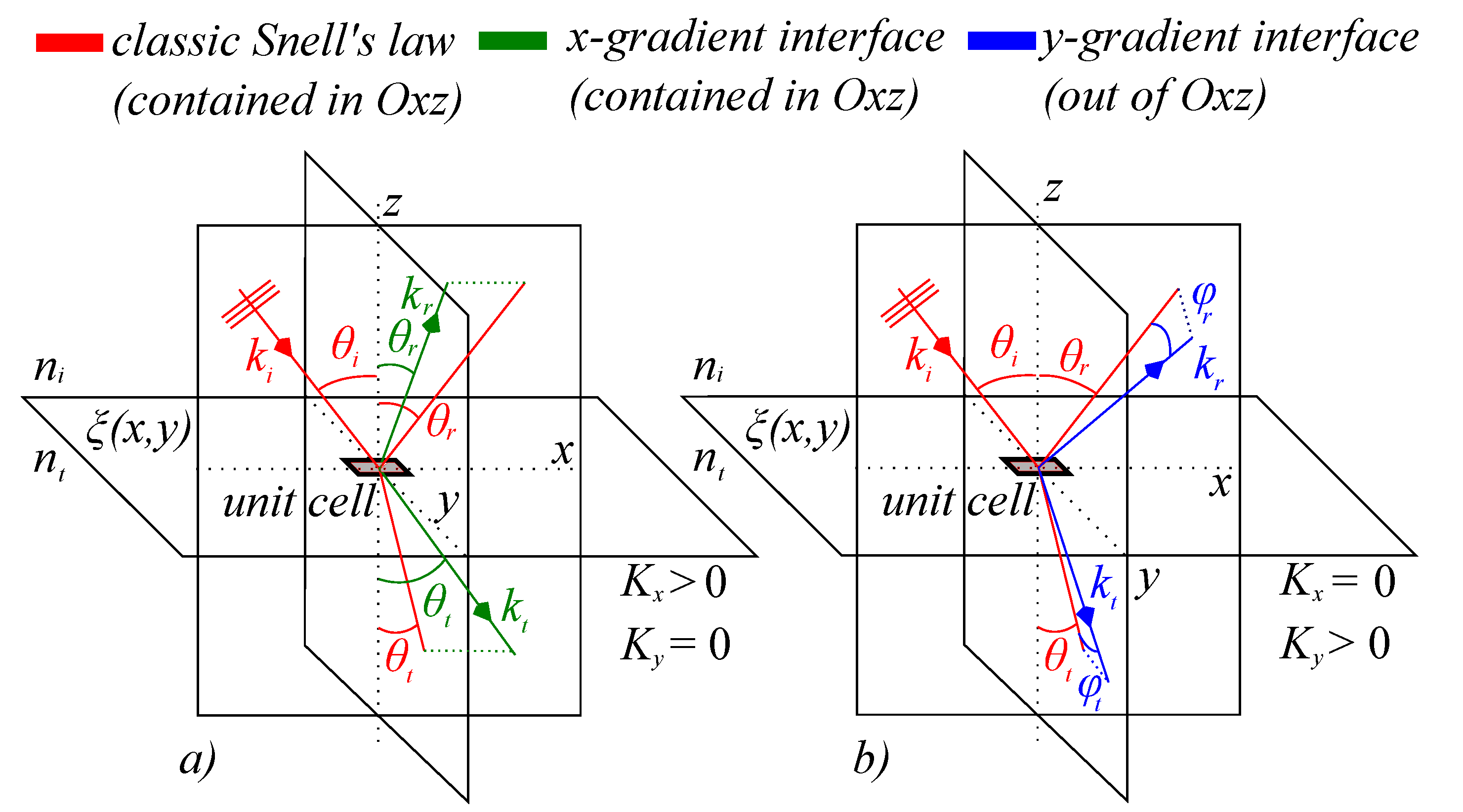
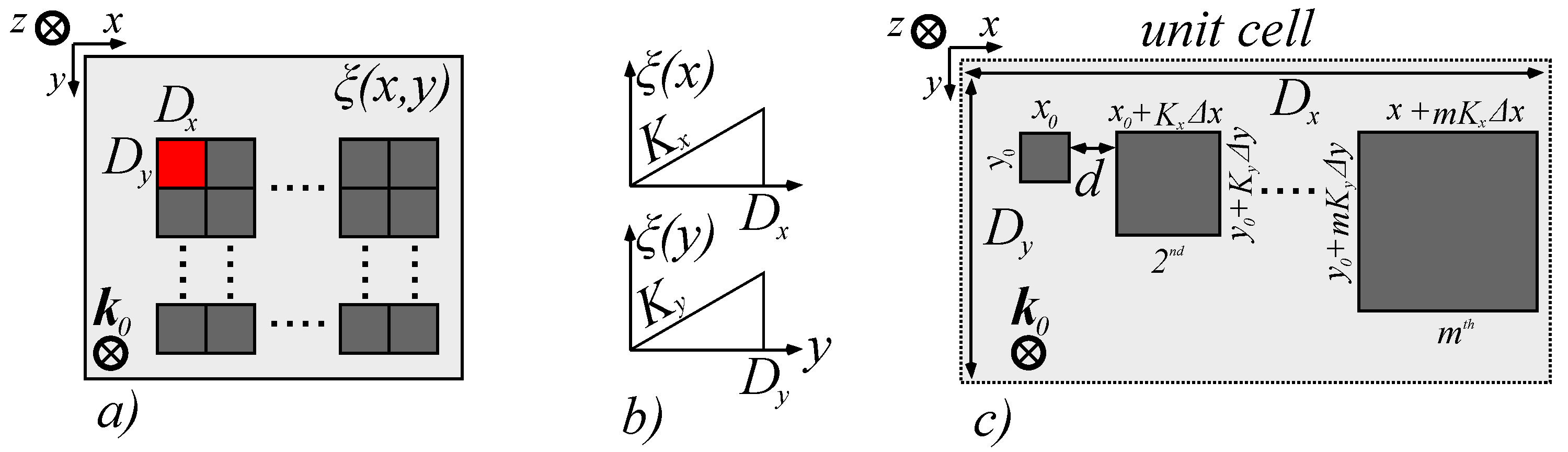
2. Theoretical Model and Simulation Conditions
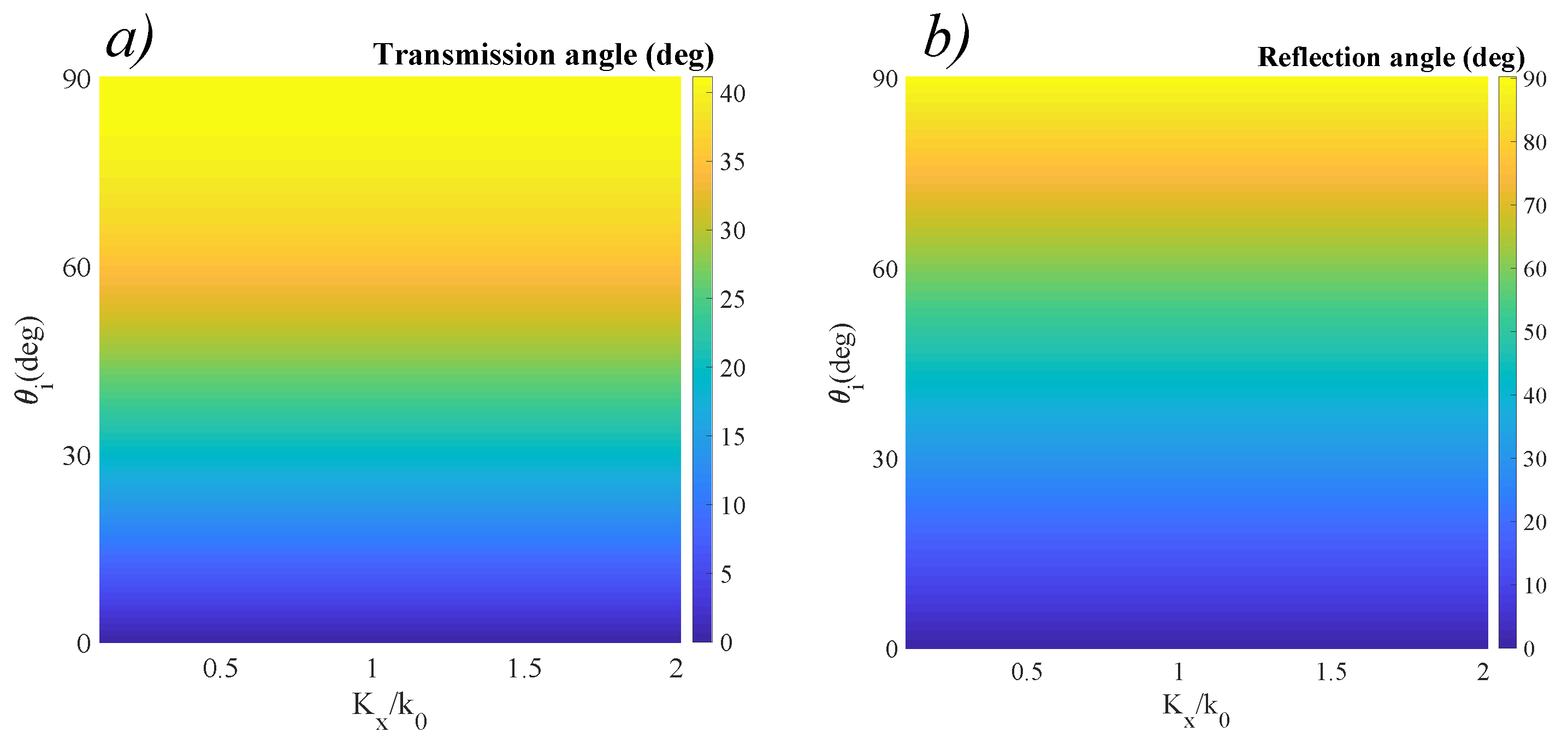
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lunghi, T.; Doutre, F.; Rambu, A.P.; Bellec, M.; De Micheli, M.P.; Apetrei, A.M.; Alibart, O.; Balebas, N.; Tascu, S.; Tanzilli, S. Broadband integrated beam splitter using spatial adiabatic passage. Opt. Express 2015, 26, 27058–27063. [Google Scholar] [CrossRef]
- Rambu, A.P.; Apetrei, A.M.; Doutre, F.; Tronche, H.; Tiron, V.; DeMicheli, M.P.; Tascu, S. Lithium niobate waveguides with high-index contrast and preserved nonlinearity fabricated by a high vacuum vapor-phase proton exchange. Photon. Res. 2020, 8, 8–16. [Google Scholar] [CrossRef] [Green Version]
- Mondain, F.; Brunel, F.; Hua, X.; Gouzien, E.; Zavatta, A.; Lunghi, T.; Doutre, F.; DeMicheli, M.P.; Tanzilli, S.; d’Auria, V. Photorefractive effect in LiNbO3-based integrated-optical circuits for continuous variable experiments. Opt. Express 2020, 28, 23176–23188. [Google Scholar] [CrossRef] [PubMed]
- Tanzilli, S.; Tittel, H.; De Riedmatten, H.; Zbinden, H.; Baldi, P.; DeMicheli, M.P.; Ostrowsky, D.B.; Gisin, N. PPLN waveguide for quantum communication. Eur. Phys. J. D Mol. Plasma Phys. 2002, 18, 155–160. [Google Scholar] [CrossRef] [Green Version]
- Kaiser, F.; Vegyris, P.; Martin, A.; Aktas, D.; DeMicheli, M.P.; Alibart, O.; Tanzilli, S. Quantum optical frequency up-conversion for polarisation entangled qubits: Towards interconnected quantum information devices. Opt. Express 2019, 27, 25603–25610. [Google Scholar] [CrossRef]
- Kaiser, F.; Issautier, A.; Ngah, L.A.; Dănilă, O.; Herrmann, H.; Sohler, W.; Martin, A.; Tanzilli, S. High-quality polarization entanglement state preparation and manipulation in standard telecommunication channels. New J. Phys. 2012, 14, 085015. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Veselago, V.G. Electrodynamics of materials with negative index of refraction. J. Phys. Usp. 2003, 46, 764–768. [Google Scholar] [CrossRef]
- Pendry, J.B.; Holden, A.J.; Stewart, W.J.; Youngs, I. Extremely low frequency plasmons in metallic mesostructures. Phys. Rev. Lett. 1996, 76. [Google Scholar] [CrossRef] [Green Version]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85. [Google Scholar] [CrossRef]
- Smith, D.R.; Padilla, W.; Vier, D.C.; Nemat-Nasser, S.C.; Schultz, S. Negative permeability from split ring resonator arrays. In Proceedings of the Conference Digest. 200 Conference on Lasers and Electro-Optics Europe (Cat. No. 00TH8505), Nice, France, 10–15 September 2000. [Google Scholar]
- Smith, D.R.; Padilla, W.J.; Vier, D.C.; Nemat-Nasser, S.C.; Schultz, S. Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 2000, 84, 4184–4187. [Google Scholar] [CrossRef] [Green Version]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Veselago, V.; Braginsky, L.; Shkover, V.; Hafner, C. Negative refractive index materials. J. Comp. Theor. Nanosci. 2006, 3, 189–218. [Google Scholar] [CrossRef]
- Sihvola, A. Ubi Materia, ibi Geometria. Proc. Bianisotropics. 2000, pp. 299–303. Available online: users.aalto.fi (accessed on 24 April 2021).
- Lindell, I.V.; Sihvola, A. Soft-and-hard/DB boundary conditions defined by a skewon-axion medium. IEEE Trans. Antenna Propag. 2013, 61, 768–774. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Ting, C.W.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef] [Green Version]
- Arbabi, E.; Arbabi, A.; Kamali, S.M.; Horie, Y.; Faraon, A. Controlling the sign of chromatic dispersion in diffractive optics with dielectric metasurfaces. Optica 2017, 4, 625–632. [Google Scholar] [CrossRef]
- Sawant, R.; Bhumkar, P.; Zhu, A.Y.; Ni, P.; Capasso, F.; Genevet, P. Mitigating chromatic dispersion with hybrid optical metasurfaces. Adv. Mat. 2019, 31. [Google Scholar] [CrossRef]
- Munk, B.A. Frequency Selective Surfaces: Theory and Design; Wiley Interscience: Hoboken, NJ, USA, 2000. [Google Scholar]
- Pu, M.; Feng, Q.; Wang, M.; Chenggang, H.; Huang, C.; Ma, X.; Zhao, Z.; Wang, C.; Luo, X. Ultrathin broadband nearly perfect absorber with symmetrical coherent illumination. Opt. Express 2012, 20, 2246–2254. [Google Scholar] [CrossRef] [PubMed]
- Correas-Serrano, D.; Gomez-Diaz, J.S.; Tymchenko, M.; Alù, A. Nonlocal response of hyperbolic metasurfaces. Opt. Express 2015, 23, 29434–29448. [Google Scholar] [CrossRef]
- Pors, A.; Bozhevolnyi, S.I. Plasmonic metasurfaces for efficient phase control in reflection. Opt. Express 2013, 21, 27438–27451. [Google Scholar] [CrossRef] [PubMed]
- Leonhardt, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Ji, C.; Mock, J.; Chin, J.Y.; Cui, T.J.; Smith, D.R. Broadband ground-plane cloak. Science 2009, 323, 366. [Google Scholar] [CrossRef] [PubMed]
- Debus, C.; Bolivar, P.H. Frequency selective surfaces for high sensitivity terahertz sensing. Appl. Phys. Lett. 2007, 91. [Google Scholar] [CrossRef]
- Christofi, A.; Kawaguchi, Y.; Alù, A.; Khanikaev, A.B. Giant enhancement of Faraday rotation due to electromagnetically induced transparency in all-dielectric magneto-optical metasurfaces. Opt. Lett. 2018, 43, 1838–1841. [Google Scholar] [CrossRef] [PubMed]
- Liberal, I.; Li, Y.; Engheta, N. Reconfigurable epsilon near-zero metasurfaces via photonic doping. Nanophotonics 2018, 7. [Google Scholar] [CrossRef]
- Lee, C.; Choi, H.J.; Jeong, H. Tunable metasurfaces for visible and SWIR applications. Nano Converg. 2020, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gomez-Diaz, J.S.; Tymchenko, M.; Alù, A. Hyperbolic metasurfaces: Surface plasmons, light-matter interactions, and physical implementation using graphene strips. Opt. Mat. Express 2015, 5, 2313–2329. [Google Scholar] [CrossRef]
- Yang, Y.; Qin, P.; Lin, X.; Li, E.; Wang, Z.; Zhang, B.; Chen, H. Type-I hyperbolic metasurfaces for highly-squeezed designer polaritons with negative group velocity. Nat. Comm. 2019, 10. [Google Scholar] [CrossRef] [Green Version]
- Hu, G.; Krasnok, A.; Mazor, Y.; Qiu, C.W.; Alù, A. Moiré Hyperbolic Metasurfaces. Nano Lett. 2020, 20, 3217–3224. [Google Scholar] [CrossRef]
- Babicheva, V.E.; Evlyukhin, A.B. Resonant lattice Kerker effect in metasurfaces with electric and magnetic optical responses. Las. Phot. Rev. 2017, 11. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Kivshar, Y.S. Generalized Kerker effects in nanophotonics and meta-optics. Opt. Express 2018, 26, 13085–13105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmidt, R.; Slobozhanyuk, A.; Belov, P.; Webb, A. Flexible and compact hybrid metasurfaces for enhanced ultra high field magnetic resonance imaging. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [PubMed]
- Kang, E.S.H.; Chaharsougi, M.S.; Rossi, S.; Jonnson, M.P. Hybrid plasmonic metasurfaces. J. Appl. Phys. 2019, 126, 140901. [Google Scholar] [CrossRef]
- Zhou, C.; Li, S.; Fan, M.; Wang, X.; Xu, Y.; Weiwei, X.; Xiao, S.; Hu, M.; Liu, J. Optical radiation manipulation by Si-Ge2Sb2Te5 hybrid metasurfaces. Opt. Express 2020, 28, 9690–9701. [Google Scholar] [CrossRef] [PubMed]
- Bărar, A.; Dănilă, O.; Mănăilă-Maximean, D.; Loiko, V.A. Active spectral absorption control in a tunable liquid crystal/metamaterial structure by polarization plane rotation. In Proceedings of the 4th International Conference on Nanotechnologies and Biomedical Engineering, Chisinau, Moldova, 18–21 September 2020; pp. 299–303. [Google Scholar]
- Gao, S.; Park, C.S.; Lee, S.S.; Choi, D.Y. All-dielectric metasurfaces for simultaneously realizing polarization rotation and wavefront shaping of visible light. Nanoscale 2019, 11, 4083–4090. [Google Scholar] [CrossRef]
- Yang, W.; Xiao, S.; Song, Q.; Liu, Y.; Wu, Y.; Wang, S.; Yu, J.; Han, J.; Tsai, D.P. All-dielectric metasurface for high-performance structural color. Nat. Commun. 2020, 11. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, H.; Rahim, A.A.; Maab, H.; Ali, M.M.; Mahmood, N.; Naureen, S. Phase engineering with all-dielectric metasurfaces for focused-optical-vortex (FOV) beams with high cross-polarization efficiency. Opt. Mat. Express 2020, 10, 434–448. [Google Scholar] [CrossRef]
- Kowerdziej, R.; Jaroszewicz, L. Tunable dual-band liquid crystal based near-infrared perfect metamaterial absorber with high-loss metal. Liq. Cryst. 2019, 46, 1568–1573. [Google Scholar] [CrossRef]
- Kowerdziej, R.; Wróbel, J.; Kula, P. Ultrafast electrical switching of nanostructured metadevice with dual-frequency liquid crystal. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef] [Green Version]
- Pancharatnam, S. Generalized theory of interference and its applications. Part I. Coherent pencils. Proc. Indian Acad. Sci. A 1956, 44, 247–262. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. A 1984, 392, 45–57. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, L.; Hu, D.; Chen, S.; Xie, S.; Lu, Y.; Cao, Y.; Zhu, Z.; Jin, L.; Guan, B.O.; et al. Full-visible multifunctional aluminium metasurfaces by in situ anisotropic thermoplasmonic laser printing. Nanoscale Horiz. 2019, 4, 601–609. [Google Scholar] [CrossRef]
- Shirmanesh, G.K.; Sokhoyan, R.; Wu, P.C.; Atwater, H.A. Electro-optically tunable multifunctional metasurfaces. ACS Nano 2020, 14, 6912–6920. [Google Scholar] [CrossRef] [PubMed]
- Shanei, M.M.; Fathi, D.; Ghasemifard, F.; Quedovo-Teruel, O. All-silicon reconfigurable metasurfaces for multifunction and tunable performance at optical frequencies based on glide symmetry. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef]
- Sun, S.; Yang, K.Y.; Wang, C.M.; Juan, T.K.; Chen, W.T.; Liao, C.Y.; He, Q.; Xiao, S.; Kung, W.T.; Guo, G.Y.; et al. High-efficiency broadband anomalous reflection by gradient metasurfaces. Nano Lett. 2012, 12, 6223–6229. [Google Scholar] [CrossRef] [PubMed]
- Aieta, F.; Genevet, P.; Yu, N.; Kats, M.A.; Gaburro, Z.; Capasso, F. Out-of-plane reflection and refraction of light by anisotropic optical antenna metasurfaces with phase discontinuities. Nano Lett. 2012, 12, 1702–1706. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, H.; Wang, F.; Meng, H.; Guo, J.; Li, J.; Wei, Z. High-fficiency, near-diffraction limited, dielectric metasurface lenses based on crystalline Titanium dioxide at visible wavelengths. Nanomaterials 2018, 8, 288. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danila, O.; Manaila-Maximean, D. Bifunctional Metamaterials Using Spatial Phase Gradient Architectures: Generalized Reflection and Refraction Considerations. Materials 2021, 14, 2201. https://doi.org/10.3390/ma14092201
Danila O, Manaila-Maximean D. Bifunctional Metamaterials Using Spatial Phase Gradient Architectures: Generalized Reflection and Refraction Considerations. Materials. 2021; 14(9):2201. https://doi.org/10.3390/ma14092201
Chicago/Turabian StyleDanila, Octavian, and Doina Manaila-Maximean. 2021. "Bifunctional Metamaterials Using Spatial Phase Gradient Architectures: Generalized Reflection and Refraction Considerations" Materials 14, no. 9: 2201. https://doi.org/10.3390/ma14092201





