Computational Approaches of Quasi-Static Compression Loading of SS316L Lattice Structures Made by Selective Laser Melting
Abstract
1. Introduction
1.1. Lightweight Structures
1.2. Computational Approaches
2. Materials and Methods
2.1. Powder Material
2.2. Lattice Structure
2.3. Multi-Strut Tensile Samples
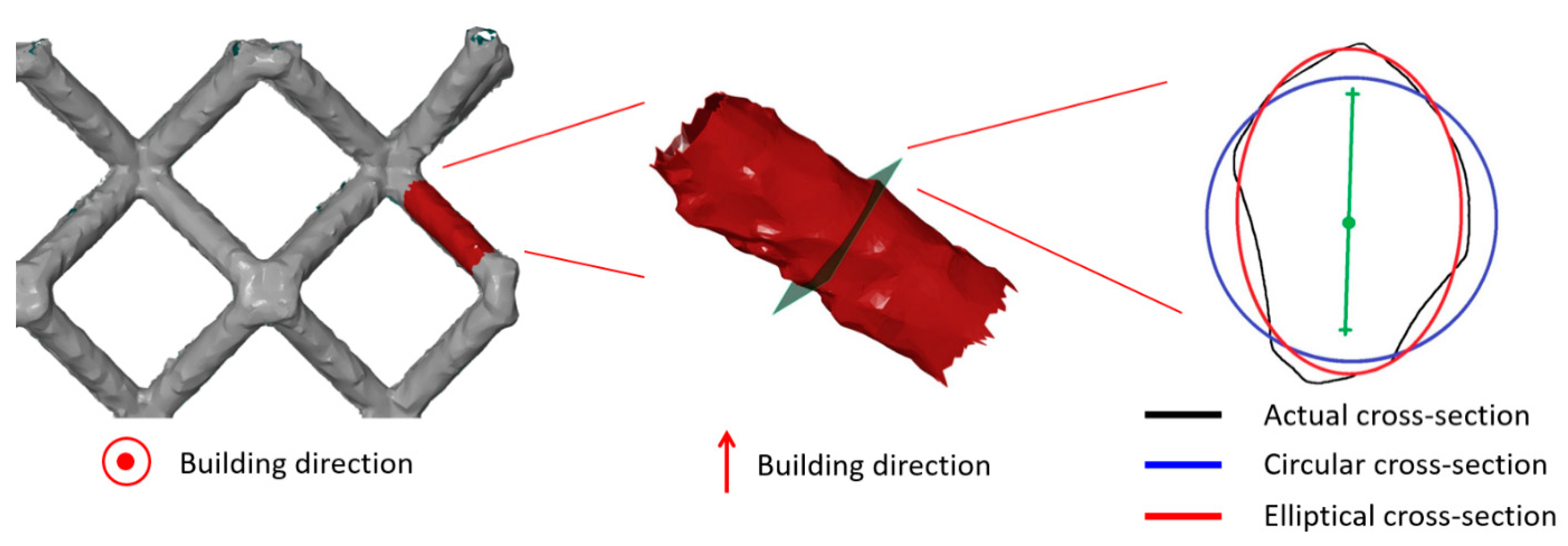
2.4. Dimension and Shape Analysis
2.5. Quasi-Static Mechanical Tests
2.6. Analytical Formulation
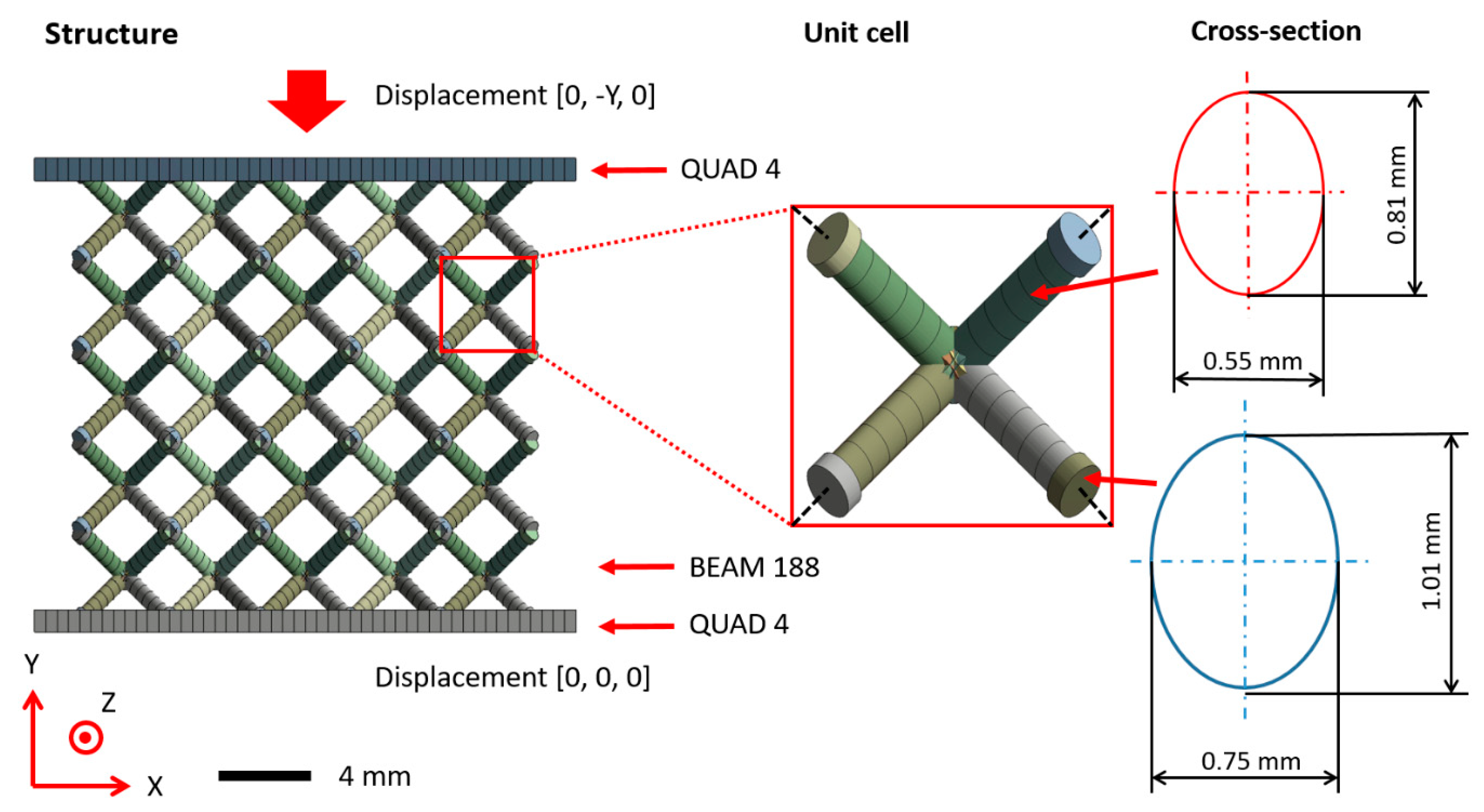
2.7. Finite Element Analysis
2.7.1. Solid Element Model (Continuum Model)
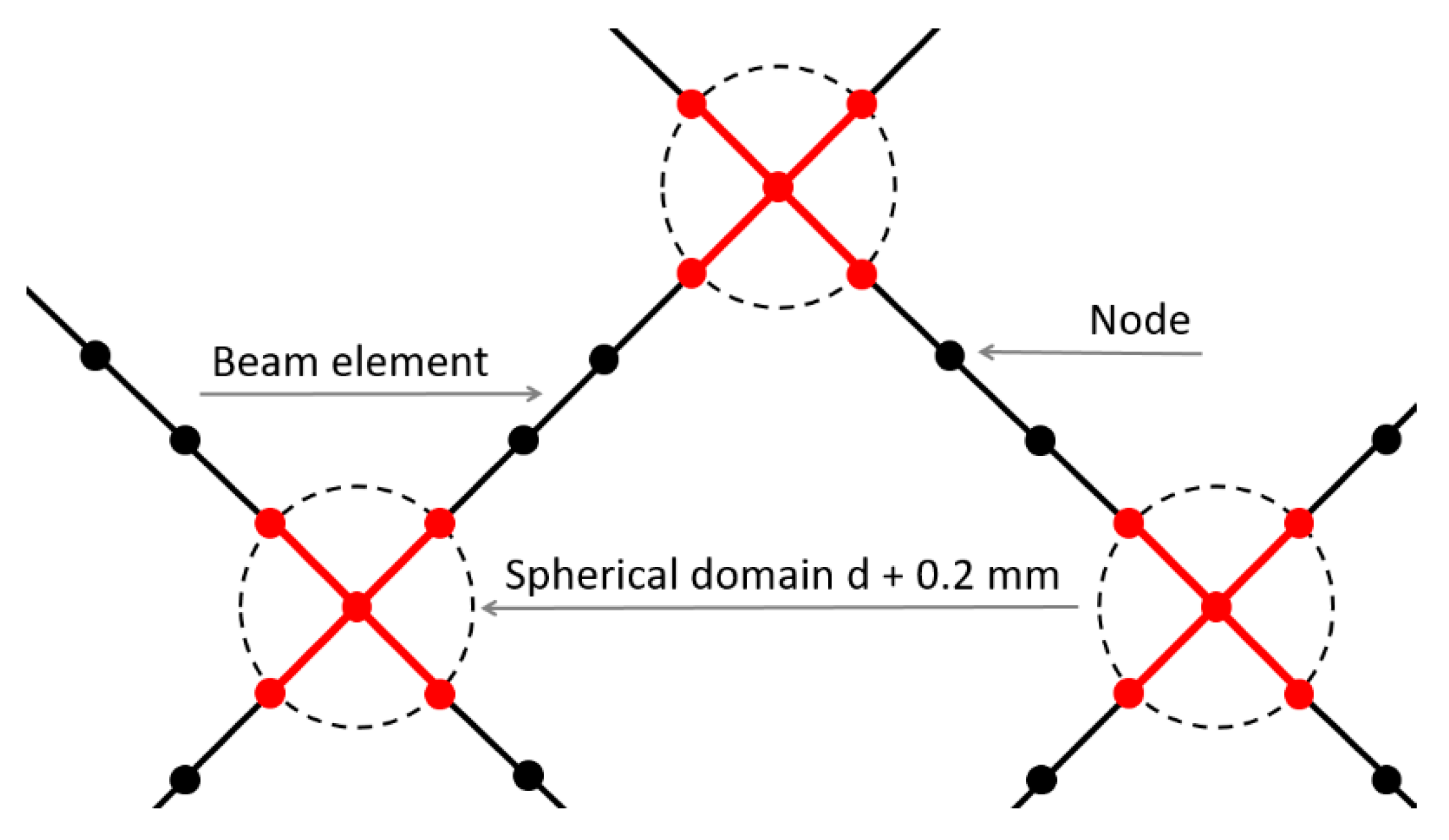
2.7.2. Beam Element Model
3. Results and Discussion
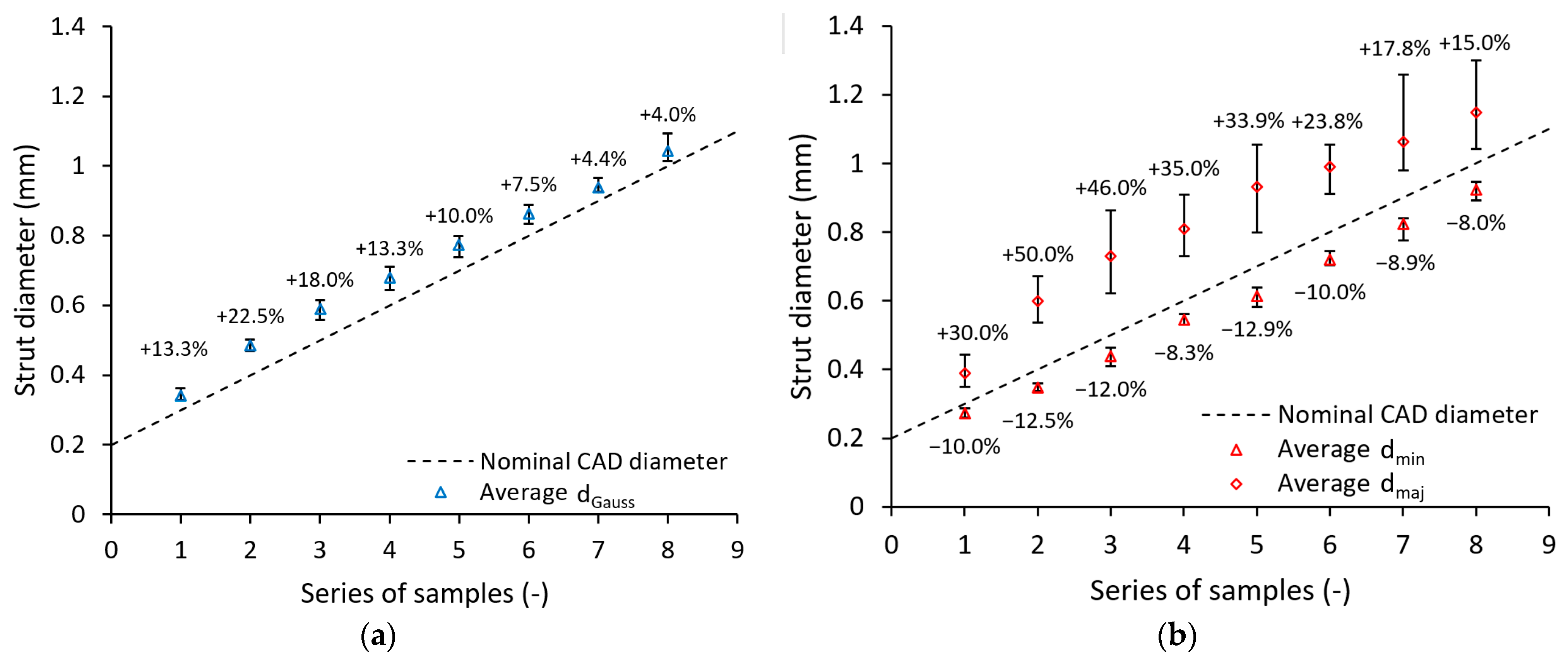
3.1. Strut Dimension Analysis/Samples Morphology
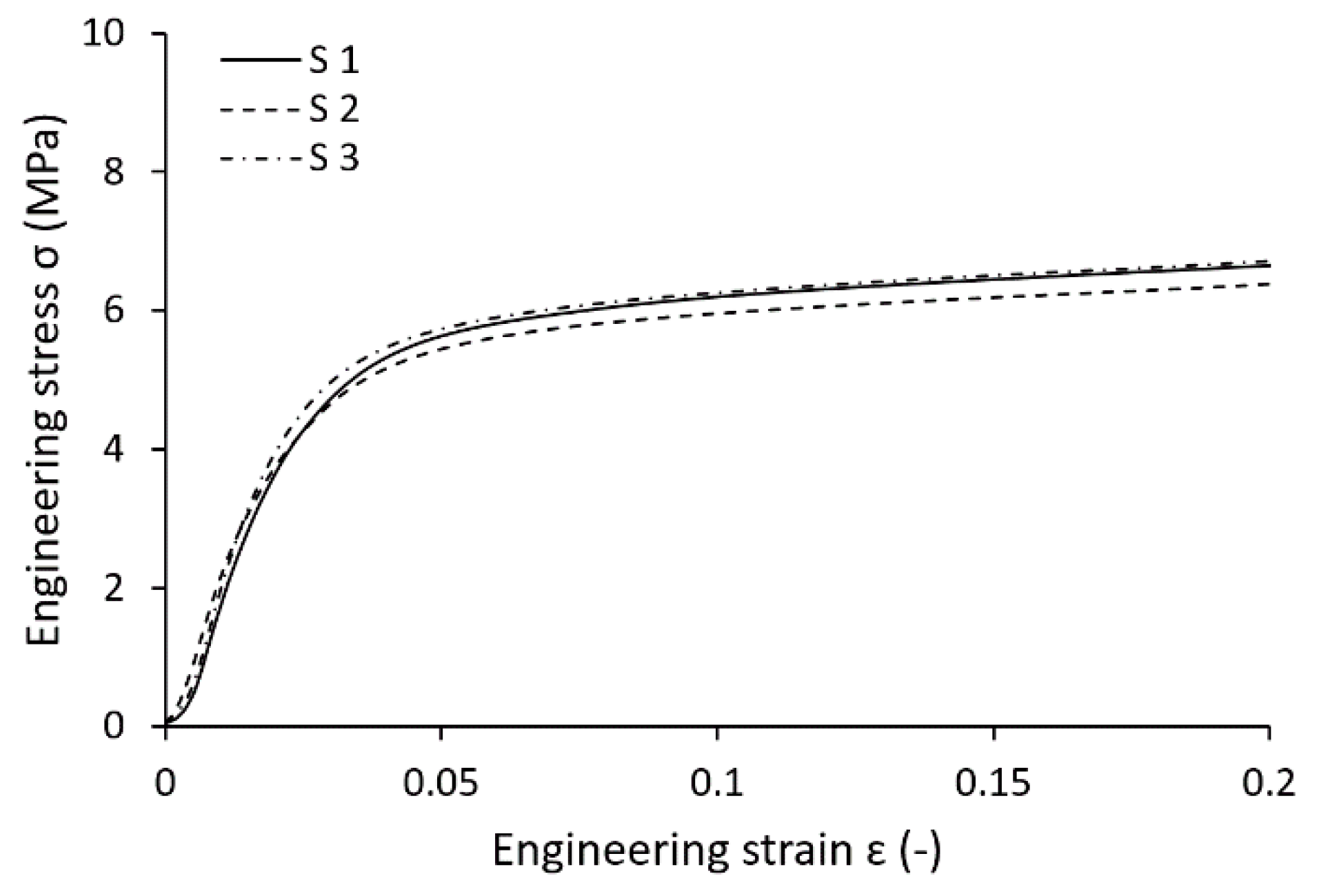
3.2. Multi-Strut Tensile Test Evaluation
- Young’s modulus Es and yield strength Rp0.2% determined by testing of multi-strut tensile samples achieved only 57% and 75% of the conventional samples values;
- Young’s modulus Es obtained by multi-strut tensile samples testing is approximately 49% lower compared to the results achieved by single strut samples testing combined with the numerical correction presented by Tsopanos [36] and Smith [3]. Contrary to this, yield strength Rp0.2% was more than two times higher compared to previous studies;
- A good correlation of mechanical properties between multi-strut samples test and Gümrük [32] study was found. Young’s modulus Es and yield strength Rp0.2% values deviated up to 5%;
- A good correlation of mechanical properties between conventional samples and the data sheet from SLM Solutions was found. Young’s modulus Es, yield strength Rp0.2%, and elongation at break A values deviated up to 7%.
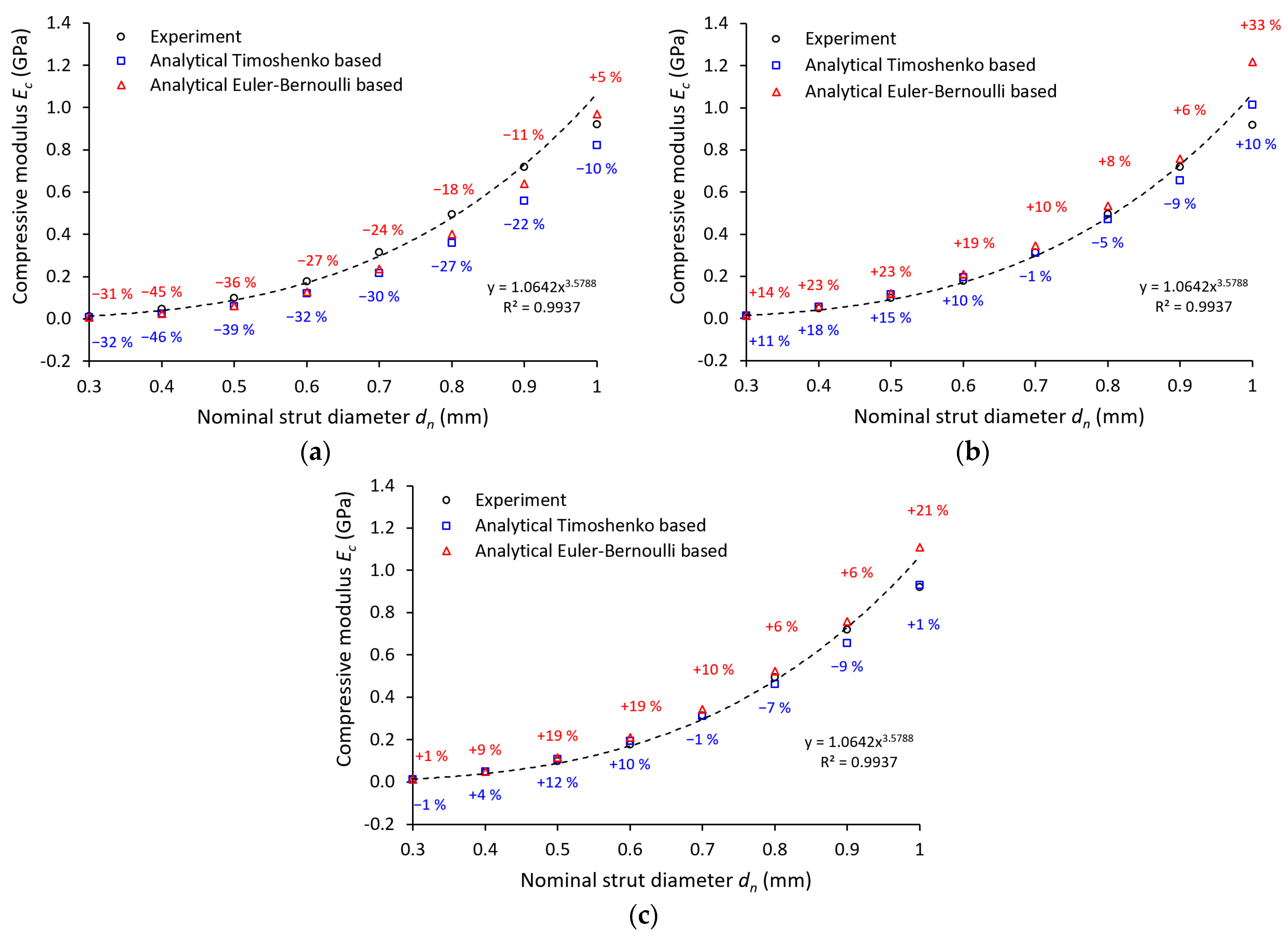
3.3. Comparison of Analytical Approaches and Experiment
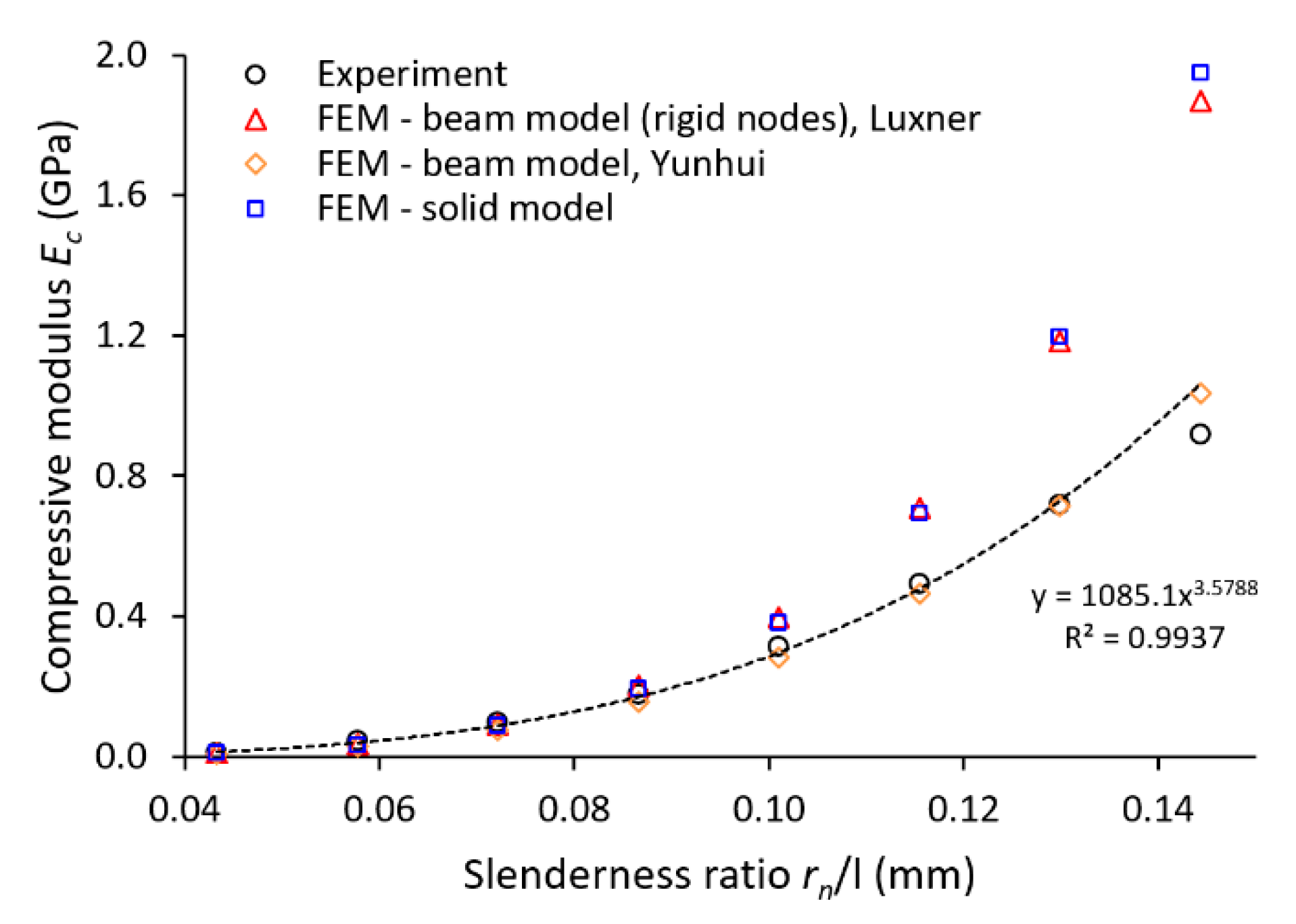
3.4. Comparison of FEM and Experiment
3.4.1. Linear Material
3.4.2. Non-Linear Material
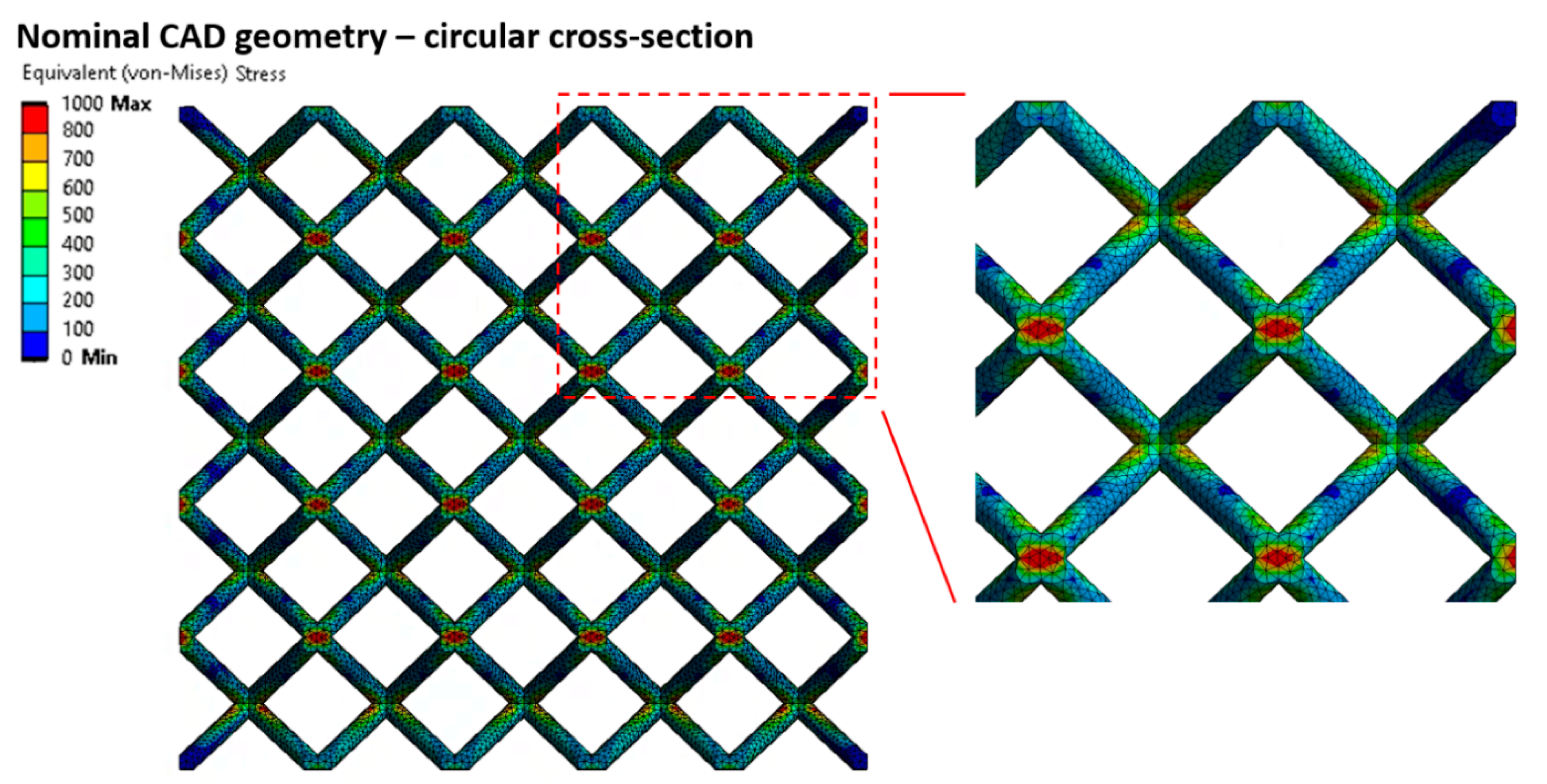
3.4.3. Comparison with Specific Structured Component
4. Conclusions
- It is efficient to use specially designed tensile samples that consist of more thin struts to determine the actual mechanical properties of lattice structures. A good correlation (up to 5%) between mechanical properties determined in this study and described in the literature [32] was found. The analytical models support the credibility of the mechanical properties in the linear-elastic regime;
- The geometrical imperfections can acquire different significance across variating strut diameter for one structure manufactured with the same process parameters and different geometrical parameters, e.g., strut diameter;
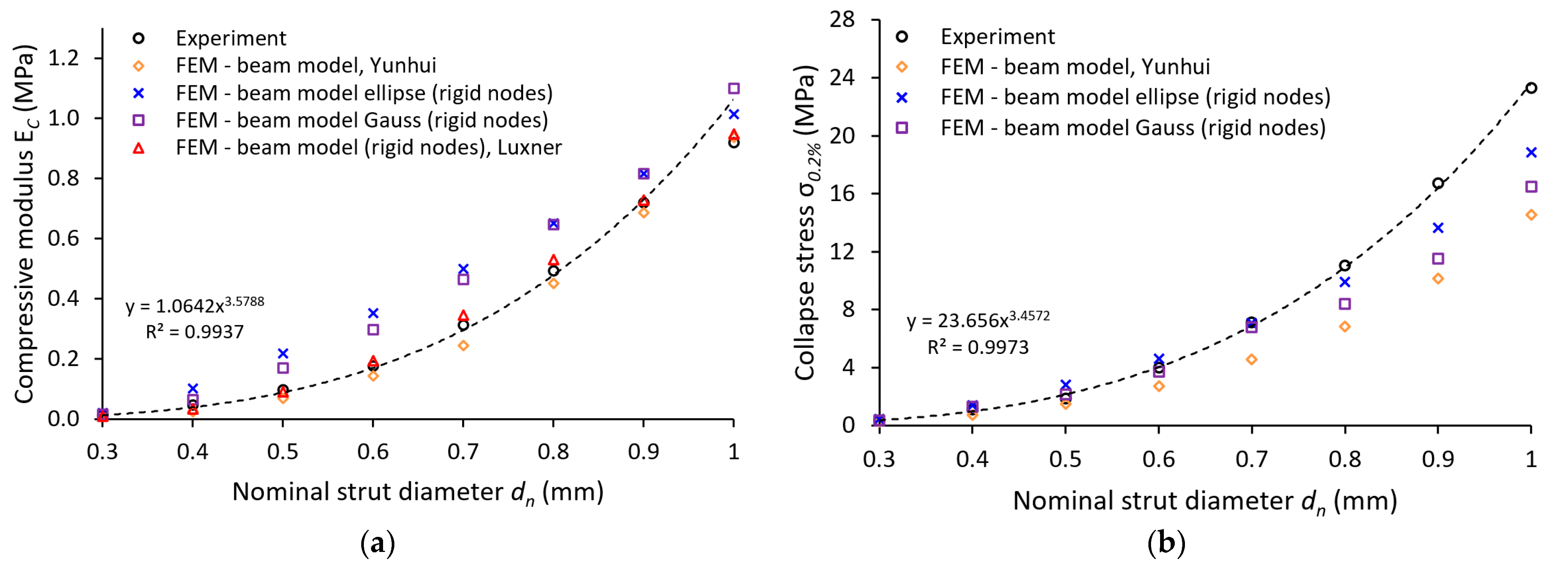
- The FE analyses with solid and beam element models can predict the lattice structure compressive modulus with similar accuracy if an artificial stiffness increase in the vicinity of nodes is used within the beam element model;
- The significance of geometrical imperfections increased after reaching 0.2% deformation beyond the linear regime (collapse strain). Including the imperfections improve the accuracy of calculations for both introduced approaches, whereas the change of cross-section to the elliptical seems to be more effective than the change to Gaussian circular for all diameters in the tested range;
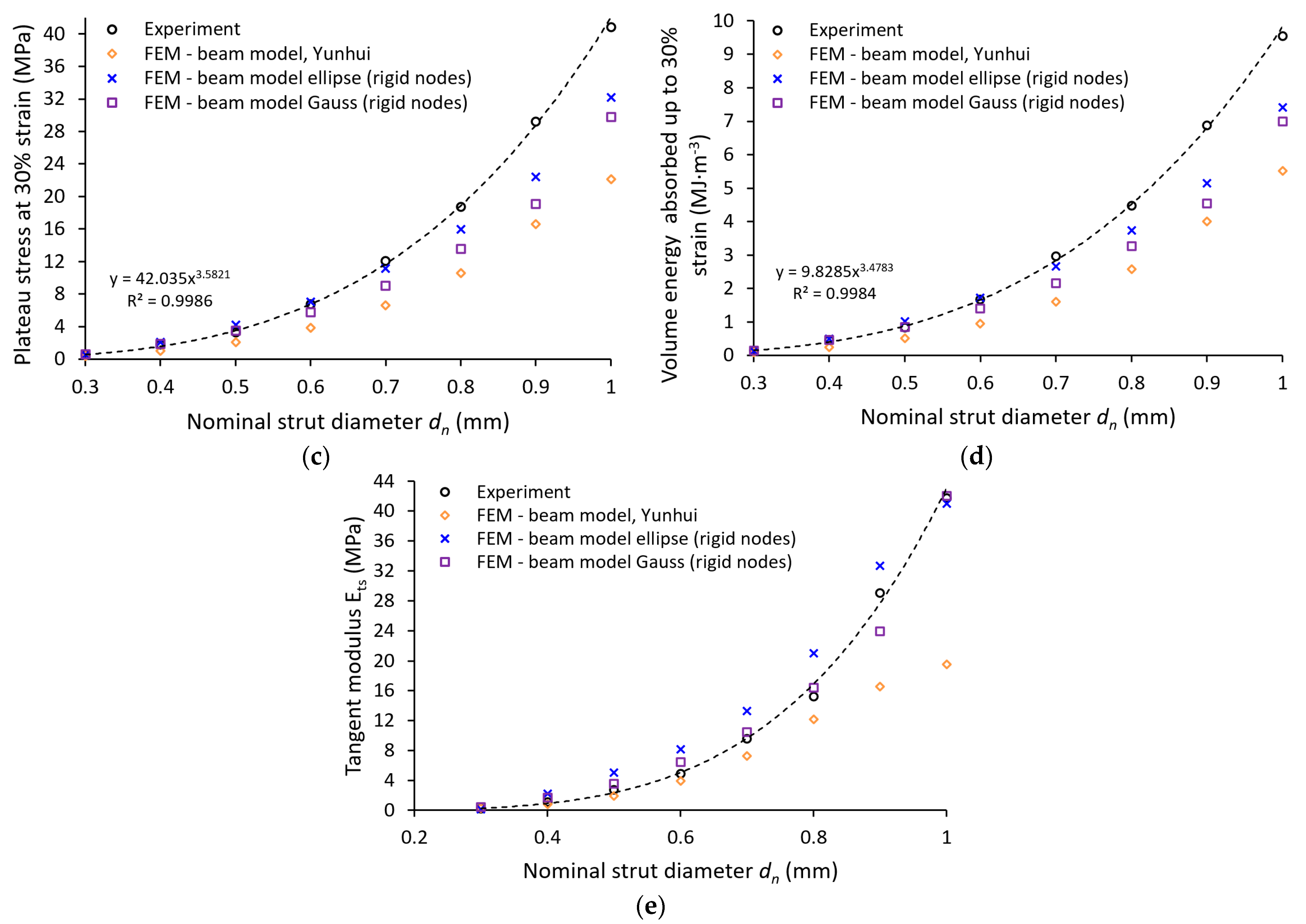
- The calculated levels of engineering stress compared to experiments in the area of lattice structure progressive collapse (30% deflection of structure) exhibit lower values with increasing nominal strut diameter. This phenomenon can indicate different values of mechanical properties of different strut diameters;
- According to the FE simulation, an increment of partly melted material has a bigger significance for the loading force transmission. The finding is similar to the study of Vrana [31], who determined geometrical imperfections for AlSi10Mg with similar methods. It would be interesting to investigate the strut diameters beyond the range of diameters in this study (nominal CAD diameter > 1 mm) to determine the influence of the described imperfections in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | additive manufacturing |
| BCC | Body-centered cubic |
| FEA | finite element analysis |
| SLM | Selective laser melting |
| FCC | face-centered cubic |
| CAD | computer-aided design |
| µ-CT | micro computed tomography |
| Q10 | 10% quantile of particles distribution |
| Q50 | 50% quantile of particles distribution |
| Q90 | 90% quantile of particles distribution |
| elastic modulus of lattice structure | |
| elastic modulus of bulk material | |
| Poisson’s constant of bulk material | |
| rn | nominal strut radius |
| l | half of unit cell diagonal |
| m | weight of sample |
| ma | measured weight of sample |
| mn | nominal CAD weight of sample |
| σ0.2% | collapse stress (0.2% structure strain) |
| Rm | ultimate tensile strength |
| Φn | nominal volume fraction |
| dn | nominal strut diameter |
| Sn | cross-section area of nominal strut diameter |
| dGauss | diameter given by Gauss distribution |
| SGauss | cross-section area of Gauss strut diameter |
| dmaj | major axis diameter |
| dmin | minor axis diameter |
| Sellipse | cross-section area of elliptical strut |
| Rp0.2% | yield strength (0.2% proof stress) |
| Et | tangent modulus |
| Ec | structure compressive modulus |
| σ | engineering stress |
| Ɛ | engineering strain |
| Ets | tangent modulus of structure |
| A | elongation at break |
| Ea | volume energy absorbed |
References
- Bonatti, C.; Mohr, D. Mechanical Performance of Additively-Manufactured Anisotropic and Isotropic Smooth Shell-Lattice Materials: Simulations & Experiments. J. Mech. Phys. Solids 2019. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 2014; ISBN 9781139878326. [Google Scholar]
- Smith, M.; Guan, Z.; Cantwell, W.J. Finite Element Modelling of the Compressive Response of Lattice Structures Manufactured Using the Selective Laser Melting Technique. Int. J. Mech. Sci. 2013, 67, 28–41. [Google Scholar] [CrossRef]
- Harris, J.A.; Winter, R.E.; McShane, G.J. Impact Response of Additively Manufactured Metallic Hybrid Lattice Materials. Int. J. Impact Eng. 2017, 104, 177–191. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A. Isotropic Constitutive Models for Metallic Foams. J. Mech. Phys. Solids 2000, 48, 1253–1283. [Google Scholar] [CrossRef]
- Rashed, M.G.; Ashraf, M.; Mines, R.A.W.; Hazell, P.J. Metallic Microlattice Materials: A Current State of the Art on Manufacturing, Mechanical Properties and Applications. Mater. Des. 2016, 95, 518–533. [Google Scholar] [CrossRef]
- Banhart, J. Manufacture, Characterisation and Application of Cellular Metals and Metal Foams. Prog. Mater. Sci. 2001, 46, 559–632. [Google Scholar] [CrossRef]
- Salimon, A.; Bréchet, Y.; Ashby, M.F.; Greer, A.L. Potential Applications for Steel and Titanium Metal Foams. J. Mater. Sci. 2005, 40, 5793–5799. [Google Scholar] [CrossRef]
- Ozdemir, Z.; Hernandez-Nava, E.; Tyas, A.; Warren, J.A.; Fay, S.D.; Goodall, R.; Todd, I.; Askes, H. Energy Absorption in Lattice Structures in Dynamics: Experiments. Int. J. Impact Eng. 2016, 89, 49–61. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Spierings, A.B.; Mohr, D. Additively-Manufactured Metallic Micro-Lattice Materials for High Specific Energy Absorption under Static and Dynamic Loading. Acta Mater. 2016, 116, 14–28. [Google Scholar] [CrossRef]
- Ozdemir, Z.; Tyas, A.; Goodall, R.; Askes, H. Energy Absorption in Lattice Structures in Dynamics: Nonlinear FE Simulations. Int. J. Impact Eng. 2017, 102. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.; Zhang, T.; Zhou, H. Improved Mechanical Properties and Energy Absorption of BCC Lattice Structures with Triply Periodic Minimal Surfaces Fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef]
- Labeas, G.; Ptochos, E. Investigation of Sandwich Structures with Innovative Cellular Metallic Cores under Low Velocity Impact Loading. Plast. Rubber Compos. 2013, 42, 194–202. [Google Scholar] [CrossRef]
- Xiao, L.; Song, W. Additively-Manufactured Functionally Graded Ti-6Al-4V Lattice Structures with High Strength under Static and Dynamic Loading: Experiments. Int. J. Impact Eng. 2018, 111, 255–272. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Z.; Zhou, S.; Shao, J.; Wu, X. Novel Negative Poisson’s Ratio Lattice Structures with Enhanced Stiffness and Energy Absorption Capacity. Materials 2018, 11, 1095. [Google Scholar] [CrossRef]
- Vrana, R.; Vaverka, O.; Cervinek, O.; Pantelejev, L.; Hurnik, J.; Koutny, D.; Palousek, D. Heat Treatment of the SLM Processed Lattice Structure Made of AlSi10Mg and Its Effect on the Impact Energy Absorption. In Proceedings of the Conference: Euro PM2019 Congress & Exhibition, Maastricht, The Netherlands, 13–16 October 2019; p. 6. [Google Scholar]
- Maskery, I.; Hussey, A.; Panesar, A.; Aremu, A.; Tuck, C.; Ashcroft, I.; Hague, R. An Investigation into Reinforced and Functionally Graded Lattice Structures. J. Cell. Plast. 2017, 53, 151–165. [Google Scholar] [CrossRef]
- Zhang, L.; Feih, S.; Daynes, S.; Chang, S.; Wang, M.Y.; Wei, J.; Lu, W.F. Energy Absorption Characteristics of Metallic Triply Periodic Minimal Surface Sheet Structures under Compressive Loading. Addit. Manuf. 2018, 23, 505–515. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Mohr, D. Stiffness and Specific Energy Absorption of Additively-Manufactured Metallic BCC Metamaterials Composed of Tapered Beams. Int. J. Mech. Sci. 2018, 141, 101–116. [Google Scholar] [CrossRef]
- Al-Saedi, D.S.J.; Masood, S.H.; Faizan-Ur-Rab, M.; Alomarah, A.; Ponnusamy, P. Mechanical Properties and Energy Absorption Capability of Functionally Graded F2BCC Lattice Fabricated by SLM. Mater. Des. 2018, 144, 32–44. [Google Scholar] [CrossRef]
- Mines, R.A.W.; Tsopanos, S.; Shen, Y.; Hasan, R.; McKown, S.T. Drop Weight Impact Behaviour of Sandwich Panels with Metallic Micro Lattice Cores. Int. J. Impact Eng. 2013, 60, 120–132. [Google Scholar] [CrossRef]
- Crupi, V.; Kara, E.; Epasto, G.; Guglielmino, E.; Aykul, H. Static Behavior of Lattice Structures Produced via Direct Metal Laser Sintering Technology. Mater. Des. 2017, 135, 246–256. [Google Scholar] [CrossRef]
- Vrána, R.; Koutný, D.; Paloušek, D.; Pantělejev, L.; Jaroš, J.; Zikmund, T.; Kaiser, J. Selective Laser Melting Strategy for Fabrication of Thin Struts Usable in Lattice Structures. Materials 2018, 11, 1763. [Google Scholar] [CrossRef]
- Lei, H.; Li, C.; Meng, J.; Zhou, H.; Liu, Y.; Zhang, X.; Wang, P.; Fang, D. Evaluation of Compressive Properties of SLM-Fabricated Multi-Layer Lattice Structures by Experimental Test and μ-CT-Based Finite Element Analysis. Mater. Des. 2019, 169, 107685. [Google Scholar] [CrossRef]
- Luxner, M.H.; Stampfl, J.; Pettermann, H.E. Linear and Nonlinear Numerical Investigations of Regular Open Cell Structures. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Anaheim, CA, USA, 13–19 November 2004; American Society of Mechanical Engineers, Aerospace Division (Publication) AD: New York, NY, USA, 2004; Volume 47004, pp. 469–475. [Google Scholar]
- Luxner, M.H.; Stampfl, J.; Pettermann, H.E. Finite Element Modeling Concepts and Linear Analyses of 3D Regular Open Cell Structures. J. Mater. Sci. 2005, 40, 5859–5866. [Google Scholar] [CrossRef]
- Luxner, M.H.; Woesz, A.; Stampfl, J.; Fratzl, P.; Pettermann, H.E. A Finite Element Study on the Effects of Disorder in Cellular Structures. Acta Biomater. 2009, 5, 381–390. [Google Scholar] [CrossRef] [PubMed]
- Karamooz Ravari, M.R.; Kadkhodaei, M.; Badrossamay, M.; Rezaei, R. Numerical Investigation on Mechanical Properties of Cellular Lattice Structures Fabricated by Fused Deposition Modeling. Int. J. Mech. Sci. 2014, 88, 154–161. [Google Scholar] [CrossRef]
- Dong, G.; Zhao, Y.F. Numerical and Experimental Investigation of the Joint Stiffness in Lattice Structures Fabricated by Additive Manufacturing. Int. J. Mech. Sci. 2018, 148, 475–485. [Google Scholar] [CrossRef]
- Geng, X.; Ma, L.; Liu, C.; Zhao, C.; Yue, Z.F. A FEM Study on Mechanical Behavior of Cellular Lattice Materials Based on Combined Elements. Mater. Sci. Eng. A 2018, 712, 188–198. [Google Scholar] [CrossRef]
- Vrána, R.; Cervinek, O.; Manas, P.; Koutný, D.; Paloušek, D. Dynamic Loading of Lattice Structure Made by Selective Laser Melting-Numerical Model with Substitution of Geometrical Imperfections. Materials 2018, 11, 2129. [Google Scholar] [CrossRef] [PubMed]
- Gümrük, R.; Mines, R.A.W. Compressive Behaviour of Stainless Steel Micro-Lattice Structures. Int. J. Mech. Sci. 2013, 68, 125–139. [Google Scholar] [CrossRef]
- Li, P.; Wang, Z.; Petrinic, N.; Siviour, C.R. Deformation Behaviour of Stainless Steel Microlattice Structures by Selective Laser Melting. Mater. Sci. Eng. A 2014, 614, 116–121. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, Z.; Liang, J.; Ge, J. Determination of the Strength of a Multilayer BCC Lattice Structure with Face Sheets. Int. J. Mech. Sci. 2019, 152, 568–575. [Google Scholar] [CrossRef]
- Lozanovski, B.; Leary, M.; Tran, P.; Shidid, D.; Qian, M.; Choong, P.; Brandt, M. Computational Modelling of Strut Defects in SLM Manufactured Lattice Structures. Mater. Des. 2019, 171, 107671. [Google Scholar] [CrossRef]
- Tsopanos, S.; Mines, R.A.W.; McKown, S.; Shen, Y.; Cantwell, W.J.; Brooks, W.; Sutcliffe, C.J. The Influence of Processing Parameters on the Mechanical Properties of Selectively Laser Melted Stainless Steel Microlattice Structures. J. Manuf. Sci. Eng. Trans. ASME 2010, 132, 0410111–04101112. [Google Scholar] [CrossRef]
- Amani, Y.; Dancette, S.; Delroisse, P.; Simar, A.; Maire, E. Compression Behavior of Lattice Structures Produced by Selective Laser Melting: X-Ray Tomography Based Experimental and Finite Element Approaches. Acta Mater. 2018, 159, 395–407. [Google Scholar] [CrossRef]
- SLM Solutions. Material Data Sheet. Fe-Alloy 316L (1.4404)[1]. Available online: https://www.slm-solutions.com/fileadmin/Content/Powder/MDS/MDS_Fe-Alloy_316L_0820_V0.91_EN_LS.pdf (accessed on 10 October 2019).
- Gümrük, R.; Mines, R.A.W.; Karadeniz, S. Determination of Strain Rate Sensitivity of Micro-Struts Manufactured Using the Selective Laser Melting Method. J. Mater. Eng. Perform. 2018, 27, 1016–1032. [Google Scholar] [CrossRef]
- Koutny, D.; Vrana, R.; Palousek, D. Dimensional Accuracy of Single Beams of AlSi10Mg Alloy and 316L Stainless Steel Manufactured by SLM. In Proceedings of the 5th International Conference on Additive Technologies iCAT2014, Vienna, Austria, 16–17 October 2014; Pogacar, D., Ed.; Interesansa Zavod: Ljubljana, Slovenia, 2014. [Google Scholar]
- Palousek, D.; Omasta, M.; Koutny, D.; Bednar, J.; Koutecky, T.; Dokoupil, F. Effect of Matte Coating on 3D Optical Measurement Accuracy. Opt. Mater. 2015, 40. [Google Scholar] [CrossRef]
- Ushijima, K.; Cantwell, W.J.; Mines, R.A.W.; Tsopanos, S.; Smith, M. An Investigation into the Compressive Properties of Stainless Steel Micro-Lattice Structures. J. Sandw. Struct. Mater. 2011, 13, 303–329. [Google Scholar] [CrossRef]
- Yang, Y.; Shan, M.; Zhao, L.; Qi, D.; Zhang, J. Multiple Strut-Deformation Patterns Based Analytical Elastic Modulus of Sandwich BCC Lattices. Mater. Des. 2019, 181, 107916. [Google Scholar] [CrossRef]
- Ren, X.; Xiao, L.; Hao, Z. Multi-Property Cellular Material Design Approach Based on the Mechanical Behaviour Analysis of the Reinforced Lattice Structure. Mater. Des. 2019, 174, 107785. [Google Scholar] [CrossRef]
- Werner, B.; Todt, M.; Pettermann, H.E. Nonlinear Finite Element Study of Beams with Elasto-Plastic Damage Behavior in the Post-Buckling Regime. PAMM 2019, 19, 2. [Google Scholar] [CrossRef]
- Labeas, G.N.; Sunaric, M.M. Investigation on the Static Response and Failure Process of Metallic Open Lattice Cellular Structures. Strain 2010, 46, 195–204. [Google Scholar] [CrossRef]
- Trevisan, F.; Calignano, F.; Lorusso, M.; Pakkanen, J.; Aversa, A.; Ambrosio, E.P.; Lombardi, M.; Fino, P.; Manfredi, D. On the Selective Laser Melting (SLM) of the AlSi10Mg Alloy: Process, Microstructure, and Mechanical Properties. Materials 2017, 10, 76. [Google Scholar] [CrossRef] [PubMed]
- Qiu, C.; Yue, S.; Adkins, N.J.E.; Ward, M.; Hassanin, H.; Lee, P.D.; Withers, P.J.; Attallah, M.M. Influence of Processing Conditions on Strut Structure and Compressive Properties of Cellular Lattice Structures Fabricated by Selective Laser Melting. Mater. Sci. Eng. A 2015, 628, 188–197. [Google Scholar] [CrossRef]










| Elem. | Fe | C | Si | Mn | Cr | Mo | Ni |
|---|---|---|---|---|---|---|---|
| wt.% | Bal. | 0.03 | 0.8 | 1.8 | 17.5 | 2.2 | 11.3 |
| dn | dGauss | SGauss/Sn | dmaj | dmin | Sellipse/Sn |
|---|---|---|---|---|---|
| (mm) | (mm) | (%) | (mm) | (mm) | (%) |
| 0.3 | 0.34 | +13.7 | 0.39 | 0.27 | +41.4 |
| 0.4 | 0.49 | +21.5 | 0.60 | 0.35 | +108.3 |
| 0.5 | 0.59 | +18.0 | 0.73 | 0.44 | +46.2 |
| 0.6 | 0.68 | +13.4 | 0.81 | 0.55 | +34.9 |
| 0.7 | 0.77 | +10.5 | 0.93 | 0.61 | +33.2 |
| 0.8 | 0.86 | +7.9 | 0.99 | 0.72 | +23.8 |
| 0.9 | 0.94 | +4.1 | 1.06 | 0.82 | +18.1 |
| 1 | 1.04 | +4.2 | 1.15 | 0.92 | +14.9 |
| Es | Rp0.2% | Et | Rm | A | |
|---|---|---|---|---|---|
| (GPa) | (MPa) | (MPa) | (MPa) | (%) | |
| Multi-strut tensile samples | 94 ± 10 | 338 ± 20 | 787 | 397 | 5.3 |
| Conventional samples | 166 ± 15 | 450 ± 5 | 89 | 541 | 40.7 |
| Experiment | Simulations | |||||||
|---|---|---|---|---|---|---|---|---|
| Beam Element | Beam Element Gauss | Beam Element Ellipse | ||||||
| Ɛ | σ | Ea | σ | Ea | σ | Ea | σ | Ea |
| (-) | (MPa) | (MJ·m−3) | (MPa) | (MJ·m−3) | (MPa) | (MJ·m−3) | (MPa) | (MJ·m−3) |
| 0.1 | 21.24 | 1.88 | 16.84 | 1.4 | 19.96 | 1.65 | 18.94 | 1.56 |
| 0.2 | 23.51 | 4.17 | 19.41 | 3.18 | 23.09 | 3.77 | 22.2 | 3.58 |
| 0.3 | 29.61 | 6.69 | 22.15 | 5.26 | 26.41 | 6.24 | 25.66 | 5.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Červinek, O.; Werner, B.; Koutný, D.; Vaverka, O.; Pantělejev, L.; Paloušek, D. Computational Approaches of Quasi-Static Compression Loading of SS316L Lattice Structures Made by Selective Laser Melting. Materials 2021, 14, 2462. https://doi.org/10.3390/ma14092462
Červinek O, Werner B, Koutný D, Vaverka O, Pantělejev L, Paloušek D. Computational Approaches of Quasi-Static Compression Loading of SS316L Lattice Structures Made by Selective Laser Melting. Materials. 2021; 14(9):2462. https://doi.org/10.3390/ma14092462
Chicago/Turabian StyleČervinek, Ondřej, Benjamin Werner, Daniel Koutný, Ondřej Vaverka, Libor Pantělejev, and David Paloušek. 2021. "Computational Approaches of Quasi-Static Compression Loading of SS316L Lattice Structures Made by Selective Laser Melting" Materials 14, no. 9: 2462. https://doi.org/10.3390/ma14092462
APA StyleČervinek, O., Werner, B., Koutný, D., Vaverka, O., Pantělejev, L., & Paloušek, D. (2021). Computational Approaches of Quasi-Static Compression Loading of SS316L Lattice Structures Made by Selective Laser Melting. Materials, 14(9), 2462. https://doi.org/10.3390/ma14092462






