An Effective Strategy to Maintain the CALPHAD Atomic Mobility Database of Multicomponent Systems and Its Application to Hcp Mg–Al–Zn–Sn Alloys
Abstract
1. Introduction
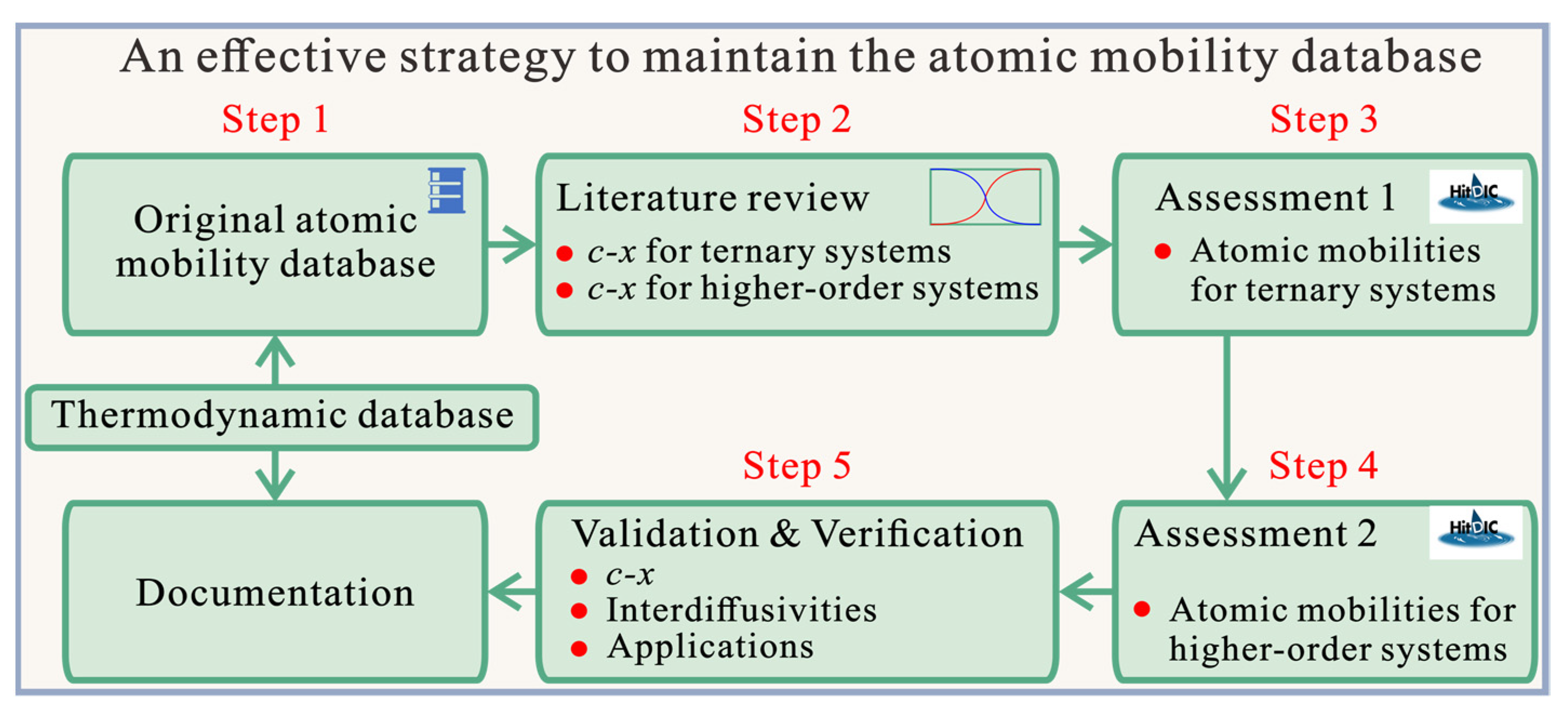
2. An Effective Strategy to Maintain the CALPHAD Atomic Mobility Database of Multicomponent Systems
- The original atomic mobility descriptions of the target multicomponent system, together with the thermodynamic descriptions, should be ready or re-constructed according to the corresponding publication(s).
- A critical review of all the composition–distance profiles of diffusion multiples/couples in ternary and higher-order systems available in the literature should be conducted both before and after the publication/release of the original atomic mobility database.
- The atomic mobility descriptions in each boundary ternary system should be updated by means of the HitDIC software based on the reviewed composition–distance profiles. It should be noted that the atomic mobility descriptions in all the boundary binaries are fixed during the entire stage. Moreover, the reliability of the updated atomic mobilities should be validated by the experimental composition–distance profiles as well as the evaluated interdiffusion coefficients available in the literature.
- Based on the updated atomic mobilities of boundary ternary systems, all the composition–distance profiles in the higher-order systems should be input into the HitDIC software to assess the possible interaction parameters in high-order systems. The interaction parameters in higher-order systems are introduced if their addition can really improve the fit to most of the experimental composition profiles. During this step, it should be noted that the interaction parameters of ternary atomic mobilities can be updated if a better fit to the experimental composition profiles in higher-order system can be achieved.
- One needs to validate the updated atomic mobility database by comprehensively comparing the predicted diffusion properties with the experimental ones in all the related ternary, quaternary, and higher-order systems, verify the updated atomic mobility database by applying real applications if available, and finalize the documentation.
3. Literature Review on Diffusion Information in Hcp Mg–Al–Zn–Sn Alloys
4. Results and Discussion
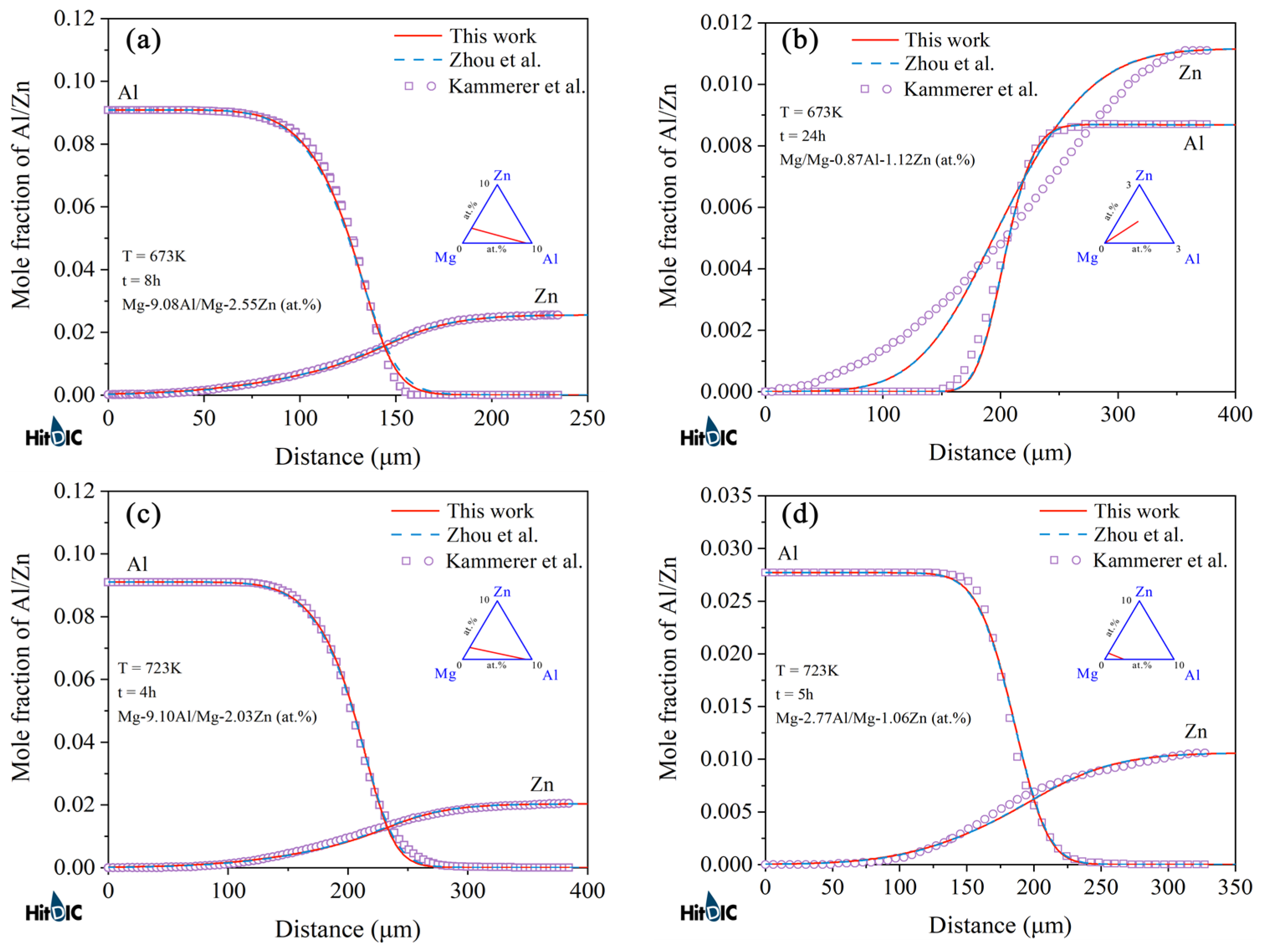
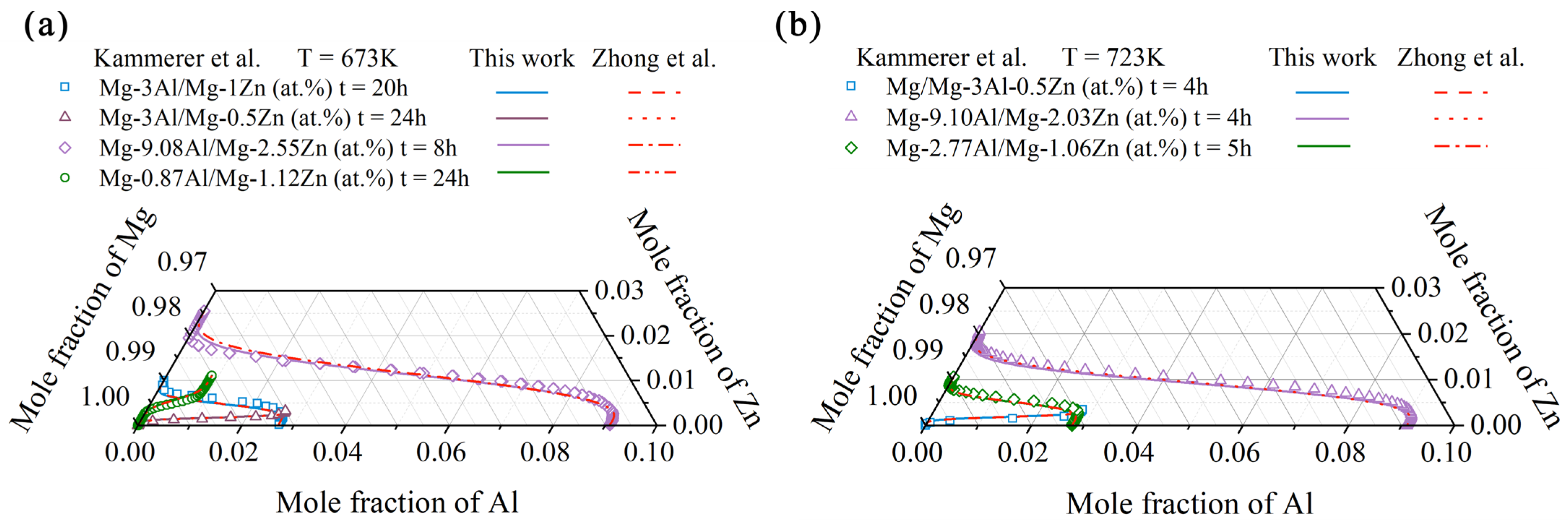
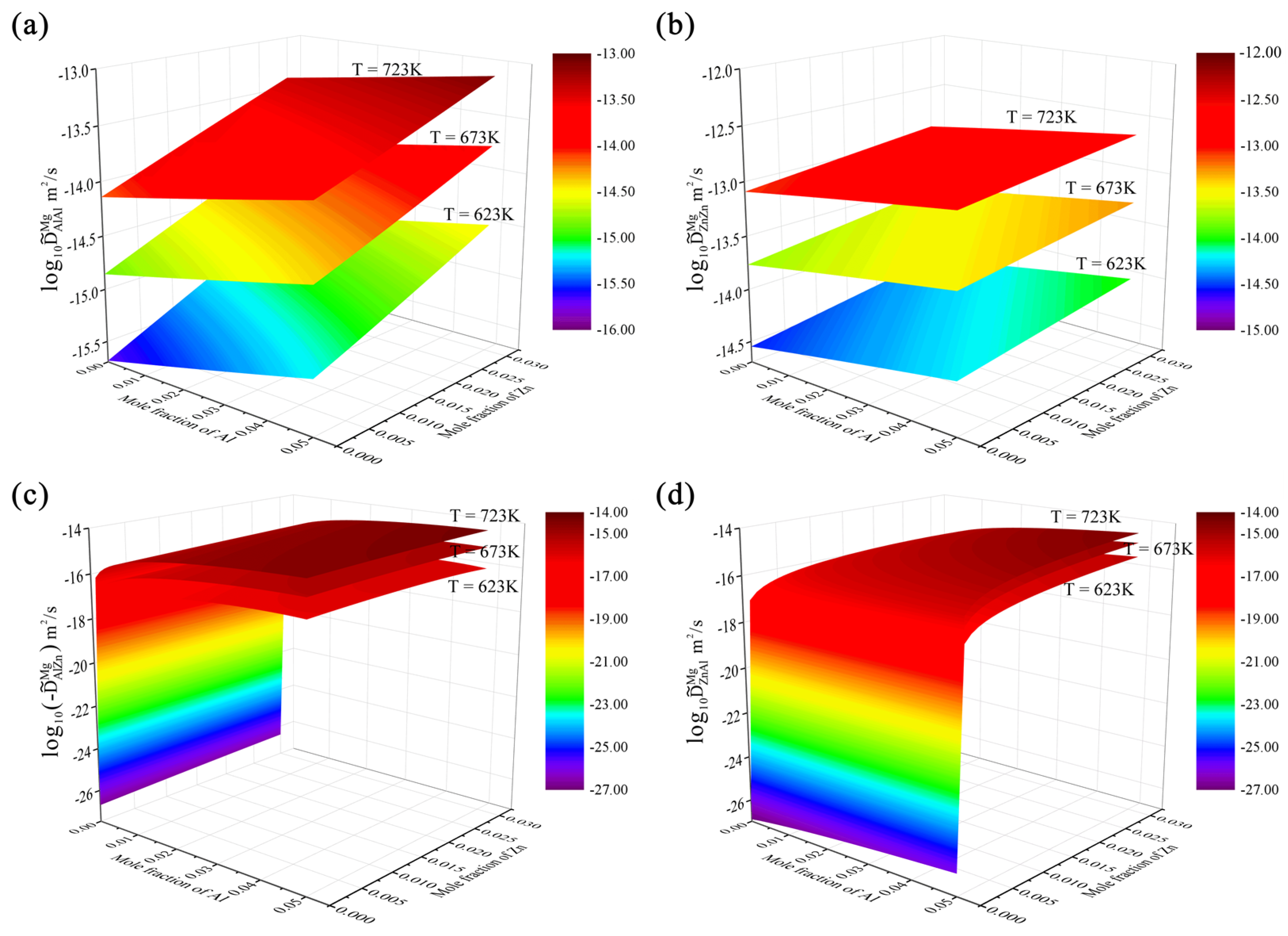
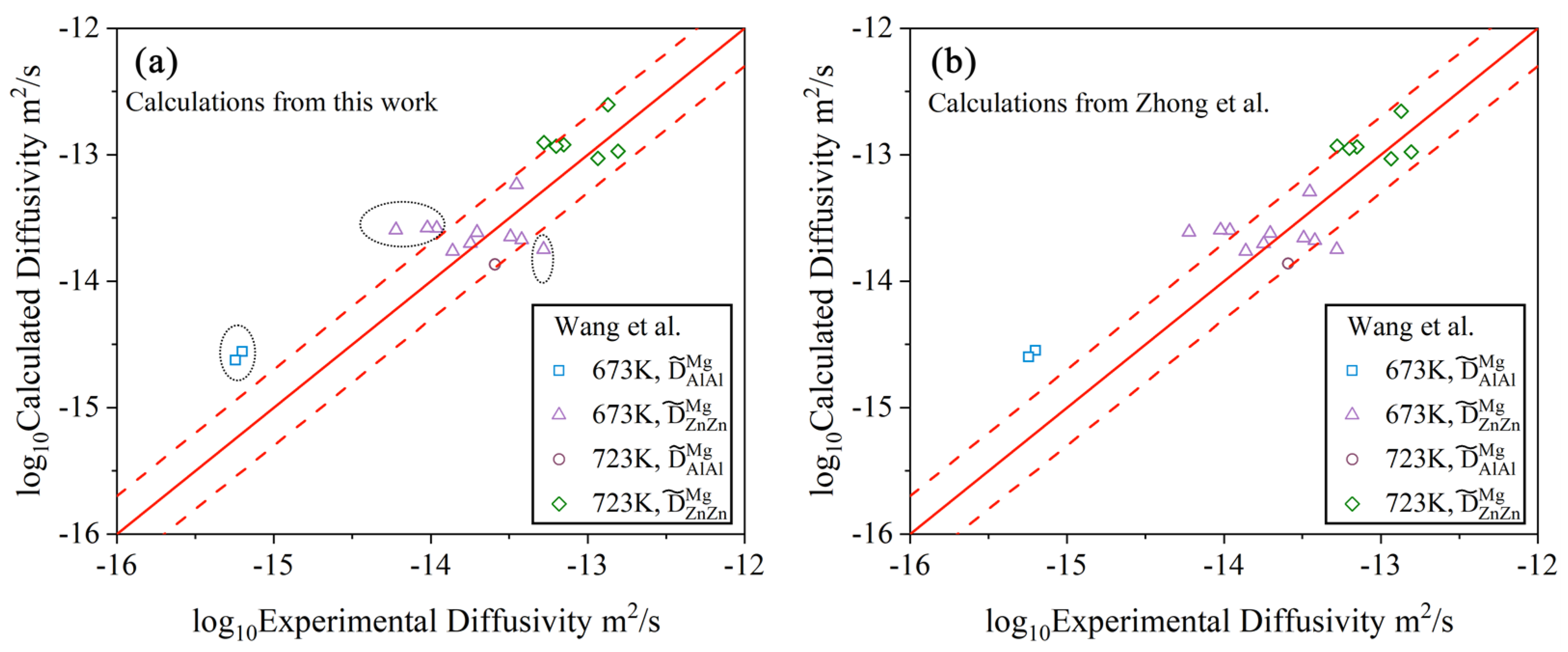
4.1. Hcp Mg–Al–Zn Ternary System
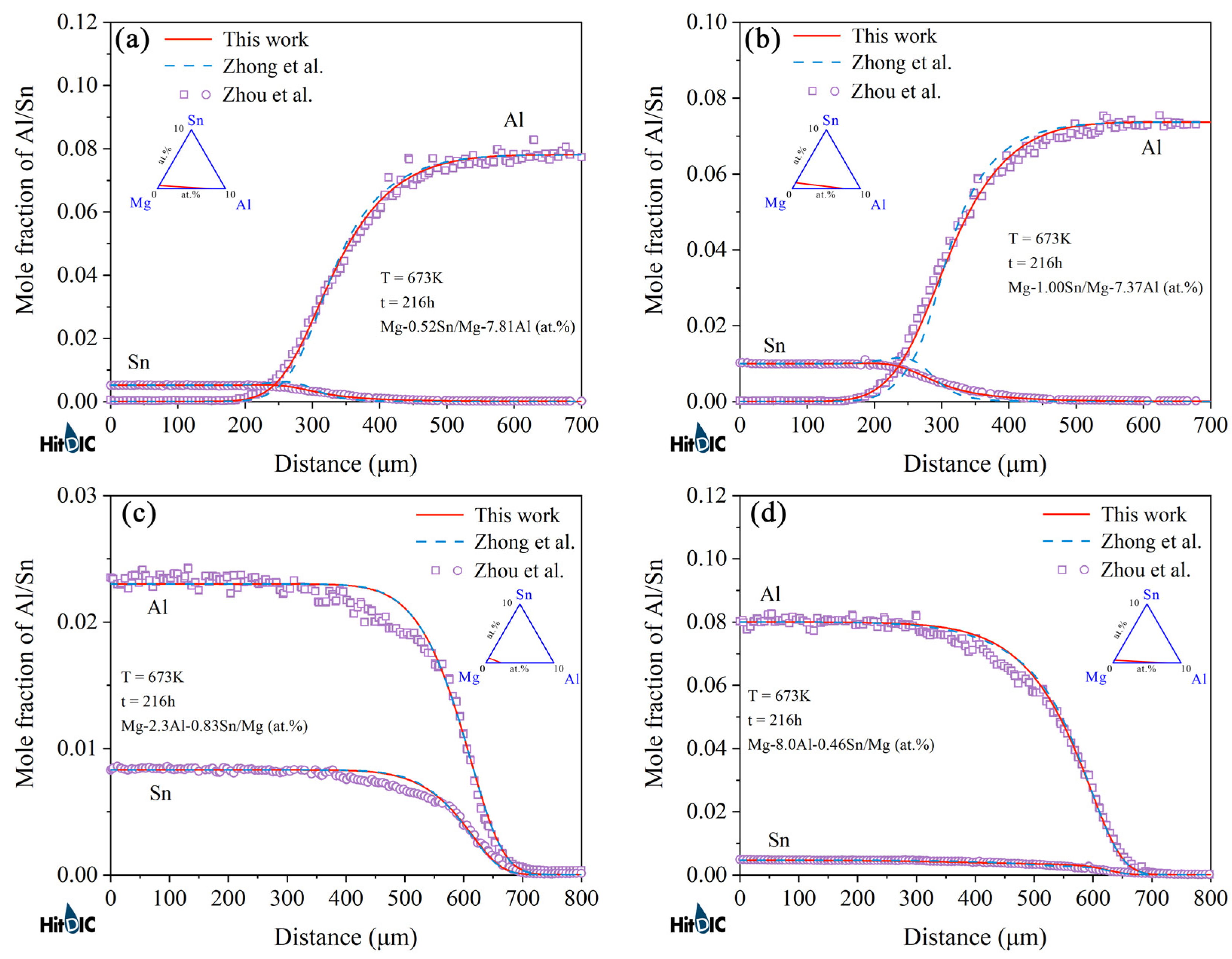
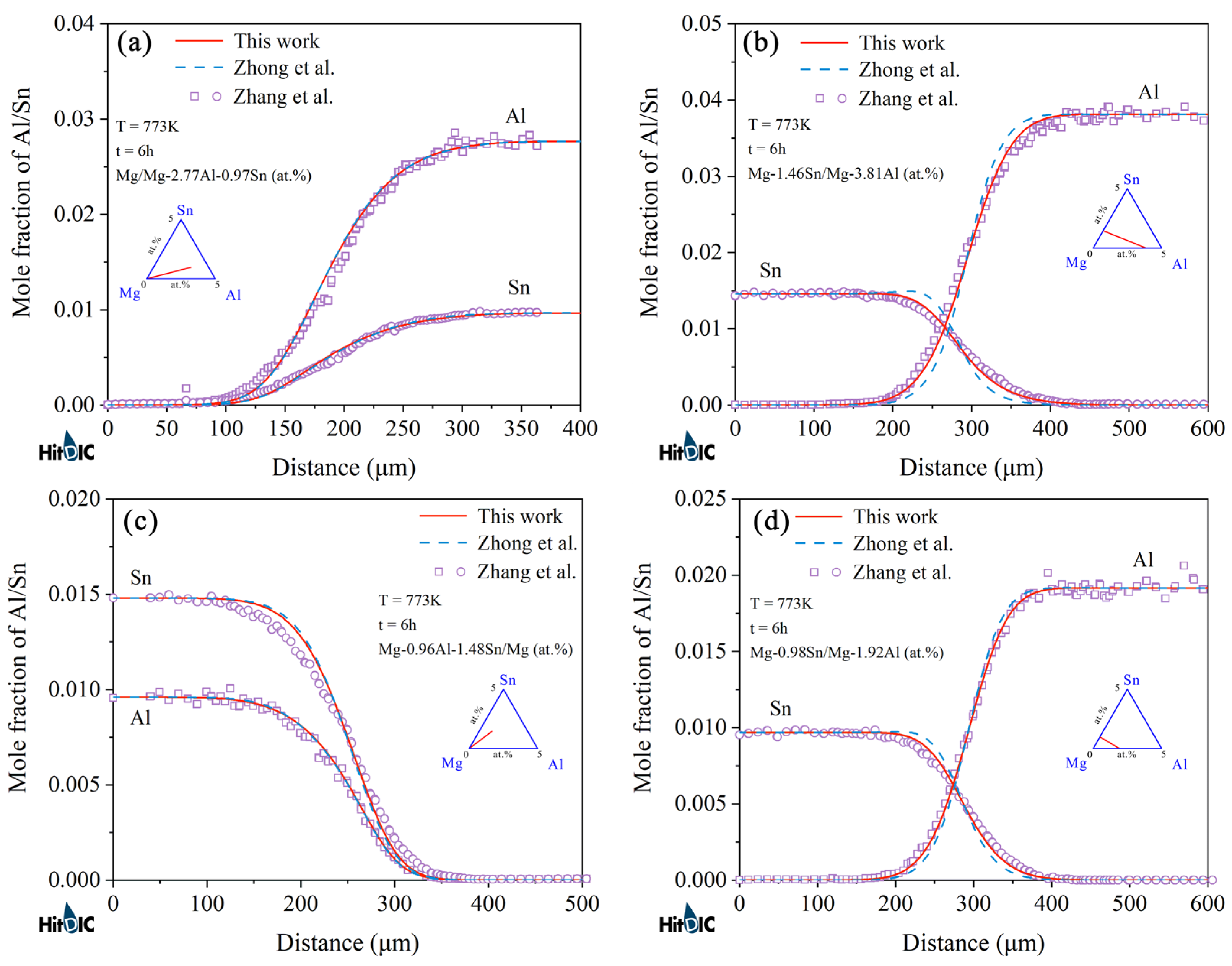
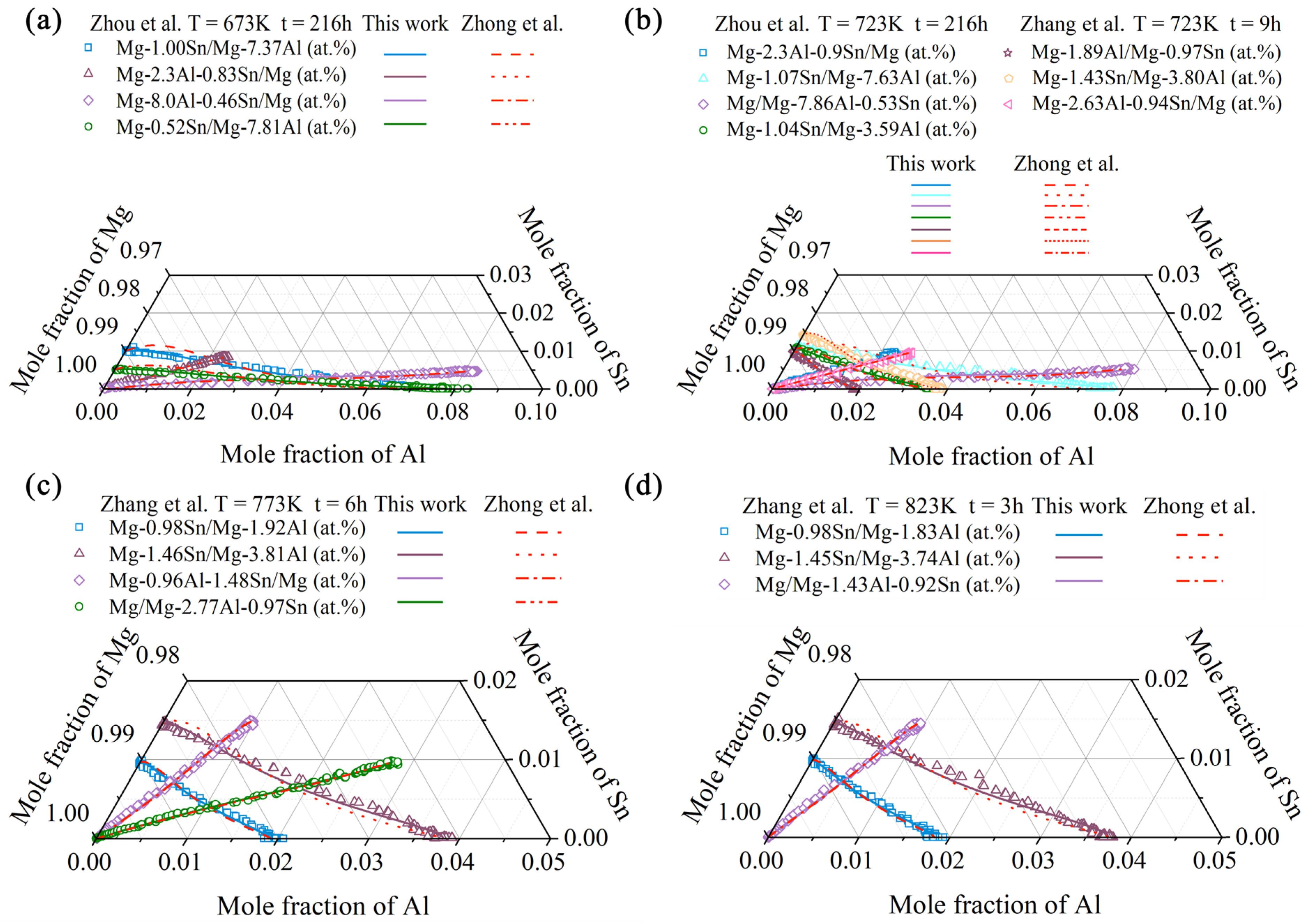
4.2. Hcp Mg–Al–Sn Ternary System
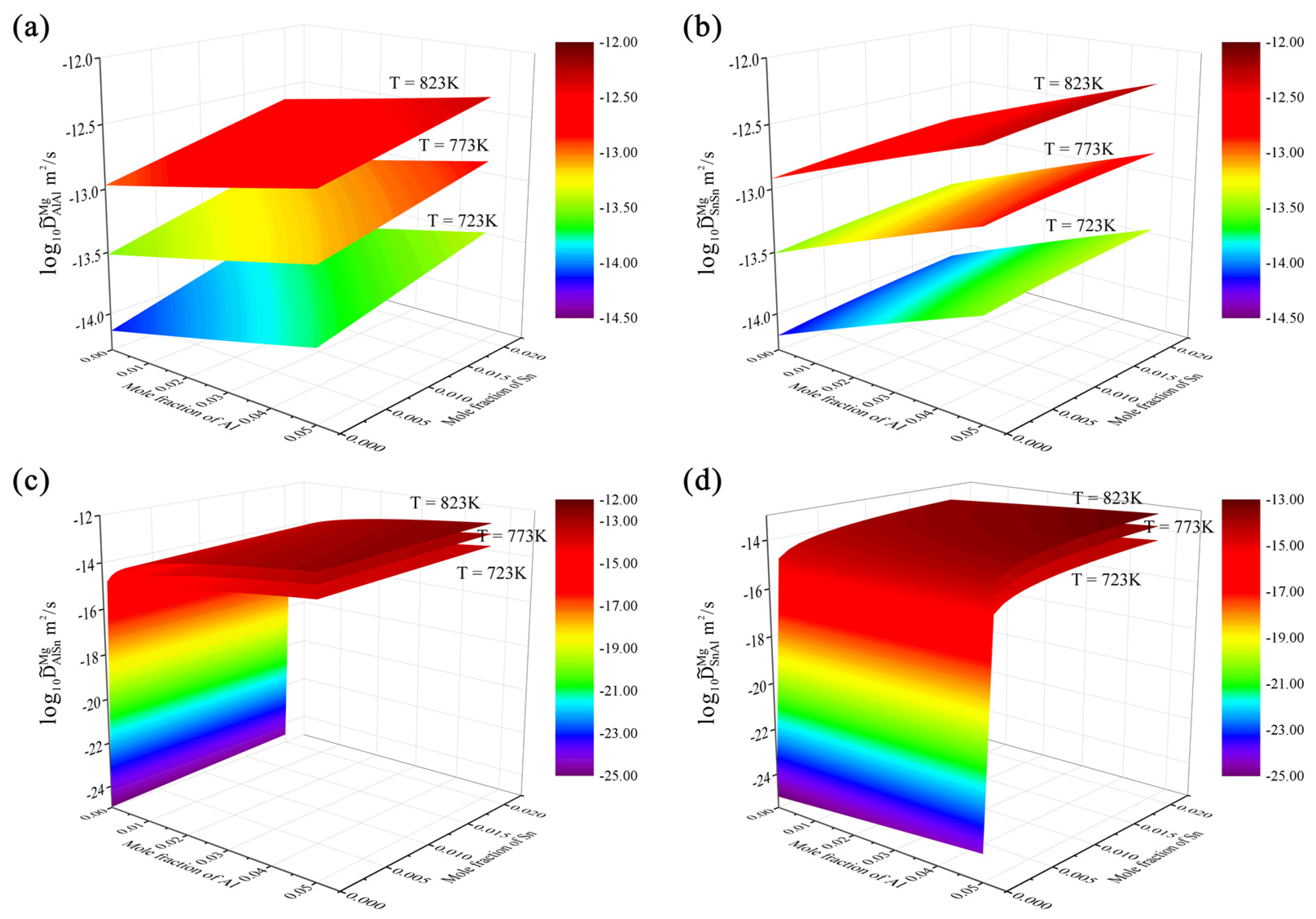
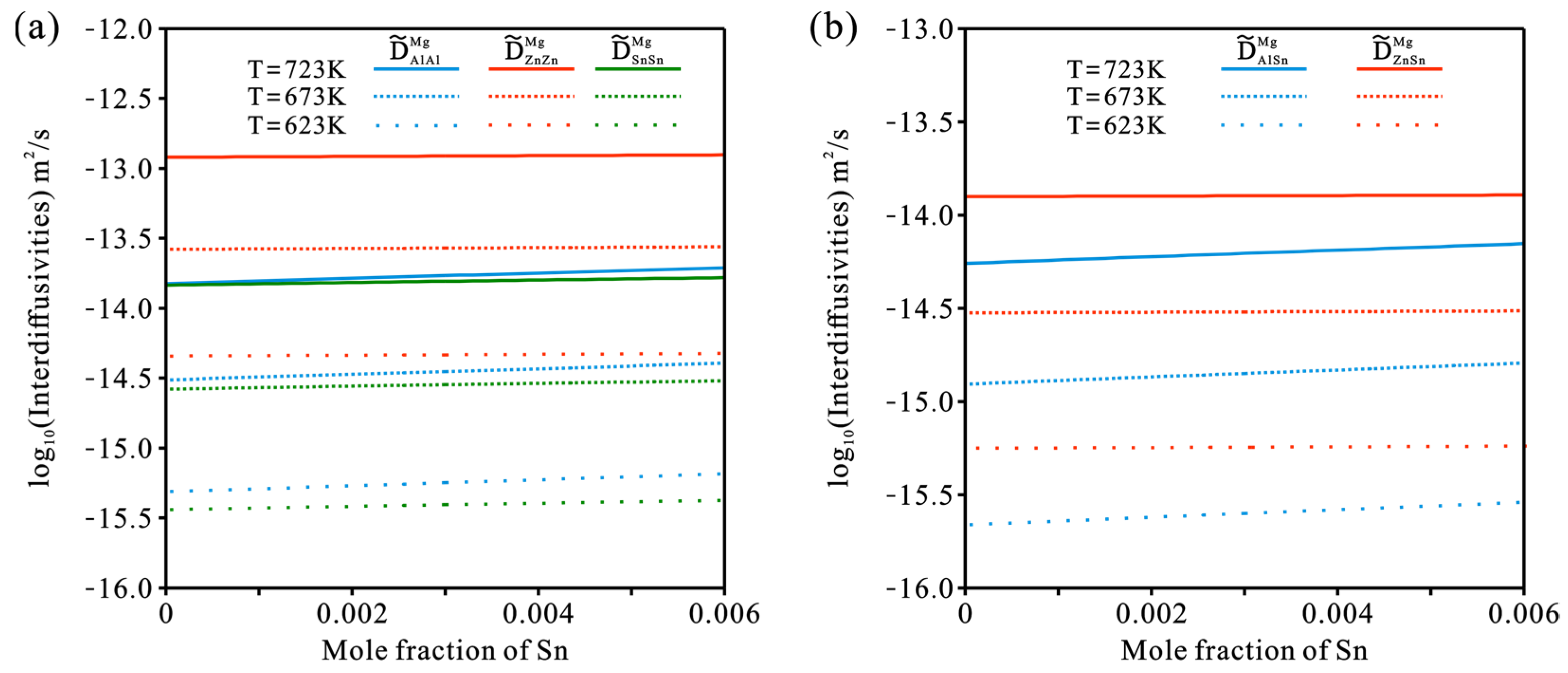
4.3. Hcp Mg–Al–Zn–Sn Quaternary System
5. Conclusions
- A general and effective strategy for the maintenance of the CALPHAD atomic mobility database of multicomponent systems was developed based on the pragmatic numerical inverse method and HitDIC software;
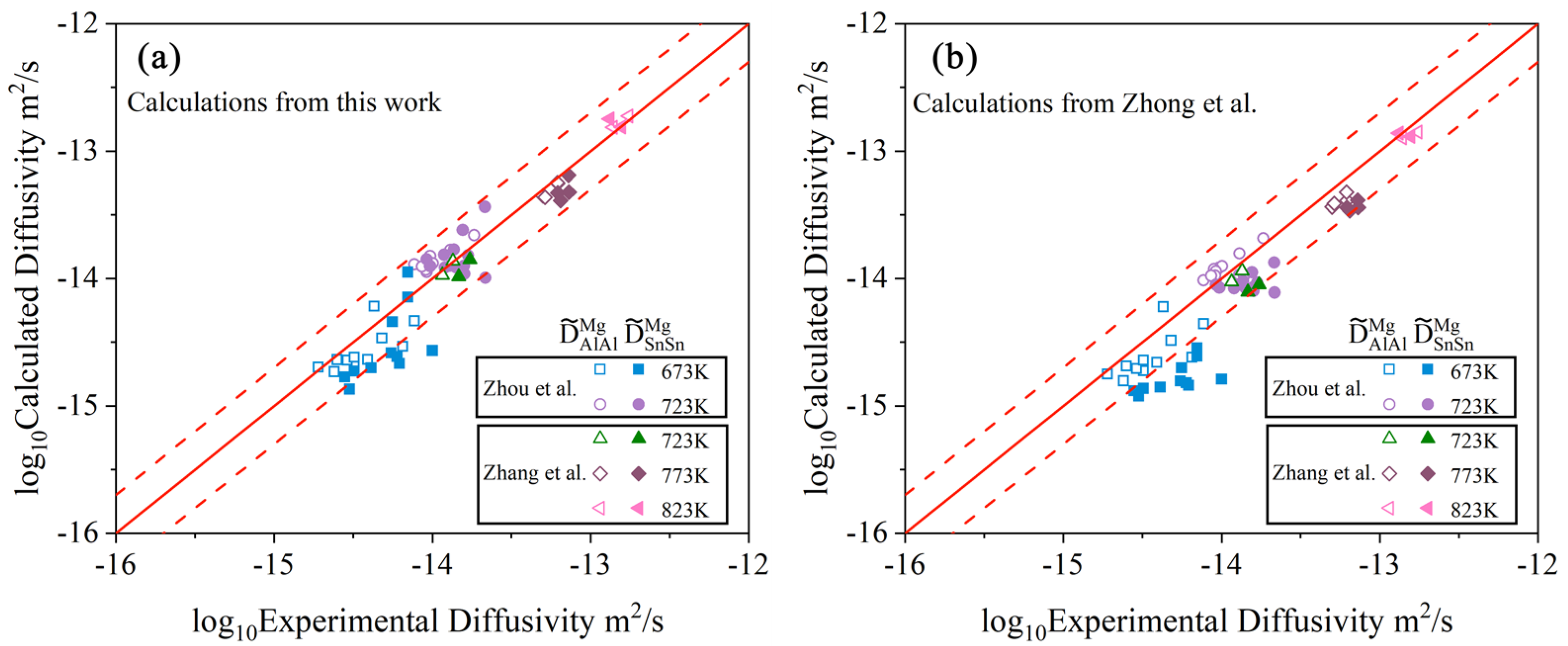
- Following the newly proposed strategy, the atomic mobility descriptions of the hcp Mg–Al–Zn and Mg–Al–Sn ternary systems were updated based on the experimental composition profiles in the respective ternary systems. It was found that the presently updated atomic mobilities of the hcp Mg–Al–Zn system provided a good fit for all of the experimental diffusion properties as did the previous assessment [32] using the traditional approach, while the presently updated atomic mobilities of the hcp Mg–Al–Sn system showed better agreement with the experimental diffusion properties than the previous assessment [32] using the traditional approach. Moreover, the variation trend of inter-diffusivities of the hcp Mg–Al–Zn and Mg–Al–Sn systems with the temperature and solute (i.e., Al, Zn, and Sn) concentrations was also fully analyzed;
- Based on the updated atomic mobility descriptions of the hcp Mg–Al–Zn and Mg–Al–Sn systems, together with only one set of composition–distance profiles, the atomic mobility descriptions of the hcp Mg–Al–Zn–Sn quaternary system were further updated following the newly proposed strategy. A real improvement in the reproduction of experimental data was achieved by the present work compared with the previous assessment. Furthermore, the influence of Sn concentration and temperature on the inter-diffusivities of the hcp Mg–Al–Zn–Sn quaternary alloys was also illustrated;
- It is anticipated that the presently proposed strategy can serve as a standard for maintaining the CALPHAD atomic mobility database of different multicomponent systems.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, A.A.; Fu, P.; Peng, L.; Kang, X.; Li, Z.; Zhu, T. Solidification Microstructure and Mechanical Properties of Cast Magnesium-Aluminum-Tin Alloys. Metall. Mater. Trans. A 2012, 43, 360–368. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, L. Thermodynamic description of the quaternary Al-Si-Mg-Sc system and its application to the design of novel Sc-additional A356 alloys. Mater. Des. 2017, 116, 427–437. [Google Scholar] [CrossRef]
- Cheng, K.; Chen, W.; Liu, D.; Zhang, L.; Du, Y. Analysis of the Cermak–Rothova method for determining the concentration dependence of ternary interdiffusion coefficients with a single diffusion couple. Scr. Mater. 2014, 76, 5–8. [Google Scholar] [CrossRef]
- Andersson, J.; Ågren, J. Models for numerical treatment of multicomponent diffusion in simple phases. J. Appl. Phys. 1992, 72, 1350–1355. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Q. Chapter 6—CALPHAD-Type Modeling of Diffusion Kinetics in Multicomponent Alloys. In Handbook of Solid State Diffusion; Paul, A., Divinski, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; Volume 1, pp. 321–362. [Google Scholar]
- Vaidya, M.; Trubel, S.; Murty, B.S.; Wilde, G.; Divinski, S.V. Ni tracer diffusion in CoCrFeNi and CoCrFeMnNi high entropy alloys. J. Alloys Compd. 2016, 688, 994–1001. [Google Scholar] [CrossRef]
- Mantina, M.; Wang, Y.; Arroyave, R.; Chen, L.; Liu, Z.; Wolverton, C. First-principles calculation of self-diffusion coefficients. Phys. Rev. Lett. 2008, 100, 215901. [Google Scholar] [CrossRef]
- Wang, J.; Hou, T. Application of molecular dynamics simulations in molecular property prediction II: Diffusion coefficient. J. Comput. Chem. 2011, 32, 3505–3519. [Google Scholar] [CrossRef]
- Hall, L.D. An analytical method of calculating variable diffusion coefficients. J. Chem. Phys. 1953, 21, 87–89. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, J.; Wu, X.; Deng, C.; Zhang, L. An Effective Approach to Acquire the Impurity Diffusion Coefficients in Binary Alloys with Quantified Uncertainties. Metals 2021, 11, 809. [Google Scholar] [CrossRef]
- Matano, C. On the relation between the diffusion-coefficients and concentrations of solid metals. Jpn. J. Phys. 1933, 8, 109–113. [Google Scholar]
- Kirkaldy, J.S.; Young, D.J. Diffusion in the Condensed State; The Institute of Metals: London, UK, 1987. [Google Scholar]
- Wu, X.; Zhong, J.; Zhang, L. A general approach to quantify the uncertainty of interdiffusion coefficients in binary, ternary and multicomponent systems evaluated using Matano-based methods. Acta Mater. 2020, 188, 665–676. [Google Scholar] [CrossRef]
- Paul, A. A pseudobinary approach to study interdiffusion and the Kirkendall effect in multicomponent systems. Philos. Mag. 2013, 93, 2297–2315. [Google Scholar] [CrossRef]
- Esakkiraja, N.; Paul, A. A novel concept of pseudo ternary diffusion couple for the estimation of diffusion coefficients in multicomponent systems. Scr. Mater. 2018, 147, 79–82. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, L.; Du, Y.; Tang, C.; Huang, B. A pragmatic method to determine the composition-dependent interdiffusivities in ternary systems by using a single diffusion couple. Scr. Mater. 2014, 90–91, 53–56. [Google Scholar] [CrossRef]
- Chen, W.; Zhong, J.; Zhang, L. An augmented numerical inverse method for determining the composition-dependent interdiffusivities in alloy systems by using a single diffusion couple. MRS Commun. 2016, 6, 295–300. [Google Scholar] [CrossRef]
- Xu, H.; Chen, W.; Zhang, L.; Du, Y.; Tang, C. High-throughput determination of the composition-dependent interdiffusivities in Cu-rich fcc Cu–Ag–Sn alloys at 1073 K. J. Alloys Compd. 2015, 644, 687–693. [Google Scholar] [CrossRef]
- Xu, H.; Cheng, K.; Zhong, J.; Wu, X.; Wei, M.; Zhang, L. Determination of accurate interdiffusion coefficients in fcc Ag-In and Ag-Cu-In alloys: A comparative study on the Matano method with distribution function and the numerical inverse method with HitDIC. J. Alloys Compd. 2019, 798, 26–34. [Google Scholar] [CrossRef]
- McCall, D.W.; Douglass, D.C. Diffusion in binary solutions. J. Chem. Phys. 1967, 71, 987–997. [Google Scholar] [CrossRef]
- DeHoff, R.; Kulkarni, N. The trouble with diffusion. Mater. Res. 2002, 5, 209–229. [Google Scholar] [CrossRef]
- Zhong, J.; Chen, L.; Zhang, L. Automation of diffusion database development in multicomponent alloys from large number of experimental composition profiles. NPJ Comput. Mater. 2021, 7, 35. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, L.; Wu, X.; Chen, L.; Deng, C. A novel computational framework for establishment of atomic mobility database directly from composition profiles and its uncertainty quantification. J. Mater. Sci. Technol. 2020, 48, 163–174. [Google Scholar] [CrossRef]
- Luo, A.A. Magnesium casting technology for structural applications. J. Magnes. Alloys 2013, 1, 2–22. [Google Scholar] [CrossRef]
- Luo, A.A. Recent magnesium alloy development for elevated temperature applications. Int. Mater. Rev. 2004, 49, 13–30. [Google Scholar] [CrossRef]
- Gontarz, A.; Drozdowski, K.; Michalczyk, J.; Wiewiórowska, S.; Pater, Z.; Tomczak, J.; Samołyk, G.; Winiarski, G.; Surdacki, P. Forging of Mg–Al–Zn Magnesium Alloys on Screw Press and Forging Hammer. Materials 2021, 14, 32. [Google Scholar] [CrossRef]
- Aldalur, E.; Suárez, A.; Veiga, F. Metal transfer modes for Wire Arc Additive Manufacturing Al-Mg alloys: Influence of heat input in microstructure and porosity. J. Mater. Process. Technol. 2021, 297, 117271. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, X.; Kang, N.; Hu, Y.; Chen, J.; Huang, W. Strength-ductility synergy of selective laser melted Al-Mg-Sc-Zr alloy with a heterogeneous grain structure. Addit. Manuf. 2020, 34, 101260. [Google Scholar] [CrossRef]
- Liang, J.Y. Effects of Sn on Mechanical Properties of Magnesium Alloy AZ61. Appl. Mech. Mater. 2012, 204–208, 4161–4164. [Google Scholar] [CrossRef]
- Mahmudi, R.; Moeendarbari, S. Effects of Sn additions on the microstructure and impression creep behavior of AZ91 magnesium alloy. Mater. Sci. Eng. A 2013, 566, 30–39. [Google Scholar] [CrossRef]
- Jung, I.C.; Kim, Y.K.; Cho, T.H.; Oh, S.H.; Kim, T.E.; Shon, S.W.; Kim, W.T.; Kim, D.H. Suppression of discontinuous precipitation in AZ91 by addition of Sn. Met. Mater. Int. 2014, 20, 99–103. [Google Scholar] [CrossRef]
- Zhong, W.; Zhao, J.-C. A comprehensive diffusion mobility database comprising 23 elements for magnesium alloys. Acta Mater. 2020, 201, 191–208. [Google Scholar] [CrossRef]
- Bryan, Z.L.; Alieninov, P.; Berglund, I.S.; Manuel, M.V. A diffusion mobility database for magnesium alloy development. Calphad 2015, 48, 123–130. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, C.; Liu, Y.; Wen, S.; Liu, S.; Huang, Y.; Hort, N.; Du, Y. Interdiffusion and atomic mobility in hcp Mg–Al–Sn alloys. J. Alloys Compd. 2021, 871, 159517. [Google Scholar] [CrossRef]
- Kammerer, C.C.; Kulkarni, N.S.; Warmack, B.; Sohn, Y.H. Interdiffusion in Ternary Magnesium Solid Solutions of Aluminum and Zinc. J. Phase Equilib. Diffus. 2016, 37, 65–74. [Google Scholar] [CrossRef]
- Wang, J.; Li, N.; Wang, C.; Beltran, J.I.; Llorca, J.; Cui, Y. Computational study of atomic mobility in hcp Mg–Al–Zn ternary alloys. Calphad 2016, 54, 134–143. [Google Scholar] [CrossRef][Green Version]
- Zhou, Z.; Gu, Y.; Xu, G.; Guo, Y.; Cui, Y. Diffusion research in HCP Mg–Al–Sn ternary alloys. Calphad 2020, 68, 101710. [Google Scholar] [CrossRef]
- Whittle, D.P.; Green, A. The measurement of diffusion coefficient in ternary systems. Scr. Metall. 1974, 8, 883–884. [Google Scholar] [CrossRef]
- Cheng, T.; Tang, Y.; Zhang, L. Update of thermodynamic descriptions of the binary Al-Sn and ternary Mg–Al–Sn systems. Calphad 2019, 64, 354–363. [Google Scholar] [CrossRef]
- Cheng, T.; Zhang, L. Thermodynamic Descriptions of the Quaternary Mg–Al–Zn–Sn System and Their Experimental Validation. In Magnesium Technology 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 269–279. [Google Scholar]
- Cheng, T.; Zhang, L.-J. Thermodynamic re-assessment of the Al-Sn-Zn ternary system. J. Min. Metall. Sect. B-Metall. 2019, 55, 439–449. [Google Scholar] [CrossRef]
- Liang, P.; Tarfa, T.; Robinson, J.; Wagner, S.; Ochin, P.; Harmelin, M.; Seifert, H.; Lukas, H.; Aldinger, F. Experimental investigation and thermodynamic calculation of the Al–Mg–Zn system. Thermochim. Acta 1998, 314, 87–110. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, L.; Du, Y.; Xu, H.; Jin, Z. Ternary diffusion in Cu-rich fcc Cu–Al–Si alloys at 1073 K. J. Alloys Compd. 2013, 566, 156–163. [Google Scholar] [CrossRef]
- Du, Y.; Chang, Y.; Huang, B.; Gong, W.; Jin, Z.; Xu, H.; Yuan, Z.; Liu, Y.; He, Y.; Xie, F.-Y. Diffusion coefficients of some solutes in fcc and liquid Al: Critical evaluation and correlation. Mater. Sci. Eng. A 2003, 363, 140–151. [Google Scholar] [CrossRef]
- Dong, X.; Fu, J.; Wang, J.; Yang, Y. Microstructure and tensile properties of as-cast and as-aged Mg-6Al-4Zn alloys with Sn addition. Mater. Des. 2013, 51, 567–574. [Google Scholar] [CrossRef]



| Type of Diffusion Couple (in at.%) | Diffusion Temperature (K) | Diffusion Time (h) | References | Code |
|---|---|---|---|---|
| Mg–Al–Zn ternary system | ||||
| Mg-9.08Al/Mg-2.55Zn | 673 | 8 | [35] | ▲ |
| Mg/Mg-0.87Al-1.12Zn | 24 | △ | ||
| Mg-3Al/Mg-1Zn | 20 | △ | ||
| Mg-3Al/Mg-0.5Zn | 24 | △ | ||
| Mg-9.10Al/Mg-2.03Zn | 723 | 4 | [35] | ▲ |
| Mg-2.77Al/Mg-1.06Zn | 5 | ▲ | ||
| Mg/Mg-3Al-0.5Zn | 4 | △ | ||
| Mg/Mg-8.41Al-0.45Zn | 663 | 144 | [33] | △ |
| Mg/Mg-8.50Al-0.41Zn | 708 | 144 | [33] | △ |
| Mg–Al–Sn ternary system | ||||
| Mg-0.52Sn/Mg-7.81Al | 673 | 216 | [37] | ▲ |
| Mg-1.00Sn/Mg-7.37Al | 216 | ▲ | ||
| Mg-2.30Al-0.83Sn/Mg | 216 | ▲ | ||
| Mg-8.00Al-0.46Sn/Mg | 216 | ▲ | ||
| Mg-1.04Sn/Mg-3.59Al | 723 | 216 | [37] | ▲ |
| Mg-1.07Sn/Mg-7.63Al | 216 | ▲ | ||
| Mg/Mg-7.86Al-0.53Sn | 216 | ▲ | ||
| Mg-2.3Al-0.9Sn/Mg | 216 | ▲ | ||
| Mg-2.63Al-0.94Sn/Mg | 723 | 9 | [34] | ▲ |
| Mg-1.43Sn/Mg-3.80Al | 9 | ▲ | ||
| Mg-1.89Al/Mg-0.97Sn | 9 | ▲ | ||
| Mg/Mg-2.77Al-0.97Sn | 773 | 6 | [34] | ▲ |
| Mg-1.46Sn/Mg-3.81Al | 6 | ▲ | ||
| Mg-0.96Al-1.48Sn/Mg | 6 | ▲ | ||
| Mg-0.98Sn/Mg-1.92Al | 6 | ▲ | ||
| Mg/Mg-1.43Al-0.92Sn | 823 | 3 | [34] | ▲ |
| Mg-1.45Sn/Mg-3.74Al | 3 | ▲ | ||
| Mg-0.98Sn/Mg-1.83Al | 3 | ▲ | ||
| Mg–Al–Zn–Sn quaternary system | ||||
| Mg-0.64Al-0.04Sn-0.59Zn/Mg-0.79Al-2.42Sn-0.66Zn | 773 | 250 | [33] | ▲ |
| Mobility | Parameters | References |
|---|---|---|
| Mobility of Mg | = −125,748.3 − 86.924 × T | [32] |
| = −105,022.4 − 100.826 × T | [32] | |
| = −97,239.0 − 87.338 × T | [32] | |
| = −76,913.9 − 71.922 × T | [32] | |
| = 154,978.2 | [32] | |
| Mobility of Al | = −115,705.9 − 104.143 × T | [32] |
| = −133,378.9 − 86.232 × T | [32] | |
| = −97,239.0 − 87.338 × T | [32] | |
| = −76,913.9 − 71.922 × T | [32] | |
| = 125,172.6 | [32] | |
| = 313,977.051 | This work | |
| = 214,599.609 | This work | |
| Mobility of Zn | = −97,239.0 − 87.338 × T | [32] |
| = −125,731.0 − 76.734 × T | [32] | |
| = −115,705.9 − 104.143 × T | [32] | |
| = −76,913.9 − 71.922 × T | [32] | |
| = 80,988.7 | [32] | |
| = 90,957.031 | This work | |
| = −11,209.270 | This work | |
| Mobility of Sn | = −76,913.9 − 71.922 × T | [32] |
| = −143,787.3 − 72.615 × T | [32] | |
| = −115,705.9 − 104.143 × T | [32] | |
| = −97,239.0 − 87.338 × T | [32] | |
| = −162,023.5 | [32] | |
| = 191,345.215 | This work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, T.; Zhong, J.; Zhang, L. An Effective Strategy to Maintain the CALPHAD Atomic Mobility Database of Multicomponent Systems and Its Application to Hcp Mg–Al–Zn–Sn Alloys. Materials 2022, 15, 283. https://doi.org/10.3390/ma15010283
Cheng T, Zhong J, Zhang L. An Effective Strategy to Maintain the CALPHAD Atomic Mobility Database of Multicomponent Systems and Its Application to Hcp Mg–Al–Zn–Sn Alloys. Materials. 2022; 15(1):283. https://doi.org/10.3390/ma15010283
Chicago/Turabian StyleCheng, Ting, Jing Zhong, and Lijun Zhang. 2022. "An Effective Strategy to Maintain the CALPHAD Atomic Mobility Database of Multicomponent Systems and Its Application to Hcp Mg–Al–Zn–Sn Alloys" Materials 15, no. 1: 283. https://doi.org/10.3390/ma15010283
APA StyleCheng, T., Zhong, J., & Zhang, L. (2022). An Effective Strategy to Maintain the CALPHAD Atomic Mobility Database of Multicomponent Systems and Its Application to Hcp Mg–Al–Zn–Sn Alloys. Materials, 15(1), 283. https://doi.org/10.3390/ma15010283







