Optimization of Polymer Processing: A Review (Part I—Extrusion)
Abstract
:1. Introduction
- Use the simulation tools on a trial-and-error basis. This is obviously expensive and inefficient and relies on the capability of the user to input progressively more appropriate boundary conditions.
- Adopt an optimization procedure, whereby the process modelling package is used judiciously by an optimization algorithm, in order to define a “best” solution, or a Pareto optimal solution (see below). Practical polymer processing problems generally involve multiple, often conflicting, criteria (for example, maximizing output while minimizing viscous dissipation and mechanical energy consumption in plasticating single-screw extrusion); hence this approach is usually labelled as multi-objective optimization.
2. Need for Optimization in Polymer Processing
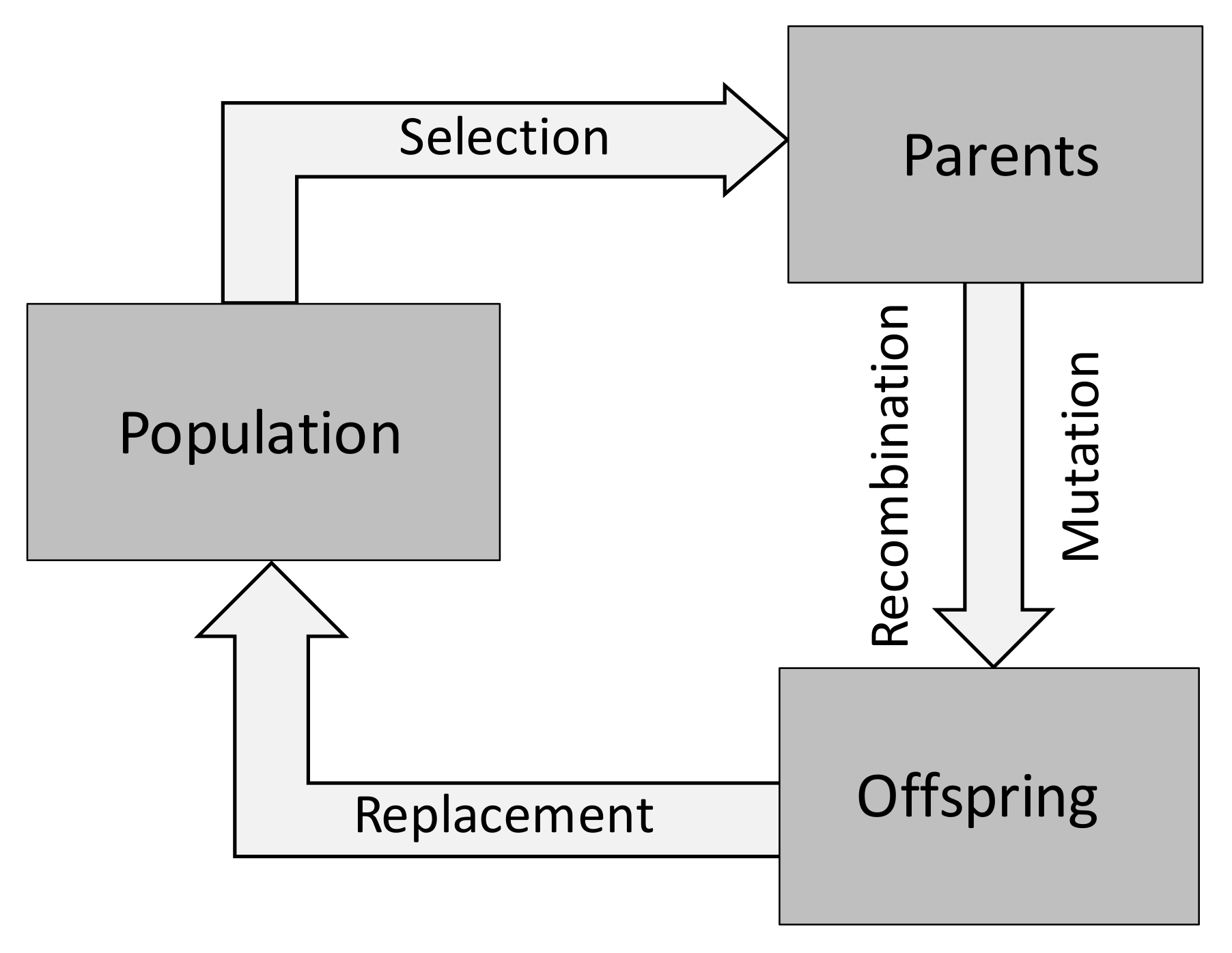
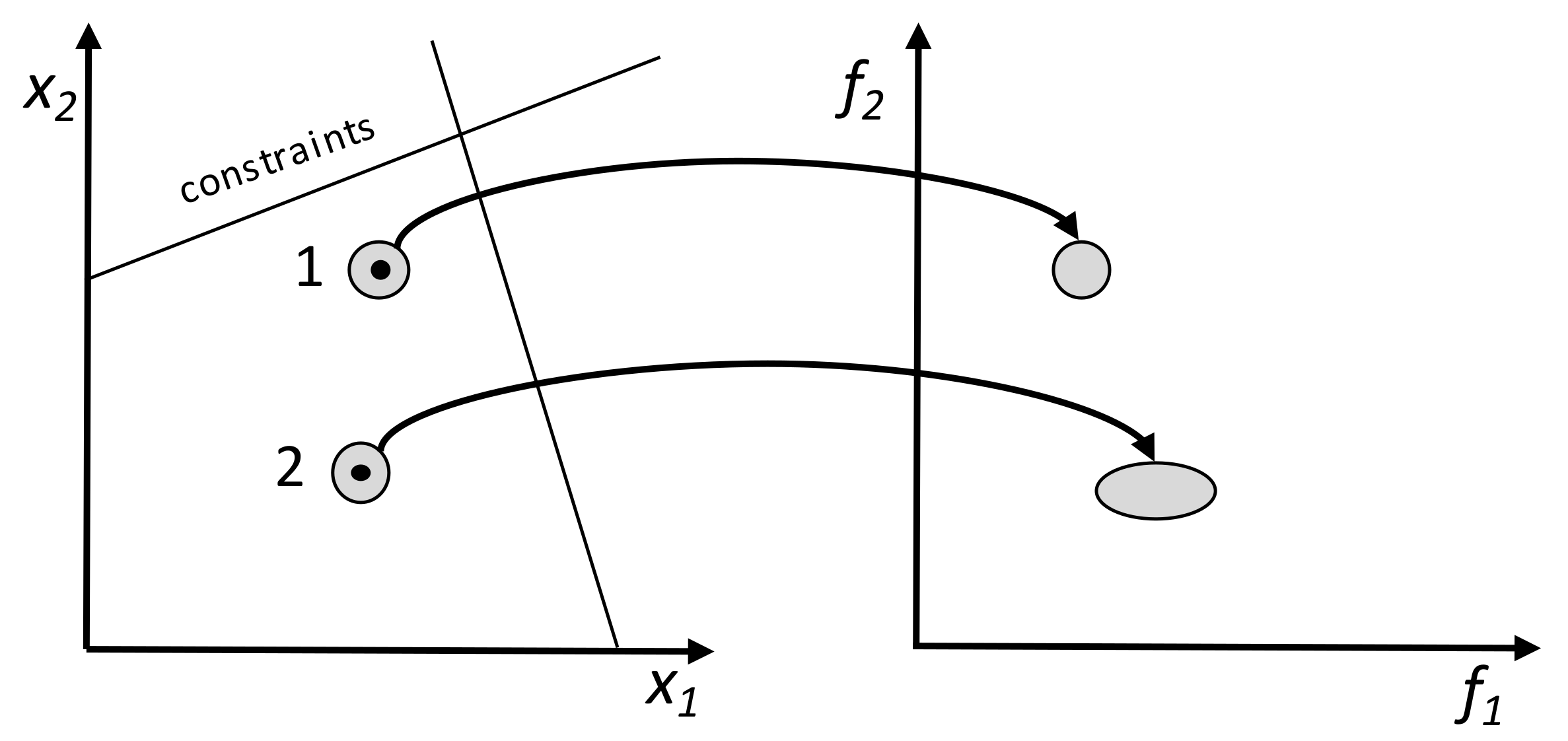
3. Multi-Objective Optimization
4. Optimization Algorithms in Polymer Processing
4.1. Methodology
- Objective function. It can be Single Objective (SO), Aggregated Product (AP), Aggregated Sum (AS), or Multi-Objective (MO).
- Optimization algorithm, e.g., Empirical, Regression, Direct, Gradient, Augmented Lagrangian (AL), Pattern Search (PS), Expert System (ES), Evolutionary Algorithm (EA), Differential Evolution (DE), Ant Colony Optimization (ACO), Stochastic Local Search (SLS), or Two-Phase Local Search (TPLS).
- Modelling approach: unidimensional (1D), two-dimensional (2D) and three-dimensional (3D), using Analytical (A), Finite Differences (FD), Finite Volumes (FV) or Finite Elements (FE) approaches; whenever relevant, the actual software used is identified.
- Decision variables, i.e., parameters to optimize. The aim can be to define the Operating Conditions (OC), Screw Design (SD), Screw Configuration (SC) (the last two will be explained below), or Die Geometry (DG). The number of variables considered in the problem is indicated between brackets in the tables below.
- Other characteristics, related with the process/modelling, the optimization, or others.
4.2. Single-Screw Extrusion
| Objective Function | Optimization Algorithm | Modelling Approach | Decision Variables | Other Characteristics | Authors (Year) Reference |
|---|---|---|---|---|---|
| SO | Direct | 1D-A | SD | Step-by-step | Helmy and Parnaby (1976) [38] |
| SO | Empirical | 1D-A | SD | Grooves | Potente et al. (1992) [39] |
| SO | ES | 1D-A | OC + SD | Worteberg et al. (1994) [40] | |
| SO | Empirical | 1D-A | SD | Step-by-step | Chung (1998, 2016) [8,41] |
| SO | Empirical | 1D-A | SD | Zone-by-zone | Rauwendaal (1986) [42] |
| SO | AL | 3D-N | SD | Altinkaynak (2010) [43] | |
| AP | Empirical | 1D-A | OC | Potente et al. (1993, 1994, 1996) [44,45,46] | |
| AP | Regression | 1D-A | SD | Statistical | Potente and Zelleröhr (1997) [47] |
| AP | Regression | 1D-A | SD | DOE | Potent and Krell (1997) [48] |
| AP(3) | Regression | 1D-A | OC(2) + SD(1) | Wilczyński et al. (2001, 2003) [49,50] | |
| AP(3) | Regression | 1D-A | OC(2) + SD(1) | Wilczyński et al. (2004) [51] | |
| AS(3) | Regression | 1D-A | SD | Thibodeau and Lafleur (2000) [52,53] | |
| AS(2) | EA | 1D-A | OC(2) + SD(1) | Nastaj and Wilczyński (2018) [54] | |
| AS(2) | EA | 1D-A | OC(2) + SD(1) | Starve-feed | Nastaj and Wilczyński (2020) [55] |
| AS(2) | DE + PS | Experimental | OC(1) | Various techniques | Abeykoon et al. (2011) [56] |
| AS(4) | EA | 2D-N | OC(4) | Gaspar-Cunha et al. (1998) [57] | |
| AS(4) + MO(4) | EA | 2D-N | OC(4) | Covas et al. (1999) [58] | |
| MO(7) | EA | 2D-N | SD(6) | Gaspar-Cunha et al. (2001) [59] | |
| MO(5) | EA | 2D-N | SD(5) | Barrier screws | Covas et al. (2004) [60] |
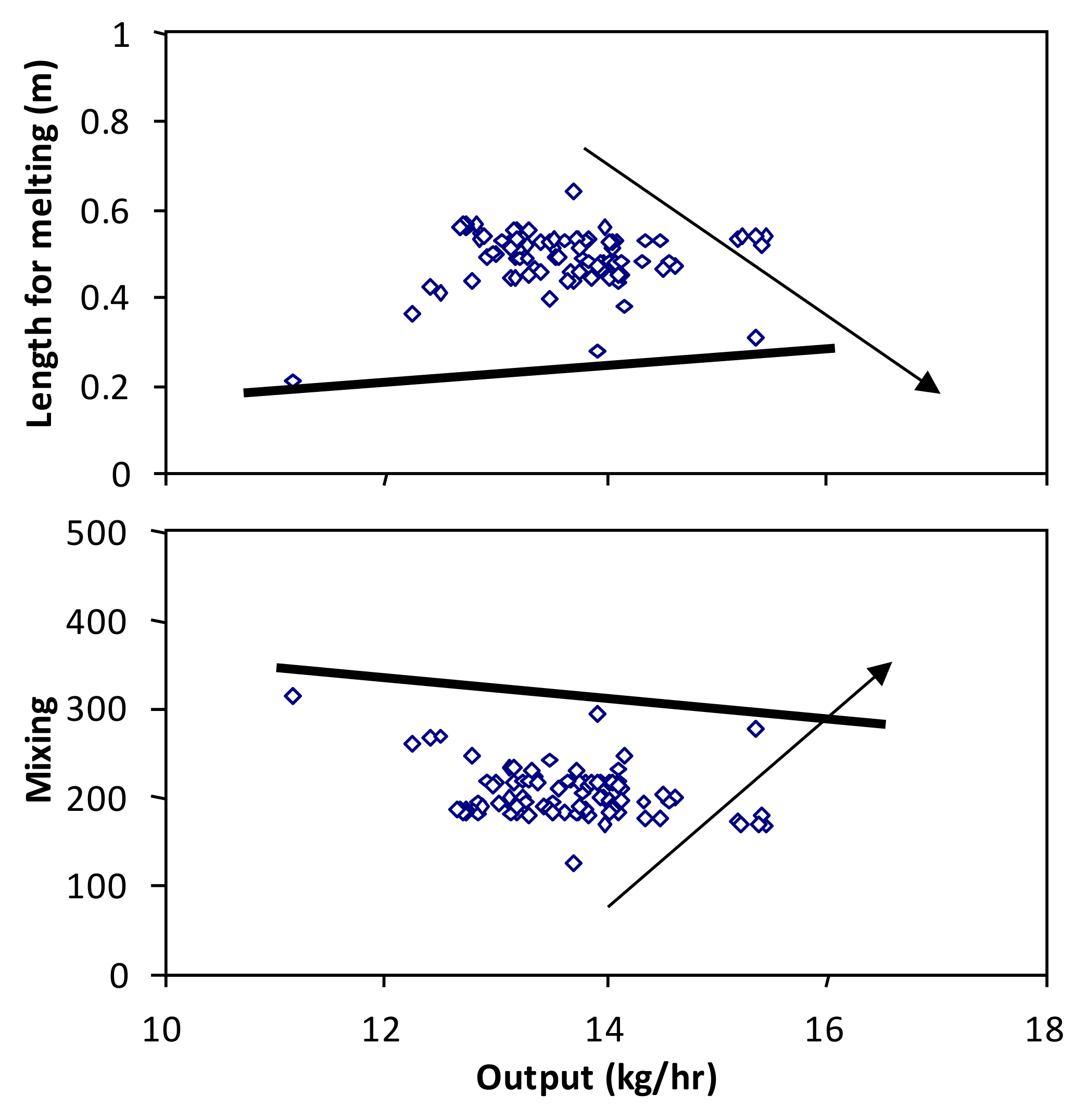
| MO(2) | EA | 2D-N | OC(4) + SD(6) | Mixing | Domingues at al. (2012) [61] |
| MO(5) | EA | 2D-N | SD(4) | Barrier screws | Gaspar-Cunha et al. (2006) [62] |
| MO(19) | EA | 2D-N | OC(3) | Scale-up | Covas and Gaspar-Cunha (2009) [63] |
| MO(9) | EA | 2D-N | SD(4) | Scale-up | Gaspar-Cunha and Covas (2014) [64] |
| MO(3) | EA | 2D-N | SD(4) | Robustness + DM | Denysiuk et al. (2018) [65] |
| MO(5) | EA | 2D-N | OC(4) + SD86) | Innovization | Deb et al. (2014) [66] |
4.3. Twin-Screw Extrusion
| Objective Function | Optimization Algorithm | Modelling Approach | Decision Variables | Other Characteristics | Authors (Year) Reference |
|---|---|---|---|---|---|
| Not defined | Empirical | 1D-A | Not defined | Potente et al. (1994, 1999) [67,68] | |
| SO | Empirical | Experimental | Not-defined | Mixing | Vainio et al. (1995) [69] |
| SO(2) | Regression | 1D-Ludovic | OC(3) + SD(1) | Reactive Extrusion | Berzin et al. (2007) [70] |
| SO | Regression | Experimental | OC(2) | Counter-rotating | Maridass and Gupta (2004) [71] |
| SO(2) | Regression | Experimental | OC | Reactive Extrusion | Ulitzsh et al. (2020) [72] |
| SO(2) | Regression | Experimental | OC(2) | Scale-up | Fukuda et al. (2015) [73] |
| AP(3) | Gradient | 1D-A | SD(2) | Conv. elements | Potente and Thümen (2006) [74] |
| AS(2) | EA | 2D-numerical | OC(1) + SD(1) | Reactive Extrusion | Zhang et al. (2015) [75] |
| AS + MO(6) | EA | 1D-Ludovic | OC(4) | Gaspar-Cunha et al. (2002) [76] | |
| MO(7+2) | EA | 1D-Ludovic | OC(4) + SC(10) | Reactive Extrusion | Gaspar-Cunha et al. (2005) [78] |
| MO(5)(7) | EA | 1D-Ludovic | SD(4) + SC(10) | Robustness | Covas et al. (2004) [60] |
| MO(3) | SLS | 2D-FD | SC(14) | Teixeira et al. (2011) [79] | |
| MO(3) | EA + ACO + SLS + TPLS | 2D-FD | SC(14) | Teixeira et al. (2012) [81] | |
| MO(3) | ACO + TPLS | 2D-FD | SC(14) | Teixeira et al. (2014) [82] | |
| MO(3) | EA | 1D-Ludovic | OC(1) + SC(14) | Reactive Extrusion | Teixeira et al. (2011) [83] |
| MO(3) | EA | 2D-FD | SD(1) + SC(8) | Scale-up | Gaspar-Cunha and Covas (2011) [84] |
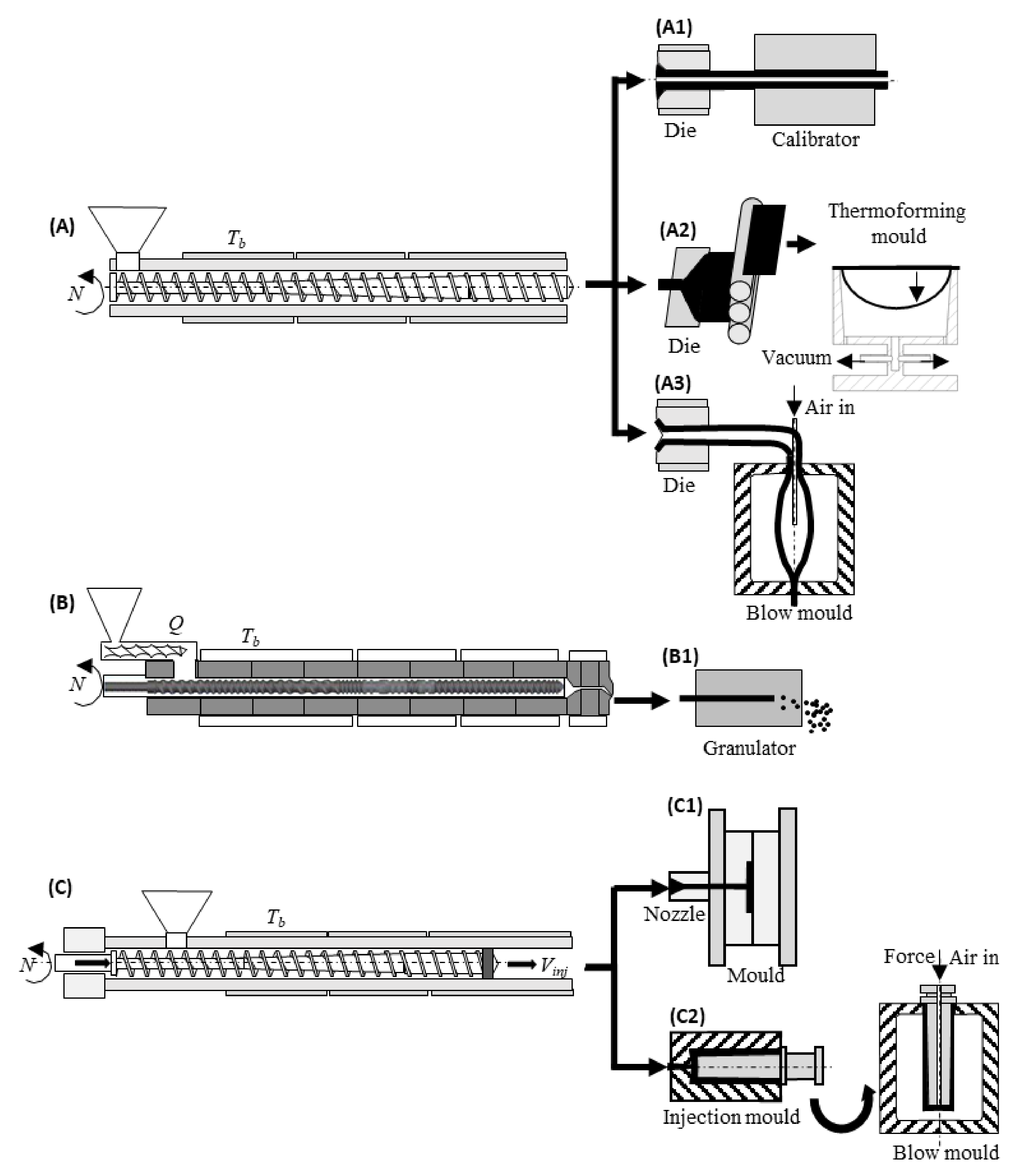
4.4. Dies and Calibrators
- (i)
- Using a manifold, i.e., use a larger channel upstream to distribute the flow transversally, prior to its progress downstream. The die geometry is such that a central flow stream has a shorter path in the manifold and a longer path in the shallower parallel zone, while the reverse occurs for a flow stream near to the edges. This approach is frequently adopted for the production of cast film and sheet, wire insulation, and in extrusion blow moulding.
- (ii)
- Using a cylindrical mandrel to convert the circular flow from the extruder into an annular flow. Since the classical torpedo-type solution with its supports (known as spider legs) creates unbalanced flow and strong weld lines, it was progressively replaced by basket-type dies and spiral mandrel dies. The mandrels of the latter are designed in such a way that the flow from the extruder is divided into individual melts that feed helical channels with decreasing depth along their length in the mandrel. Thus, the helical flow is gradually converted into an axial annular flow.
- (iii)
- Change gradually from the inlet circular channel into the desired cross-section. The design of dies for hollow profiles, or for profiles containing thickness differences in their cross-section is particularly challenging.
4.4.1. Manifold Dies
4.4.2. Mandrel Dies
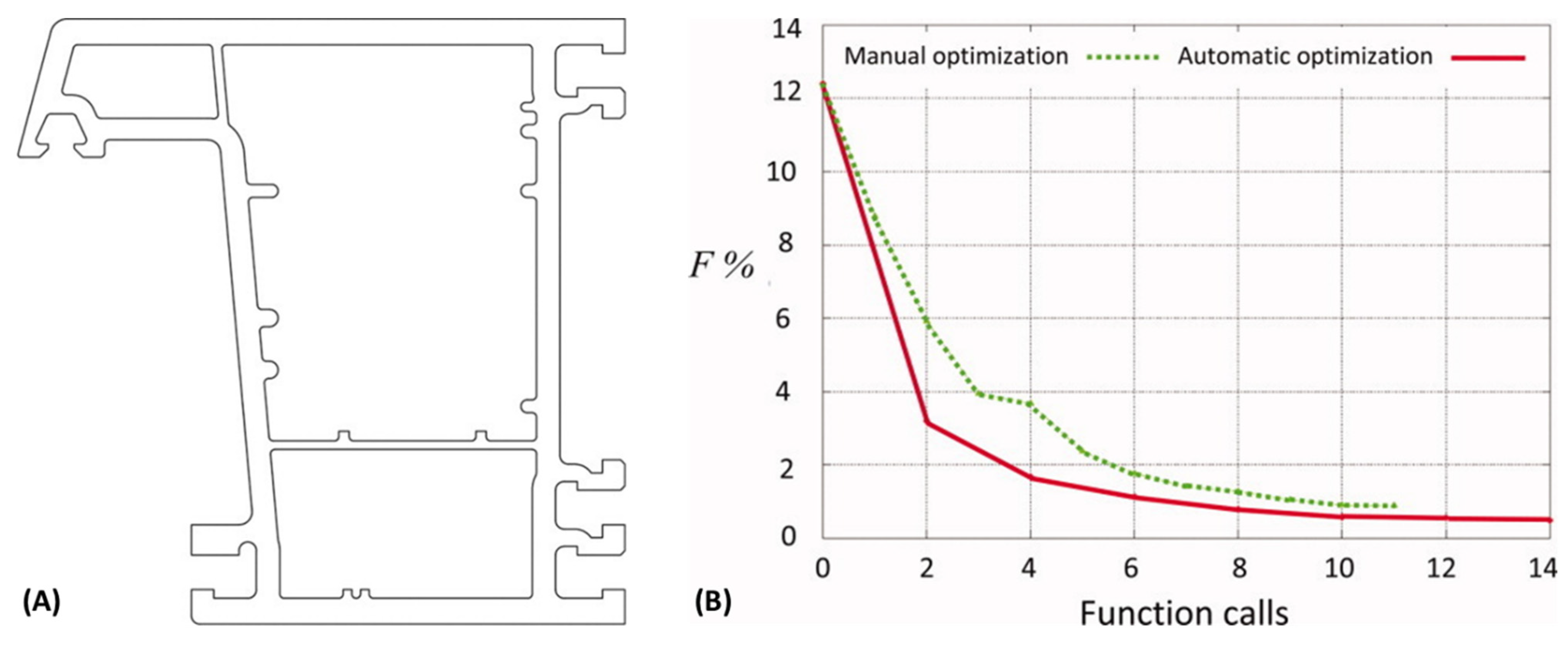
4.4.3. Profile Dies
| Objective Function | Optimization Algorithm | Modelling Approach | Decision Variables | Other Characteristics | Authors (Year) Reference |
|---|---|---|---|---|---|
| SO | Empirical | 3D-N | GP | IEP | Legat and Marchal (1993) [127] |
| SO | Empirical | 3D-N | GP | IEP | Tran-Cong and Phan-Thien (1988) [129] |
| SO | Empirical | A | GP | Hurez et al. (1996) [130] | |
| SO | Empirical | 3D-N | GP | Švábík et al. (1999) [131] | |
| SO | Empirical | 3D-N | GP | IEP | Gifford (2003) [132] |
| SO | Empirical | 3D-N | GP(3) | Rezaei Shahreza et al. (2010) [133] | |
| SO | Simplex | 3D-N | GP | Coupez et al. (1999) [134] | |
| SO | Regression | 3D-N | MP | Ready and Schaub (1999) [135] | |
| SO | Regression | 3D-N | GP(22) | Elgeti et al. (2012) [136] | |
| SO | Regression | 3D-N | GP(171) | IEP | Pauli et al. (2013) [137] |
| SO | Gradient | 3D-N | MP | Sienz et al. (1998, 2010) [138,139] | |
| SO | Gradient | 3D-N | GP | Szarvasy et al. (2000) [140] | |
| SO | ES | 3D-N | MP | Sienz et al. (1999) [141] | |
| SO | Gradient | 2D-N | KP | Ettinger et al. (2004, 2004) [142,143] | |
| SO | Gradient | 2D-N | KP(2-46] | Sienz et al. (2012) [144] | |
| SO | SA | 3D-N | GP(3) | Yilmaz et al. (2014) [145] | |
| SO | Feedback Control | 3D-N | GP | IEP | Spanjaards et al. (2021) [146] |
| WS(2) | Simplex | 3D-N | GP | Nóbrega et al. (2002, 2003) [147,148,149] | |
| WS(2) | Simplex | 3D-N | GP | Carneiro et al. (2004) [150] | |
| WS(4) | Gradient | 3D-N | GP(8) | Zhang et al. (2019) [154] |
4.4.4. Calibrators
| Objective function | Optimization Algorithm | Modelling Approach | Decision Variables | Other Characteristics | Authors (Year) Reference |
|---|---|---|---|---|---|
| SO | Simplex | 3D-N | GP(5) | - | Nóbrega and Carneiro (2005) [156] |
| AS(2) | Empirical | 3D-N | GP(n) | - | Duan and Zhang (2014) [158] |
| AS(2) | Gradient | 3D-N | GP(48) | - | Fradette et al. (1996) [155] |
| AS(2) | EA | 3D-N | GP(n) | - | Ren et al. (2010) [159] |
| MO | EA | 3D-N | GP(8) | - | Nóbrega et al. (2008) [157] |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Plastics the Facts 2020, Plastics Europe: Association of Plastics Manufactures. Available online: https://www.plasticseurope.org/en/resources/publications/4312-plastics-facts-2020 (accessed on 18 May 2021).
- Tadmor, Z.; Gogos, C.G. Principles of Polymer Processing, 2nd ed.; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Maddock, B.H. A Visual Analysis of Flow and Mixing in Extruder Screws. SPE J. 1959, 15, 383–389. [Google Scholar]
- Agassant, J.F.; Avenas, P.; Sergent, J.-P.; Carreau, P.J. Polymer Processing: Principles and Modeling; Carl Hanser Verlag: Munich, Germany, 1991. [Google Scholar]
- Osswald, A.T.; Hernández-Ortiz, P.J. Polymer Processing: Modeling and Simulation; Carl Hanser Verlag: Munich, Germany, 2006. [Google Scholar]
- Baird, G.D.; Collias, I.D. Polymer Processing: Principles and Design, 2nd ed.; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Gooneie, A.; Schuschnigg, S.; Holzer, C. A Review of Multiscale Computational Methods in Polymeric Materials. Polymers 2017, 9, 16. [Google Scholar] [CrossRef]
- Chan, I.C. A Scientific Approach to Screw Design. J. Reinf. Plast. Compos. 1998, 17, 1096–1109. [Google Scholar]
- Carneiro, O.; Nóbrega, J.M.; Pinho, F.T.; Oliveira, P.J. Computer Aided rheological Design of Extrusion Dies for Profiles. J. Mater. Process. Technol. 2001, 114, 75–86. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, H.; Chugh, T.; Guo, D.; Miettinen, K. Data-Driven Evolutionary Optimization: An Overview and Case Studies. IEEE Trans. Evol. Comput. 2019, 23, 442–458. [Google Scholar] [CrossRef]
- Ibañez, R.; Casteran, F.; Argerich, C.; Ghnatios, C.; Hascoet, N.; Ammar, A.; Cassagnau, P.; Chinesta, F. On the Data-Driven Modeling of Reactive Extrusion. Fluids 2020, 5, 94. [Google Scholar] [CrossRef]
- Kasat, R.B.; Ray, A.K.; Gupta, S.K. Applications of Genetic Algorithm in Polymer Science and Engineering. Mater. Manuf. Process. 2003, 18, 523–532. [Google Scholar] [CrossRef]
- Oduguwa, V.; Tiwari, A.; Roy, R. Evolutionary computing in manufacturing industry: An overview of recent applications. Appl. Soft Comput. 2005, 5, 281–299. [Google Scholar] [CrossRef]
- Nastaj, A.; Wilczyński, K. Optimization and Scale-Up for Polymer Extrusion. Polymers 2021, 13, 1547. [Google Scholar] [CrossRef] [PubMed]
- Denysiuk, R.; Gonçalves, N.; Pinto, R.; Silva, H.; Duarte, F.; Nunes, J.; Gaspar-Cunha, A. Optimization of Injection Stretch Blow Molding: Part I—Defining Part Thickness Profile. Int. Polym. Process. 2019, 34, 314–323. [Google Scholar] [CrossRef]
- Pinto, R.S.; Silva, H.M.; Duarte, F.M.; Nunes, J.P.; Gaspar-Cunha, A. Neuroevolutionary Multiobjective Optimization of Injection Stretch Blow Molding Process in the Blowing Phase. Comput. Methods Appl. Sci. 2021, 55, 307–318. [Google Scholar] [CrossRef]
- Deb, K. Optimization for Engineering Design: Algorithms and Examples; Prentice-Hall: New Delhi, India, 1995. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Carlos Coello, C.; Lamont, B.G.; van Veldhuizen, A.D. Evolutionary Algorithms for Solving Multi-Objective Problems, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer: Boston, MA, USA, 2012. [Google Scholar]
- Afsar, B.; Miettinen, K.; Ruiz, F. Assessing the Performance of Interactive Multiobjective Optimization Methods: A Survey. ACM Comput. Surv. 2021, 54, 85. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; Technical Report 103; Computer Engineering and Networks Laboratory (TIK), Swiss Federal Institute of Technology (ETH): Zurich, Switzerland, 2001. [Google Scholar]
- Li, H.; Zhang, Q. Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2009, 13, 284–302. [Google Scholar] [CrossRef]
- Zitzler, E.; Künzli, S. Indicator-Based Selection in Multiobjective Search. In Parallel Problem Solving from Nature—PPSN VIII. PPSN 2004; Lecture Notes in Computer Science 2004, 3242; Yao, X., Burke, E.D., Lozano, J.A., Smith, J., Merelo-Guervós, J.J., Bullinaria, J.A., Rowe, J.E., Tiňo, P., Kabán, A., Schwefel, H.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 832–842. [Google Scholar]
- Beume, N.; Naujoks, B.; Emmerich, M. SMS-EMOA: Multiobjective selection based on dominated hypervolume. Eur. J. Oper. Res. 2007, 181, 1653–1669. [Google Scholar] [CrossRef]
- Emmerich, M.; Beume, N.; Naujoks, B. An EMO Algorithm Using the Hypervolume Measure as Selection Criterion. In Proceedings of the Evolutionary Multi-Criterion Optimization (EMO 2005), Guanajuato, Mexico, 9–11 March 2005. [Google Scholar]
- McMullen, P.R. An ant colony optimization approach to addressing a JIT sequencing problem with multiple objectives. Artif. Intell. Eng. 2001, 15, 309–317. [Google Scholar] [CrossRef]
- Mason, K.; Duggan, J.; Howley, E. Multi-objective dynamic economic emission dispatch using particle swarm optimisation variants. Neurocomputing 2017, 270, 188–197. [Google Scholar] [CrossRef]
- Suman, B.; Kumar, P. A survey of simulated annealing as a tool for single and multiobjective optimization. J. Oper. Res. Soc. 2006, 57, 1143–1160. [Google Scholar] [CrossRef]
- Mezura-Montes, E.; Reyes-Sierra, M.; Coello, C.A.C. Multi-objective Optimization Using Differential Evolution: A Survey of the State-of-the-Art. In Advances in Differential Evolution. Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2008; Volume 143, pp. 173–196. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Covas, J.A. Robustness in Multi-Objective Optimization Using Evolutionary Algorithms. Comput. Optim. Appl. 2008, 39, 75–96. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Ferreira, J.; Recio, G. Evolutionary Robustness Analysis for Multi-Objective Optimisation: Benchmark Problems. Struct. Multidiscip. Optim. 2014, 49, 771–793. [Google Scholar] [CrossRef]
- Ferreira, J.; Fonseca, C.; Gaspar-Cunha, A. Methodology to Select Solutions for Multi-Objective Optimization Problems: Weighted Stress Function Method. J. Multi-Crit. Decis. Anal. 2017, 24, 103–120. [Google Scholar] [CrossRef]
- Underwood, W.M. Experimental method for designing extrusion screws. Chem. Eng. Prog. 1962, 58, 59–65. [Google Scholar]
- Tadmor, Z.; Klein, I. Engineering Principles of Plasticating Extrusion; Van Nostrand Reinhold Co.: New York, NY, USA, 1970. [Google Scholar]
- Maddock, B.H.; Smith, D.J. Extruder Design by Computer Printout. SPE J. 1972, 28, 12–17. [Google Scholar]
- Helmy, H.A.A.; Parnaby, J. Computer–Aided Optimal Melt Screw Design. Polym. Eng. Sci. 1976, 16, 437–449. [Google Scholar] [CrossRef]
- Potente, H.; Hanhart, W.; Klarholz, B.; Schöppner, V. Optimizing extruder screws by simulation. Kunstst. Plast 1992, 82, 939–944. [Google Scholar]
- Wortberg, J.; Klarholz, B.; Meyer-Katona, S. Expert-knowledge-based analysis of extrusion process. Kunstst. Plast 1994, 84, 26–30. [Google Scholar]
- Chung, I.C. Screw Design, High Performance Screws, and Scale-Up, in Extrusion of Polymers: Theory & Practice, 3rd ed.; Carl Hanser Verlag GmbH & Co.: Munich, Germany, 2019; pp. 309–364. [Google Scholar]
- Rauwendaal, C. Polymer Extrusio; Hanser Publishers: Munich, Germany, 1986. [Google Scholar]
- Altinkaynak, A. Three Dimensional Finite Element Simulation of Polymer Melting and Flow in a Single-Screw Extruder: Optimization of Screw Channel Geometry. Ph.D. Thesis, Michigan Technological University, Houghton, MI, USA, 2010. [Google Scholar] [CrossRef]
- Potente, H.; Klarholz, B. Systematic Optimisation of Single-Screw Plasticating Units. In Proceedings of the PPS 9 Annual Meeting, Manchester, UK, 5–8 April 1993; pp. 353–354. [Google Scholar]
- Potente, H.; Klarholz, B. A Computer Aided Engineering Concept for the Design and Optimisation of a Single-Screw Plasticating Units. In Proceedings of the PPS 10 Annual Meeting, Akron, OH, USA, 5–8 April 1994; pp. 35–36. [Google Scholar]
- Potente, H.; Zelleröhr, M. Quality-Functions for the Optimisation of Single-Screw Plasticating Units. In Proceedings of the PPS 12 Annual Meeting, Sorrento, Italy, 27–31 May 1996; pp. 345–346. [Google Scholar]
- Potente, H.; Zelleröhr, M. Optimisation of Single-Screw Extruders with Statistical Methods. In Proceedings of the PPS13 Annual Meeting, Secausus, NY, USA, 10–13 June 1997. [Google Scholar]
- Potente, H.; Krell, B. Screw optimization by means of DOE and multiple regression. In Proceedings of the 55th Annual Technical Conferences of the Society of Plastics Engineers (ANTEC 1997), Toronto, ON, Canada, 27 April–2 May 1997; pp. 135–139. [Google Scholar]
- Wilczyński, K.; Nastaj, A.; Krutysz, P. Optymalizacja Procesu Wytłaczania Jednoślimakowego Tworzyw Sztucznych. Metoda Statystyczna. Mechanik 2003, 10, 618. [Google Scholar]
- Wilczyñski, K. SSEM: A computer model for a polymer single-screw extrusion. J. Mater. Process. Technol. 2001, 109, 308–313. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Abramczyk, P. Optymalizacja Procesu Wytłaczania Jednoślimakowego Tworzyw Sztucznych. Metoda Sieci Neuronowych. Mechanik 2004, 7, 470. [Google Scholar]
- Thibodeau, C.A.; Lafleur, P.G. Computer Design and Screw Optimization. In Proceedings of the 58th Annual Technical Conference of the Society of Plastics Engineers (ANTEC 2000), Orlando, FL, USA, 7–11 May 2000; pp. 276–282. [Google Scholar]
- Thibodeau, C.A.; Lafleur, P.G. Computer Design and Screw Optimization. In Proceedings of the Polymer Processing Society 16th Annual Meeting (PPS-16), Shanghai, China, 18–23 June 2000; p. 15. [Google Scholar]
- Nastaj, A.; Wilczyński, K. Process Optimization for Single Screw Extrusion of Polymeric Materials-Simulation Studies. Polimery 2018, 63, 297–304. [Google Scholar] [CrossRef]
- Nastaj, A.; Wilczyński, K. Optimization for Starve Fed/Flood Fed Single Screw Extrusion of Polymeric Materials. Polymers 2020, 12, 149. [Google Scholar] [CrossRef] [Green Version]
- Abeykoon, C.; Li, K.; McAfee, M.; Martin, P.J.; Niu, Q.; Kelly, A.L.; Deng, J. A new model based approach for the prediction and optimisation of thermal homogeneity in single screw extrusion. Control Eng. Pract. 2011, 19, 862–874. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Covas, J.A.; Oliveira, P. Optimization of Polymer Extrusion With Genetic Algorithms. IMA J. Math. Appl. Bus. Ind. 1998, 9, 267–277. [Google Scholar] [CrossRef]
- Covas, J.A.; Cunha, A.G.; Oliveira, P. An Optimization Approach to Practical Problems in Plasticating Single Screw Extrusion. Polym. Eng. Sci. 1999, 39, 443–456. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Covas, J.A. The Design of Extrusion Screw: An Optimization Approach. Int. Polym. Proc. 2001, 16, 229–240. [Google Scholar] [CrossRef] [Green Version]
- Covas, J.A.; Gaspar-Cunha, A. Optimisation-Based Design of Extruders. Plast. Rubber Compos. Macromol. Eng. 2004, 33, 416–425. [Google Scholar] [CrossRef]
- Domingues, N.; Gaspar-Cunha, A.; Covas, J.A. A Quantitative Approach to Assess the Mixing Ability of Single Screw Extruders for Polymer Extrusion. J. Polym. Eng. 2012, 32, 81–94. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Gonçalves, L.; Covas, J.A. Application of Evolutionary Algorithms to the Design of Barrier Screws for Single Screw Extruders. In Applied Soft Computing Technologies: The Challenge of Complexity; Abraham, A., Baets, B., Koppen, M., Nickolay, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 763–774. [Google Scholar]
- Covas, J.A.; Gaspar-Cunha, A. Extrusion Scale-up: An Optimization-based Methodology. Int. Polym. Proc. 2009, 24, 67–82. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Covas, J.A. A Universal Engineering Scale-Up Approach Using Multi-Objective Optimization. Int. J. Nat. Lang. Comput. 2014, 4, 17–30. [Google Scholar] [CrossRef] [Green Version]
- Denysiuk, R.; Recio, G.; Covas, J.A.; Gaspar-Cunha, A. Using Multiobjective Optimization Algorithms and Decision Making Support to Solve Polymer Extrusion Problems. Polym. Eng. Sci. 2018, 58, 493–502. [Google Scholar] [CrossRef]
- Deb, K.; Bandaru, S.; Greiner, D.; Gaspar-Cunha, A.; Tutum, C.C. An Integrated Approach to Automated Innovization for Discovering Useful Design Principles: Case Studies from Engineering. Appl. Soft Comput. 2014, 15, 42–56. [Google Scholar] [CrossRef] [Green Version]
- Potente, H.; Ansahl, J.; Klarholz, B. Design of Tightly Intermeshing Co-Rotating Twin Screw Extruders. Int. Polym. Proc. 1994, 9, 11–25. [Google Scholar] [CrossRef]
- Potente, H.; Bastian, M.; Flecke, J. Design of a compounding extruder by means of the SIGMA simulation software. Adv. Polym. Technol. 1999, 18, 147–170. [Google Scholar] [CrossRef]
- Vainio, T.P.; Harlin, A.; Seppälä, J.V. Screw optimization of a co-rotating twin-screw extruder for a binary immiscible blend. Polym. Eng. Sci. 1995, 35, 225–232. [Google Scholar] [CrossRef]
- Berzin, F.; Tara, A.; Vergnes, B. Optimization and scale-up of starch cationization in a twin screw extruder. Polym. Eng. Sci. 2007, 47, 814–823. [Google Scholar] [CrossRef]
- Maridass, B.; Gupta, B.R. Performance optimization of a counter rotating twin screw extruder for recycling natural rubber vulcanizates using response surface methodology. Polym. Test. 2004, 23, 377–385. [Google Scholar] [CrossRef]
- Ulitzsch, S.; Bäuerle, T.; Chassé, T.; Lorenz, G.; Kandelbauer, A. Optimizing the Process Efficiency of Reactive Extrusion in the Synthesis of Vinyltrimethoxysilane-Grafted Ethylene-Octene-Copolymer (EOC-g-VTMS) by Response Surface Methodology. Polymers 2020, 12, 2798. [Google Scholar] [CrossRef]
- Fukuda, G.; Bigio, D.I.; Andersen, P.; Wetzel, M. A new scale-up approach for dispersive mixing in twin-screw compounding. AIP Conf. Proc. 2015, 1664, 100007. [Google Scholar]
- Potente, H.; Thümen, A. Method for the Optimisation of Screw Elements for Tightly Intermeshing, Co-rotating Twin Screw Extruders. Int. Polym. Proc. 2006, 21, 149–154. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, M.; Jia, Y. Multi-objective optimization of reactive extrusion by genetic algorithms. J. Appl. Polym. Sci. 2015, 132, 41862. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Poulesquen, A.; Vergnes, B.; Covas, J.A. Optimization of Processing Conditions for Polymer Twin-Screw Extrusion. Int. Polym. Proc. 2002, 17, 201–213. [Google Scholar] [CrossRef]
- Vergnes, B.; Della Valle, G.; Delamare, L. A global computer software for polymer flows in corotating twin screw extruders. Polym. Eng. Sci. 1998, 38, 1781. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Covas, J.A.; Vergnes, B. Defining the Configuration of Co-Rotating Twin-Screw Extruders with Multiobjective Evolutionary Algorithms. Polym. Eng. Sci. 2005, 45, 1159–1173. [Google Scholar] [CrossRef]
- Teixeira, C.; Covas, J.A.; Stützle, T.; Gaspar-Cunha, A. Engineering an Efficient Two-Phase Local Search Algorithm for the Co-Rotating Twin-Screw Extruder Configuration Problem. Int. Trans. Oper. Res. 2011, 18, 271–291. [Google Scholar] [CrossRef]
- Teixeira, C.; Gaspar-Cunha, A.; Covas, J.A. Flow and Heat Transfer along the Length of a Co-Rotating Twin Screw Extruder. Polym. Plast. Technol. Eng. 2012, 51, 1567–1577. [Google Scholar] [CrossRef]
- Teixeira, C.; Covas, J.A.; Stützle, T.; Gaspar-Cunha, A. Multi-Objective Ant Colony Optimization for the Twin-Screw Configuration Problem. Eng. Optim. 2012, 44, 351–371. [Google Scholar] [CrossRef] [Green Version]
- Teixeira, C.; Covas, J.A.; Stützle, T.; Gaspar-Cunha, A. Hybrid Algorithms for the Twin-Screw Extrusion Configuration Problem. Appl. Soft Comput. 2014, 23, 298–307. [Google Scholar] [CrossRef]
- Teixeira, C.; Covas, J.A.; Berzin, F.; Vergnes, B.; Gaspar-Cunha, A. Application of Evolutionary Algorithms to the Definition of the Optimal Twin-Screw Extruder Configuration for Starch Cationization. Polym. Eng. Sci. 2011, 51, 330–340. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Covas, J.A. A Scaling-up Methodology for Co-Rotating Twin-Extruders. In Proceedings of the 27th Annual Meeting of the Polymer Processing Society (PPS-27), Marrakesh, Morocco, 10–14 May 2011; pp. 1–6. [Google Scholar]
- Rakos, R.; Sebastian, D. Design and optimization of extrusion dies using computer based simulations. Adv. Polym. Technol. 1990, 10, 297–307. [Google Scholar] [CrossRef]
- Matsubara, Y. Geometry design of a coat-hanger die with uniform flow rate and residence time across the die width. Polym. Eng. Sci. 1997, 19, 169–172. [Google Scholar] [CrossRef]
- Matsubara, Y. Design of coat-hanger sheeting dies based on ratio of residence times in manifold and slot. Polym. Eng. Sci. 1980, 20, 716–719. [Google Scholar] [CrossRef]
- Matsubara, Y. Residence time distribution of polymer melt in the T-die. Polym. Eng. Sci. 1980, 20, 212–214. [Google Scholar] [CrossRef]
- Matsubara, Y. Flat die geometry—A note. Polym. Eng. Sci. 1988, 28, 1275. [Google Scholar] [CrossRef]
- Winter, H.H.; Fritz, H.G. Design of dies for the extrusion of sheets and annular parisons: The distribution problem. Polym. Eng. Sci. 1986, 26, 543–553. [Google Scholar] [CrossRef]
- Liu, T.J.; Hong, C.N.; Chen, K.C. Computer-aided analysis of a linearly tapered coat-hanger die. Polym. Eng. Sci. 1988, 28, 1517–1526. [Google Scholar] [CrossRef]
- Lee, K.Y.; Liu, T.J. Design and analysis of a dual-cavity coat-hanger die. Polym. Eng. Sci. 1989, 29, 1066–1075. [Google Scholar] [CrossRef]
- Liu, T.J.; Liu, L.D.; Tsou, J.D. A unified lubrication approach for the design of a coat-hanger die. Polym. Eng. Sci. 1994, 34, 541–550. [Google Scholar] [CrossRef]
- Yu, Y.W.; Liu, T.J. A simple numerical approach for the optimal design of an extrusion die. J. Polym. Res. 1998, 5, 1–7. [Google Scholar] [CrossRef]
- Na, S.Y.; Kim, D.H. Three-dimensional modelling of non-newtonian fluid flow in a coat-hanger die. Korean J. Chem. Eng. 1995, 12, 236–243. [Google Scholar] [CrossRef]
- Huang, Y.; Gentle, C.R.; Hull, J.B. A comprehensive 3-D analysis of polymer melt flow in slit extrusion dies. Adv. Polym. Technol. 2004, 23, 111–124. [Google Scholar] [CrossRef]
- Chen, C.; Jen, P.; Lai, F.S. Optimization of the coathanger manifold via computer simulation and an orthogonal array method. Polym. Eng. Sci. 1997, 37, 188–196. [Google Scholar] [CrossRef]
- Razeghiyadaki, A.; Zhang, D.; Wei, D.; Perveen, A. Optimization of Polymer Extrusion Die Based on Response Surface Method. Processes 2020, 8, 1043. [Google Scholar] [CrossRef]
- Razeghiyadaki, A.; Wei, D.; Perveen, A.; Zhang, D. A Multi-Rheology Design Method of Sheeting Polymer Extrusion Dies Based on Flow Network and the Winter–Fritz Design Equation. Polymers 2021, 13, 1924. [Google Scholar] [CrossRef]
- Lebaal, N.; Schmidt, F.M.; Puissant, S. Optimization of 3D die extrusion using response surface method. In Proceedings of the 9th International Conference on Material Forming ESAFORM, Glasgow, UK, 26–28 April 2006; pp. 703–706. [Google Scholar]
- Lebaal, N.; Schmidt, F.; Puissant, S. Design and optimization of three-dimensional extrusion dies, using constraint optimization algorithm. Finite Elem. Anal. Design 2009, 45, 333–340. [Google Scholar] [CrossRef]
- Lebaal, N.; Schmidt, F.; Puissant, S. Optimisation of extrusion flat die design and die wall temperature distribution, using Kriging and response surface method. Int. J. Mater. Prod. Technol. 2010, 38, 307. [Google Scholar] [CrossRef]
- Lebaal, N.; Puissant, S.; Schmidt, F.M.; Schläfli, D. An optimization method with experimental validation for the design of extrusion wire coating dies for a range of different materials and operating conditions. Polym. Eng. Sci. 2012, 52, 2675–2687. [Google Scholar] [CrossRef] [Green Version]
- Smith, D.E.; Tortorelli, D.A.; Tucker, C.L. Optimal design for polymer extrusion. Part I: Sensitivity analysis for nonlinear steady-state systems. Comput. Methods Appl. Mech. Eng. 1998, 167, 283–302. [Google Scholar] [CrossRef]
- Smith, D.E.; Tortorelli, D.A.; Tucker, C.L. Optimal design for polymer extrusion. Part II: Sensitivity analysis for weakly-coupled nonlinear steady-state systems. Comput. Methods Appl. Mech. Eng. 1998, 167, 303–323. [Google Scholar] [CrossRef]
- Smith, D.E. Design sensitivity analysis and optimization for polymer sheet extrusion and mold filling processes. Int. J. Numer. Methods Eng. 2003, 57, 1381–1411. [Google Scholar] [CrossRef]
- Smith, D.E. An optimisation-based approach to compute sheeting die designs for multiple operating conditions. In Proceedings of the Annual Technical Conference of the SPE --ANTEC 2003, Nashville, TN, USA, 4–8 May 2003; pp. 315–319. [Google Scholar]
- Sun, Y.; Gupta, M. Optimization of a flat die geometry. In Proceedings of the SPE Annual Technical Conference, Chicago, IL, USA, 16–20 May 2004; pp. 3307–3311. [Google Scholar]
- Bates, S.J.; Pittman, J.F.T.; Sienz, J.; Langley, D.S. Enhancing slit die performance by optimization of restrictor profiles. Polym. Eng. Sci. 2003, 43, 1500–1511. [Google Scholar] [CrossRef]
- Sienz, J.; Bates, S.J.; Pittman, J.F.T. Flow restrictor design for extrusion slit dies for a range of materials: Simulation and comparison of optimization techniques. Finite Elem. Anal. Design 2006, 42, 430–453. [Google Scholar] [CrossRef]
- Michaeli, W.; Kaul, S. Approach of an Automatic Extrusion Die Optimization. J. Polym. Eng. 2004, 24. [Google Scholar] [CrossRef]
- Meng, K.; Zhao, Z.L. Optimal Design of the Curvilinear Tapered Coat-Hanger Die. Appl. Mech. Mater. 2011, 121–126, 1014–1018. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, X. Optimization of air flow field of the melt blowing slot die via numerical simulation and genetic algorithm. J. Appl. Polym. Sci. 2010, 115, 1540–1545. [Google Scholar] [CrossRef]
- Meng, K.; Wang, X.; Huang, X. Optimal design of the coat-hanger die used for producing melt-blown fabrics by finite element method and evolution strategies. Polym. Eng. Sci. 2009, 49, 354–358. [Google Scholar] [CrossRef]
- Meng, K.; Wang, X.H.; Chen, Q.G. Analysis and Design of a Broad-Width Coat-Hanger Die in the Melt Blowing Process. Fibres Text. East. Eur. 2012, 20, 44–47. [Google Scholar]
- Han, W.; Wang, X. Optimal geometry design of the coat-hanger die with uniform outlet velocity and minimal residence time. J. Appl. Polym. Sci. 2012, 123, 2511–2516. [Google Scholar] [CrossRef]
- Smith, D.; Wang, Q. Optimal Polymer Sheeting Die Design for Multiple Operation Conditions. In Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, CA, USA, 19–22 April 2004. [Google Scholar]
- Smith, D.E.; Wang, Q. Optimization-based design of polymer sheeting dies using generalized Newtonian fluid models. Polym. Eng. Sci. 2005, 45, 953–965. [Google Scholar] [CrossRef]
- Wang, Q.; Smith, D.E. Analysis of the fluid–structure interaction in the optimization-based design of polymer sheeting dies. J. Appl. Polym. Sci. 2006, 103, 3994–4004. [Google Scholar] [CrossRef]
- Wang, Q.; Smith, D. Incorporating Fluid-Structure Interaction in the Optimization-Based Design of Polymer Sheeting Dies. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006. [Google Scholar]
- Zhang, H.; Chen-Yu, W.; Chai, Y.; Guan, T.Y. Structure optimisation of coat-hanger die based on the multi-objective and design of experiment analysis. Int. J. Theor. Appl. Multiscale Mech. 2020, 3, 206–228. [Google Scholar] [CrossRef]
- Lee, P.C.; Dietsche, L.; Dooley, J.; Parashar, S. Improving Film Die Flow Uniformity Using Optimization Methods Coupled with Finite Element Computational Fluid Dynamics (CFD) Analysis. Int. Polym. Proc. 2015, 30, 51–62. [Google Scholar] [CrossRef]
- Han, W.; Wang, X. Multi-objective optimization of the coat-hanger die for melt-blowing process. Fibers Polym. 2012, 13, 626–631. [Google Scholar] [CrossRef]
- Han, W.; Wang, X. Optimal geometry design of double coat-hanger die for melt blowing process. Fibers Polym. 2014, 15, 1190–1196. [Google Scholar] [CrossRef]
- Huang, C.C. A systematic approach for the design of a spiral mandrel die. Polym. Eng. Sci. 1998, 38, 573–582. [Google Scholar] [CrossRef]
- Mu, Y.; Zhao, G.; Wu, X.; Zhang, C. An optimization strategy for die design in the low-density polyethylene annular extrusion process based on FES/BPNN/NSGA-II. Int. J. Adv. Manuf. Technol. 2010, 50, 517–532. [Google Scholar] [CrossRef]
- Legat, V.; Marchal, J.M. Die design: An implicit formulation for the inverse problem. Int. J. Numer. Methods Fluids 1993, 16, 29–42. [Google Scholar] [CrossRef]
- Pittman, J. Computer-aided design and optimization of profile extrusion dies for thermoplastics and rubber: A review. Proc. Inst. Mech. Eng. Part E J. Proc. Mech. Eng. 2011, 225, 280–321. [Google Scholar] [CrossRef]
- Tran-Cong, T.; Phan-Thien, N. Die design by a boundary element method. J. Non-Newton. Fluid Mech. 1998, 30, 37–46. [Google Scholar] [CrossRef]
- Hurez, P.; Tanguy, P.A.; Blouin, D. A new design procedure for profile extrusion dies. Polym. Eng. Sci. 1996, 36, 626–635. [Google Scholar] [CrossRef]
- Švábík, J.; Plaček, L.; Sáha, P. Profile Die Design Based on Flow Balancing: Balancing with Flow Separation. Int. Polym. Proc. 1999, 14, 247–253. [Google Scholar] [CrossRef]
- Gifford, W.A. Compensating for die swell in the design of profile dies. Polym. Eng. Sci. 2003, 43, 1657–1665. [Google Scholar] [CrossRef]
- Rezaei, S.A.; Behravesh, A.H.; Bakhshi, J.M.; Soury, E. Design, optimization, and manufacturing of a multiple-thickness profile extrusion die with a cross flow. Polym. Eng. Sci. 2010, 50, 2417–2424. [Google Scholar] [CrossRef]
- Coupez, Y.; Isaac, A.; Nouatin, H. Optimisation in forming using the simplex method and preliminary results on an explicit 3D viscoelastic solution. In Proceedings of the 2nd ESAFORM, Guimaraes, Portugal, 13–16 April 1999; pp. 477–480. [Google Scholar]
- Reddy, M.P.; Schaub, E.G. Design and optimisation of three dimensional extrusion dies using adaptive finite element method. In Proceedings of the ANTEC 1999, Kaneohe, HI, USA, 2–6 May 1999; pp. 63–67. [Google Scholar]
- Elgeti, S.; Probst, M.; Windeck, C.; Behr, M.; Michaeli, W.; Hopmann, C. Numerical shape optimization as an approach to extrusion die design. Finite Elem. Anal. Design 2012, 61, 35–43. [Google Scholar] [CrossRef]
- Pauli, L.; Behr, M.; Elgeti, S. Towards shape optimization of profile extrusion dies with respect to homogeneous die swell. J. Non-Newton. Fluid Mech. 2013, 200, 79–87. [Google Scholar] [CrossRef]
- Sienz, J.; Da Silva, C.E.K.; Hinton, E.; Szarvasy, I. Optimisation of PVC window profile dies. In Computational Mechanics New Trends and Applications; Idelsohn, S., Oñate, E., Dvorkin, E., Eds.; ©CIMNE: Barcelona, Spain, 1998. [Google Scholar]
- Sienz, J.; Goublomme, A.; Luege, M. Sensitivity analysis for the design of profile extrusion dies. Comput. Struct. 2010, 88, 610–624. [Google Scholar] [CrossRef]
- Szarvasy, I.; Sienz, J.; Pittman, J.F.T.; Hinton, E. Computer aided optimisation of profile extrusion dies: Definition and assessment of the objective function. Int. Polym. Proc. 2000, 15, 28–39. [Google Scholar] [CrossRef]
- Sienz, J.; Da Silva, C.E.K.; Hinton, E.; Pittman, J.F.T.; Marchal, J.M. Expert-system driven optimisation of extrusion dies. In Proceedings of the 1st ASMO UK/ISSMO Conference on Engineering Design Optimization, Ilkley, UK, 8–9 July 1999; pp. 337–344. [Google Scholar]
- Ettinger, H.J.; Sienz, J.; Pittman, J.F.T.; Polynkin, A. Parameterization and optimization strategies for the automated design of uPVC extrusion dies. Struct. Multidiscip. Optim. 2004, 28, 180–194. [Google Scholar] [CrossRef]
- Ettinger, H.J. Development of Optimization and Parameterization Techniques Applied to Extrusion die Design Optimization of PVC Profile Dies. Ph.D. Thesis, Swansea University, Swansea, UK, 2004. [Google Scholar]
- Ettinger, H.; Pittman, J.F.T.; Sienz, J. Optimization-driven design of dies for profile extrusion: Parameterization, strategy, and performance. Polym. Eng. Sci. 2012, 53, 189–203. [Google Scholar] [CrossRef]
- Yilmaz, O.; Gunes, H.; Kirkkopru, K. Optimization of a profile extrusion die for flow balance. Fibers Polym. 2014, 15, 753–761. [Google Scholar] [CrossRef]
- Spanjaards, M.M.A.; Hulsen, M.A.; Anderson, P.D. Die shape optimization for extrudate swell using feedback control. J. Non-Newton. Fluid Mech. 2021, 293, 104552. [Google Scholar] [CrossRef]
- Nobrega, J.M.; Carneiro, O.S.; Oliveira, O.S.; Pinho, F.T. Flow balance optimisation of profile dies. In Proceedings of the PPS18, Guimaraes, Portugal, 16–20 June 2002. [Google Scholar]
- Nobrega, J.M.; Carneiro, O.S.; Pinho, F.T.; Oliveira, P.J. Optimisation of the flow distribution in profile extrusion dies. In Proceedings of the ANTEC 2002, San Francisco, CA, USA, 5–9 May 2002; pp. 122–126. [Google Scholar]
- Nobrega, J.M.; Carneiro, O.S.; Oliveira, P.J.; Pinho, F.T. Flow balancing in extrusion dies for thermoplastic profiles. Part I. Automatic design. Int. Polym. Proc. 2003, 18, 298–306. [Google Scholar] [CrossRef]
- Carneiro, O.S.; Nobrega, J.M. Recent developments in automatic die design for profile extrusion. Plast. Rubber Compos. 2004, 33, 400–408. [Google Scholar] [CrossRef]
- Carneiro, O.S.; Nobrega, J.M.; Oliveira, P.J.; Pinho, F.T. Flow balancing in extrusion dies for thermoplastics profiles, Part II. Influence of the design strategy. Int. Polym. Proc. 2003, 18, 307–312. [Google Scholar] [CrossRef] [Green Version]
- Nobrega, J.M.; Carneiro, O.S.; Pinho, F.T. Flow balancing in extrusion dies for thermoplastic profiles. Part III: Experimental assessment. Int. Polym. Process. 2004, 19, 225–235. [Google Scholar] [CrossRef]
- Carneiro, O.S.; Nobrega, J.M.; Pinho, F.T.; Oliveira, P.J. Automatic balancing of profile extrusion dies: Experimental assessment. In Proceedings of the ANTEC 2004, Chicago, IL, USA, 16–20 May 2004; pp. 91–95. [Google Scholar]
- Zhang, G.; Huang, X.; Li, S.; Deng, T. Optimized Design Method for Profile Extrusion Die Based on NURBS Modeling. Fibers Polym. 2019, 20, 1733–1741. [Google Scholar] [CrossRef]
- Fradette, L.; Tanguy, P.A.; Thibault, F.; Sheehy, P.; Blouin, D.; Hurez, P. Optimal Design in Profile Extrusion Calibration. J. Polym. Eng. 1995, 14, 295–322. [Google Scholar] [CrossRef]
- Nóbrega, J.M.; Carneiro, O.S. Recent Developments in Profile Extrusion: Automatic Design of Extrusion Dies and Calibrators. In Proceedings of the Anais do 9º Congresso Brasileiro de Polímeros, Campina Grande, Brazil, 7-11 de October 2007. [Google Scholar]
- Nóbrega, J.M.; Carneiro, O.S.; Gaspar-Cunha, A.; Goncalves, N. Design of Calibrators for Profile Extrusion—Optimizing Multi-Step Systems. Int. Polym. Proc. 2008, 23, 331–338. [Google Scholar] [CrossRef]
- Duan, L.; Zhang, Y. Optimization Design in Cooling Channels of Calibrator for Plastic Profile Extrusion Based on Numerical Simulation. Appl. Mech. Mater. 2014, 494–495, 677–680. [Google Scholar] [CrossRef]
- Ren, L.; Yang, R.; Zhang, W. Topology and Shape Optimization Design in Cooling System of Vacuum Calibrator for Plastic Profile Extrusion. In Proceedings of the 2010 International Conference on E-Product E-Service and E-Entertainment, Henan, China, 7–9 November 2010. [Google Scholar]

| Objective Function | Optimization Algorithm | Modelling Approach | Decision Variables | Other Characteristics | Authors (Year) Reference |
|---|---|---|---|---|---|
| Not defined | Empirical | 1D-A | DG | Various dies | Rakos and Sebastian (1990) [85] |
| SO | Empirical | 1D-A | DG(1) | CH | Matsubara (1979, 1980) [86,87] |
| SO | Empirical | 1D-A | DG(1) | T-die | Matsubara (1980, 1988) [88,89] |
| SO | Empirical | 1D-A | DG(3) | CH | Winter and Fritz (1986) [90] |
| SO | Empirical | 3D-N | DG(3) | CH | Liu et al. (1988, 1994) [91] |
| SO | Empirical | 3D-N | DG(4) | TCH, 2 cavities | Lee and Liu (1989) [92] |
| SO | Empirical | 3D-N | DG(3) | CH | Liu et al. (1988, 1994) [93] |
| SO | Empirical | 3D-N | DG(4) | TCH | Yu and Liu (1998) [94] |
| SO | Empirical | 3D-N | DG(3) | CH | Na and Kim (1995) [95] |
| SO | Empirical | 2D-N | DG(2) | CH | Huang et al. (2004) [96] |
| SO | Regression | 1D-A | OC(1) + DG(3) | CH | Chen et al. (1997) [97] |
| SO | Regression | 3D-N | DG(5) | CH | Razeghiyadaki et al. (2020, 2021) [98,99] |
| SO | SQP + Regression | 3D-N | DG(1) | CH | Lebaal et al. (2006) [100] |
| SO | SQP + Regression | 3D-N | DG(4) | CH | Lebaal et al. (2009) [101] |
| SO | SQP + Regression | 3D-N | OC(3) + DG(1) | CH | Lebaal et al. (2010) [102] |
| SO | SQP + Regression | 3D-N | DG(4) | CH (wire) | Lebaal et al. (2012) [103] |
| SO | Gradient | 3D-N | DG(2) | CH | Smith et al. (1998, 1998) [104,105] |
| SO | Gradient | 3D-N | OC(1) + DG(2) | CH | Smith (2003) [106] |
| SO | Gradient | 3D-N | DG(811) | CH, Robustness | Smith (2003) [107] |
| SO | Gradient | 3D-N | DG(9) | CH | Sun and Gupta (2004) [108] |
| SO | Gradient | 3D-N | DG(5) | CH, Restrictor | Bates et al. (2003) [109] |
| SO | Regression + Gradient + EA | 3D-N | DG(5) | CH, Restrictor | Siens et al. (2006) [110] |
| SO | EA | 3D-N | DG(n) | CH | Michaeli and Kaul (2004) [111] |
| SO | EA | 3D-N | DG(2) | CH | Meng and Zhao (2011) [112] |
| SO | EA | 3D-N | DG(4) | Slot die | Sun and Wang (2010) [113] |
| SO | EA | 3D-N | DG(2) | Blow: 2-CH | Meng et al. (2009, 2012) [114,115] |
| AS(2) | Regression | 3D-N | DG(3) | CH | Han and Wang (2012) [116] |
| AS(n) | Gradient | 3D-N | OC(1) + DG(2) | CH, Robustness | Smith and Wang (2004) [117] |
| AS(n) | Gradient | 3D-N | OC(1) + DG(2) | CH | Smith and Wang (2005) [118] |
| AS(n) | SQP | 3D-N | OC(1) + DG(2) | CH | Wang and Smith (2006) [119,120] |
| AS(3) | EA | 3D-N | OC() + DG() | CH | Zhang et al. (2020) [121] |
| MO(2) | DOE, RSM, EA | 3D-N | DG(3/8/12) | CH | Lee et al. (2015) [122] |
| MO(2) | EA | 3D-N | DG(3) | CH | Han and Wang (2012) [123] |
| AS(2) & MO(2) | Regression + EA | 3D-N | DG(1) | Blow: 2-CH | Han and Wang (2014) [124] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaspar-Cunha, A.; Covas, J.A.; Sikora, J. Optimization of Polymer Processing: A Review (Part I—Extrusion). Materials 2022, 15, 384. https://doi.org/10.3390/ma15010384
Gaspar-Cunha A, Covas JA, Sikora J. Optimization of Polymer Processing: A Review (Part I—Extrusion). Materials. 2022; 15(1):384. https://doi.org/10.3390/ma15010384
Chicago/Turabian StyleGaspar-Cunha, António, José A. Covas, and Janusz Sikora. 2022. "Optimization of Polymer Processing: A Review (Part I—Extrusion)" Materials 15, no. 1: 384. https://doi.org/10.3390/ma15010384
APA StyleGaspar-Cunha, A., Covas, J. A., & Sikora, J. (2022). Optimization of Polymer Processing: A Review (Part I—Extrusion). Materials, 15(1), 384. https://doi.org/10.3390/ma15010384








