On the Localization of Persistent Currents Due to Trapped Magnetic Flux at the Stacking Faults of Graphite at Room Temperature
Abstract
:1. Introduction
Assumptions and Experimental Restrictions to Observe Room Temperature Superconductivity in Graphite
2. Magnetic Force Microscopy and Monopole Model Description
2.1. Magnetic Force Microscopy
2.2. Cantilever Tip Approximation
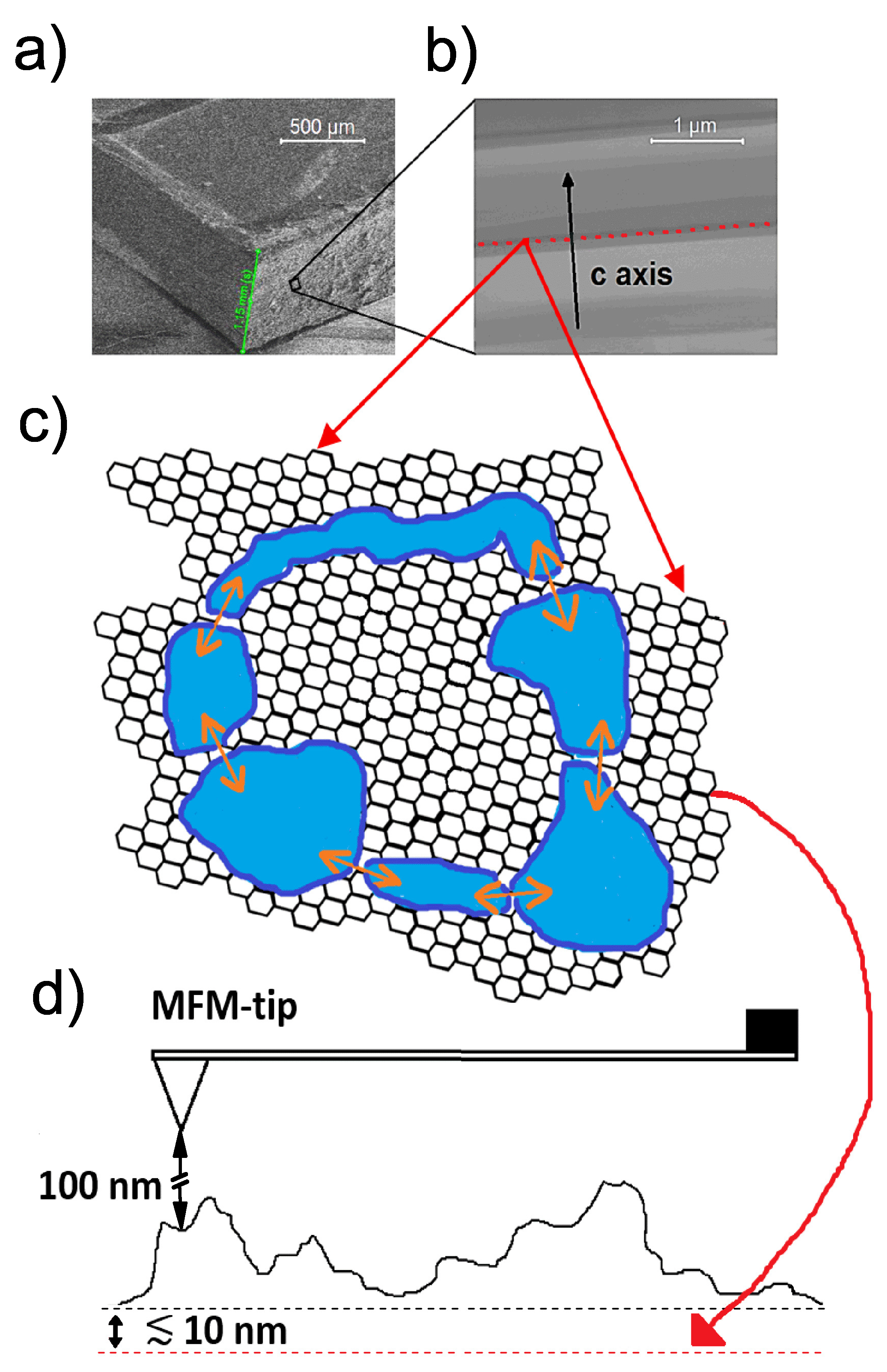
3. Experimental Setup, Sample Preparation, and Precharacterization
4. Results and Discussion
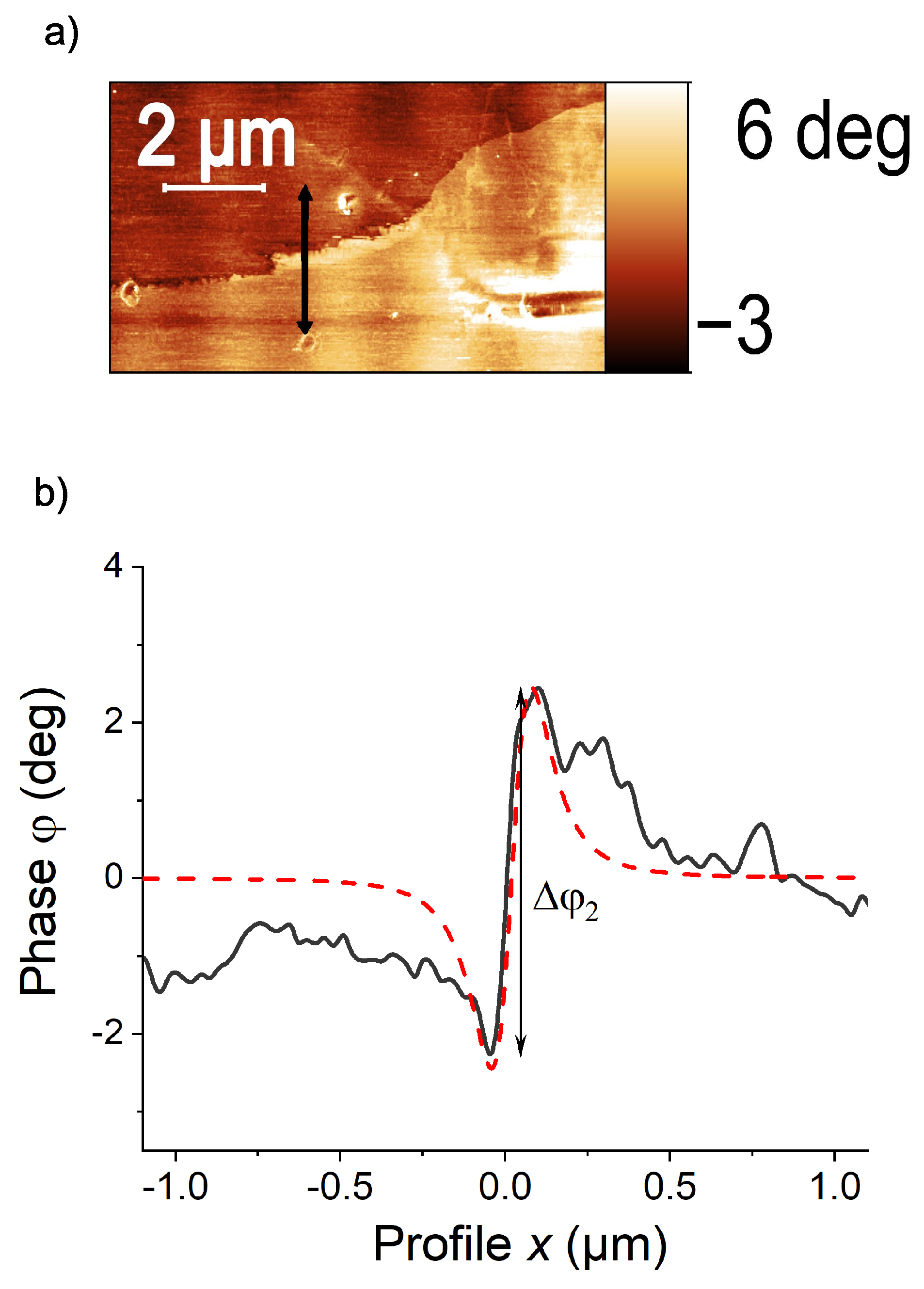
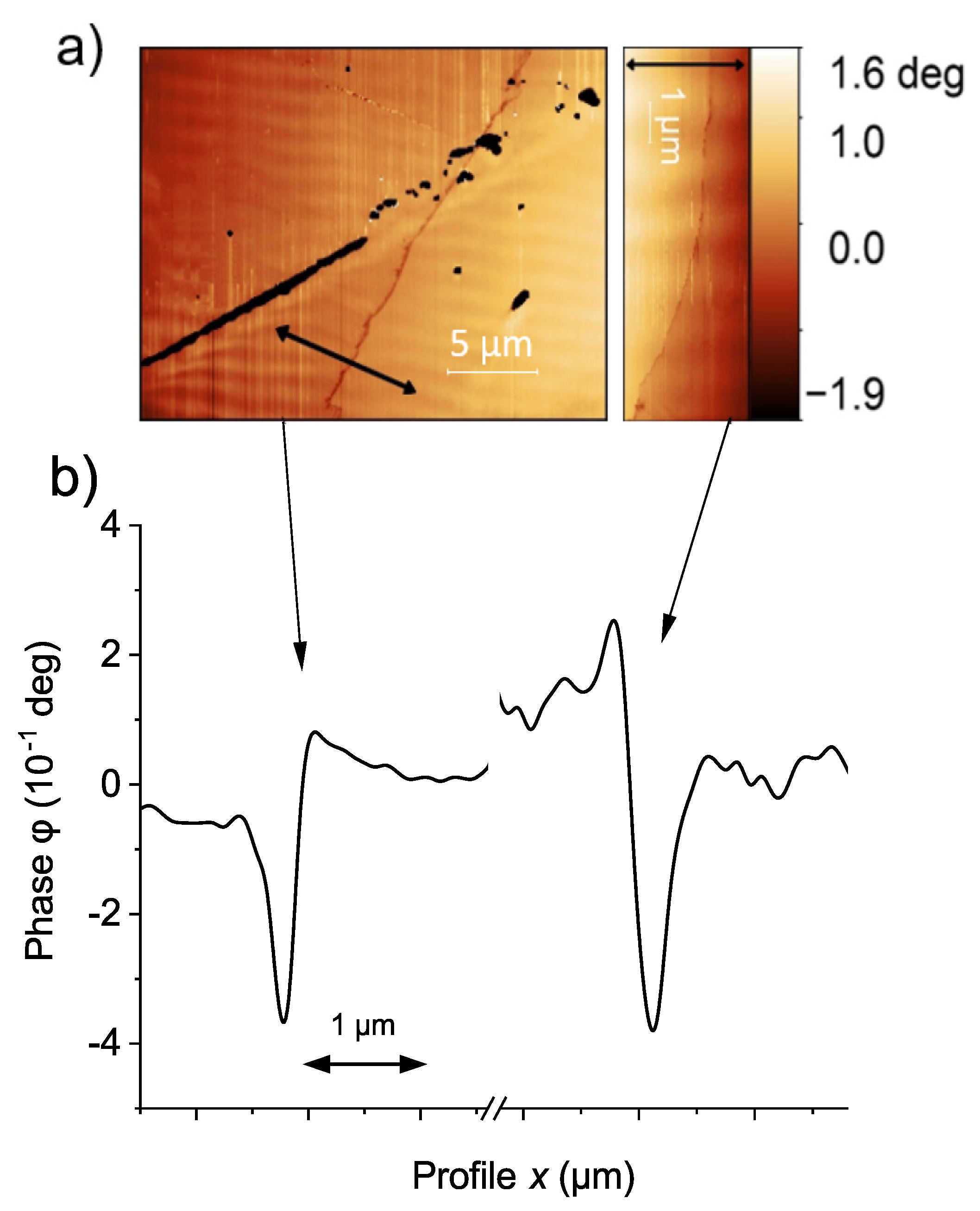
4.1. The MFM Phase Signal at the Current Path
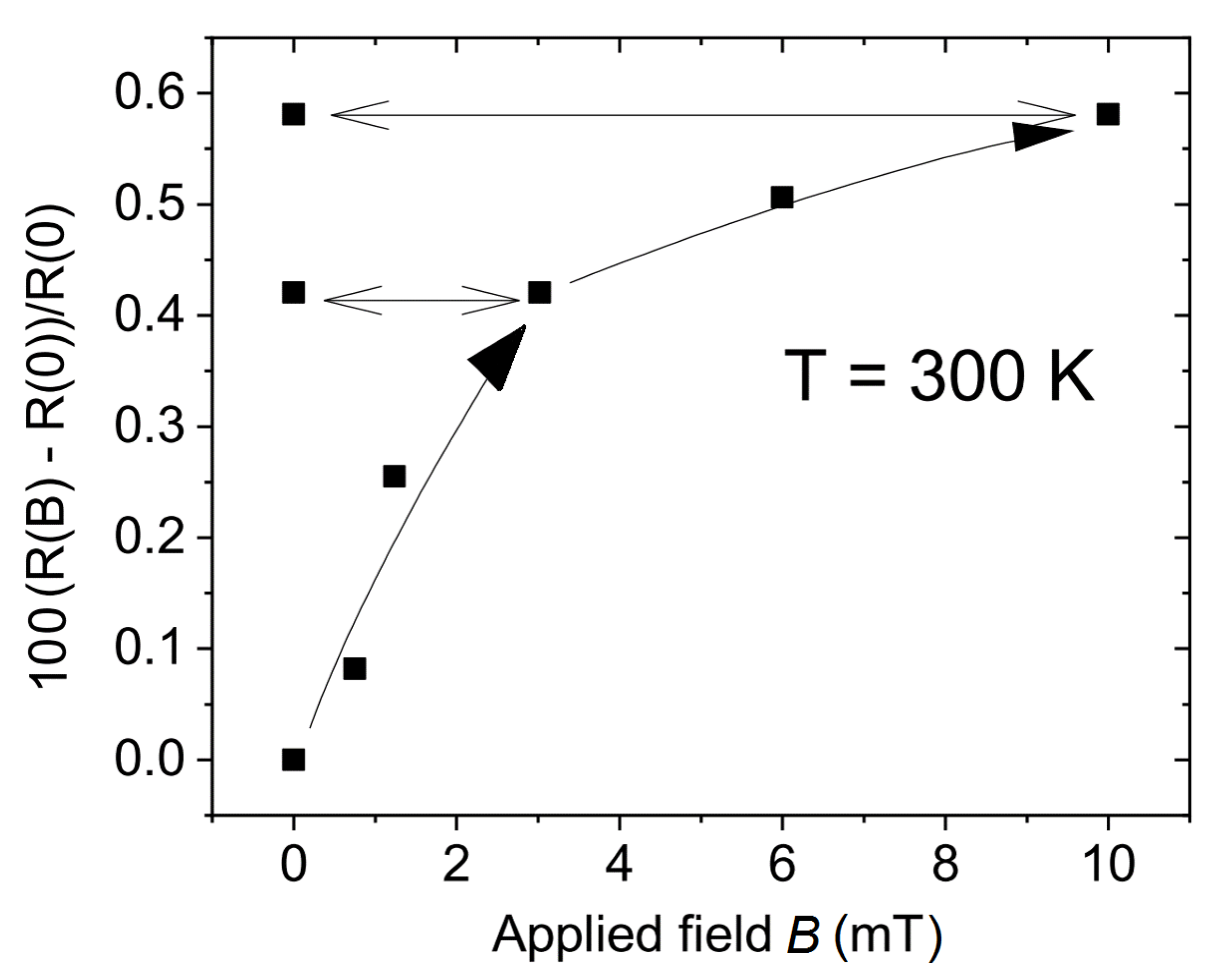
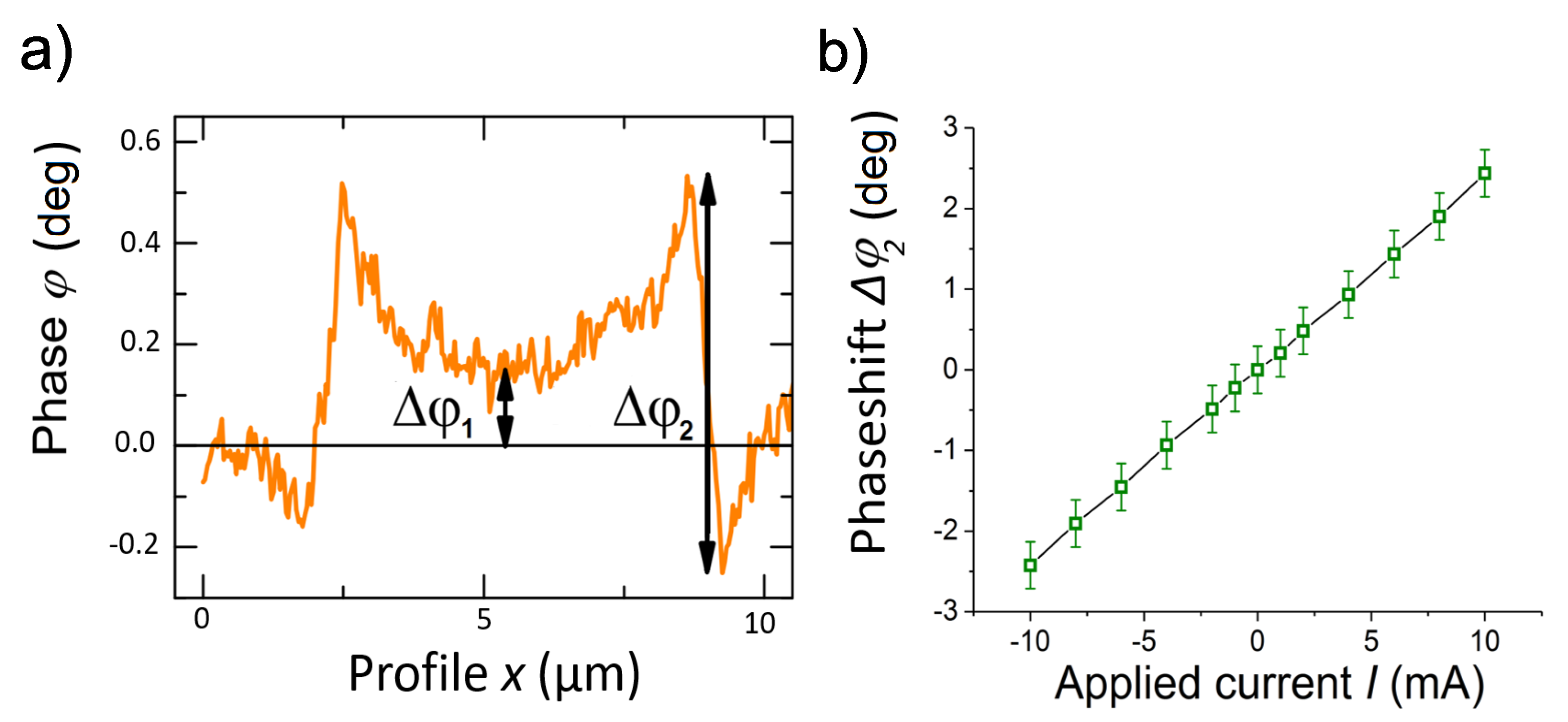
4.2. Influence of the Applied Magnetic Field on the Remanent Current Value
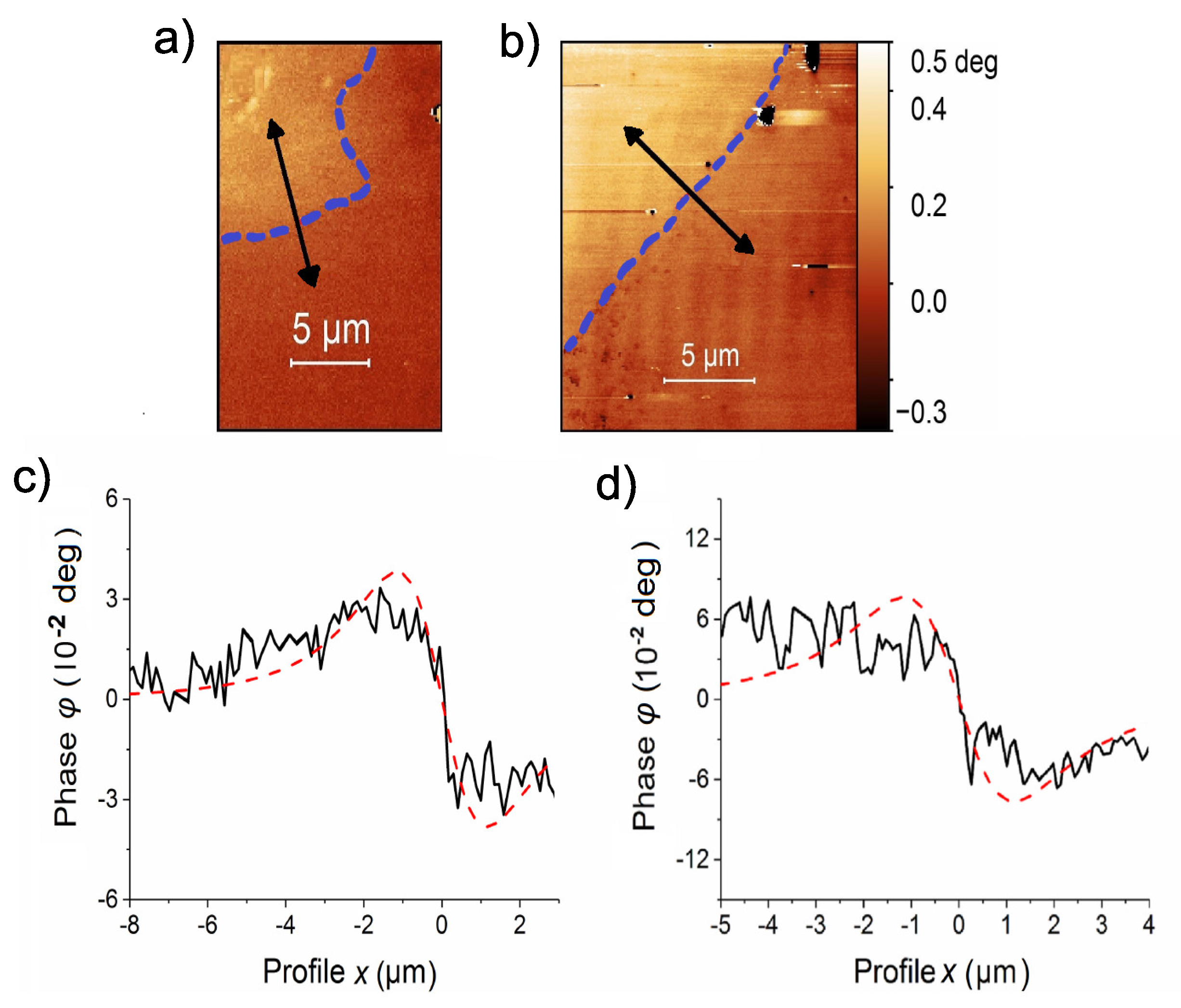
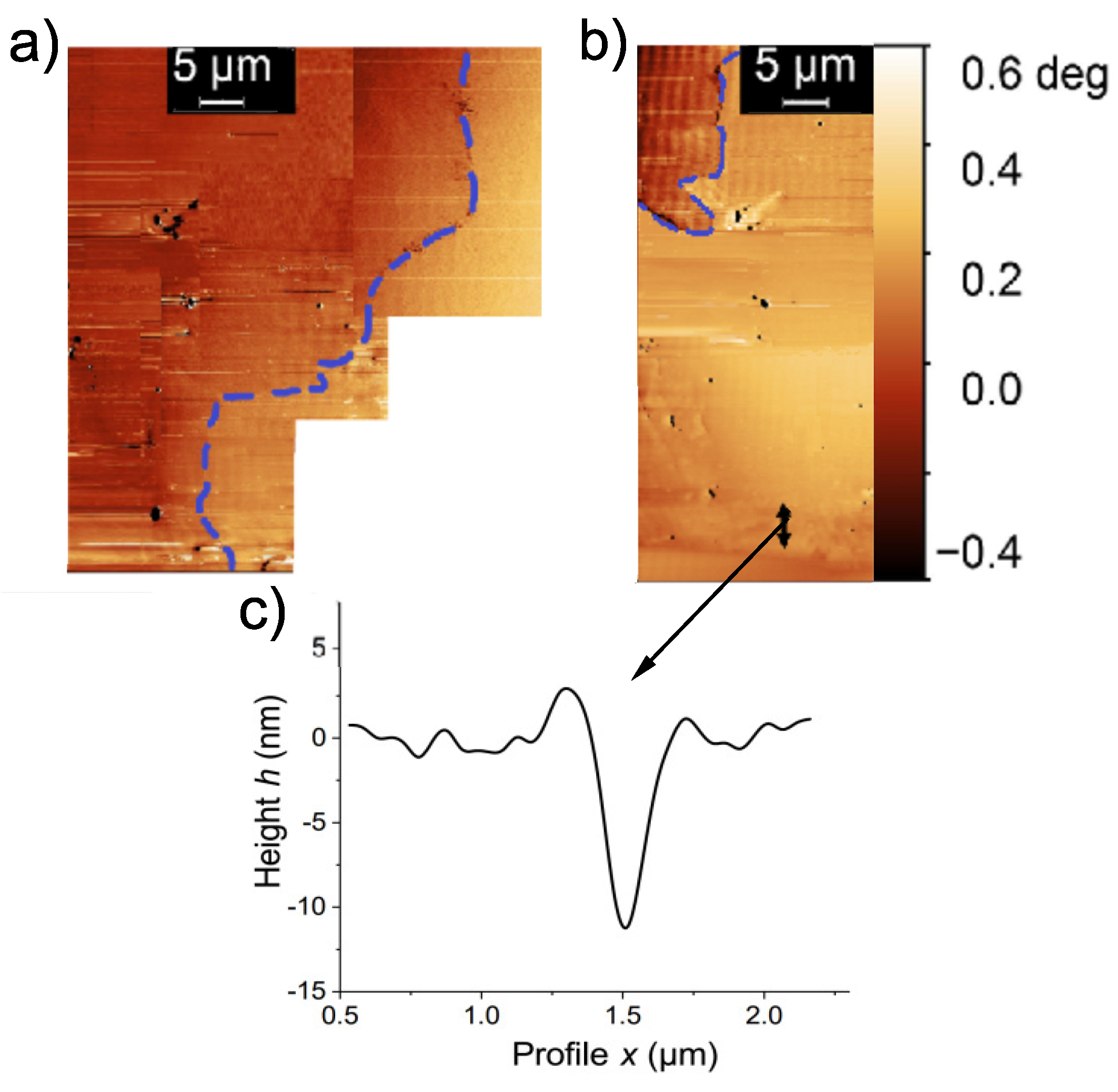
4.3. How Deep Is the SF of Interest?
4.4. Estimate of the Absolute Value of the Current
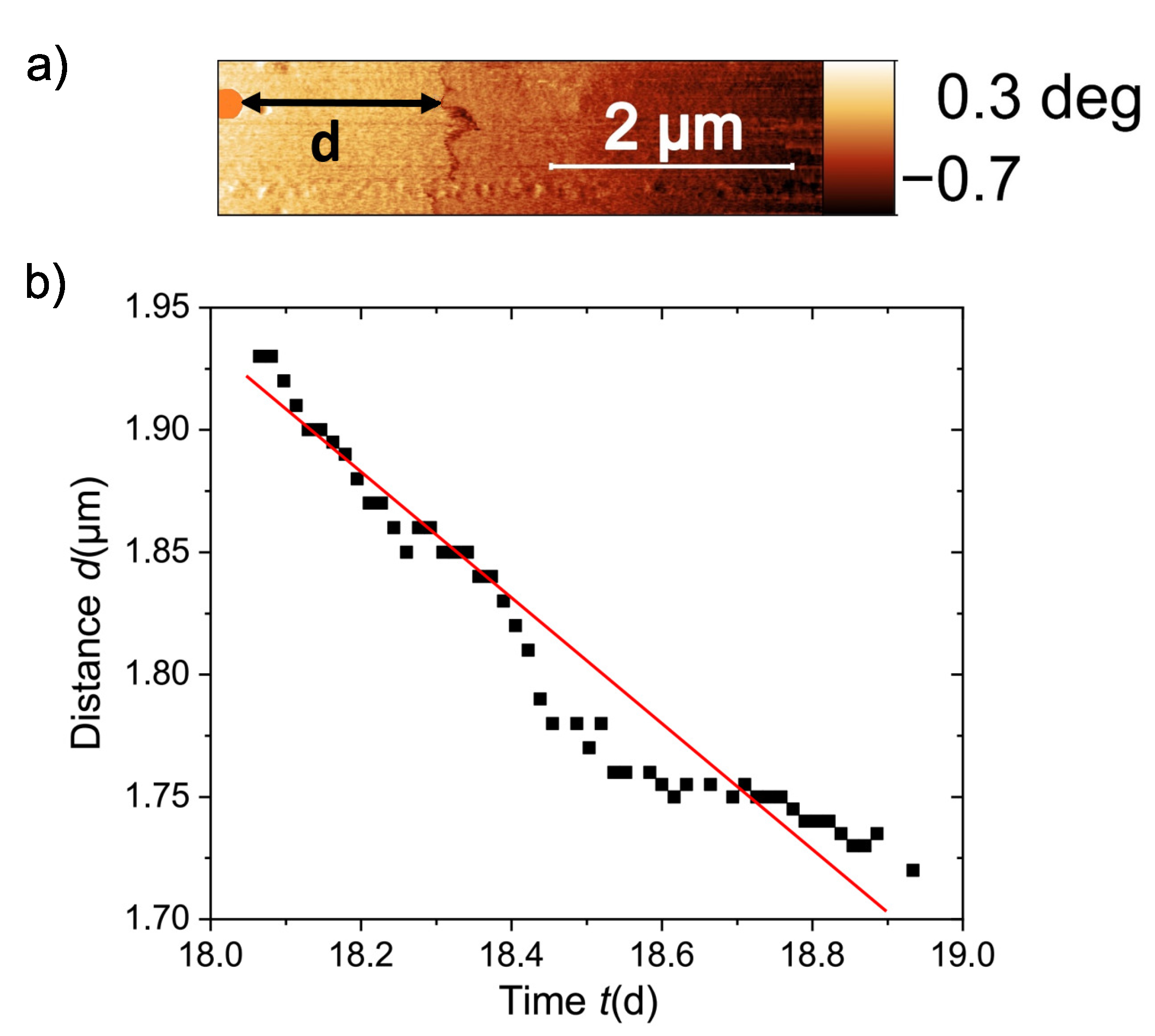
4.5. Flux Creep
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kopnin, N.B.; Heikkilä, T.T.; Volovik, G.E. High-temperature surface superconductivity in topological flat-band systems. Phys. Rev. B 2011, 83, 220503. [Google Scholar] [CrossRef] [Green Version]
- Kopnin, N.B.; Ijäs, M.; Harju, A.; Heikkilä, T.T. High-temperature surface superconductivity in rhombohedral graphite. Phys. Rev. B 2013, 87, 140503. [Google Scholar] [CrossRef] [Green Version]
- Kopnin, N.B.; Heikkilä, T.T. Surface Superconductivity in Rhombohedral Graphite. In Carbon-Based Superconductors: Towards High-Tc Superconductivity; Chapter 9; Haruyama, J., Jenny Stanford Publishing, Eds.; Taylor & Francis Group: London, UK, 2014; pp. 231–263. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Xie, T.; Taniguchi, T.; Watanabe, K.; Young, A.F. Superconductivity in rhombohedral trilayer graphene. Nature 2021, 598, 434–438. [Google Scholar] [CrossRef]
- Muñoz, W.A.; Covaci, L.; Peeters, F. Tight-binding description of intrinsic superconducting correlations in multilayer graphene. Phys. Rev. B 2013, 87, 134509. [Google Scholar] [CrossRef] [Green Version]
- Volovik, G.E. Graphite, Graphene, and the Flat Band Superconductivity. JETP Lett. 2018, 107, 516–517. [Google Scholar] [CrossRef] [Green Version]
- Esquinazi, P.; Heikkilä, T.T.; Lysogoskiy, Y.V.; Tayurskii, D.A.; Volovik, G.E. On the superconductivity of graphite interfaces. JETP Lett. 2014, 100, 336–339. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef]
- Cea, T.; Walet, N.R.; Guinea, F. Twists and the Electronic Structure of Graphitic Materials. Nano Lett. 2019, 19, 8683–8689. [Google Scholar] [CrossRef] [Green Version]
- Mohanta, N.; Taraphder, A. Phase segregation of superconductivity and ferromagnetism at the LaAlO3/SrTiO3 interface. J. Phys. Condens. Matter 2014, 26, 025705. [Google Scholar] [CrossRef] [Green Version]
- Boschker, H.; Manske, D.; Mannhart, J. Gedeihliche Grenzflächen. Phys. J. 2016, 15, 37–42. [Google Scholar]
- Wang, L.; Ma, X.; Xue, Q.K. Interface high-temperature superconductivity. Supercond. Sci. Technol. 2016, 29, 123001. [Google Scholar] [CrossRef] [Green Version]
- Gitsu, D.V.; Grozav, A.F.; Kistol, V.G.; Leporda, L.I.; Muntyanu, F.M. Experimental observation of a superconducting phase with Tc ≃ 8.5 K in large-angle bismuth bicrystals. JETP Lett. 1992, 55, 403–407. [Google Scholar]
- Muntyanu, F.M.; Leporda, L.I. Restructuring of the energy spectrum in large angle bismuth bicrystals. Phys. Solid State 1995, 37, 298–299. [Google Scholar]
- Muntyanu, F.M.; Gilewski, A.; Nenkov, K.; Zaleski, A.J.; Chistol, V. Fermi-surface rearrangement in Bi bicrystals with twisting superconducting crystallite interfaces. Phys. Rev. B 2007, 76, 014532. [Google Scholar] [CrossRef]
- Tang, E.; Fu, L. Strain-Induced Helical Flat Band and Interface Superconductivity in Topological Crystalline Insulators. Nat. Phys. 2014, 10, 964–969. [Google Scholar] [CrossRef] [Green Version]
- Fogel, N.Y.; Pokhila, A.S.; Bomze, Y.V.; Sipatov, A.Y.; Fedorenko, A.I.; Shekhter, R.I. Novel Superconducting Semiconducting Superlattices: Dislocation-Induced Superconductivity? Phys. Rev. Lett. 2001, 86, 512–515. [Google Scholar] [CrossRef] [Green Version]
- Fogel, N.Y.; Buchstab, E.I.; Bomze, Y.V.; Yuzephovich, O.I.; Mikhailov, M.Y.; Sipatov, A.Y.; Pashitskii, E.A.; Shekhter, R.I.; Jonson, M. Direct evidence for interfacial superconductivity in two-layer semiconducting heterostructures. Phys. Rev. B 2006, 73, 161306. [Google Scholar] [CrossRef]
- Antonowicz, K. Possible superconductivity at room temperature. Nature 1974, 247, 358–360. [Google Scholar] [CrossRef]
- Antonowicz, K. The Effect of Microwaves on DC Current in an Al-Carbon-Al Sandwich. Phys. Stat. Sol. (a) 1975, 28, 497–502. [Google Scholar] [CrossRef]
- Kopelevich, Y.; Esquinazi, P. Ferromagnetism and Superconductivity in Carbon-based Systems. J. Low Temp. Phys. 2007, 146, 629–639. [Google Scholar] [CrossRef] [Green Version]
- Scheike, T.; Esquinazi, P.; Setzer, A.; Böhlmann, W. Granular superconductivity at room temperature in bulk highly oriented pyrolytic graphite samples. Carbon 2013, 59, 140–149. [Google Scholar] [CrossRef] [Green Version]
- Precker, C.E.; Esquinazi, P.D.; Champi, A.; Barzola-Quiquia, J.; Zoraghi, M.; Muiños-Landin, S.; Setzer, A.; Böhlmann, W.; Spemann, D.; Meijer, J.; et al. Identification of a possible superconducting transition above room temperature in natural graphite crystals. New J. Phys. 2016, 18, 113041. [Google Scholar] [CrossRef]
- Stiller, M.; Esquinazi, P.D.; Barzola-Quiquia, J.; Precker, C.E. Local Magnetic Measurements of Trapped Flux through a Permanent Current Path in Graphite. J. Low Temp. Phys. 2018, 191, 105–121. [Google Scholar] [CrossRef] [Green Version]
- Scheike, T.; Böhlmann, W.; Esquinazi, P.; Barzola-Quiquia, J.; Ballestar, A.; Setzer, A. Can Doping Graphite Trigger Room Temperature Superconductivity? Evidence for Granular High-Temperature Superconductivity in Water-Treated Graphite Powder. Adv. Mater. 2012, 24, 5826–5831. [Google Scholar] [CrossRef]
- Saad, M.; Gilmutdinov, I.F.; Kiiamov, A.G.; Tayurskii, D.A.; Nikitin, S.I.; Yusupov, R.V. Observation of Persistent Currents in Finely Dispersed Pyrolytic Graphite. JETP Lett. 2018, 107, 37–41. [Google Scholar] [CrossRef]
- Ballestar, A.; Barzola-Quiquia, J.; Scheike, T.; Esquinazi, P. Evidence of Josephson-coupled superconducting regions at the interfaces of highly oriented pyrolytic graphite. New J. Phys. 2013, 15, 023024. [Google Scholar] [CrossRef] [Green Version]
- Ballestar, A.; Esquinazi, P.; Böhlmann, W. Granular superconductivity below 5 K in SPI-II pyrolytic graphite. Phys. Rev. B 2015, 91, 014502. [Google Scholar] [CrossRef] [Green Version]
- Pierucci, D.; Sediri, H.; Hajlaoui, M.; Girard, J.C.; Brumme, T.; Calandra, M.; Velez-Fort, E.; Patriarche, G.; Silly, M.G.; Ferro, G.; et al. Evidence for Flat Bands near the Fermi Level in Epitaxial Rhombohedral Multilayer Graphene. ACS Nano 2015, 9, 5432–5439. [Google Scholar] [CrossRef]
- Henck, H.; Avila, J.; Ben Aziza, Z.; Pierucci, D.; Baima, J.; Pamuk, B.; Chaste, J.; Utt, D.; Bartos, M.; Nogajewski, K.; et al. Flat electronic bands in long sequences of rhombohedral-stacked graphene. Phys. Rev. B 2018, 97, 245421. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Shi, Y.; Zakharov, A.A.; Syväjärvi, M.; Yakimova, R.; Uhrberg, R.I.G.; Sun, J. Flat-Band Electronic Structure and Interlayer Spacing Influence in Rhombohedral Four-Layer Graphene. Nano Lett. 2018, 18, 5862–5866. [Google Scholar] [CrossRef]
- Ariskina, R.; Schnedler, M.; Esquinazi, P.D.; Champi, A.; Stiller, M.; Hergert, W.; Dunin-Borkowski, R.E.; Ebert, P.; Venus, T.; Estrela-Lopis, I. Influence of surface band bending on a narrow band gap semiconductor: Tunneling atomic force studies of graphite with Bernal and rhombohedral stacking orders. Phys. Rev. Mater. 2021, 5, 044601. [Google Scholar] [CrossRef]
- Brihuega, I.; Mallet, P.; González-Herrero, H.; de Laissardière, G.T.; Ugeda, M.M.; Magaud, L.; Gómez-Rodríguez, J.M.; Ynduráin, F.; Veuillen, J.Y. Unraveling the Intrinsic and Robust Nature of van Hove Singularities in Twisted Bilayer Graphene by Scanning Tunneling Microscopy and Theoretical Analysis. Phys. Rev. Lett. 2012, 109, 196802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kelly, B.T. Physics of Graphite; Applied Science Publishers: London, UK, 1981. [Google Scholar]
- Lin, Q.; Li, T.; Liu, Z.; Song, Y.; He, L.; Hu, Z.; Guo, Q.; Ye, H. High-resolution TEM observations of isolated rhombohedral crystallites in graphite blocks. Carbon 2012, 50, 2369–2371. [Google Scholar] [CrossRef]
- Hattendorf, S.; Georgi, A.; Liebmann, M.; Morgenstern, M. Networks of ABA and ABC stacked graphene on mica observed by scanning tunneling microscopy. Surf. Sci. 2013, 610, 53–58. [Google Scholar] [CrossRef] [Green Version]
- Ballestar, A.; Heikkilä, T.T.; Esquinazi, P. Interface size dependence of the Josephson critical behaviour in pyrolytic graphite. Superc. Sci. Technol. 2014, 27, 115014. [Google Scholar] [CrossRef] [Green Version]
- Guimpel, J.; de la Cruz, M.E.; de la Cruz, F.; Fink, H.J.; Laborde, O.; Villegier, J.C. Size dependence of the superconducting critical temperature and fields of Nb/Al multilayers. J. Low Temp. Phys. 1986, 63, 151–165. [Google Scholar] [CrossRef]
- Oreg, Y.; Finkel’stein, A. Suppression of Tc in superconducting amorphous wires. Phys. Rev. Lett. 1999, 83, 191. [Google Scholar] [CrossRef] [Green Version]
- Fukuyama, H. Localization and superconductivity. Physica 1984, 126B, 306–313, reprinted in Ebisawa, H.; Fukuyama, H.; Maekawa, S. J. Phys. Soc. Jpn. 1985, 54, 2257. [Google Scholar]
- Senoussi, S.; Aguillon, C.; Hadjoudj, S. The contribution of the intergrain currents to the low field hysteresis cycle of granular superconductors and the connection with the micro- and macrostructures. Phys. C 1991, 175, 215–225. [Google Scholar] [CrossRef]
- Esquinazi, P.D. Ordered Defects: A Roadmap towards room temperature Superconductivity and Magnetic Order. arXiv 2019, arXiv:1902.07489. [Google Scholar]
- Balaev, D.A.; Gokhfeld, D.M.; Dubrovski, A.A.; Popkov, S.I.; Shaikhutdinov, K.; Petrov, M.I. Magnetoresistance hysteresis in granular HTSCs as a manifestation of the magnetic flux trapped by superconducting grains in YBCO + CuO composites. J. Exp. Theor. Phys. 2007, 105, 1174–1183. [Google Scholar] [CrossRef]
- Kopelevich, Y.; Esquinazi, P.; Torres, J.; Moehlecke, S. Ferromagnetic- and superconducting-like behavior of graphite. J. Low Temp. Phys. 2000, 119, 691–702. [Google Scholar] [CrossRef]
- Straver, E.W.J.; Hoffman, J.E.; Auslaender, O.; Rugar, D. Magnetic Force Microscopy: Comparison and Validation of Different Magnetic Force Microscopy Calibration Schemes. Appl. Phys. Lett. 2008, 93, 172514. [Google Scholar] [CrossRef] [Green Version]
- Di Giorgio, C.; Bobba, F.; Cucolo, A.M.; Scarfato, A.; Moore, S.A.; Karapetrov, G.; D’Agostino, D.; Novosad, V.; Yefremenko, V.; Iavarone, M. Observation of superconducting vortex clusters in S/F hybrids. Sci. Rep. 2016, 6, 38557. [Google Scholar] [CrossRef] [PubMed]
- Han, K.H.; Spemann, D.; Esquinazi, P.; Höhne, R.; Riede, V.; Butz, T. Ferromagnetic spots in graphite produced by proton irradiation. Adv. Mater. 2003, 15, 1719–1722. [Google Scholar] [CrossRef]
- Esquinazi, P.; Spemann, D.; Höhne, R.; Setzer, A.; Han, K.H.; Butz, T. Induced magnetic ordering by proton irradiation in graphite. Phys. Rev. Lett. 2003, 91, 227201. [Google Scholar] [CrossRef] [Green Version]
- Martinez-Martin, D.; Jaafar, M.; Perez, R.; Gomez-Herrero, J.; Asenjo, A. Upper Bound for the Magnetic Force Gradient in Graphite. Phys. Rev. Lett. 2010, 105, 257203. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Muñoz, M.; Steplecaru, C.S.; Hao, C.; Bai, M.; García, N.; Schindler, K.; Esquinazi, P. Electrostatic Force Microscopy on Oriented Graphite Surfaces: Coexistence of Insulating and Conducting Behaviors. Phys. Rev. Lett. 2006, 97, 076805, See the comment on by Sadewasser, S.; Glatzel, T. Phys. Rev. Lett. 2007, 98, 269701, and the reply by Lu et al. Idem 2007, 98, 269702. See also Proksch, R. Appl. Phys. Lett. 2006, 89, 113121. [Google Scholar] [CrossRef] [Green Version]
- Baumeister, W.; Griitter, P.; Guckenberger, R.; Güntherodt, H.; Hartmann, T.; Heinzelmann, H.; Mamin, H.; Meyer, E.; Pohl, D.; Rugar, D.; et al. Scanning Tunneling Microscopy II; Springer: Berlin, Germany, 1992. [Google Scholar]
- Kirtley, J. Fundamental studies of superconductors using scanning magnetic imaging. Rep. Prog. Phys. 2010, 73, 126501. [Google Scholar] [CrossRef] [Green Version]
- Precker, C.E.; Barzola-Quiquia, J.; Esquinazi, P.D.; Stiller, M.; Chan, M.K.; Jaime, M.; Zhang, Z.; Grundmann, M. Record-Breaking Magnetoresistance at the Edge of a Microflake of Natural Graphite. Adv. Eng. Mater. 2019, 21, 1970039. [Google Scholar] [CrossRef]
- Vlasko-Vlasov, V.K.; Welp, U.; Crabtree, G.W.; Gunter, D.; Kabanov, V.; Nikitenko, V.I. Meissner holes in superconductors. Phys. Rev. B 1997, 56, 5622. [Google Scholar] [CrossRef]
- Corte-León, H.; Neu, V.; Manzin, A.; Barton, C.; Tang, Y.; Gerken, M.; Klapetek, P.; Schumacher, H.W.; Kazakova, O. Controlled Manipulation of Individual Vortices in a Superconductor. Small 2020, 16, 1906144. [Google Scholar] [CrossRef] [Green Version]
- Esquinazi, P. Graphite and its hidden superconductivity. Pap. Phys. 2013, 5, 050007. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ariskina, R.; Stiller, M.; Precker, C.E.; Böhlmann, W.; Esquinazi, P.D. On the Localization of Persistent Currents Due to Trapped Magnetic Flux at the Stacking Faults of Graphite at Room Temperature. Materials 2022, 15, 3422. https://doi.org/10.3390/ma15103422
Ariskina R, Stiller M, Precker CE, Böhlmann W, Esquinazi PD. On the Localization of Persistent Currents Due to Trapped Magnetic Flux at the Stacking Faults of Graphite at Room Temperature. Materials. 2022; 15(10):3422. https://doi.org/10.3390/ma15103422
Chicago/Turabian StyleAriskina, Regina, Markus Stiller, Christian E. Precker, Winfried Böhlmann, and Pablo D. Esquinazi. 2022. "On the Localization of Persistent Currents Due to Trapped Magnetic Flux at the Stacking Faults of Graphite at Room Temperature" Materials 15, no. 10: 3422. https://doi.org/10.3390/ma15103422
APA StyleAriskina, R., Stiller, M., Precker, C. E., Böhlmann, W., & Esquinazi, P. D. (2022). On the Localization of Persistent Currents Due to Trapped Magnetic Flux at the Stacking Faults of Graphite at Room Temperature. Materials, 15(10), 3422. https://doi.org/10.3390/ma15103422






