High-Selectivity Bandpass Filter with Controllable Attenuation Based on Graphene Nanoplates
Abstract
1. Introduction
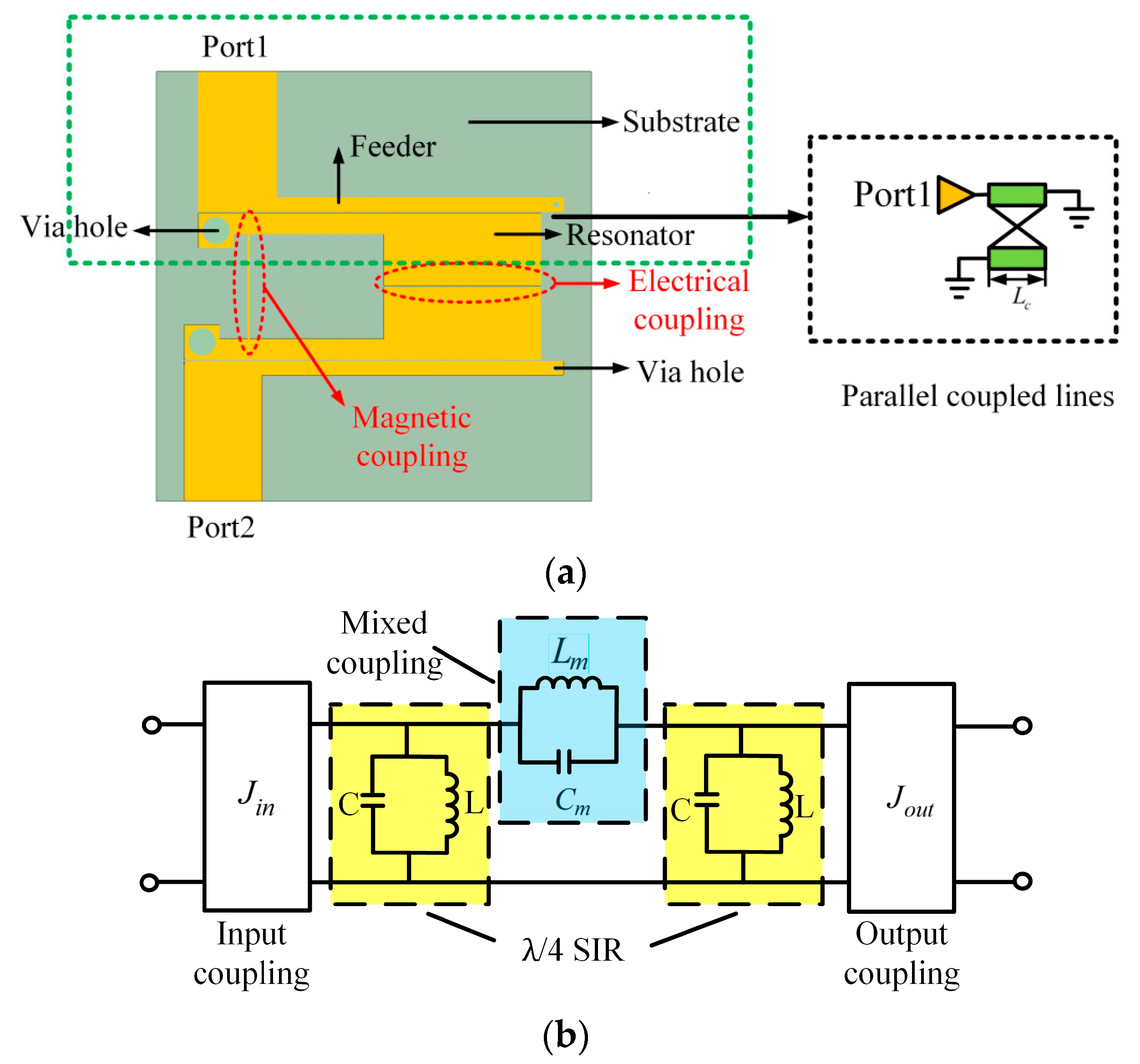
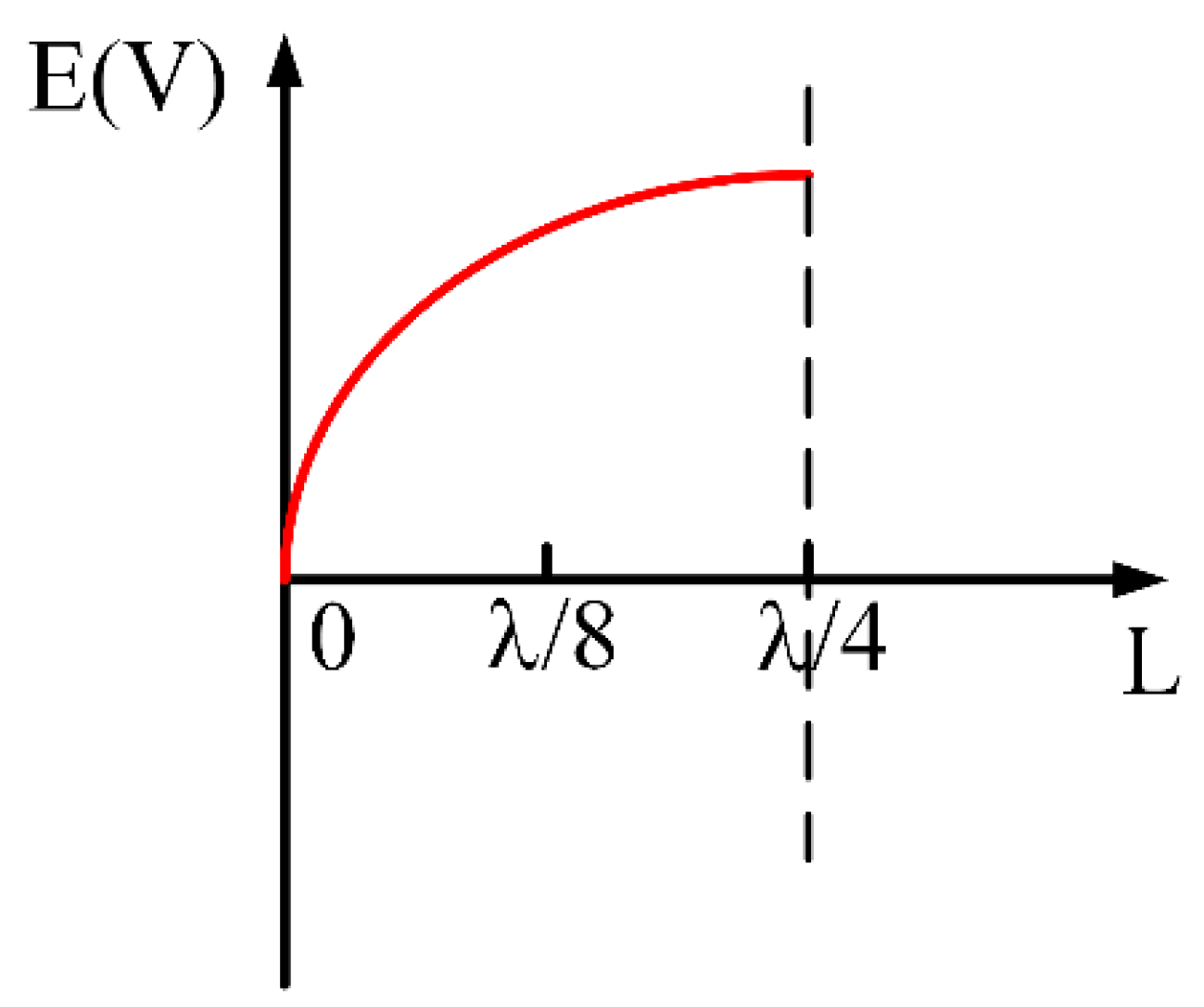
2. Materials and Methods
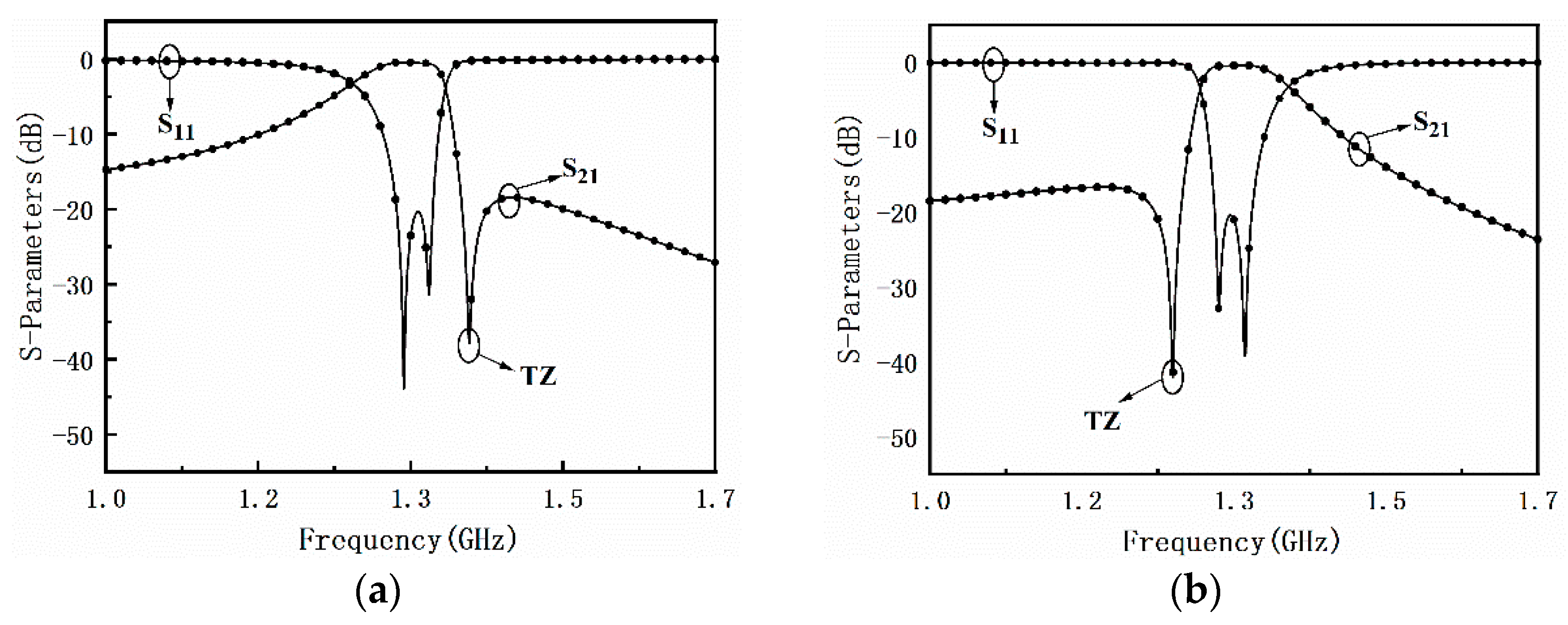
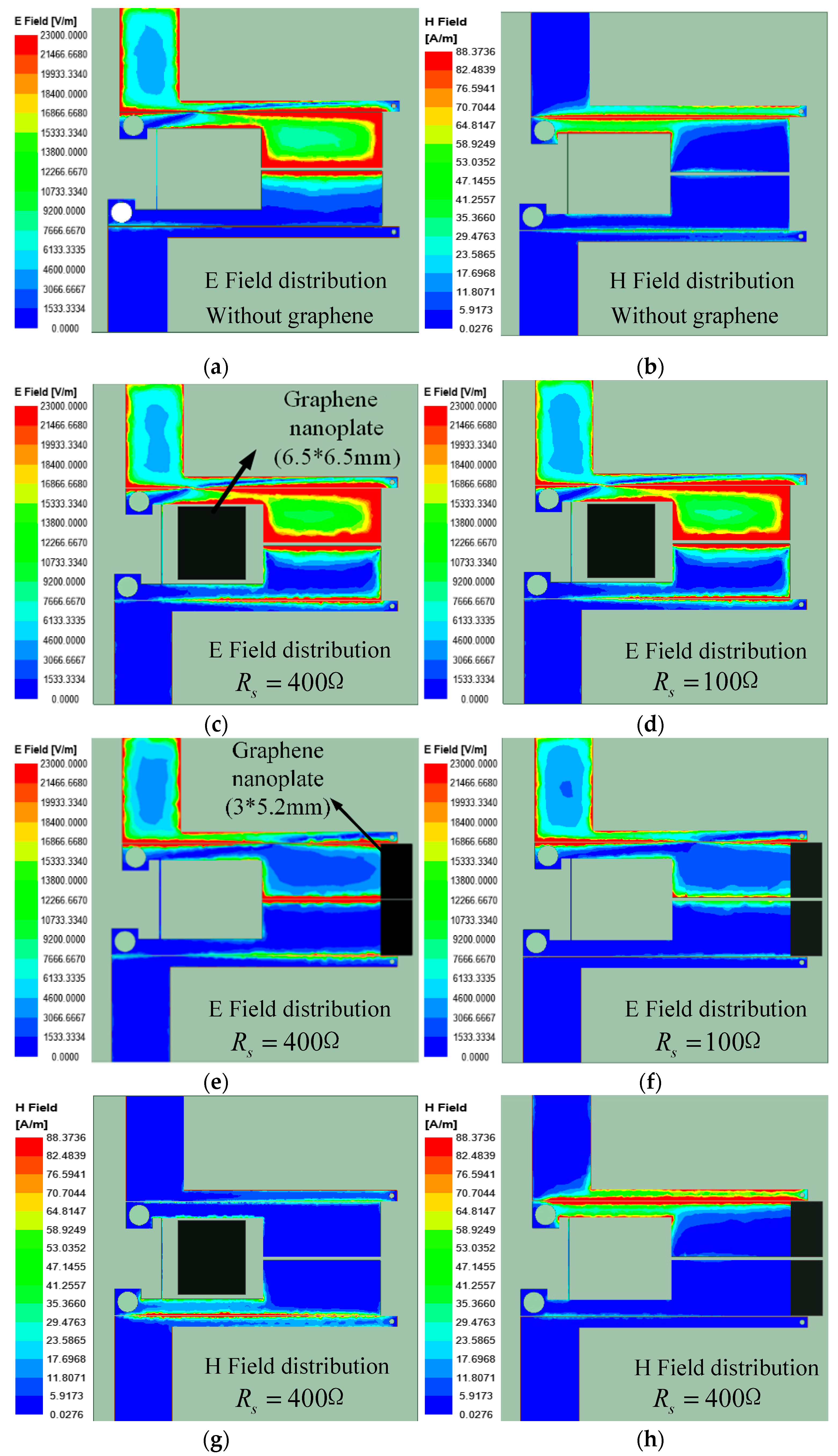
3. Experiment Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Poniatowska, A.; Trzaskowska, P.A.; Trzaskowski, M.; Ciach, T. Physicochemical and Biological Properties of Graphene-Oxide-Coated Metallic Materials. Materials 2021, 14, 5752. [Google Scholar] [CrossRef] [PubMed]
- Chae, H.-R.; Kim, I.-C.; Kwon, Y.-N. Acid-Resistance Enhancement of Thin-Film Composite Membrane Using Barrier Effect of Graphene Oxide Nanosheets. Materials 2021, 14, 3151. [Google Scholar] [CrossRef] [PubMed]
- Han, C.; Zhong, R.; Liang, Z.; Yang, L.; Fang, Z.; Wang, Y.; Ma, A.; Wu, Z.; Hu, M.; Liu, D.; et al. Independently Tunable Multipurpose Absorber with Single Layer of Metal-Graphene Metamaterials. Materials 2021, 14, 284. [Google Scholar] [CrossRef] [PubMed]
- Bozzi, M.; Pierantoni, L.; Bellucci, S. Applications of graphene atmicrowave frequencies. Radioengineering 2015, 24, 661–669. [Google Scholar] [CrossRef]
- Meng, N.; Fernández, J.F.; Lancry, O.; Pichonat, E.; Vignaud, D.; Dambrine, G.; Happy, H. RF characterization of epitaxial graphene nanoribbon field effect transistor. In Proceedings of the IEEE MTT-S International Microwave Symposium, Baltimore, MD, USA, 5–10 June 2011; pp. 1–3. [Google Scholar]
- Dragoman, M.; Neculoiu, D.; Dragoman, D.; Deligeorgis, G.; Konstantinidis, G.; Cismaru, A.; Coccetti, F.; Plana, R. Graphene for microwaves. IEEE Microw. Mag. 2010, 11, 81–86. [Google Scholar] [CrossRef]
- Pierantoni, L.; Mencarelli, D.; Bozzi, M.; Moro, R.; Bellucci, S. Microwave applications of graphene for tunable devices. In Proceedings of the 9th European Microwave Conference, Rome, Italy, 6–9 October 2014; pp. 512–515. [Google Scholar]
- Bellucci, S.; Bozzi, M.; Cataldo, A.; Moro, R.; Mencarelli, D.; Pierantoni, L. Graphene as a tunable resistor. In Proceedings of the International Semiconductor Conference (CAS), Sinaia, Romania, 13–15 October 2014; pp. 17–20. [Google Scholar]
- Pierantoni, L.; Mencarelli, D.; Bozzi, M.; Moro, R.; Bellucci, S. Graphene-based electronically tunable microstrip attenuator. Nanomater. Nanotechnology 2014, 4, 18. [Google Scholar] [CrossRef][Green Version]
- Li, H.; Mirihanage, W.; Smith, A.D.; Donoghue, J.; Fernando, A. Strain based electrical resistance behaviour of graphene-coated elastomeric yarns. Mater. Lett. 2020, 273, 127948. [Google Scholar] [CrossRef]
- Guo, R.; Liu, W.; Zhang, Y.; Hou, Z.; He, C.; Li, J. Multi-channels electrode parallel structure graphene photodetector with high performance. Mater. Lett. 2020, 260, 126948. [Google Scholar] [CrossRef]
- Yasir, M.; Savi, P.; Bistarelli, S.; Cataldo, A.; Bozzi, M.; Perregrini, L.; Bellucci, S. A Planar Antenna with Voltage-Controlled Frequency Tuning Based on Few-Layer Graphene. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2380–2383. [Google Scholar] [CrossRef]
- Pierantoni, L.; Mencarelli, D.; Bozzi, M.; Moro, R.; Moscato, S.; Perregrini, L.; Micciulla, F.; Cataldo, A.; Bellucci, S. Broadband Microwave Attenuator Based on Few Layer Graphene Flakes. IEEE Trans. Microw. Theory Tech. 2015, 63, 2491–2497. [Google Scholar] [CrossRef]
- Yasir, M.; Bistarelli, S.; Cataldo, A.; Bozzi, M.; Perregrini, L.; Bellucci, S. Enhanced tunable microstrip attenuator based on few layer graphene flakes. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 332–334. [Google Scholar] [CrossRef]
- Wu, B.; Fan, C.; Feng, X.; Zhao, Y.-T.; Ning, J.; Wang, D.; Su, T. Dynamically Tunable Filtering Attenuator Based on Graphene Integrated Microstrip Resonators. IEEE Trans. Microw. Theory Tech. 2020, 68, 5270–5278. [Google Scholar] [CrossRef]
- Zhang, A.-Q.; Lu, W.-B.; Liu, Z.-G.; Chen, H.; Huang, B.-H. Dynamically tunable substrate-integrated-waveguide attenuator using grapheme. IEEE Trans. Microw. Theory Tech. 2018, 66, 3081–3089. [Google Scholar] [CrossRef]
- Ilić, A.Ž.; Bukvić, B.M.; Budimir, D.; Ilić, M.M. Tuning the Filter Responses with Graphene Based Resonators. In Proceedings of the 2019 International Conference on Electromagnetics in Advanced Applications (ICEAA), Granada, Spain, 9–13 September 2019; pp. 151–152. [Google Scholar] [CrossRef]
- Zhou, W.; Xia, W.; Zhang, J.; He, D.; Liu, C.; Wu, Z. Flexible Graphene Based Films for Stepped Impedance Lowpass Microstrip Filter. In Proceedings of the 2018 IEEE International Conference on Computational Electromagnetics (ICCEM), Chengdu, China, 26–28 March 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, Y.; Zu, H.; Fan, C.; Lu, W. Tunable Grounded Coplanar Waveguide Attenuator Based on Graphene Nanoplates. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 330–332. [Google Scholar] [CrossRef]
- Zhu, F.; Hong, W.; Chen, J.-X.; Wu, K. Quarter-wavelength stepped-impedance resonator filter with mixed electric and magnetic coupling. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 90–92. [Google Scholar] [CrossRef]


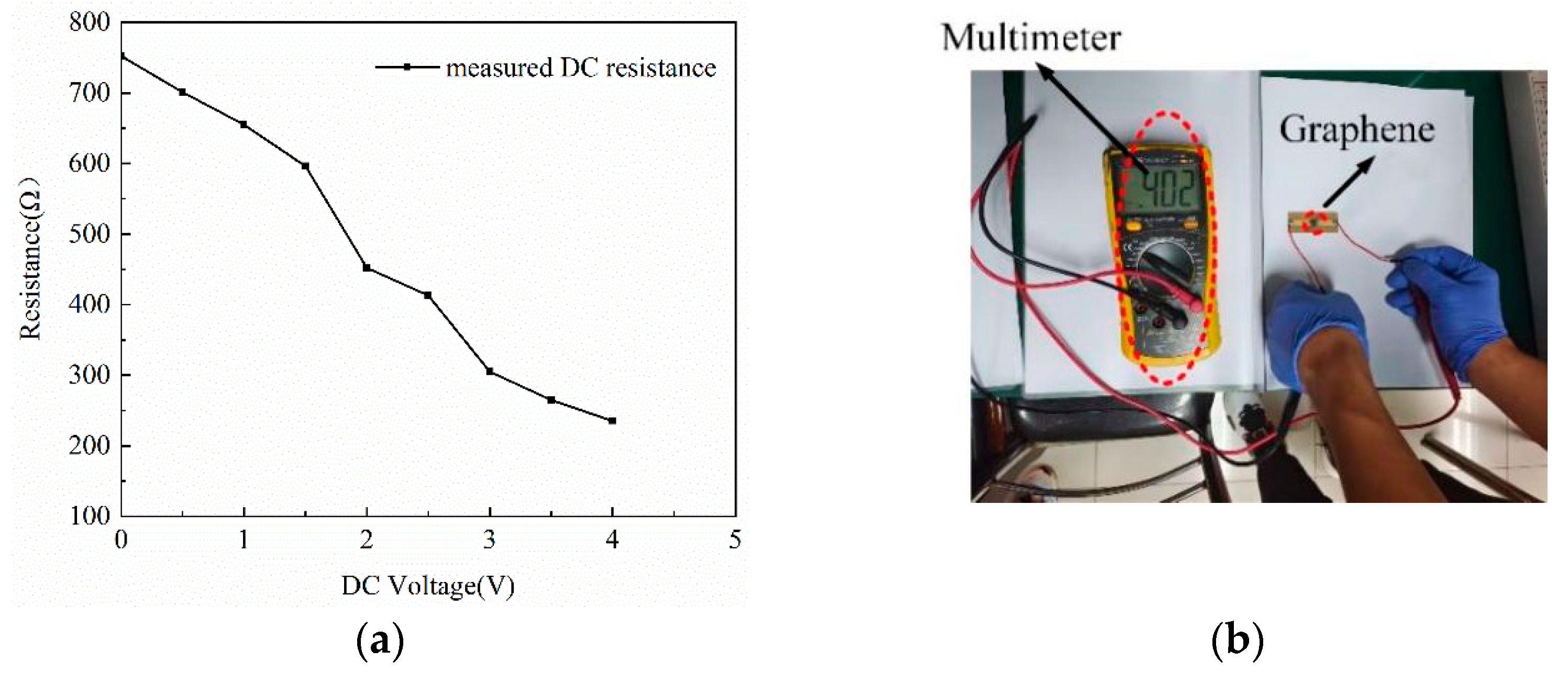

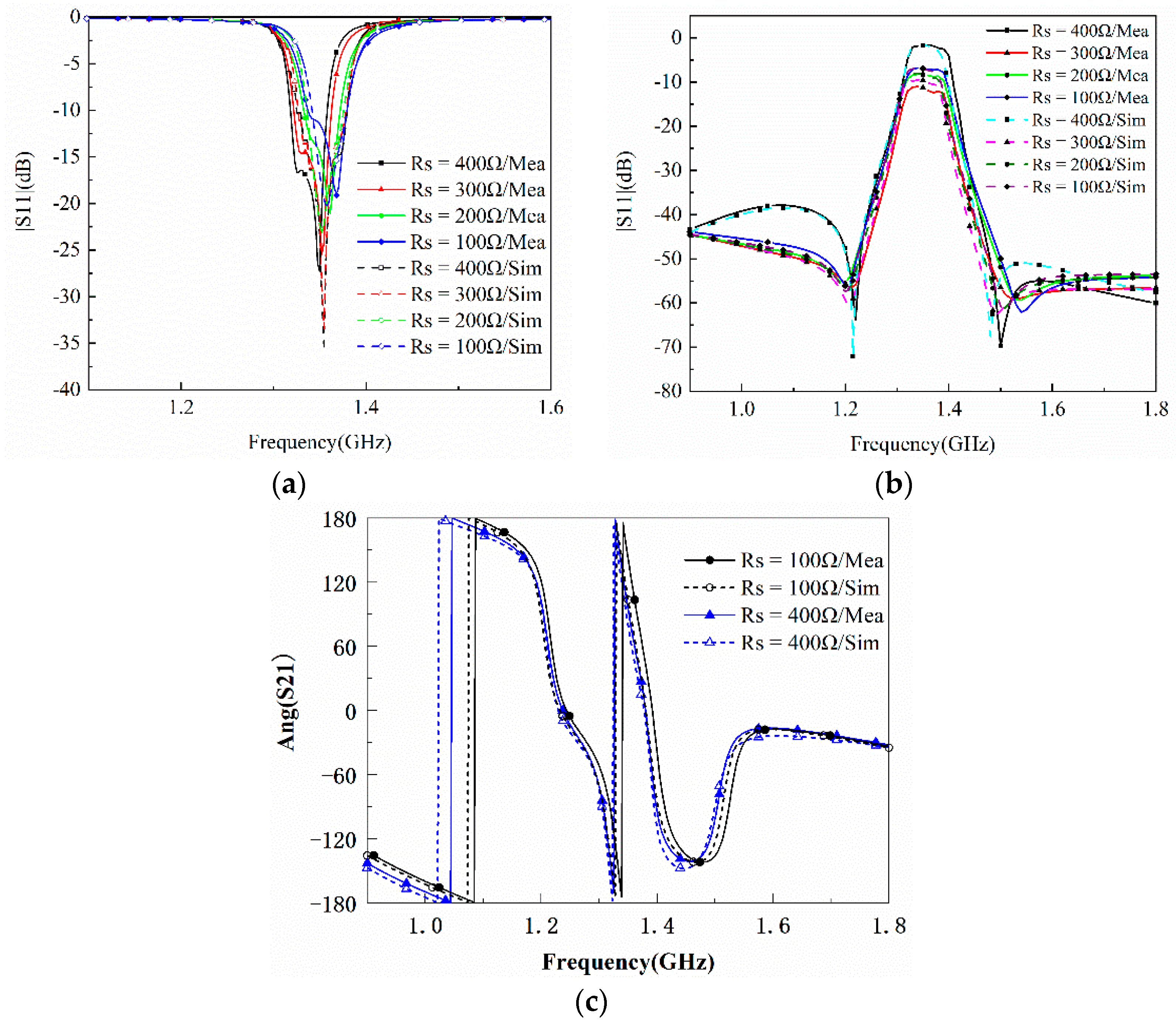
| Ref. | |S21| (dB) | |S11| (dB) | Filter Response | Transmission Zeros | Rectangle Coefficient | Structure |
|---|---|---|---|---|---|---|
| [13] | 5–10.5 | <5 | No | No | / | Graphene + MS |
| [14] | 0.3–14 | <5 | No | No | / | Graphene + MS |
| [15] | 1.7–8.4 | <10 | Yes | 1 | 4.6 | Graphene + HMSIW |
| [16] | 3–15 | <15 | No | No | / | Graphene + SIW |
| [19] | 2.5–14 | <10 | No | No | / | Graphene + GCPW |
| This Work | 1.64–11.13 | <10 | Yes | 2 | 2.12 | Graphene + MS |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Zhang, J.; Zhao, Y.; Li, L.; Su, T.; Fan, C.; Wu, B. High-Selectivity Bandpass Filter with Controllable Attenuation Based on Graphene Nanoplates. Materials 2022, 15, 1694. https://doi.org/10.3390/ma15051694
Chen J, Zhang J, Zhao Y, Li L, Su T, Fan C, Wu B. High-Selectivity Bandpass Filter with Controllable Attenuation Based on Graphene Nanoplates. Materials. 2022; 15(5):1694. https://doi.org/10.3390/ma15051694
Chicago/Turabian StyleChen, Jianzhong, Jiali Zhang, Yutong Zhao, Liang Li, Tao Su, Chi Fan, and Bian Wu. 2022. "High-Selectivity Bandpass Filter with Controllable Attenuation Based on Graphene Nanoplates" Materials 15, no. 5: 1694. https://doi.org/10.3390/ma15051694
APA StyleChen, J., Zhang, J., Zhao, Y., Li, L., Su, T., Fan, C., & Wu, B. (2022). High-Selectivity Bandpass Filter with Controllable Attenuation Based on Graphene Nanoplates. Materials, 15(5), 1694. https://doi.org/10.3390/ma15051694







