Using the Smith-Watson-Topper Parameter and Its Modifications to Calculate the Fatigue Life of Metals: The State-of-the-Art
Abstract
:1. Introduction
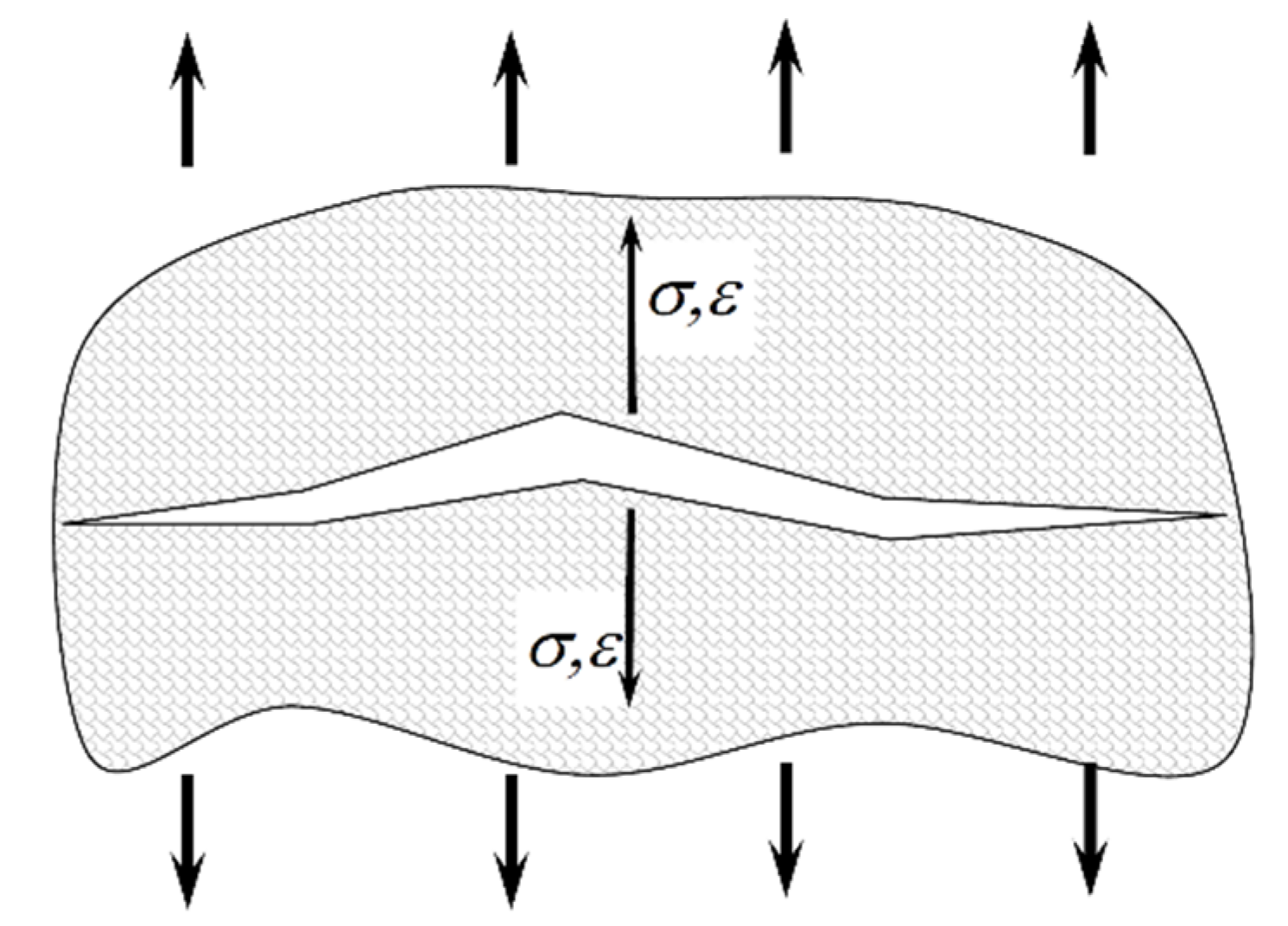
2. Definition of Original Smith-Watson-Topper Parameter
3. The Smith-Watson-Topper Parameter Defined by Normal Values
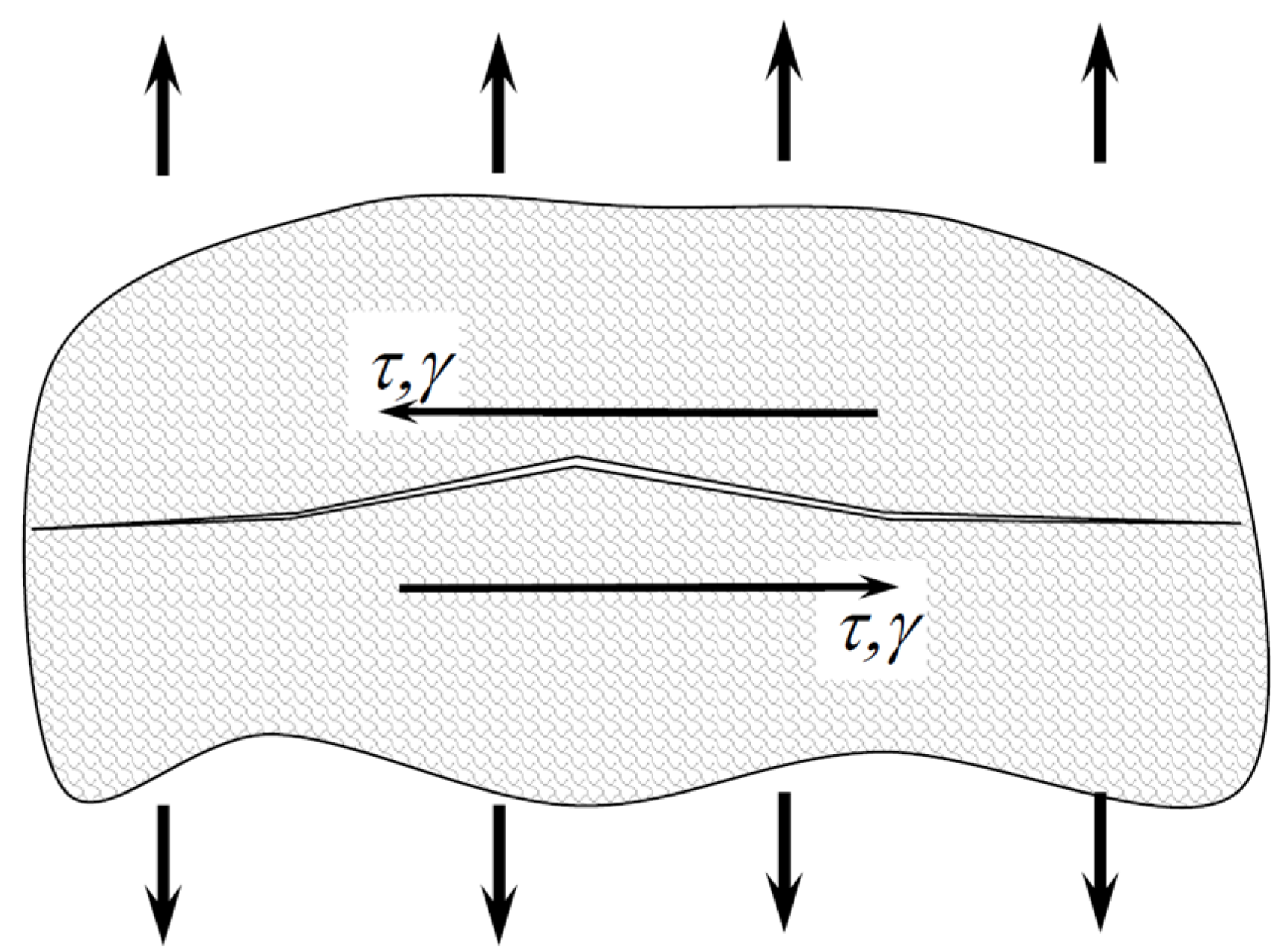
4. Smith-Watson-Topper Parameter Defined by Shear Values
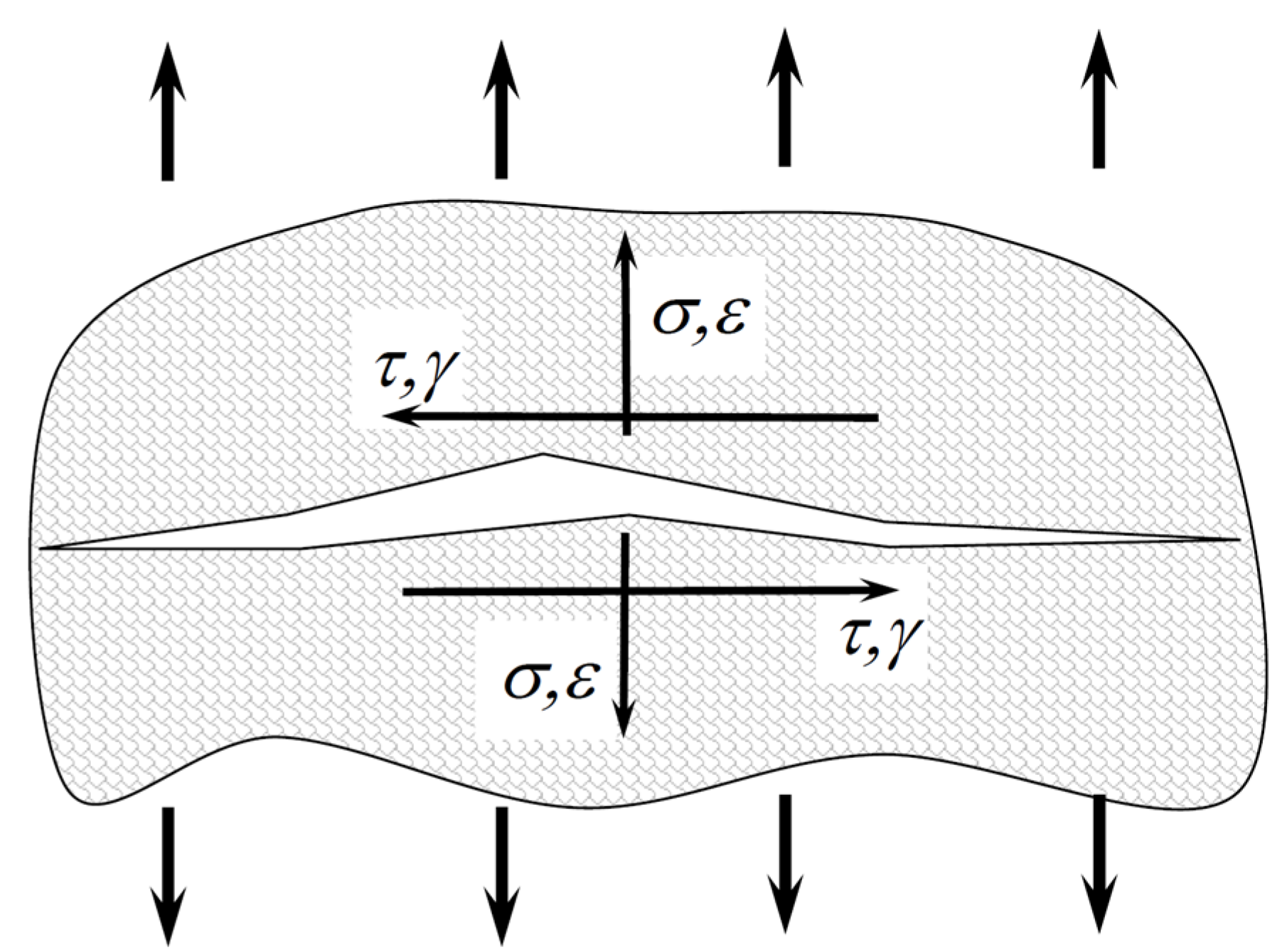
5. The Smith-Watson-Topper Parameter Defined by Normal and Shear Values
6. Energy Fatigue Characteristics
7. Discussion
8. Conclusions
- By studying the literature on fatigue failure of materials, one can notice a significant increase in the number of fatigue life estimation models, which at first glance seem to be new ideas, but analyzing them carefully, one can see that some of them are based on the same idea as that proposed by Smith-Watson-Topper (SWT), which has been presented in detail in this paper.
- All proposals related to the analyzed SWT parameter were defined in the critical plane.
- By analyzing all the damage parameters and the corresponding fatigue characteristics, it can be concluded that parameters in which the fatigue life is determined from the fatigue characteristics that arise on the basis of two load states (tension–compression and bilateral shear) have the greatest potential.
- In the future, calculations should be performed according to the selected presented models, based on the available experimental research, with particular emphasis on two fatigue characteristics.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| b | exponent of the fatigue limit |
| bo | exponent of the shear fatigue limit |
| c | exponent of the plastic fatigue strain |
| co | exponent of the plastic shear fatigue strain |
| DPn | damage parameter |
| E | Young’s modulus of elasticity |
| G | shear modulus |
| J | material constant |
| k | material fitting parameter |
| Nf | number of cycles to failure |
| β | coefficient taking into account the best fit for a given material |
| plastic strain tensor | |
| normal strain amplitude | |
| εn* | normal strain excursion between adjacent turning points of the maximum shear strain range on the critical plane |
| coefficient of the plastic fatigue strain | |
| material-dependent exponent | |
| shear strain amplitude | |
| coefficient of the plastic shear fatigue strain | |
| maximum shear strain | |
| coefficient of the fatigue limit | |
| stress tensor | |
| σh | hydrostatic stress |
| maximum normal stress | |
| σu | ultimate strength |
| σy | yield strength |
| (στ)max | maximum shear and tensile stress product value |
| shear coefficient of the fatigue limit | |
| maximum shear stress | |
| υ | elastic Poisson’s ratio |
References
- Garud, Y.S. A New Approach to the Evaluation of Fatigue under Multiaxial Loadings. J. Eng. Mater. Technol. 1981, 103, 118–125. [Google Scholar] [CrossRef]
- Smith, K.N.; Watson, P.; Toper, T.H. A stress–strain function for the fatigue of metals. J. Mater. 1970, 5, 767–778. [Google Scholar]
- Wang, Y. Evaluation and comparison of several multiaxial fatigue criteria. Int. J. Fatigue 2004, 26, 17–25. [Google Scholar] [CrossRef]
- Kamal, M.; Rahman, M.M. Advances in fatigue life modeling: A review. Renew. Sustain. Energy Rev. 2018, 82, 940–949. [Google Scholar] [CrossRef]
- You, B.-R.; Lee, S.-B. A critical review on multiaxial fatigue assessments of metals. Int. J. Fatigue 1996, 18, 235–244. [Google Scholar] [CrossRef]
- Cui, W. A state-of-the-art review on fatigue life prediction methods for metal structures. J. Mar. Sci. Technol. 2002, 7, 43–56. [Google Scholar] [CrossRef]
- Meggiolaro, M.A.; Tupiassú, J.; De Castro, P.; Carlos, A.; Miranda, O. Evaluation of multiaxial stress-strain models and fatigue life prediction methods under proportional loading. Mech. Solids Braz. Braz. Soc. Mech. Sci. Eng. 2009, 2009, 365–384. [Google Scholar]
- Skibicki, D.; Pejkowski, Ł. Low-cycle multiaxial fatigue behaviour and fatigue life prediction for CuZn37 brass using the stress-strain models. Int. J. Fatigue 2017, 102, 18–36. [Google Scholar] [CrossRef]
- Lu, C.; Melendez, J.; Martinez-Esnaola, J.M. A universally applicable multiaxial fatigue criterion in 2D cyclic loading. Int. J. Fatigue 2018, 110, 95–104. [Google Scholar] [CrossRef]
- Zhu, H.; Wu, H.; Lu, Y.; Zhong, Z. A novel energy-based equivalent damage parameter for multiaxial fatigue life prediction. Int. J. Fatigue 2019, 121, 1–8. [Google Scholar] [CrossRef]
- Arora, P.; Gupta, S.K.; Samal, M.; Chattopadhyay, J. Development of new critical plane model for assessment of fatigue life under multi-axial loading conditions. Int. J. Fatigue 2019, 129, 105209. [Google Scholar] [CrossRef]
- Esmaeili, F.; Chakherlou, T.; Zehsaz, M. Prediction of fatigue life in aircraft double lap bolted joints using several multiaxial fatigue criteria. Mater. Des. 2014, 59, 430–438. [Google Scholar] [CrossRef]
- Cruces, A.S.; Lopez-Crespo, P.; Moreno, B.; Antunes, F.V. Multiaxial Fatigue Life Prediction on S355 Structural and Offshore Steel Using the SKS Critical Plane Model. Metals 2018, 8, 1060. [Google Scholar] [CrossRef] [Green Version]
- Han, C.; Chen, X.; Kim, K. Evaluation of multiaxial fatigue criteria under irregular loading. Int. J. Fatigue 2002, 24, 913–922. [Google Scholar] [CrossRef]
- Lei, B.-M.; Tran, V.-X.; Taheri, S.; le Roux, J.-C.; Curtit, F.; He, M.; Wan, L.; Zhou, Y. Toward consistent fatigue crack initiation criteria for 304L austenitic stainless steel under multi-axial loads. Int. J. Fatigue 2015, 75, 57–68. [Google Scholar] [CrossRef] [Green Version]
- Yu, Z.-Y.; Zhu, S.-P.; Liu, Q.; Liu, Y. Multiaxial Fatigue Damage Parameter and Life Prediction without Any Additional Material Constants. Materials 2017, 10, 923. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.-P.; Yu, Z.-Y.; Correia, J.; De Jesus, A.M.; Berto, F. Evaluation and comparison of critical plane criteria for multiaxial fatigue analysis of ductile and brittle materials. Int. J. Fatigue 2018, 112, 279–288. [Google Scholar] [CrossRef]
- Chen, X.; Song, J.; Kim, K.S. Low cycle fatigue life prediction of 63Sn–37Pb solder under proportional and non-proportional loading. Int. J. Fatigue 2006, 28, 757–766. [Google Scholar] [CrossRef]
- Boeller, C.; Seeger, T. Materials Data for Cyclic Loading, Part A: Unalloyed Steels. In Materials Data for Cyclic Loading; Materials Science Monographs 42A; Elsevier: Amsterdam, The Netherlands, 1987; Available online: https://www.elsevier.com/books/materials-data-for-cyclic-loading/boller/978-0-444-42871-4 (accessed on 10 May 2022).
- Boeller, C.; Seeger, T. Materials Data for Cyclic Loading, Part B: Low-alloyed Steels. In Materials Data for Cyclic Loading; Materials Science Monographs 42B; Elsevier: Amsterdam, The Netherlands, 1987; Available online: https://www.elsevier.com/books/materials-data-for-cyclic-loading/boller/978-0-444-42872-1 (accessed on 10 May 2022).
- Boeller, C.; Seeger, T. Materials Data for Cyclic Loading, Part C: High-alloyed Steels. In Materials Data for Cyclic Loading; Materials Science Monographs 42C; Elsevier: Amsterdam, The Netherlands, 1987; Available online: https://www.elsevier.com/books/materials-data-for-cyclic-loading/boller/978-0-444-42874-5 (accessed on 10 May 2022).
- Boeller, C.; Seeger, T. Materials Data for Cyclic Loading, Part D: Aluminium and Titanium Alloys. In Materials Data for Cyclic Loading; Materials Science Monographs 42D; Elsevier: Amsterdam, The Netherlands, 1987; Available online: https://www.elsevier.com/books/materials-data-for-cyclic-loading/boller/978-0-444-42873-8 (accessed on 10 May 2022).
- Boeller, C.; Seeger, T. Materials Data for Cyclic Loading, Part E: Cast and weldedmaterials. In Materials Data for Cyclic Loading; Materials Science Monographs 42E; Elsevier: Amsterdam, The Netherlands, 1987; Available online: https://www.elsevier.com/books/materials-data-for-cyclic-loading/boller/978-0-444-42870-7 (accessed on 10 May 2022).
- Boeller, C.; Seeger, T. Materials Data for Cyclic Loading, Suplement 1. In Materials Data for Cyclic Loading; Materials Science Monographs 61; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Zhang, W.; Akid, R. Effect of biaxial mean stress on cyclic stress-strain response and behaviour of short fatigue cracks in a high strength spring steel. Fatigue Fract. Eng. Mater. Struct. 1997, 20, 167–177. [Google Scholar] [CrossRef]
- Salerno, G.; Magnabosco, R.; Neto, C.D.M. Mean strain influence in low cycle fatigue behavior of AA7175-T1 aluminum alloy. Int. J. Fatigue 2007, 29, 829–835. [Google Scholar] [CrossRef]
- Walker, K. The Effect of Stress Ratio During Crack Propagation and Fatigue for 2024-T3 and 7075-T6 Aluminum. In Effects of Environment and Complex Load History on Fatigue Life; ASTM International: West Conshohocken, PA, USA, 2009; pp. 1–14. [Google Scholar] [CrossRef]
- Lv, Z.; Huang, H.-Z.; Wang, H.-K.; Gao, H.; Zuo, F.-J. Determining the Walker exponent and developing a modified Smith-Watson-Topper parameter model. J. Mech. Sci. Technol. 2016, 30, 1129–1137. [Google Scholar] [CrossRef]
- Wehner, T.; Fatemi, A. Effects of mean stress on fatigue behaviour of a hardened carbon steel. Int. J. Fatigue 1991, 13, 241–248. [Google Scholar] [CrossRef]
- Bergmann, J.; Seeger, T. On the Influence of Cyclic Stress-Strain Curves, Damage Parameters, and Various Evaluation Concepts on the Life Prediction by the Local Approach. In Proceedings of the 2nd European Conference on Fracture, VDI-Report of Progress. Darmstadt, Germany, 9–11 October 1979; Volume 18. [Google Scholar]
- Nihei, M.; Heuler, P.; Boller, C.; Seeger, T. Evaluation of mean stress effect on fatigue life by use of damage parameters. Int. J. Fatigue 1986, 8, 119–126. [Google Scholar] [CrossRef]
- Roberts, R.; Erdogan, F. The effect of mean stress on fatigue crack propagation in plates under extension and bending. J. Fluids Eng. 1967, 89, 885–892. [Google Scholar] [CrossRef]
- Socie, D.F. Multiaxial Fatigue Damage Models. J. Eng. Mater. Technol. 1987, 109, 293–298. [Google Scholar] [CrossRef]
- Navarro, C.; Muñoz, S.; Dominguez, J. On the use of multiaxial fatigue criteria for fretting fatigue life assessment. Int. J. Fatigue 2008, 30, 32–44. [Google Scholar] [CrossRef]
- Szolwinski, M.P.; Farris, T.N. Observation, analysis and prediction of fretting fatigue in 2024-T351 aluminum alloy. Wear 1998, 221, 24–36. [Google Scholar] [CrossRef]
- Yu, Z.-Y.; Zhu, S.-P.; Liu, Q.; Liu, Y. A New Energy-Critical Plane Damage Parameter for Multiaxial Fatigue Life Prediction of Turbine Blades. Materials 2017, 10, 513. [Google Scholar] [CrossRef] [Green Version]
- Suman, S.; Kallmeyer, A.; Smith, J. Development of a multiaxial fatigue damage parameter and life prediction methodology for non-proportional loading. Frat. Integrità Strutt. 2016, 10, 224–230. [Google Scholar] [CrossRef]
- Glinka, G.; Shen, G.; Plumtree, A. A multiaxial fatigue strain energy density parameter related to the critical fracture plane. Fatigue Fract. Eng. Mater. Struct. 1995, 18, 37–46. [Google Scholar] [CrossRef]
- Kanchanomai, C.; Miyashita, Y.; Mutoh, Y. Strain-rate effects on low cycle fatigue mechanism of eutectic Sn–Pb solder. Int. J. Fatigue 2002, 24, 987–993. [Google Scholar] [CrossRef]
- Hao, M.-F.; Zhu, S.-P.; Liao, D. New strain energy-based critical plane approach for multiaxial fatigue life prediction. J. Strain Anal. Eng. Des. 2019, 54, 310–319. [Google Scholar] [CrossRef]
- Chen, X.; Xu, S.; Huang, D. A critical plane-strain energy density criterion for multiaxial low-cycle fatigue life under non-proportional loading. Fatigue Fract. Eng. Mater. Struct. 1999, 22, 679–686. [Google Scholar] [CrossRef]
- Gupta, S.K.; Fisch, T.M.; Schuler, X.; Roos, E. A critical plane based model for fatigue assessment under fixed and rotating principal direction loading. In Proceedings of the 21st International Conference on Structural Mechanics in Reactor Technology, New Delhi, India, 6–11 November 2011; p. 624. [Google Scholar]
- Calvo, S.; Canales, M.; Gómez, C.; Valdés, J.; Núñez, J. Probabilistic formulation of the multiaxial fatigue damage of Liu. Int. J. Fatigue 2011, 33, 460–465. [Google Scholar] [CrossRef]
- Liu, K.; Wang, J.-A. An energy method for predicting fatigue life, crack orientation, and crack growth under multiaxial loading conditions. Int. J. Fatigue 2001, 23, 129–134. [Google Scholar] [CrossRef]
- Chu, C.C.; Conle, F.A.; Bonnen, J.J. Multiaxial stress- strain modeling and fatigue life prediction of sea axle shafts. ASTM Spec. Tech. Publ. 1993, 1191, 37. [Google Scholar]
- Bonnen, J.; Topper, T. The effect of bending overloads on torsional fatigue in normalized 1045 steel. Int. J. Fatigue 1999, 21, 23–33. [Google Scholar] [CrossRef]
- Li, J.; Sun, Q.; Zhang, Z.; Qiao, Y.-J.; Liu, J. A modification of Smith-Watson-Topper damage parameter for fatigue life prediction under non-proportional loading. Fatigue Fract. Eng. Mater. Struct. 2012, 35, 301–316. [Google Scholar] [CrossRef]
- Pan, W.-F.; Hung, C.-Y.; Chen, L.-L. Fatigue life estimation under multiaxial loadings. Int. J. Fatigue 1999, 21, 3–10. [Google Scholar] [CrossRef]
- Rolović, R.; Tipton, S.M. Energy based critical plane approach to multiaxial fatigue analysis. ASTM Spec. Tech. Publ. 1999, 1999, 599–613. [Google Scholar] [CrossRef]
- Ince, A.; Glinka, G. A generalized fatigue damage parameter for multiaxial fatigue life prediction under proportional and non-proportional loadings. Int. J. Fatigue 2014, 62, 34–41. [Google Scholar] [CrossRef]
- Jiang A fatigue criterion for general multiaxial loading. Fatigue Fract. Eng. Mater. Struct. 2000, 23, 19–32. [CrossRef]
- Jiang, Y.; Hertel, O.; Vormwald, M. An experimental evaluation of three critical plane multiaxial fatigue criteria. Int. J. Fatigue 2007, 29, 1490–1502. [Google Scholar] [CrossRef]
- Benedetti, M.; Fontanari, V.; Bandini, M.; Taylor, D. Multiaxial fatigue resistance of shot peened high-strength aluminum alloys. Int. J. Fatigue 2014, 61, 271–282. [Google Scholar] [CrossRef]
- “Fatigue and Stress Analyses of Rolling Contact”, Yanyao Roger Jiang and Huseyin Sehitoglu, February 1992 (UILU-ENG 92-3602).|Fracture Control Program-Illinois. n.d. Available online: https://fcp.mechse.illinois.edu/fcp_report161/ (accessed on 14 December 2020).
- Abbadi, M.; Belouettar, S.; Muzzo, P.; Kremer, P.; Oussouaddi, O.; Zeghloul, A. On low cycle fatigue life of nickel-based superalloy valve membranes under non-proportional cyclic loading. Int. J. Fatigue 2008, 30, 1160–1168. [Google Scholar] [CrossRef]
- Varvani-Farahani, A. A new energy-critical plane parameter for fatigue life assessment of various metallic materials subjected to in-phase and out-of-phase multiaxial fatigue loading conditions. Int. J. Fatigue 2000, 22, 295–305. [Google Scholar] [CrossRef]
- Jahed, H.; Varvanifarahani, A. Upper and lower fatigue life limits model using energy-based fatigue properties. Int. J. Fatigue 2006, 28, 467–473. [Google Scholar] [CrossRef]
- Xue, L.; Shang, D.-G.; Li, D.-H.; Li, L.-J.; Liu, X.-D.; Chen, H. Equivalent energy-based critical plane fatigue damage parameter for multiaxial LCF under variable amplitude loading. Int. J. Fatigue 2020, 131, 105350. [Google Scholar] [CrossRef]
- Łagoda, T. Energy models for fatigue life estimation under uniaxial random loading. Part II: Verification of the model. Int. J. Fatigue 2001, 23, 481–489. [Google Scholar] [CrossRef]
- Łagoda, T.; Ogonowski, P. Criteria of multiaxial random fatigue based on stress, strain and energy parameters of damage in the critical plane. Mater. Werkst. 2005, 36, 429–437. [Google Scholar] [CrossRef]
- Walat, K.; Kurek, M.; Ogonowski, P.; Łagoda, T. The multiaxial random fatigue criteria based on strain and energy damage parameters on the critical plane for the low-cycle range. Int. J. Fatigue 2012, 37, 100–111. [Google Scholar] [CrossRef]
- Plumtree, A.; Cheng, G. A fatigue damage parameter for off-axis unidirectional fibre-reinforced composites. Int. J. Fatigue 1999, 21, 849–856. [Google Scholar] [CrossRef]
- Petermann, J.; Plumtree, A. A unified fatigue failure criterion for unidirectional laminates. Compos. Part A Appl. Sci. Manuf. 2001, 32, 107–118. [Google Scholar] [CrossRef]
- Roostaei, A.A.; Jahed, H. Multiaxial cyclic behaviour and fatigue modelling of AM30 Mg alloy extrusion. Int. J. Fatigue 2017, 97, 150–161. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łagoda, T.; Vantadori, S.; Głowacka, K.; Kurek, M.; Kluger, K. Using the Smith-Watson-Topper Parameter and Its Modifications to Calculate the Fatigue Life of Metals: The State-of-the-Art. Materials 2022, 15, 3481. https://doi.org/10.3390/ma15103481
Łagoda T, Vantadori S, Głowacka K, Kurek M, Kluger K. Using the Smith-Watson-Topper Parameter and Its Modifications to Calculate the Fatigue Life of Metals: The State-of-the-Art. Materials. 2022; 15(10):3481. https://doi.org/10.3390/ma15103481
Chicago/Turabian StyleŁagoda, Tadeusz, Sabrina Vantadori, Karolina Głowacka, Marta Kurek, and Krzysztof Kluger. 2022. "Using the Smith-Watson-Topper Parameter and Its Modifications to Calculate the Fatigue Life of Metals: The State-of-the-Art" Materials 15, no. 10: 3481. https://doi.org/10.3390/ma15103481
APA StyleŁagoda, T., Vantadori, S., Głowacka, K., Kurek, M., & Kluger, K. (2022). Using the Smith-Watson-Topper Parameter and Its Modifications to Calculate the Fatigue Life of Metals: The State-of-the-Art. Materials, 15(10), 3481. https://doi.org/10.3390/ma15103481





