Flexural Performance of Encased Pultruded GFRP I-Beam with High Strength Concrete under Static Loading
Abstract
:1. Introduction
2. Experimental Program
2.1. Details of the Tested Specimens
2.2. Material Properties
2.3. Experimental Setup and Instrumentations
3. Experimental Results and Discussion
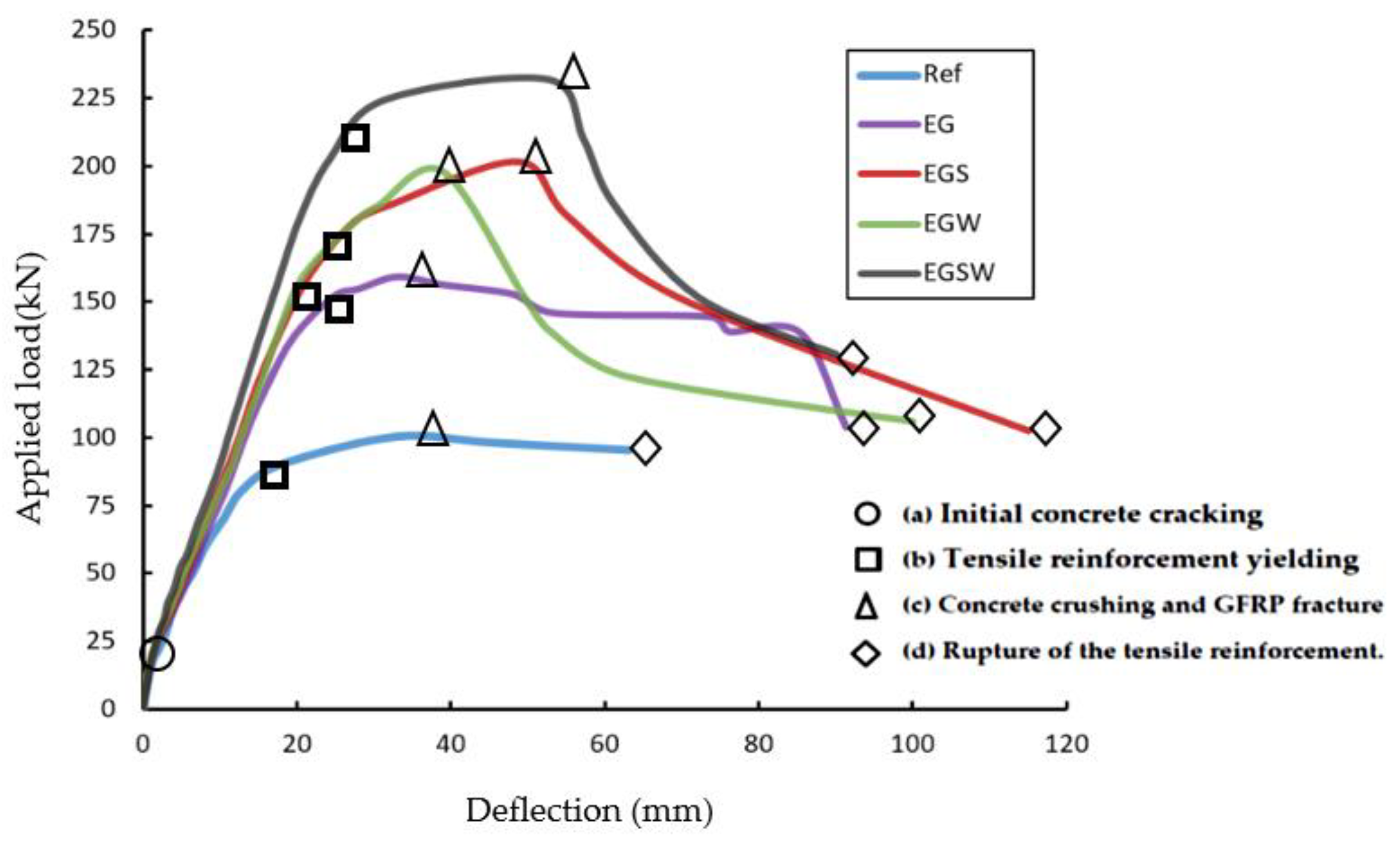
3.1. Load-Deflection Curves
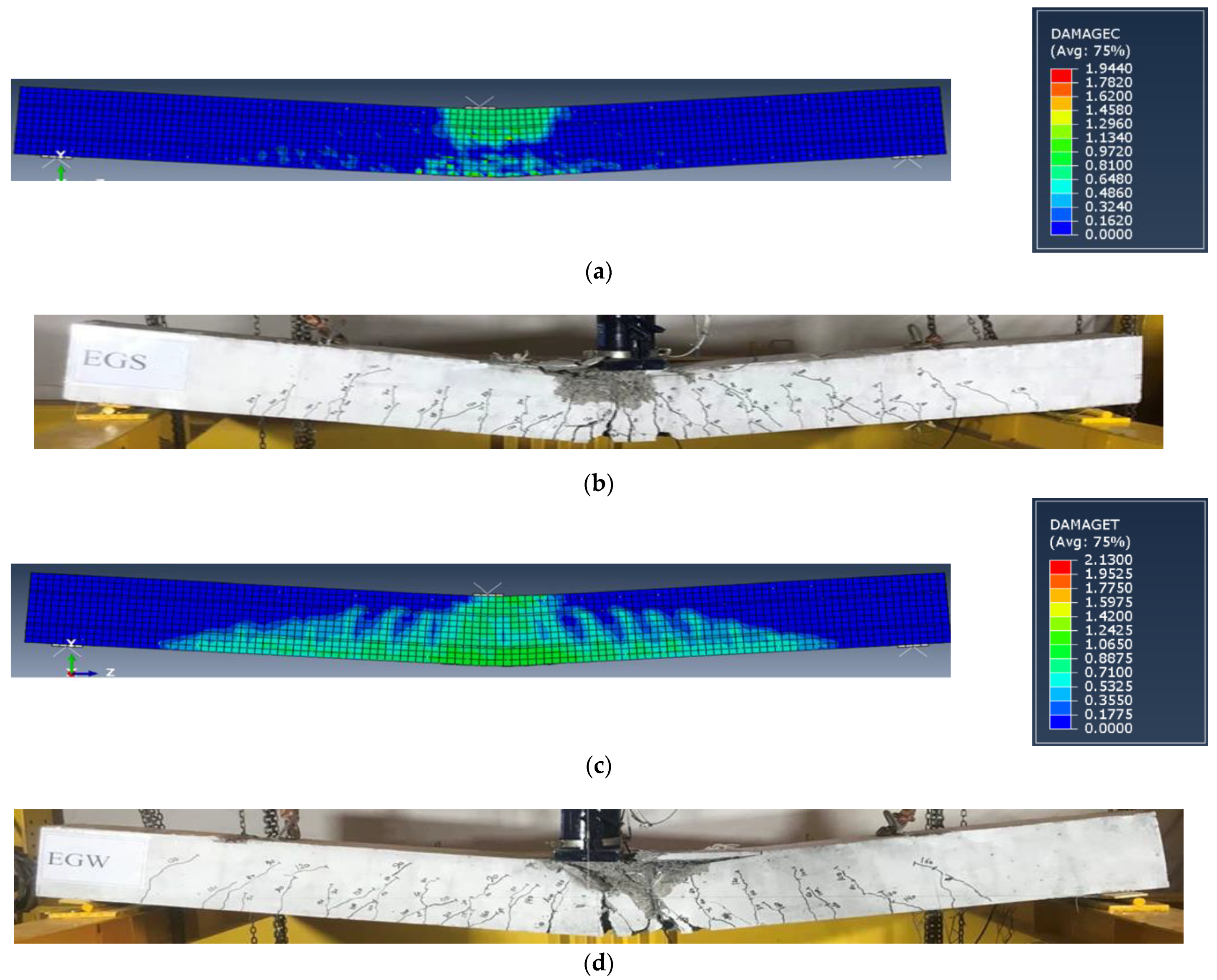
3.2. Crack Patterns and Failure Modes
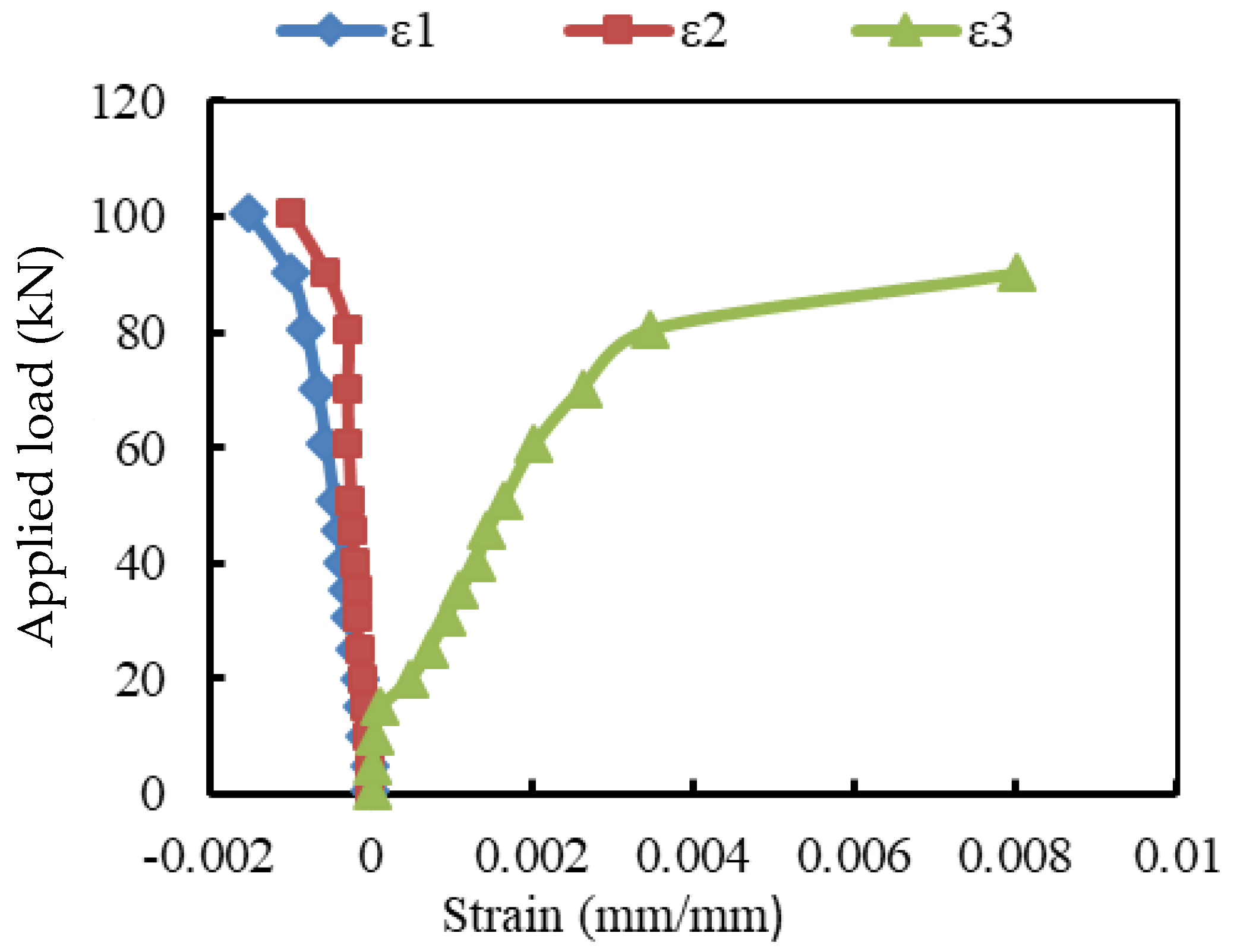
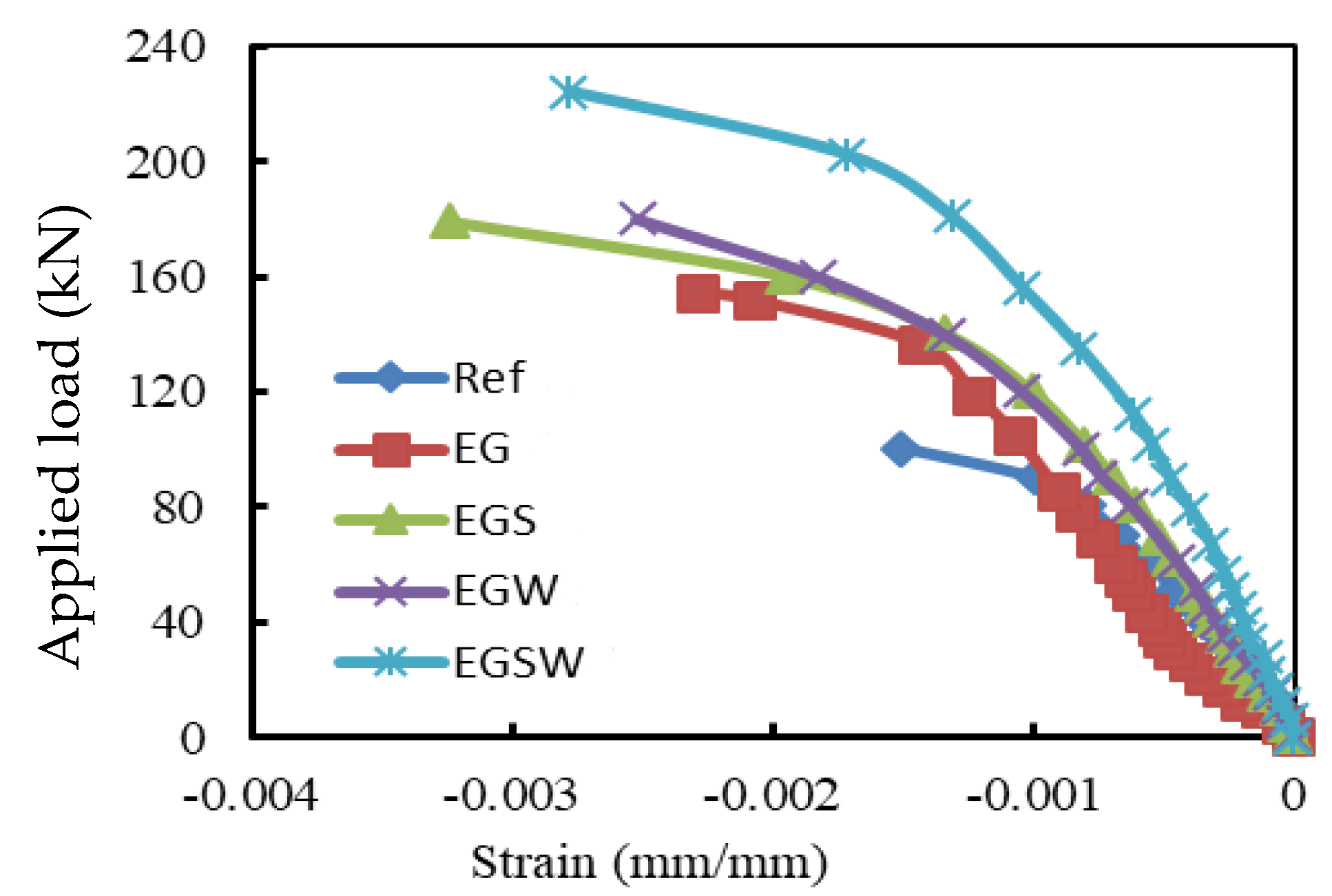
3.3. Load-Strain Relationships
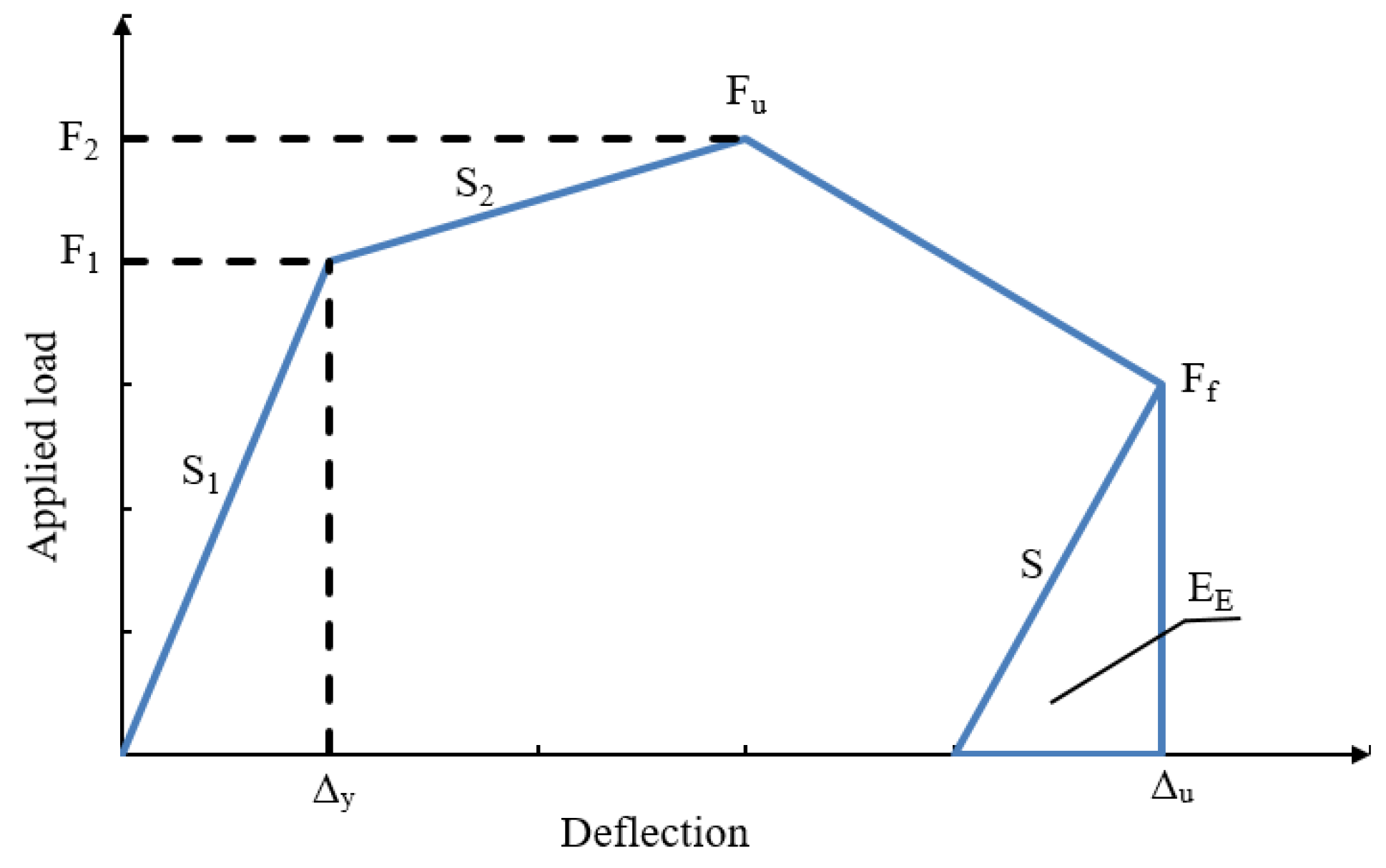
3.4. Ductility
4. Numerical Modeling
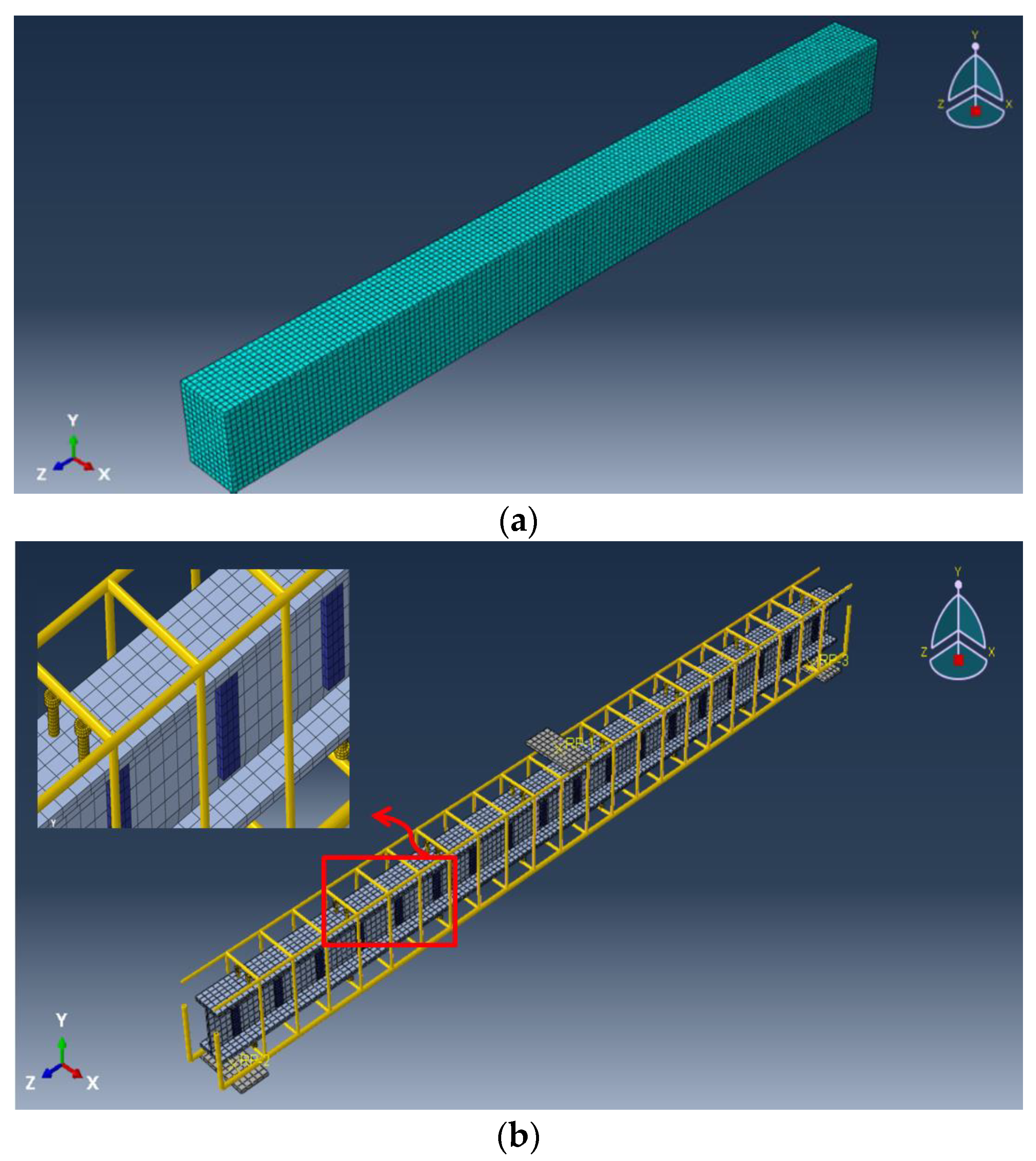
4.1. FE Modelling of Encased Beam
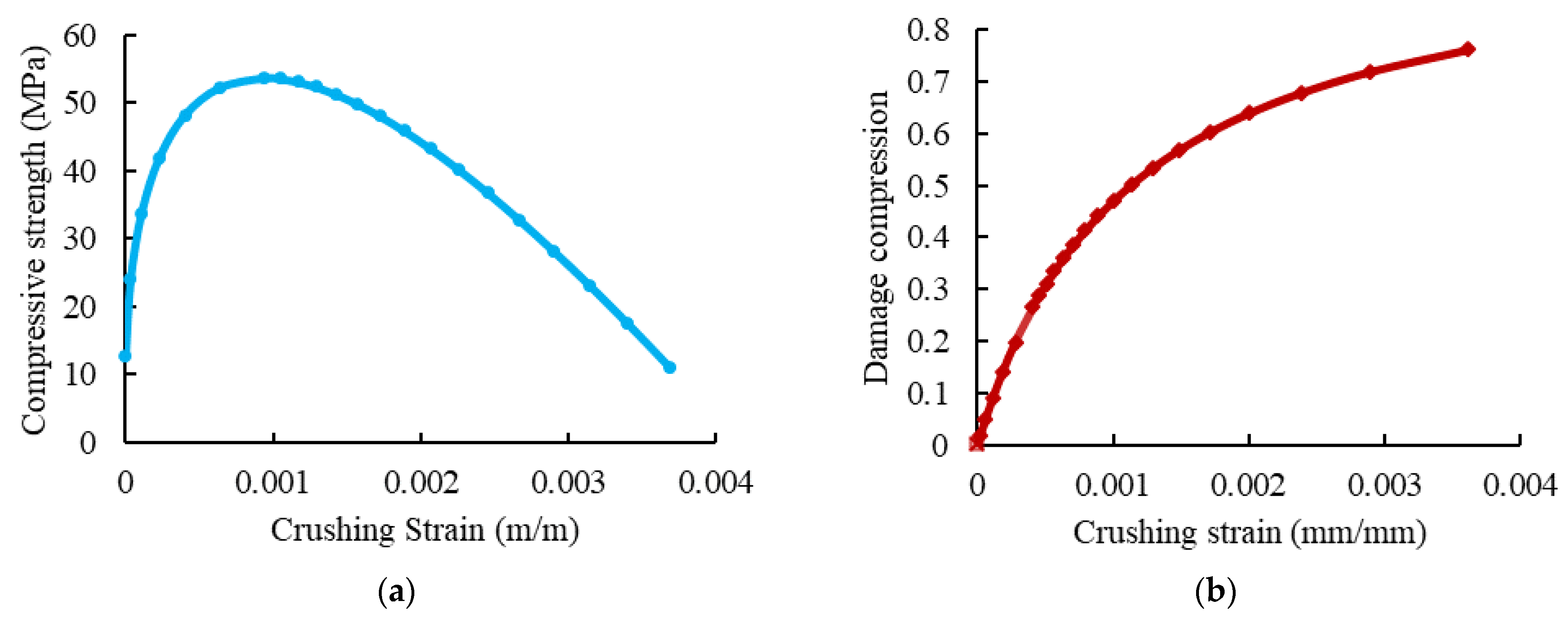
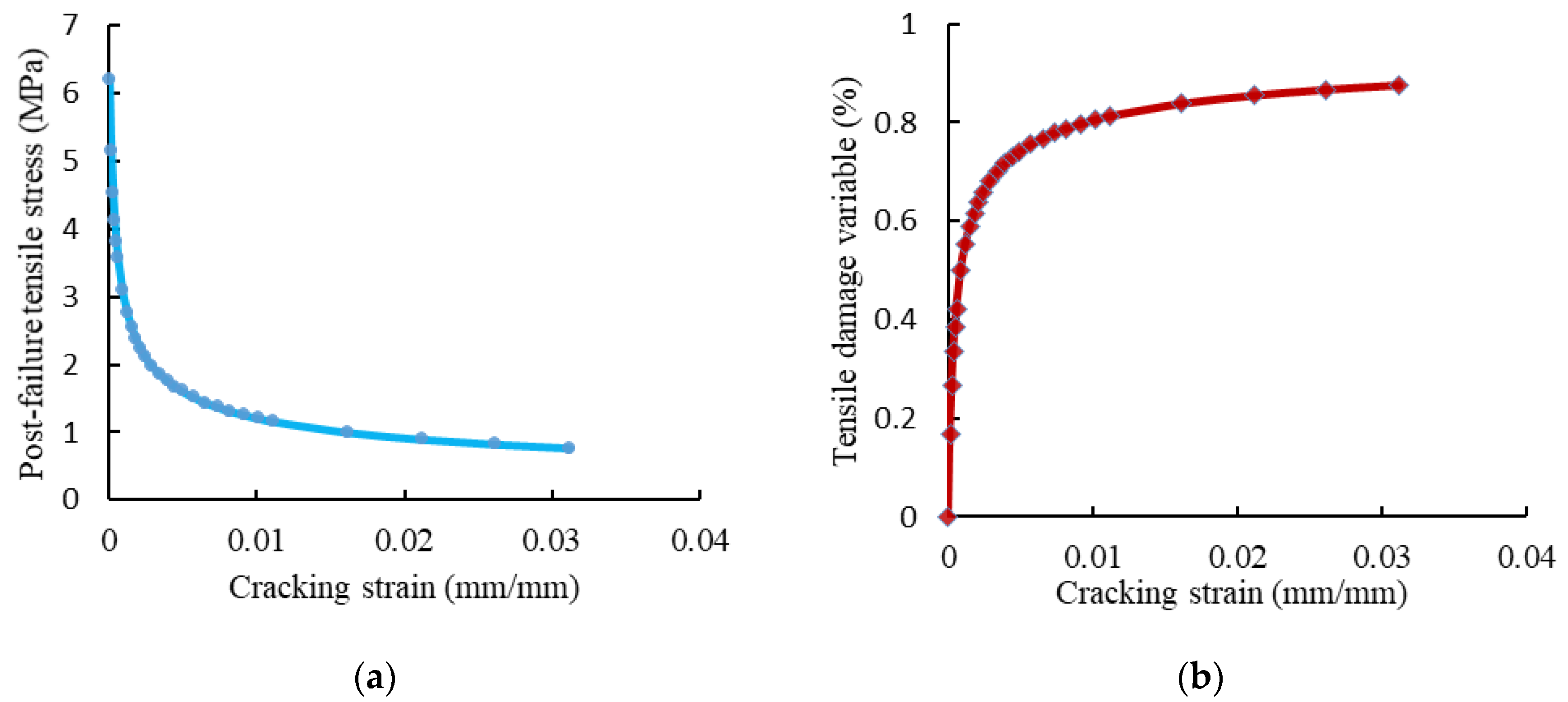
4.2. Material Modeling
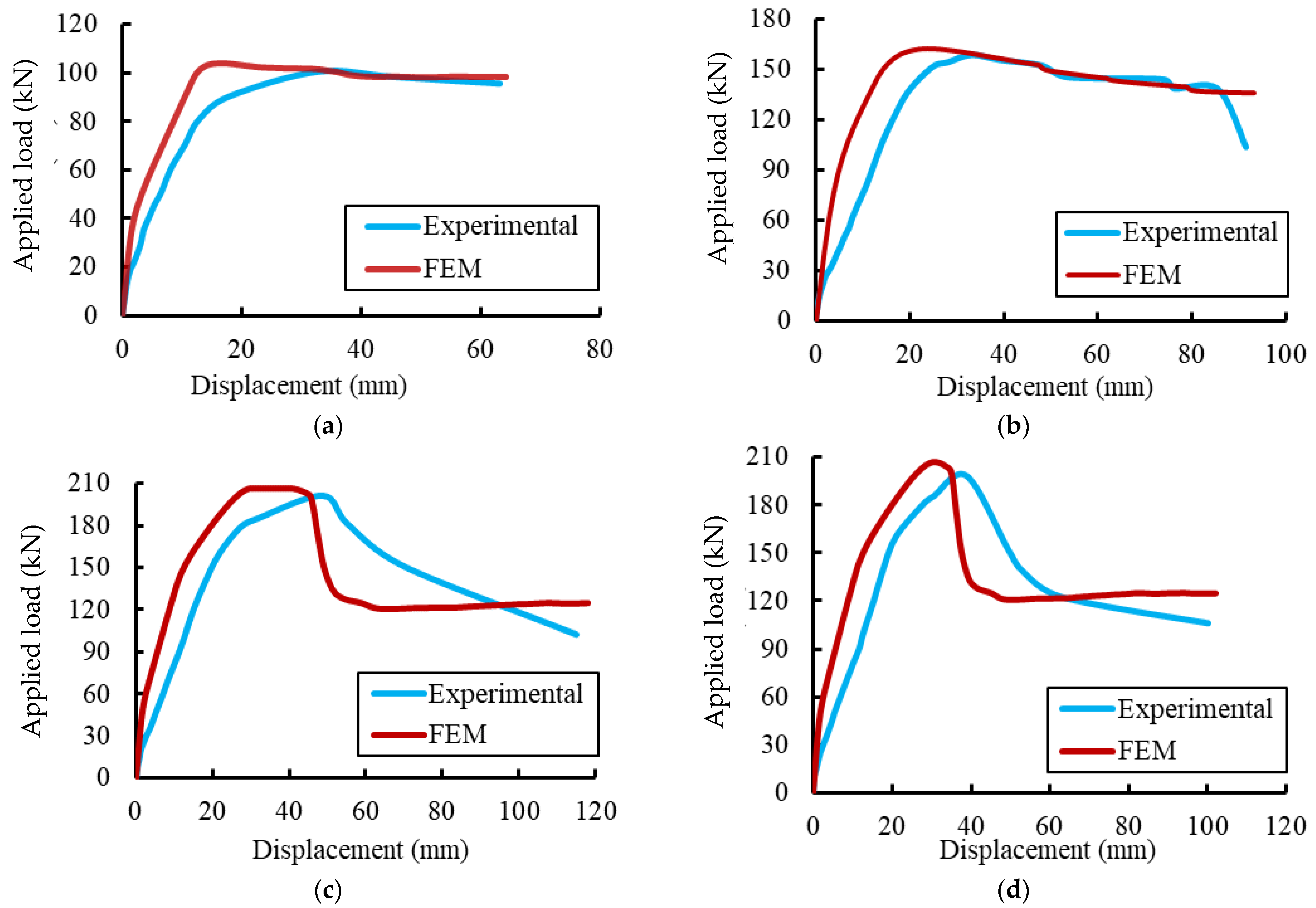
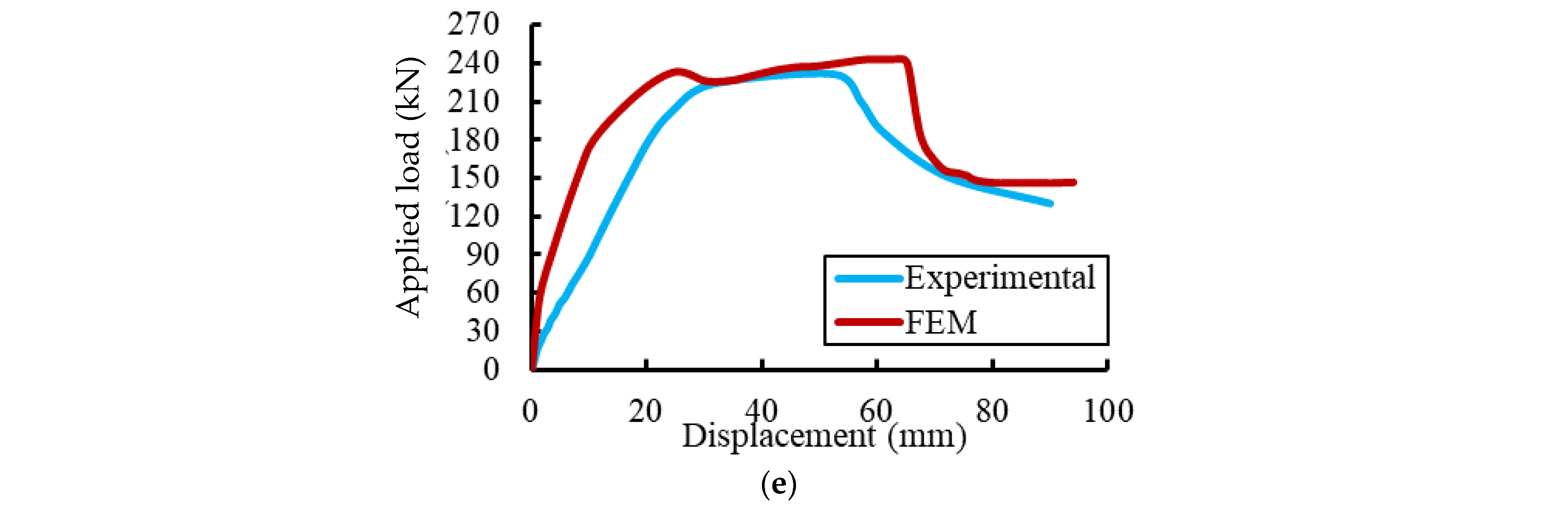
4.3. Validations of the FE Results
5. Parametric Study
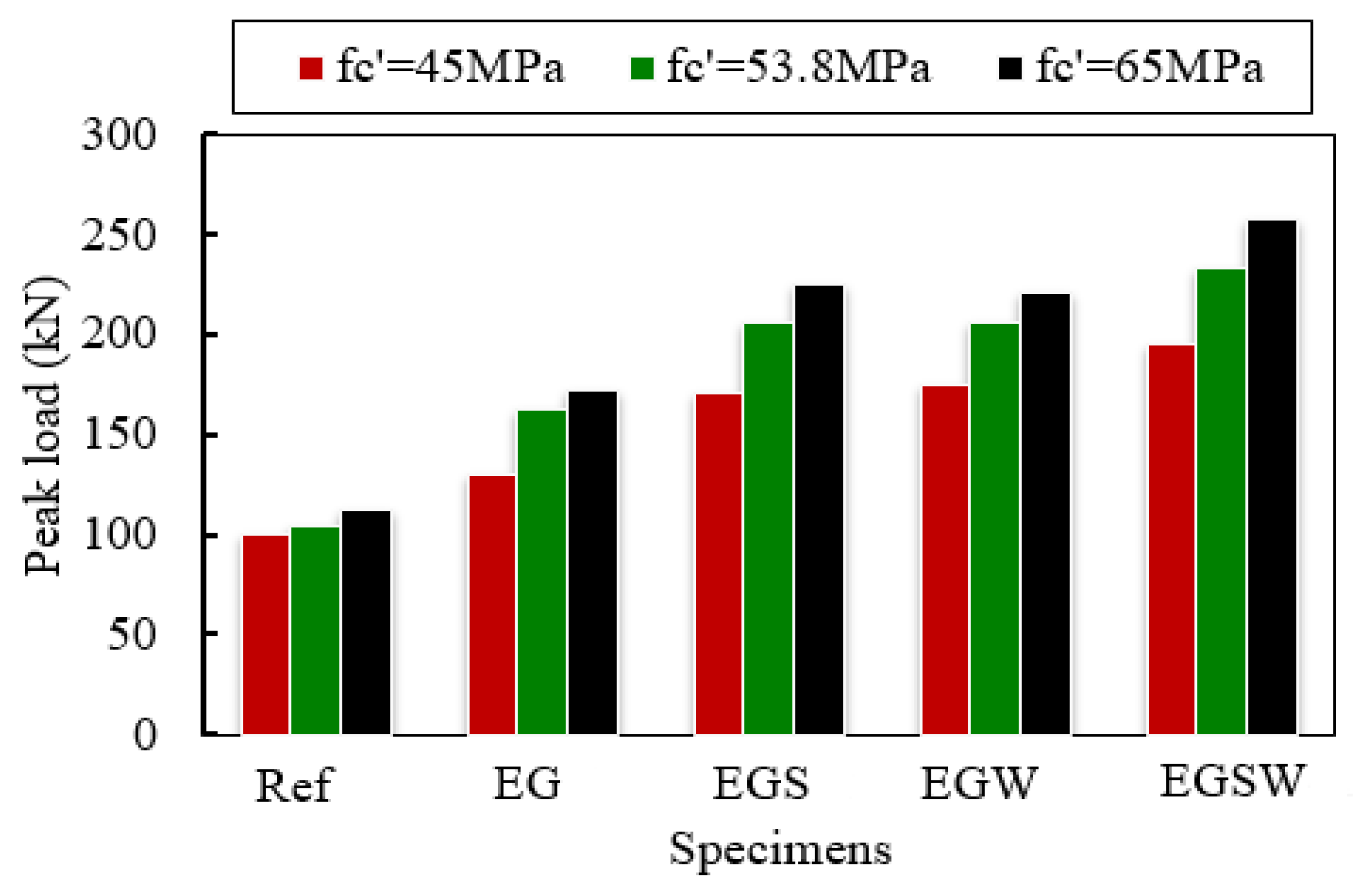
5.1. Effect of the Concrete Compressive Strength
5.2. Effect of the Tensile Strength of the GFRP Beam
6. Conclusions
- Encasing the GFRP beam with concrete enhanced the peak load by 58.3%. Using shear connectors, web stiffeners, and both improved the peak loads by 100.6%, 97.3%, and 130.8%, respectively, relative to the classical reinforced concrete. The shear connectors and web stiffeners increased the beams’ rigidity. In addition, the GFRP beams improved the ductility by 21.6% relative to the reference one. Moreover, the shear connectors, web stiffeners, and both improved the ductility by 185.5%, 119.8%, and 128.4%, respectively, relative to the reference beam.
- The strains of the pultruded GFRP beams increased almost linearly until failure. The GFRP beams contributed to providing more strength to the encased beams. The contribution of the GFRP beams increased by adding the studs and web stiffeners because the bottom flanges of these beams exhibited additional strains due to increasing the composite interaction with concrete.
- The peak loads increased with increasing the compressive strength of concrete. For the reference beam without a GFRP beam, the peak load increased by 3.76% and 11.92% for the compressive strength of 53.8 MPa and 65 MPa, respectively. However, the most enhancements in the peak loads were for the encased beam, which were 24.78% and 32.32% for the compressive strengths of 53.8 MPa 65 MPa, respectively, with respect to the compressive strength of 45 MPa.
- The peak loads and the corresponding mid-span deflections increased as the tensile strength of GFRP increased. The increase in the peak loads ranged between 6% and 18% when the tensile strength was 347.5 MPa, while the improvements ranged between 14% and 27% for the tensile strength of 416 MPa.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, C.; Yin, X.; Liu, Y.; Guo, R.; Xian, G. Long-term service evaluation of a pultruded carbon/glass hybrid rod exposed to elevated temperature, hydraulic pressure and fatigue load coupling. Int. J. Fatigue 2020, 134, 105480. [Google Scholar] [CrossRef]
- Li, C.; Guo, R.; Xian, G.; Li, H. Innovative compound-type anchorage system for a large-diameter pultruded carbon/glass hybrid rod for bridge cable. Mater. Struct. 2020, 53, 73. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, X.L.; Xian, G.; Wu, G.; Raman, R.K.S.; Al-Saadi, S. Effect of sustained load and seawater and sea sand concrete environment on durability of basalt- and glass-fibre reinforced polymer (B/GFRP) bars. Corros. Sci. 2018, 138, 200–218. [Google Scholar] [CrossRef]
- AL-Baghdady, H.A.; Sabah, A. Behavior of RC Beams Strengthened with NSM-CFRP Strips Subjected to Fire Exposure. Eng. Technol. Appl. Sci. Res. 2021, 11, 7782–7787. [Google Scholar] [CrossRef]
- ACI Committee 363. ACI PRC-363-10 Report on High-Strength Concrete; American Concrete Institute: Farmington Hills, MI, USA, 2010. [Google Scholar]
- Chalangaran, N.; Farzampour, A.; Paslar, N.; Fatemi, H. Experimental Investigation of Sound Transmission Loss in Concrete Containing Recycled Rubber Crumbs. Adv. Concr. Constr. 2021, 11, 447–454. [Google Scholar] [CrossRef]
- Chalangaran, N.; Farzampour, A.; Paslar, N. Nano Silica and Metakaolin Effects on the Behavior of Concrete Containing Rubber Crumbs. CivilEng 2020, 1, 264–274. [Google Scholar] [CrossRef]
- Farzampour, A. Compressive Behavior of Concrete under Environmental Effects. Compressive Strength Concr. 2019, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Farzampour, A. Temperature and humidity effects on behavior of grouts. Adv. Concr. Constr. 2017, 5, 659–669. [Google Scholar] [CrossRef]
- Li, X.; Lv, H.; Zhou, S. Flexural behavior of GFRP-reinforced concrete encased steel composite beams. Constr. Build. Mater. 2012, 28, 255–262. [Google Scholar] [CrossRef]
- Youssef, J. Behavior of GFRP Reinforced and GFRP Encased Square Concrete Members under Different Loading Conditions. Ph.D. Thesis, School of Civil, Mining and Environmental Engineering, University of Wollongong, Wollongong, Australia, 2017. [Google Scholar]
- Estep, D.D. Bending and Shear Behavior of Pultruded Glass Fiber Reinforced Polymer Composite Beams with Closed and Open Sections. Master’s Thesis, West Virginia University, Morgantown, WV, USA, 2014. [Google Scholar] [CrossRef]
- Boller, K.H. Effect of Long-Term Loading on Glass-Reinforced Plastic Laminates; No. 2039; United States Department of Agriculture, Forest Service, Forest Products Laboratory: Washington, DC, USA, 1965.
- Ascione, F.; Mancusi, G.; Spadea, S.; Lamberti, M.; Lebon, F.; Maurel-Pantel, A. On the flexural behavior of GFRP beams obtained by bonding simple panels: An experimental investigation. Compos. Struct. 2015, 131, 55–65. [Google Scholar] [CrossRef] [Green Version]
- Yuan, J.S.; Hadi, M.N.S. Bond-slip behavior between GFRP I-section and concrete. Compos. Part B Eng. 2017, 130, 76–89. [Google Scholar] [CrossRef] [Green Version]
- Hadi, M.N.S.; Yuan, J.S. Experimental investigation of composite beams reinforced with GFRP I-beam and steel bars. Constr. Build. Mater. 2017, 144, 462–474. [Google Scholar] [CrossRef] [Green Version]
- Ibrahim, T.H.; Allawi, A.A.; El-Zohairy, A. Impact Behavior of Composite Reinforced Concrete Beams with Pultruded I-GFRP Beam. Materials 2022, 15, 441. [Google Scholar] [CrossRef] [PubMed]
- Allawi, A.A.; Ali, S.I. Flexural Behavior of Composite GFRP Pultruded I-Section Beams under Static and Impact Loading. Civ. Eng. J. 2020, 6, 143–2158. [Google Scholar] [CrossRef]
- Hoe, K.W.; Ramli, M. Indicative performance of fiber-reinforced polymer (FRP) encased beam in flexure. Constr. Build. Mater. 2013, 48, 780–788. [Google Scholar] [CrossRef]
- Gemi, L.; Madenci, E.; Özkiliç, Y.O. Investigation of Reinforced Concrete-Filled Pultruded Beams Strengthened by GFRP Composite. In Proceedings of the International Aluminum-Themed Engineering and Natural Sciences Conference, Seydişehir, Turkey, 4–6 October 2019; pp. 313–316. [Google Scholar]
- Almusallam, T.H. Behavior of Normal and High-Strength Concrete Cylinders Confined with E-Glass/Epoxy Composite Laminates. Compos. Part B Eng. J. 2006, 38, 629–639. [Google Scholar] [CrossRef]
- El-nemr, A.; Ahmed, E.A.; Benmokrane, B. Flexural Behavior and Serviceability of Normal-and High-Strength Concrete Beams Reinforced with Glass Fiber-Reinforced Polymer Bars. ACI Struct. J. 2013, 110, 1077–1087. [Google Scholar]
- Saleh, N.; Ashour, A.; Lam, D.; Sheehan, T. Experimental Investigation of Bond Behaviour of Two Common GFRP Bar Types in High–Strength Concrete. Constr. Build. Mater. 2019, 201, 610–622. [Google Scholar] [CrossRef] [Green Version]
- ASTM Designation C39-39M; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. Annual Book of ASTM Standards. ASTM International: West Conshohocken, PA, USA, 2001.
- ASTM Designation C469-469M; Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression. ASTM International: West Conshohocken, PA, USA, 2001.
- ASTM A615/A615M-18; Standard Test Method for Deformed and Plain Carbon-Steel Bars for Concrete Reinforcement. Annual Book of ASTM Standards. American Association State Highway and Transportation Officials Standard AASHTO No.: M 31: West Conshohocken, PA, USA, 2018.
- ASTM Designation D695-15; Standard Test Method for Compressive Properties of Rigid Plastics. Annual Book of ASTM Standards. American International: West Conshohocken, PA, USA, 2015.
- European Standard EN ISO 527-4; Determination of Tensile Properties of Plastics. Part 4: Test Conditions for Isotropic and Orthotropic Fiber-Reinforced Plastic Composites, No. 1109a. International Organization for Standardization: Geneva, Switzerland, 2021.
- Yuan, J. Flexural Behavior of Composite Beams Reinforced with GFRP I-Section. Ph.D. Thesis, School of Civil, Mining and Environmental Engineering, University of Wollongong, Wollongong, Australia, 2017. [Google Scholar]
- Abaqus, A. Computer Software for Finite Element Analysis; Dassault Systems Simulia: Johnston, RI, USA, 2017. [Google Scholar]
- Ibrahim, T.H.; Allawi, A.A.; El-Zohairy, A. Experimental and FE Analysis of Composite RC Beams with Encased Pultruded GFRP I-Beam under Static Loads. J. Adv. Struct. Eng. 2022; in press. [Google Scholar]
- Nunes, F.; Silvestre, N.; Correia, J.R. Progressive Damage Analysis of Web Crippling of GFRP Pultruded I-Sections. J. Compos. Constr. 2016, 21, 04016104. [Google Scholar] [CrossRef]
- ACI 318-19. Building Code Requirements for Structural Concrete (ACI 318-19) Commentary on Building; Code Requirements for Structural Concrete (ACI 318R-19); American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]
- Earij, A.; Alfano, G.; Cashell, K.; Zhou, X. Nonlinear three–dimensional finite–element modeling of reinforced–concrete beams: Computational challenges and experimental validation. Eng. Fail. Anal. 2017, 82, 92–115. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Chern, J.G.; You, C.M. Deformation of Progressively Cracking Partially Prestressed Concrete Beams. PCI J. 1992, 37, 74–85. [Google Scholar] [CrossRef] [Green Version]
- Hashin, Z. Failure criteria for unidirectional fiber composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Almeida-Fernandes, L.; Silvestre, N.; Correia, J.R.; Arruda, M. Compressive transverse fracture behaviour of pultruded GFRP materials: Experimental study and numerical calibration. Compos. Struct. 2020, 247, 112453. [Google Scholar] [CrossRef]
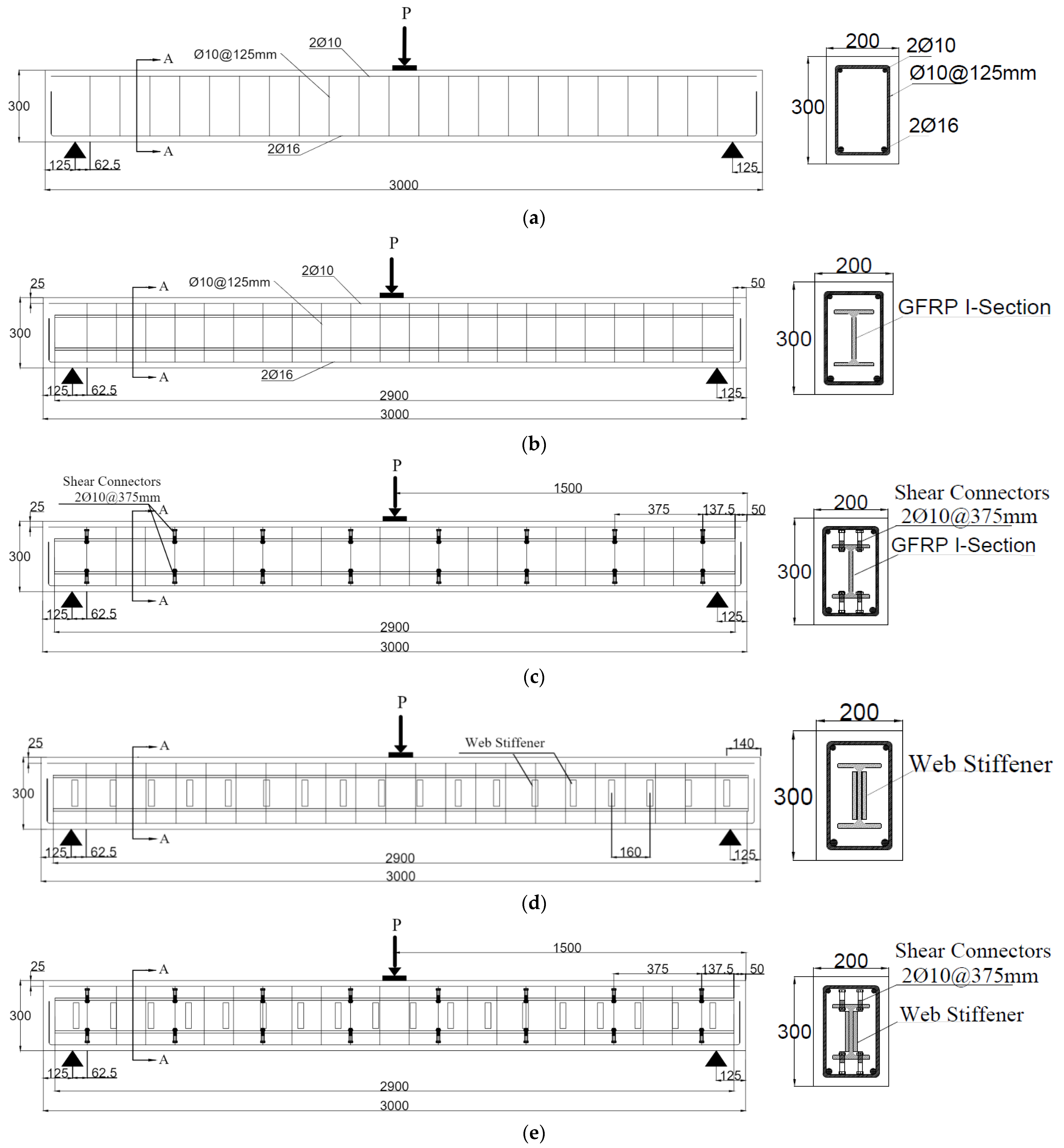







| Specimen Encoding | GFRP I-Section | Shear Connectors | Web Stiffeners |
|---|---|---|---|
| Ref | - | - | - |
| EG | - | - | |
| EGS | - | ||
| EGW | - | ||
| EGSW |
| Cement (kg/m3) | Fine Aggregate (kg/m3) | Coarse Aggregate (kg/m3) | Water (kg/m3) | Admixture (kg/m3) | |
|---|---|---|---|---|---|
| Amount | 475 | 880 | 910 | 165 | 15.25 |
| Mechanical Properties | Value (MPa) | Geometrical Properties | Value |
|---|---|---|---|
| Transverse Compressive Strength | 118.3 | Area | 3300 mm2 |
| Longitudinal Compressive Strength | 326.14 | Perimeter | 680 mm |
| Longitudinal Tensile Strength | 347.5 | Moment of inertia | 11,647,500 mm4 |
| Longitudinal Modulus of elasticity | 27,100 | Mass | 5.94 kg/m |
| Transverse Modules of elasticity | 6800 | Web and flange thickness | 10 mm |
| Specimens | Initial Crack Load (kN) | % Change | Ultimate Load (kN) | % Change | Central Displacement (mm) | % Change |
|---|---|---|---|---|---|---|
| Ref | 19.93 | - | 100.46 | - | 32.80 | - |
| EG | 20.24 | +1.5 | 159.04 | +58.3 | 33.07 | +0.8 |
| EGS | 19.73 | −1.0 | 201.54 | +100.6 | 48.68 | +48.4 |
| EGW | 20.12 | 0.9 | 198.24 | +97.3 | 38.96 | +18.8 |
| EGSW | 22.26 | +11.7 | 231.88 | +130.8 | 52.56 | +60.2 |
| Specimens | Strain in Concrete ε1 (mm/mm) | Change (%) | Strain in Compression Reinforcement ε2 (mm/mm) | Change (%) | Strain in Tensile Reinforcement ε3 (mm/mm) | Change (%) |
|---|---|---|---|---|---|---|
| Ref | 0.0015 | - | 0.001 | - | 0.008 | - |
| EG | 0.0023 | 53 | 0.0055 | 450 | 0.0116 | 45 |
| EGS | 0.0032 | 116 | 0.0065 | 550 | 0.0115 | 44 |
| EGW | 0.0025 | 68 | 0.00615 | 515 | 0.0145 | 81 |
| EGSW | 0.0028 | 85 | 0.00588 | 488 | 0.011 | 38 |
| Specimen | Slope S1 | Slope S2 | Slope S | Total Energy ET (kN·mm) | Elastic Energy EE (kN·mm) | Ductility μE | % Change |
|---|---|---|---|---|---|---|---|
| Ref | 6.1 | 0.9 | 5.1 | 5443 | 900 | 3.52 | - |
| EG | 6.3 | 0.9 | 6.1 | 11,933 | 1576 | 4.28 | 21.6 |
| EGS | 6.8 | 1 | 6.1 | 16,344 | 852 | 10.05 | 185.5 |
| EGW | 6.7 | 1.6 | 6.3 | 12,962 | 895 | 7.74 | 119.8 |
| EGSW | 7.6 | 0.4 | 7.4 | 17,397 | 1154 | 8.04 | 128.4 |
| Mechanical Properties Data | Value (N/mm) |
|---|---|
| Longitudinal tensile fracture energy | 4.76 |
| Longitudinal compressive fracture energy | 0.375 |
| Transverse tensile fracture energy | 5 |
| Transverse compressive fracture energy | 0.55 |
| Beam | Exp. Results | FE Results | Change (%) | |||
|---|---|---|---|---|---|---|
| Ultimate Load Pu (kN) | Max. Disp. (mm) | Ultimate Load Pu (kN) | Max. Disp. (mm) | Ultimate Load | Max. Disp. | |
| Ref | 100.46 | 63 | 104.24 | 64.11 | 3.7 | 1.76 |
| EG | 159.04 | 91 | 162.51 | 93.19 | 2.18 | 2.4 |
| EGS | 201.55 | 115 | 206.02 | 120.12 | 2.22 | 4.45 |
| EGW | 198.24 | 100 | 206.67 | 102.24 | 4.25 | 2.24 |
| EGSW | 231.88 | 90 | 233.96 | 94.07 | 0.90 | 4.52 |
| Beams | Compressive Strength (MPa) | Peak Load Pu (kN) | Deflection at Peak Load (mm) | Increase in Load (%) | Reduction in Deflection (%) |
|---|---|---|---|---|---|
| 45 | 100.46 | 18.32 | - | - | |
| Ref | 53.8 | 104.24 | 16.56 | 3.76 | 9.61 |
| 65 | 112.43 | 15.33 | 11.92 | 16.32 | |
| 45 | 130.23 | 26.38 | - | - | |
| EG | 53.8 | 162.51 | 23.70 | 24.78 | 10.38 |
| 65 | 172.32 | 18.41 | 32.32 | 43.29 | |
| 45 | 171.47 | 42.38 | - | - | |
| EGS | 53.8 | 206.02 | 40.59 | 20.15 | 4.22 |
| 65 | 225.03 | 31.05 | 31.24 | 26.73 | |
| 45 | 174.33 | 40.25 | - | - | |
| EGW | 58.3 | 206.67 | 31.14 | 18.55 | 22.63 |
| 65 | 221.27 | 27.39 | 26.93 | 31.95 | |
| 45 | 195.88 | 27.51 | - | - | |
| EGSW | 53.8 | 233.96 | 25.37 | 19.44 | 7.78 |
| 65 | 258.23 | 19.08 | 31.83 | 30.64 |
| Beam | Tensile Strength of GFRP (MPa) | Peak Load Pu (kN) | Deflection at Peak Load (mm) | Increase in Peak Load (%) | Increasing in Deflection (%) |
|---|---|---|---|---|---|
| 258 | 153.9 | 21.23 | - | - | |
| EG | 347.5 | 162.51 | 23.70 | 5.59 | 11.63 |
| 416 | 175.59 | 24.83 | 14.09 | 16.96 | |
| 258 | 187.43 | 28.38 | - | - | |
| EGS | 347.5 | 206.02 | 40.59 | 9.92 | 43.02 |
| 416 | 217.81 | 41.50 | 16.21 | 46.23 | |
| 258 | 174.05 | 27.97 | - | - | |
| EGW | 347.5 | 206.67 | 31.14 | 18.74 | 11.33 |
| 416 | 218.27 | 40.32 | 25.41 | 44.15 | |
| 258 | 197.33 | 19.75 | - | - | |
| EGSW | 347.5 | 233.96 | 25.37 | 18.56 | 28.45 |
| 416 | 251.43 | 26.40 | 27.42 | 33.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmood, E.M.; Allawi, A.A.; El-Zohairy, A. Flexural Performance of Encased Pultruded GFRP I-Beam with High Strength Concrete under Static Loading. Materials 2022, 15, 4519. https://doi.org/10.3390/ma15134519
Mahmood EM, Allawi AA, El-Zohairy A. Flexural Performance of Encased Pultruded GFRP I-Beam with High Strength Concrete under Static Loading. Materials. 2022; 15(13):4519. https://doi.org/10.3390/ma15134519
Chicago/Turabian StyleMahmood, Enas M., Abbas A. Allawi, and Ayman El-Zohairy. 2022. "Flexural Performance of Encased Pultruded GFRP I-Beam with High Strength Concrete under Static Loading" Materials 15, no. 13: 4519. https://doi.org/10.3390/ma15134519
APA StyleMahmood, E. M., Allawi, A. A., & El-Zohairy, A. (2022). Flexural Performance of Encased Pultruded GFRP I-Beam with High Strength Concrete under Static Loading. Materials, 15(13), 4519. https://doi.org/10.3390/ma15134519








