An Energy-Based Method for Lifetime Assessment on High-Strength-Steel Welded Joints under Different Pre-Strain Levels
Abstract
1. Introduction
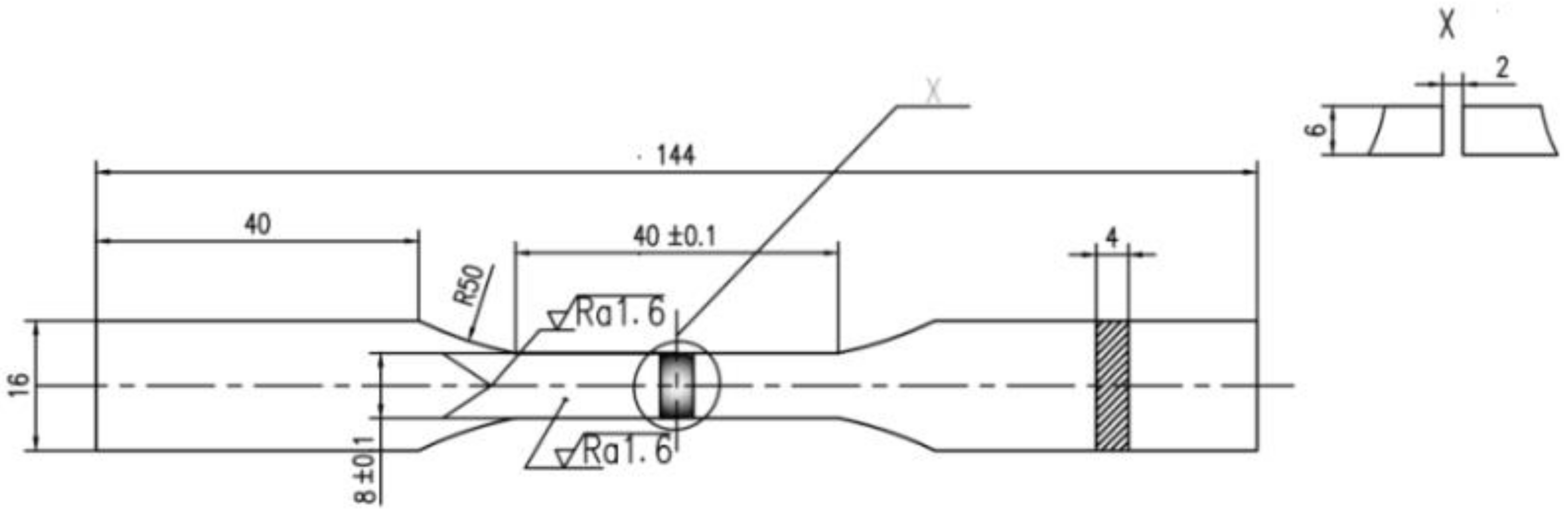
2. Experimental Work
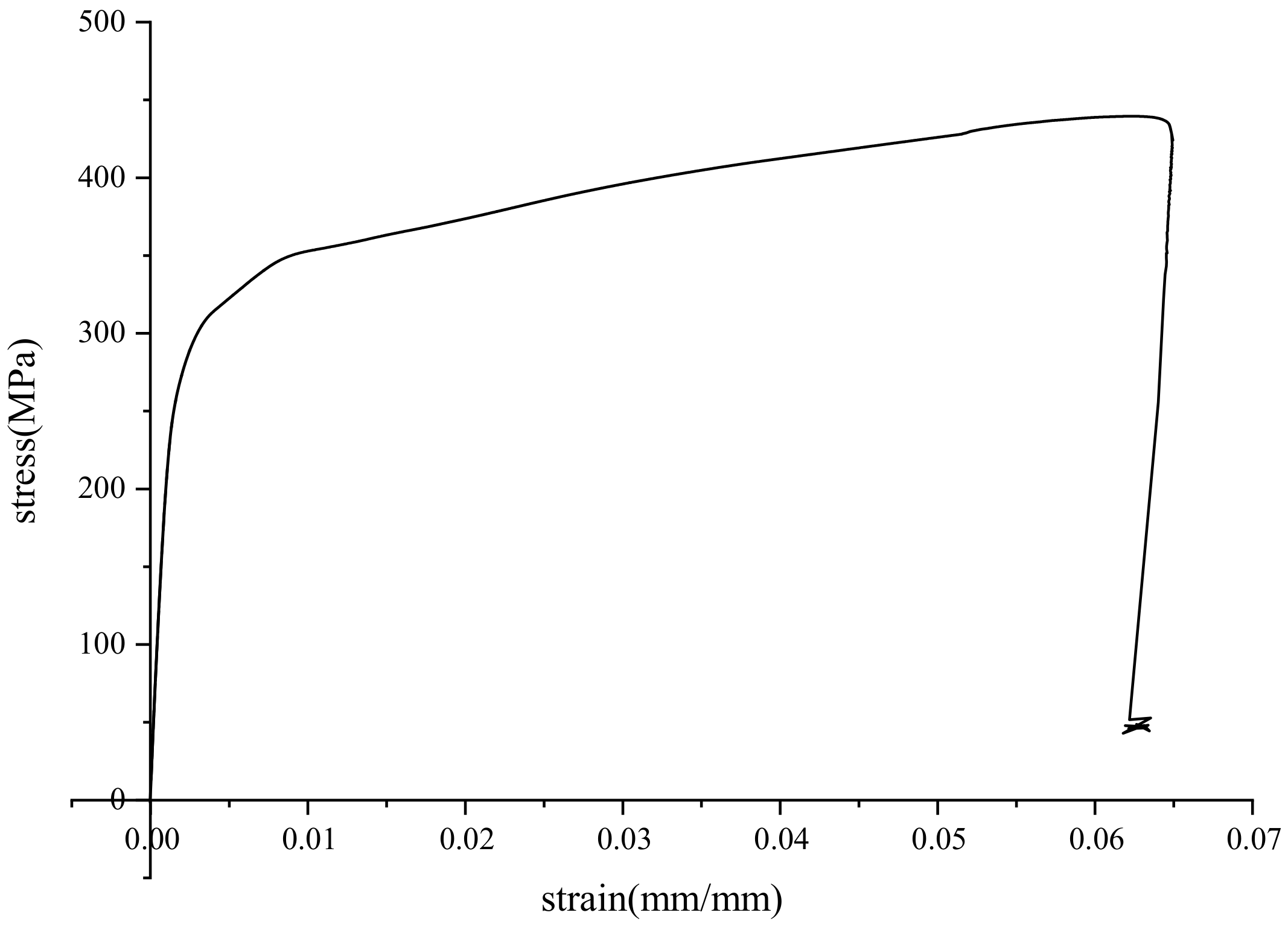
2.1. Tensile Test
2.2. Fatigue Test
3. Results and Discussion
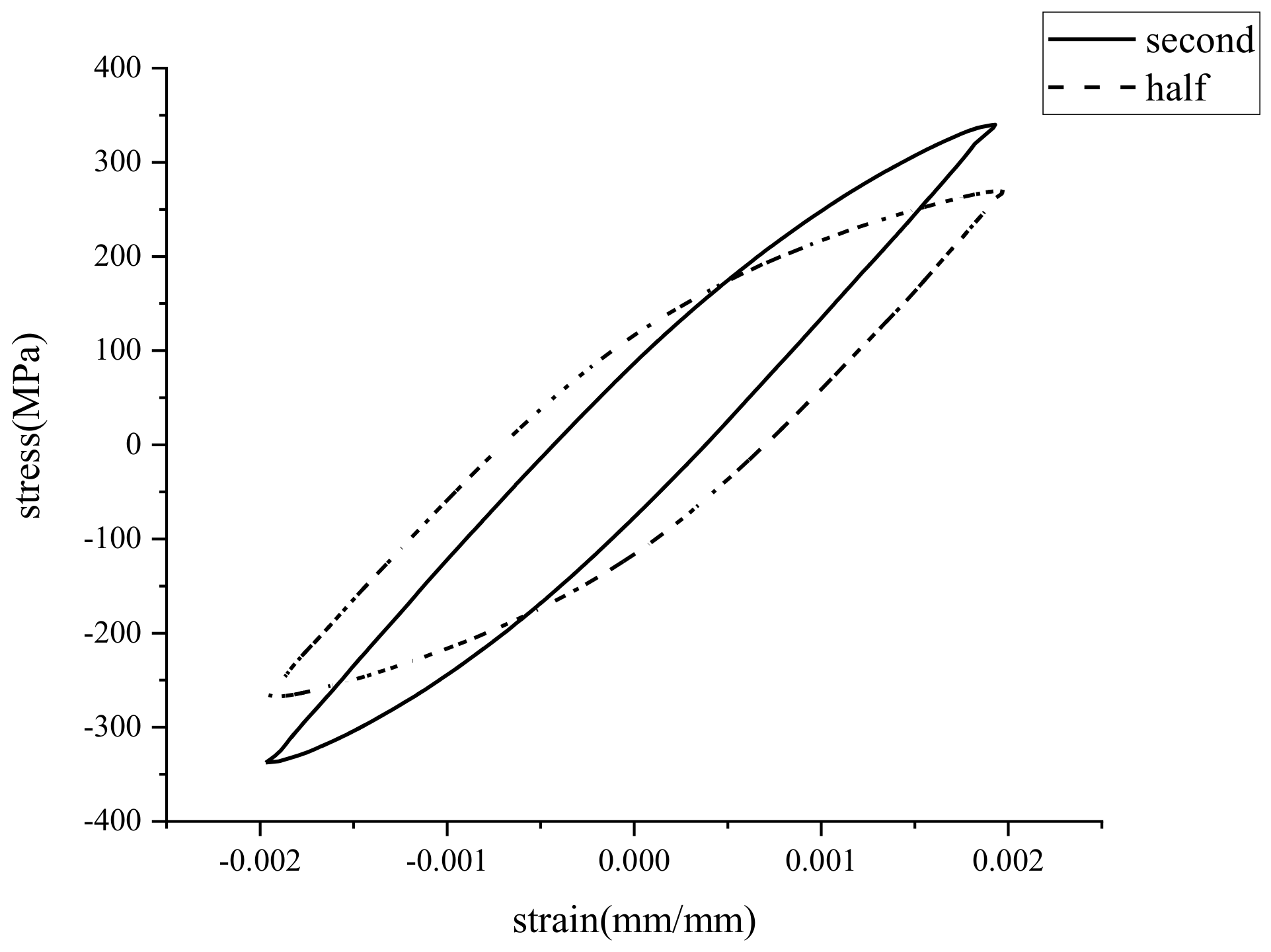
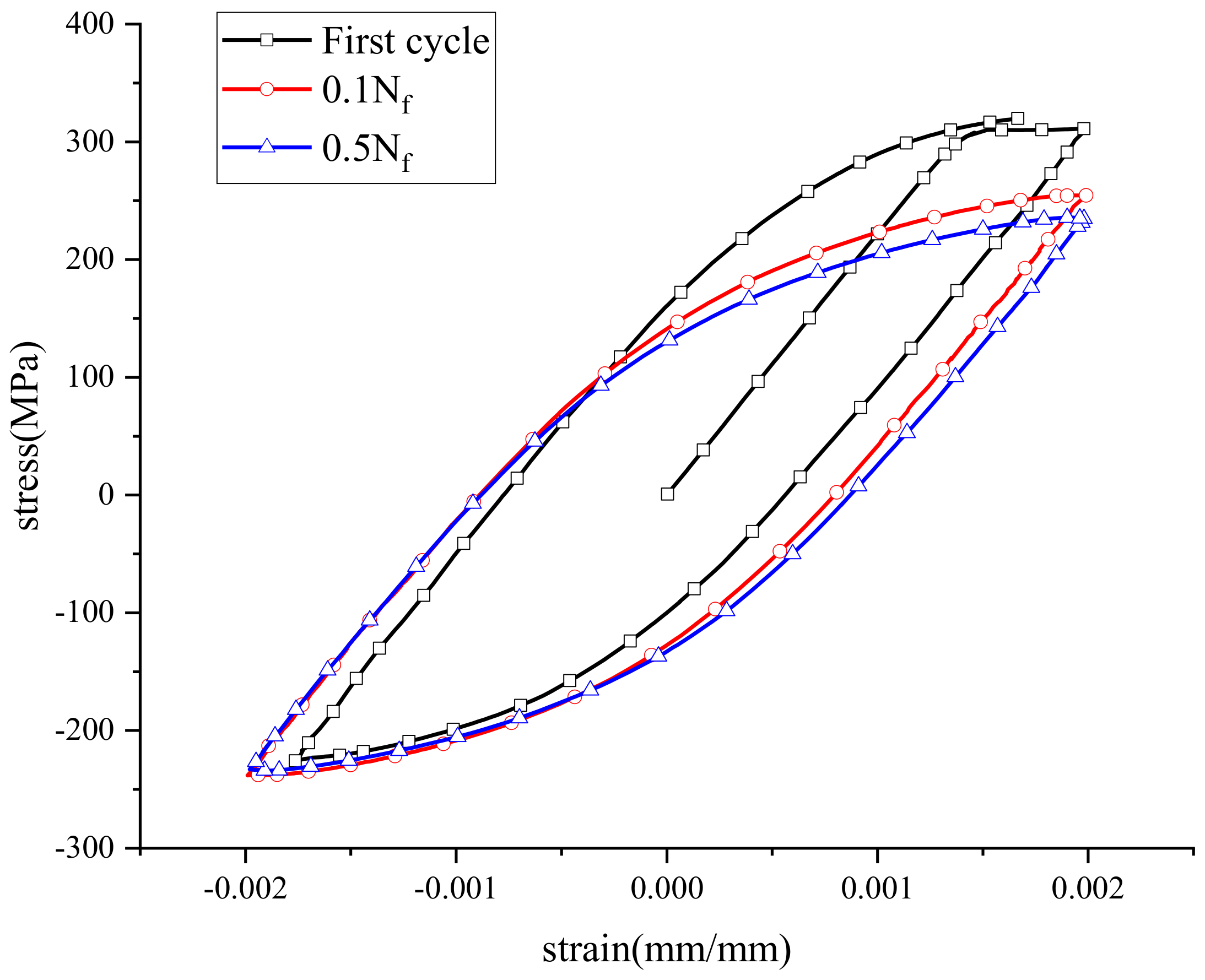
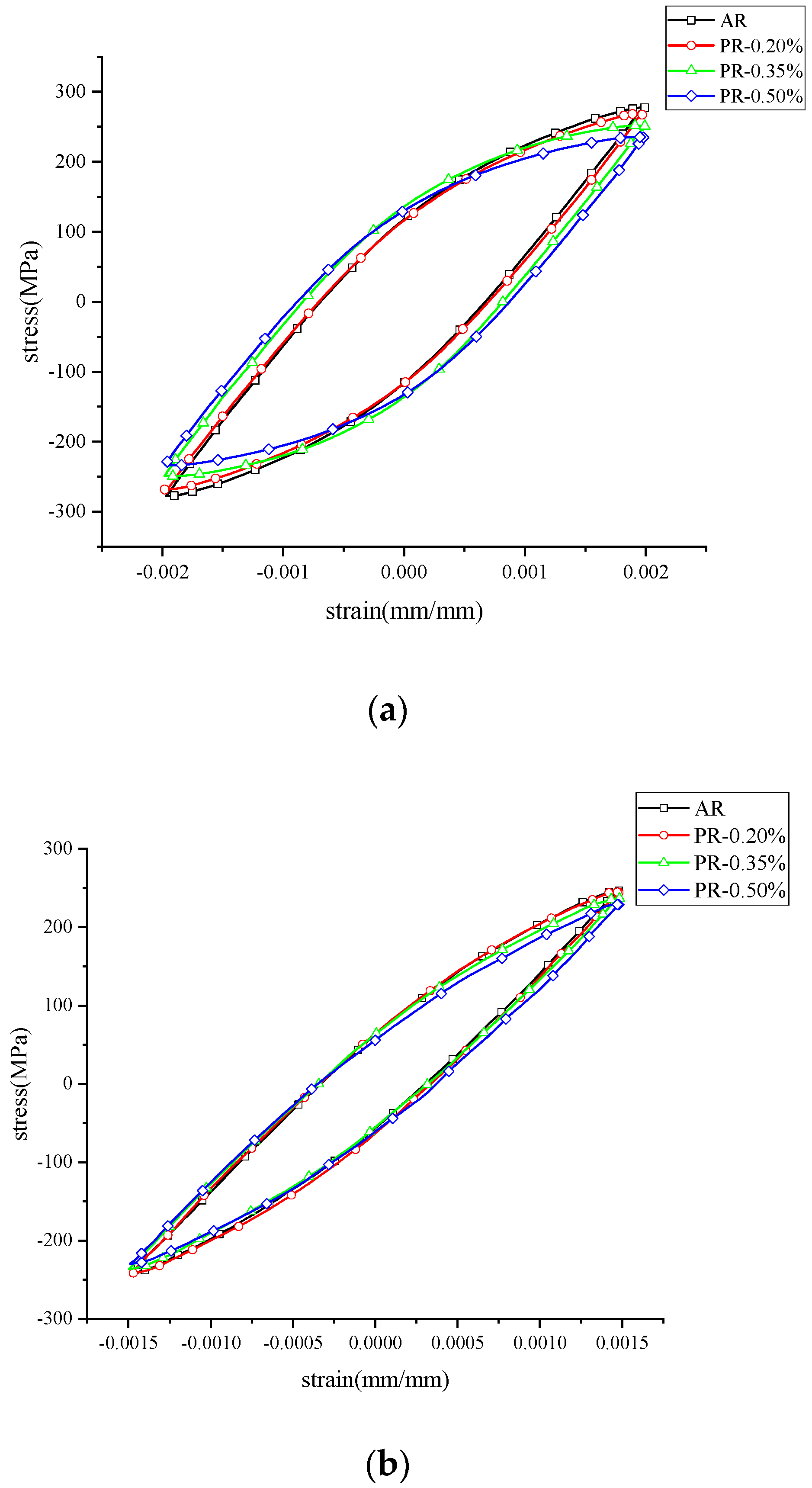
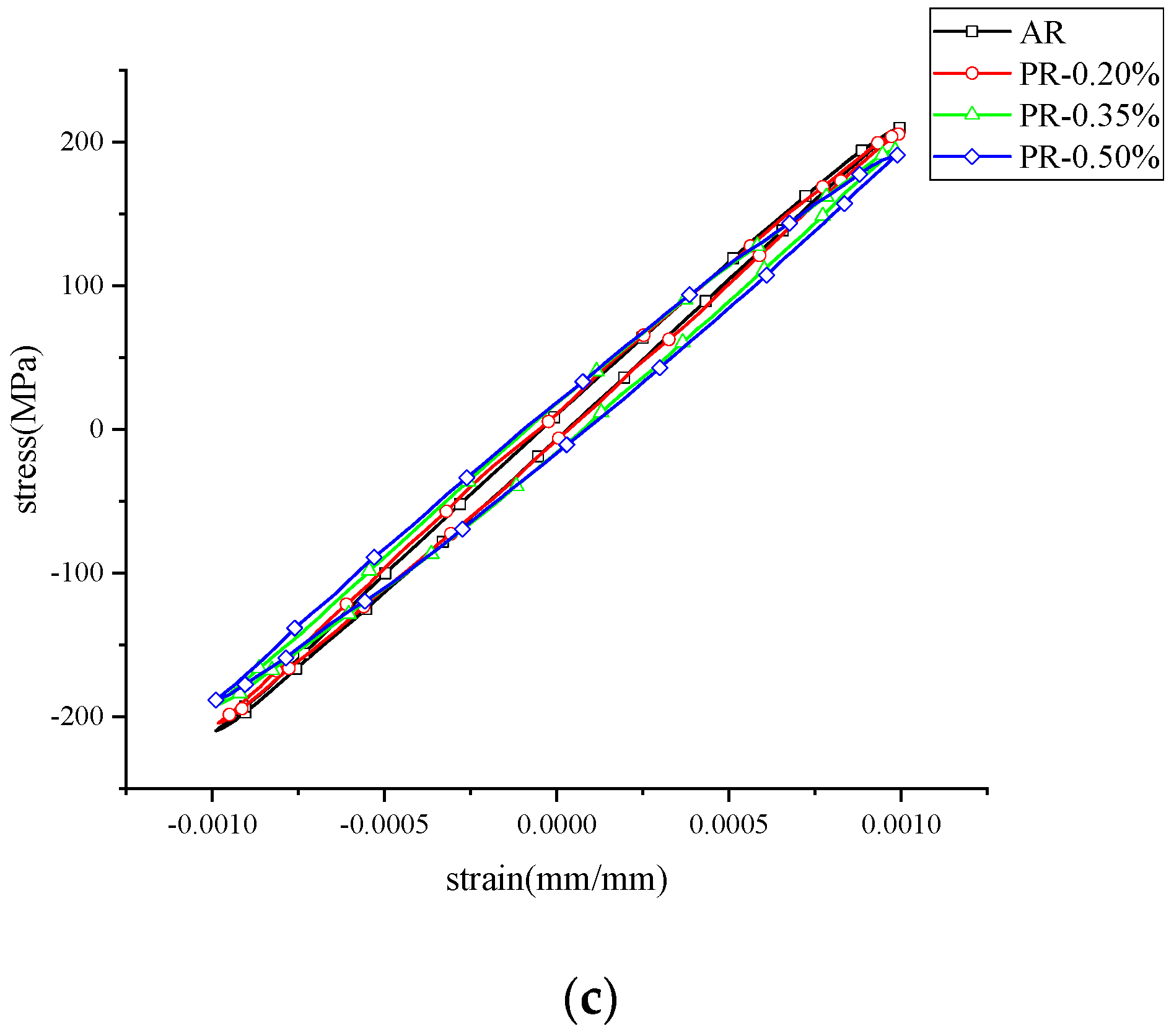
3.1. Effect of Pre-Strain on Fatigue Behavior
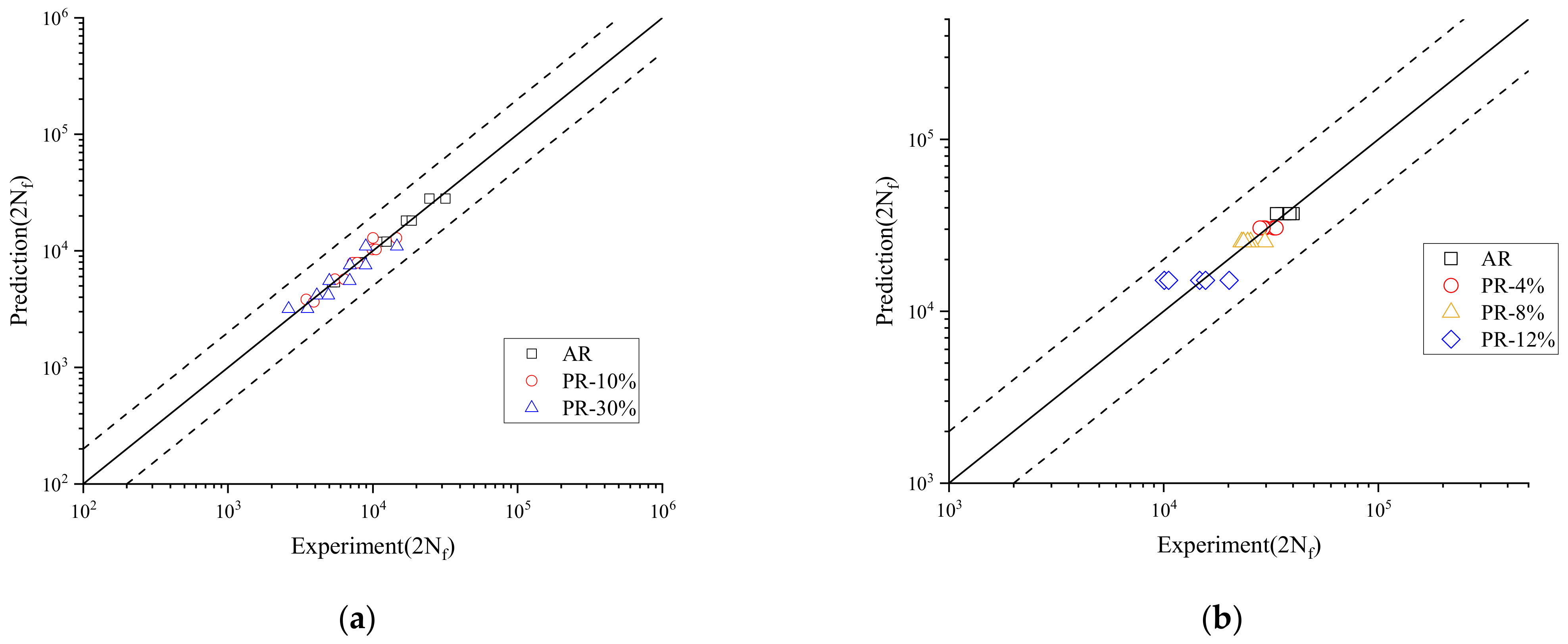
3.2. Fatigue Life Prediction of Welded Joints under Pre-Strain
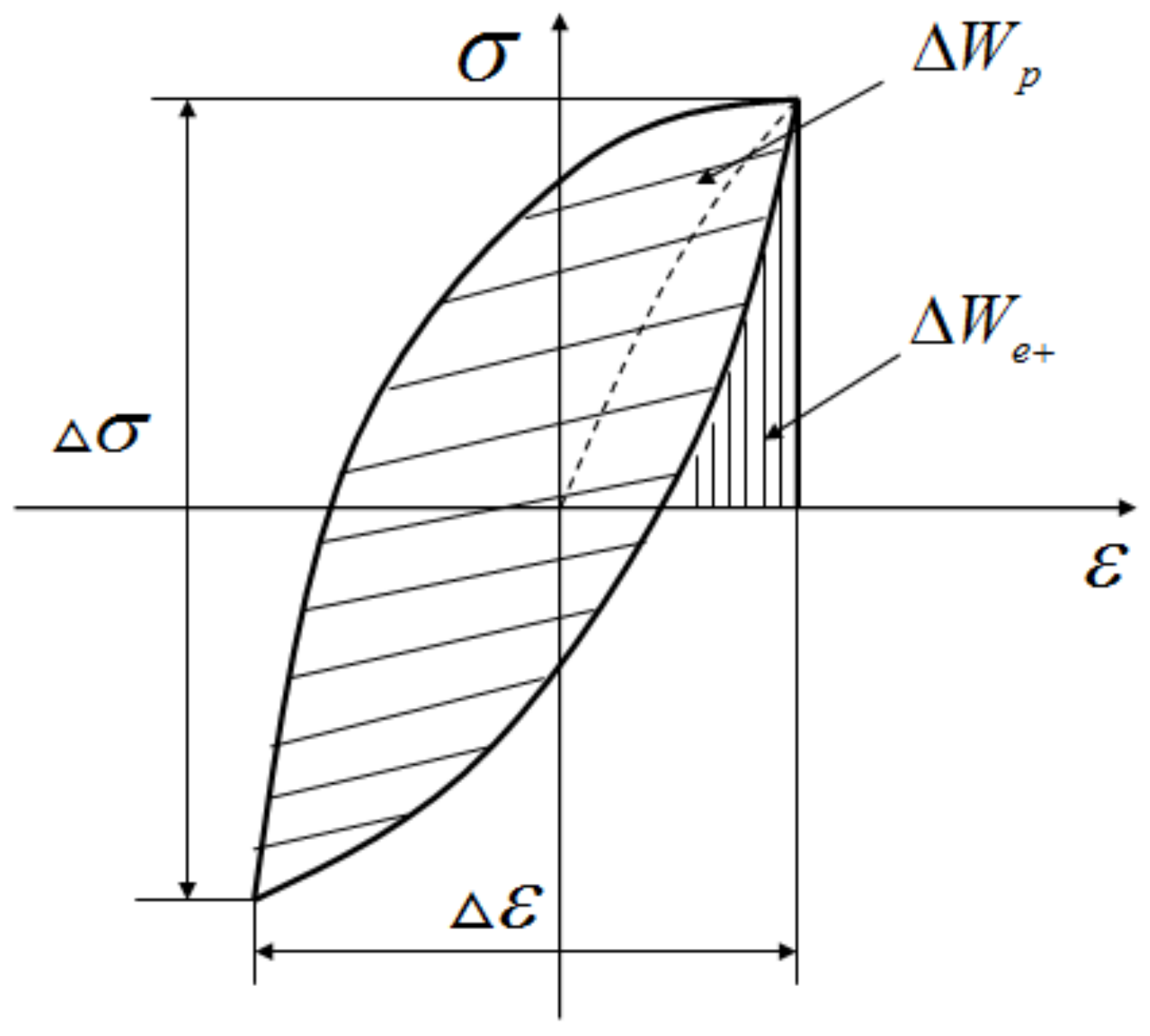
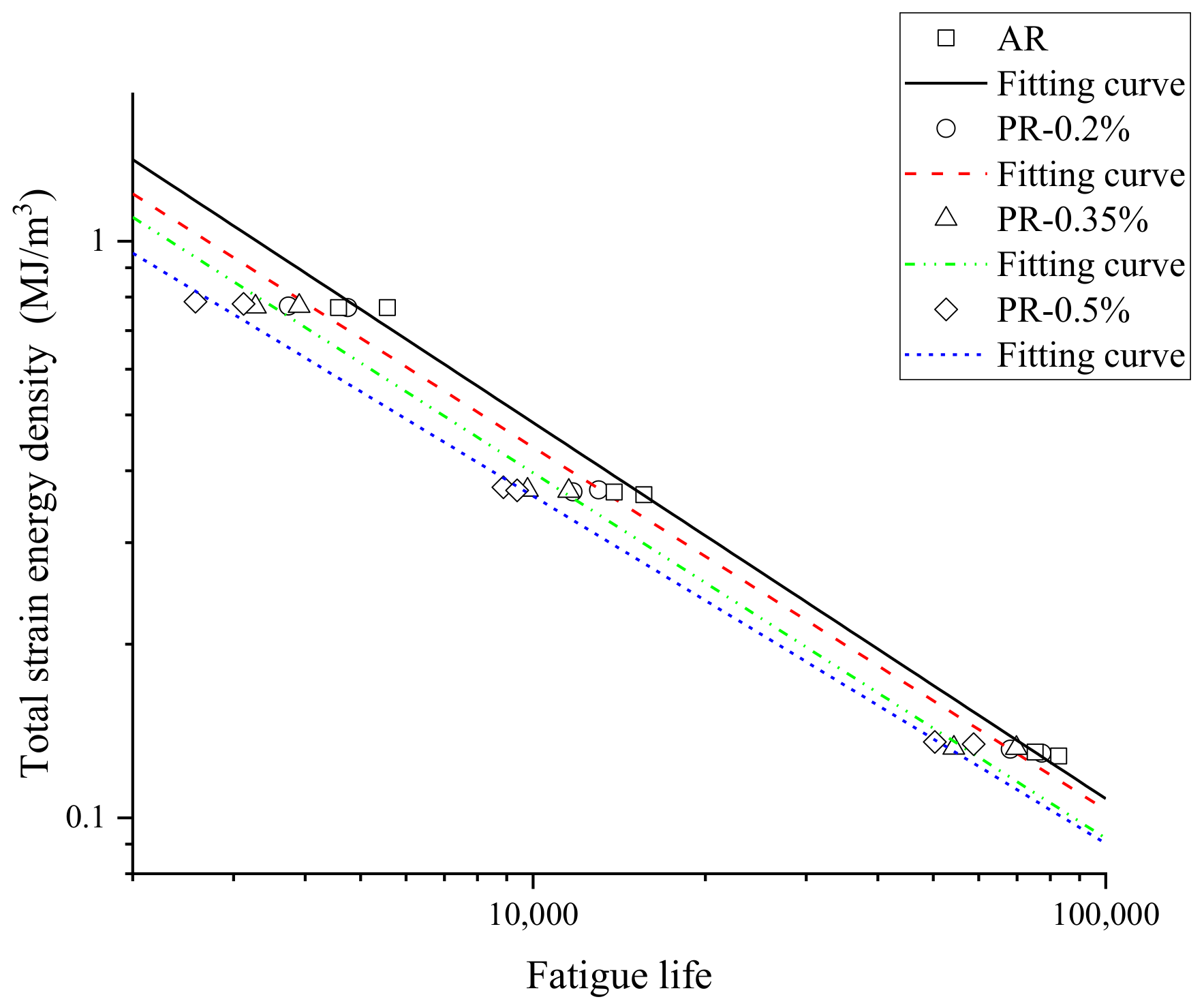
3.2.1. Strain Energy Density Method
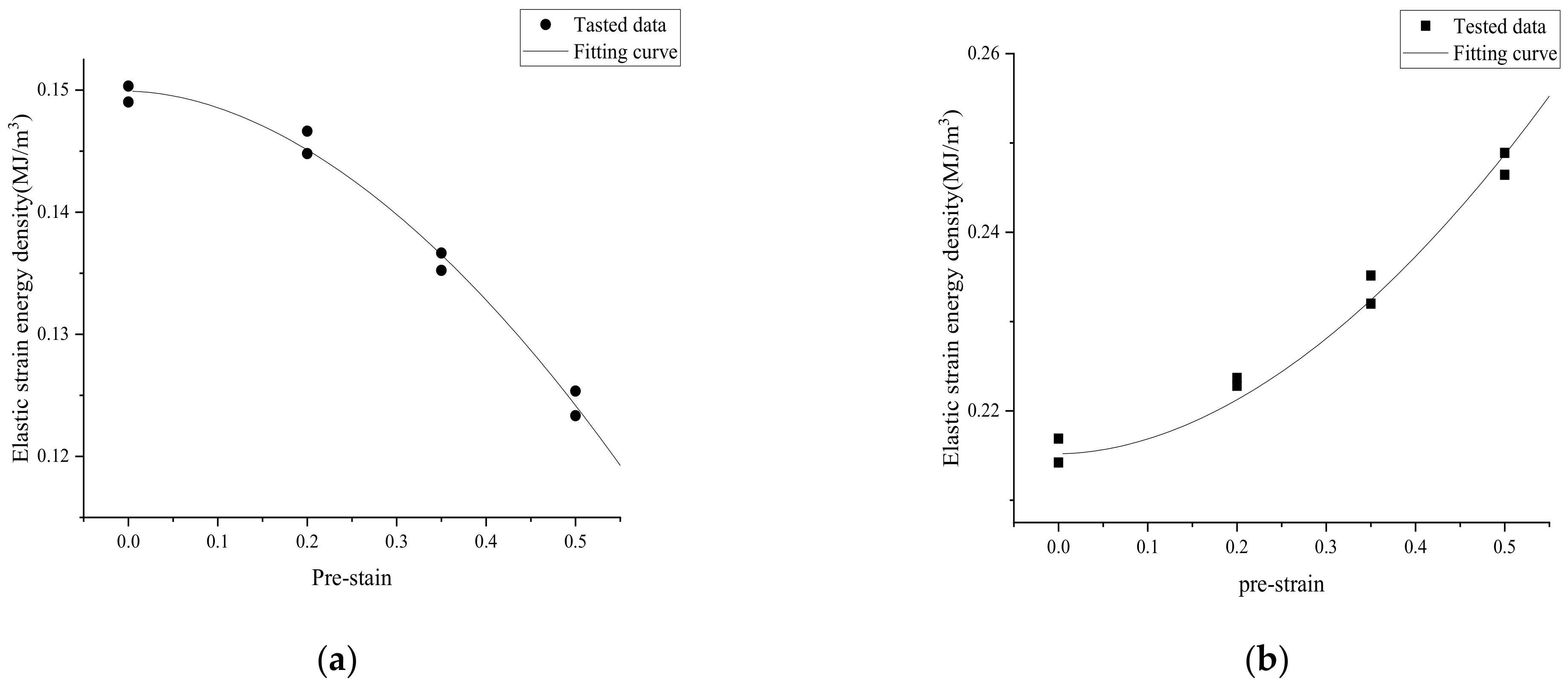
3.2.2. Strain Energy Density Method under Pre-Strain
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Lin, Y.; Zhou, H.; Zhang, Y.; Shi, Y. Progress in the brittle fracture and fatigue of high-strength steels and their welds. Prog. Steel Build. Struct. 2012, 14, 21–28. [Google Scholar]
- Xu, F.; Yang, L.; Zhang, Y.; Jiang, W.; Xiong, Y.; Liu, P. Effects of pre-strain on microstructure, texture and mechanical properties of HSLA. J. Plast. Eng. 2020, 27, 103–109. [Google Scholar]
- Li, J.; Zhang, P.; Lu, L.; Lv, F.; Miao, X.; Chang, L.; Zhou, B.; He, X.; Zhou, C. Effect of pre-strain on fatigue crack growth behavior for commercial pure titanium at ambient temperature. Int. J. Fatigue 2018, 117, 27–38. [Google Scholar] [CrossRef]
- Xiao, G.; Jing, H.; Xu, L.; Ji, J.; Li, W. Research on fracture toughness of high-strength structural steel with prestrain at low temperature. Trans. China Weld. Inst. 2011, 32, 41–44. [Google Scholar]
- Chang, L.; Ma, T.; Wen, J.; Zhou, B.; Li, J.; He, X.; Zhou, C. The distinct influences of pre-strain on low cycle fatigue behavior of CP-Ti along rolling direction at different strain amplitudes. Mater. Sci. Eng. A 2019, 763, 235–247. [Google Scholar] [CrossRef]
- Belattar, A.; Keller, C.; Taleb, L. Multiscale analysis of the pre-hardening effect on the cyclic behavior and fatigue life of 304L stainless steel. Mater. Sci. Eng. A 2016, 662, 468–480. [Google Scholar] [CrossRef]
- Marnier, G.; Keller, C.; Taleb, L. Fatigue of OFHC pure copper and 316L stainless steel subjected to prior tensile and cyclic prestrains. Int. J. Fatigue 2016, 91, 204–219. [Google Scholar] [CrossRef]
- Julie, C.; Ali, F.; Said, T. Fatigue behavior of stainless steel 304L including strain hardening, prestraining, and mean stress effects. J. Eng. Mater. Technol. 2010, 132, 021008. [Google Scholar]
- Branco, R.; Costa, J.D.; Borrego, L.P.; Wu, S.C.; Long, X.Y.; Antunes, F.V. Effect of tensile pre-strain on low-cycle fatigue behaviour of 7050-T6 aluminium alloy. Eng. Fail. Anal. 2020, 114, 104592. [Google Scholar] [CrossRef]
- Kariya, M.; Hatano, K.; Horibe, S. Influence of compressive pre-strain on tensile fatigue in two types of aluminum alloys. J. Mater. Eng. Perform. 2010, 19, 1205–1207. [Google Scholar] [CrossRef]
- Al-Rubaie, K.S.; Marcio, A.; Dilermando, N.; Katia, R. Effect of pre-strain on the fatigue life of 7050–T7451 aluminium alloy. Mater. Sci. Eng. A 2007, 464, 141–150. [Google Scholar] [CrossRef]
- Ghosal, P.; Paul, S.K.; Das, B.; Chinara, M.; Arora, K.S. Notch fatigue performance of DP600 steel under different pre-straining paths. Theor. Appl. Fract. Mech. 2020, 108, 102630. [Google Scholar] [CrossRef]
- Slota, J.; Jurcisin, M.; Tomas, M.; Spisak, E. Cyclic test of DP600 steel under tension-compression load for different pre-strain levels. Key Eng. Mater. 2015, 635, 71–74. [Google Scholar] [CrossRef]
- Das, B.; Singh, A.; Paul, S.K. Low cycle fatigue performance of DP600 steel under various pre-straining paths. Int. J. Fatigue 2020, 132, 265–277. [Google Scholar] [CrossRef]
- Das, B.; Singh, A.; Arora, K.S.; Shome, M.; Paul, S.K. Influence of pre-straining path on high cycle fatigue performance of DP 600 steel. Int. J. Fatigue 2019, 126, 369–380. [Google Scholar] [CrossRef]
- Wu, Y. Effect of Pre-Strain on the Fatigue Behavior of Extruded AZ31 Alloys. IOP Conf. Ser. Mater. Sci. Eng. 2017, 230, 012005. [Google Scholar] [CrossRef]
- Park, S.H.; Hong, S.G.; Lee, J.H.; Kim, S.H.; Cho, Y.R.; Yoon, J.; Lee, C.S. Effects of pre-tension on fatigue behavior of rolled magnesium alloy. Mater. Sci. Eng. A 2017, 680, 351–358. [Google Scholar] [CrossRef]
- Ozaki, J.; Yosida, M.; Horibe, S. The effect of pre-compressive strain on the fatigue life of the AZ31 magnesium alloy. Mater. Sci. Eng. A 2014, 604, 192–195. [Google Scholar] [CrossRef]
- White, B.C.; White, R.E.; Jordon, J.B.; Allison, P.G.; Rushing, T.; Garcia, L. The effect of tensile pre-straining on fatigue crack initiation mechanisms and mechanical behavior of AA7050 friction stir welds. Mater. Sci. Eng. A 2018, 763, 228–238. [Google Scholar] [CrossRef]
- Jia, D.; Wang, Y.; Cui, J.; Liao, X.; Gu, H. Experimental research on fatigue performance and fracture mechanism of Q345QD butt welds. Ind. Constr. 2017, 47, 175–180. [Google Scholar]
- An, G.; Park, J.U.; Ohata, M.; Minami, F. Pre-strain effect of on fracture performance of high-strength steel welds. J. Mech. Sci. Technol. 2018, 32, 3145–3151. [Google Scholar] [CrossRef]
- Al-Rubaie, K.S.; Barroso, E.K.L.; Godefroid, L.B. Fatigue crack growth analysis of pre-strained 7475-T7351 aluminum alloy. Int. J. Fatigue 2005, 28, 934–942. [Google Scholar] [CrossRef]
- Al-Rubaie, K.S.; Barroso, E.K.L.; Godefroid, L.B. Statistical modeling of fatigue crack growth rate in pre-strained 7475-T7351 aluminum alloy. Mater. Sci. Eng. A 2007, 486, 585–595. [Google Scholar] [CrossRef][Green Version]
- Le, Q.; Kang, H.; Kridli, G.; Khosrovaneh, A.; Yan, B. Modified strain-life equation to consider the effect of different prestrain paths for dual phase sheet steel. J. Mater. Process. Technol. 2008, 209, 3525–3531. [Google Scholar] [CrossRef]
- Chang, L.; Ma, T.; Zhou, B.; Wen, J.; He, X.; Zhou, C. Comprehensive investigation of fatigue behavior and a new strain-life model for CP-Ti under different loading conditions. Int. J. Fatigue 2019, 129, 105220. [Google Scholar] [CrossRef]
- An, G.; Park, J.; Ohata, M.; Minami, F. Fracture assessment of weld joints of high-strength steel in pre-strained condition. Appl. Sci. 2019, 9, 1306. [Google Scholar] [CrossRef]
- Xu, K.; Qiao, G.; Wang, J.; Li, H.; Xiao, F. Effect of plastic pre-strain on the fatigue properties of welded joints of X80 LSAW pipes. Int. J. Fatigue 2020, 139, 105788. [Google Scholar] [CrossRef]
- Jin, X.; Ji, S.; Liu, C.; Shi, S.; Chen, X. Comparison of low cycle fatigue behavior of 304 stainless steels induced by tensile and torsional pre-strain. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 2247–2258. [Google Scholar] [CrossRef]
- Wu, H.; Hamada, S.; Noguchi, H. Pre-strain effect on fatigue strength characteristics of SUH660 plain specimens. Int. J. Fatigue 2013, 55, 291–298. [Google Scholar] [CrossRef]
- Song, S.; Lee, J.; Lee, T.; Lee, C. Effect of the amount and temperature of pre-strain on tensile and low-cycle fatigue properties of Fe-17Mn-0.5C TRIP/TWIP steel. Mater. Sci. Eng. A 2017, 696, 493–502. [Google Scholar] [CrossRef]
- Gao, L.; Sun, C.; Zhuang, M.; Hou, M. Fatigue life prediction of HTRB630E steel bars based on modified coffin-manson model under pre-strain. Structures 2022, 38, 28–39. [Google Scholar] [CrossRef]
- Kim, Y.W.; Kim, G.; Hong, S.G.; Lee, C.S. Energy-based approach to predict the fatigue life behavior of pre-strained Fe–18Mn TWIP steel. Mater. Sci. Eng. A 2011, 528, 4696–4702. [Google Scholar] [CrossRef]
- You, X.; Liu, Y.; Cui, S.; Wang, R.; Wang, Q. Low cycle fatigue behaviors of Q345B steel and welded joint. J. Sichuan Univ. (Eng. Sci. Ed.) 2015, 47, 112–117. [Google Scholar]
- Peng, J.; Li, K.; Dai, Q. Mechanical properties of pre-strained austenitic stainless steel from the view of energy density. Results Phys. 2018, 10, 187–193. [Google Scholar] [CrossRef]
- Mi, C.; Gu, Z.; Jian, H.; Zhang, Y.; Li, W.; Yu, B. Frame weldment fatigue life prediction of electric dump trucks based on modified strain energy density method. China Mech. Eng. 2019, 30, 96–104. [Google Scholar]
- Sun, H.; Wei, K.; Yang, X.; Xiao, Z.; Wu, Y. Effects of pre-strain and annealing on the fatigue properties of complex phase steel CP800. Int. J. Fatigue 2020, 131, 105364. [Google Scholar] [CrossRef]



| C | Si | Mn | P | S | Al | Fe | |
|---|---|---|---|---|---|---|---|
| Q345 | 0.16 | 0.30 | 1.23 | 0.015 | 0.003 | 0.035 | Bal. |
| Material Properties | Welded Joint | Q345 |
|---|---|---|
| Elastic modulus (GPa) | 205.4 | 209.5 |
| Yield strength (MPa) | 325.1 | 351.9 |
| Tensile strength (MPa) | 440.6 | 512.8 |
| Poisson’s ratio | 0.28 | 0.29 |
| Strain Amplitude | Number of Specimens | Elastic Strain Energy Density (MJ/m3) | Plastic Strain Energy Density (MJ/m3) | Total Strain Energy Density (MJ/m3) | Fatigue Life (Cycle) |
|---|---|---|---|---|---|
| 0.2% | 4 | 0.18757 | 0.57942 | 0.766996 | 4578 |
| 6 | 0.18603 | 0.58115 | 0.767188 | 5570 | |
| 17 | 0.181211 | 0.59079 | 0.772001 | 3744 | |
| 19 | 0.179952 | 0.58701 | 0.766962 | 4746 | |
| 32 | 0.169569 | 0.6021 | 0.771669 | 3907 | |
| 34 | 0.171722 | 0.59772 | 0.769442 | 3276 | |
| 47 | 0.161759 | 0.62347 | 0.785229 | 2573 | |
| 51 | 0.160656 | 0.61795 | 0.778606 | 3124 | |
| 0.15% | 8 | 0.149018 | 0.21422 | 0.363238 | 15623 |
| 10 | 0.150322 | 0.21689 | 0.367212 | 13,863 | |
| 22 | 0.146631 | 0.22368 | 0.370311 | 13,027 | |
| 28 | 0.144796 | 0.22281 | 0.367606 | 11,744 | |
| 33 | 0.13665 | 0.23201 | 0.36866 | 11,548 | |
| 38 | 0.135235 | 0.23516 | 0.370395 | 9780 | |
| 45 | 0.125347 | 0.24888 | 0.374227 | 8879 | |
| 55 | 0.123323 | 0.24643 | 0.369753 | 9380 | |
| 0.1% | 11 | 0.107484 | 0.02254 | 0.130024 | 75,328 |
| 14 | 0.106637 | 0.02135 | 0.127987 | 82,798 | |
| 29 | 0.10293 | 0.02649 | 0.12942 | 77,326 | |
| 31 | 0.103823 | 0.02771 | 0.131533 | 68,173 | |
| 37 | 0.097021 | 0.03502 | 0.132041 | 69,813 | |
| 44 | 0.095916 | 0.03632 | 0.132236 | 54,311 | |
| 50 | 0.088879 | 0.04528 | 0.134159 | 58,809 | |
| 59 | 0.08862 | 0.04679 | 0.13541 | 50,282 |
| −0.219 | −3.948 | 197.3 | −0.6524 | −183.4 | 0.305 | 902.2 | 3.764 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mi, C.; Huang, Z.; Wang, H.; Zhang, D.; Xiong, T.; Jian, H.; Tang, J.; Yu, J. An Energy-Based Method for Lifetime Assessment on High-Strength-Steel Welded Joints under Different Pre-Strain Levels. Materials 2022, 15, 4558. https://doi.org/10.3390/ma15134558
Mi C, Huang Z, Wang H, Zhang D, Xiong T, Jian H, Tang J, Yu J. An Energy-Based Method for Lifetime Assessment on High-Strength-Steel Welded Joints under Different Pre-Strain Levels. Materials. 2022; 15(13):4558. https://doi.org/10.3390/ma15134558
Chicago/Turabian StyleMi, Chengji, Zhonglin Huang, Haibo Wang, Dong Zhang, Tao Xiong, Haigen Jian, Jiachang Tang, and Jianwu Yu. 2022. "An Energy-Based Method for Lifetime Assessment on High-Strength-Steel Welded Joints under Different Pre-Strain Levels" Materials 15, no. 13: 4558. https://doi.org/10.3390/ma15134558
APA StyleMi, C., Huang, Z., Wang, H., Zhang, D., Xiong, T., Jian, H., Tang, J., & Yu, J. (2022). An Energy-Based Method for Lifetime Assessment on High-Strength-Steel Welded Joints under Different Pre-Strain Levels. Materials, 15(13), 4558. https://doi.org/10.3390/ma15134558





