Stress Component Decoupling Analysis Based on Large Numerical Aperture Objective Lens, an Impractical Approach
Abstract
1. Introduction
2. Materials and Experiments
2.1. Physical Experiments
2.2. Simulation Experiments
3. Models and Methods
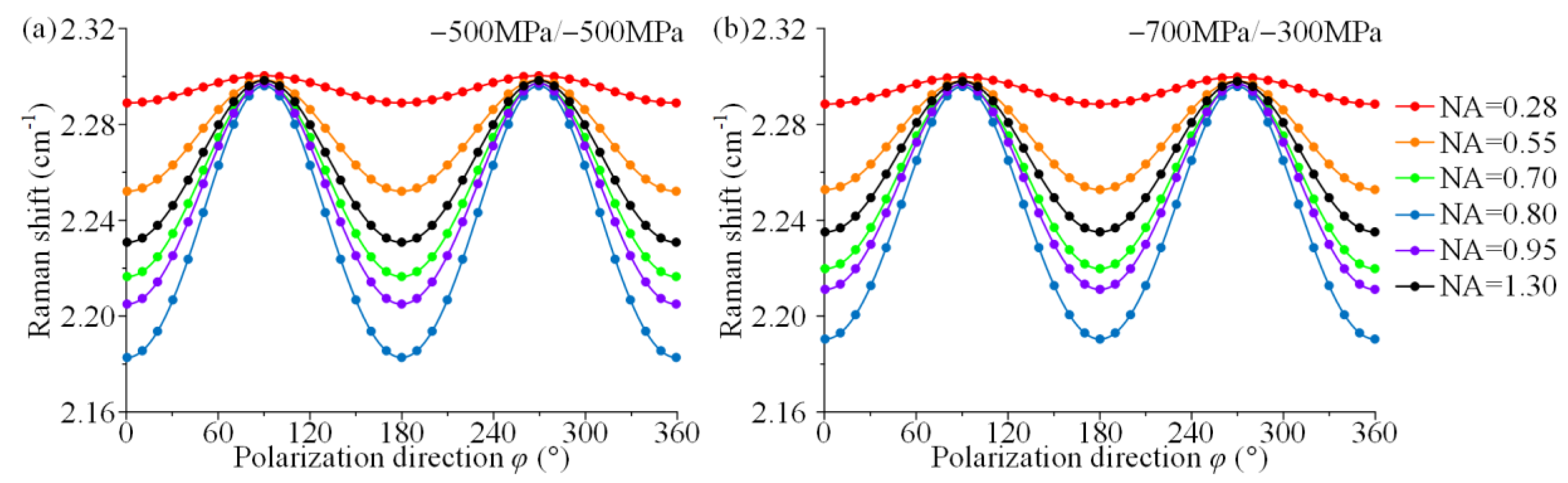
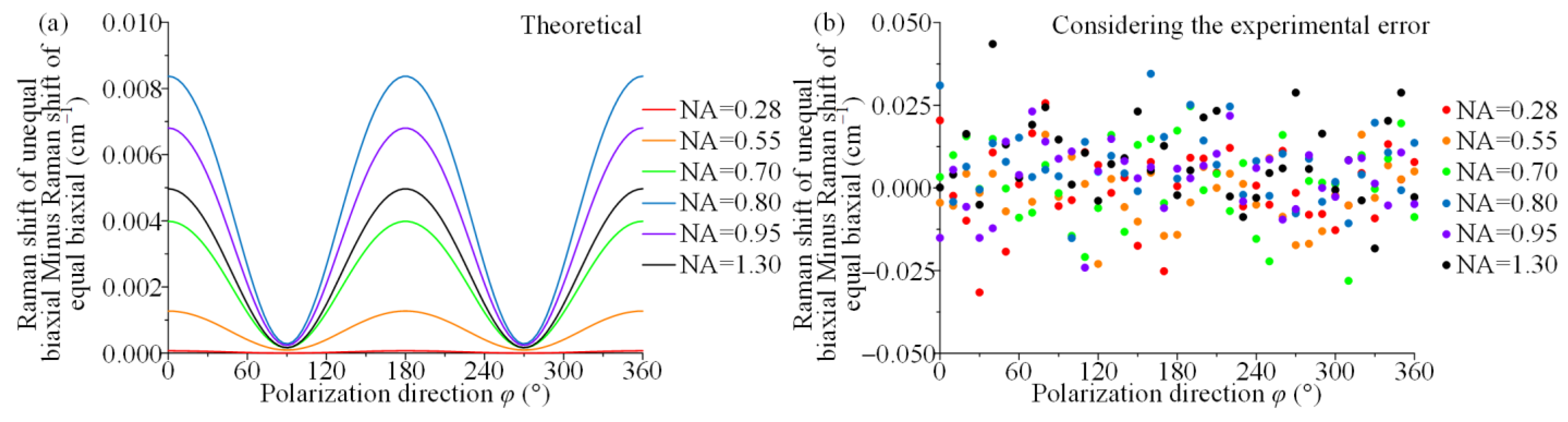
4. Results and Discussion
5. Conclusions
- The backscattering Raman can give a relatively accurate sum of the principal stresses in {100} c-Si, regardless of the NA size. However, decoupling analysis of the in-plane stress components cannot be achieved.
- This work finds that the principal stress sum is more than 98.7% of the total Raman shift, which is close to 100% by analysing the theoretical model and simulation experiment results. The principal stress difference part, which can represent the variability of stress state, has a subtle weight in the total Raman shift.
- The Raman shift variation caused by stress state is much smaller than the resolution of existing micro-Raman system, which cannot be identified in the experimental results with the combination of various experimental errors.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Parton, E.; Verheyen, P. Strained silicon—The key to sub-45 nm CMOS. III-Vs Rev. 2006, 19, 28–31. [Google Scholar] [CrossRef][Green Version]
- Chidambaram, P.R.; Bowen, C.; Chakravarthi, S.; Machala, C.; Wise, R. Fundamentals of silicon material properties for successful exploitation of strain engineering in modern CMOS manufacturing. IEEE Trans. Electron. Dev. 2006, 53, 944–964. [Google Scholar] [CrossRef]
- Calabretta, M.; Sitta, A.; Oliveri, S.M.; Sequenzia, G. An Integrated Approach to Optimize Power Device Performances by Means of Stress Engineering. In Design Tools and Methods in Industrial Engineering; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2020; pp. 481–491. [Google Scholar]
- Dhar, S.; Ungersbock, E.; Kosina, H.; Grasser, T.; Selberherr, S. Electron mobility model for (100) stressed silicon including strain-dependent mass. IEEE Trans. Nanotechnol. 2007, 6, 97–100. [Google Scholar] [CrossRef]
- Lafuente-Sampietro, A.; Utsumi, H.; Boukari, H.; Kuroda, S.; Besombes, L. Individual Cr atom in a semiconductor quantum dot: Optical addressability and spin-strain coupling. Phys. Rev. B 2016, 93, 161301. [Google Scholar] [CrossRef]
- Wang, Y.L.; Wang, Y.; Xu, C.; Zhang, X.W.; Mei, L.; Wang, M.; Xia, Y.; Zhao, P.; Wang, H.T. Domain-boundary independency of Raman spectra for strained graphene at strong interfaces. Carbon 2018, 134, 37–42. [Google Scholar] [CrossRef]
- Jin, Y.; Ren, Q.; Liu, J.; Zhang, Y.; Zheng, H.; Zhao, P. Stretching graphene to 3.3% strain using formvar-reinforced flexible substrate. Exp. Mech. 2022, 62, 761–767. [Google Scholar] [CrossRef]
- Yao, Q.Z.; Qi, Y.Z.; Zhang, J.; Zhang, S.; Zhao, P.; Wang, H.T.; Feng, X.Q.; Li, Q.Y. Impacts of the substrate stiffness on the anti-wear performance of graphene. AIP Adv. 2019, 9, 075317. [Google Scholar] [CrossRef]
- Wang, Y.L.; Zhou, X.C.; Jin, Y.H.; Zhang, X.W.; Zhang, Z.L.; Wang, Y.; Liu, J.L.; Wang, M.; Xia, Y.; Zhao, P.; et al. Strain-dependent Raman analysis of the G* band in graphene. Phys. Rev. B 2019, 100, 241407. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Zhang, X.W.; Wang, Y.L.; Wang, Y.; Zhang, Y.; Xu, C.; Zou, Z.X.; Wu, Z.H.; Xia, Y.; Zhao, P.; et al. Crack propagation and fracture toughness of graphene probed by raman spectroscopy. ACS Nano 2019, 13, 10327–10332. [Google Scholar] [CrossRef]
- Xie, H.M.; Han, B.; Song, H.B.; Li, X.F.; Kang, Y.L.; Zhang, Q. In-situ measurements of electrochemical stress/strain fields and stress analysis during an electrochemical process. J. Mech. Phys. Solids 2021, 156, 104602. [Google Scholar] [CrossRef]
- Song, H.B.; Na, R.; Hong, C.Y.; Zhang, G.; Li, X.F.; Kang, Y.L.; Zhang, Q.; Xie, H.M. In situ measurement and mechanism analysis of the lithium storage behavior of graphene electrodes. Carbon 2022, 188, 146–154. [Google Scholar] [CrossRef]
- Xie, H.M.; Zhang, Q.; Song, H.B.; Shi, B.Q.; Kang, Y.L. Modeling and in situ characterization of lithiation-induced stress in electrodes during the coupled mechano-electro-chemical process. J. Power Sources 2017, 342, 896–903. [Google Scholar] [CrossRef]
- Xie, H.M.; Song, H.B.; Guo, J.G.; Kang, Y.L.; Yang, W.; Zhang, Q. In situ measurement of rate-dependent strain/stress evolution and mechanism exploration in graphene electrodes during electrochemical process. Carbon 2019, 144, 342–350. [Google Scholar] [CrossRef]
- Xie, H.M.; Kang, Y.L.; Song, H.B.; Zhang, Q. Real-time measurements and experimental analysis of material softening and total stresses of Si-composite electrode. J. Power Sources 2019, 424, 100–107. [Google Scholar] [CrossRef]
- Adu, K.W.; Xiong, Q.; Gutierrez, H.R.; Chen, G.; Eklund, P.C. Raman scattering as a probe of phonon confinement and surface optical modes in semiconducting nanowires. Appl. Phys. A 2006, 85, 287–297. [Google Scholar] [CrossRef]
- Ma, L.L.; Fan, X.J.; Qiu, W. Polarized Raman spectroscopy-stress relationship considering shear stress effect. Opt. Lett. 2019, 44, 4682–4685. [Google Scholar] [CrossRef]
- Ma, L.L.; Xing, H.D.; Li, Q.; Wang, J.S.; Qiu, W. Raman stress measurement of crystalline silicon desensitizes shear stress: Only on {001} crystal plane. Jpn. J. Appl. Phys. 2018, 57, 080307. [Google Scholar] [CrossRef]
- Loechelt, G.H.; Cave, N.G.; Menéndez, J. Polarized off-axis Raman spectroscopy: A technique for measuring stress tensors in semiconductors. J. App. Phys. 1999, 86, 6164–6180. [Google Scholar] [CrossRef]
- Fu, D.H.; He, X.Y.; Ma, L.L.; Xing, H.D.; Meng, T.; Chang, Y.; Qiu, W. The 2-axis stress component decoupling of {100} c-Si by using oblique backscattering micro-Raman spectroscopy. Sci. China Phys. Mech. 2020, 63, 55–61. [Google Scholar] [CrossRef]
- Ma, L.L.; Xing, H.D.; Ding, Q.; Han, Y.T.; Li, Q.; Qiu, W. Analysis of residual stress around a Berkovich nano-indentation by micro-Raman spectroscopy. AIP Adv. 2019, 9, 015010. [Google Scholar] [CrossRef]
- Miyatake, T.; Pezzotti, G. Tensor-resolved stress analysis in silicon MEMS device by polarized Raman spectroscopy. Phys. Status Solidi A 2011, 208, 1151–1158. [Google Scholar] [CrossRef]
- De Wolf, I. High-resolution stress and temperature measurements in semiconductor devices using micro-Raman spectroscopy. In Proceedings of the International Symposium on Photonics and Applications, Singapore, 29 November 1999; Volume 3897, pp. 239–252. [Google Scholar]
- Lee, C.J.; Pezzotti, G.; Okui, Y.; Nishino, S. Raman microprobe mapping of residual microstresses in 3C-SiC film epitaxial lateral grown on patterned Si (1 1 1). Appl. Surf. Sci. 2004, 228, 10–16. [Google Scholar] [CrossRef]
- Kosemura, D.; Ogura, A. Transverse-optical phonons excited in Si using a high-numerical-aperture lens. Appl. Phys. Lett. 2010, 96, 212106. [Google Scholar] [CrossRef]
- Brunner, K.; Abstereiter, G.; Kolbesen, B.O.; Meul, H.W. Strain at Si-SiO2 interfaces studied by Micron-Raman spectroscopy. Appl. Surf. Sci. 1989, 39, 116–126. [Google Scholar] [CrossRef]
- Büchler, A.; Beinert, A.; Kluska, S.; Haueisen, V.; Romer, P.; Heinz, F.D.; Glatthaar, M.; Schubert, M.C. Enabling stress determination on alkaline textured silicon using Raman spectroscopy. Energy Procedia 2017, 124, 18–23. [Google Scholar] [CrossRef]
- Ossikovski, R.; Nguyen, Q.; Picardi, G.; Schreiber, J.; Morin, P. Theory and experiment of large numerical aperture objective Raman microscopy: Application to the stress-tensor determination in strained cubic materials. J. Raman Spectrosc. 2008, 39, 661–672. [Google Scholar] [CrossRef]
- Poborchii, V.; Tada, T.; Kanayama, T. Observation of the forbidden doublet optical phonon in Raman spectra of strained Si for stress analysis. Appl. Phys. Lett. 2010, 97, 041915. [Google Scholar] [CrossRef]
- Qiu, Z.; Im, J.; Huang, R.; Ho, P.S. Extension of micro-Raman spectroscopy for full-component stress characterization of TSV structures. In Proceedings of the IEEE 63rd Electronic Components and Technology Conference, Las Vegas, NV, USA, 28–31 May 2013; pp. 397–401. [Google Scholar]
- Becker, M.; Scheel, H.; Christiansen, S.; Strunk, H.P. Grain orientation, texture, and internal stress optically evaluated by micro-Raman spectroscopy. J. Appl. Phys. 2007, 101, 7148. [Google Scholar] [CrossRef]
- Chang, Y.; He, S.S.; Sun, M.Y.; Xiao, A.X.; Zhao, J.X.; Ma, L.L.; Qiu, W. Angle-Resolved Intensity of In-Axis/Off-Axis Polarized Micro-Raman Spectroscopy for Monocrystalline Silicon. J. Spectrosc. 2021, 2021, 2860007. [Google Scholar] [CrossRef]
- Chang, Y.; Xiao, A.X.; Li, R.B.; Wang, M.J.; He, S.S.; Sun, M.Y.; Wang, L.Z.; Qu, C.Y.; Qiu, W. Angle-Resolved Intensity of Polarized Micro-Raman Spectroscopy for 4H-SiC. Crystals 2021, 11, 626. [Google Scholar] [CrossRef]
- Gouadec, G.; Colomban, P. Raman Spectroscopy of nanomaterials: How spectra relate to disorder, particle size and mechanical properties. Prog. Cryst. Growth Charact. Mater. 2007, 53, 1–56. [Google Scholar] [CrossRef]
- Gouadec, G.; Colomban, P.; Bansal, N.P. Raman Study of Hi-Nicalon-Fiber-Reinforced Celsian Composites: II, Residual Stress in Fiberss. J. Am. Ceram. Soc. 2001, 84, 1136–1142. [Google Scholar] [CrossRef]
- Ma, L.L.; Zheng, J.X.; Fan, X.J.; Qiu, W. Determination of stress components in a complex stress condition using micro-Raman spectroscopy. Opt. Express 2021, 29, 30319–30326. [Google Scholar] [CrossRef] [PubMed]
- Qiu, W.; Ma, L.L.; Li, Q.; Xing, H.D.; Cheng, C.L.; Huang, G.Y. A general metrology of stress on crystalline silicon with random crystal plane by using micro-Raman spectroscopy. Acta Mech. Sin. 2018, 34, 1095–1107. [Google Scholar] [CrossRef]
- Qiu, W.; He, S.S.; Chang, Y.; Ma, L.L.; Qu, C.Y. Error Analysis for Stress Component Characterization Based on Polarized Raman Spectroscopy. Exp. Mech. 2022, 62, 1007–1015. [Google Scholar] [CrossRef]


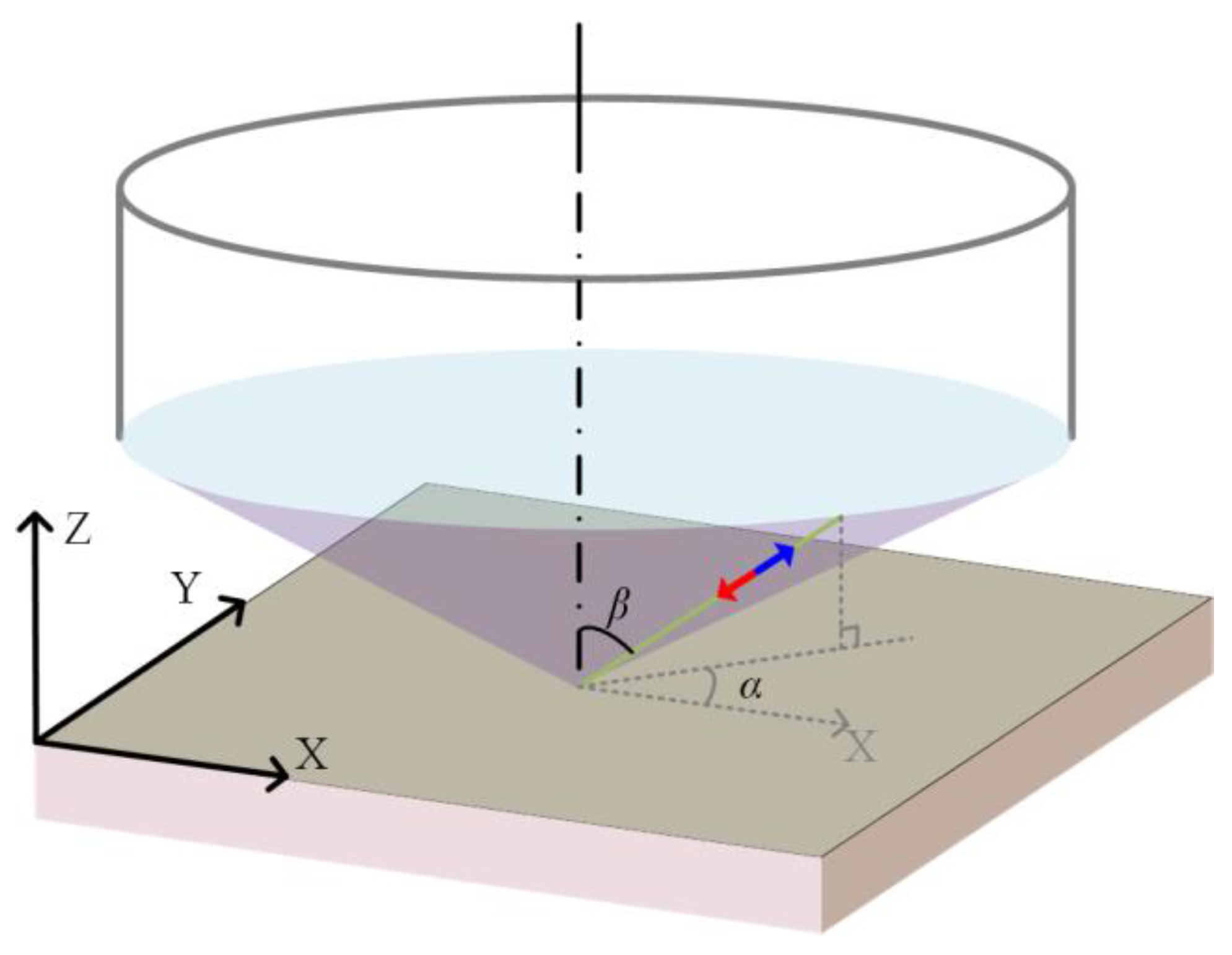
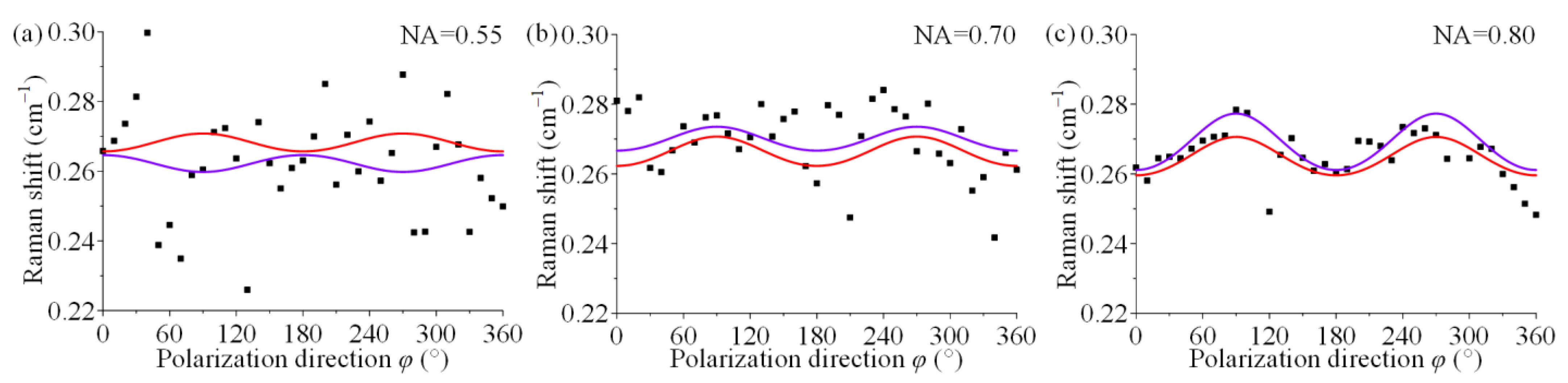

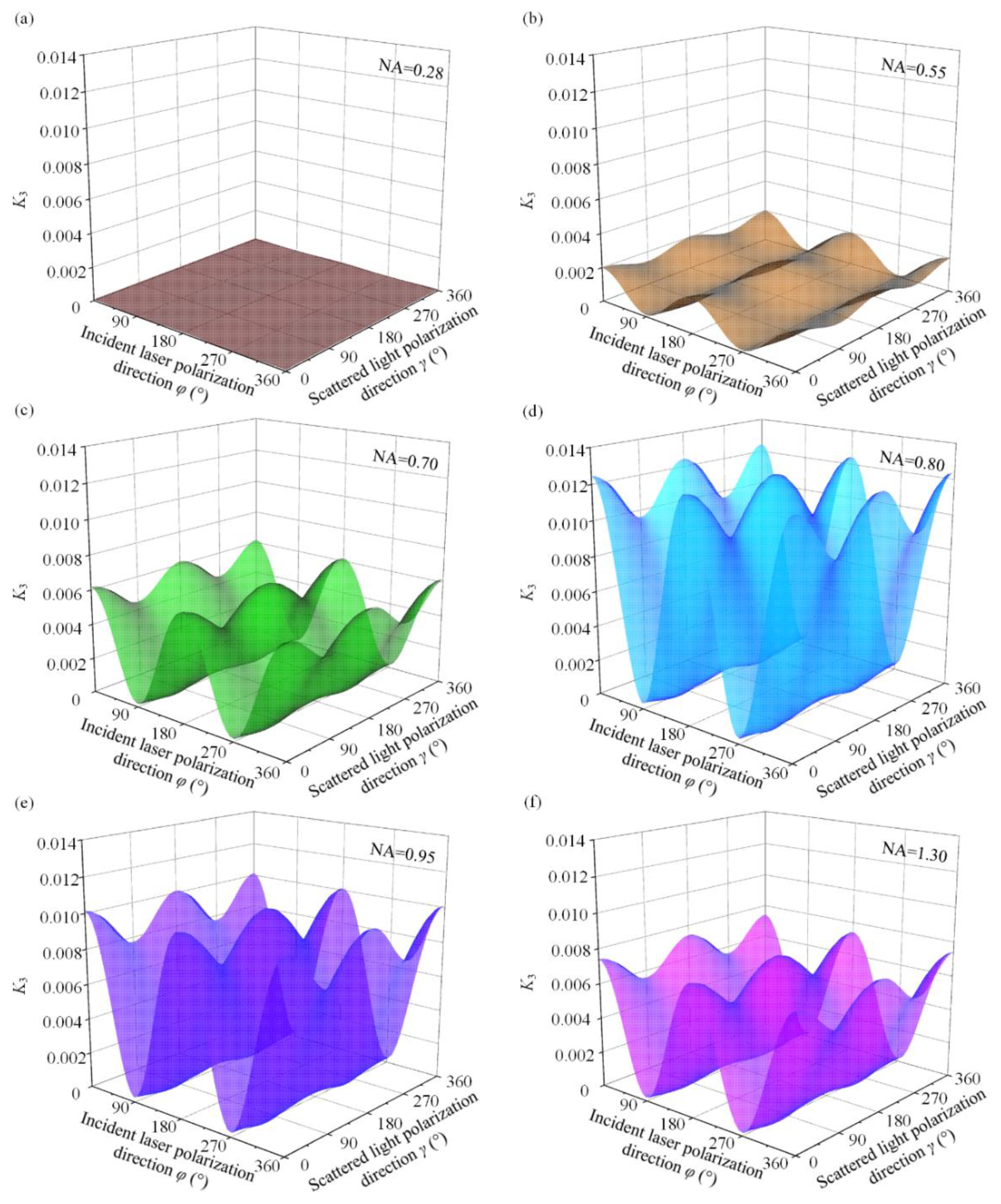
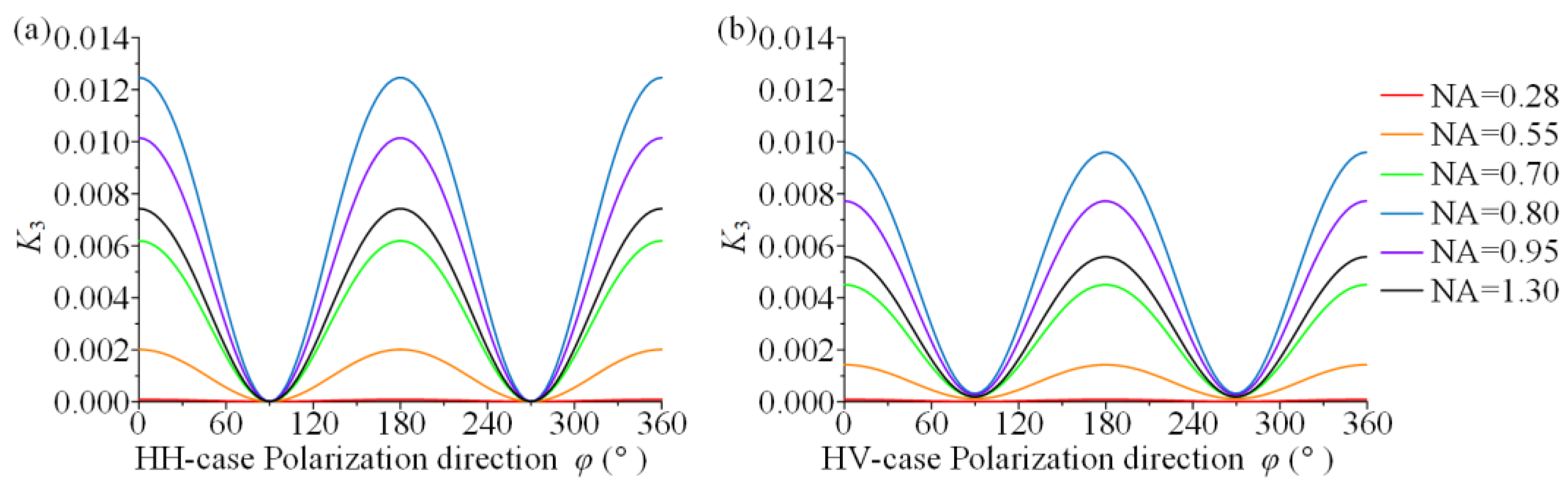
| σ11/MPa | σ22/MPa | τ12/MPa | (σ11 + σ22)/MPa | |
|---|---|---|---|---|
| Sample 1 | −117.60 | −0.24 | −5.34 | −117.84 |
| Sample 2 | −29.39 | −29.39 | −29.39 | −58.78 |
| a1 | b1 | c1 | −a2 | −b2 | −c2 | |
|---|---|---|---|---|---|---|
| NA = 0.20 | 0.0105 | 0.0006 | 0.0048 | 0 * | 0 * | 0.0004 |
| NA = 0.28 | 0.0209 | 0.0011 | 0.0097 | 0.0003 | 0 * | 0 * |
| NA = 0.42 | 0.0495 | 0.0026 | 0.0225 | 0.0023 | 0.0009 | 0.0007 |
| NA = 0.55 | 0.0909 | 0.0041 | 0.0397 | 0.0059 | 0.0004 | 0.0023 |
| NA = 0.70 | 0.1684 | 0.0066 | 0.0663 | 0.0198 | 0.0007 | 0.0080 |
| NA = 0.80 | 0.2526 | 0.0084 | 0.0916 | 0.0446 | 0.0012 | 0.0157 |
| NA = 0.95 | 0.1957 | 0.0065 | 0.0710 | 0.0346 | 0.0010 | 0.0121 |
| NA = 1.30 | 0.1360 | 0.0045 | 0.0493 | 0.0240 | 0.0007 | 0.0084 |
| Sample 1 | Sample 2 | |||
|---|---|---|---|---|
| Average Relative Error of Stress Components | Relative Error of Principal Stress Sums | Average Relative Error of Stress Components | Relative Error of Principal Stress Sums | |
| NA = 0.55 | 346,100.00% | 4.37% | 43.73% | 0.82% |
| NA = 0.70 | 17,882.77% | 1.02% | 351.43% | 0.17% |
| NA = 0.80 | 5001.38% | 2.54% | 98.98% | 0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.; Fu, D.; Sun, M.; He, S.; Qiu, W. Stress Component Decoupling Analysis Based on Large Numerical Aperture Objective Lens, an Impractical Approach. Materials 2022, 15, 4616. https://doi.org/10.3390/ma15134616
Chang Y, Fu D, Sun M, He S, Qiu W. Stress Component Decoupling Analysis Based on Large Numerical Aperture Objective Lens, an Impractical Approach. Materials. 2022; 15(13):4616. https://doi.org/10.3390/ma15134616
Chicago/Turabian StyleChang, Ying, Donghui Fu, Mingyuan Sun, Saisai He, and Wei Qiu. 2022. "Stress Component Decoupling Analysis Based on Large Numerical Aperture Objective Lens, an Impractical Approach" Materials 15, no. 13: 4616. https://doi.org/10.3390/ma15134616
APA StyleChang, Y., Fu, D., Sun, M., He, S., & Qiu, W. (2022). Stress Component Decoupling Analysis Based on Large Numerical Aperture Objective Lens, an Impractical Approach. Materials, 15(13), 4616. https://doi.org/10.3390/ma15134616







