Experimental Tests and Numerical Simulations on the Ballistic Impact Response of a Highly Inhomogeneous Aluminium Foam
Abstract
:1. Introduction
2. Characterisation of the Aluminium Foam Material
2.1. Aluminium Foam Material
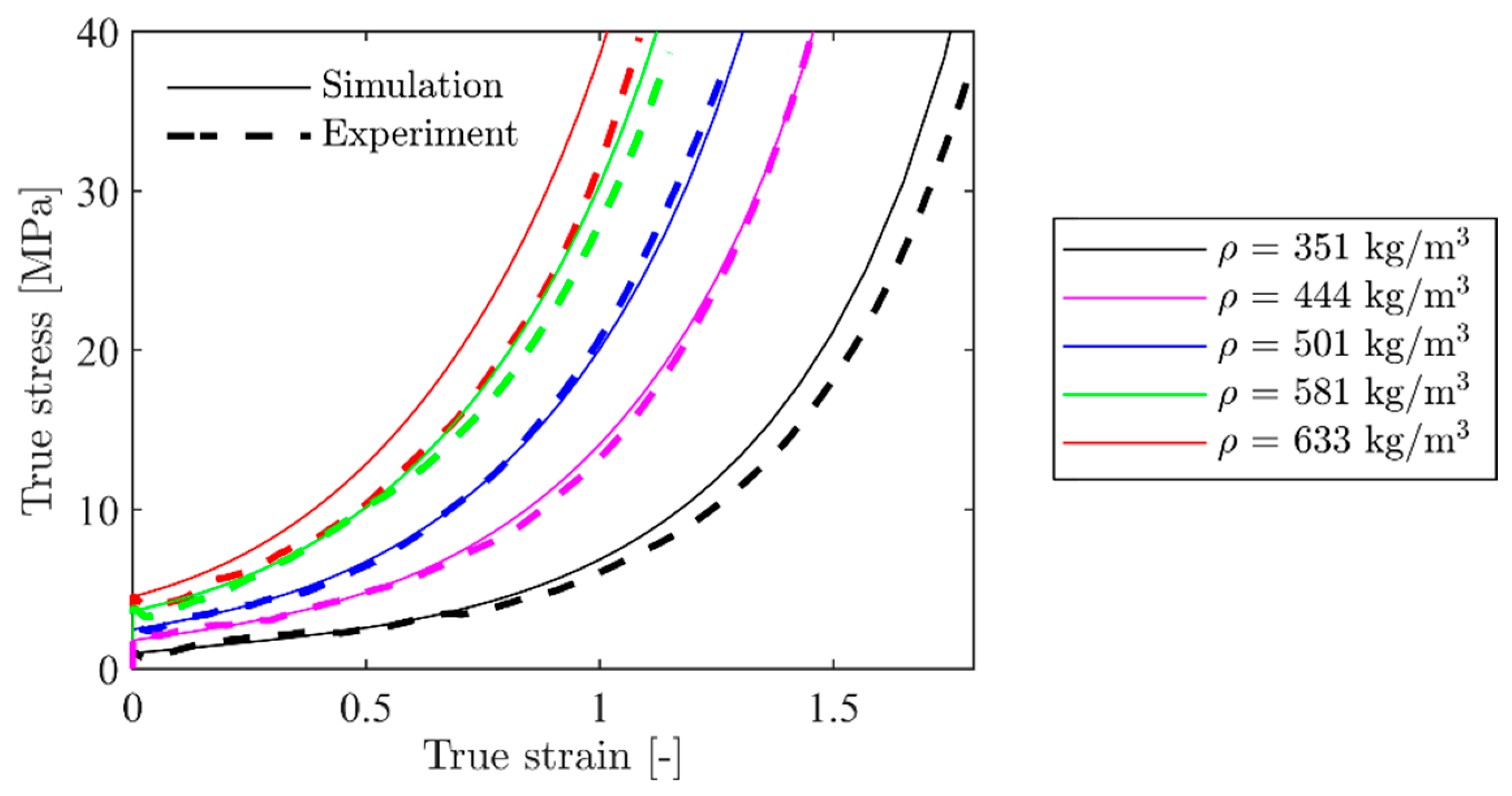
2.2. Mechanical Behaviour of the Aluminium Foam
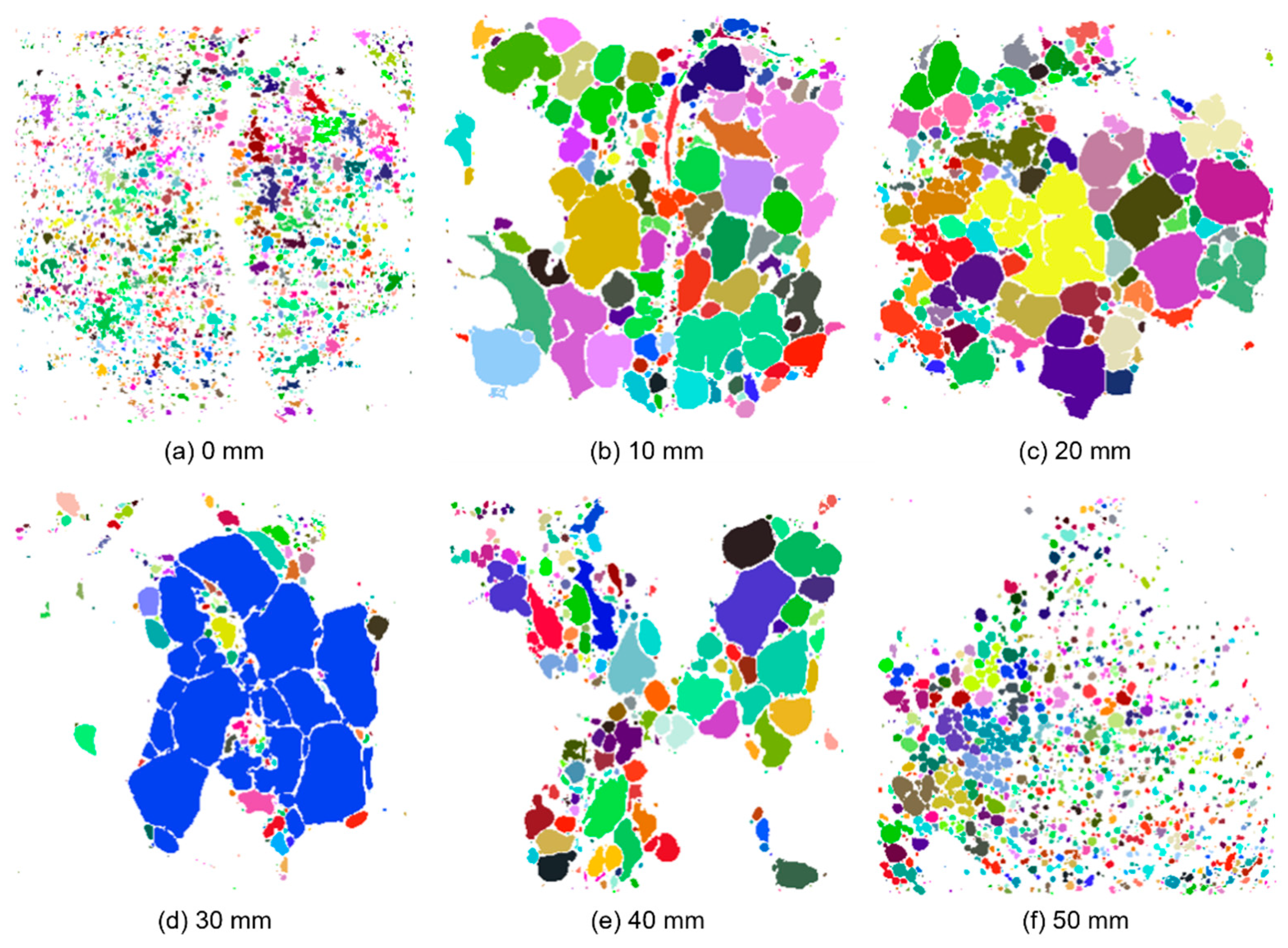
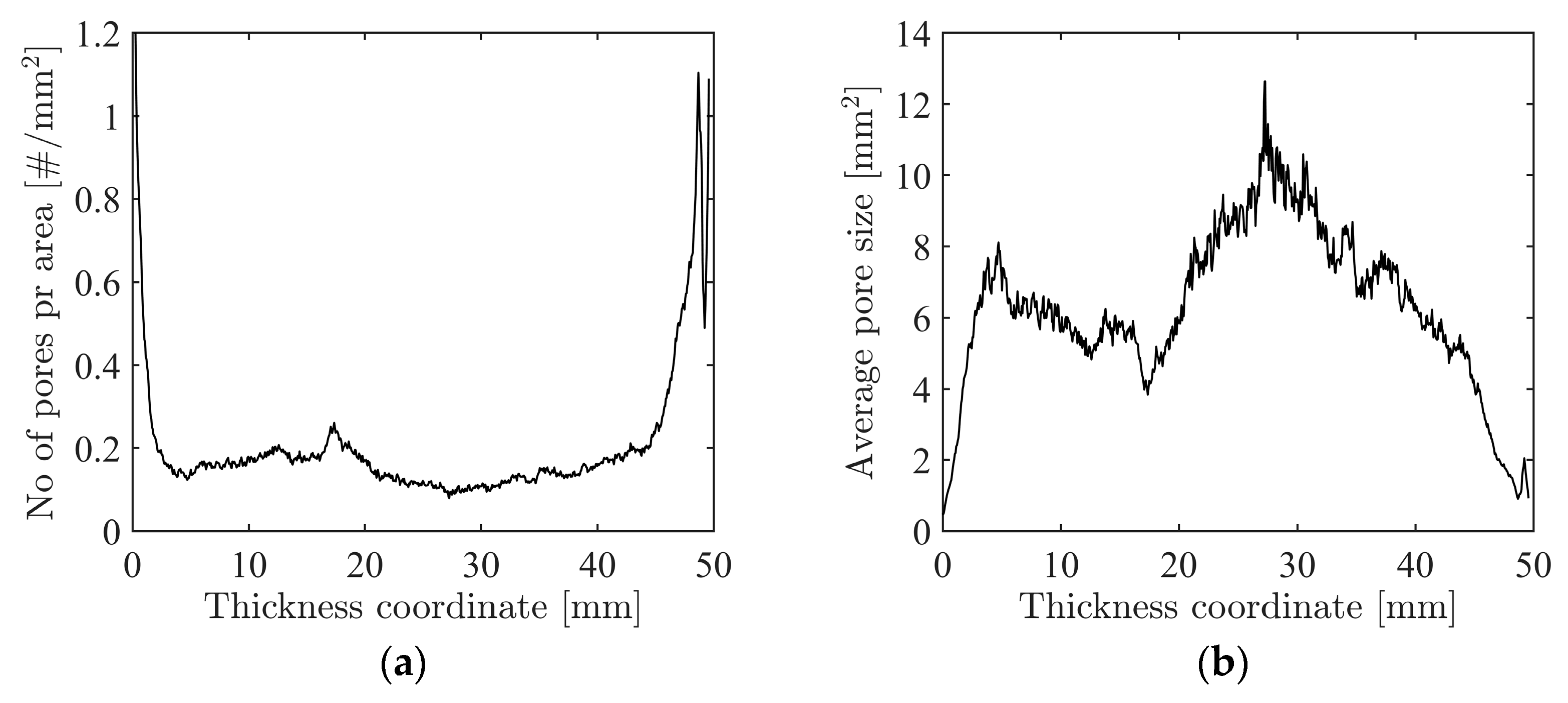
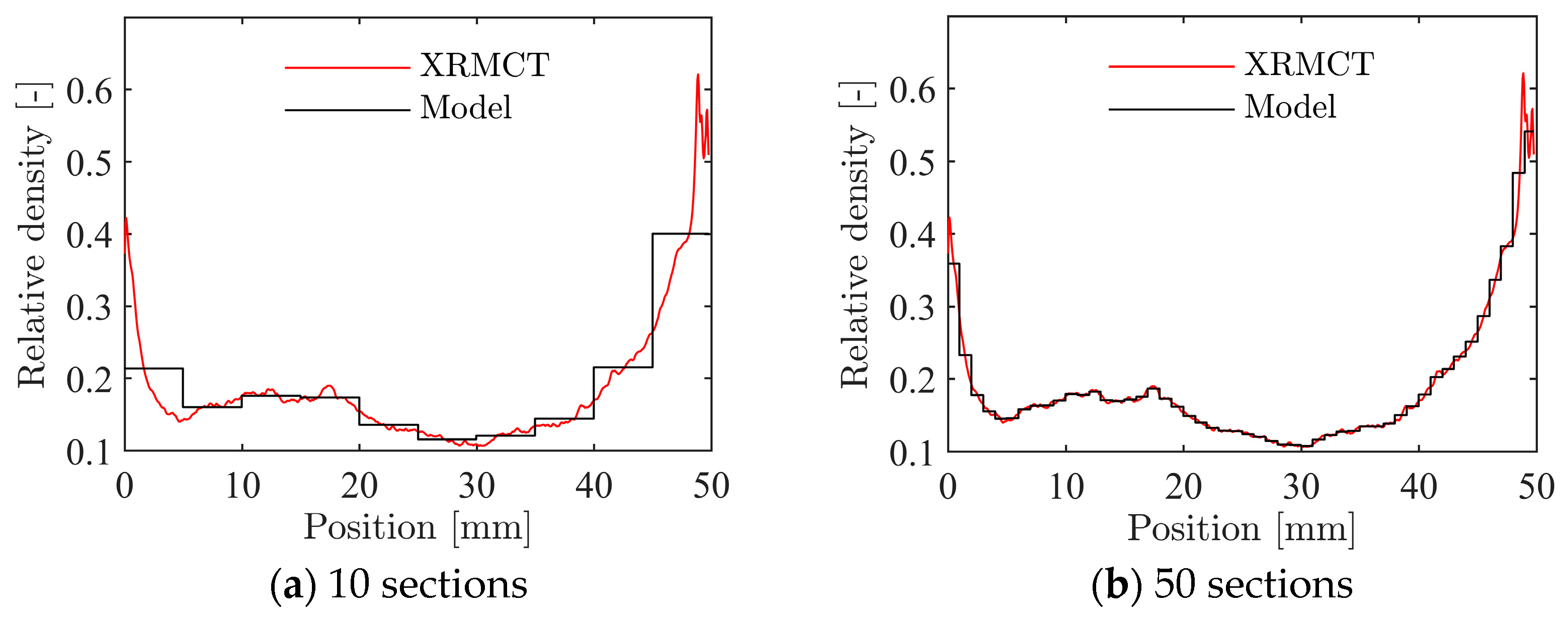
2.3. X-ray Micro Computed Tomography
3. Component Tests
3.1. Experimental Setup
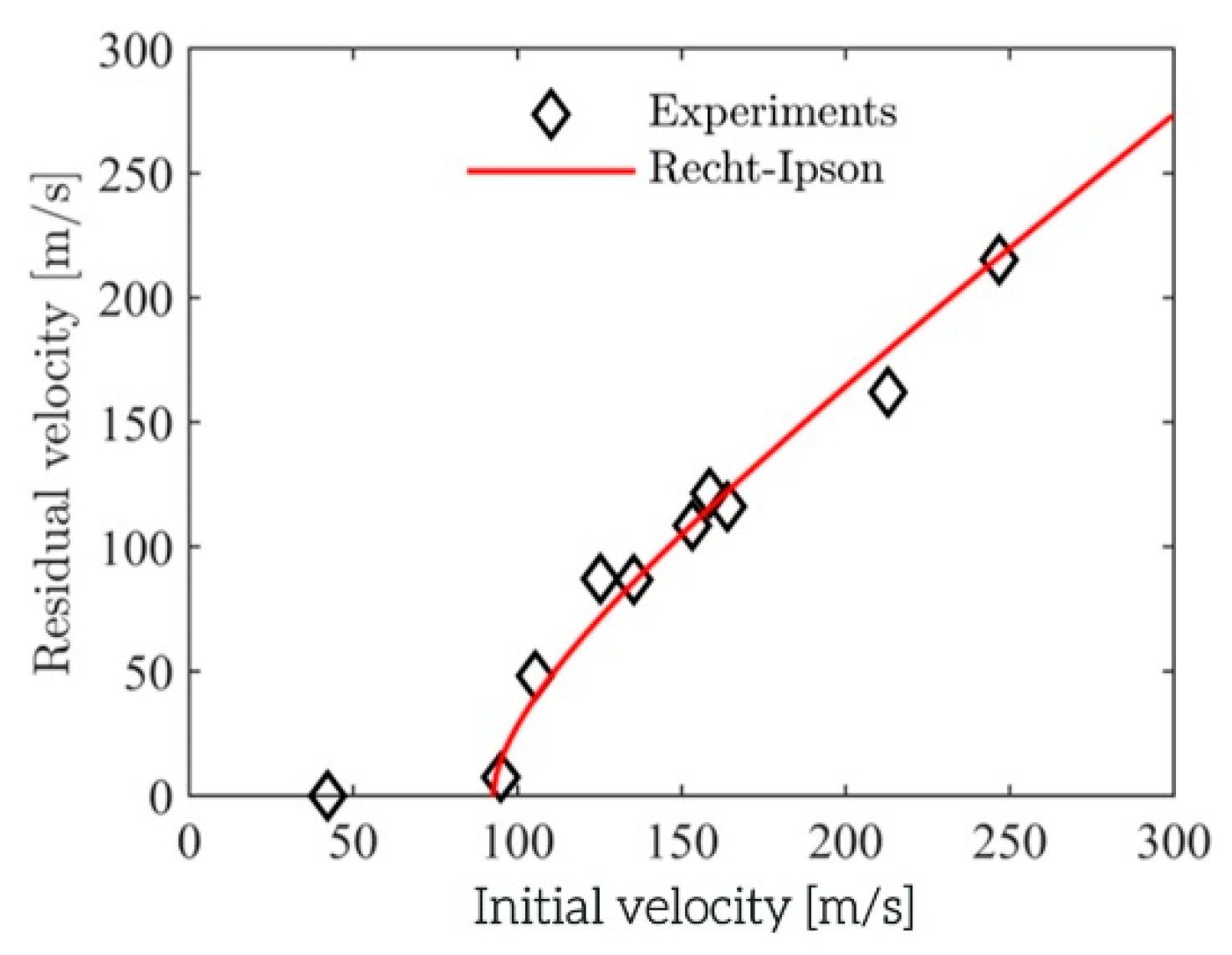
3.2. Experimental Results
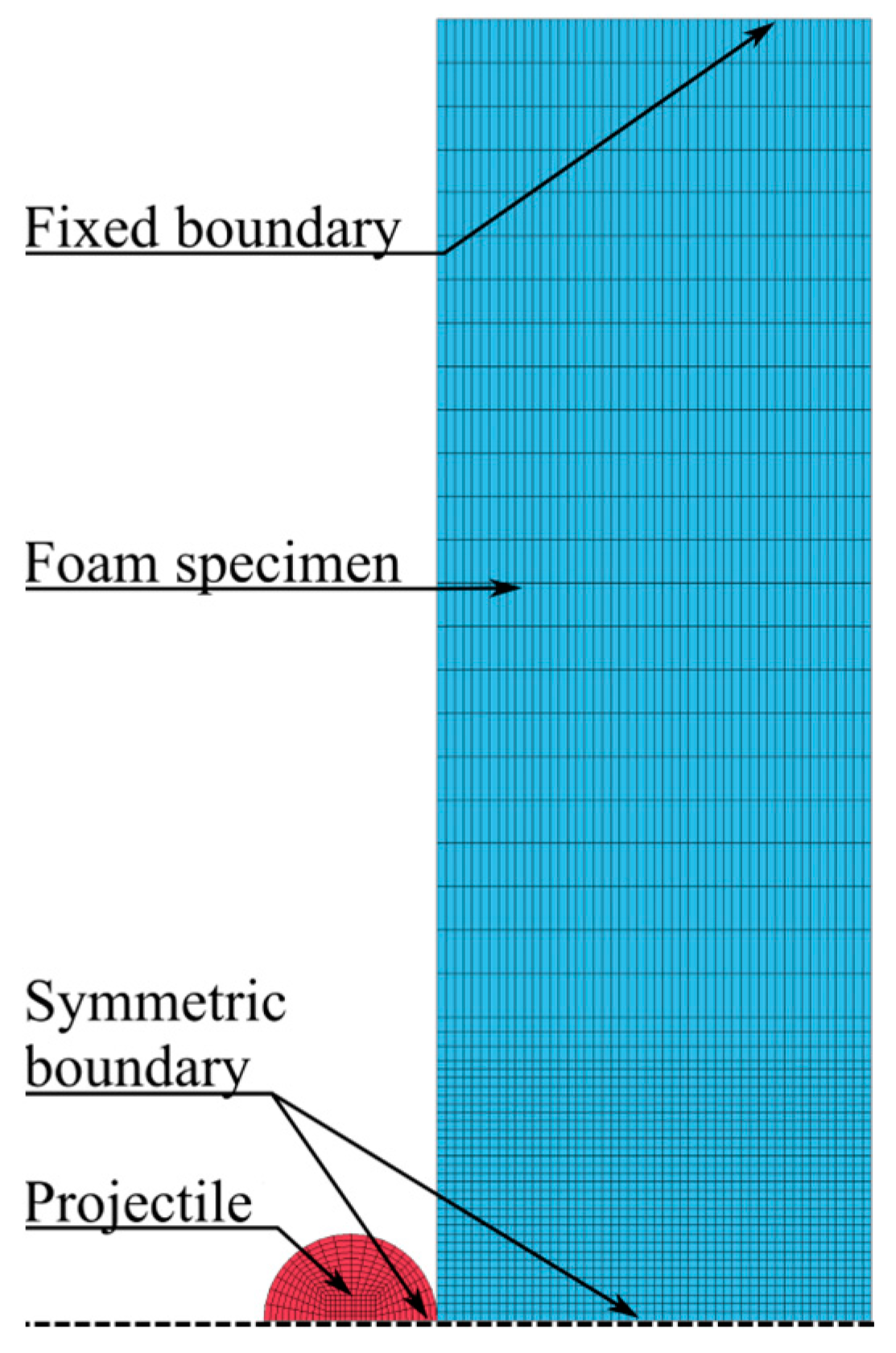
4. Numerical Simulations
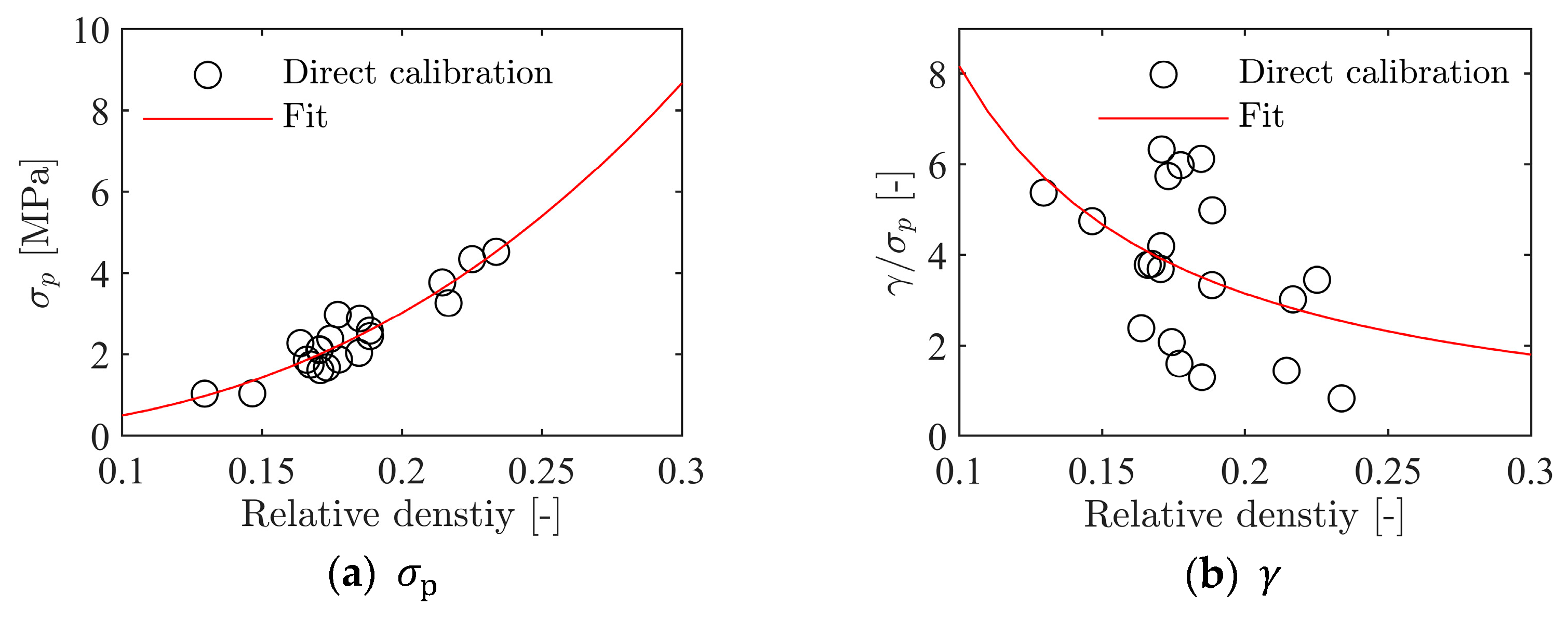
4.1. Constitutive Relation and Fracture Criteria
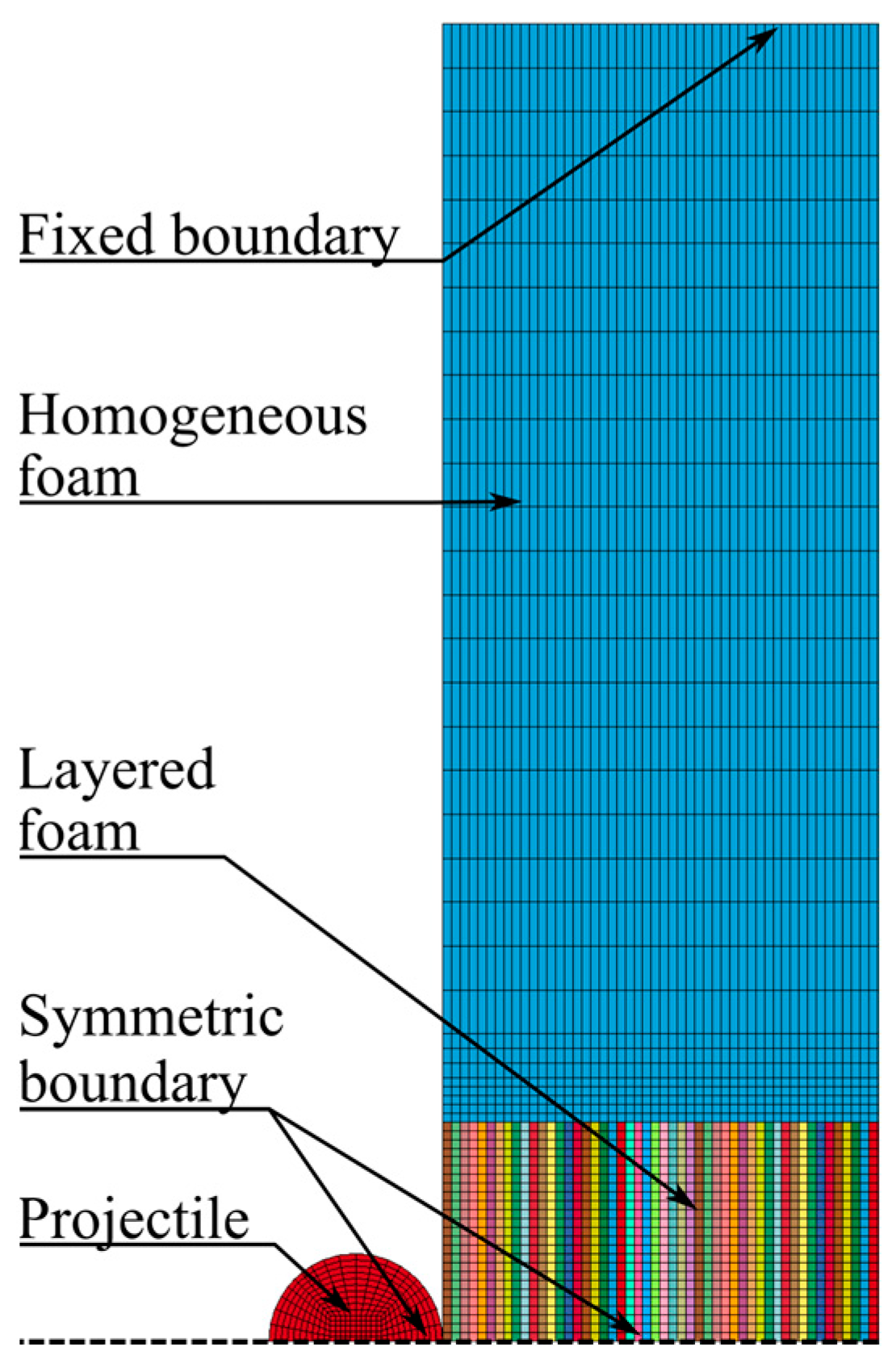
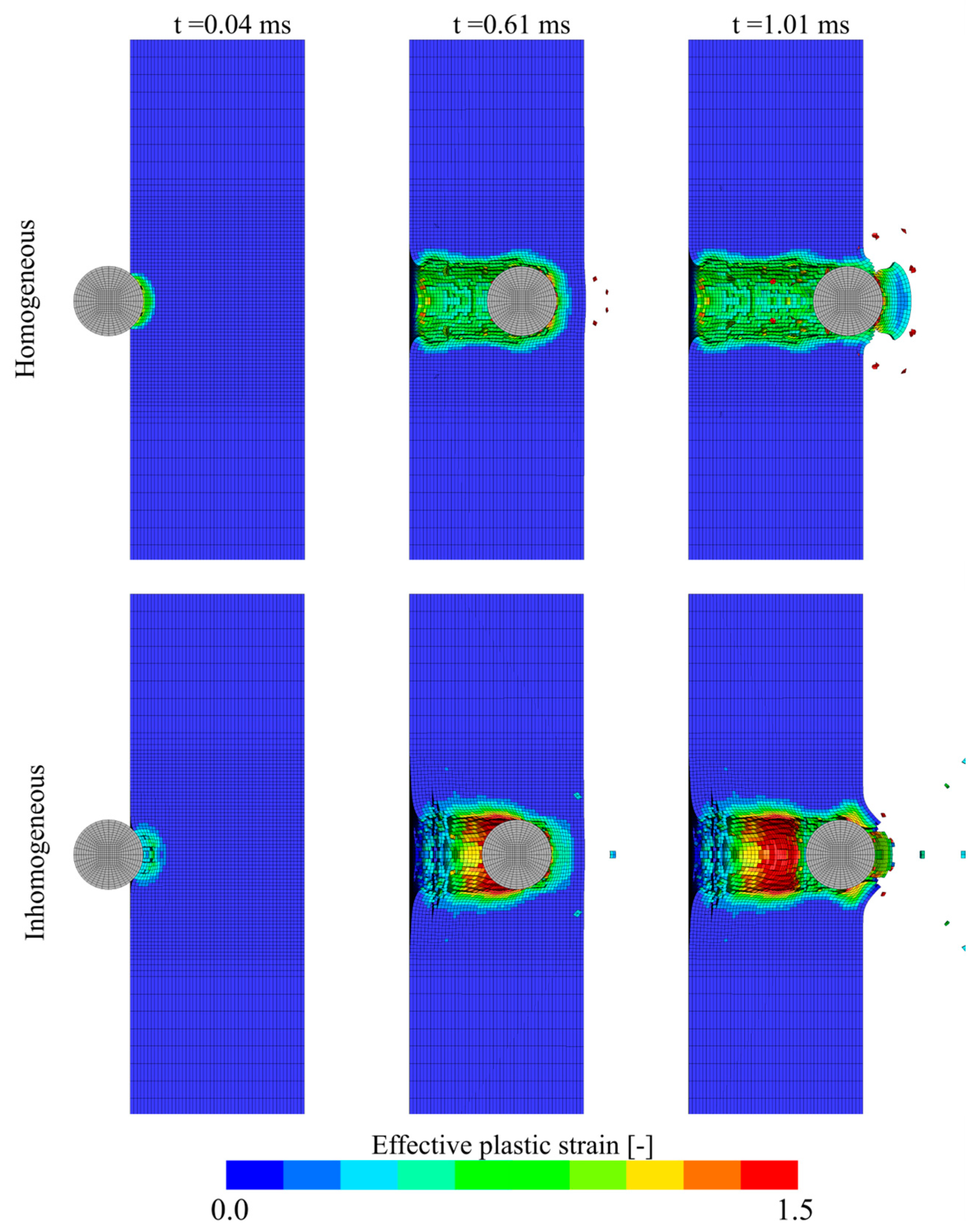
4.2. Homogeneous Foam Model
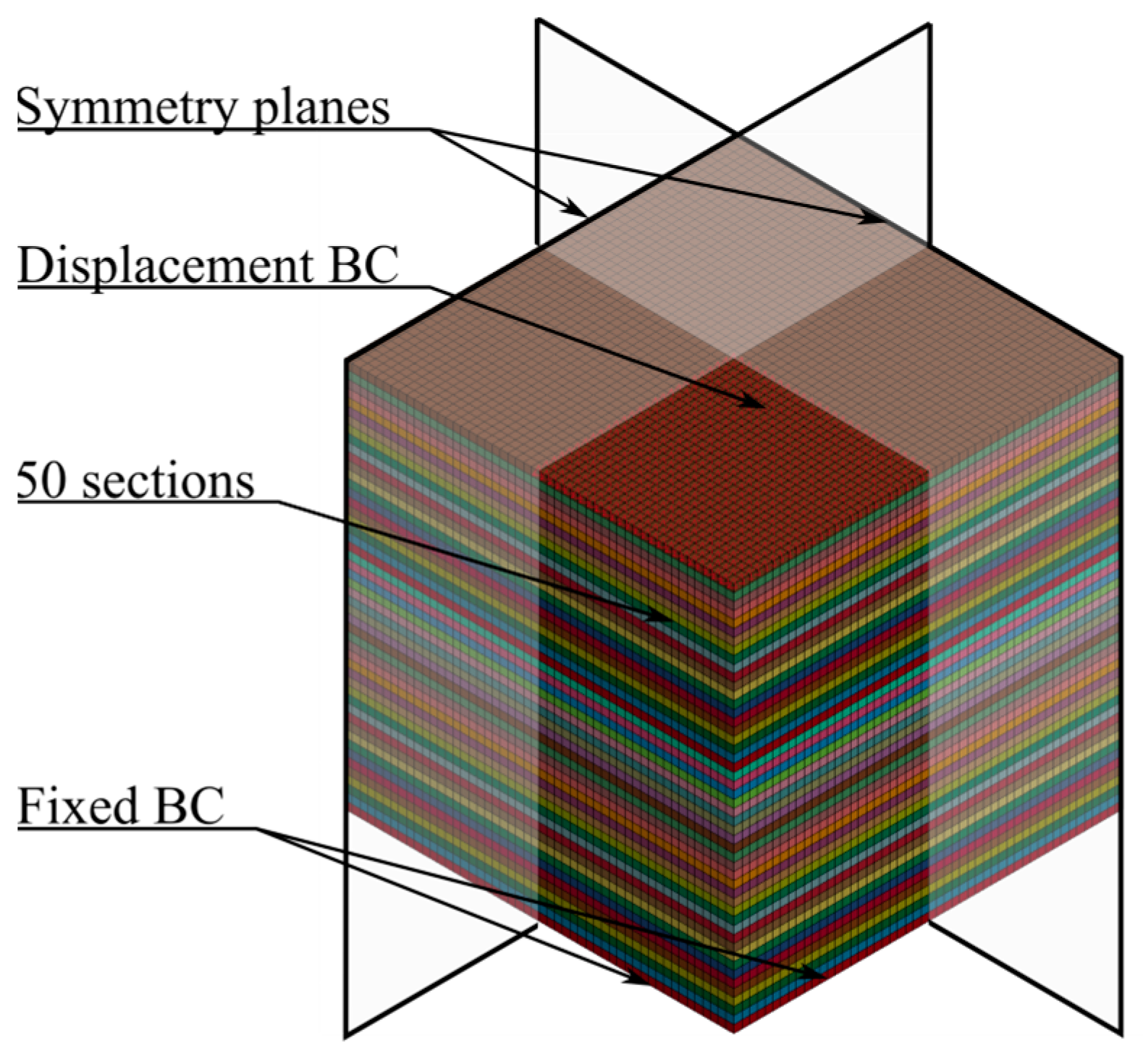
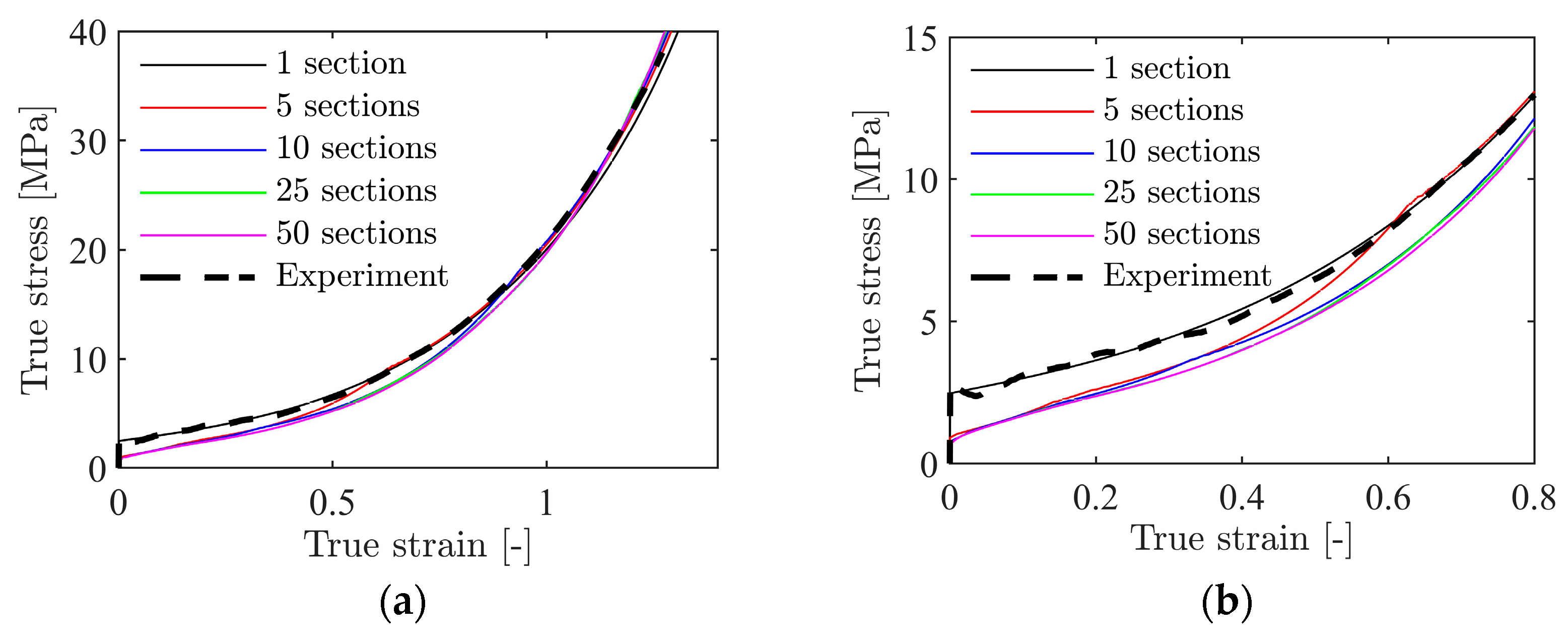
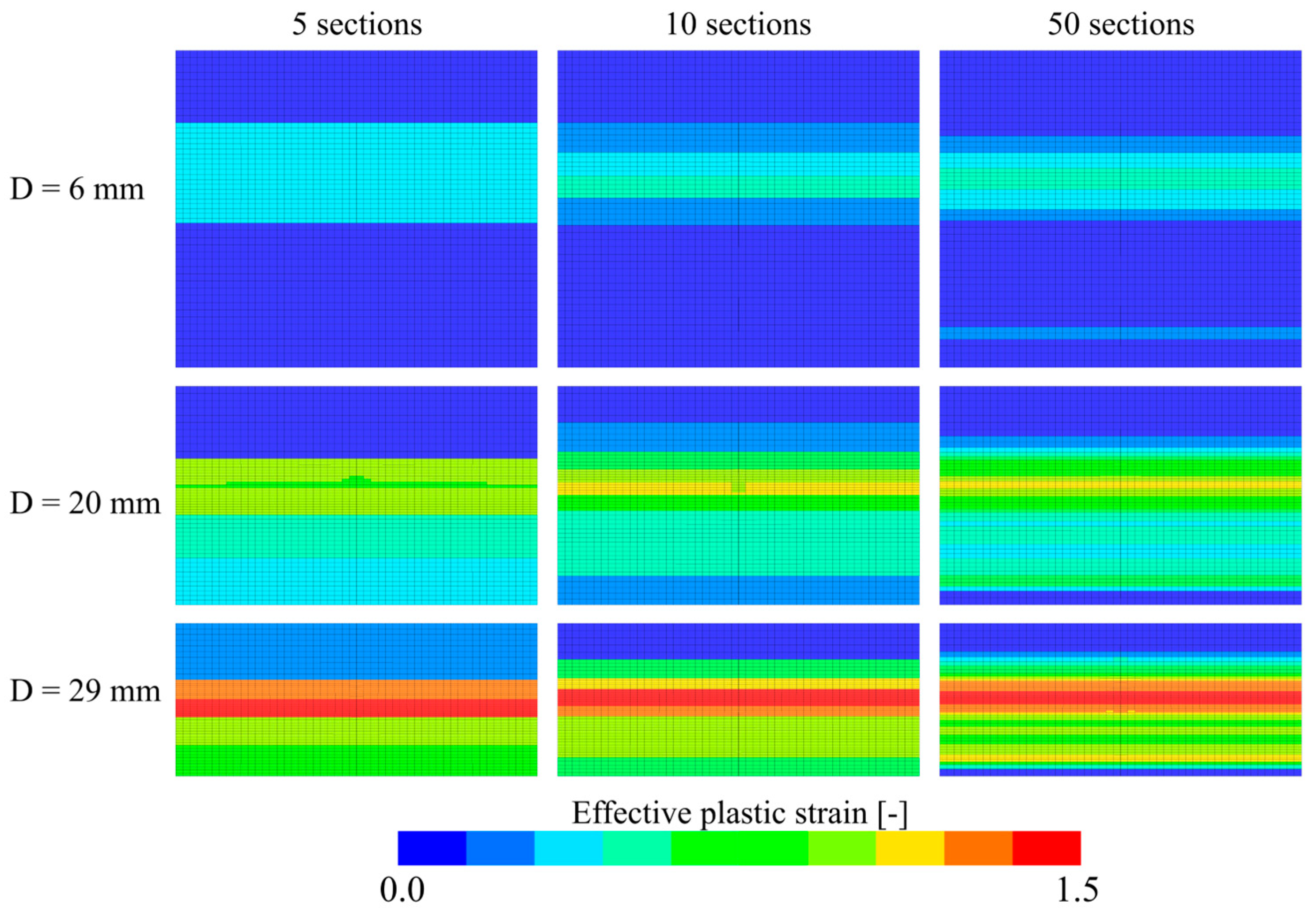
4.3. Inhomogeneous Foam Model
5. Concluding Remarks
- Aluminium foams produced by the powder compaction method may have a highly inhomogeneous and complex pore structure with a strong variation in density distribution throughout the spatial dimensions that affect the mechanical properties of the material and causes a significant spread in the stress-strain response.
- Although complex, post-processing of XRMCT data can be used to accurately characterise the topology and morphology of the foam and provide pore statistics that can be used to understand and optimise the behaviour of the material.
- The ballistic perforation resistance of the aluminium foam can be readily determined in a gas gun facility. Even though the material was complex, the penetration and perforation process was similar with limited fragmentation independent of impact velocity, and the spread in the experimental results was low.
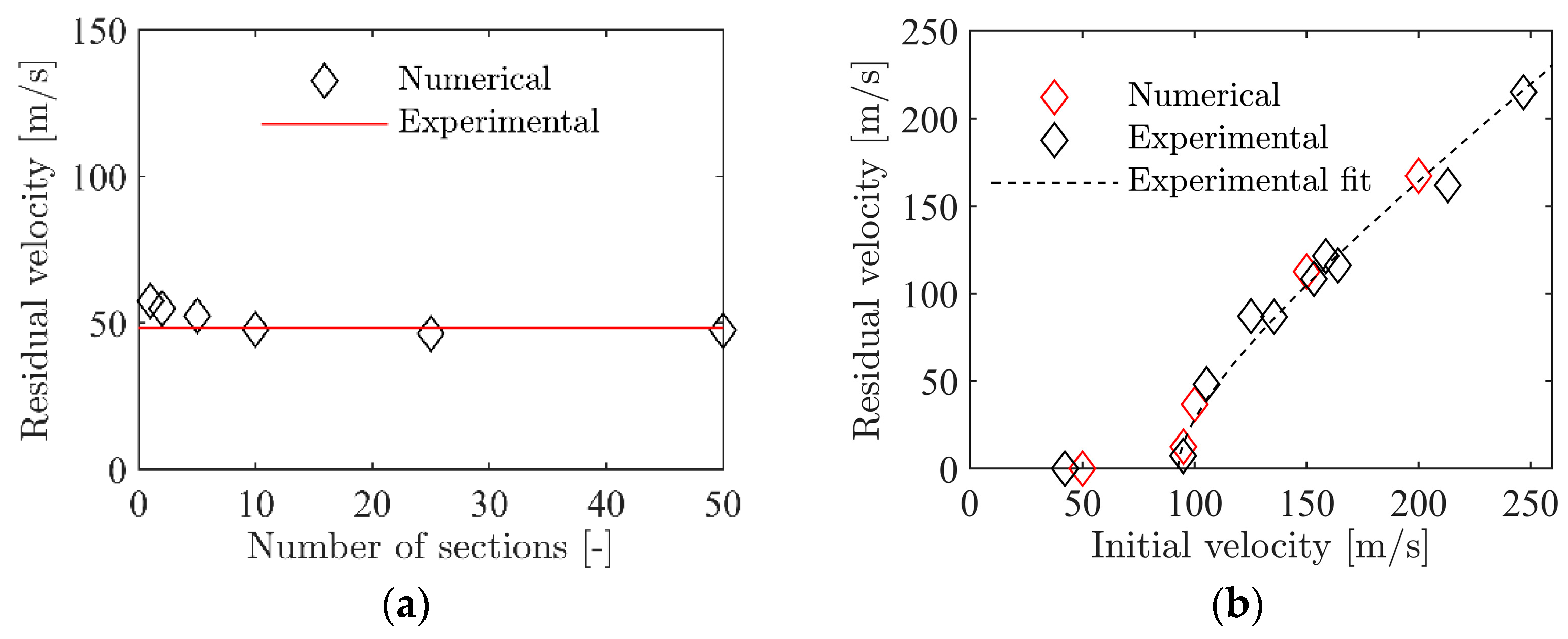
- Numerical simulations using a crushable foam model available in LS-DYNA gave excellent predictions of the ballistic limit velocity and curve, independent of whether the constitutive relation was directly calibrated based on material tests or XRMCT data.
- It was, however, found necessary to calibrate the fracture criterion by inverse modelling of one of the ballistic impact tests to have reliable fracture predictions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mackerle, J. Finite Element Analyses of Sandwich Structures: A Bibliography (1980–2001); Engineering Computations: Swansea, UK, 2002; pp. 206–245. [Google Scholar]
- Brekken, K.A.; Reyes, A.; Berstad, T.; Langseth, M.; Børvik, T. Sandwich panels with polymeric foam cores exposed to blast loading: An experimental and numerical investigation. Appl. Sci. 2020, 10, 9061. [Google Scholar] [CrossRef]
- Reyes, A.; Børvik, T. Low velocity impact of crash components with steel skins and polymer foam cores. Int. J. Impact Eng. 2019, 132, 103297. [Google Scholar] [CrossRef]
- Reyes, A.; Børvik, T. Quasi-static behaviour of crash components with steel skins and polymer foam cores. Mater. Today Commun. 2018, 17, 541–553. [Google Scholar] [CrossRef]
- Tarlochan, F. Sandwich Structures for Energy Absorption Applications: A Review. Materials 2021, 14, 4731. [Google Scholar] [CrossRef]
- Zhang, Z.-J.; Huang, L.; Li, B.-C.; Chen, T.; Zhang, Q.-C.; Jin, F. Design of a novel multi-walled tube-reinforced aluminum foam for energy absorption. Compos. Struct. 2021, 276, 114584. [Google Scholar] [CrossRef]
- Marsavina, L.; Kováčik, J.; Linul, E. Experimental validation of micromechanical models for brittle aluminium alloy foam. Theor. Appl. Fract. Mech. 2016, 83, 11–18. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Sun, Y.; Li, Q.M. Dynamic compressive behaviour of cellular materials: A review of phenomenon, mechanism and modelling. Int. J. Impact Eng. 2018, 112, 74–115. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Zheng, Z.; Yu, J. Low-velocity perforation behavior of composite sandwich panels with aluminum foam core. J. Sandwich Struct. Mater. 2012, 15, 92–109. [Google Scholar] [CrossRef]
- Babakhani, A.; Golestanipour, M.; Zebarjad, S.M. Modelling of aluminium foam core sandwich panels under impact perforation. Mater. Sci. Technol. 2016, 32, 1330–1337. [Google Scholar] [CrossRef]
- Golestanipour, M.; Babakhani, A.; Zebarjad, S.M. High-velocity perforation behaviour of sandwich panels with Al/SiCp composite foam core. J. Compos. Mater. 2020, 54, 1483–1495. [Google Scholar] [CrossRef]
- Hou, W.; Zhu, F.; Lu, G.; Fang, D.-I. Ballistic impact experiments of metallic sandwich panels with aluminium foam core. Int. J. Impact Eng. 2010, 37, 1045–1055. [Google Scholar] [CrossRef]
- Reyes, A.; Hopperstad, O.S.; Langseth, M. Aluminum foam-filled extrusions subjected to oblique loading: Experimental and numerical study. Int. J. Solids Struct. 2004, 41, 1645–1675. [Google Scholar] [CrossRef]
- Børvik, T.; Hopperstad, O.S.; Reyes, A.; Langseth, M.; Solomos, G.; Dyngeland, T. Empty and foam-filled circular aluminium tubes subjected to axial and oblique quasistatic loading. Int. J. Crashworthiness 2003, 8, 481–494. [Google Scholar] [CrossRef]
- Radford, D.D.; Deshpande, V.S.; Fleck, N.A. The use of metal foam projectiles to simulate shock loading on a structure. Int. J. Impact Eng. 2005, 31, 1152–1171. [Google Scholar] [CrossRef]
- Radford, D.D.; McShane, G.J.; Deshpande, V.S.; Fleck, N.A. The response of clamped sandwich plates with metallic foam cores to simulated blast loading. Int. J. Solids Struct. 2006, 43, 2243–2259. [Google Scholar] [CrossRef] [Green Version]
- Banhart, J.; Seeliger, H. Aluminium Foam Sandwich Panels: Manufacture, Metallurgy and Applications. Adv. Eng. Mater. 2008, 10, 793–802. [Google Scholar] [CrossRef]
- Banhart, J.; Seeliger, H.-W. Recent Trends in Aluminum Foam Sandwich Technology. Adv. Eng. Mater. 2012, 14, 1082–1087. [Google Scholar] [CrossRef]
- Hommel, P.; Roth, D.; Binz, H. Derivation of motivators for the use of aluminum foam sandwich and advantageous applications. Proc. Des. Soc. 2021, 1, 933–942. [Google Scholar] [CrossRef]
- Hommel, P.; Roth, D.; Binz, H. Deficits in the application of aluminum foam sandwich: An industrial perspective. Proc. Des. Soc. 2020, 1, 927–936. [Google Scholar] [CrossRef]
- Epasto, G.; Distefano, F.; Mozafari, H.; Linul, E.; Crupi, V. Nondestructive Evaluation of Aluminium Foam Panels Subjected to Impact Loading. Appl. Sci. 2021, 11, 1148. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, Z.; Yu, T.; Xin, D. Mechanical properties and energy absorption capabilities of aluminium foam sandwich structure subjected to low-velocity impact. Constr. Build. Mater. 2021, 273, 121996. [Google Scholar] [CrossRef]
- Elnasri, I.; Zhao, H. Impact perforation of sandwich panels with aluminum foam core: A numerical and analytical study. Int. J. Impact Eng. 2016, 96, 50–60. [Google Scholar] [CrossRef]
- Zhao, H.; Elnasri, I.; Girard, Y. Perforation of aluminium foam core sandwich panels under impact loading—An experimental study. Int. J. Impact Eng. 2007, 34, 1246–1257. [Google Scholar] [CrossRef]
- Qi, C.; Yang, S.; Yang, L.-J.; Wei, Z.-Y.; Lu, Z.-H. Blast resistance and multi-objective optimization of aluminum foam-cored sandwich panels. Compos. Struct. 2013, 105, 45–57. [Google Scholar] [CrossRef]
- Ren, C.-X.; Hu, Z.-F.; Yao, C.; Mo, F. Experimental study on the quasi-static compression behavior of multilayer aluminum foam sandwich structure. J. Alloys Compd. 2019, 810, 151860. [Google Scholar] [CrossRef]
- Morton, D. Characterization and Modeling of the Mechanical Behavior of Polymer Foam. Ph.D. Thesis, Department of Structural Engineering, Norwegian University of Science and Technology, Trondheim, Norway, 2021. [Google Scholar]
- Zhang, X.; Chen, Q.; Gao, J.; Wang, M.; Zhang, Y.; Cai, Z. Numerical Study on the Plastic Forming of Doubly Curved Surfaces of Aluminum Foam Sandwich Panel Using 3D Voronoi Model. Metals 2021, 11, 675. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Q.-M.; Cai, Z.-Y. Prediction and prevention of fracture defect in plastic forming for aluminum foam sandwich panel. J. Mater. Res. Technol. 2021, 15, 1145–1154. [Google Scholar] [CrossRef]
- Ko, Y.K.; Lee, J.S.; Huh, H.; Kim, H.K.; Park, S.H. Prediction of fracture in hub-hole expanding process using a new ductile fracture criterion. J. Mater. Proc. Technol. 2007, 187, 358–362. [Google Scholar] [CrossRef]
- Maire, E.; Withers, P.J. Quantitative X-ray tomography. Int. Mater. Rev. 2014, 59, 1–43. [Google Scholar] [CrossRef] [Green Version]
- Maire, E.; Fazekas, A.; Salvo, L.; Dendievel, R.; Youssef, S.; Cloetens, P.; Letang, J.M. X-ray tomography applied to the characterization of cellular materials. Related finite element modeling problems. Compos. Sci. Technol. 2003, 63, 2431–2443. [Google Scholar] [CrossRef]
- Maire, E.; Buffière, J.Y.; Salvo, L.; Blandin, J.J.; Ludwig, W.; Létang, J.M. On the application of X-ray microtomography in the field of materials science. Adv. Eng. Mater. 2001, 3, 539–546. [Google Scholar] [CrossRef]
- Crupi, V.; Epasto, G.; Guglielmino, E. Comparison of aluminium sandwiches for lightweight ship structures: Honeycomb vs. foam. Marine Struct. 2013, 30, 74–96. [Google Scholar] [CrossRef]
- Petit, C.; Maire, E.; Meille, S.; Adrien, J. Two-scale study of the fracture of an aluminum foam by X-ray tomography and finite element modeling. Mater. Des. 2017, 120, 117–127. [Google Scholar] [CrossRef]
- Vestrum, O.; Langseth, M.; Børvik, T. Finite element modeling of porous polymer pipeline coating using X-ray micro computed tomography. Compos. Part B Eng. 2019, 172, 406–415. [Google Scholar] [CrossRef]
- Vestrum, O.; Dæhli, L.E.B.; Hopperstad, O.S.; Børvik, T. Constitutive modeling of a graded porous polymer based on X-ray computed tomography. Mater. Des. 2020, 188, 108449. [Google Scholar] [CrossRef]
- Vestrum, O.; Langseth, M.; Børvik, T. Finite element analysis of porous polymer coated pipelines subjected to impact. Int. J. Impact Eng. 2021, 152, 103825. [Google Scholar] [CrossRef]
- Havel Metal Foam. Available online: https://en.havel-mf.com/ (accessed on 10 January 2022).
- Uberalli, G.; Ferraris, S. Al-based metal foams (AMF) as permanent cores in casting: State-of-the-art and future perspectives. Metals 2020, 10, 1592. [Google Scholar] [CrossRef]
- Campana, F.; Cortese, L.; Pilone, D. Property variations in large AlSi7 alloy foam ingots. Mater. Sci. Eng. A 2012, 556, 400–407. [Google Scholar] [CrossRef]
- eCorr–SIMLab–NTNU. Available online: https://www.ntnu.edu/kt/ecorr/ (accessed on 13 January 2022).
- Deshpande, V.S.; Fleck, N.A. Isotropic models for metallic foams. J. Mech. Phys. Solids 2000, 48, 1253–1283. [Google Scholar] [CrossRef] [Green Version]
- Børvik, T.; Langseth, M.; Hopperstad, O.S.; Malo, K.A. Ballistic penetration of steel plates. Int. J. Impact Eng. 1999, 22, 855–886. [Google Scholar] [CrossRef]
- Dey, S.; Børvik, T.; Teng, X.; Wierzbicki, T.; Hopperstad, O.S. On the ballistic resistance of double-layered steel plates: An experimental and numerical investigation. Int. J. Solids Struct. 2007, 44, 6701–6723. [Google Scholar] [CrossRef] [Green Version]
- Holmen, J.K.; Solberg, J.K.; Hopperstad, O.S.; Børvik, T. Ballistic impact of layered and case-hardened steel plates. Int. J. Impact Eng. 2017, 110, 4–14. [Google Scholar] [CrossRef]
- Recht, R.F.; Ipson, T.W. Ballistic perforation dynamics. ASME J. Appl. Mech. 1960, 30, 384–390. [Google Scholar] [CrossRef]
- Available online: http://lstc.com/products/ls-dyna (accessed on 31 January 2022).
- Børvik, T.; Hopperstad, O.S.; Berstad, T.; Langseth, M. A computational model of viscoplasticity and ductile damage for impact and penetration. Eur. J. Mech. A/Solids 2001, 20, 685–712. [Google Scholar] [CrossRef]
- Hanssen, A.G.; Hopperstad, O.S.; Langseth, M. Validation of constitutive models applicable to aluminium foams. Int. J. Mech. Sci. 2002, 44, 359–406. [Google Scholar] [CrossRef]
- Reyes, A.; Hopperstad, O.S.; Berstad, T.; Hanssen, A.G.; Langseth, M. Constitutive modelling of aluminium foam including fracture and statistical variation of density. Eur. J. Mech. A/Solids 2003, 32, 815–835. [Google Scholar] [CrossRef]


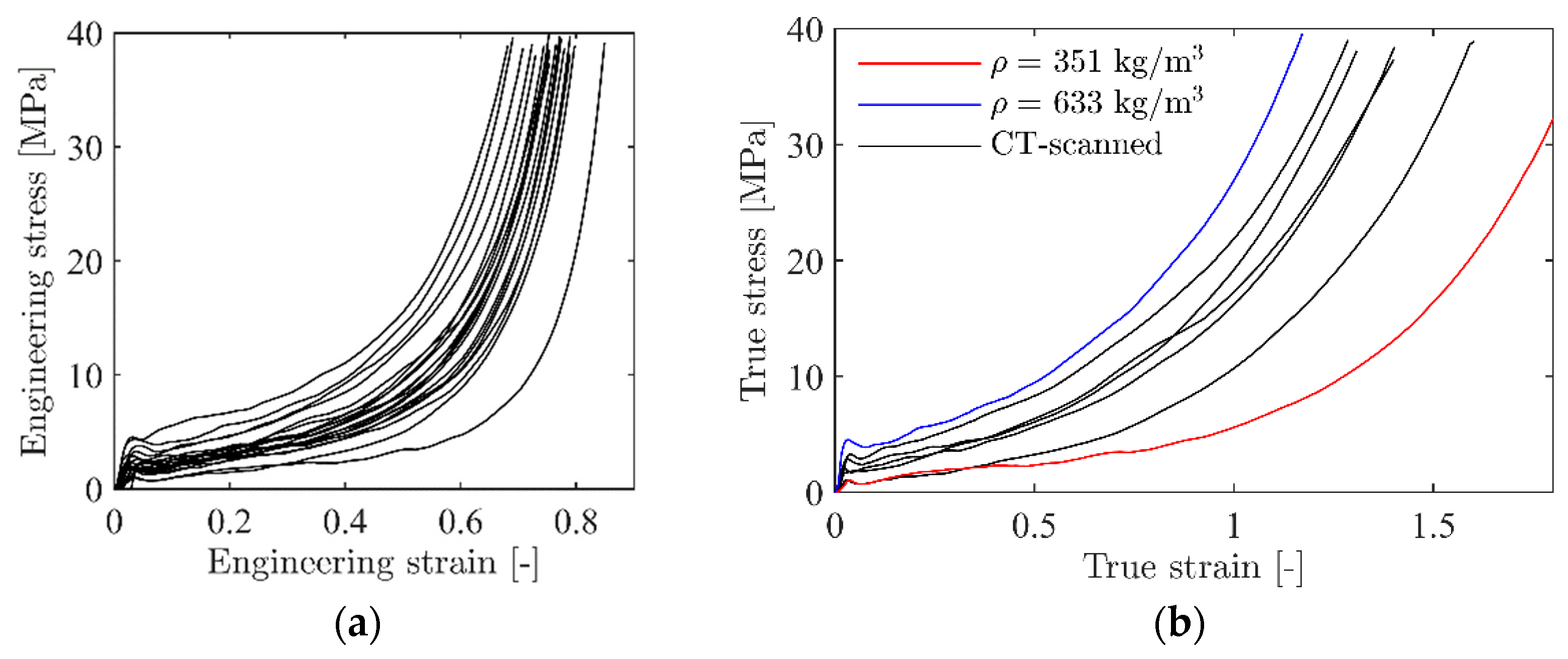

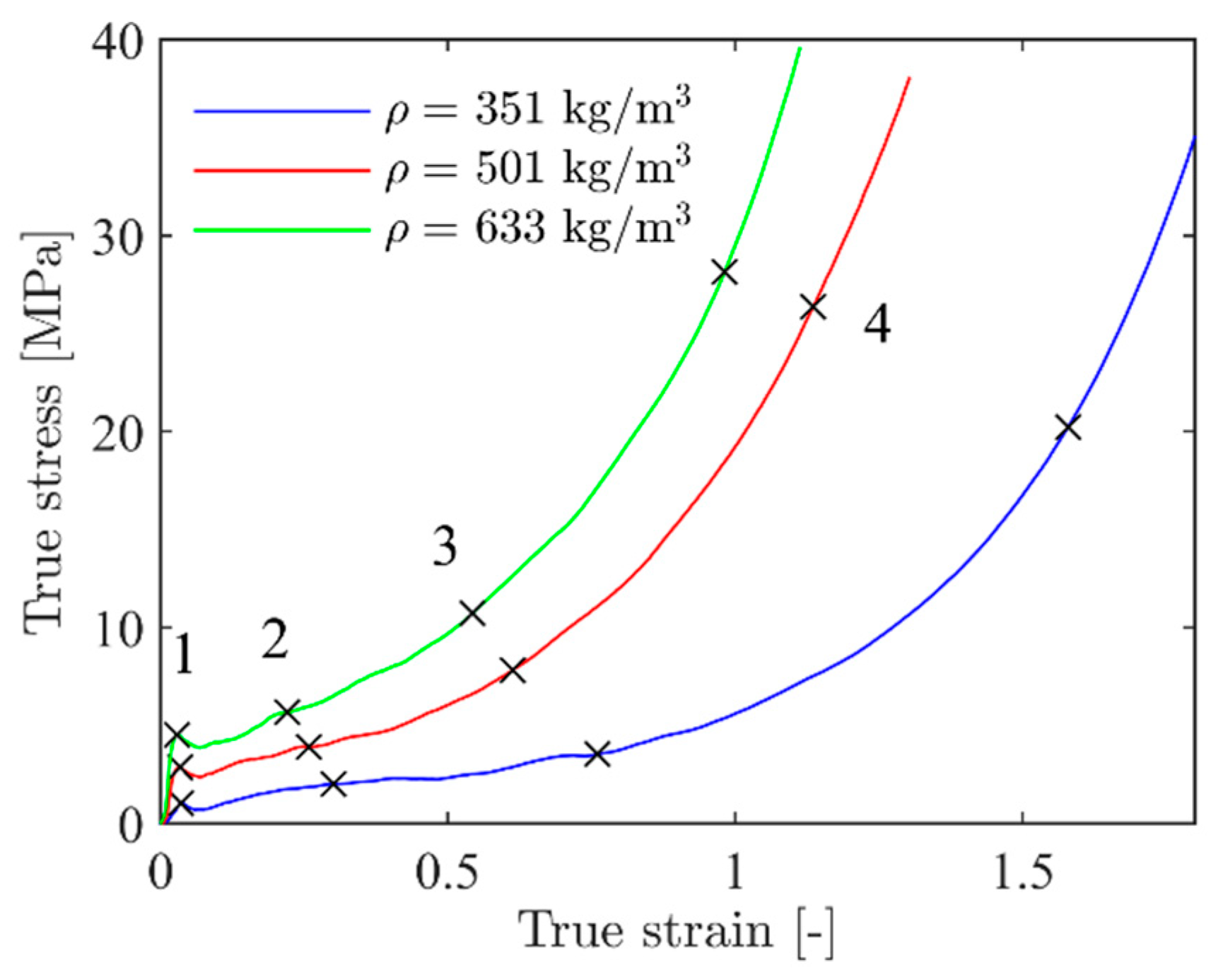













| Specimen # | Density ρ [kg/mm3] | Elastic Modulus E [GPa] | Yield Stress [MPa] | Plateau Stress [MPa] | Densification Strain [-] |
|---|---|---|---|---|---|
| 6 | 351 | 2.6 | 1.03 | 1.97 | 2.04 |
| 19 | 501 | 4.6 | 2.88 | 4.16 | 1.68 |
| 9 | 633 | 6.8 | 4.52 | 6.58 | 1.45 |
| Specimen # | Density [kg/mm3] | [MPa] | [-] | [MPa] | [MPa] | [-] | [-] |
|---|---|---|---|---|---|---|---|
| 6 | 351 | 1.03 | 2.04 | 2.04 | 2.04 | 3.86 | 12 |
| 12 | 443 | 2.27 | 1.81 | 5.41 | 1.81 | 3.15 | 4.5 |
| 19 | 501 | 2.88 | 1.68 | 1.45 | 1.68 | 2.43 | 3.2 |
| 2 | 581 | 3.77 | 1.54 | 5.45 | 1.54 | 2.01 | 1.85 |
| 9 | 633 | 4.16 | 1.45 | 1.68 | 1.45 | 2.13 | 1.4 |
| [MPa] | [-] | [-] | [-] | [-] | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1.02 | 0 | |
| 198.4 | 0.34 | 0.31 | 0.19 | 0.0046 | |
| 2.60 | −1.37 | −2.42 | −1.29 | −3.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brekken, K.A.; Vestrum, O.; Dey, S.; Reyes, A.; Børvik, T. Experimental Tests and Numerical Simulations on the Ballistic Impact Response of a Highly Inhomogeneous Aluminium Foam. Materials 2022, 15, 4651. https://doi.org/10.3390/ma15134651
Brekken KA, Vestrum O, Dey S, Reyes A, Børvik T. Experimental Tests and Numerical Simulations on the Ballistic Impact Response of a Highly Inhomogeneous Aluminium Foam. Materials. 2022; 15(13):4651. https://doi.org/10.3390/ma15134651
Chicago/Turabian StyleBrekken, Kristoffer A., Ole Vestrum, Sumita Dey, Aase Reyes, and Tore Børvik. 2022. "Experimental Tests and Numerical Simulations on the Ballistic Impact Response of a Highly Inhomogeneous Aluminium Foam" Materials 15, no. 13: 4651. https://doi.org/10.3390/ma15134651
APA StyleBrekken, K. A., Vestrum, O., Dey, S., Reyes, A., & Børvik, T. (2022). Experimental Tests and Numerical Simulations on the Ballistic Impact Response of a Highly Inhomogeneous Aluminium Foam. Materials, 15(13), 4651. https://doi.org/10.3390/ma15134651







