Fractal Permeability Model of Newtonian Fluids in Rough Fractured Dual Porous Media
Abstract
:1. Introduction
2. Fractal Theory of Fractured Dual Porous Medium
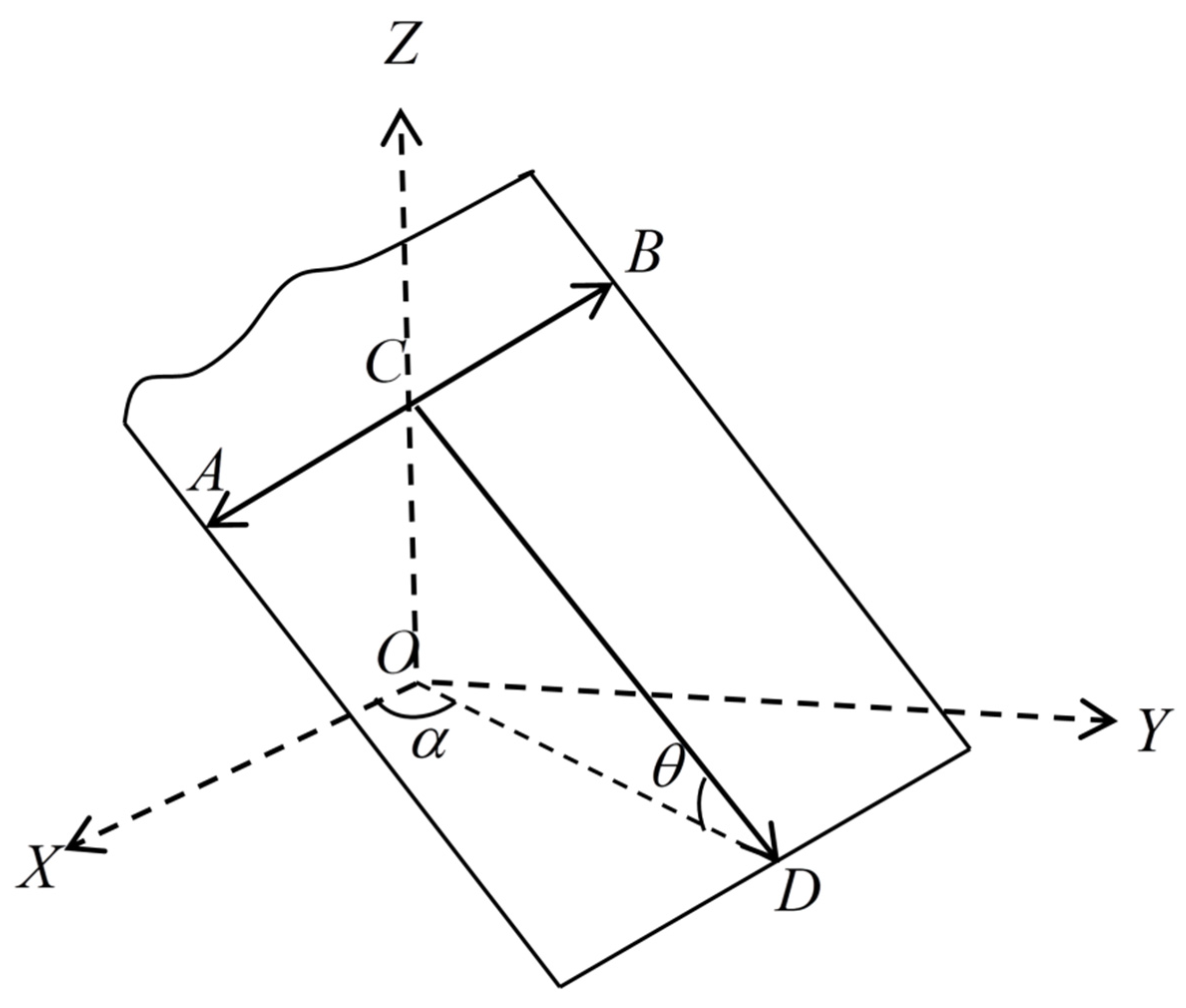
2.1. Fractal Theory of Fracture Networks
2.2. Fractal Theory of Matrix Pores
3. Characterization of Rough Surfaces of Fractured Double Porous Media
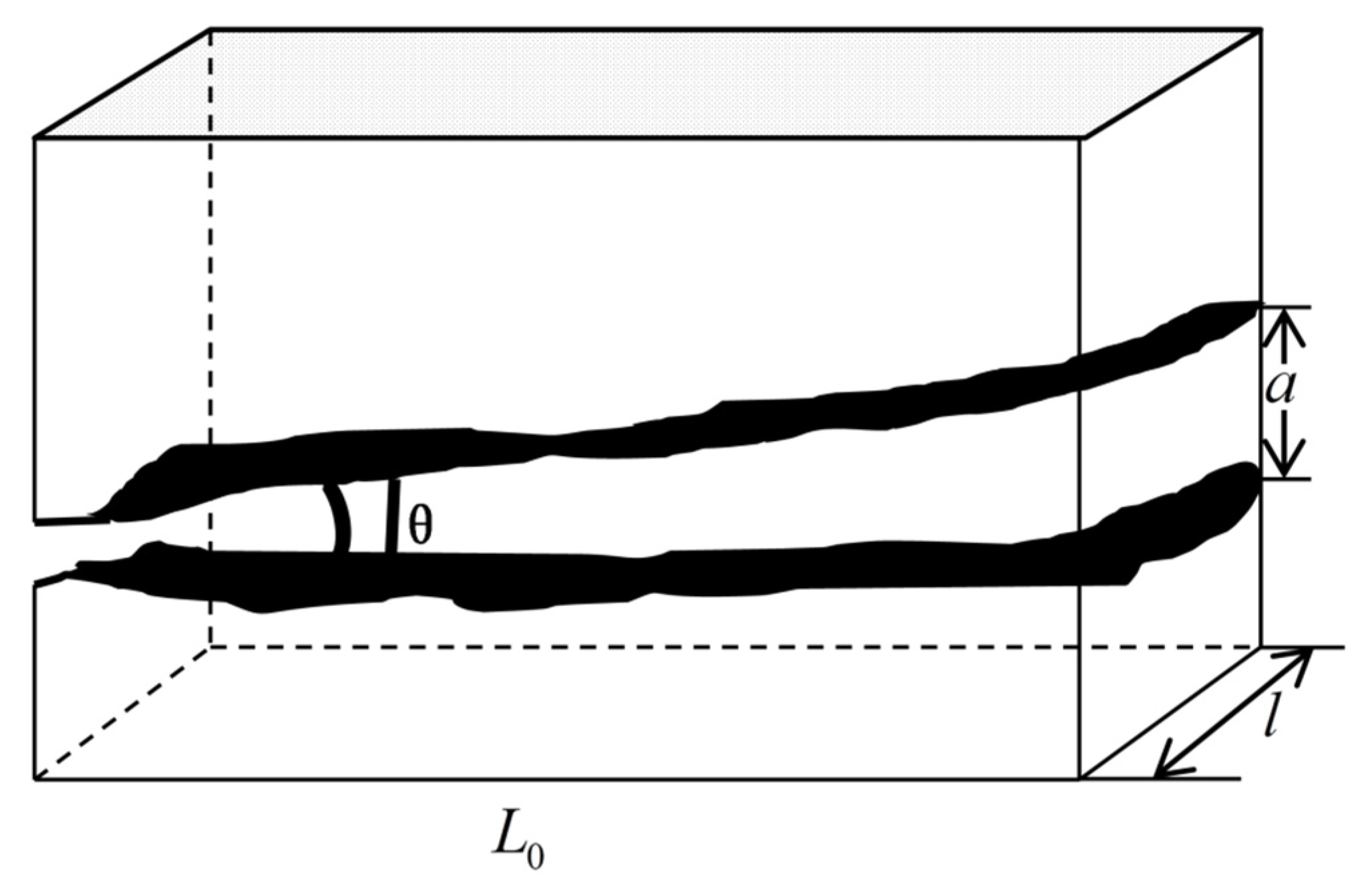
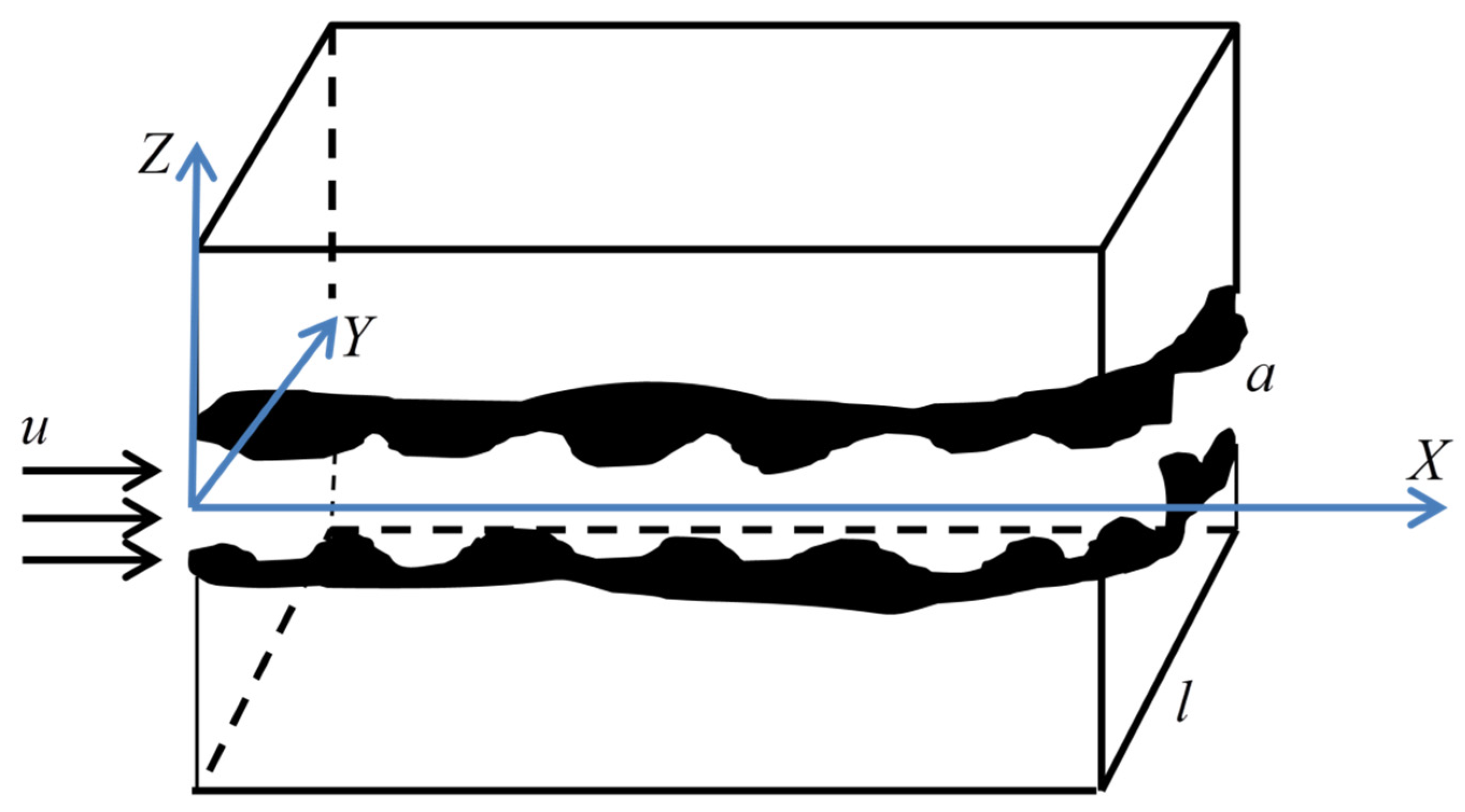
3.1. Characterization of Rough Surfaces of Fracture Networks
3.2. Characterization of Rough Surfaces of Matrix Pores
4. Fractal Model of Seepage in Rough Fractured Dual Porous Media
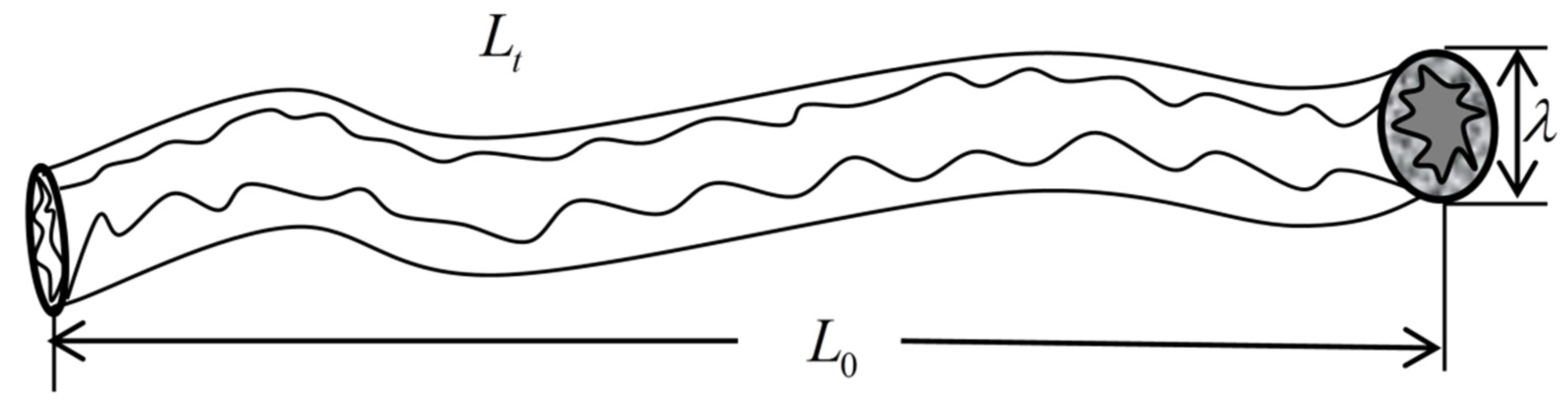
4.1. Seepage Characteristics of Rough Fracture Networks
4.2. Seepage Characteristics of Pores in Rough Matrix
4.3. Permeability Model of Rough Fractured Double Porous Media
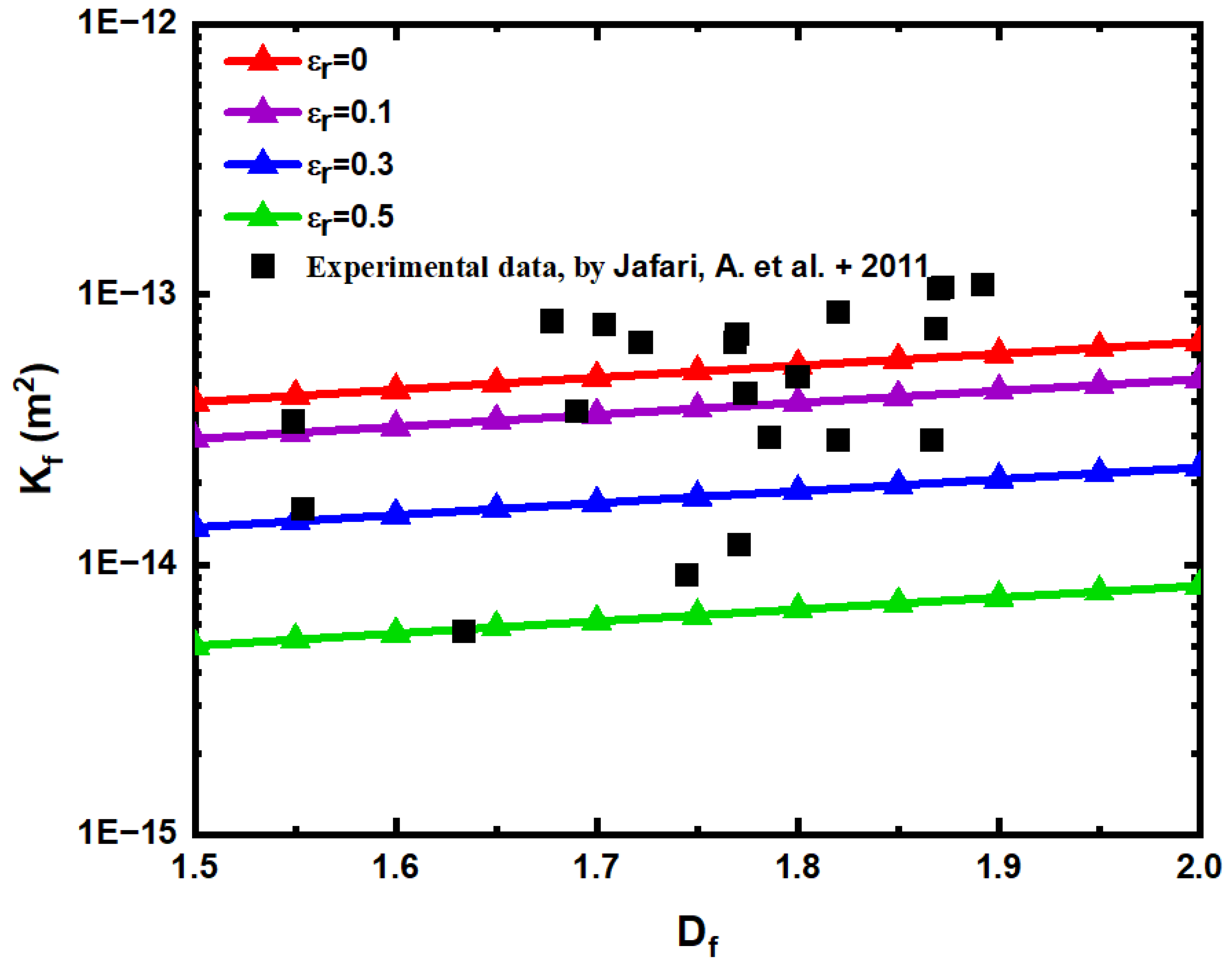
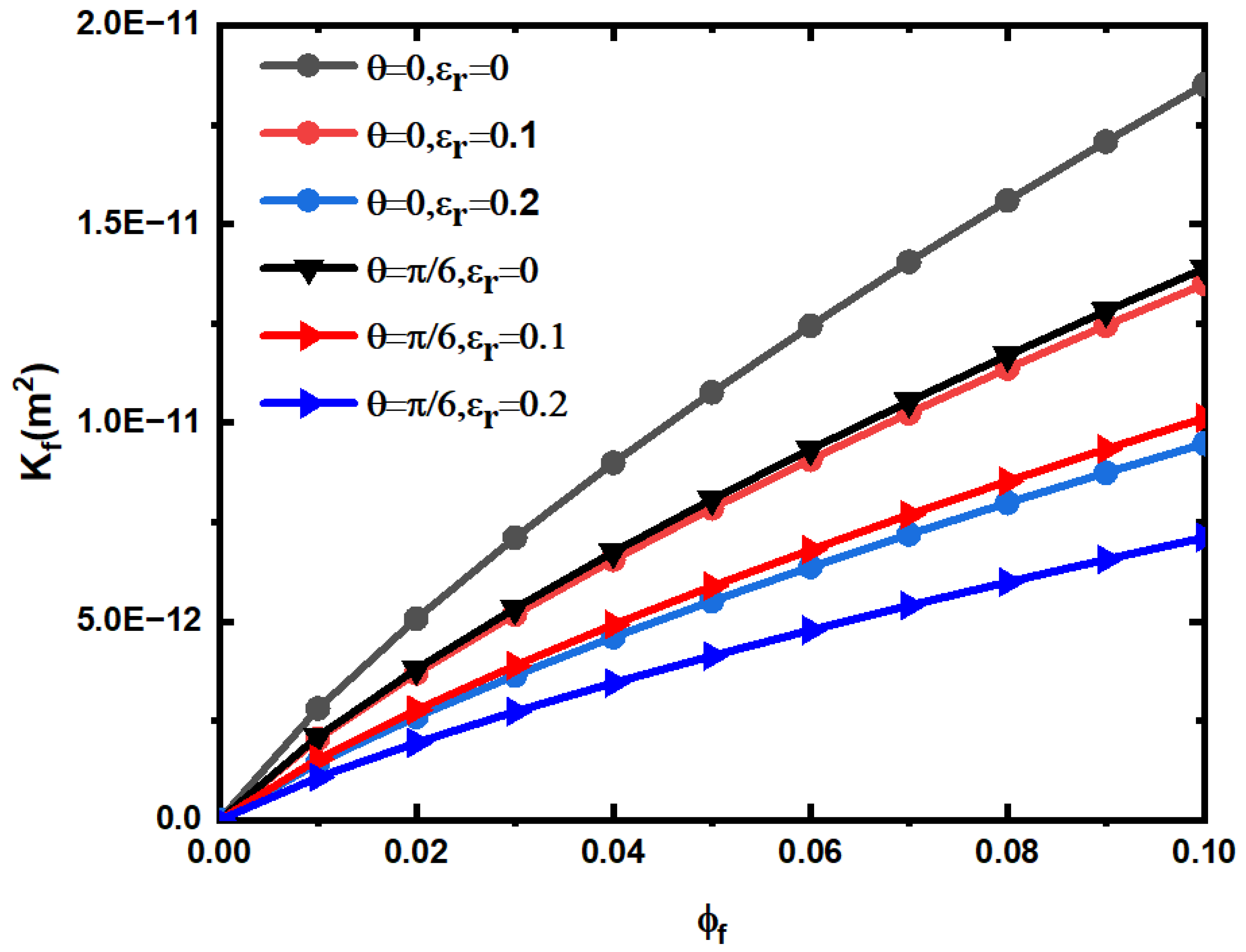
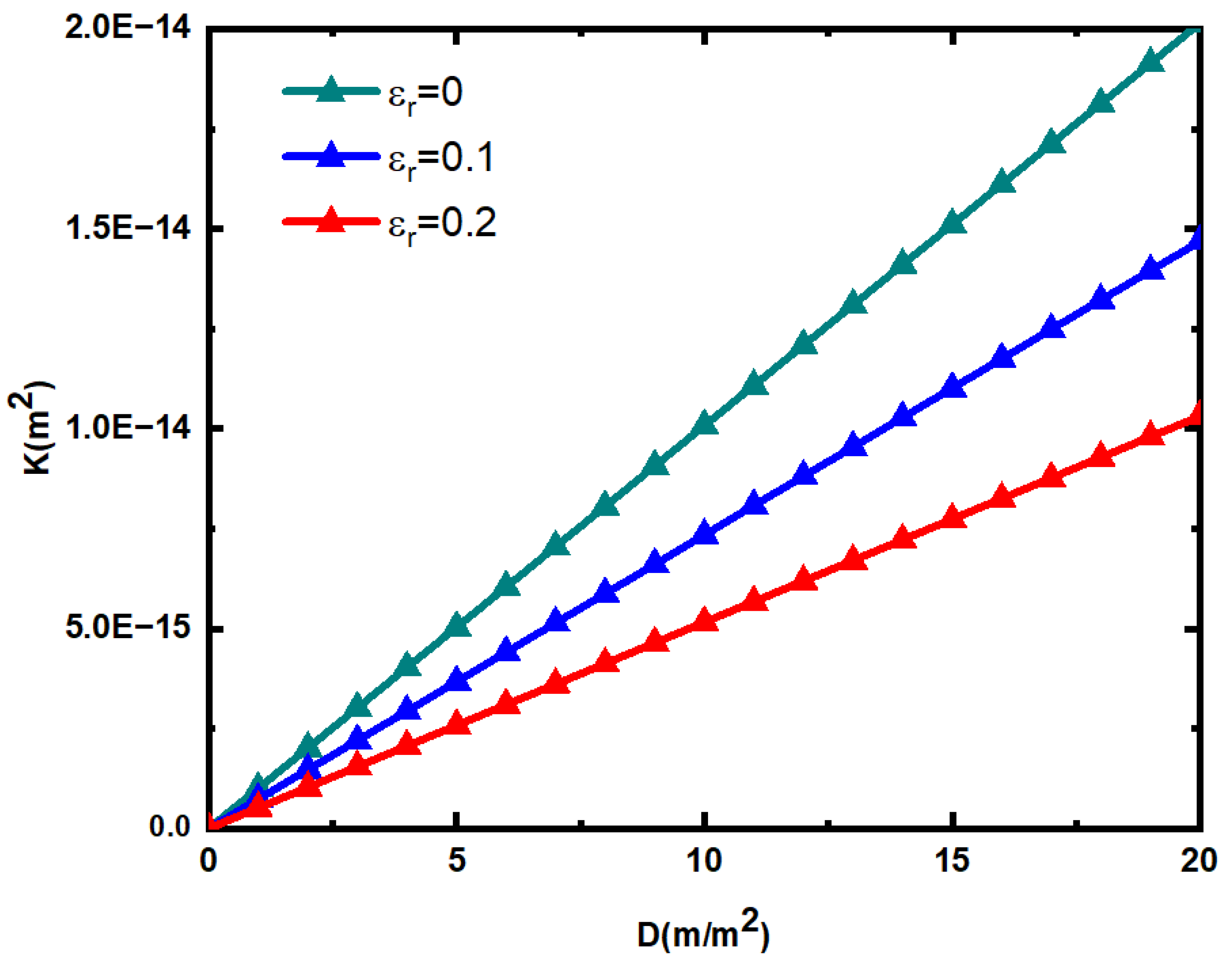
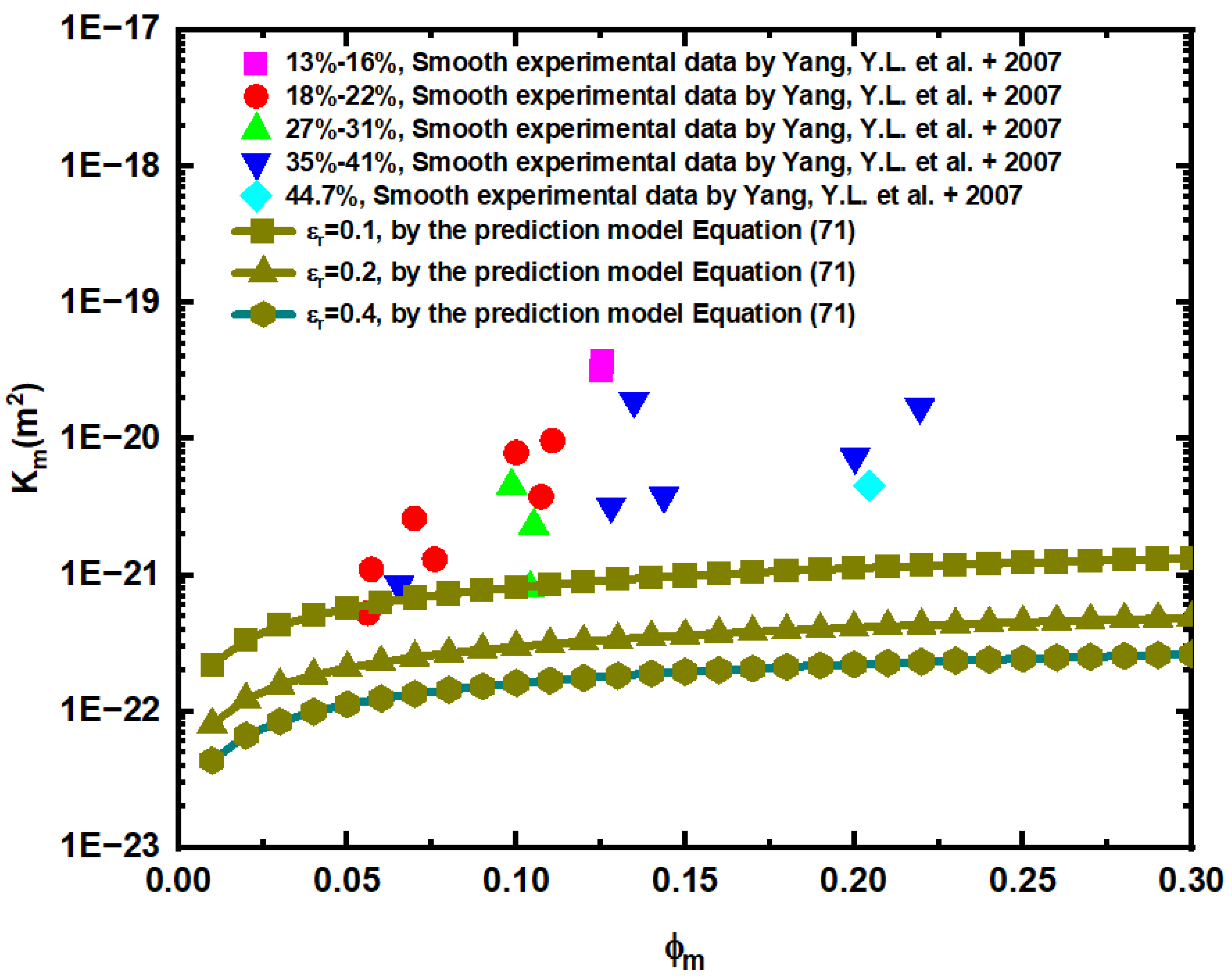
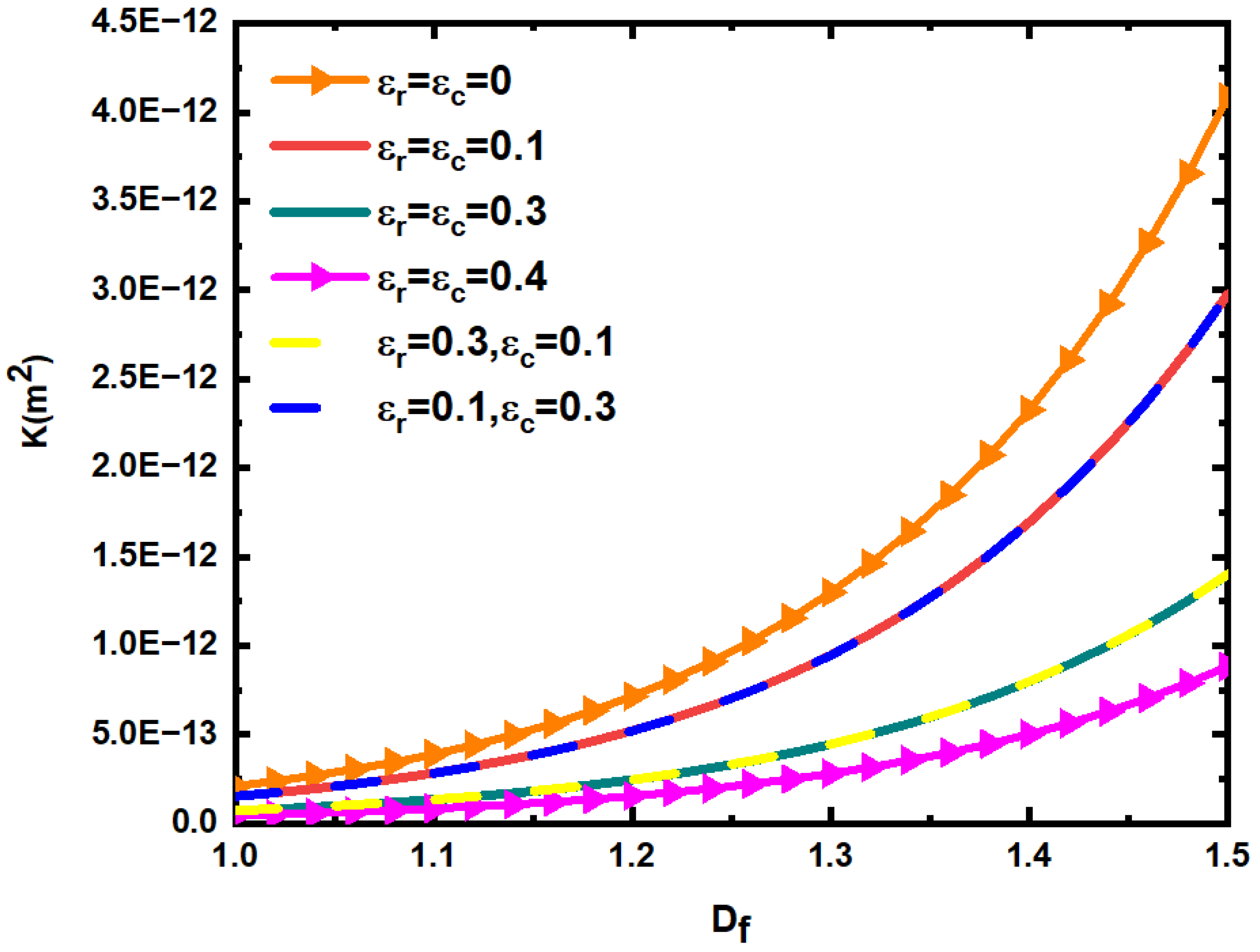
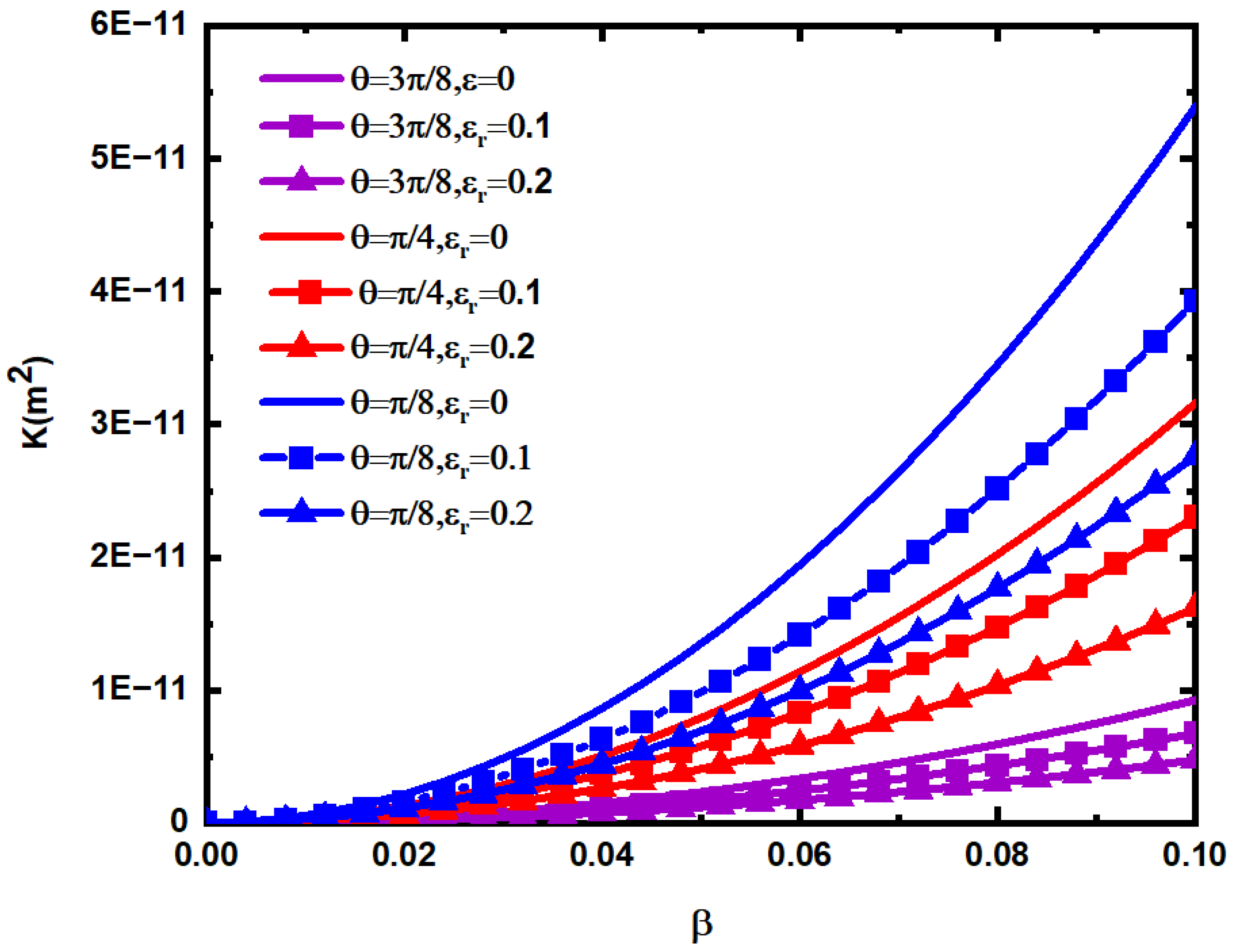
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| The opening of the fracture | |
| The trace length of the fracture | |
| The average inclination angle of fractures | |
| The average azimuth angle of fractures | |
| The ratio of fracture opening to fracture trace length | |
| The diameter of the capillary | |
| The fractal dimension of fracture trace length | |
| The fractal dimension of pore diameter | |
| The percentage of the total bottom area of all cones to the total area of fracture surface in the fracture network representative elementary volume | |
| The porosity of the fracture network | |
| The porosity of the matrix pores | |
| The effective average height of rough elements in fracture | |
| The effective average height of rough elements on rough capillaries | |
| The relative roughness of the fracture surface | |
| The relative roughness of the rough capillary bundle | |
| The average tortuosity of the capillary | |
| The average diameter of the pores | |
| The total flow of fluids through the rough fractures network representative elementary volume | |
| The total flow of fluids through the matrix representative elementary volume | |
| The permeability of the fracture network | |
| The permeability of rough matrices pores | |
| The characteristic length of the capillary | |
| The actual length of the capillary | |
| The bottom diameter of the cone | |
| The height of the cone | |
| The ratio of the height of the cone to the diameter of the base | |
| The tortuosity fractal dimension | |
| The fractal dimension of the bottom diameter of the cone | |
| The total bottom area of all cones in representative elementary volume | |
| The total area of fracture surface in representative elementary volume | |
| The total area of fracture pores | |
| The total matrix pores area | |
| The cross-section area of the representative elementary volume of the fracture network | |
| The cross-sectional area of matrix representative elementary volume | |
| The bottom area of a small cone | |
| The total volume of all cones in the representative elementary volume | |
| The volume of a small cone | |
| The fracture areal density | |
| The total flow of fluids in the fractured dual porous media | |
| The permeability of a Newtonian fluid in rough fractured double porous media | |
| The dimensionless permeability |
References
- Xiao, B.Q.; Liu, Z.J.; Zhang, Y.D.; Liang, M.C.; Long, G.B.; Zhao, Z. An investigation on spontaneous imbibition in tree-like branching network with fractal roughened surfaces. Fractals 2021, 29, 1–13. [Google Scholar] [CrossRef]
- Liu, Y.H.; Li, Z.H.; Xiao, B.Q.; Chen, H.X.; Long, G.B. A novel model for effective thermal conductivity of tree-like branching network with fractal roughened surfaces. Fractals 2021, 29, 2150165. [Google Scholar] [CrossRef]
- Xiao, B.Q.; Zhang, M.; Chen, H.X.; Cao, J.Y.; Long, G.B.; Zhao, Z. A fractal model for predicting the effective thermal conductivity of roughened porous media with microscale effect. Fractals 2021, 29, 2150114. [Google Scholar] [CrossRef]
- Li, Y.; Luo, H.W.; Li, H.T.; Liu, X.J.; Tan, Y.S.; Chen, S.N.; Cai, J.C. A brief review of dynamic capillarity effect and its characteristics in low permeability and tight reservoirs. J. Petrol. Sci. Eng. 2020, 189, 106959. [Google Scholar] [CrossRef]
- Cai, J.C.; Tian, Z.H.; Zhou, S.W.; Xiong, Y.H.; Sun, C.H.; Zeng, J.H. Controlling Factor Analysis of Microstructural Property and Storage Capacity of Deep Longmaxi Formation Shale in Sichuan Basin. Energ. Fuel. 2021, 35, 20092–20102. [Google Scholar] [CrossRef]
- Kang, Y.L.; Zhang, J.Y.; Xu, C.Y.; You, L.J.; Lin, C. The effect of geometrical morphology of rigid lost circulation material on its retention behavior in fractures. Petr. Drill. Techn. 1900, 46, 26–34. [Google Scholar]
- Pasquier, S.; Quintard, M.; Davit, Y. Modeling flow in porous media with rough surfaces: Effective slip boundary conditions and application to structured packings. Chem. Eng. Sci. 2017, 165, 131–146. [Google Scholar] [CrossRef] [Green Version]
- Liang, M.C.; Fu, C.G.; Xiao, B.Q.; Luo, L.; Wang, Z.K. A fractal study for the effective electrolyte diffusion through charged porous media. Int. J. Heat Mass Tran. 2019, 137, 365–371. [Google Scholar] [CrossRef]
- Xiao, B.Q.; Wang, W.; Zhang, X.; Long, G.B.; Chen, H.X.; Cai, H.T.; Deng, L. A novel fractal model for relative permeability of gas diffusion layer in proton exchange membrane fuel cell with capillary pressure effect. Fractals 2019, 27, 1950012. [Google Scholar] [CrossRef]
- Bonnet, E.; Bour, O.; Odling, N.E.; Davy, P.; Main, I.; Cowie, P.; Berkowitz, B. Scaling of fracture systems in geological media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.; Li, X.; Chen, Z.; Li, J.; Jiang, L. Gas transport behavior through micro fractures of shale and tight gas reservoirs. Chin. J. Theor. Appl. Mech. 2015, 47, 955–964. [Google Scholar]
- Yu, B.M.; Li, J.H. Some fractal characters of porous media. Fractals 2001, 9, 365–372. [Google Scholar] [CrossRef]
- Yu, B.M.; Cheng, P. A fractal permeability model for bi-dispersed porous media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Wang, S.F.; Wu, T.; Deng, Y.J.; Zheng, Q.S. A New Fractal Model for the Permeability of Porous Media. Chin. Quart. Mech. 2016, 37, 293–301. [Google Scholar]
- Zhu, Z.W.; Liu, J.J.; Wu, M.Y. Study on Seepage Characteristics of Fractured Porous Media Based on Fractal-Like Tree Network. In Proceedings of the International Conference on Geo-Fluid Resources Development, Wuhan, China, 27–28 October 2017; Aussino Academic Publishing House: Sydney, Australia, 2017; pp. 508–513. [Google Scholar]
- Wang, F.Y.; Jiao, L.; Zhao, J.Y.; Cai, J.C. A more generalized model for relative permeability prediction in unsaturated fractal porous media. J. Nat. Gas. Sci. Eng. 2019, 67, 82–92. [Google Scholar] [CrossRef]
- Zhang, Q.F.; Yao, J.; Huang, Z.Q.; Wang, Y.Y. A Multiscale Deep Learning Model for Fractured Porous Media. Chin. J. Comput. Phys. 2019, 36, 665–671. [Google Scholar]
- Zeng, F.H.; Zhang, T.; Yang, J.; Guo, J.C.; Zhang, Q.; Ren, W.X. A fractal permeability model for the dual-porosity media of tight gas reservoirs. Energy Explor. Exploit. 2021, 39, 224–242. [Google Scholar] [CrossRef]
- Miao, T.J.; Yang, S.S.; Long, Z.C.; Yu, B.M. Fractal analysis of permeability of dual-porosity media embedded with random fractures. Int. J. Heat Mass Tran. 2015, 88, 814–821. [Google Scholar] [CrossRef]
- Miao, T.J.; Chen, A.; Xu, Y.; Cheng, S.J.; Yu, B.T. A fractal permeability model for porous–fracture media with the transfer of fluids from porous matrix to fracture. Fractals 2019, 27, 1950121. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, G.; Gao, F.; Ye, D.; Luo, J. A Complex Network Model for Analysis of Fractured Rock Permeability. Adv. Civ. Eng. 2020, 2020, 8824082. [Google Scholar] [CrossRef]
- Wu, T.; Li, G. A fractal model of permeability for power-law fluids in porous-fracture dual media. J. Hua Zhong Norm. Univers. 2021, 55, 376–381. [Google Scholar]
- Xiong, F.S.; Gan, L.D.; Sun, W.T.; Yang, H. Characterization of reservoir permeability and analysis of influencing factors in fracture-pore media. Chin. J. Geophys. 2021, 64, 279–288. [Google Scholar]
- Qu, G.Z.; Qu, Z.Q.; Hazlett, R.D.; Freed, D.; Mustafayev, R. Geometrical description and permeability calculation about shale tensile micro-fractures. Petrol. Explor. Dev. 2016, 43, 115–120. [Google Scholar] [CrossRef]
- Yang, S.S.; Yu, B.M.; Zou, M.Q.; Liang, M.C. A fractal analysis of laminar flow resistance in roughened microchannels. Int. J. Heat Mass Tran. 2014, 77, 208–217. [Google Scholar] [CrossRef]
- Xiao, B.Q.; Huang, Q.W.; Chen, H.X.; Chen, X.B.; Long, G.B. A fractal model for capillary flow through a single tortuous capillary with roughened surfaces in fibrous porous media. Fractals 2021, 29, 2150017. [Google Scholar] [CrossRef]
- Gao, J.; Li, Z.H.; Xiao, B.Q.; Liu, Y.H.; Liang, M.C. A novel fractal model for the invasion depth of fluid through the tortuous capillary bundle with roughened surfaces in porous media. Fractals 2021, 29, 1–10. [Google Scholar] [CrossRef]
- He, Y.F.; Tian, X.R.; Dou, X.J.; Wang, X.; Tao, L.; Zhao, H.Y. Fracture permeability of shale gas reservoir considering tortuosity. Fault-Block Oil Gas. Field. 2020, 27, 613–618. [Google Scholar]
- Zhang, G.; Tian, Y.; Li, Y.J. Numerical study on the mechanism of fluid flow through single rough fractures with different JRC. Sci. Sin. Phys. Mech. Astron. 2019, 49, 30–39. [Google Scholar] [CrossRef]
- Wang, P.F.; Tan, W.H.; Ma, X.W.; Li, Z.J.; Liu, J.J.; Wu, Y.F. Experimental study of seepage characteristics of consecutive and filling fracture with different roughness levels and gap-widths. Rock Soil Mech. 2019, 40, 3062–3070. [Google Scholar]
- Li, Z.H.; Chen, S.J. Numerical simulation of seepage characteristics of fractures with different roughness. Min. Saf. Envir. Prot. 2021, 48, 6–11. [Google Scholar]
- Yu, B.M.; Lee, L.J. A fractal in-plane permeability model for fabrics. Polym. Compos. 2004, 23, 201–221. [Google Scholar] [CrossRef]
- Chen, Y.P.; Shi, M.H. Determination of permeability for porous media using fractal theory. J. T. Singhua. Univ. 2000, 40, 94–97. [Google Scholar]
- Yu, B.M. Analysis of flow in fractal porous media. Appl. Mech. Rev. 2008, 61, 50801. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Role of Fractal Geometry in Roughness Characterization and Contact Mechanics of Surfaces. J. Tribol. Trans. ASME 1990, 112, 205–216. [Google Scholar] [CrossRef]
- Miao, T.; Yu, B.; Duan, Y.; Fang, Q. A fractal analysis of permeability for fractured rocks. Int. J. Heat Mass Transf. 2015, 81, 75–80. [Google Scholar] [CrossRef]
- Zhang, X.; Sanderson, D.J. Numerical study of critical behaviour of deformation and permeability of fractured rock masses. Mar. Petrol. Geol. 1998, 15, 535–548. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Hunt, A.G.; Ewing, R.P.; Sahimi, M. Tortuosity in porous media: A critical review. Soil. Sci. Soc. Am. J. 2013, 77, 1461–1477. [Google Scholar] [CrossRef]
- Yu, B.; Li, J.H. A geometry model for tortuosity of flow path in porous media. Chin. Phys. Lett. 2004, 21, 1569–1571. [Google Scholar]
- Yu, B. Fractal character for tortuous streamtubes in porous media. Chin. Phys. Lett. 2005, 22, 158–161. [Google Scholar]
- Guo, L.X.; Jiao, L.C.; Wu, Z.S. Electromagnetic scattering from two-dimensional rough surface using the Kirchhoff Approximation. Chin. Phys. Lett. 2001, 18, 214–216. [Google Scholar]
- Poljacek, S.M.; Risovic, D.; Furic, K.; Gojo, M. Comparison of fractal and profilometric methods for surface topography characterization. Appl. Surf. Sci. 2008, 254, 3449–3458. [Google Scholar] [CrossRef]
- Yang, S.S.; Liang, M.C.; Yu, B.M.; Zou, M.Q. Permeability model for fractal porous media with rough surfaces. Microfluid. Nanofluid. 2015, 18, 1085–1093. [Google Scholar] [CrossRef]
- Yang, S.S.; Fu, H.H.; Yu, B.M. Fractal Analysis of Flow Resistance in Tree-Like Branching Networks with Roughened Microchannels. Fractals 2017, 25, 1750008. [Google Scholar] [CrossRef]
- Liang, M.C.; Yang, S.S.; Miao, T.J.; Yu, B.M. Analysis of electroosmotic characters in fractal porous media. Chem. Eng. Sci. 2015, 127, 202–209. [Google Scholar] [CrossRef]
- Khamforoush, M.; Shams, K.; Thovert, J.F.; Adler, P.M. Permeability and percolation of anisotropic three-dimensional fracture networks. Phys. Rev. E 2008, 77, 056307. [Google Scholar] [CrossRef]
- Liu, Y.T.; Ding, Z.P.; Qu, Y.G.; Zhao, C.J. The characterization of fracture orientation and the calculation of anisotropic permeability parameters of reservoirs. Acta Pet. Sinica 2011, 32, 842–846. [Google Scholar]
- Wu, H.Y.; Cheng, P. Friction factors in smooth trapezoidal silicon microchannels with different aspect ratios. Int. J. Heat Mass Tran. 2003, 46, 2519–2525. [Google Scholar] [CrossRef]
- Chen, J.; Yu, B.M.; Xu, P.; Li, Y.H. Fractal-like tree networks increasing the permeability. Phys. Rev. E 2007, 75, 056301. [Google Scholar] [CrossRef]
- Jafari, A.; Babadagli, T.F. Effective fracture network permeability of geothermal reservoirs. Geothermics 2011, 40, 25–38. [Google Scholar] [CrossRef]
- Yang, Y.L.; Aplin, A.C. Permeability and petrophysical properties of 30 natural mudstones. J. Geophys. Res. Solid Earth 2007, 112, B03206. [Google Scholar] [CrossRef]
- Perera, M.S.A.; Ranjith, P.G.; Choi, S.K.; Airey, D. Numerical simulation of gas flow through porous sandstone and its experimental validation. Fuel 2011, 90, 547–554. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Wang, M.; Zheng, S.; Zeng, S.; Gao, L. Fractal Permeability Model of Newtonian Fluids in Rough Fractured Dual Porous Media. Materials 2022, 15, 4662. https://doi.org/10.3390/ma15134662
Yang S, Wang M, Zheng S, Zeng S, Gao L. Fractal Permeability Model of Newtonian Fluids in Rough Fractured Dual Porous Media. Materials. 2022; 15(13):4662. https://doi.org/10.3390/ma15134662
Chicago/Turabian StyleYang, Shanshan, Mengying Wang, Sheng Zheng, Shuguang Zeng, and Ling Gao. 2022. "Fractal Permeability Model of Newtonian Fluids in Rough Fractured Dual Porous Media" Materials 15, no. 13: 4662. https://doi.org/10.3390/ma15134662





