Numerical Investigation of the Defects Effect in Additive Manufactured Ti-6Al-4V Struts on Deformation Behavior Based on Microtomographic Images
Abstract
:1. Introduction
2. Materials and Methods
- -
- Layering of tomographic images (cross-sections) and definition of their orientation in the software.
- -
- Binarization of the images using thresholding to separate the shape of the diamond structure from the tomographic images.
- -
- Separation of struts from diamond structures.
- -
- Triangulation of the struts’ exterior surfaces and interior pore surfaces based on generated voxel layers.
- -
- Generation of surface finite element mesh.
- -
- Conversion to solid finite element mesh.
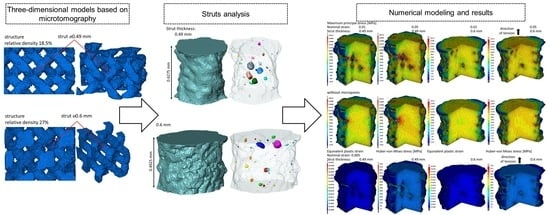
3. Results and Discussion
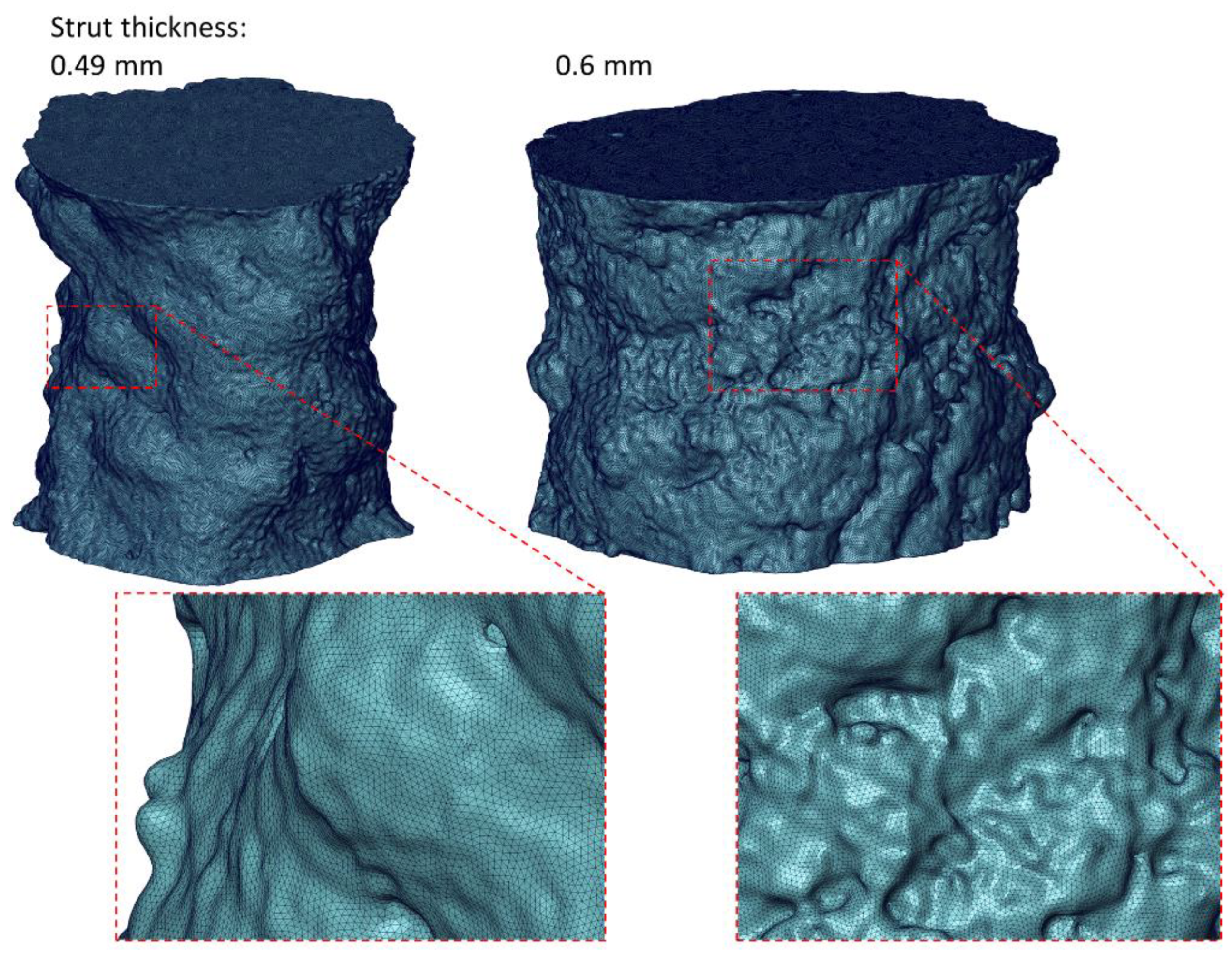
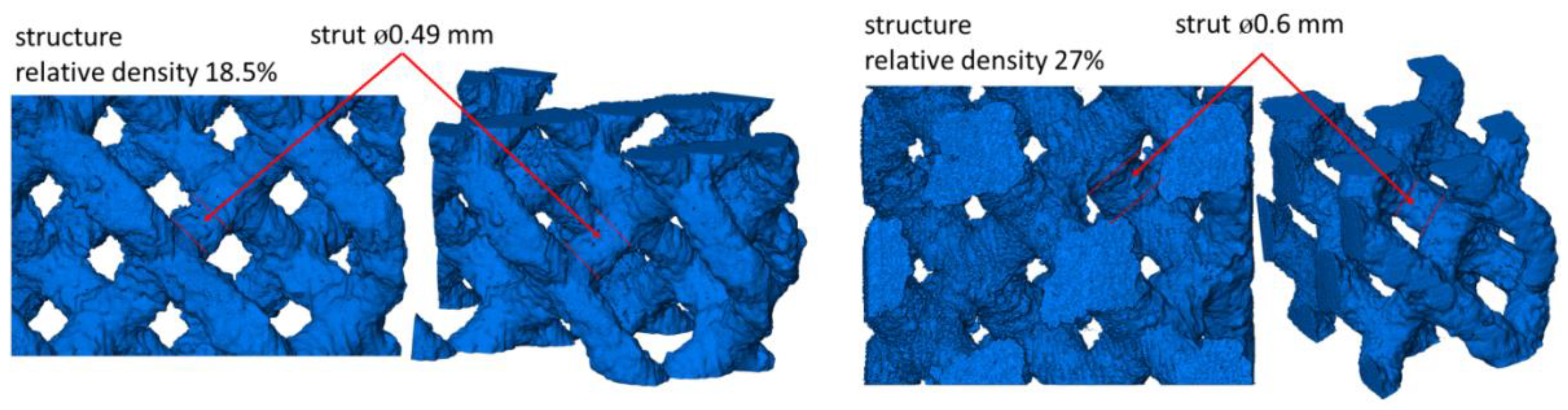
3.1. Defect Analysis Based on Micro-CT
3.2. Stress and Strain Fields in Struts
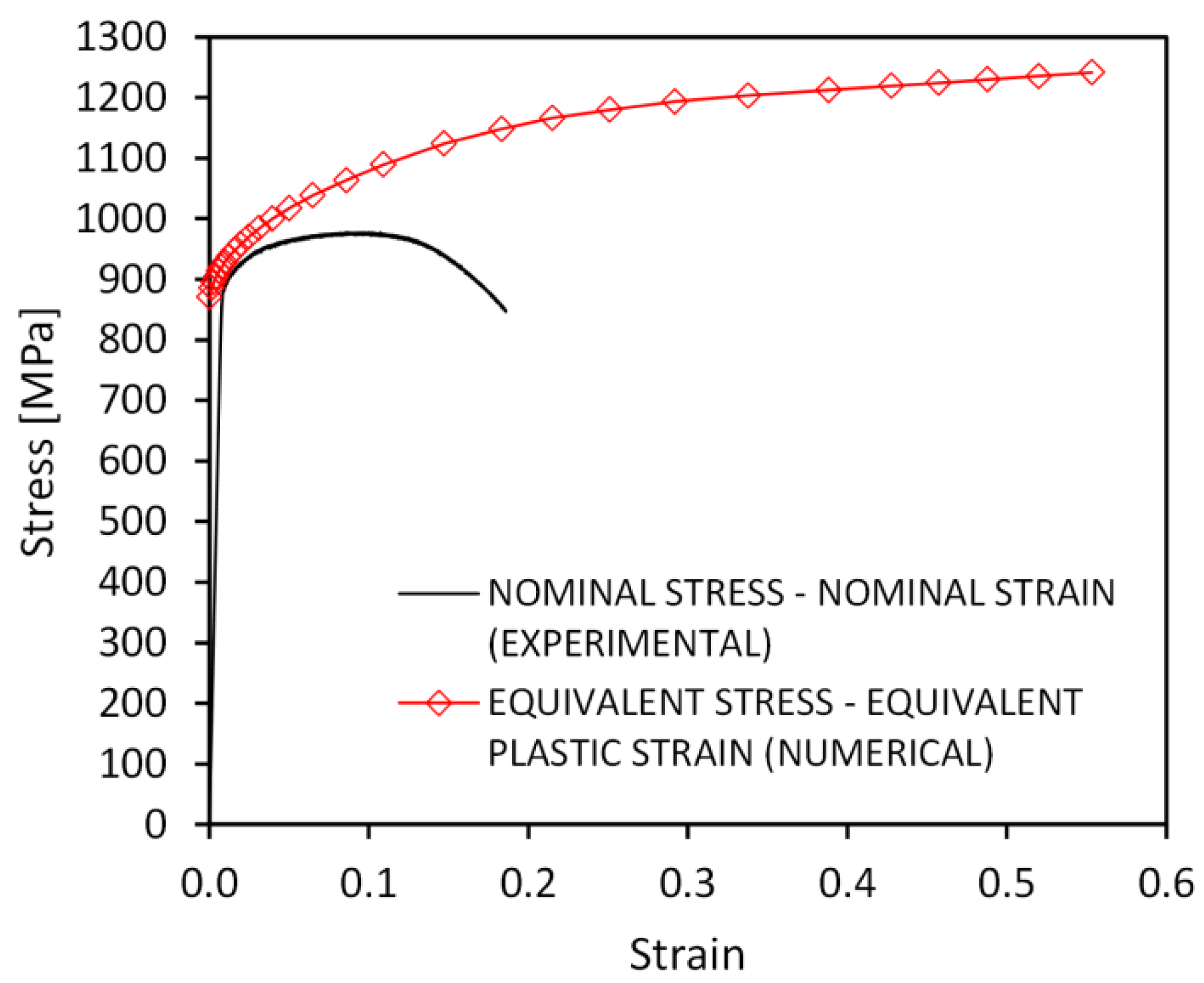
3.3. Mechanical Properties
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Jahr, H.; Zhou, J.; Zadpoor, A.A. Additively manufactured biodegradable porous metals. Acta Biomater. 2020, 115, 29–50. [Google Scholar] [CrossRef] [PubMed]
- Zadpoor, A.A. Additively manufactured porous metallic biomaterials. J. Mater. Chem. B 2019, 7, 4088–4117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suresh, S.; Sun, C.N.; Tekumalla, S.; Rosa, V.; Ling Nai, S.M.; Wong, R.C.W. Mechanical properties and in vitro cytocompatibility of dense and porous Ti–6Al–4V ELI manufactured by selective laser melting technology for biomedical applications. J. Mech. Behav. Biomed. Mater. 2021, 123, 104712. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Xu, S.; Zhou, S.; Xu, W.; Leary, M.; Choong, P.; Qian, M.; Brandt, M.; Xie, Y.M. Topological design and additive manufacturing of porous metals for bone scaffolds and orthopaedic implants: A review. Biomaterials 2016, 83, 127–141. [Google Scholar] [CrossRef] [PubMed]
- Hanks, B.; Berthel, J.; Frecker, M.; Simpson, T.W. Mechanical properties of additively manufactured metal lattice structures: Data review and design interface. Addit. Manuf. 2020, 35, 101301. [Google Scholar] [CrossRef]
- Dressler, A.D.; Jost, E.W.; Miers, J.C.; Moore, D.G.; Seepersad, C.C.; Boyce, B.L. Heterogeneities dominate mechanical performance of additively manufactured metal lattice struts. Addit. Manuf. 2019, 28, 692–703. [Google Scholar] [CrossRef]
- Liverani, E.; Rogati, G.; Pagani, S.; Brogini, S.; Fortunato, A.; Caravaggi, P. Mechanical interaction between additive-manufactured metal lattice structures and bone in compression: Implications for stress shielding of orthopaedic implants. J. Mech. Behav. Biomed. Mater. 2021, 121, 104608. [Google Scholar] [CrossRef]
- Madej, L. Digital/virtual microstructures in application to metals engineering—A review. Arch. Civ. Mech. Eng. 2017, 17, 839–854. [Google Scholar] [CrossRef]
- Doroszko, M.; Seweryn, A. Numerical modeling of the tensile deformation process of sintered 316L based on microtomography of porous mesostructures. Mater. Des. 2015, 88, 493–504. [Google Scholar] [CrossRef]
- Liu, L.; Kamm, P.; García-Moreno, F.; Banhart, J.; Pasini, D. Elastic and failure response of imperfect three-dimensional metallic lattices: The role of geometric defects induced by Selective Laser Melting. J. Mech. Phys. Solids 2017, 107, 160–184. [Google Scholar] [CrossRef]
- Lei, H.; Li, C.; Meng, J.; Zhou, H.; Liu, Y.; Zhang, X.; Wang, P.; Fang, D. Evaluation of compressive properties of SLM-fabricated multi-layer lattice structures by experimental test and μ-CT-based finite element analysis. Mater. Des. 2019, 169, 107685. [Google Scholar] [CrossRef]
- Doroszko, M.; Seweryn, A. A new numerical modelling method for deformation behaviour of metallic porous materials using X-ray computed microtomography. Mater. Sci. Eng. A 2017, 689, 142–156. [Google Scholar] [CrossRef]
- Echlin, M.P.; Burnett, T.L.; Polonsky, A.T.; Pollock, T.M.; Withers, P.J. Serial sectioning in the SEM for three dimensional materials science. Curr. Opin. Solid State Mater. Sci. 2020, 24, 100817. [Google Scholar] [CrossRef]
- Sitko, M.; Mojzeszko, M.; Rychlowski, L.; Cios, G.; Bala, P.; Muszka, K.; Madej, L. Numerical procedure of three-dimensional reconstruction of ferrite-pearlite microstructure data from SEM/EBSD serial sectioning. Procedia Manuf. 2020, 47, 1217–1222. [Google Scholar] [CrossRef]
- Zhou, M.; Zhou, H. Flame front propagation and sinter strength properties of permeable sintering bed prepared via enhanced granulation with hydrated lime. Asia-Pacific J. Chem. Eng. 2020, 16, e2592. [Google Scholar] [CrossRef]
- Ziółkowski, G.; Gruber, K.; Tokarczyk, E.; Roszak, R.; Ziegenhorn, M. X-ray Computed Tomography for the ex-situ mechanical testing and simulation of additively manufactured IN718 samples. Addit. Manuf. 2021, 45, 102070. [Google Scholar] [CrossRef]
- Doroszko, M.; Seweryn, A. Modeling of the tension and compression behavior of sintered 316L using micro computed tomography. Acta Mech. Autom. 2015, 9, 70–74. [Google Scholar] [CrossRef] [Green Version]
- Doroszko, M.; Seweryn, A. Finite element modeling of anisotropic deformation behavior of the porous materials based on microtomographic images. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2016; p. 0600012016. [Google Scholar] [CrossRef] [Green Version]
- Rowenhorst, D.J.; Nguyen, L.; Murphy-Leonard, A.D.; Fonda, R.W. Characterization of Microstructure in Additively Manufactured 316L using Automated Serial Sectioning. Curr. Opin. Solid State Mater. Sci. 2020, 24, 100819. [Google Scholar] [CrossRef]
- Doroszko, M.; Seweryn, A. Numerical modelling of the mesofracture process of sintered 316L steel under tension using microtomography. Eng. Fract. Mech. 2021, 255, 107965. [Google Scholar] [CrossRef]
- Xiao, L.; Li, S.; Song, W.; Xu, X.; Gao, S. Process-induced geometric defect sensitivity of Ti–6Al–4V lattice structures with different mesoscopic topologies fabricated by electron beam melting. Mater. Sci. Eng. A 2020, 778, 139092. [Google Scholar] [CrossRef]
- Dallago, M.; Winiarski, B.; Zanini, F.; Carmignato, S.; Benedetti, M. On the effect of geometrical imperfections and defects on the fatigue strength of cellular lattice structures additively manufactured via Selective Laser Melting. Int. J. Fatigue 2019, 124, 348–360. [Google Scholar] [CrossRef]
- Lozanovski, B.; Leary, M.; Tran, P.; Shidid, D.; Qian, M.; Choong, P.; Brandt, M. Computational modelling of strut defects in SLM manufactured lattice structures. Mater. Des. 2019, 171, 107671. [Google Scholar] [CrossRef]
- Yánez, A.; Fiorucci, M.P.; Cuadrado, A.; Martel, O.; Monopoli, D. Surface roughness effects on the fatigue behaviour of gyroid cellular structures obtained by additive manufacturing. Int. J. Fatigue 2020, 138, 105702. [Google Scholar] [CrossRef]
- Falkowska, A.; Seweryn, A.; Skrodzki, M. Strength Properties of a Porous Titanium Alloy Ti6Al4V with Diamond Structure Obtained by Laser Power Bed Fusion (LPBF). Materials 2020, 13, 5138. [Google Scholar] [CrossRef]
- Doroszko, M.; Falkowska, A.; Seweryn, A. Image-based numerical modeling of the tensile deformation behavior and mechanical properties of additive manufactured Ti–6Al–4V diamond lattice structures. Mater. Sci. Eng. A 2021, 818, 141362. [Google Scholar] [CrossRef]
- Van Hooreweder, B.; Apers, Y.; Lietaert, K.; Kruth, J.P. Improving the fatigue performance of porous metallic biomaterials produced by Selective Laser Melting. Acta Biomater. 2017, 47, 193–202. [Google Scholar] [CrossRef]
- Lietaert, K.; Cutolo, A.; Boey, D.; Van Hooreweder, B. Fatigue life of additively manufactured Ti6Al4V scaffolds under tension-tension, tension-compression and compression-compression fatigue load. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef] [Green Version]
- MSC Software Corporation. Marc® 2014.2, Product Documentation, Volume B: Element Library 2015; MSC Software Corporation: Newport Beach, CA, USA, 2015. [Google Scholar]
- Derpenski, L.; Seweryn, A. Experimental Research into Fracture of EN-AW 2024 and EW-AW 2007 Aluminum Alloy Specimens with Notches Subjected to Tension. Exp. Mech. 2011, 51, 1075–1094. [Google Scholar] [CrossRef]
- Doroszko, M.; Seweryn, A. Pore-scale numerical modelling of large deformation behaviour of sintered porous metals under compression using computed microtomography. Mech. Mater. 2020, 141, 103259. [Google Scholar] [CrossRef]
- Thermo Fisher Scientific. Avizo Software 9 User’s Guide; Thermo Fisher Scientific: Waltham, MA, USA, 2018; Volume 9, pp. 1–915. [Google Scholar]
- Derpenski, L.; Seweryn, A. Ductile fracture of EN-AW 2024 aluminum alloy specimens with notches under biaxial loading. Part 2—Numerical research and ductile fracture criterion. Theor. Appl. Fract. Mech. 2016, 84, 203–214. [Google Scholar] [CrossRef]
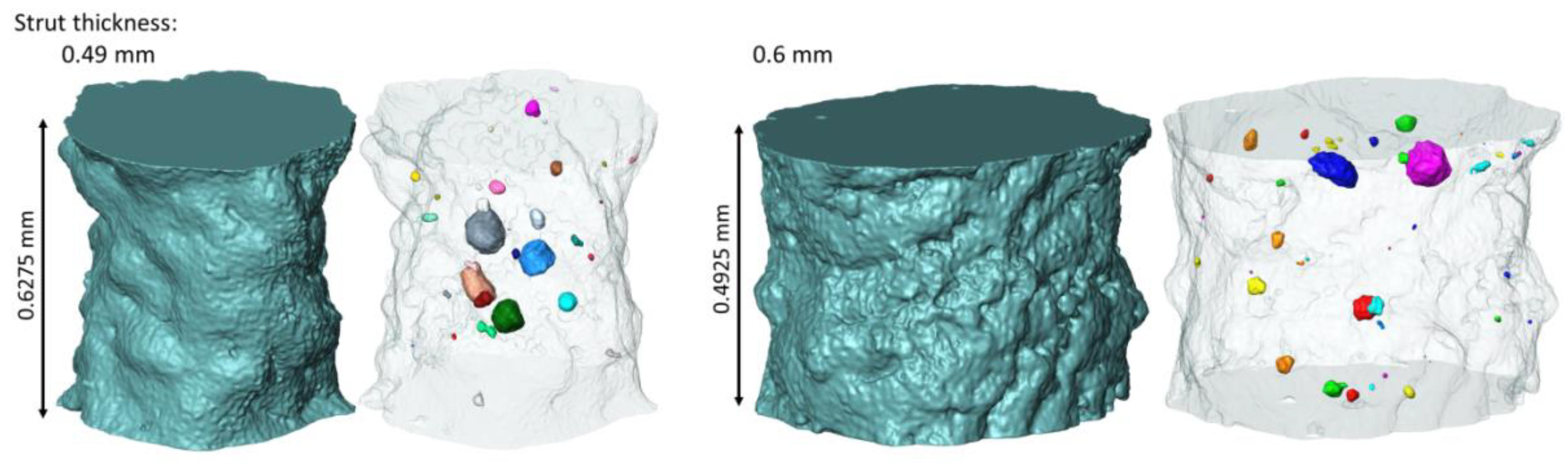
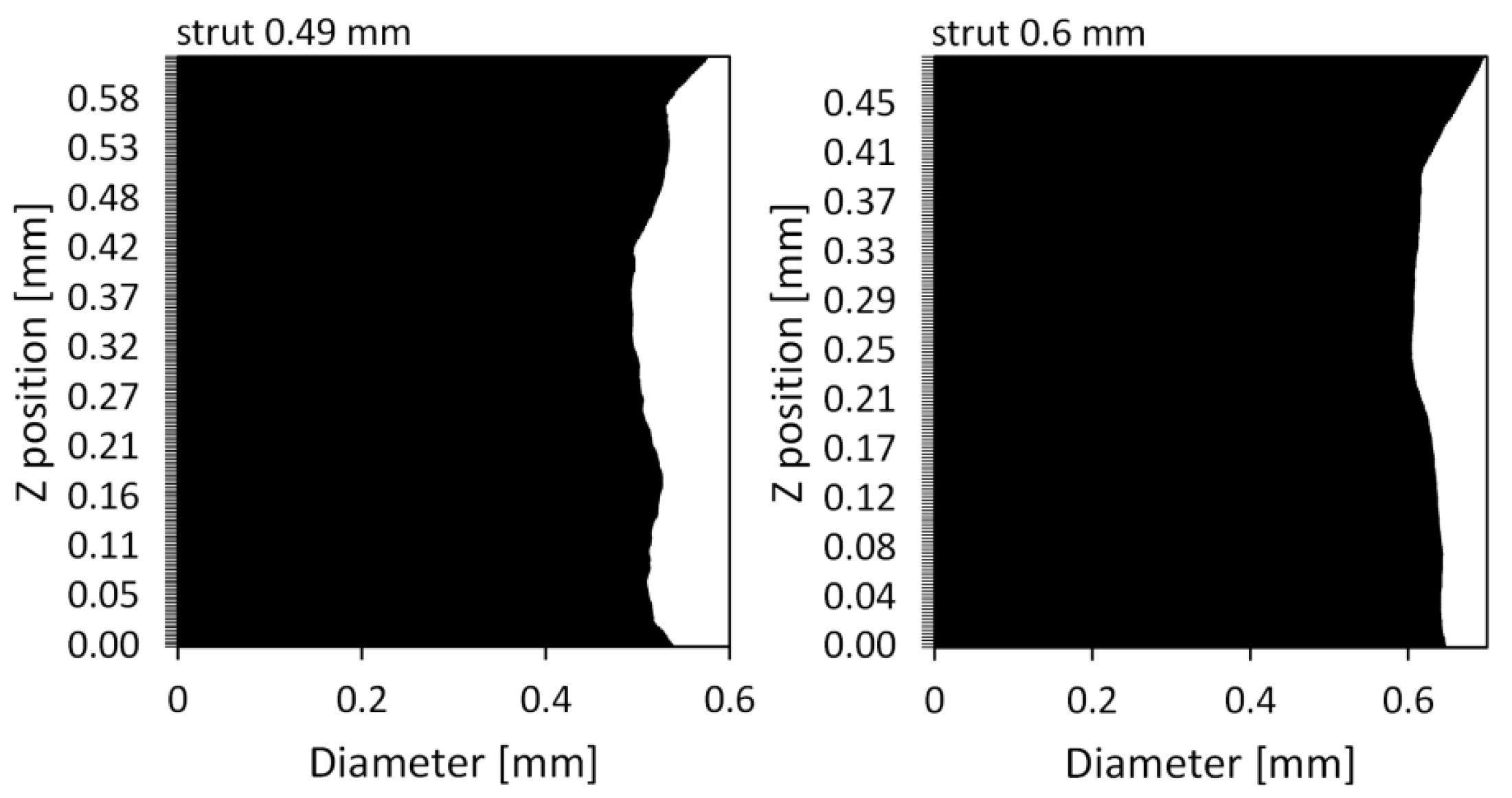
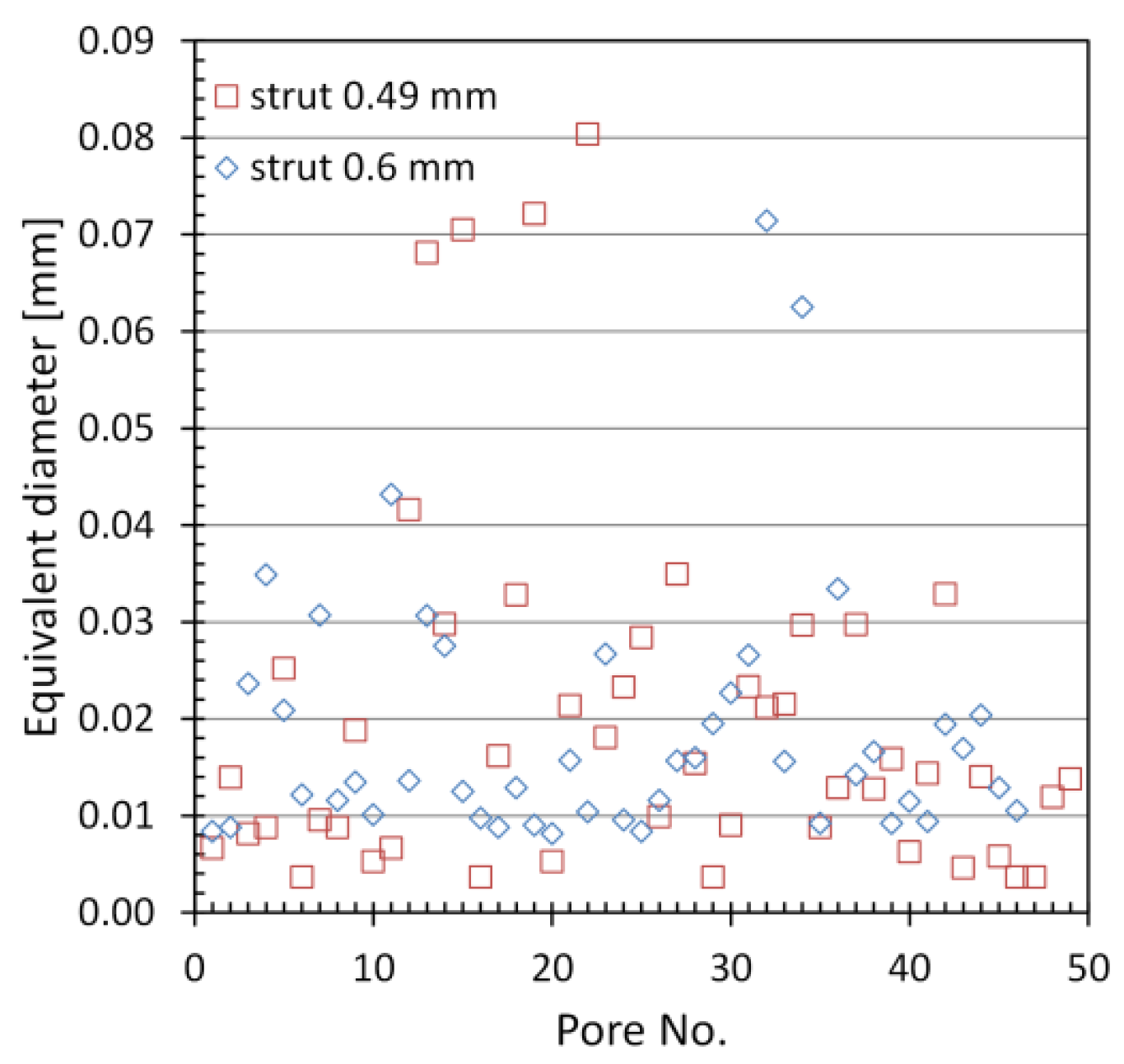
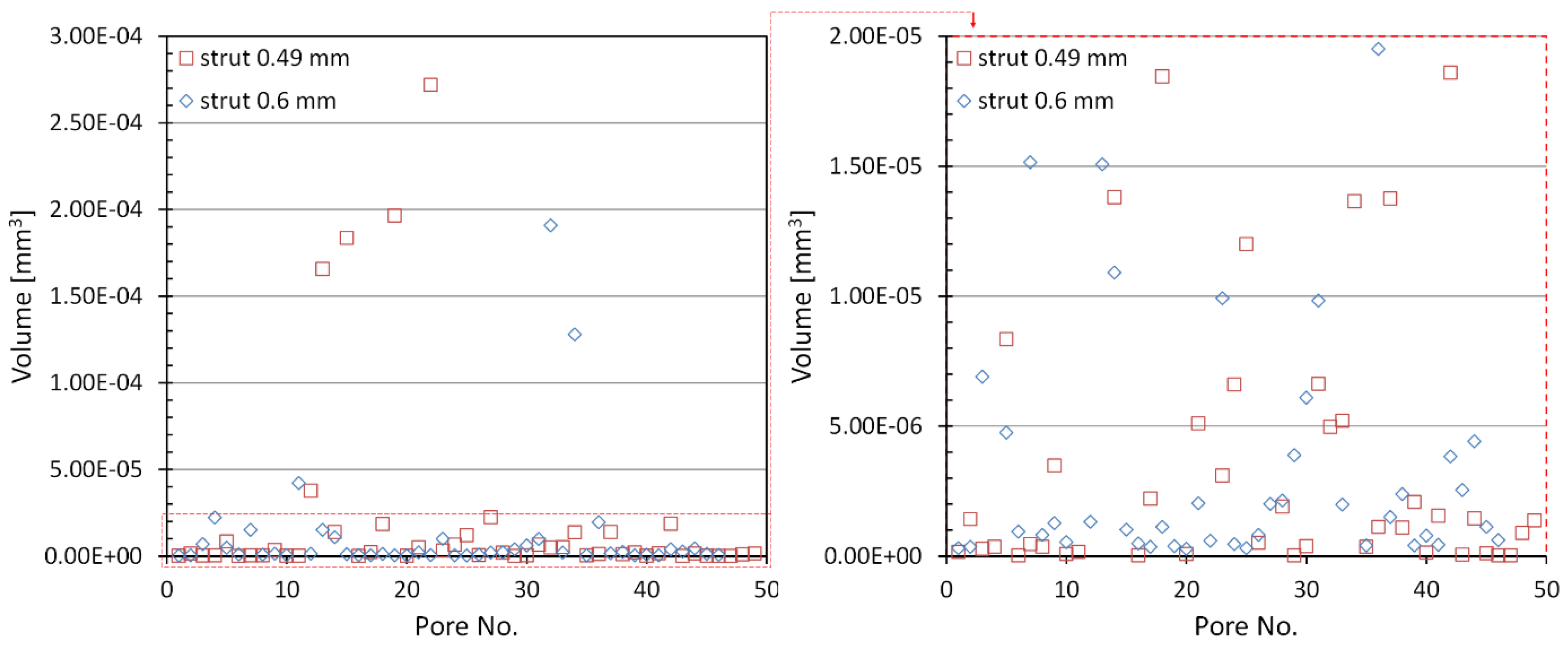

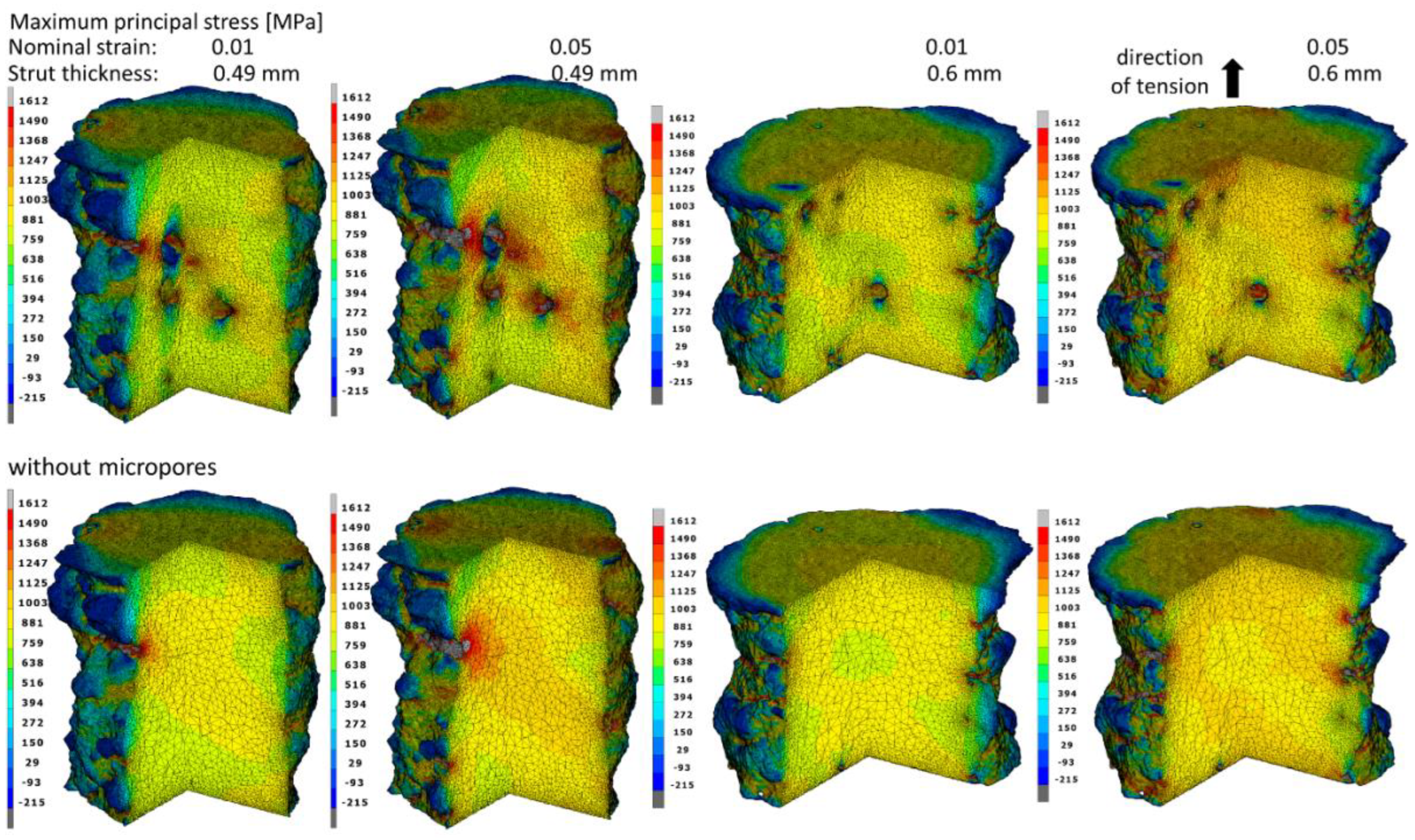
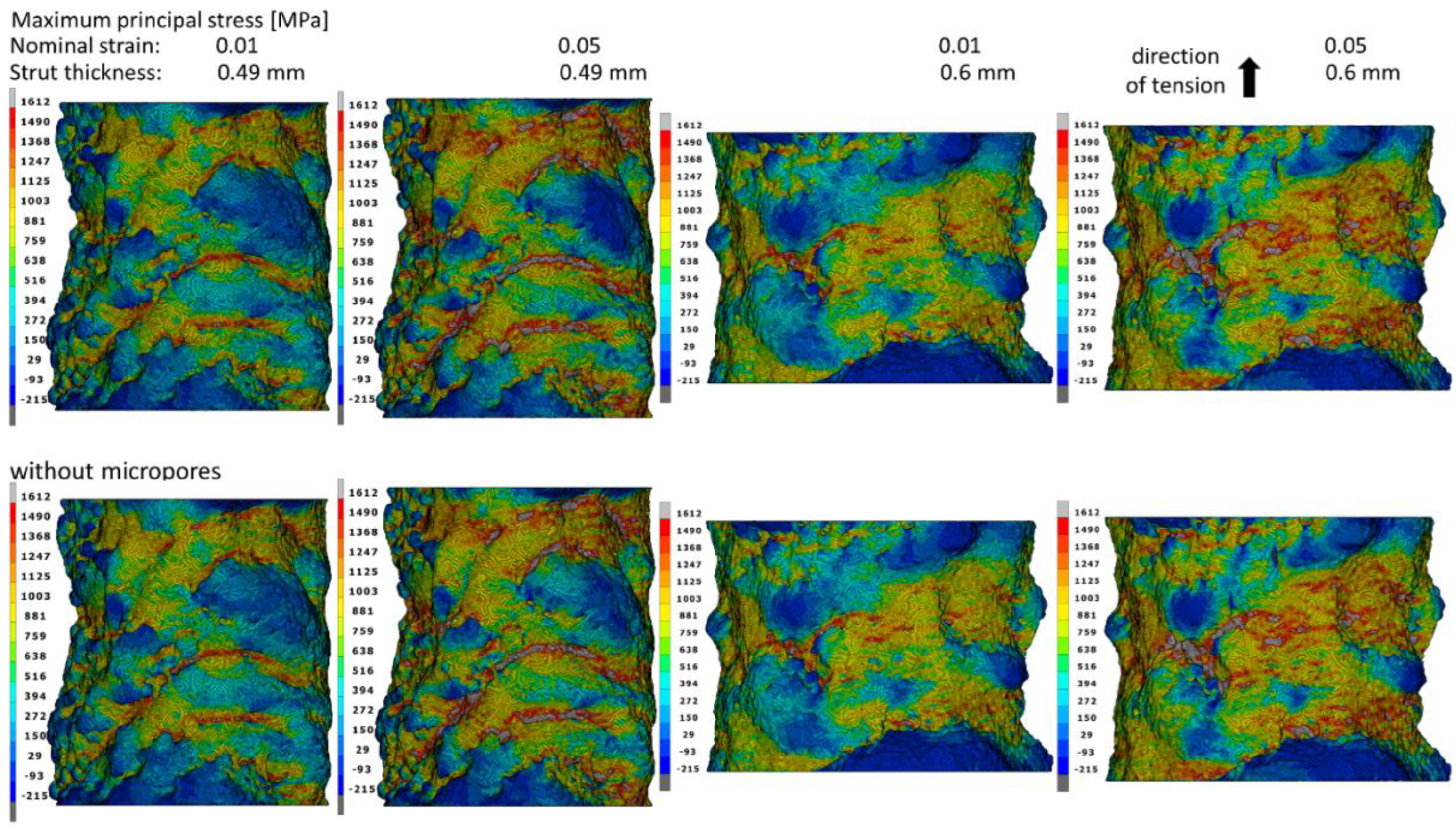

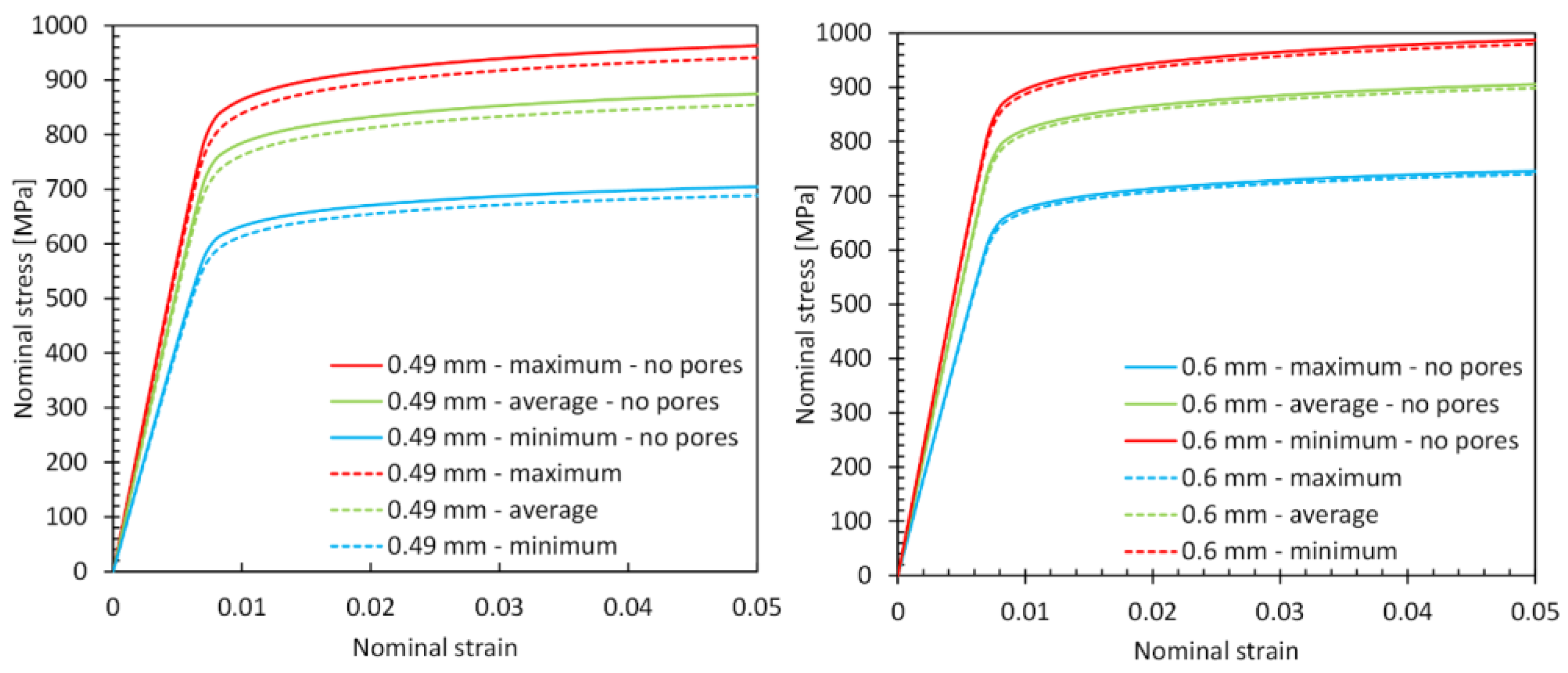
| Strut Thickness [mm] | Emin [GPa] | Eav [GPa] | Emax [GPa] | |||
|---|---|---|---|---|---|---|
| 0.49 | 83.4 | 105.4 | 114 | 607 | 754 | 831 |
| 0.49 (no pores) | 84.9 | 107.6 | 116.1 | 629 | 778 | 858 |
| 0.6 | 88.6 | 107.5 | 117.3 | 668 | 809 | 882 |
| 0.6 (no pores) | 89.2 | 108.4 | 118.2 | 672 | 818 | 893 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doroszko, M. Numerical Investigation of the Defects Effect in Additive Manufactured Ti-6Al-4V Struts on Deformation Behavior Based on Microtomographic Images. Materials 2022, 15, 4807. https://doi.org/10.3390/ma15144807
Doroszko M. Numerical Investigation of the Defects Effect in Additive Manufactured Ti-6Al-4V Struts on Deformation Behavior Based on Microtomographic Images. Materials. 2022; 15(14):4807. https://doi.org/10.3390/ma15144807
Chicago/Turabian StyleDoroszko, Michał. 2022. "Numerical Investigation of the Defects Effect in Additive Manufactured Ti-6Al-4V Struts on Deformation Behavior Based on Microtomographic Images" Materials 15, no. 14: 4807. https://doi.org/10.3390/ma15144807
APA StyleDoroszko, M. (2022). Numerical Investigation of the Defects Effect in Additive Manufactured Ti-6Al-4V Struts on Deformation Behavior Based on Microtomographic Images. Materials, 15(14), 4807. https://doi.org/10.3390/ma15144807