Steady-State Thermal Analysis of Functionally Graded Rotating Disks Using Finite Element and Analytical Methods
Abstract
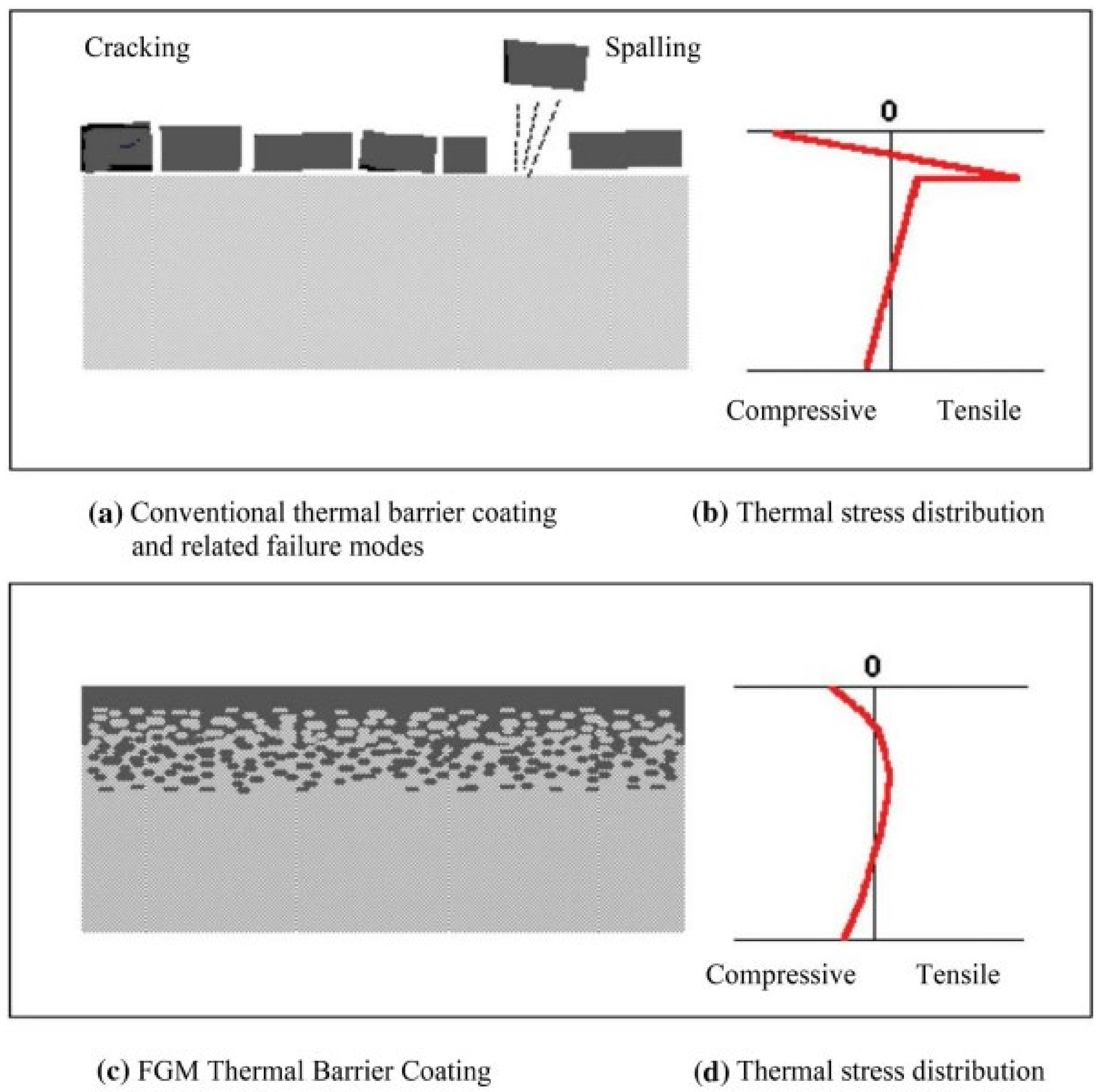
1. Introduction
2. Material Gradation Relation
3. Methodology and Problem Formulation
- In-house finite element program;
- APDL;
- Analytical solution.
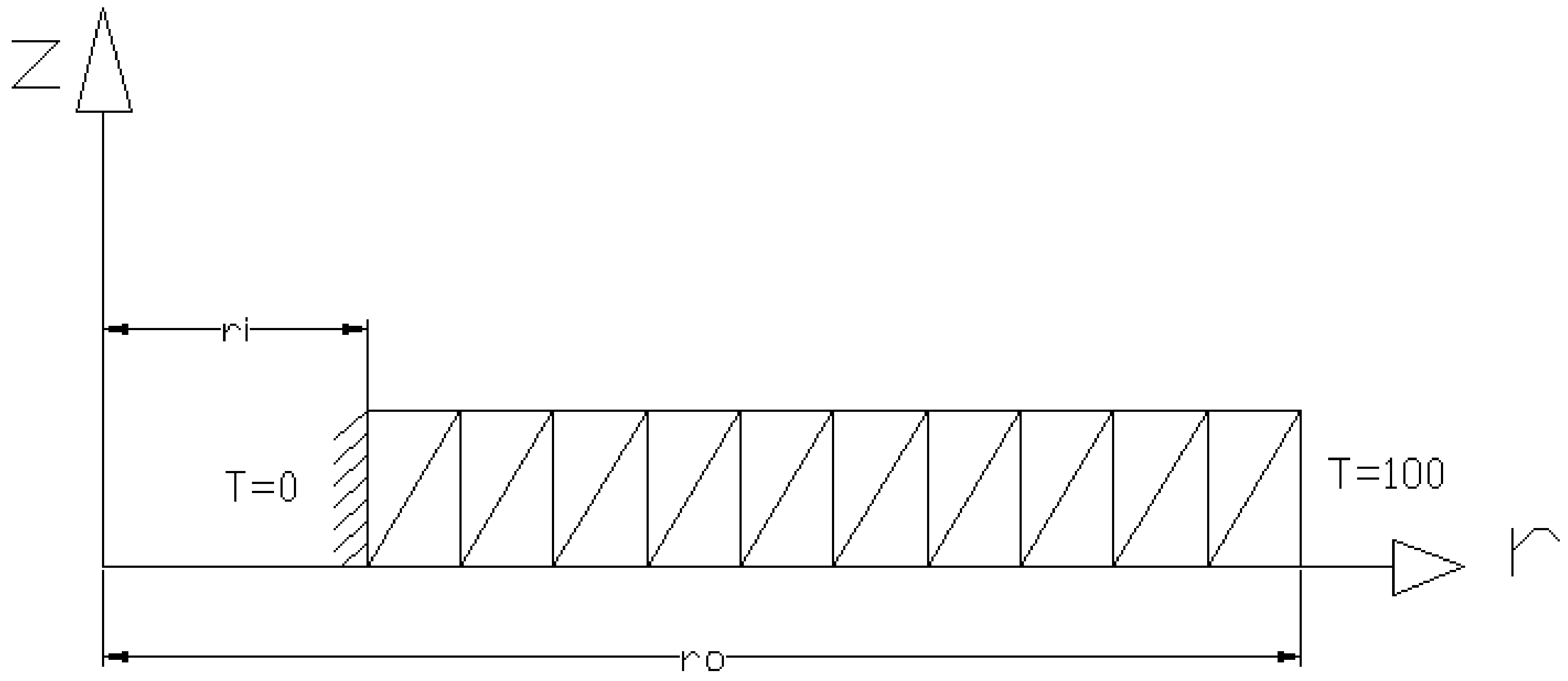
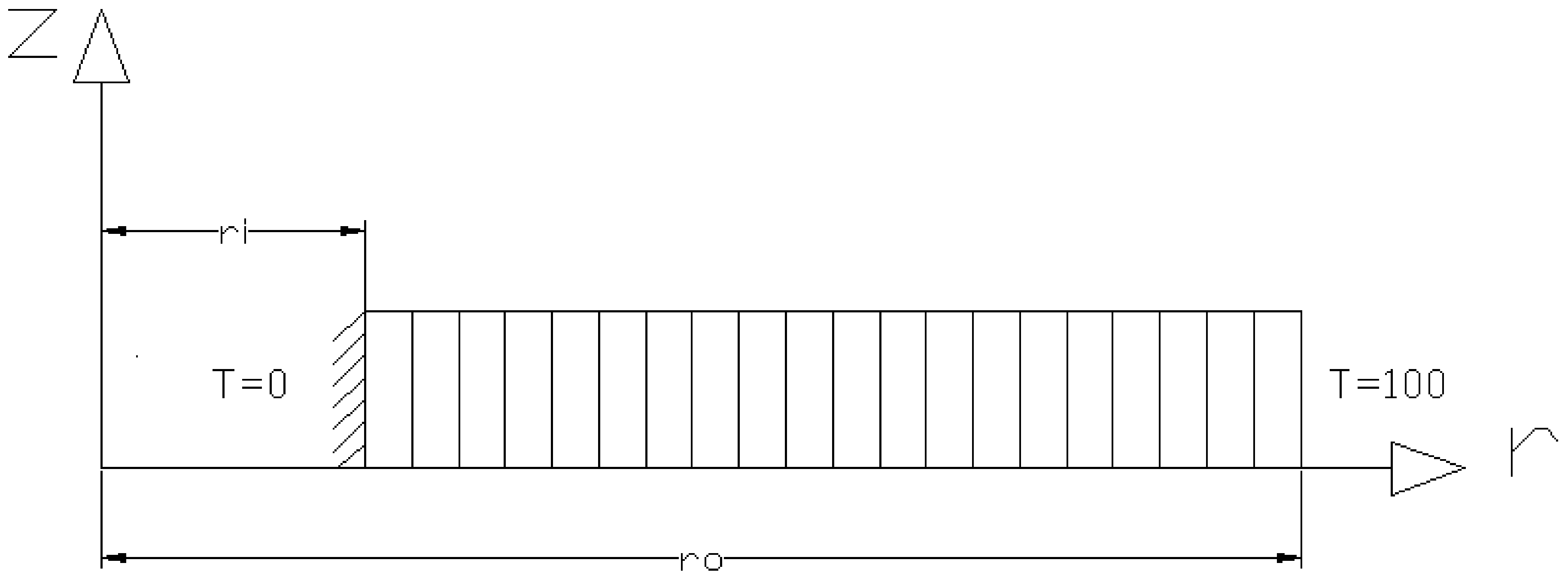
3.1. Method #1: In-House FE Program
3.2. Method #2: APDL
3.3. Method #3: Analytical Solution
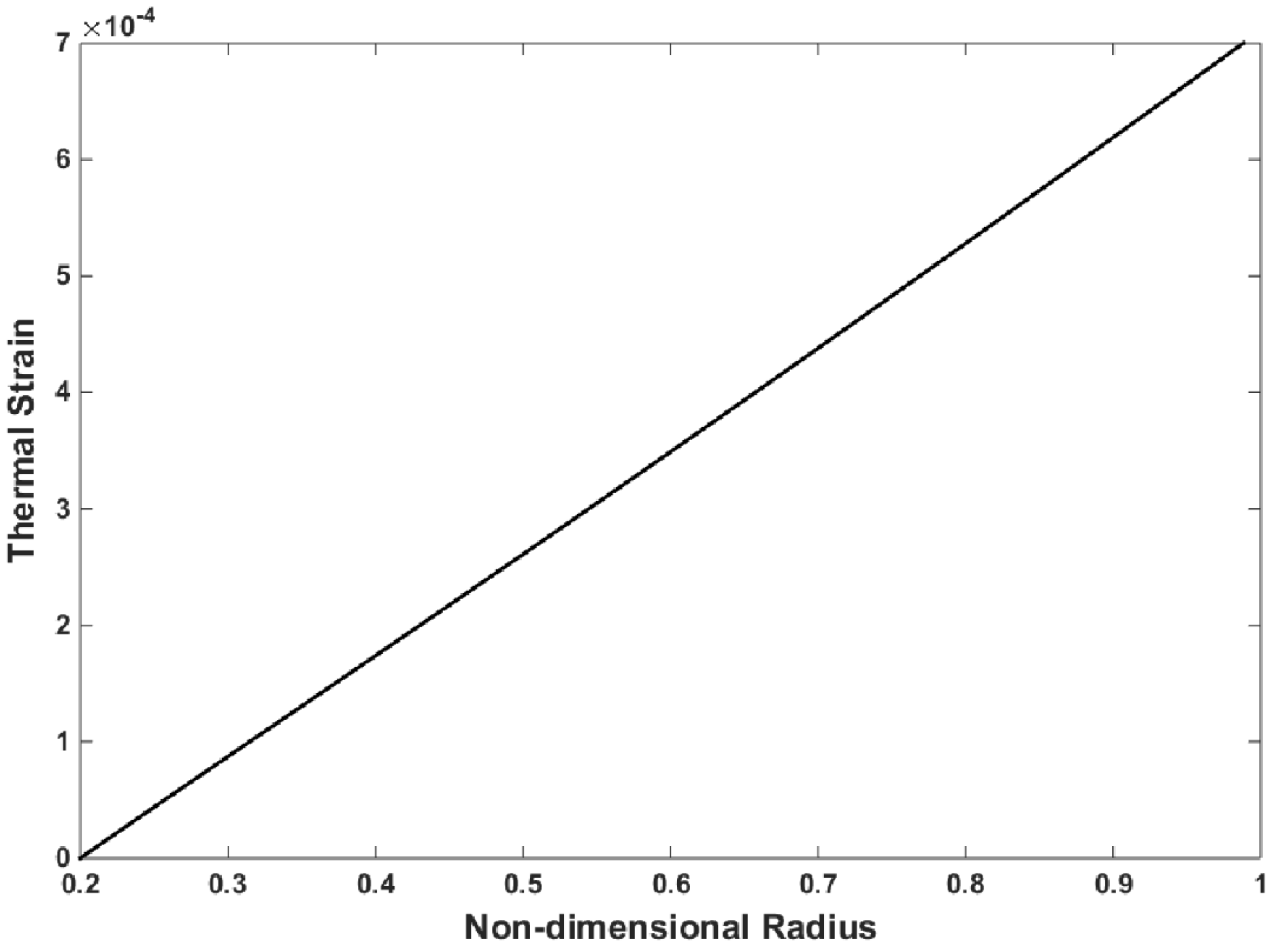
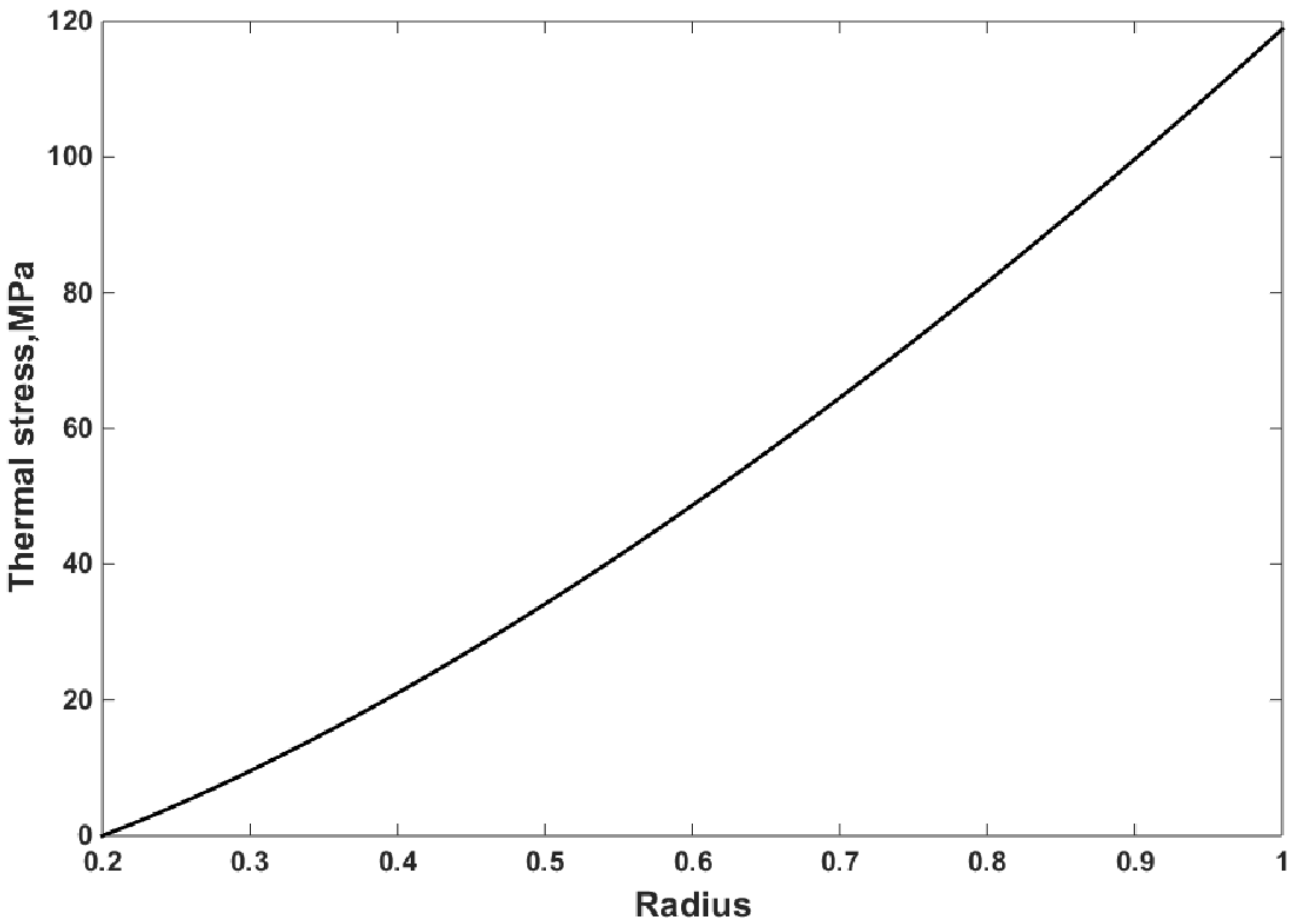
4. Thermal Stress and Strain Relations
5. Numerical Results and Discussion
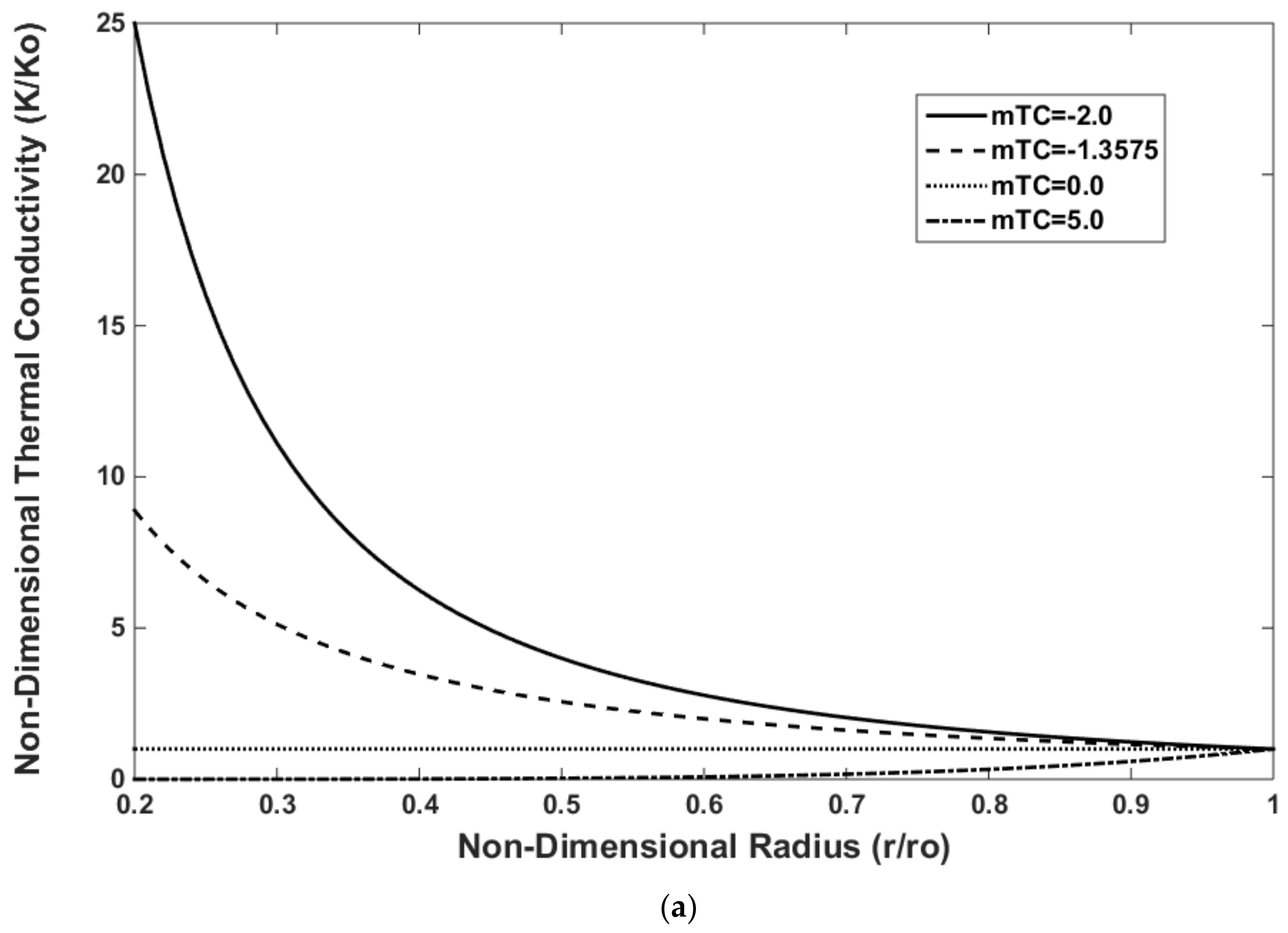
5.1. Material Property Variations in an FG Disk
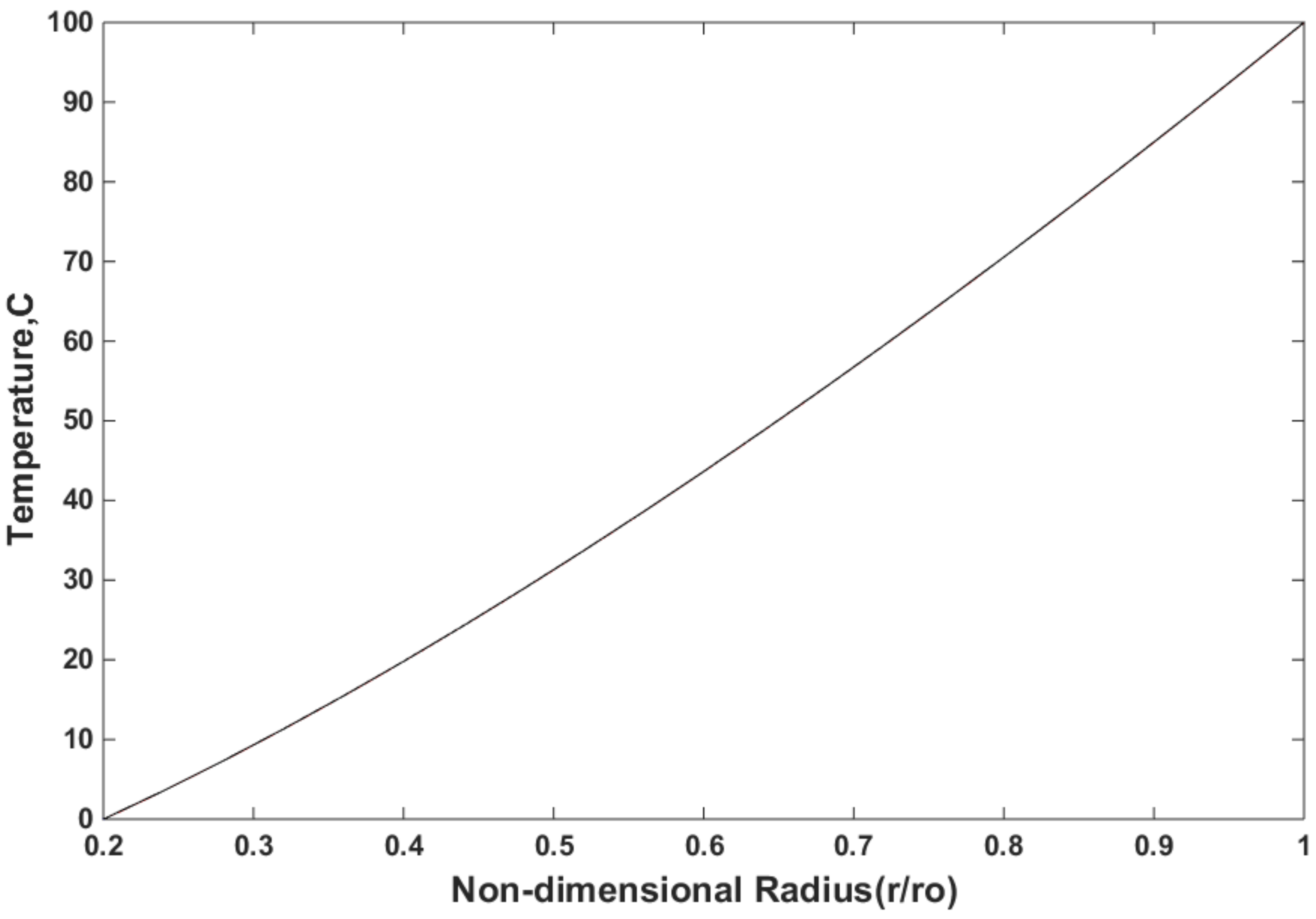
5.2. Numerical Results of the Three Methods
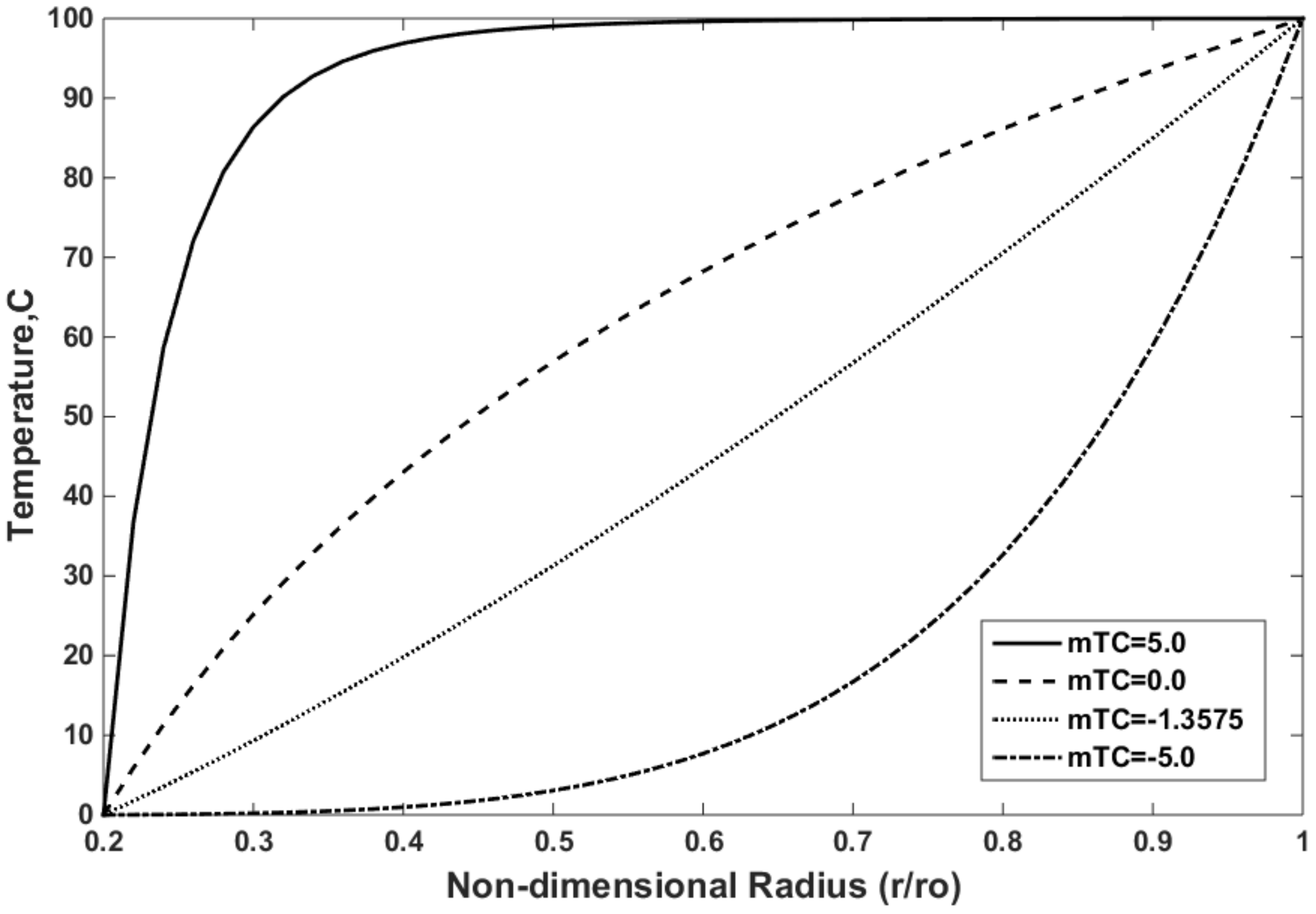
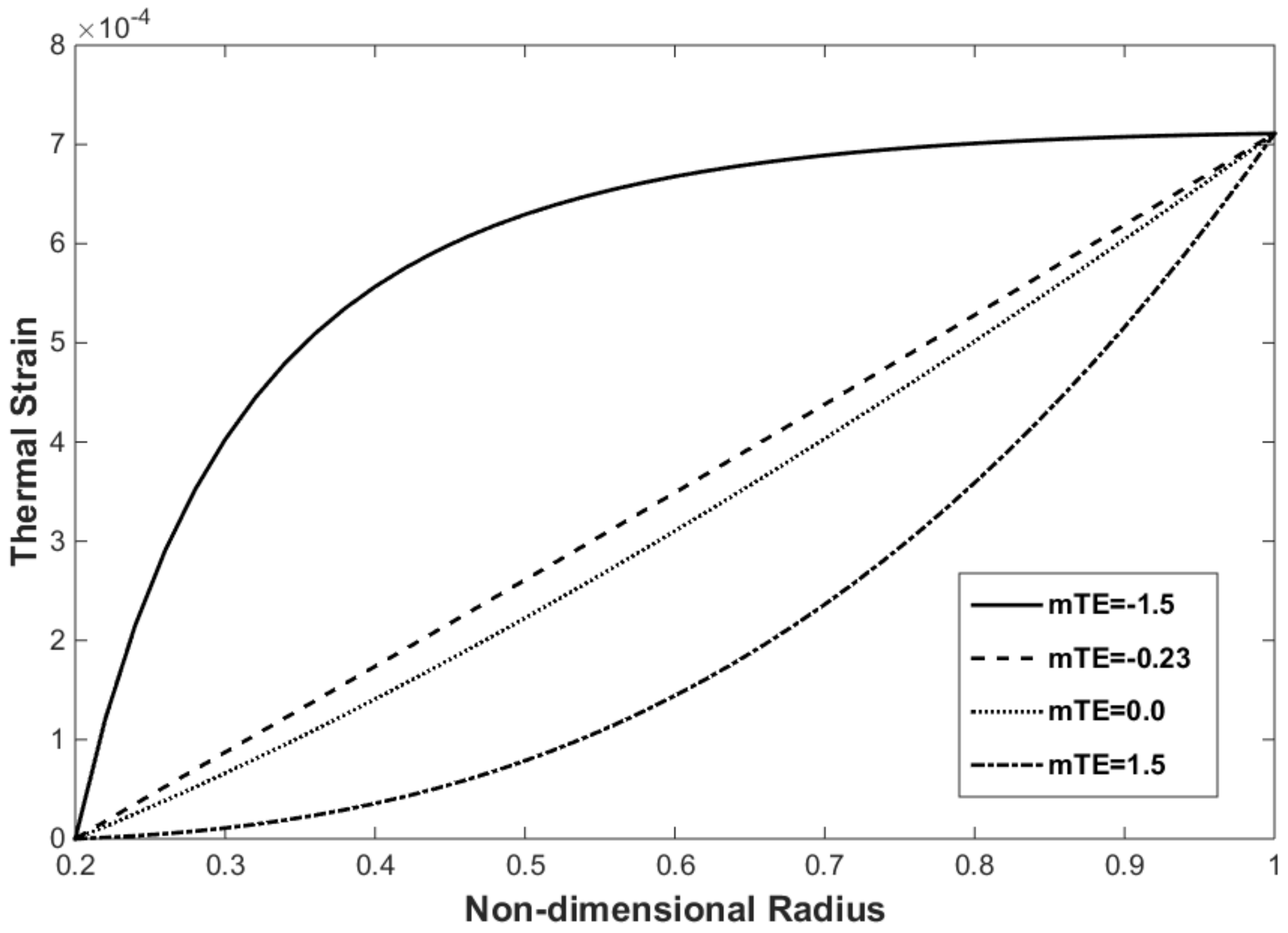
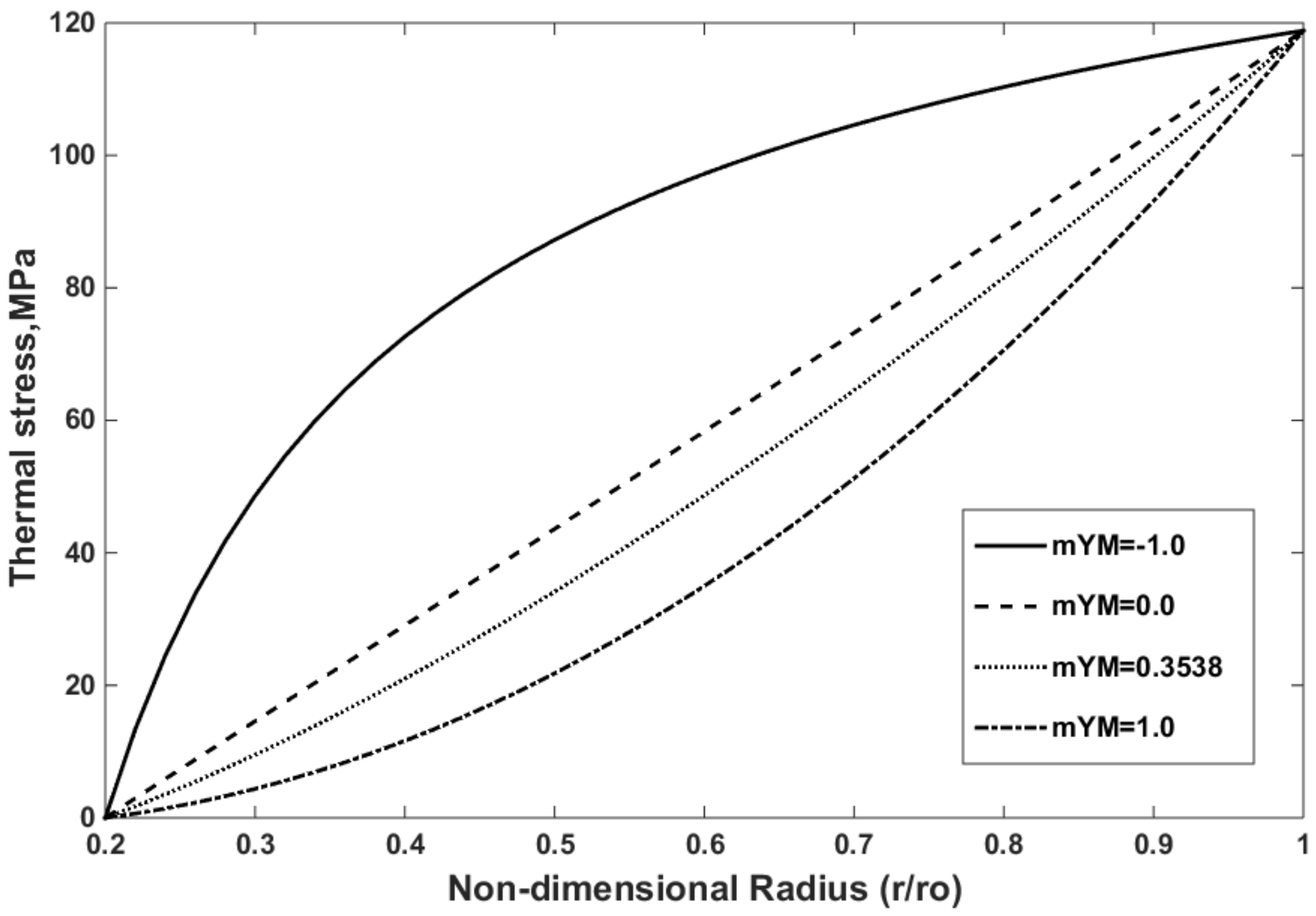
5.3. Material Gradation Parametric Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Suresh, S.; Mortensen, A. Fundamentals of Functionally Graded Materials; Massachusetts Institute of Materials; IOM Communications Ltd.: London, UK, 1998. [Google Scholar]
- Reddy, J. Analysis of functionally graded plates. Int. J. Numer. Methods Eng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Saleh, B.; Jiang, J.; Fathi, R.; Al-Hababi, T.; Xu, Q.; Wang, L.; Song, D.; Ma, A. 30 Years of functionally graded materials: An overview of manufacturing methods, Applications and Future Challenges. Compos. Part B Eng. 2020, 201, 108376. [Google Scholar] [CrossRef]
- Koizumi, M. The concept of FGM. Ceram. Trans. 1993, 34, 3–10. [Google Scholar]
- Aerospace Specification Metals, Inc. Titanium Ti–6Al–2Sn–4Zr–2Mo, Duplex Annealed. Available online: http://asm.matweb.com/search/SpecificMaterial.asp?bassnum¼MTA641 (accessed on 3 December 2003).
- Bayat, M.; Saleem, M.; Bin Sahari, B.; Hamouda, A.M.; Mahdi, E. Thermo elastic analysis of a functionally graded rotating disk with small and large deflections. Thin Walled Struct. 2007, 45, 677–691. [Google Scholar] [CrossRef]
- Bayat, M.; Saleem, M.; Sahari, B.; Hamouda, A.; Mahdi, E. Analysis of functionally graded rotating disks with variable thickness. Mech. Res. Commun. 2008, 35, 283–309. [Google Scholar] [CrossRef]
- Jabbari, M.; Bahtui, A.; Eslami, M. Axisymmetric mechanical and thermal stresses in thick short length FGM cylinders. Int. J. Press. Vessel. Pip. 2009, 86, 296–306. [Google Scholar] [CrossRef]
- Jabbari, M.; Bahtui, A.; Eslami, M.R. Axisymmetric Mechanical and Thermal Stresses in Thick Long FGM Cylinders. J. Therm. Stress. 2006, 29, 643–663. [Google Scholar] [CrossRef]
- Zenkour, A. Stress distribution in rotating composite structures of functionally graded solid disks. J. Mater. Process. Technol. 2009, 209, 3511–3517. [Google Scholar] [CrossRef]
- Eldeeb, A.; Shabana, Y.; Elsawaf, A. Thermo-elastoplastic behavior of a rotating sandwich disc made of temperature-dependent functionally graded materials. J. Sandw. Struct. Mater. 2021, 23, 1761–1783. [Google Scholar] [CrossRef]
- Erdogan, F.; Wu, B.H. Crack problems in FGM layers under thermal stresses. J. Therm. Stress. 1996, 19, 237–265. [Google Scholar] [CrossRef]
- Duc, N.D.; Bich, D.H.; Cong, P.H. Nonlinear thermal dynamic response of shear deformable FGM plates on elastic foundations. J. Therm. Stress. 2016, 39, 278–297. [Google Scholar] [CrossRef]
- Yaghmourali, Y.V.; Ahmadi, N.; Abbaspour-Sani, E. A thermal-calorimetric gas flow meter with improved isolating feature. Microsyst. Technol. 2017, 23, 1927–1936. [Google Scholar] [CrossRef]
- Choudhur, R.; Das, U.J.; Ceruti, A.; Piancastelli, L.; Frizziero, L.; Zanuccoli, G.; Ahmadpour, V. Visco-elastic effects on the three dimensional hydrodynamic flow past a vertical porous plate. Int. Inf. Eng. Technol. Assoc. 2013, 31, 1–8. [Google Scholar]
- Shahzamanian, M.M.; Partovi, A.; Wu, P.D. Finite element analysis of elastic-plastic and fracture behavior in functionally graded materials (FGMs). SN Appl. Sci. 2020, 2, 2135. [Google Scholar] [CrossRef]
- Swaminathan, K.; Sachin, H.; Rajanna, T. Buckling analysis of functionally graded materials by dynamic approach. Mater. Today Proc. 2021, 45, 172–178. [Google Scholar] [CrossRef]
- Hirane, H.; Belarbi, M.-O.; Houari, M.S.A.; Tounsi, A. On the layerwise finite element formulation for static and free vibration analysis of functionally graded sandwich plates. Eng. Comput. 2021, 1–29. [Google Scholar] [CrossRef]
- Sweidan, F.B.; Ryu, H.J. One-step functionally graded materials fabrication using ultra-large temperature gradients obtained through finite element analysis of field-assisted sintering technique. Mater. Des. 2020, 192, 108714. [Google Scholar] [CrossRef]
- Shivay, O.N.; Mukhopadhyay, S. A complete Galerkin’s type approach of finite element for the solution of a problem on modified Green-Lindsay thermoelasticity for a functionally graded hollow disk. Eur. J. Mech. A Solids 2020, 80, 103914. [Google Scholar] [CrossRef]
- Trabelsi, S.; Zghal, S.; Dammak, F. Thermo-elastic buckling and post-buckling analysis of functionally graded thin plate and shell structures. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 233. [Google Scholar] [CrossRef]
- Durodola, J.; Attia, O. Deformation and stresses in functionally graded rotating disks. Compos. Sci. Technol. 2000, 60, 987–995. [Google Scholar] [CrossRef]
- Shahzamanian, M.; Sahari, B.; Bayat, M.; Mustapha, F.; Ismarrubie, Z. Finite element analysis of thermoelastic contact problem in functionally graded axisymmetric brake disks. Compos. Struct. 2010, 92, 1591–1602. [Google Scholar] [CrossRef]
- Shahzamanian, M.; Sahari, B.; Bayat, M.; Ismarrubie, Z.; Mustapha, F. Transient and thermal contact analysis for the elastic behavior of functionally graded brake disks due to mechanical and thermal loads. Mater. Des. 2010, 31, 4655–4665. [Google Scholar] [CrossRef]
- Shahzamanian, M.M.; Sahari, B.B.; Bayat, M.; Mustapha, F.; Ismarrubie, Z.N. Elastic Contact Analysis of Functionally Graded Brake Disks Subjected to Thermal and Mechanical Loads. Int. J. Comput. Methods Eng. Sci. Mech. 2013, 14, 10–23. [Google Scholar] [CrossRef]
- Genao, F.Y.; Kim, J.; Żur, K.K. Nonlinear finite element analysis of temperature-dependent functionally graded porous micro-plates under thermal and mechanical loads. Compos. Struct. 2021, 256, 112931. [Google Scholar] [CrossRef]
- Najibi, A.; Alizadeh, P.; Ghazifard, P. Transient thermal stress analysis for a short thick hollow FGM cylinder with nonlinear temperature-dependent material properties. J. Therm. Anal. 2021, 146, 1971–1982. [Google Scholar] [CrossRef]
- Babaee, A.; Jelovica, J. Nonlinear transient thermoelastic response of FGM plate under sudden cryogenic cooling. Ocean Eng. 2021, 226, 108875. [Google Scholar] [CrossRef]
- Bidgoli, M.O.; Arefi, M.; Loghman, A. Thermoelastic behaviour of FGM rotating cylinder resting on friction bed subjected to a thermal gradient and an external torque. Aust. J. Mech. Eng. 2021, 19, 1–9. [Google Scholar] [CrossRef]
- Sarkar, P.R.; Rahman, A.S. Effect of magnetic field on the thermo-elastic response of a rotating FGM Circular disk with non-uniform thickness. J. Strain Anal. Eng. Des. 2022, 57, 116–131. [Google Scholar] [CrossRef]
- Bezzie, Y.M.; Woldemichael, D.E.; Chekol, E.T.; Admass, S.A.; Selvaraj, S.K.; Paramasivam, V. Effect of volumetric fraction index on temperature distribution in thick-walled functionally graded material made cylinder. Mater. Today Proc. 2021, 46, 7442–7447. [Google Scholar] [CrossRef]
- Swaminathan, K.; Sangeetha, D. Thermal analysis of FGM plates—A critical review of various modeling techniques and solution methods. Compos. Struct. 2017, 160, 43–60. [Google Scholar] [CrossRef]
- Jabbari, M.; Karampour, S.; Eslami, M.R. Steady state thermal and mechanical stresses of a poro-piezo-FGM hollow sphere. Meccanica 2013, 48, 699–719. [Google Scholar] [CrossRef]
- Jabbari, M.; Karampour, S.; Eslami, M.R. Radially Symmetric Steady State Thermal and Mechanical Stresses of a Poro FGM Hollow Sphere. ISRN Mech. Eng. 2011, 2011, 1–7. [Google Scholar] [CrossRef][Green Version]
- Bayat, Y.; Ghannad, M.; Torabi, H. Analytical and numerical analysis for the FGM thick sphere under combined pressure and temperature loading. Ingenieur-Archiv 2012, 82, 229–242. [Google Scholar] [CrossRef]
- Delouei, A.A.; Emamian, A.; Karimnejad, S.; Sajjadi, H.; Jing, D. Two-dimensional temperature distribution in FGM sectors with the power-law variation in radial and circumferential directions. J. Therm. Anal. 2021, 144, 611–621. [Google Scholar] [CrossRef]
- Shahzamanian, M.M.; Sahari, B.B.; Bayat, M.; Mustapha, F.; Ismarrubie, Z.N.; Shahrjerdi, A. Steady state and thermoelastic analysis of a functionally graded rotating disk. In Proceedings of the World Engineering Congress 2010, Malaysia Conference on Aerospace and Mechanical Engineering, Kuching, Sarawak, Malaysia, 2–5 August 2010; pp. 222–228. [Google Scholar]
- Kordkheili, S.H.; Naghdabadi, R. Thermoelastic analysis of a functionally graded rotating disk. Compos. Struct. 2007, 79, 508–516. [Google Scholar] [CrossRef]
- Delouei, A.A.; Emamian, A.; Karimnejad, S.; Sajjadi, H.; Jing, D. Asymmetric Conduction in an Infinite Functionally Graded Cylinder: Two-Dimensional Exact Analytical Solution Under General Boundary Conditions. J. Heat Transf. 2020, 142, 044505. [Google Scholar] [CrossRef]
- Kwon, Y.W.; Bang, H. The Finite Element Method Using MATLAB; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Available online: https://github.com/mmshahzamanian/FGM-disc_FEM_thermal-analysis/tree/main (accessed on 22 July 2022).
- Bayat, M.; Saleem, M.; Bin Sahari, B.; Hamouda, A.M.; Mahdi, E. Mechanical and thermal stresses in a functionally graded rotating disk with variable thickness due to radially symmetry loads. Int. J. Press. Vessel. Pip. 2009, 86, 357–372. [Google Scholar] [CrossRef]

| Material Properties | ||||
|---|---|---|---|---|
| Ceramic (outer surface) | ||||
| Metal (inner surface) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahzamanian, M.M.; Shahrjerdi, A.; Sahari, B.B.; Wu, P.D. Steady-State Thermal Analysis of Functionally Graded Rotating Disks Using Finite Element and Analytical Methods. Materials 2022, 15, 5548. https://doi.org/10.3390/ma15165548
Shahzamanian MM, Shahrjerdi A, Sahari BB, Wu PD. Steady-State Thermal Analysis of Functionally Graded Rotating Disks Using Finite Element and Analytical Methods. Materials. 2022; 15(16):5548. https://doi.org/10.3390/ma15165548
Chicago/Turabian StyleShahzamanian, M. M., A. Shahrjerdi, B. B. Sahari, and P. D. Wu. 2022. "Steady-State Thermal Analysis of Functionally Graded Rotating Disks Using Finite Element and Analytical Methods" Materials 15, no. 16: 5548. https://doi.org/10.3390/ma15165548
APA StyleShahzamanian, M. M., Shahrjerdi, A., Sahari, B. B., & Wu, P. D. (2022). Steady-State Thermal Analysis of Functionally Graded Rotating Disks Using Finite Element and Analytical Methods. Materials, 15(16), 5548. https://doi.org/10.3390/ma15165548






