Analytical Solution for Forced Vibration Characteristics of Rotating Functionally Graded Blades under Rub-Impact and Base Excitation
Abstract
:1. Introduction
2. Theoretical Formulations
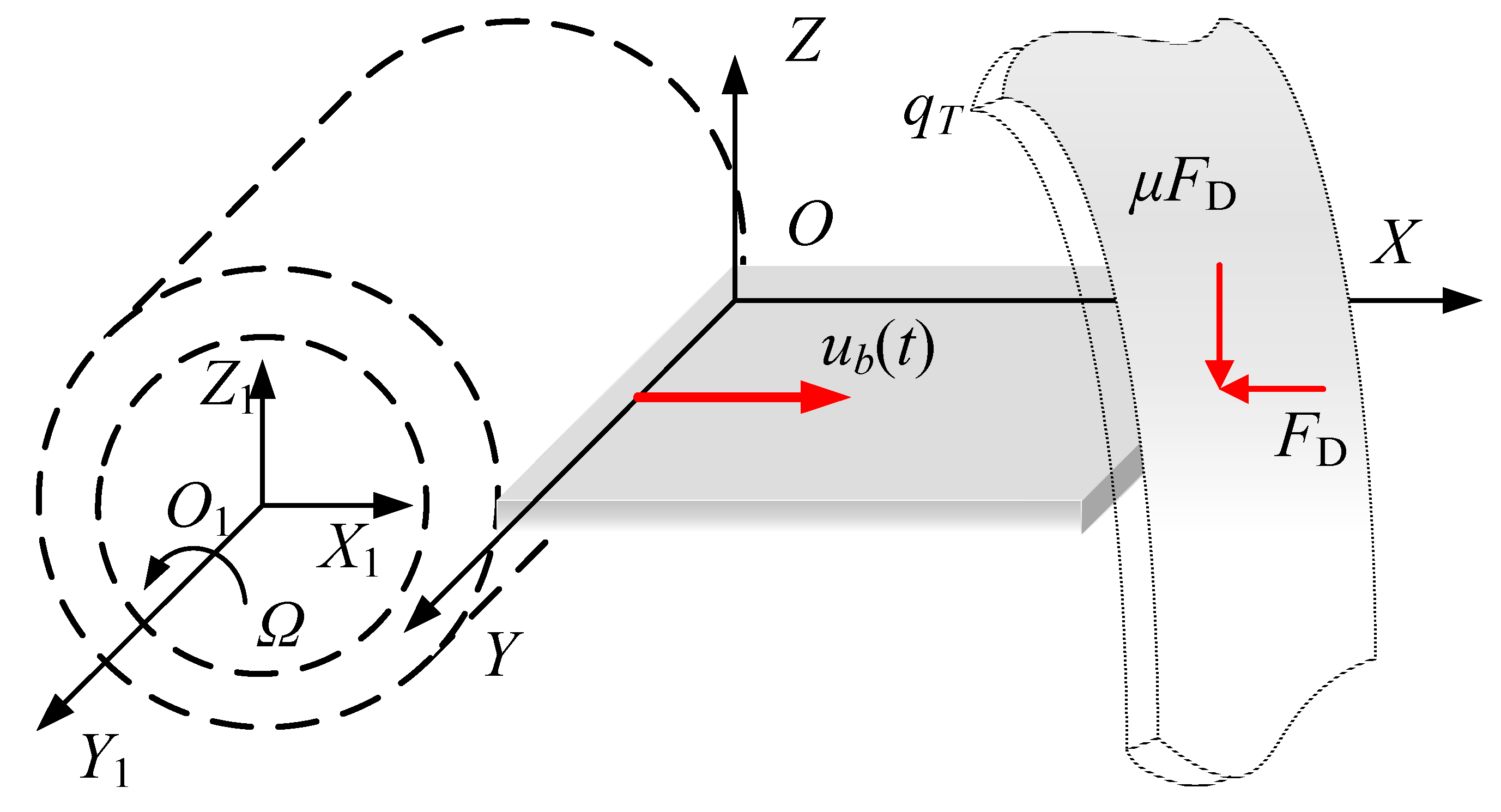
2.1. Modeling
2.2. Energy Functionals
2.3. Governing Equations
2.4. Analytic Solution for Forced Vibration
3. Results and Discussion
3.1. Validation Study
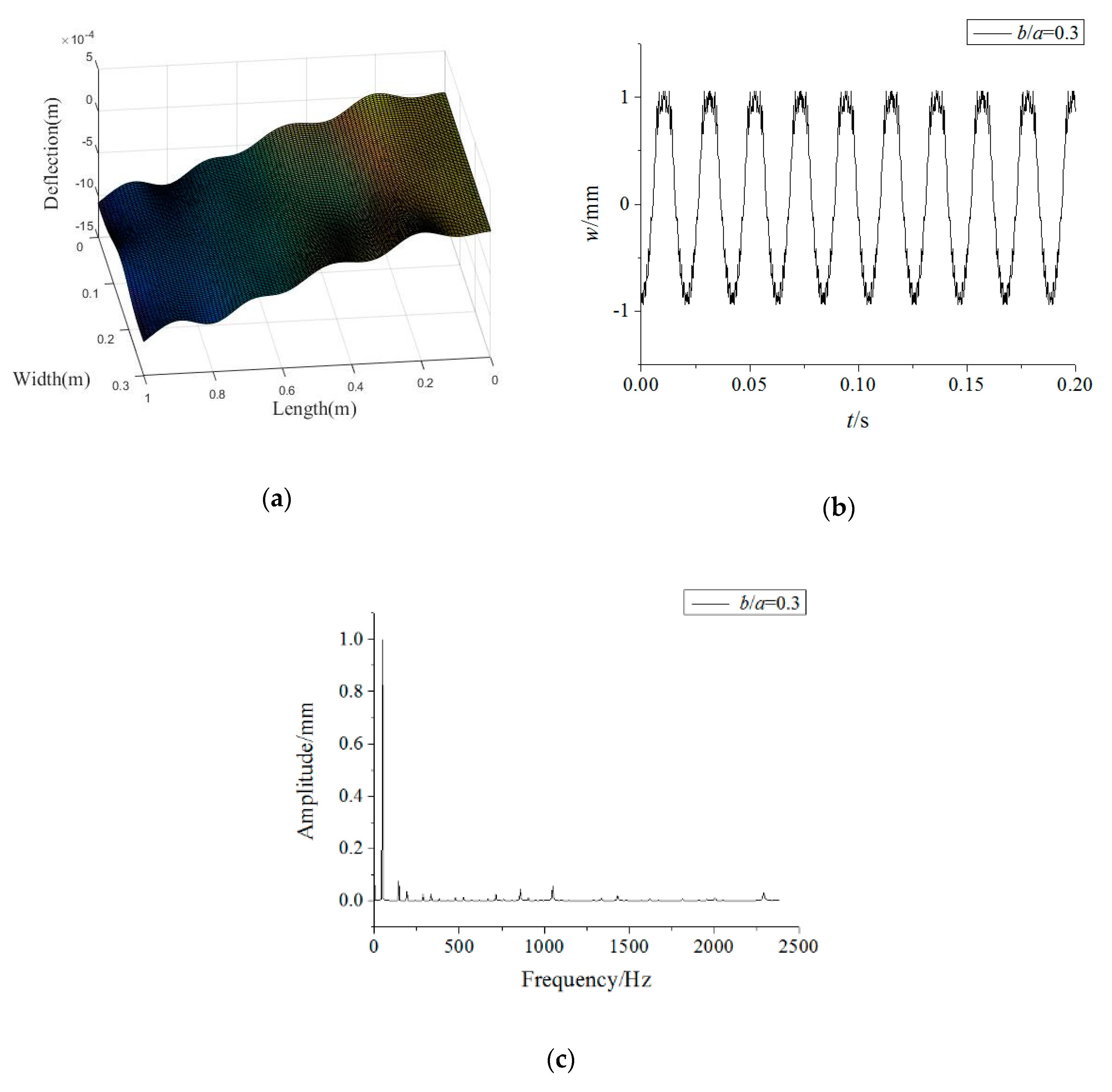
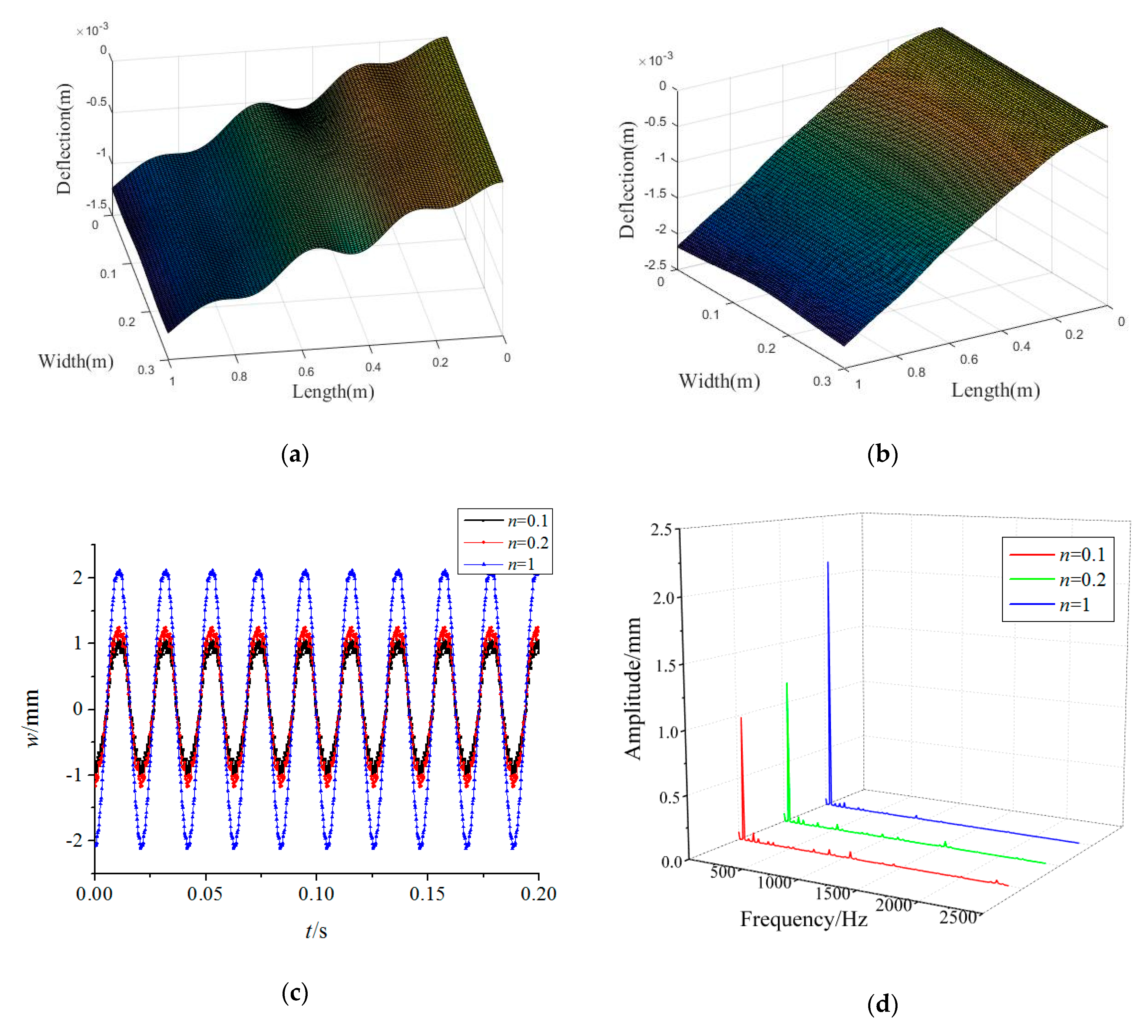
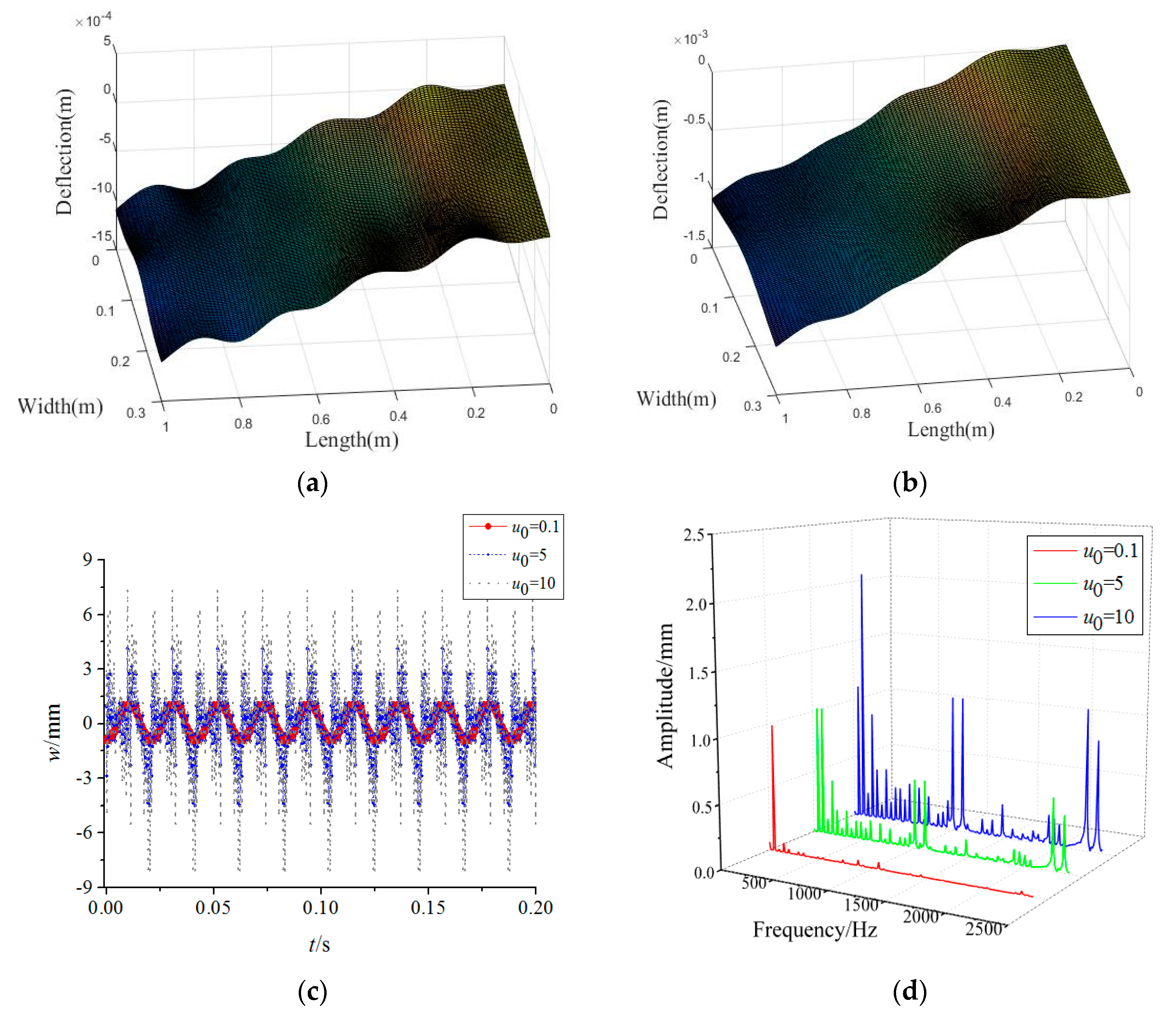
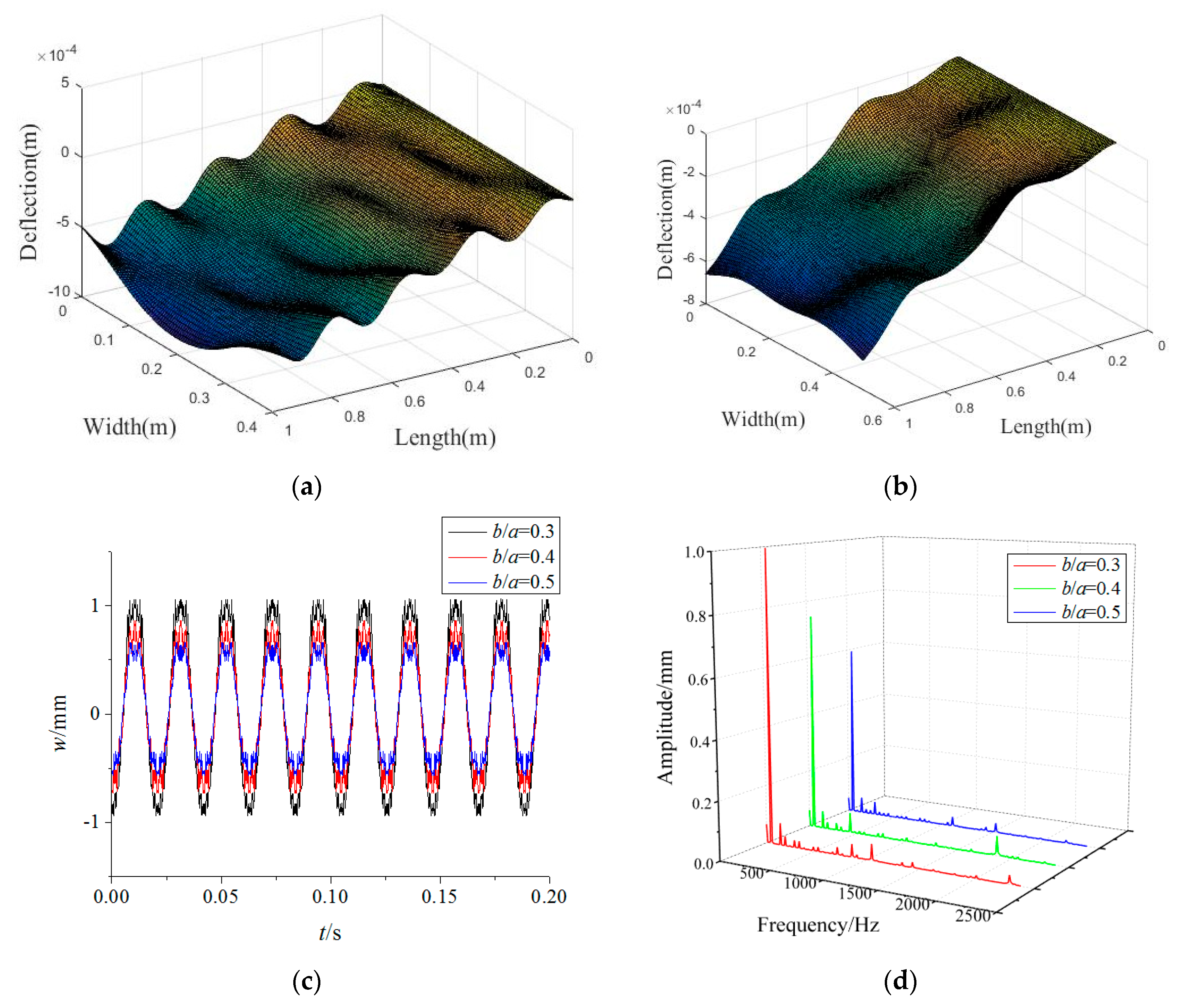
3.2. Forced Vibration Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, J.; Shaw, A.D.; Wang, C.; Gu, H.; Amoozgar, M.; Friswell, M.I.; Woods, B.K.S. Aeroelastic Model and Analysis of an Active Camber Morphing Wing. Aerosp. Sci. Technol. 2021, 111, 106534. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.; Zhao, D.; Wu, S. A Revised Contact Stiffness Model of Rough Curved Surfaces Based on the Length Scale. Tribol. Int. 2021, 164, 107206. [Google Scholar] [CrossRef]
- Arefi, M.; Loghman, A.; Mohammad Hosseini Mirzaei, M. Thermoelastic Analysis of a Functionally Graded Simple Blade Using First-Order Shear Deformation Theory. Mech. Adv. Compos. Struct. 2019, 7, 147–155. [Google Scholar]
- Ma, H.; Tai, X.Y.; Han, H.K.; Wu, Z.Y.; Wang, D.; Wen, B.C. A revised model for rubbing between rotating blade and elastic casing. J. Sound Vib. 2015, 337, 301–320. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.F.; Liu, C.; Jiang, D.X.; Behdinan, K. Casing vibration response prediction of dual–rotor–blade-casing system with blade-casing rubbing. Mech. Syst. Signal. Process. 2019, 118, 61–77. [Google Scholar] [CrossRef]
- Hou, L.; Chen, H.Z.; Chen, Y.S.; Lu, K.; Liu, Z.S. Bifurcation and stability analysis of a nonlinear rotor system subjected to constant excitation and rub-impact. Mech. Syst. Signal Process. 2019, 125, 65–78. [Google Scholar] [CrossRef]
- Xiao, S.G.; Liu, S.L.; Jiang, F.; Song, M.M.; Cheng, S.G. Nonlinear dynamic response of reciprocating compressor system with rub-impact fault caused by subsidence. J. Vib. Control. 2019, 25, 1737–1751. [Google Scholar] [CrossRef]
- Tchomeni, B.X.; Alugongo, A. Modelling and numerical simulation of vibrations induced by mixed faults of a rotor system immersed in an incompressible viscous fluid. Adv. Mech. Eng. 2018, 10, 1–21. [Google Scholar] [CrossRef]
- Wang, J.G.; Zhang, J.; Bai, R.S.; Yang, X.F.; Zhao, Y.X. Nonlinear analysis of the locomotive traction system with rub-impact and nonlinear stiffness. Adv. Mech. Eng. 2018, 10, 1–11. [Google Scholar] [CrossRef]
- Ebrahim, T.N.; Pouya, A.S.; Hamid, A. Nonlinear dynamics of a flexible rotor on tilting pad journal bearings experiencing rub-impact. Nonlinear Dyn. 2018, 94, 2937–2956. [Google Scholar]
- Zhang, Z.; Yang, F.; Zhang, H.; Zhang, T.; Wang, H.; Xu, Y.; Ma, Q. Influence of CeO2 Addition on Forming Quality and Microstructure of TiC-Reinforced CrTi4-Based Laser Cladding Composite Coating. Mater. Charact. 2021, 171, 110732. [Google Scholar] [CrossRef]
- Zhang, C.; Ali, A.; Sun, L. Investigation on Low-Cost Friction-Based Isolation Systems for Masonry Building Structures: Experimental and Numerical Studies. Eng. Struct. 2021, 243, 112645. [Google Scholar] [CrossRef]
- Hu, Y.; Qing, J.X.; Liu, Z.H.; Conrad, Z.J.; Cao, J.N.; Zhang, X.P. Hovering Efficiency Optimization of the Ducted Propeller with Weight Penalty Taken into Account. Aerosp. Sci. Technol. 2021, 117, 106937. [Google Scholar] [CrossRef]
- Minoo, N.; Kamyar, S. Functionally graded materials: A review of fabrication and properties. Appl. Mater. Today 2016, 5, 223–245. [Google Scholar]
- Yang, J.; Shen, H.S. Vibration characteristics and transient response of shear-deformation functionally graded plates in thermal environments. J. Sound Vib. 2002, 255, 579–602. [Google Scholar] [CrossRef]
- Kumar, R.; Lal, A.; Singh, B.N.; Singh, J. New transverse shear deformation theory for bending analysis of FGM plate under patch load. Compos. Struct. 2019, 208, 91–100. [Google Scholar] [CrossRef]
- Singh, S.J.; Harsha, S.P. Buckling analysis of FGM plates under uniform, linear and non-linear in-plane loading. J. Mech. Sci. Technol. 2019, 33, 1761–1767. [Google Scholar] [CrossRef]
- Do, V.N.V.; Ong, T.H.; Lee, C.H. Isogeometric analysis for nonlinear buckling of FGM plates under various types of thermal gradients. Thin-Walled Struct. 2019, 137, 448–462. [Google Scholar] [CrossRef]
- Wang, C.M.; Ke, L.L.; Chowdhury, A.N.R.; Yang, J.; Kitipornchai, S.; Fernando, D. Critical examination of midplane and neutral plane formulations for vibration analysis of FGM beams. Eng. Struct. 2017, 130, 275–281. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Buckling and bending analyses of a novel functionally graded porous plate using Chebyshev-Ritz method. ScienceDirect 2019, 19, 157–170. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Yang, Y.F.; Pan, H.G.; Zhang, H.Y.; Yuan, H.Q. Free vibration analysis of a spinning porous nanocomposite blade reinforced with graphene nanoplatelets. Materials 2022, 56, 574–586. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Jiang, Z.Y.; Zhao, Z.; Xie, L.Y.; Yuan, H.Q. Modeling and free vibration analysis of rotating hub-blade assemblies reinforced with graphene nanoplatelets. J. Strain Anal. Eng. 2021, 56, 563–573. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Ma, Y.; Zhang, H.Y.; Yang, J. Coupled Free Vibration of Spinning Functionally Graded Porous Double-Bladed Disk Systems Reinforced with Graphene Nanoplatelets. Materials 2020, 13, 5610. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.Y.; Liu, Z.F.; Pan, H.G.; Zhang, H.Y.; Yuan, H.Q. Vibration Characteristics of Functionally Graded Porous Nanocomposite Blade-disk-shaft Rotor System Reinforced with Graphene Nanoplatelets. Appl. Compos. Mater. 2021, 28, 717–731. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Jiang, L.P.; Pan, H.G.; Yang, J.; Kitipornchai, S. Coupled free vibration of a functionally graded pre-twisted blade-shaft system reinforced with graphene nanoplatelets. Compos. Struct. 2021, 262, 113362. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Ma, Y.; Zhang, H.Y.; Pan, H.G.; Cai, Y. Free vibration analysis of a rotating graphene nanoplatelet reinforced pre-twist blade-disk assembly with a setting angle. Appl. Math. Model. 2021, 93, 578–596. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Cui, Y.S.; Pan, H.G.; Yuan, H.Q.; Yang, J. Free vibration analysis of a functionally graded graphene nanoplatelet reinforced disk-shaft assembly with whirl motion. Int. J. Mech. Sci. 2021, 197, 106335. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Cui, Y.S.; Wang, Y.Q.; Pan, H.G. Vibration characteristics of graphene nanoplatelet reinforced disk-shaft rotor with eccentric mass. Mech. Adv. Mater. 2021, 1–25. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Jiang, L.P.; Yu, Y.X.; Wang, Y.Q. Study on theoretical modeling and mechanical performance of a spinning porous graphene nanoplatelet reinforced beam attached with double blades. Mech. Adv. Mater. Struct. 2022, 1–12. [Google Scholar] [CrossRef]
- Li, Z.C.; Zheng, J.X.; Sun, Q.; He, H.T. Nonlinear structural stability performance of pressurized thin-walled FGM arches under temperature variation field. Int. J. Non-Linear Mech. 2019, 113, 86–102. [Google Scholar] [CrossRef]
- Bakora, A.; Bourada, F.; Bousahla, A.A.; Tounsi, A.; Benrahou, K.H.; Tounsi, A.; I-Zahrani, M.M.A.; Mahmoud, S.R. Buckling analysis of functionally graded plates using HSDT in conjuction with the stress function method. Comput. Concr. 2021, 27, 73–83. [Google Scholar]
- Guellil, M.; Saidi, H.; Bourada, F.; Bousahla, A.A.; Tounsi, A.; I-Zahrani, M.M.A.; Hussain, M.; Mahmoud, S.R. Influences of porosity distributions and boundary conditions on mechanical bending response of functionally graded plates resting on Pasternak foundation. Steel Compos. Struct. 2021, 38, 1–15. [Google Scholar]
- Bekkaye, T.H.L.; Fahsi, B.; Bousahla, A.A.; Bourada, F.; Tounsi, A.; Benrahou, K.H.; Tounsi, A.; I-Zahrani, M.M.A. Porosity-dependent mechanical behaviors of FG plate using refined trigonometric shear deformation theory. Comput. Concr. 2020, 26, 439–450. [Google Scholar]
- Sobhy, M. Size dependent hygro-thermal buckling of porous FGM sandwich microplates and microbeams using a novel four-variable shear deformation theory. Int. J. Appl. Mech. 2020, 12, 2050017. [Google Scholar] [CrossRef]
- Sobhy, M.; Zenkour, A.M. Vibration analysis of functionally graded graphene platelet-reinforced composite doubly curved shallow shells on elastic foundations. Steel Compos. Struct. 2019, 33, 195–208. [Google Scholar]
- Guégan, A. Parameter Study of Bladed Disk/Casing Interactions through Direct Contact in Aero-Engine Assemblies. Structural Dynamics and Vibration Laboratory; McGill University Press: Montreal, QC, Canada, 2015. [Google Scholar]
- Padova, C.; Barton, J.; Dunn, M.G.; Manwaring, S.; Young, G.; Adams, M. Development of an Experimental Capability to Produce Controlled Blade Tip/Shroud Rubs at Engine Speed. J. Turbomach. Trans. Asme 2005, 127, 726–735. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear Vibrations and Stability of Shells and Plate; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Yao, M.H.; Ma, L.; Zhang, W. Nonlinear Dynamics of the High-Speed Rotating Plate. Int. J. Aerosp. Eng. 2018, 2018, 5610915. [Google Scholar] [CrossRef] [Green Version]
- Yoo, H.H.; Pierre, C. Modal Characteristic of a Rotating Rectangular Cantilever Plata. J. Sound Vib. 2003, 259, 81–96. [Google Scholar] [CrossRef]
- Zhao, J.; Tian, Q.; Hu, H.Y. Modal Analysis of a Rotating Thin Plate via Absolute Nodal Coordinate Formulation. J. Comput. Nonlinear Dyn. 2020, 6, 041013. [Google Scholar] [CrossRef]



| Dimensionless Rotating Speed | Frequency | Present | Yoo [40] | Zhao [41] |
|---|---|---|---|---|
| γ = 1 | 1st | 3.478 | 3.516 | 3.639 |
| 2nd | 8.514 | 8.533 | 8.571 | |
| 3rd | 21.325 | 21.520 | 21.469 | |
| 4th | 27.208 | 27.353 | 27.194 | |
| 5th | 31.013 | 31.206 | 31.068 | |
| γ = 2 | 1st | 3.493 | 3.596 | 4.101 |
| 2nd | 8.517 | 8.551 | 8.755 | |
| 3rd | 21.388 | 21.865 | 21.877 | |
| 4th | 27.214 | 27.384 | 27.284 | |
| 5th | 31.062 | 31.477 | 31.379 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, T.; Wang, Y.; Cui, X.; Wang, X. Analytical Solution for Forced Vibration Characteristics of Rotating Functionally Graded Blades under Rub-Impact and Base Excitation. Materials 2022, 15, 2175. https://doi.org/10.3390/ma15062175
Zhao T, Wang Y, Cui X, Wang X. Analytical Solution for Forced Vibration Characteristics of Rotating Functionally Graded Blades under Rub-Impact and Base Excitation. Materials. 2022; 15(6):2175. https://doi.org/10.3390/ma15062175
Chicago/Turabian StyleZhao, Tianyu, Yuxuan Wang, Xinze Cui, and Xin Wang. 2022. "Analytical Solution for Forced Vibration Characteristics of Rotating Functionally Graded Blades under Rub-Impact and Base Excitation" Materials 15, no. 6: 2175. https://doi.org/10.3390/ma15062175
APA StyleZhao, T., Wang, Y., Cui, X., & Wang, X. (2022). Analytical Solution for Forced Vibration Characteristics of Rotating Functionally Graded Blades under Rub-Impact and Base Excitation. Materials, 15(6), 2175. https://doi.org/10.3390/ma15062175







