Effect of Mass on the Dynamic Characteristics of Single- and Double-Layered Graphene-Based Nano Resonators
Abstract
:1. Introduction
Van Der Waal Interaction in Graphene
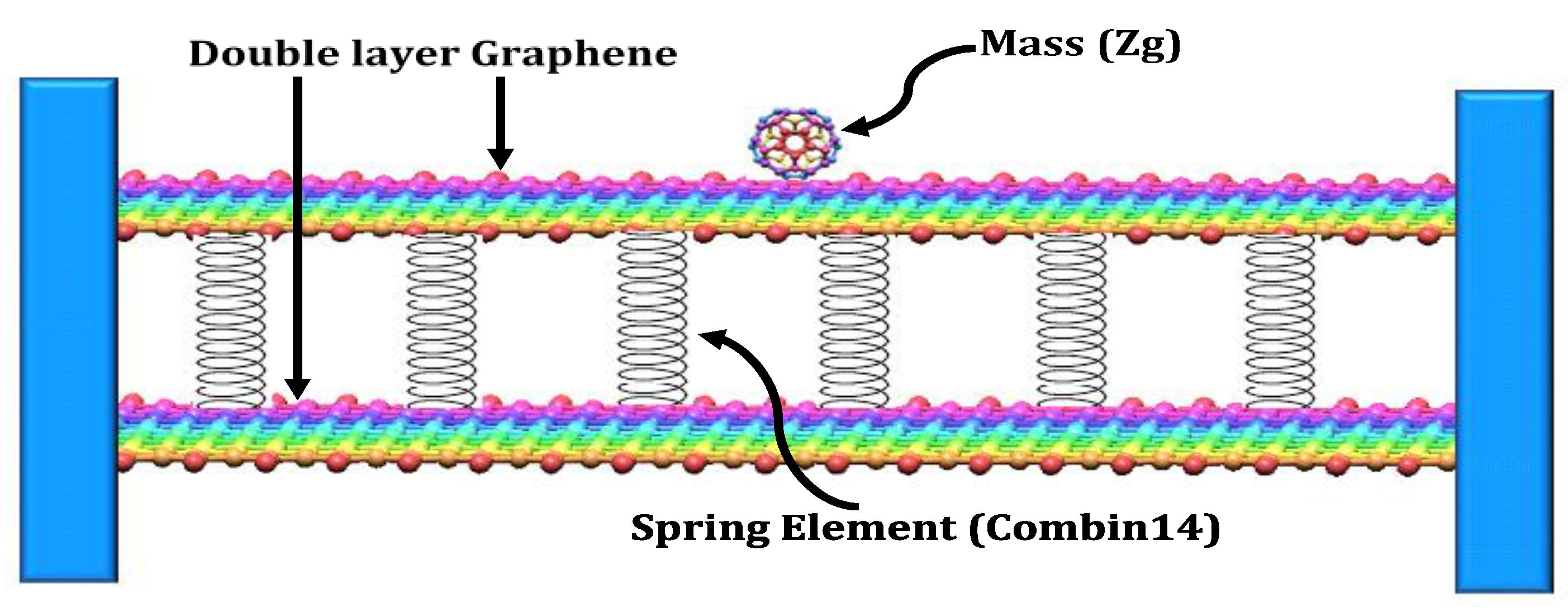
2. Interatomic Modelling of SLG and DLG
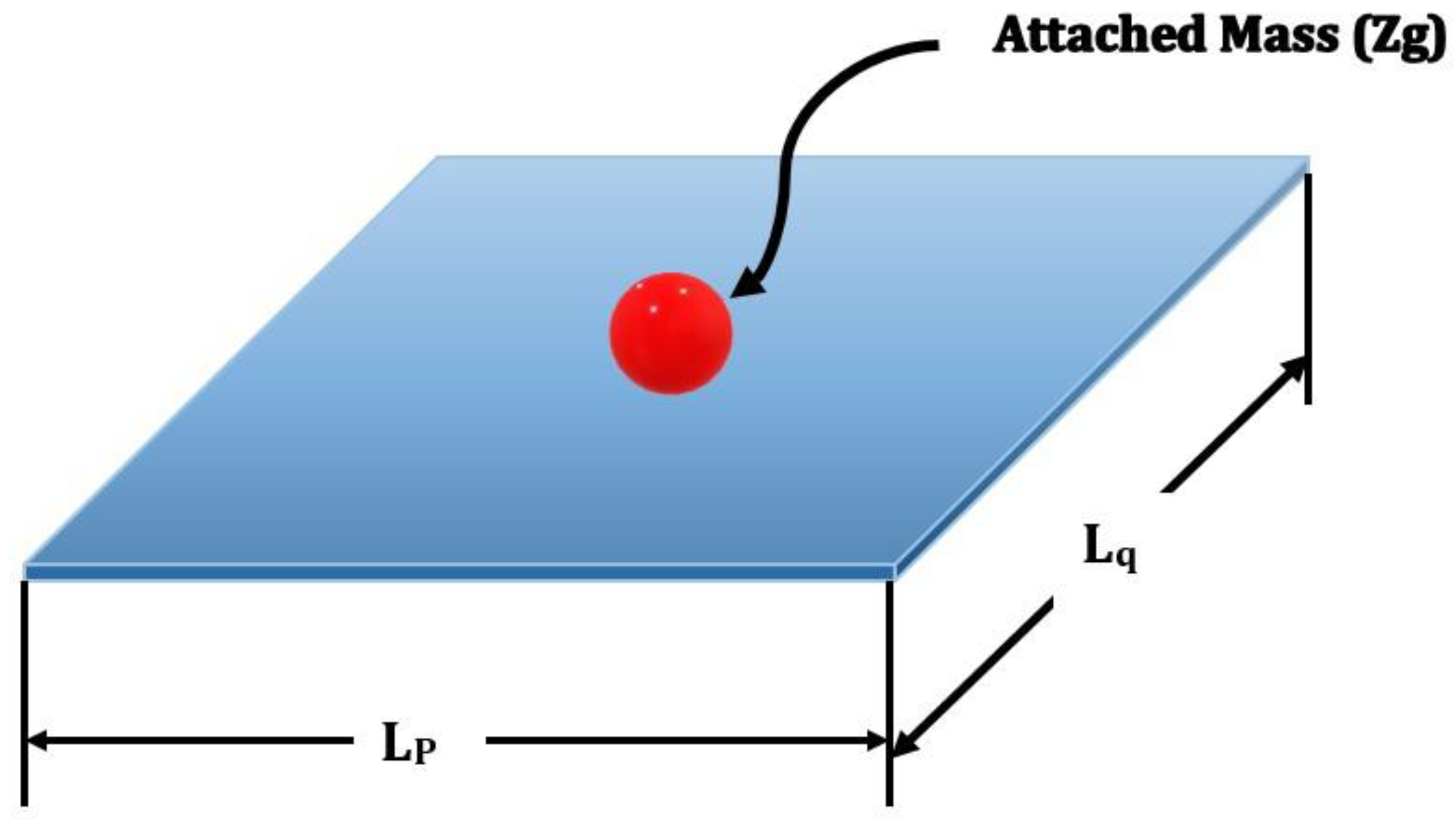
2.1. Single-Layer Graphene Sheets Analytical Approach
2.2. Validation of the Model
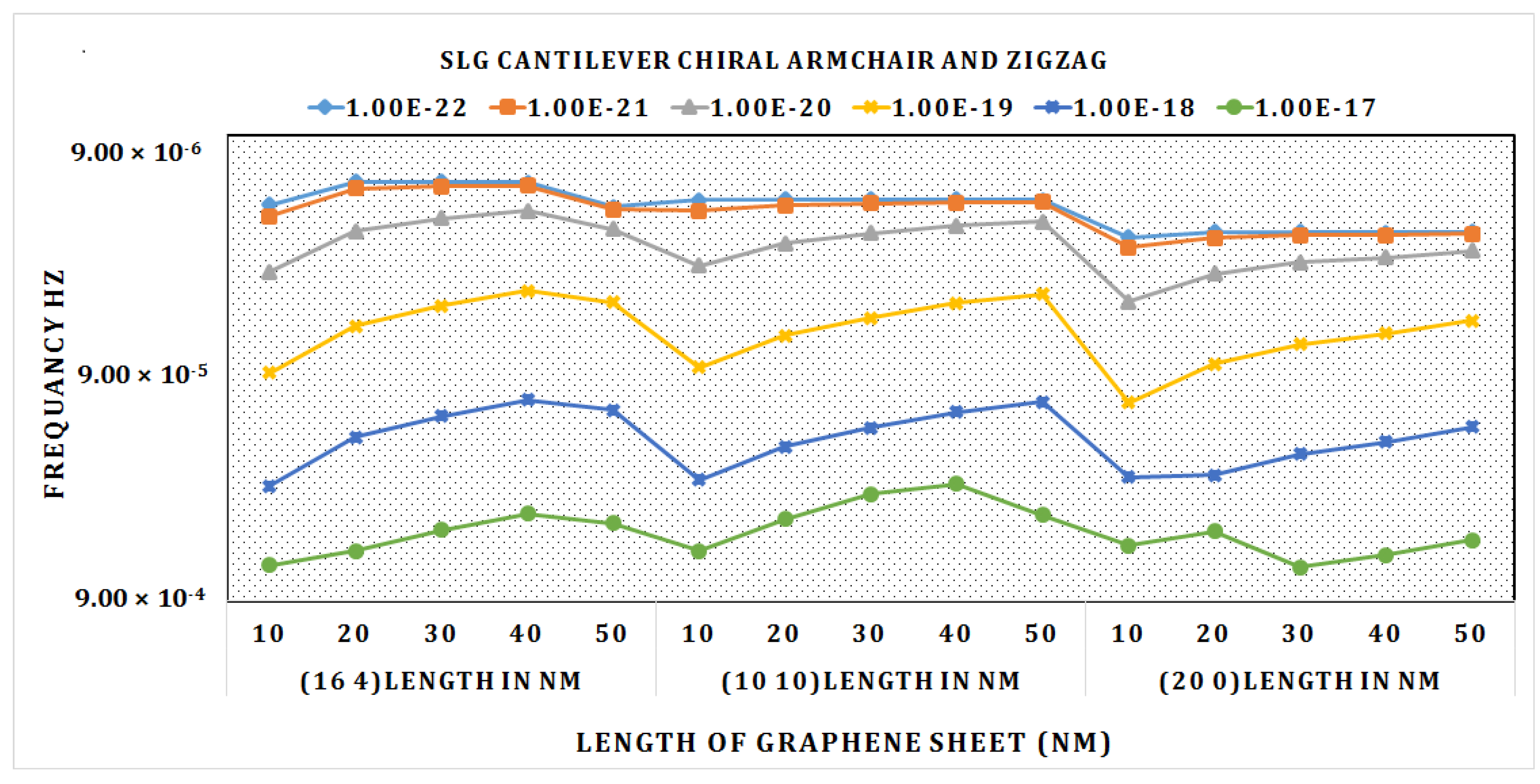
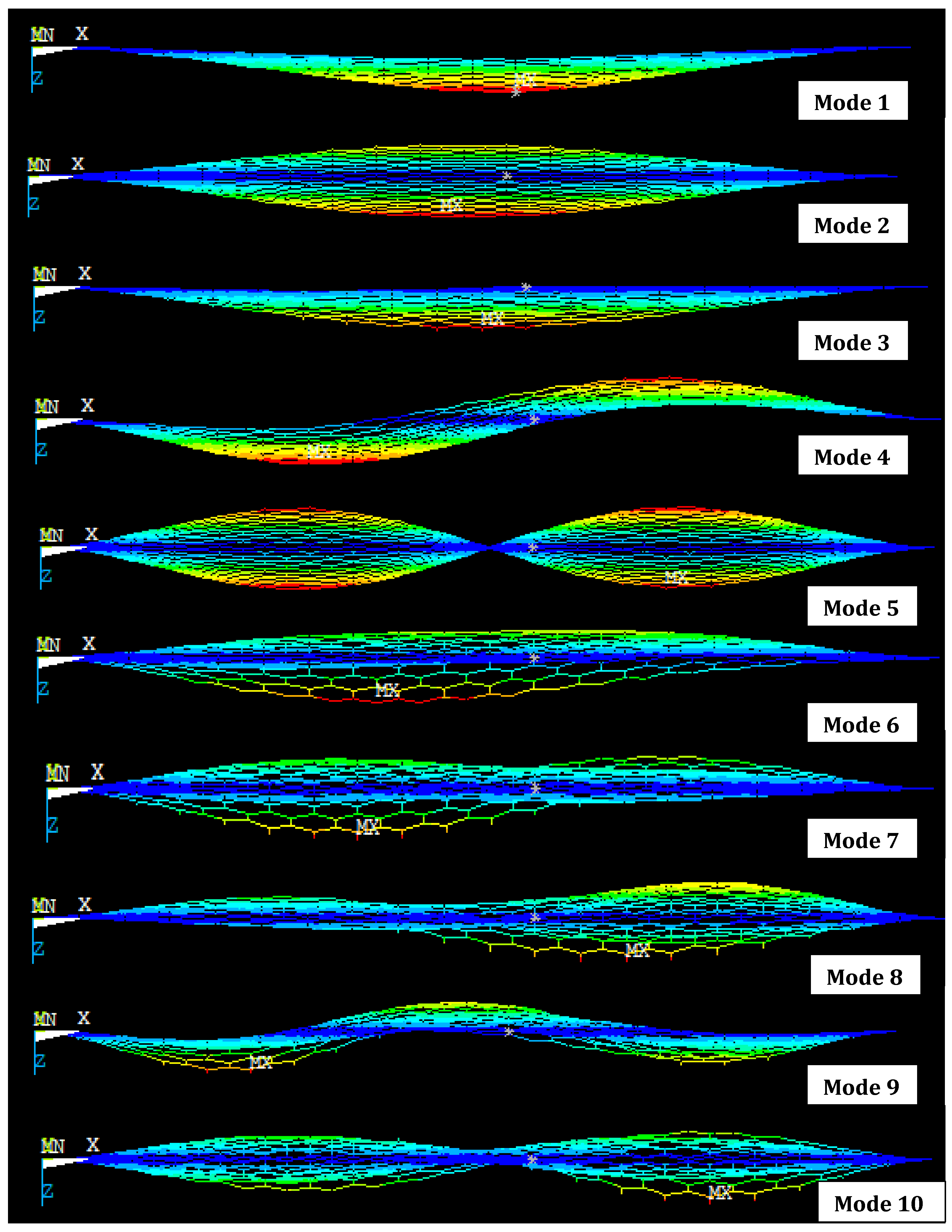
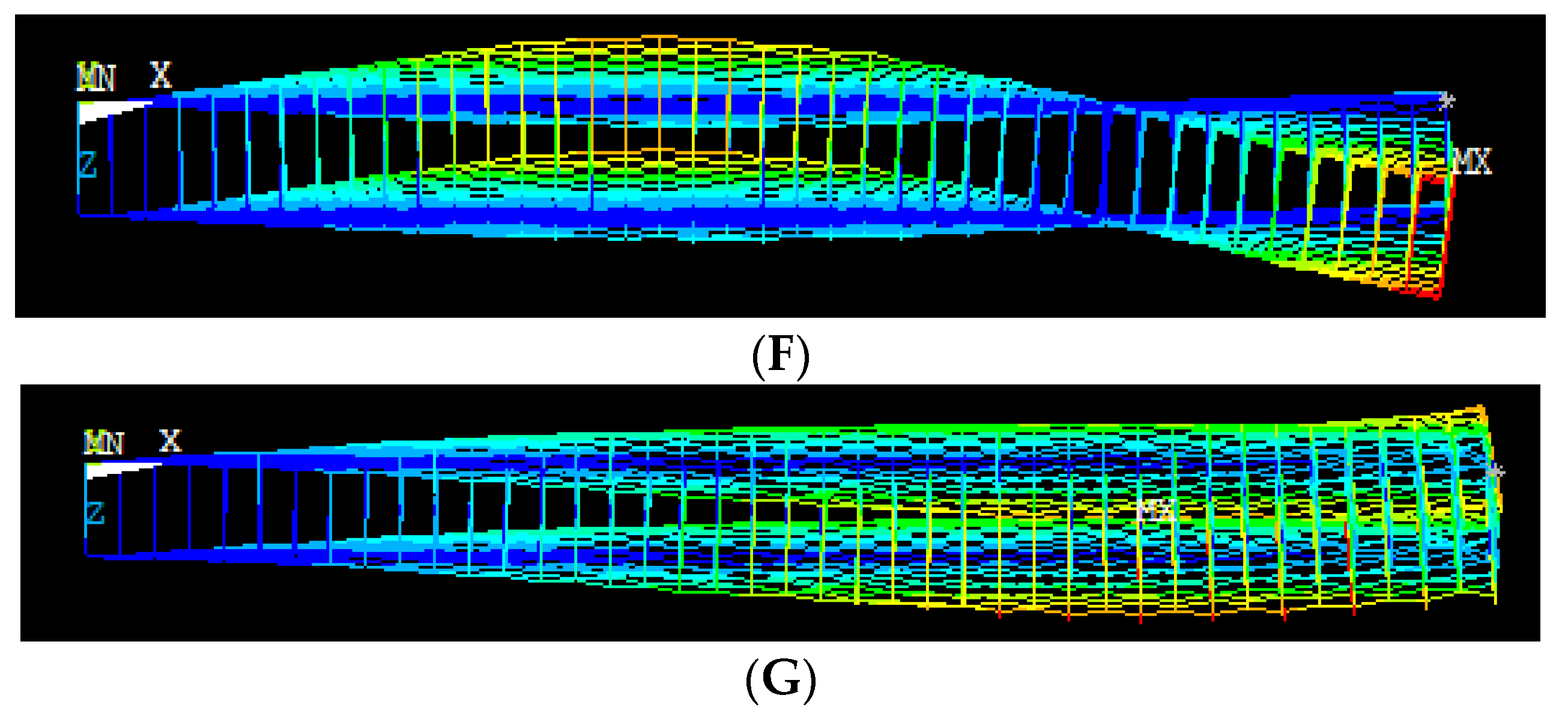
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kroto, H.W.; Heath, J.R.; O′Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Khandoker, N.; Islam, S.; Hiung, Y.S. Finite element simulation of mechanical properties of graphene sheets. IOP Conf. Series Mater. Sci. Eng. 2017, 206, 012057. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [PubMed]
- Lian, P.; Zhu, X.; Liang, S.; Li, Z.; Yang, W.; Wang, H. Large reversible capacity of high-quality graphene sheets as an anode material for lithium-ion batteries. Electrochimica Acta 2010, 55, 3909–3914. [Google Scholar] [CrossRef]
- Hassoun, J.; Bonaccorso, F.; Agostini, M.; Angelucci, M.; Betti, M.G.; Cingolani, R.; Gemmi, M.; Mariani, C.; Panero, S.; Pellegrini, V.; et al. An Advanced Lithium-Ion Battery Based on a Graphene Anode and a Lithium Iron Phosphate Cathode. Nano Lett. 2014, 14, 4901–4906. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic prop-erties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Deng, S.; Berry, V. Wrinkled, rippled and crumpled graphene: An over-view of formation mechanism, electronic properties, and applications. Mater. Today 2016, 19, 197–212. [Google Scholar] [CrossRef]
- Bolotin, K.; Sikes, K.; Jiang, Z.; Klima, M.; Fudenberg, G.; Hone, J.; Kim, P.; Stormer, H. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 2008, 146, 351–355. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Blake, P.; Katsnelson, M.I. Encyclopedia of Materials: Science and Technology, 2nd ed.; AMAZON: Seattle, WA, USA, 2008; pp. 1–6. [Google Scholar]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Kong, X.Y.; Ding, Y.; Yang, R.; Wang, Z.L. Single-crystal nanorings formed by epitaxial self-coiling of polar nanobelts. Science 2004, 303, 1348–1351. [Google Scholar] [CrossRef] [PubMed]
- Lavrik, N.V.; Sepaniak, M.J.; Datskos, P.G. Cantilever transducers as a platform for chemical and biological sensors. Rev. Sci. Instrum. 2004, 75, 2229–2253. [Google Scholar] [CrossRef]
- Haghi, A.K. Update on CNT/polymer nano-composites: From theory to applications. In Analysis and Performance of Engineering Materials; Taylor & Francis Group: Oxfordshire, UK, 2015; pp. 201–282. [Google Scholar]
- Ru, C. Axially compressed buckling of a doublewalled carbon nanotube embedded in an elastic medium. J. Mech. Phys. Solids 2001, 49, 1265–1279. [Google Scholar] [CrossRef]
- Wagner, H.D.; Lourie, O.; Zhou, X.F. Macro fragmentation and micro fragmentation phenomena in composite materials. Compos. Part A Appl. Sci. Manuf. 1999, 30, 59–66. [Google Scholar] [CrossRef]
- Rouhi, S.; Ansari, R. Atomistic finite element model for axial buckling and vibration analysis of single-layered graphene sheets. Phys. E Low-Dimens. Syst. Nanostructures 2011, 44, 764–772. [Google Scholar] [CrossRef]
- Wang, C.M.; Tan, V.B.C.; Zhang, Y.Y. Timoshenko beam model for vi-bration analysis of multi-walled carbon nanotubes. J. Sound Vib. 2006, 294, 1060–1072. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Wang, C.M.; Tan, V.B.C. Assessment of Timoshenko beam models for vibrational behavior of single-walled carbon nanotubes using molec-ular dynamics. Adv. Appl. Math. Mech. 2009, 1, 89–106. [Google Scholar]
- Lee, H.-L.; Chang, W.-J. A closed-form solution for critical buckling temperature of a single-walled carbon nanotube. Phys. E Low-Dimens. Syst. Nanostructures 2009, 41, 1492–1494. [Google Scholar] [CrossRef]
- Odegard, G.M.; Gates, T.S.; Nicholson, L.M.; Wise, K.E. Equiva-lent-continuum modeling of nano-structured materials. Compos. Sci. Technol. 2002, 62, 1869–1880. [Google Scholar] [CrossRef]
- Blagov, E.V.; Klimchitskaya, G.L.; Mostepanenko, V.M. Van der Waals interaction between a microparticle and a single-walled carbon nanotube. Phys. Rev. 2007, 75, 235413. [Google Scholar] [CrossRef]
- Lifshitz, E.M.; Pitaevskii, L.P. Statistical Physics, Pt. II; Pergamon: Oxford, UK, 1980. [Google Scholar]
- Patel, A.M.; Joshi, A.Y. Vibration analysis of double wall carbon nanotube based resonators for zeptogram level mass recognition. Comput. Mater. Sci. 2013, 79, 230–238. [Google Scholar] [CrossRef]
- Patel Ajay, M.; Joshi, A.Y. Effect of Waviness on the Dynamic Characteris-tics of Double Walled Carbon Nanotubes. Nanosci. Nano Technol. Lett. 2014, 6, 1–9. [Google Scholar] [CrossRef]
- Patel, A.M.; Joshi, A.Y. Investigating the influence of surface devia-tions in double walled carbon nanotube based nanomechanical sensors. Comput. Mater. Sci. 2014, 89, 157–164. [Google Scholar] [CrossRef]
- Li, C.; Chou, T.-W. A structural mechanics approach for the analysis of carbon nanotubes. Int. J. Solids Struct. 2003, 40, 2487–2499. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Giannopoulos, G.I.; Kakavas, P.A.; Anifantis, N.K. Evaluation of the effective mechanical properties of single walled carbon nanotubes using a spring based finite element approach. Comput. Meterials Sci. 2008, 41, 561–569. [Google Scholar] [CrossRef]
- Cornell, W.D.; Bally, C.I.; Gould, I.R.; Merz, K.M.; Feguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
- Li, C.; Chou, T.W. Vibrational behaviors of multi-walled-carbon-nanotube-based nanomechanical resonators. Appl. Phys. Lett. 2004, 84, 121–123. [Google Scholar] [CrossRef]
- Wang, J.; He, X.; Kitipornchai, S.; Zhang, H. Geometrical nonlinear free vibration of multi-layered graphene sheets. J. Phys. D Appl. Phys. 2011, 44, 135401. [Google Scholar] [CrossRef]
- Shi, J.X.; Ni, Q.Q.; Lei, X.W.; Natsuki, T. Nonlocal vibration of embed-ded double-layer graphene nanoribbons in in-phase and anti-phase modes. Phys. E Low-Dimens. Syst. Nanostructures 2012, 44, 1136–1141. [Google Scholar] [CrossRef]
- Natsuki, T.; Shi, J.X.; Ni, Q.Q. Vibration analysis of circular dou-ble-layered graphene sheets. J. Appl. Phys. 2012, 111, 044310. [Google Scholar] [CrossRef]
- Hill, E.W.; Vijayaragahvan, A.; Novoselov, K. Graphene sensors. IEEE Sens. J. 2011, 11, 3161–3170. [Google Scholar] [CrossRef]
- Jiang, J.W.; Park, H.S.; Rabczuk, T. Enhancing the mass sensitivity of graphene nanoresonators via nonlinear oscillations: The effective strain mechanism. Nanotechnology 2012, 23, 475501. [Google Scholar] [CrossRef]
- Sakhaee-Pour, A.; Ahmadian, M.T.; Vafai, A. Application of Single-Layered Graphene Sheets as Mass Sensors and Atomistic Dust Detectors. ASME Int. Mech. Eng. Congr. Expo. 2007, 4305, 99–104. [Google Scholar] [CrossRef]
- Dai, M.D.; Kim, C.W.; Eom, K. Nonlinear vibration behavior of gra-phene resonators and their applications in sensitive mass detection. Nanoscale Re-Search Lett. 2012, 7, 1–10. [Google Scholar]
- Shen, Z.B.; Tang, H.L.; Li, D.K.; Tang, G.J. Vibration of single-layered graphene sheet-based nanomechanical sensor via nonlocal Kirchhoff plate theory. Comput. Mater. Sci. 2012, 61, 200–205. [Google Scholar] [CrossRef]
- Lee, H.L.; Yang, Y.C.; Chang, W.J. Mass detection using a gra-phene-based nanomechanical resonator. Jpn. J. Appl. Phys. 2013, 52, 025101. [Google Scholar] [CrossRef]
- Natsuki, T.; Shi, J.-X.; Ni, Q.-Q. Vibration analysis of nanomechanical mass sensor using double-layered graphene sheets resonators. J. Appl. Phys. 2013, 114, 094307. [Google Scholar] [CrossRef]
- Lu, P.; Zhang, P.Q.; Lee, H.P.; Wang, C.M.; Reddy, J.N. Non-local elas-tic plate theories. Proceedings of the Royal Society A: Mathematical. Phys. Eng. Sci. 2007, 463, 3225–3240. [Google Scholar]
- Polizzotto, C. Nonlocal elasticity and related variational principles. Int. J. Solids Struct. 2001, 38, 7359–7380. [Google Scholar] [CrossRef]
- Arash, B.; Wang, Q. A review on the application of nonlocal elastic models in modeling of carbon nanotubes and graphenes. Comput. Mater. Sci. 2012, 51, 303–313. [Google Scholar] [CrossRef]
- Kitipornchai, S.; He, X.Q.; Liew, K.M. Continuum model for the vibra-tion of multilayered graphene sheets. Phys. Rev. B 2005, 72, 075443. [Google Scholar] [CrossRef]
- Shi, J.X.; Natsuki, T.; Lei, X.W.; Ni, Q.Q. Equivalent Young’s modulus and thickness of graphene sheets for the continuum mechanical models. Appl. Phys. Lett. 2014, 104, 223101. [Google Scholar] [CrossRef]
- Narendar, S.; Gopalakrishnan, S. Nonlocal scale effects on wave prop-agation in multi-walled carbon nanotubes. Comput. Mater. Sci. 2009, 47, 526–538. [Google Scholar] [CrossRef]
- Amirian, B.; Hosseini-Ara, R.; Moosavi, H. Thermo-mechanical vibra-tion of short carbon nanotubes embedded in pasternak foundation based on nonlocal elasticity theory. Shock. Vib. 2013, 20, 821–832. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, C.M.; Zhang, Y.Y. Calibration of nonlocal scaling effect parameter for free vibration of carbon nanotubes by molecular dynamics. J. Appl. Phys. 2007, 101, 024305. [Google Scholar] [CrossRef]
- Natsuki, T. Theoretical analysis of vibration frequency of graphene sheets used as nanomechanical mass sensor. Electronics 2015, 4, 723–738. [Google Scholar] [CrossRef]
- Prekodravac, J.R.; Kepić, D.P.; Colmenares, J.C.; Giannakoudakis, D.A.; Jovanović, S.P. A comprehensive review on selected graphene synthesis methods: From electrochemical exfoliation through rapid thermal annealing towards biomass pyrolysis. J. Mater. Chem. C 2021, 9, 6722–6748. [Google Scholar] [CrossRef]
- Kamedulski, P.; Lukaszewicz, J.; Witczak, L.; Szroeder, P.; Ziolkowski, P. The Importance of Structural Factors for the Electrochemical Performance of Graphene/Carbon Nanotube/Melamine Powders towards the Catalytic Activity of Oxygen Reduction Reaction. Materials 2021, 14, 2448. [Google Scholar] [CrossRef]
- Maniadi, A.; Vamvakaki, M.; Suchea, M.; Tudose, I.V.; Popescu, M.; Romanitan, C.; Pachiu, C.; Ionescu, O.N.; Viskadourakis, Z.; Kenanakis, G.; et al. Effect of Graphene Nanoplatelets on the Structure, the Morphology, and the Dielectric Behavior of Low-Density Polyethylene Nanocomposites. Materials 2020, 13, 4776. [Google Scholar] [CrossRef]













| Graphene Type | Single Layer | Length of Graphene | FEA Method Frequency (Hz) | Analytical Method [53] Frequency (Hz) |
|---|---|---|---|---|
| Armchair | (6, 6) | 10 | 1.0136 × 108 | 1.0235 × 108 |
| (8, 8) | 20 | 7.5488 × 107 | 7.5887 × 107 | |
| Zigzag | (12, 0) | 10 | 7.3185 × 107 | 7.3574 × 107 |
| (20, 0) | 20 | 2.5121 × 107 | 2.5489 × 107 | |
| Chiral | (8, 4) | 10 | 9.5844 × 107 | 9.5987 × 107 |
| (12, 4) | 20 | 4.7985 × 107 | 4.8042 × 107 |
| Length of Sheet (Nm) | Mass (gm) | ||||||
|---|---|---|---|---|---|---|---|
| 1.00 × 10−22 | 1.00 × 10−21 | 1.00 × 10−20 | 1.00 × 10−19 | 1.00 × 10−18 | 1.00 × 10−17 | 1.00 × 10−16 | |
| DLG Zigzag (6, 6) | |||||||
| 10 | 1.71 × 108 | 1.62 × 108 | 1.14 × 108 | 4.57 × 107 | 1.49 × 107 | 4.73 × 106 | 1.50 × 106 |
| 20 | 1.97 × 108 | 1.92 × 108 | 1.52 × 108 | 6.82 × 107 | 2.26 × 107 | 7.19 × 106 | 2.28 × 106 |
| 30 | 2.14 × 108 | 2.10 × 108 | 1.75 × 108 | 8.22 × 107 | 2.74 × 107 | 8.73 × 106 | 2.76 × 106 |
| 40 | 2.26 × 108 | 2.23 × 108 | 1.94 × 108 | 9.57 × 107 | 3.22 × 107 | 1.02 × 107 | 3.24 × 106 |
| 50 | 2.36 × 108 | 2.33 × 108 | 2.03 × 108 | 9.63 × 107 | 3.20 × 107 | 1.02 × 107 | 3.21 × 106 |
| DLG Zigzag (8, 8) | |||||||
| 10 | 9.35 × 107 | 8.99 × 107 | 6.75 × 107 | 2.89 × 107 | 9.55 × 106 | 3.03 × 106 | 9.60 × 105 |
| 20 | 1.10 × 108 | 1.08 × 108 | 9.00 × 107 | 4.41 × 107 | 1.50 × 107 | 4.77 × 106 | 1.51 × 106 |
| 30 | 1.21 × 108 | 1.19 × 108 | 1.04 × 108 | 5.50 × 107 | 1.90 × 107 | 6.06 × 106 | 1.92 × 106 |
| 40 | 1.30 × 108 | 1.29 × 108 | 1.15 × 108 | 6.32 × 107 | 2.20 × 107 | 7.01 × 106 | 2.22 × 106 |
| 50 | 1.38 × 108 | 1.37 × 108 | 1.24 × 108 | 6.93 × 107 | 2.41 × 107 | 7.68 × 106 | 2.43 × 106 |
| DLG Zigzag (10, 10) | |||||||
| 10 | 5.95 × 107 | 5.76 × 107 | 4.50 × 107 | 2.02 × 107 | 6.72 × 106 | 2.14 × 106 | 6.76 × 105 |
| 20 | 6.71 × 107 | 6.60 × 107 | 5.70 × 107 | 2.99 × 107 | 1.04 × 107 | 3.32 × 106 | 1.05 × 106 |
| 30 | 7.59 × 107 | 7.50 × 107 | 6.73 × 107 | 3.84 × 107 | 1.37 × 107 | 4.39 × 106 | 1.39 × 106 |
| 40 | 8.17 × 107 | 8.10 × 107 | 7.43 × 107 | 4.48 × 107 | 1.63 × 107 | 5.22 × 106 | 1.65 × 106 |
| 50 | 8.66 × 107 | 8.60 × 107 | 8.00 × 107 | 4.99 × 107 | 1.83 × 107 | 5.88 × 106 | 1.86 × 106 |
| DLG Armchair (12, 0) | |||||||
| 10 | 1.14 × 108 | 1.11 × 108 | 9.29 × 107 | 4.57 × 107 | 1.55 × 107 | 4.96 × 106 | 1.57 × 106 |
| 20 | 1.45 × 108 | 1.42 × 108 | 1.18 × 108 | 5.69 × 107 | 1.93 × 107 | 6.14 × 106 | 1.94 × 106 |
| 30 | 1.58 × 108 | 1.56 × 108 | 1.33 × 108 | 6.57 × 107 | 2.22 × 107 | 7.06 × 106 | 2.24 × 106 |
| 40 | 1.65 × 108 | 1.63 × 108 | 1.43 × 108 | 7.21 × 107 | 2.44 × 107 | 7.77 × 106 | 2.46 × 106 |
| 50 | 1.74 × 108 | 1.72 × 108 | 1.53 × 108 | 7.78 × 107 | 2.62 × 107 | 8.34 × 106 | 2.64 × 106 |
| DLG Armchair (16, 0) | |||||||
| 10 | 7.39 × 107 | 7.14 × 107 | 5.52 × 107 | 2.44 × 107 | 8.11 × 106 | 2.58 × 106 | 8.16 × 105 |
| 20 | 8.30 × 107 | 8.15 × 107 | 7.00 × 107 | 3.63 × 107 | 1.25 × 107 | 4.01 × 106 | 1.27 × 106 |
| 30 | 9.04 × 107 | 8.92 × 107 | 7.92 × 107 | 4.35 × 107 | 1.53 × 107 | 4.88 × 106 | 1.54 × 106 |
| 40 | 9.49 × 107 | 9.39 × 107 | 8.51 × 107 | 4.90 × 107 | 1.73 × 107 | 5.55 × 106 | 1.76 × 106 |
| 50 | 1.01 × 108 | 1.00 × 108 | 9.22 × 107 | 5.44 × 107 | 1.93 × 107 | 6.18 × 106 | 1.96 × 106 |
| DLG Armchair (20, 0) | |||||||
| 10 | 5.46 × 107 | 5.29 × 107 | 4.18 × 107 | 1.90 × 107 | 6.35 × 106 | 2.02 × 106 | 6.39 × 105 |
| 20 | 5.05 × 107 | 4.97 × 107 | 4.34 × 107 | 2.34 × 107 | 8.20 × 106 | 2.62 × 106 | 8.31 × 105 |
| 30 | 5.46 × 107 | 5.41 × 107 | 4.95 × 107 | 3.01 × 107 | 1.11 × 107 | 3.57 × 106 | 1.13 × 106 |
| 40 | 5.72 × 107 | 5.67 × 107 | 5.26 × 107 | 3.30 × 107 | 1.23 × 107 | 3.95 × 106 | 1.25 × 106 |
| 50 | 6.14 × 107 | 6.10 × 107 | 5.72 × 107 | 3.73 × 107 | 1.40 × 107 | 4.53 × 106 | 1.43 × 106 |
| Length of Sheet (Nm) | Mass (gm) | ||||||
|---|---|---|---|---|---|---|---|
| 1.00 × 10−22 | 1.00 × 10−21 | 1.00 × 10−20 | 1.00 × 10−19 | 1.00 × 10−18 | 1.00 × 10−17 | 1.00 × 10−16 | |
| DLG Zigzag (6, 6) | |||||||
| 10 | 6.81 × 108 | 6.58 × 108 | 4.89 × 108 | 1.96 × 108 | 6.36 × 107 | 2.02 × 107 | 6.38 × 106 |
| 20 | 7.01 × 108 | 6.89 × 108 | 5.62 × 108 | 2.30 × 108 | 7.45 × 107 | 2.36 × 107 | 7.47 × 106 |
| 30 | 6.77 × 108 | 6.70 × 108 | 5.71 × 108 | 2.35 × 108 | 7.59 × 107 | 2.41 × 107 | 7.61 × 106 |
| 40 | 7.15 × 108 | 7.09 × 108 | 6.04 × 108 | 2.39 × 108 | 7.71 × 107 | 2.44 × 107 | 7.73 × 106 |
| 50 | 7.17 × 108 | 7.13 × 108 | 6.11 × 108 | 2.40 × 108 | 7.74 × 107 | 2.45 × 107 | 7.76 × 106 |
| DLG Zigzag (8, 8) | |||||||
| 10 | 4.46 × 108 | 4.35 × 108 | 3.49 × 108 | 1.54 × 108 | 5.10 × 107 | 1.62 × 107 | 5.13 × 106 |
| 20 | 4.55 × 108 | 4.50 × 108 | 3.96 × 108 | 1.93 × 108 | 6.42 × 107 | 2.04 × 107 | 6.46 × 106 |
| 30 | 4.82 × 108 | 4.78 × 108 | 4.35 × 108 | 2.12 × 108 | 7.00 × 107 | 2.22 × 107 | 7.03 × 106 |
| 40 | 4.88 × 108 | 4.85 × 108 | 4.50 × 108 | 2.18 × 108 | 7.14 × 107 | 2.27 × 107 | 7.17 × 106 |
| 50 | 4.73 × 108 | 4.71 × 108 | 4.45 × 108 | 2.17 × 108 | 7.12 × 107 | 2.26 × 107 | 7.15 × 106 |
| DLG Zigzag (10, 10) | |||||||
| 10 | 3.13 × 108 | 3.07 × 108 | 2.56 × 108 | 1.23 × 108 | 4.12 × 107 | 1.31 × 107 | 4.15 × 106 |
| 20 | 3.30 × 108 | 3.27 × 108 | 2.96 × 108 | 1.62 × 108 | 5.58 × 107 | 1.78 × 107 | 5.63 × 106 |
| 30 | 3.51 × 108 | 3.49 × 108 | 3.26 × 108 | 1.86 × 108 | 6.35 × 107 | 2.02 × 107 | 6.40 × 106 |
| 40 | 3.58 × 108 | 3.57 × 108 | 3.39 × 108 | 1.96 × 108 | 6.64 × 107 | 2.11 × 107 | 6.68 × 106 |
| 50 | 3.51 × 108 | 3.50 × 108 | 3.37 × 108 | 1.99 × 108 | 6.69 × 107 | 2.13 × 107 | 6.73 × 106 |
| DLG Armchair (12, 0) | |||||||
| 10 | 4.45 × 108 | 4.38 × 108 | 3.81 × 108 | 1.94 × 108 | 6.62 × 107 | 2.11 × 107 | 6.68 × 106 |
| 20 | 5.24 × 108 | 5.17 × 108 | 4.42 × 108 | 2.02 × 108 | 6.65 × 107 | 2.11 × 107 | 6.68 × 106 |
| 30 | 5.35 × 108 | 5.32 × 108 | 4.81 × 108 | 2.22 × 108 | 7.25 × 107 | 2.30 × 107 | 7.27 × 106 |
| 40 | 5.37 × 108 | 5.35 × 108 | 4.93 × 108 | 2.25 × 108 | 7.34 × 107 | 2.33 × 107 | 7.36 × 106 |
| 50 | 5.39 × 108 | 5.38 × 108 | 5.05 × 108 | 2.26 × 108 | 7.36 × 107 | 2.33 × 107 | 7.38 × 106 |
| DLG Armchair (16, 0) | |||||||
| 10 | 3.37 × 108 | 3.29 × 108 | 2.69 × 108 | 1.23 × 108 | 4.11 × 107 | 1.31 × 107 | 4.14 × 106 |
| 20 | 3.67 × 108 | 3.63 × 108 | 3.26 × 108 | 1.71 × 108 | 5.81 × 107 | 1.85 × 107 | 5.85 × 106 |
| 30 | 3.69 × 108 | 3.66 × 108 | 3.42 × 108 | 1.90 × 108 | 6.45 × 107 | 2.05 × 107 | 6.50 × 106 |
| 40 | 3.72 × 108 | 3.70 × 108 | 3.52 × 108 | 2.00 × 108 | 6.72 × 107 | 2.14 × 107 | 6.77 × 106 |
| 50 | 3.75 × 108 | 3.74 × 108 | 3.63 × 108 | 2.05 × 108 | 6.83 × 107 | 2.17 × 107 | 6.86 × 106 |
| DLG Armchair (20, 0) | |||||||
| 10 | 2.98 × 108 | 2.92 × 108 | 2.43 × 108 | 1.16 × 108 | 3.90 × 107 | 1.24 × 107 | 3.93 × 106 |
| 20 | 2.47 × 108 | 2.44 × 108 | 2.25 × 108 | 1.34 × 108 | 4.74 × 107 | 1.52 × 107 | 4.80 × 106 |
| 30 | 2.69 × 108 | 2.68 × 108 | 2.54 × 108 | 1.61 × 108 | 5.72 × 107 | 1.83 × 107 | 5.79 × 106 |
| 40 | 2.82 × 108 | 2.81 × 108 | 2.70 × 108 | 1.77 × 108 | 6.23 × 107 | 1.99 × 107 | 6.30 × 106 |
| 50 | 2.78 × 108 | 2.77 × 108 | 2.71 × 108 | 1.82 × 108 | 6.37 × 107 | 2.03 × 107 | 6.42 × 106 |
| Length of Sheet (Nm) | Mass (gm) | ||||||
|---|---|---|---|---|---|---|---|
| 1.00 × 10−22 | 1.00 × 10−21 | 1.00 × 10−20 | 1.00 × 10−19 | 1.00 × 10−18 | 1.00 × 10−17 | 1.00 × 10−16 | |
| DLG Zigzag (6,6) | |||||||
| 10 | 1.43 × 107 | 1.06 × 107 | 4.53 × 106 | 1.49 × 106 | 4.74 × 105 | 1.50 × 105 | 1.00 × 105 |
| 20 | 1.51 × 107 | 1.37 × 107 | 8.12 × 106 | 2.96 × 106 | 9.50 × 105 | 3.01 × 105 | 1.01 × 105 |
| 30 | 1.51 × 107 | 1.41 × 107 | 9.19 × 106 | 3.51 × 106 | 1.14 × 106 | 3.60 × 105 | 1.14 × 105 |
| 40 | 1.52 × 107 | 1.44 × 107 | 9.97 × 106 | 3.94 × 106 | 1.28 × 106 | 4.06 × 105 | 1.28 × 105 |
| 50 | 1.63 × 107 | 1.56 × 107 | 1.14 × 107 | 4.64 × 106 | 1.52 × 106 | 4.81 × 105 | 1.52 × 105 |
| DLG Zigzag (8,8) | |||||||
| 10 | 8.13 × 106 | 7.11 × 106 | 3.86 × 106 | 1.36 × 106 | 4.35 × 105 | 1.38 × 105 | 1.00 × 105 |
| 20 | 8.24 × 106 | 7.65 × 106 | 4.92 × 106 | 1.87 × 106 | 6.05 × 105 | 1.92 × 105 | 1.01 × 105 |
| 30 | 8.33 × 106 | 7.90 × 106 | 5.57 × 106 | 2.25 × 106 | 7.35 × 105 | 2.33 × 105 | 2.00 × 105 |
| 40 | 8.44 × 106 | 8.10 × 106 | 6.03 × 106 | 2.55 × 106 | 8.41 × 105 | 2.67 × 105 | 1.12 × 105 |
| 50 | 1.13 × 107 | 1.09 × 107 | 8.10 × 106 | 3.39 × 106 | 1.11 × 106 | 3.53 × 105 | 1.12 × 105 |
| DLG Zigzag (10,10) | |||||||
| 10 | 5.18 × 106 | 4.63 × 106 | 2.66 × 106 | 9.58 × 105 | 3.07 × 105 | 1.00 × 105 | 1.00 × 105 |
| 20 | 5.21 × 106 | 4.90 × 106 | 3.34 × 106 | 1.32 × 106 | 4.29 × 105 | 1.36 × 105 | 1.01 × 105 |
| 30 | 5.21 × 106 | 5.00 × 106 | 3.71 × 106 | 1.58 × 106 | 5.20 × 105 | 1.65 × 105 | 1.03 × 105 |
| 40 | 5.21 × 106 | 5.05 × 106 | 4.00 × 106 | 1.83 × 106 | 6.11 × 105 | 1.94 × 105 | 1.12 × 105 |
| 50 | 5.20 × 106 | 5.07 × 106 | 4.17 × 106 | 1.99 × 106 | 6.74 × 105 | 2.15 × 105 | 1.13 × 105 |
| DLG Armchair (12,0) | |||||||
| 10 | 1.07 × 107 | 9.15 × 106 | 4.76 × 106 | 1.65 × 106 | 5.27 × 105 | 1.67 × 105 | 1.00 × 105 |
| 20 | 1.13 × 107 | 1.04 × 107 | 6.50 × 106 | 2.44 × 106 | 7.87 × 105 | 2.50 × 105 | 1.69 × 105 |
| 30 | 1.13 × 107 | 1.07 × 107 | 7.43 × 106 | 2.97 × 106 | 9.06 × 105 | 2.87 × 105 | 1.10 × 105 |
| 40 | 1.12 × 107 | 1.07 × 107 | 7.62 × 106 | 3.10 × 106 | 1.01 × 106 | 3.21 × 105 | 1.03 × 105 |
| 50 | 1.13 × 107 | 1.09 × 107 | 8.10 × 106 | 3.38 × 106 | 1.11 × 106 | 3.52 × 105 | 1.11 × 105 |
| DLG Armchair (16,0) | |||||||
| 10 | 5.93 × 106 | 5.24 × 106 | 2.91 × 106 | 1.03 × 106 | 3.31 × 105 | 1.05 × 105 | 1.00 × 105 |
| 20 | 6.23 × 106 | 5.84 × 106 | 3.91 × 106 | 1.53 × 106 | 4.95 × 105 | 1.57 × 105 | 1.01 × 105 |
| 30 | 6.24 × 106 | 5.95 × 106 | 4.31 × 106 | 1.78 × 106 | 5.84 × 105 | 1.85 × 105 | 1.03 × 105 |
| 40 | 6.19 × 106 | 5.97 × 106 | 4.56 × 106 | 1.98 × 106 | 6.57 × 105 | 2.09 × 105 | 1.12 × 105 |
| 50 | 6.26 × 106 | 6.08 × 106 | 4.82 × 106 | 2.19 × 106 | 7.31 × 105 | 2.32 × 105 | 1.13 × 105 |
| DLG Armchair (20,0) | |||||||
| 10 | 3.56 × 106 | 3.20 × 106 | 1.85 × 106 | 6.69 × 105 | 2.15 × 105 | 1.19 × 105 | 1.00 × 105 |
| 20 | 3.75 × 106 | 3.54 × 106 | 2.46 × 106 | 9.86 × 105 | 3.22 × 105 | 1.02 × 105 | 1.00 × 105 |
| 30 | 3.76 × 106 | 3.62 × 106 | 2.76 × 106 | 1.21 × 106 | 3.99 × 105 | 1.27 × 105 | 1.03 × 105 |
| 40 | 3.73 × 106 | 3.62 × 106 | 2.90 × 106 | 1.34 × 106 | 4.50 × 105 | 1.43 × 105 | 1.12 × 105 |
| 50 | 3.77 × 106 | 3.69 × 106 | 3.09 × 106 | 1.54 × 106 | 5.25 × 105 | 1.67 × 105 | 1.19 × 105 |
| Length of Sheet (Nm) | Mass (gm) | ||||||
|---|---|---|---|---|---|---|---|
| 1.00 × 10−22 | 1.00 × 10−21 | 1.00 × 10−20 | 1.00 × 10−19 | 1.00 × 10−18 | 1.00 × 10−17 | 1.00 × 10−16 | |
| DLG Zigzag (6, 6) | |||||||
| 10 | 9.59 × 107 | 8.49 × 107 | 4.70 × 107 | 1.66 × 107 | 5.31 × 106 | 1.68 × 106 | 5.32 × 105 |
| 20 | 9.86 × 107 | 9.20 × 107 | 5.76 × 107 | 2.10 × 107 | 6.74 × 106 | 2.14 × 106 | 6.75 × 105 |
| 30 | 9.88 × 107 | 9.41 × 107 | 6.09 × 107 | 2.21 × 107 | 7.10 × 106 | 2.25 × 106 | 7.11 × 105 |
| 40 | 9.90 × 107 | 9.54 × 107 | 6.25 × 107 | 2.27 × 107 | 7.27 × 106 | 2.30 × 106 | 7.28 × 105 |
| 50 | 1.07 × 108 | 1.03 × 108 | 6.51 × 107 | 2.34 × 107 | 7.49 × 106 | 2.37 × 106 | 7.50 × 105 |
| DLG Zigzag (8, 8) | |||||||
| 10 | 3.54 × 107 | 3.27 × 107 | 2.07 × 107 | 7.81 × 106 | 2.52 × 106 | 7.99 × 105 | 2.53 × 105 |
| 20 | 7.38 × 106 | 7.33 × 106 | 6.83 × 106 | 4.38 × 106 | 1.64 × 106 | 5.29 × 105 | 1.68 × 105 |
| 30 | 5.45 × 107 | 5.26 × 107 | 3.88 × 107 | 1.56 × 107 | 5.06 × 106 | 1.60 × 106 | 5.07 × 105 |
| 40 | 5.51 × 107 | 5.36 × 107 | 4.02 × 107 | 1.61 × 107 | 5.23 × 106 | 1.66 × 106 | 5.24 × 105 |
| 50 | 7.33 × 107 | 7.14 × 107 | 5.11 × 107 | 1.94 × 107 | 6.25 × 106 | 1.98 × 106 | 6.26 × 105 |
| DLG Zigzag (10, 10) | |||||||
| 10 | 3.40 × 107 | 3.15 × 107 | 2.01 × 107 | 7.58 × 106 | 2.45 × 106 | 7.77 × 105 | 2.46 × 105 |
| 20 | 3.42 × 107 | 3.29 × 107 | 2.43 × 107 | 1.02 × 107 | 3.33 × 106 | 1.06 × 106 | 3.35 × 105 |
| 30 | 3.56 × 107 | 3.46 × 107 | 2.73 × 107 | 1.19 × 107 | 3.91 × 106 | 1.24 × 106 | 3.93 × 105 |
| 40 | 3.43 × 107 | 3.36 × 107 | 2.77 × 107 | 1.25 × 107 | 4.12 × 106 | 1.31 × 106 | 4.14 × 105 |
| 50 | 3.43 × 107 | 3.38 × 107 | 2.84 × 107 | 1.28 × 107 | 4.21 × 10−01 | 1.34 × 106 | 4.23 × 105 |
| DLG Armchair (12, 0) | |||||||
| 10 | 6.95 × 107 | 6.17 × 107 | 3.45 × 107 | 1.23 × 107 | 3.45 × 107 | 1.24 × 106 | 3.93 × 105 |
| 20 | 7.29 × 107 | 6.85 × 107 | 4.51 × 107 | 1.70 × 107 | 5.49 × 106 | 1.74 × 106 | 5.50 × 105 |
| 30 | 7.31 × 107 | 7.01 × 107 | 4.86 × 107 | 1.85 × 107 | 5.97 × 106 | 1.89 × 106 | 5.99 × 105 |
| 40 | 7.26 × 107 | 7.03 × 107 | 4.98 × 107 | 6.10 × 106 | 1.93 × 106 | 1.93 × 106 | 6.11 × 105 |
| 50 | 7.33 × 107 | 7.12 × 107 | 5.04 × 107 | 1.90 × 107 | 6.14 × 106 | 1.94 × 106 | 6.15 × 105 |
| DLG Armchair (16, 0) | |||||||
| 10 | 3.84 × 107 | 3.50 × 107 | 2.12 × 107 | 7.81 × 106 | 2.52 × 106 | 7.97 × 105 | 2.52 × 105 |
| 20 | 4.02 × 107 | 3.83 × 107 | 2.76 × 107 | 1.12 × 107 | 3.66 × 106 | 1.16 × 106 | 3.67 × 105 |
| 30 | 4.03 × 107 | 3.90 × 107 | 3.01 × 107 | 1.28 × 107 | 4.19 × 106 | 1.33 × 106 | 4.21 × 105 |
| 40 | 3.99 × 107 | 3.91 × 107 | 3.14 × 107 | 1.35 × 107 | 4.44 × 106 | 1.41 × 106 | 4.46 × 105 |
| 50 | 4.03 × 107 | 3.96 × 107 | 3.22 × 107 | 1.38 × 107 | 4.53 × 106 | 1.44 × 106 | 4.55 × 105 |
| DLG Armchair (20, 0) | |||||||
| 10 | 2.31 × 107 | 2.15 × 107 | 1.41 × 107 | 5.38 × 106 | 1.74 × 106 | 5.52 × 105 | 1.75 × 105 |
| 20 | 2.41 × 107 | 2.33 × 107 | 1.77 × 107 | 7.67 × 106 | 2.54 × 106 | 8.06 × 105 | 2.55 × 105 |
| 30 | 2.42 × 107 | 2.36 × 107 | 1.93 × 107 | 8.99 × 106 | 3.01 × 106 | 9.58 × 105 | 3.03 × 105 |
| 40 | 2.40 × 107 | 2.36 × 107 | 2.00 × 107 | 9.66 × 106 | 3.25 × 106 | 1.03 × 106 | 3.27 × 105 |
| 50 | 2.42 × 107 | 2.39 × 107 | 2.07 × 107 | 1.02 × 107 | 3.42 × 106 | 1.09 × 106 | 3.44 × 105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makwana, M.; Patel, A.M.; Oza, A.D.; Prakash, C.; Gupta, L.R.; Vatin, N.I.; Dixit, S. Effect of Mass on the Dynamic Characteristics of Single- and Double-Layered Graphene-Based Nano Resonators. Materials 2022, 15, 5551. https://doi.org/10.3390/ma15165551
Makwana M, Patel AM, Oza AD, Prakash C, Gupta LR, Vatin NI, Dixit S. Effect of Mass on the Dynamic Characteristics of Single- and Double-Layered Graphene-Based Nano Resonators. Materials. 2022; 15(16):5551. https://doi.org/10.3390/ma15165551
Chicago/Turabian StyleMakwana, Manisha, Ajay M. Patel, Ankit D. Oza, Chander Prakash, Lovi Raj Gupta, Nikolai Ivanovich Vatin, and Saurav Dixit. 2022. "Effect of Mass on the Dynamic Characteristics of Single- and Double-Layered Graphene-Based Nano Resonators" Materials 15, no. 16: 5551. https://doi.org/10.3390/ma15165551









