Deformation Characteristics, Formability and Springback Control of Titanium Alloy Sheet at Room Temperature: A Review
Abstract
:1. Introduction
2. Deformation Characteristics of Titanium Alloys
2.1. Strain and Stress Behaviors at Room Temperature
2.2. Formability at Room Temperature
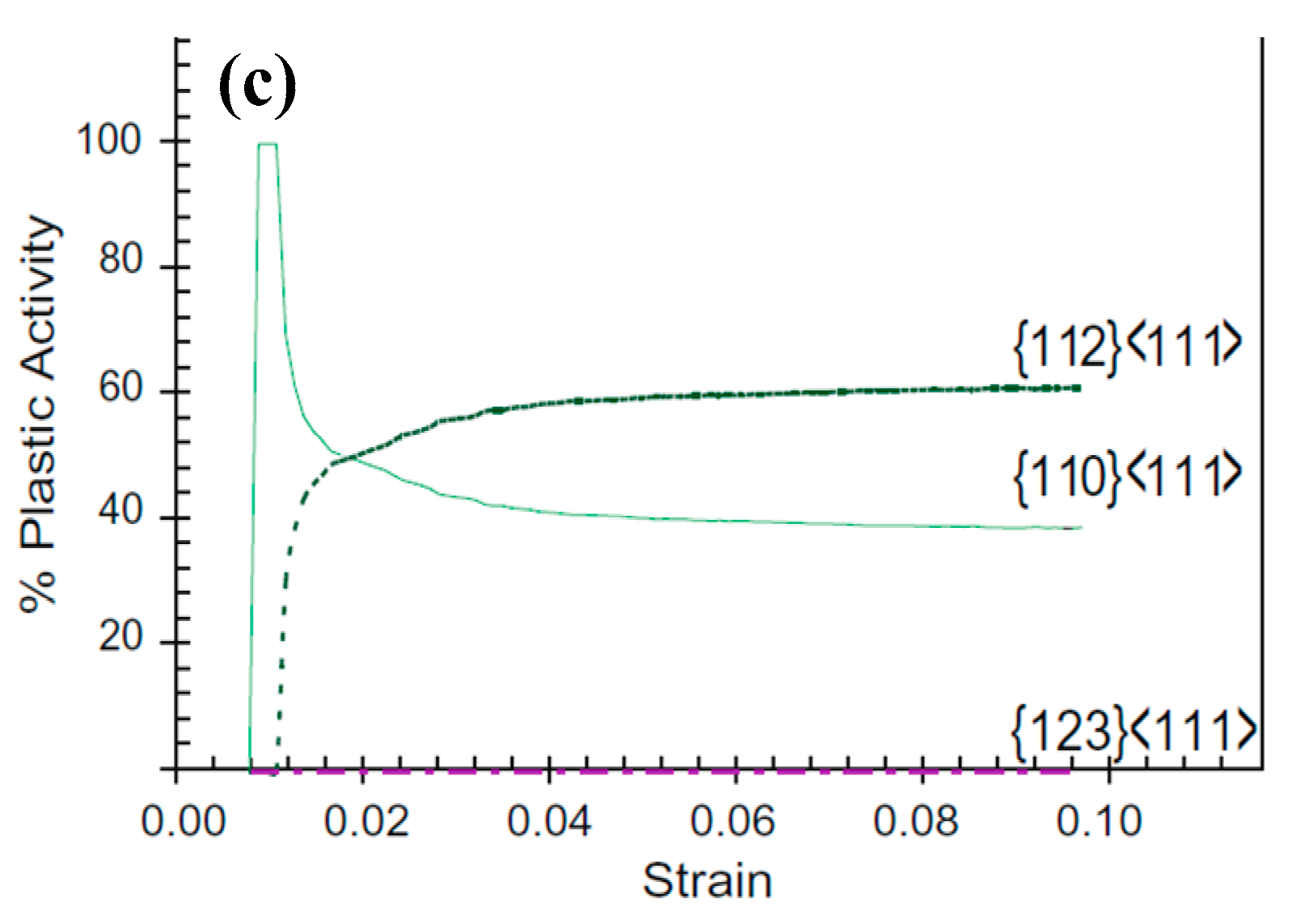
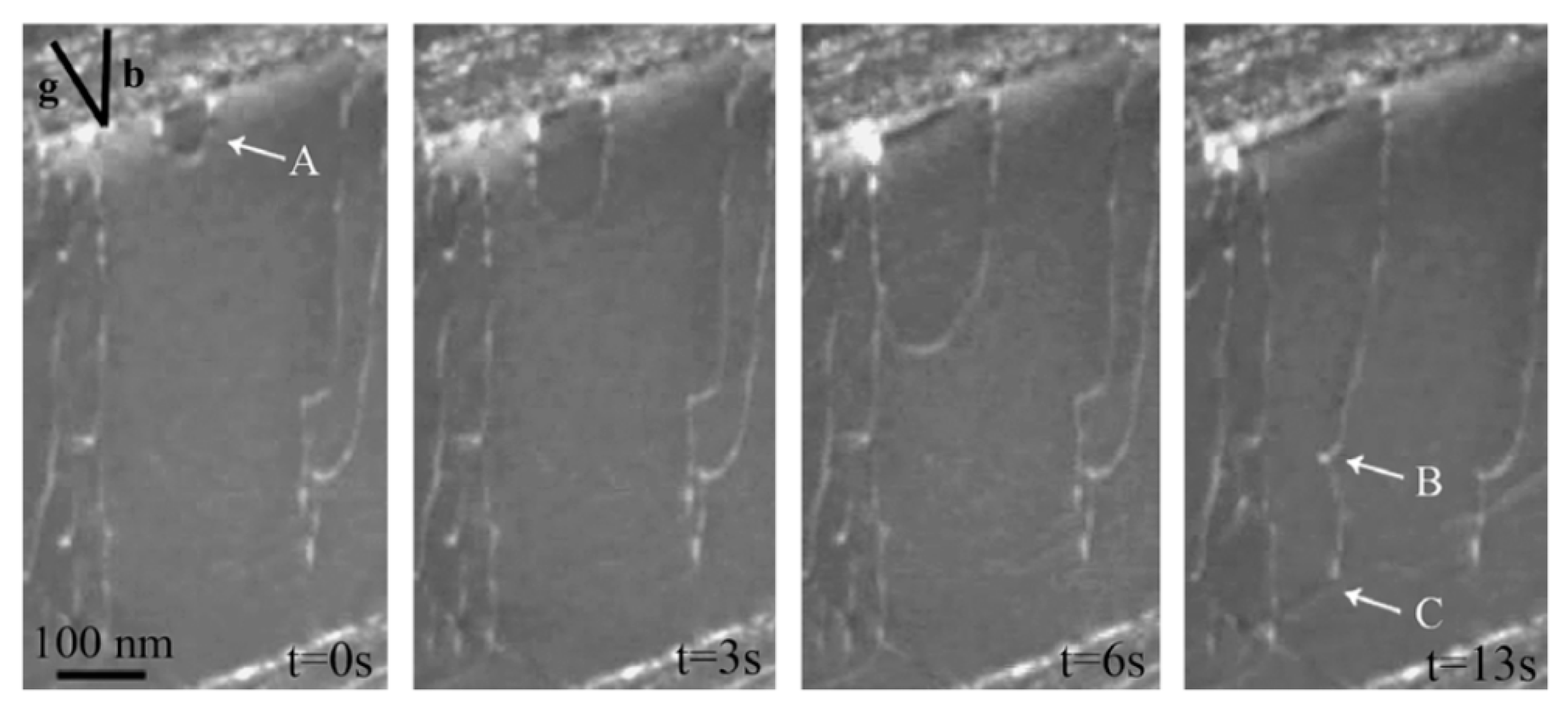
2.3. Deformation Mechanisms of Titanium Alloys
3. Springback Prediction and Control
3.1. Prediction Methods of Springback Behaviors
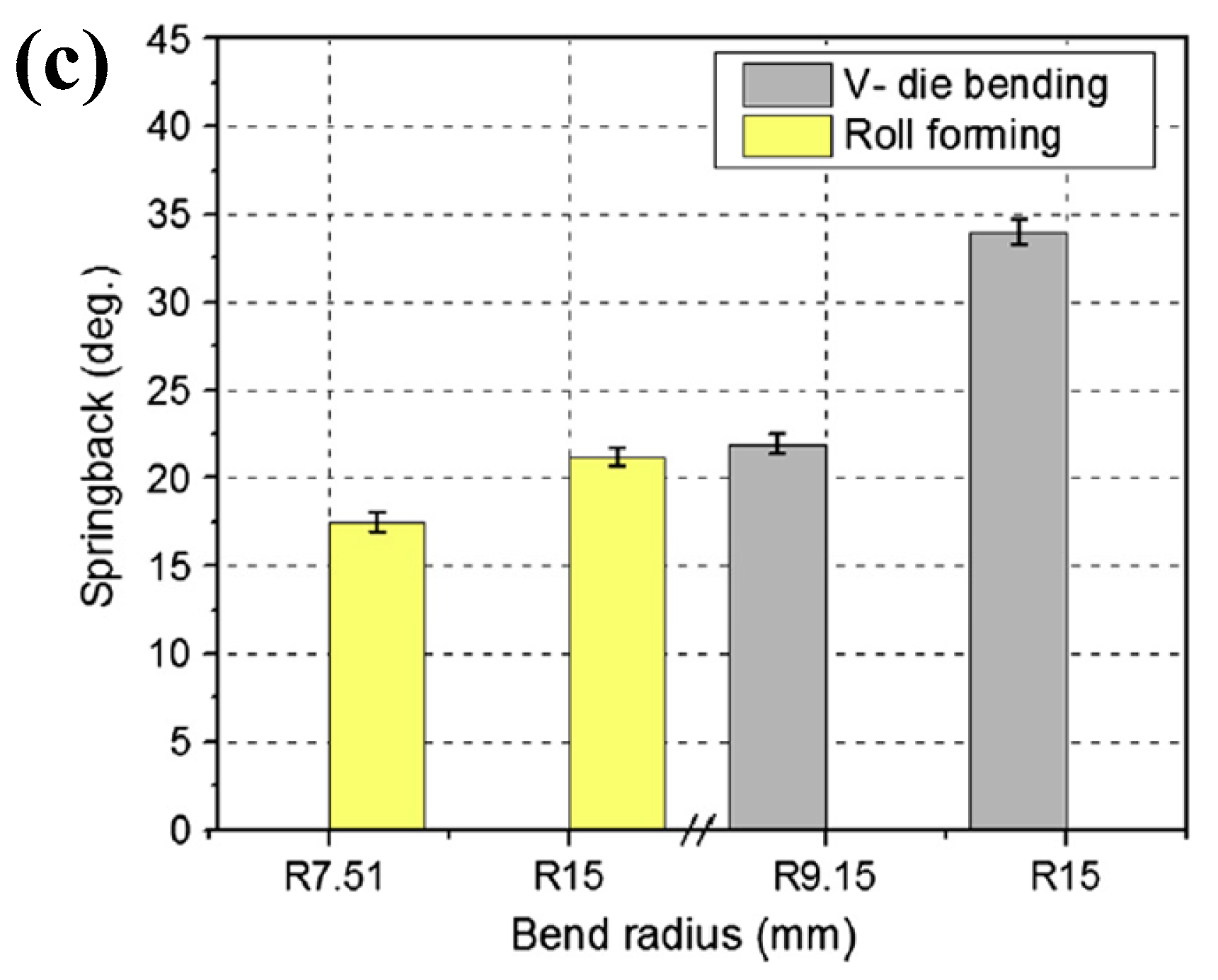
3.2. Springback Control Methods
3.2.1. Optimization of Loading Paths and Process Parameters
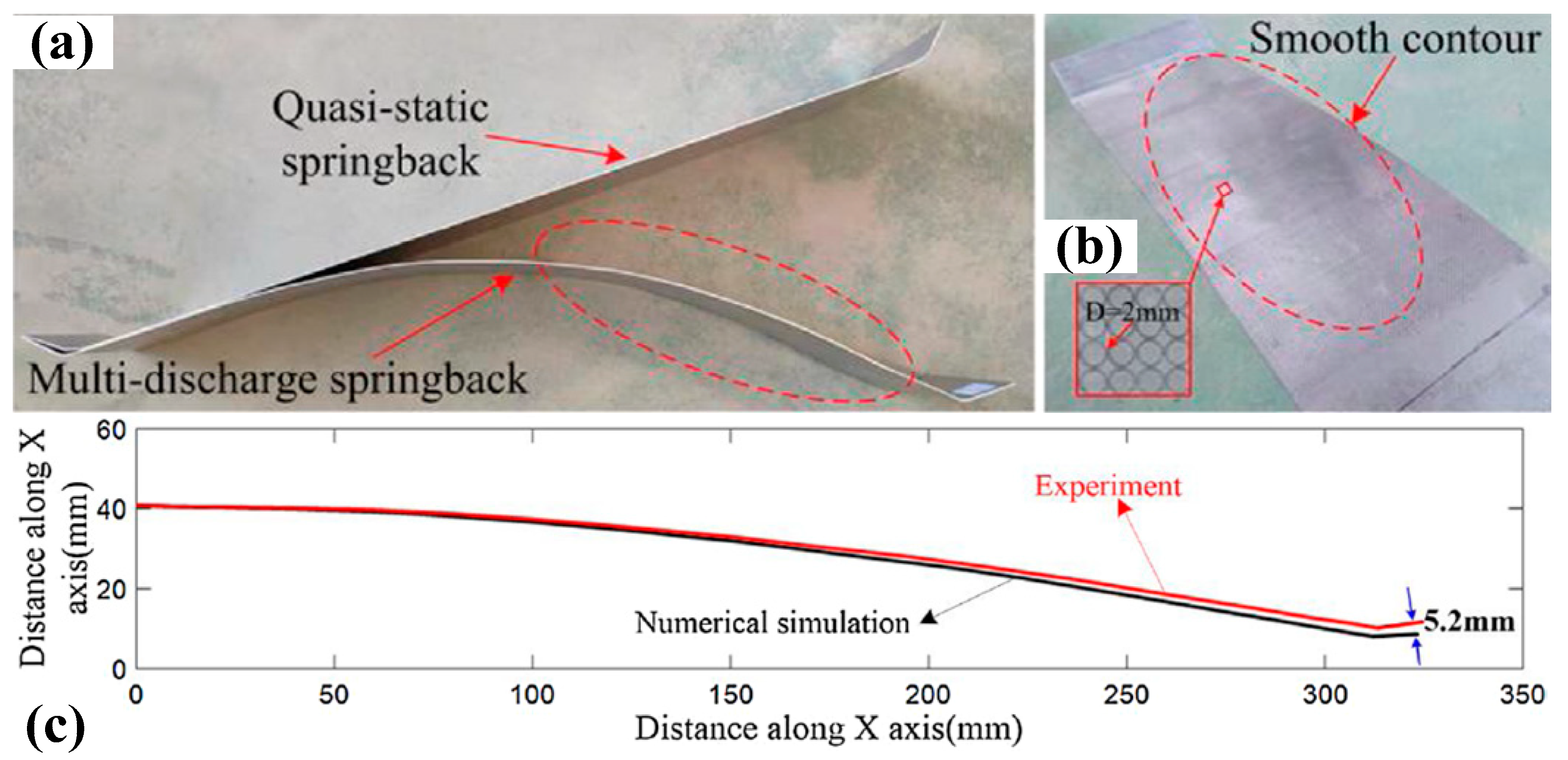
3.2.2. Mechanisms of Springback Induction and Reduction
4. Summary and Perspective
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Banerjee, D.; Williams, J.C. Perspectives on titanium science and Technology. Acta Mater. 2013, 61, 844–879. [Google Scholar] [CrossRef]
- Zhang, J.H.; Li, X.X.; Xu, D.S.; Yang, R. Recent progress in the simulation of microstructure evolution in titanium alloys. Prog. Nat. Sci.-Mater. 2019, 29, 295–304. [Google Scholar] [CrossRef]
- Zhang, X.S.; Chen, Y.J.; Hu, J.L. Recent advances in the development of aerospace materials. Prog. Aerosp. Sci. 2018, 97, 22–34. [Google Scholar] [CrossRef]
- Brian, J.H.; Brian, W.M.; Brian, W.; Samuel, J.K.; Thomas, K.A.; David, A.B.; Iman, G.; Andrew, H.B.; Christina, V.H.; Harlow, D.G.; et al. Predicting tensile properties of Ti-6Al-4V produced via directed energy deposition. Acta Mater. 2017, 133, 120–133. [Google Scholar]
- Park, C.H.; Ko, Y.G.; Park, J.W.; Lee, C.S. Enhanced superplasticity utilizing dynamic globularization of Ti-6Al-4V alloy. Mater. Sci. Eng. A 2008, 496, 150–158. [Google Scholar] [CrossRef]
- Liu, X.C.; Kopec, M.; Fakir, O.E.; Qu, H.T.; Wang, Y.Q.; Wang, L.L.; Li, Z.Q. Characterisation of the interfacial heat transfer coefficient in hot stamping of titanium alloys. Int. Commun. Heat. Mass. 2020, 113, 104535. [Google Scholar] [CrossRef]
- Seshacharyulu, T.; Medeiros, S.C.; Frazier, W.G.; Prasad, Y.V.R.K. Hot working of commercial Ti-6Al-4V with an equiaxed α-β microstructure: Materials modeling considerations. Mater. Sci. Eng. A 2000, 284, 184–194. [Google Scholar] [CrossRef]
- Semiatin, S.L.; Seetharaman, V.; Weiss, I. Flow behavior and globularization kinetics during hot working of Ti-6Al-4V with a colony alpha microstructure. Mater. Sci. Eng. A 1999, 263, 257–271. [Google Scholar] [CrossRef]
- Maeno, T.; Tomobe, M.; Mori, K.I.; Ikeda, Y. Hot stamping of titanium alloy sheets using partial contact heating. Procedia Manuf. 2018, 15, 1149–1155. [Google Scholar] [CrossRef]
- Deng, T.S.; Li, D.S.; Li, X.Q.; Ding, P.; Zhao, K. Hot stretch bending and creep forming of titanium alloy profile. In Proceedings of the 11th International Conference on Technology of Plasticity, Nagoya, Japan, 19–24 October 2014; Volume 81, pp. 1792–1798. [Google Scholar]
- Ao, D.W.; Chu, X.R.; Yang, Y.; Lin, S.X.; Gao, J. Effect of electropulsing on springback during V-bending of Ti-6Al-4V titanium alloy sheet. Int. J. Adv. Manuf. Technol. 2018, 96, 3197–3207. [Google Scholar] [CrossRef]
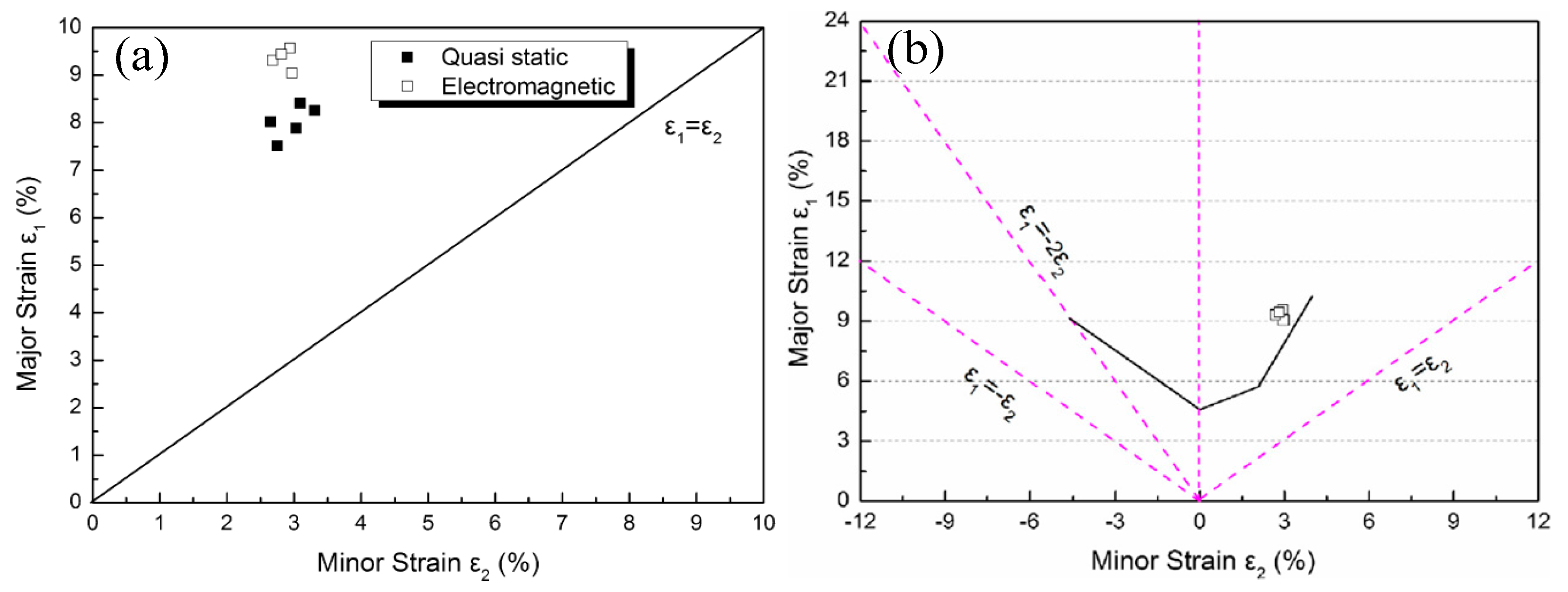
- Du, Z.H.; Yan, Z.Q.; Cui, X.H.; Chen, B.G.; Yu, H.L.; Qiu, D.Y.; Xia, W.Z.; Deng, Z.S. Springback control and large skin manufacturing by high-speed vibration using electromagnetic forming. J. Mater. Process. Technol. 2022, 299, 117340. [Google Scholar] [CrossRef]
- Zong, Y.Y.; Liu, P.; Guo, B.; Shan, D.B. Springback evaluation in hot v-bending of Ti-6Al-4V alloy sheets. Int. J. Adv. Manuf. Technolnol. 2015, 76, 577–585. [Google Scholar] [CrossRef]
- Odenberger, E.-L.; Oldenburg, M.; Thilderkvist, P.; Stoehr, T.; Lechler, J.; Merklein, M. Tool development based on modelling and simulation of hot sheet metal forming of Ti-6Al-4V titanium alloy. J. Mater. Process. Technol. 2011, 211, 1324–1335. [Google Scholar] [CrossRef]
- Cui, X.H.; Mo, J.H.; Li, J.J.; Yu, H.L.; Wang, Q.S. Reduction of springback in V-shaped parts using electromagnetic impulse calibration. In Proceedings of the International Conference on the Technolnology of Plasticity (ICTP 2017), Cambridge, UK, 17–22 September 2017; Volume 207, pp. 801–806. [Google Scholar]
- Fan, X.G.; Zhang, Y.; Gao, P.F.; Lei, Z.N.; Zhan, M. Deformation behavior and microstructure evolution during hot working of a coarse-grained Ti-5Al-5Mo-5V-3Cr-1Zr titanium alloy in beta phase field. Mater. Sci. Eng. A 2017, 694, 24–32. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, K.; Sun, Z.G.; Xin, R.L. Simultaneous improvement of strength and elongation of laser melting deposited Ti-6Al-4V titanium alloy through three-stage heat treatment. J. Mater. Process. Technol. 2022, 306, 117607. [Google Scholar] [CrossRef]
- Pons, M.; Caillet, M.; Galerie, A. Ion implantation into metals to prevent high temperature oxidation. Nucl. Instrum. Meth. A 1983, 209, 1011–1017. [Google Scholar] [CrossRef]
- Yuan, B.G.; Zheng, Y.B.; Wang, Y.J.; Gong, L.Q. Hydrogen absorption characteristics and microstructural evolution of TC21 titanium alloy. Trans. Nonferrous Met. Soc. China 2016, 26, 599–606. [Google Scholar] [CrossRef]
- Yuan, B.G.; Qian, D.; Tang, A.C.; Song, Y.X.; Zhang, X.X.; Huang, Z.Y. Characteristic and kinetics of hydrogen absorption during the heat preservation stage and the cooling stage of TC21 alloy. Int. J. Hydrogen Energy 2022, 47, 10315–10330. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, J.; Wang, Y.; Wang, Y.; Li, Z. Strain-rate-dependent tensile response of Ti-5Al-2.5Sn alloy. Materials 2019, 12, 659. [Google Scholar] [CrossRef]
- Xiao, D.W.; Li, Y.L.; Hu, S.S.; Cai, L.C. High strain rate deformation behavior of Zirconium at elevated temperatures. J. Mater. Sci. Technolnol. 2010, 26, 878–882. [Google Scholar] [CrossRef]
- Paese, E.; Geier, M.; Homrich, R.P.; Rosa, P.; Rossi, R. Sheet metal electromagnetic forming using a flat spiral coil: Experiments, modeling, and validation. J. Mater. Process. Technolnol. 2019, 263, 408–422. [Google Scholar] [CrossRef]
- Xiao, A.; Huang, C.Q.; Yan, Z.Q.; Cui, X.H.; Wang, S.P. Improved forming capability of 7075 aluminum alloy using electrically assisted electromagnetic forming. Mater. Charact. 2022, 183, 111615. [Google Scholar] [CrossRef]
- Xie, X.Y.; Yu, H.P.; Zhong, Y. Investigation on deformation of DP600 steel sheets in electric-pulse triggered energetic materials forming. Int. J. ADV Manuf. Technol. 2022, 120, 3911–3923. [Google Scholar] [CrossRef]
- Cheng, J.; Green, D.E.; Golovashchenko, S.F. Formability enhancement of DP600 steel sheets in electro-hydraulicdie forming. J. Mater. Process. Technol. 2017, 244, 178–189. [Google Scholar] [CrossRef]
- Akbari Mousavi, S.A.A.; Riahi, M.; Hagh Parast, A. Experimental and numerical analyses of explosive free forming. J. Mater. Process. Technol. 2007, 187–188, 512–516. [Google Scholar] [CrossRef]
- Wang, S.H.; Lang, L.H.; Lin, L.J. Investigation on the punching quality of hybrid impact hydroforming. Appl. Mech. Mater. 2014, 602–605, 520–523. [Google Scholar] [CrossRef]
- Kiliclar, Y.; Demir, O.K.; Engelhardt, M.; Rozgi’ce, M.; Vladimirov, I.N.; Wulfinghoff, S.; Weddeling, C.; Gies, S.; Klose, C.; Reese, S.; et al. Experimental and numerical investigation of increased formability incombined quasi-static and high-speed forming processes. J. Mater. Process. Technol. 2016, 237, 254–269. [Google Scholar] [CrossRef]
- Dong, P.X.; Li, Z.Z.; Feng, S.; Wu, Z.L.; Cao, Q.L.; Li, L.; Chen, Q.; Han, X.T. Fabrication of titanium bipolar plates for proton exchange membrane fuel cells by uniform pressure electromagnetic forming. Int. J. Hydrogen Energy 2021, 46, 38768–38781. [Google Scholar] [CrossRef]
- Ma, H.J.; Huang, L.; Tian, Y.; Li, J.J. Effects of strain rate on dynamic mechanical behavior and microstructure evolution of 5A02-O aluminum alloy. Mater. Sci. Eng. A 2014, 606, 233–239. [Google Scholar] [CrossRef]
- Yan, Z.Q.; Xiao, A.; Zhao, P.; Cui, X.H.; Yu, H.L.; Lin, Y.H. Deformation behavior of 5052 aluminum alloy sheets during electromagnetic hydraulic forming. Int. J. Mach. Tool. Manuf. 2022, 179, 103916. [Google Scholar] [CrossRef]
- Harding, J.; Macdougall, D.A.S. A constitutive relation and failure criterion for Ti5Al3V alloy at impact rates of strain. J. Mech. Phys. Solids 1999, 47, 1157–1185. [Google Scholar]
- Wang, Y.L.; Hui, S.X.; Liu, R.; Ye, W.J.; Yu, Y.; Kayumov, R. Dynamic response and plastic deformation behavior of Ti-5Al-2.5Sn ELI and Ti-8Al-1Mo-1V alloys under high-strain rate. Rare Met. 2014, 33, 127–133. [Google Scholar] [CrossRef]
- Tamirisakandala, S.; Vedam, B.V.; Bhat, R.B. Recent Advances in the deformation Processing of Titanium Alloys. J. Mater. Eng. Perform. 2003, 12, 661–673. [Google Scholar] [CrossRef]
- Tang, C.G.; Zhu, J.H.; Zhou, H.J. A phenomenon and analysis of plasticity-increasing induced by high strain rate some metallic materials. J. Mater. Res. 1996, 1, 19–24. (In Chinese) [Google Scholar]
- Hammer, J.T.; Yatnalkar, R.S.; Seidt, J.D.; Gilat, A. Plastic deformation of Ti-6Al-4V plate over a wide range of loading conditions. Dyn. Behav. Mater. 2013, 1, 165–170. [Google Scholar]
- Zhang, J.; Wang, Y. Tension behavior of Ti-6.6Al-3.3Mo-1.8Zr-0.29Si alloy over a wide range of strain rates. Mater. Lett. 2014, 124, 113–116. [Google Scholar] [CrossRef]
- Ran, C.; Chen, P.W.; Li, L.; Zhang, W.F.; Liu, Y.L.; Zhang, X. High-strain-rate plastic deformation and fracture behaviour of Ti-5Al-5Mo-5V-1Cr-1Fe titanium alloy at room temperature. Mech. Mater. 2018, 116, 3–10. [Google Scholar] [CrossRef]
- Li, F.Q.; Mo, J.H.; Li, J.J.; Huang, L.; Fan, W.; Fang, J.X. Effects of deformation rate on ductility of Ti-6Al-4V material. In Proceedings of the 11th International Conference on Technology of Plasticity, Nagoya, Japan, 19–24 October 2014; Volume 81, pp. 754–759. [Google Scholar]
- Khan, A.S.; Suh, Y.S.; Kazmi, R. Quasi-static and dynamic loading responses and constitutive modeling of titanium alloys. Int. J. Plasticity 2004, 20, 2233–2248. [Google Scholar] [CrossRef]
- Gilles, G.; Hammami, W.; Libertiaux, V.; Cazacu, O.; Yoon, J.H.; Kuwabara, T.; Habraken, A.M.; Duchêne, L. Experimental characterization and elasto-plastic modeling of the quasi-static mechanical response of TA-6V at room temperature. Int. J. Solids Struct. 2011, 48, 1277–1289. [Google Scholar] [CrossRef]
- Tang, B.T.; Wang, Q.F.; Guo, N.; Li, X.S.; Wang, Q.L.; Ghiotti, A.; Bruschi, S.; Luo, Z.A. Modeling anisotropic ductile fracture behavior of Ti-6Al-4V titanium alloy for sheet forming applications at room temperature. Int. J. Solids Struct. 2020, 207, 178–195. [Google Scholar] [CrossRef]
- Zhang, S.H.; Ma, Y.; Xu, Y.; El-Aty, A.A.; Chen, D.Y.; Shang, Y.L.; Pokrovsky, A.I. Effect of impact hydroforming loads on the formability of AA5A06 sheet metal. International Deep Drawing Research Group 37th Annual Conference. IOP Conf. Ser. Mater. Sci. Eng. 2018, 418, 012114. [Google Scholar]
- Chen, D.Y.; Zhang, S.H.; Xu, Y.; Ma, Y.; Song, H.W.; Xia, L.L. Description of stress-strain response and evaluation of the formability for Al-Cu-Mg alloy under the impact hydroforming. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Chennai, India, 16–17 September 2020; Volume 967, p. 012028. [Google Scholar]
- El-Aty, A.A.; Xu, Y.; Zhang, S.H.; Ha, S.; Ma, Y.; Chen, D.Y. Impact of high strain rate deformation on the mechanical behavior, fracture mechanisms and anisotropic response of 2060 Al-Cu-Li alloy. J. Adv. Res. 2019, 18, 19–37. [Google Scholar] [CrossRef] [PubMed]
- Xia, L.L.; Zhang, S.H.; Xu, Y.; Chen, S.F.; El-Aty, A.A.; Pokrovskyd, A.I.; Bakinovskayad, A.A. Study of the ductility enhancement of 5A90 Al-Mg-Li alloy sheets with stress relaxation. Philos. Mag. 2021, 23, 2449–2472. [Google Scholar] [CrossRef]
- Kikuchi, S.; Mori, T.; Kubozono, H.; Nakai, Y.; Kawabata, M.O.; Ameyama, K. Evaluation of near-threshold fatigue crack propagation in harmonic-structured CP titanium with a bimodal grain size distribution. Eng. Fract. Mech. 2017, 181, 77–86. [Google Scholar] [CrossRef]
- Sun, Q.J.; Wang, G.C.; Li, M.Q. The superplasticity and microstructure evolution of TC11 titanium alloy. Mater. Lett. 2011, 32, 3893–3899. [Google Scholar] [CrossRef]
- Sergueeva, A.V.; Stolyarov, V.V.; Valiev, R.Z.; Mukherjee, A.K. Advanced mechanical properties of pure titanium with ultrafine grained structure. Scr. Mater. 2001, 45, 747–752. [Google Scholar] [CrossRef]
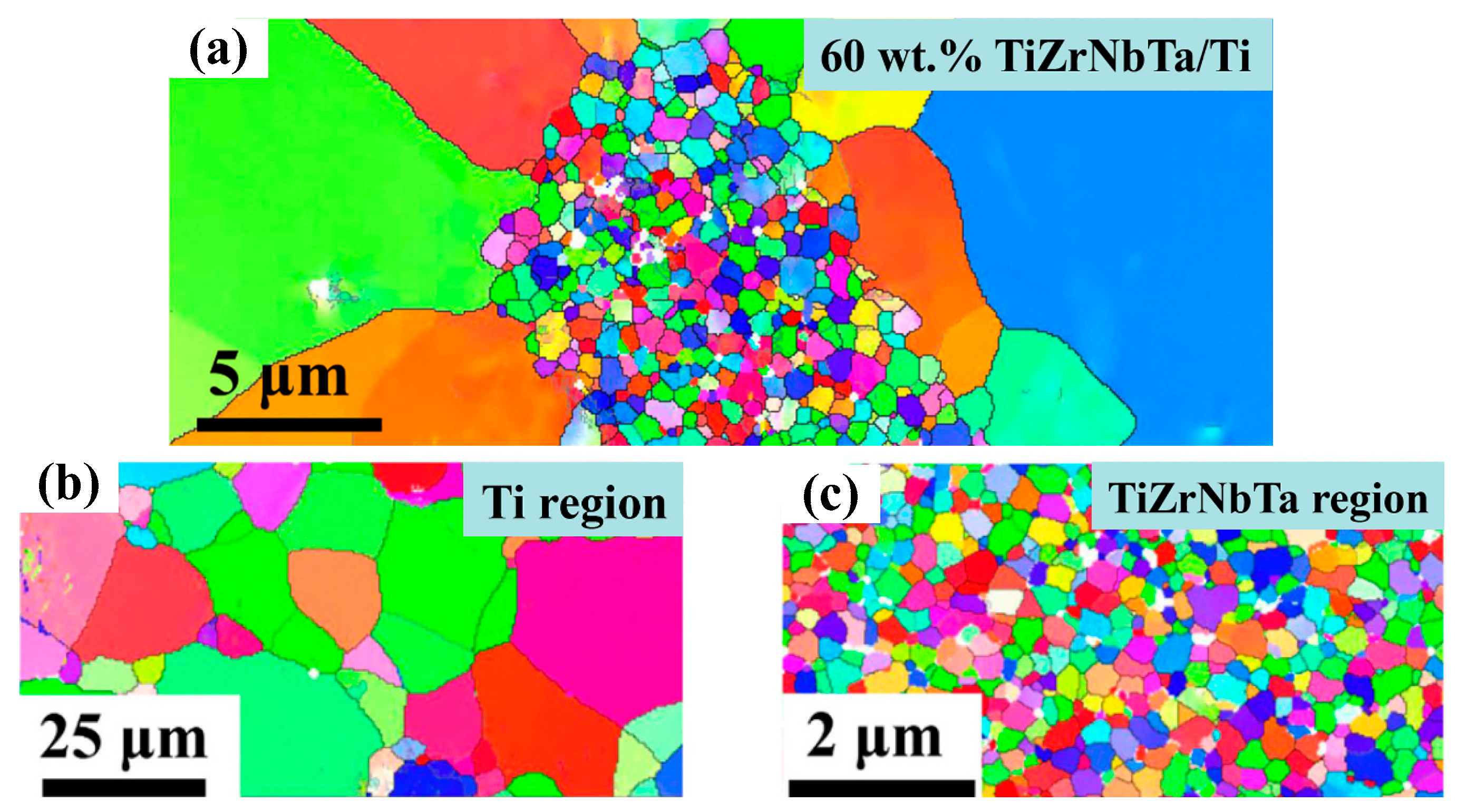
- Xiang, T.; Du, P.; Bao, W.Z.; Cai, Z.Y.; Li, K.; Xie, G.Q. Bimodal grain size structure design to optimize the mechanical properties of TiZrNbTa high entropy alloys/Ti composites. Mater. Sci. Eng. A 2022, 849, 143488. [Google Scholar] [CrossRef]
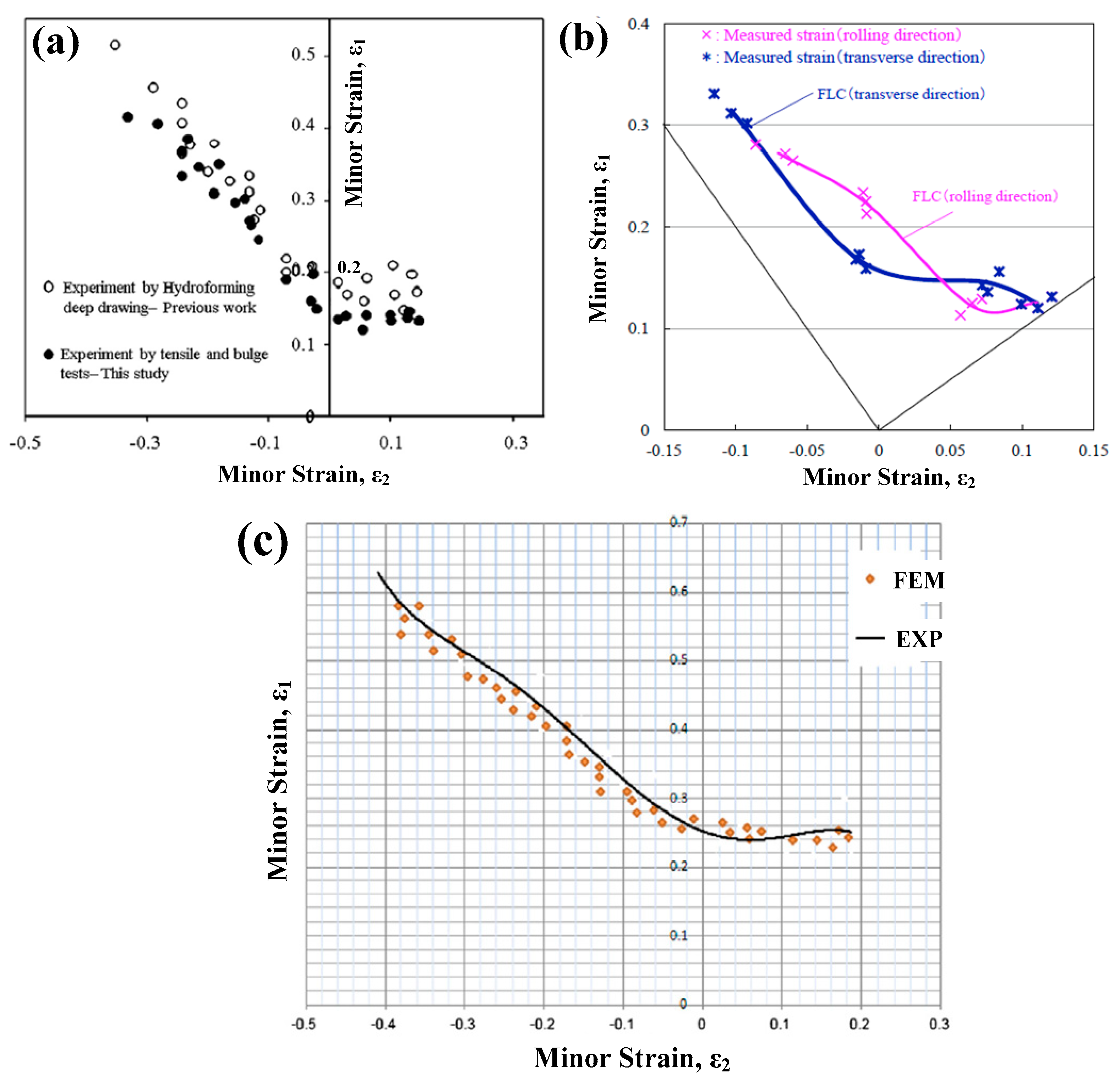
- Djavanroodi, F.; Ebrahimi, M.; Janbakhsh, M. A study on the stretching potential, anisotropy behavior and mechanical properties of AA7075 and Ti-6Al-4V alloys using forming limit diagram: An experimental, numerical and theoretical approaches. Results Phys. 2019, 14, 102496. [Google Scholar] [CrossRef]
- Djavanroodi, F.; Derogar, A. Experimental and numerical evaluation of forming limit diagram for Ti6Al4V titanium and Al6061-T6 aluminum alloys sheets. Mater. Des. 2010, 31, 4866–4875. [Google Scholar] [CrossRef]
- Okude, Y.; Saito, Y.; Iwaoka, T. Forming limit diagram with anisotropy considering of Ti-6A1-4V sheets and prediction of ductile fracture by experiment and FEA. In Proceedings of the 17th International Conference on Metal Forming, Procedia Manufacturing, Toyohashi, Japan, 16–19 September 2018; Volume 15, pp. 931–939. [Google Scholar]
- Morawińskia, Ł.; Jasiński, C.; Kocańda, A. Determination of the formability limits for Grade 1 titanium sheet by means of ALSAD method. In Proceedings of the International Conference on the Technology of Plasticity, Cambridge, UK, 17–22 September 2017; Volume 207, pp. 538–543. [Google Scholar]
- Yoganjaneyulu, G.; Sathiya Narayanan, C.; Narayanasamy, R. Investigation on the fracture behavior of titanium grade 2 sheets by using the single point incremental forming process. J. Manuf. Process. 2018, 35, 197–204. [Google Scholar] [CrossRef]
- Li, F.Q.; Mo, J.H.; Li, J.J.; Huang, L.; Zhou, H.Y. Formability of Ti-6Al-4V titanium alloy sheet in magnetic pulse bulging. Mater. Des. 2013, 52, 337–344. [Google Scholar] [CrossRef]
- Feng, F.; Li, J.J.; Chen, R.C.; Huang, L.; Su, H.L.; Fan, S. Multi-point die electromagnetic incremental forming for large-sized sheet metals. J. Manuf. Process. 2021, 62, 458–470. [Google Scholar] [CrossRef]
- Bruno, E.J. High-Velocity Forming of Metals; American Society of Tool and Manufacturing Engineers: Detroit, MI, USA, 1968. [Google Scholar]
- Davies, R.; Austin, E.R. Developments in High Speed Metal Forming; Industrial Press: South Norwalk, CT, USA, 1970. [Google Scholar]
- Chachin, V. Electro-hydraulic processing of engineering materials. Minsk. Sci. Eng. Pin. Russ. 1978, 1978, 184. [Google Scholar]
- Zheng, Q.L.; Yu, H.P.; Cai, X.H. Formability and deformation behavior of DP600 steel sheets during a hybrid quasi-static/dynamic forming process. Int. J. ADV Manuf. Technol. 2020, 110, 2169–2180. [Google Scholar] [CrossRef]
- Zheng, Q.L.; Yu, H.P. Hyperplasticity mechanism in DP600 sheets during electrohydraulic free forming. J. Mater. Process. Technol. 2020, 279, 116582. [Google Scholar] [CrossRef]
- Maris, C.; Hassannejadasl, A.; Green, D.E.; Cheng, J.; Golovashchenko, S.F.; Gillard, A.J.; Liang, Y.T. Comparison of quasi-static and electrohydraulic free forming limitsfor DP600 and AA5182 sheets. J. Mater. Process. Technol. 2016, 235, 206–219. [Google Scholar] [CrossRef]
- Gillard, A.J.; Golovashchenko, S.F.; Mamutov, A.V. Effect of quasi-static prestrain on the formability of dual phase steels in electrohydraulic forming. J. Manuf. Process. 2013, 15, 201–218. [Google Scholar] [CrossRef]
- He, F.M.; Zheng, T.; Wang, N.; Hu, Z.Y. Explosive forming of thin-wall semi-spherical parts. Mater. Lett. 2000, 45, 133–137. [Google Scholar]
- Nasiri, S.; Sadegh-Yazdi, M.; Mousavi, S.M.; Ziya-Shamami, M.; Mostofi, T.M. Repeated underwater explosive forming: Experimental investigation and numerical modeling based on coupled Eulerian-Lagrangian approach. Thin-Wall. Struct. 2022, 172, 108860. [Google Scholar] [CrossRef]
- Lang, L.H.; Wang, S.H.; Yang, C.L. Investigation on the innovative impact hydroforming Technolnology. In Proceedings of the 11th International Conference on Numerical Methods in Industrial Forming Processes AIP Conference Proceedings, Shenyang, China, 6–10 July 2013; Volume 1532, pp. 791–798. [Google Scholar]
- Khodko, O.; Zaytsev, V.; Sukaylo, V.; Verezub, N.; Scicluna, S. Experimental and numerical investigation of processes that occur during high velocity hydroforming Technolnologies: An example of tubular blank free bulging during hydrodynamic forming. J. Manuf. Process. 2015, 20, 304–313. [Google Scholar] [CrossRef]
- Akst, O.; Djakow, E.; Homberg, W. Some aspects regarding the use of a pneumomechanical high speed forming process. In Proceedings of the 5th International Conference on High Speed Forming, Dortmund, Germany, 24–26 April 2012; pp. 23–32. [Google Scholar]
- Niaraki, R.J.; Fazli, A.; Soltanpour, M. Electromagnetically activated high-speed hydroforming process: A novel process to overcome the limitations of the electromagnetic forming process. CIRP J. Manuf. Sci. Technol. 2019, 27, 21–30. [Google Scholar] [CrossRef]
- Hajializadeh, F.; Mashhadi, M.M. Investigation and numerical analysis of impulsive hydroforming of aluminum 6061-T6 tube. J. Manuf. Processes 2015, 20, 257–273. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, S.F.; Chen, D.Y.; Banabic, D.; Song, H.W.; Xu, Y.; Zhang, S.H.; Fan, X.S.; Wang, Q. Determination of the forming limit of impact hydroforming by frictionless full zone hydraulic forming test. Int. J. Mater. Form. 2021, 14, 1221–1232. [Google Scholar] [CrossRef]
- Chen, D.Y.; Xu, Y.; Zhang, S.H.; Ma, Y.; El-Aty, A.A.; Banabic, D.; Pokrovsky, A.I.; Bakinovskay, A.A. A novel method to evaluate the high strain rate formability of sheet metals under impact hydroforming. J. Mater. Process. Technol. 2021, 287, 116553. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, Y.; Zhang, S.H.; Banabic, D.; El-Aty, A.A.; Chen, D.Y.; Cheng, M.; Song, H.W.; Pokrovsky, A.I.; Chen, G.Q. Investigation on formability enhancement of 5A06 aluminium sheet by impact hydroforming. CIRP J. Manuf. Sci. Technol. 2018, 67, 281–284. [Google Scholar] [CrossRef]
- Fan, X.S. On Key Technolnology of Impact Hydroforming Process of Titanium Alloy Part; University of Jinan: Jinan, China, 2021. (In Chinese) [Google Scholar]
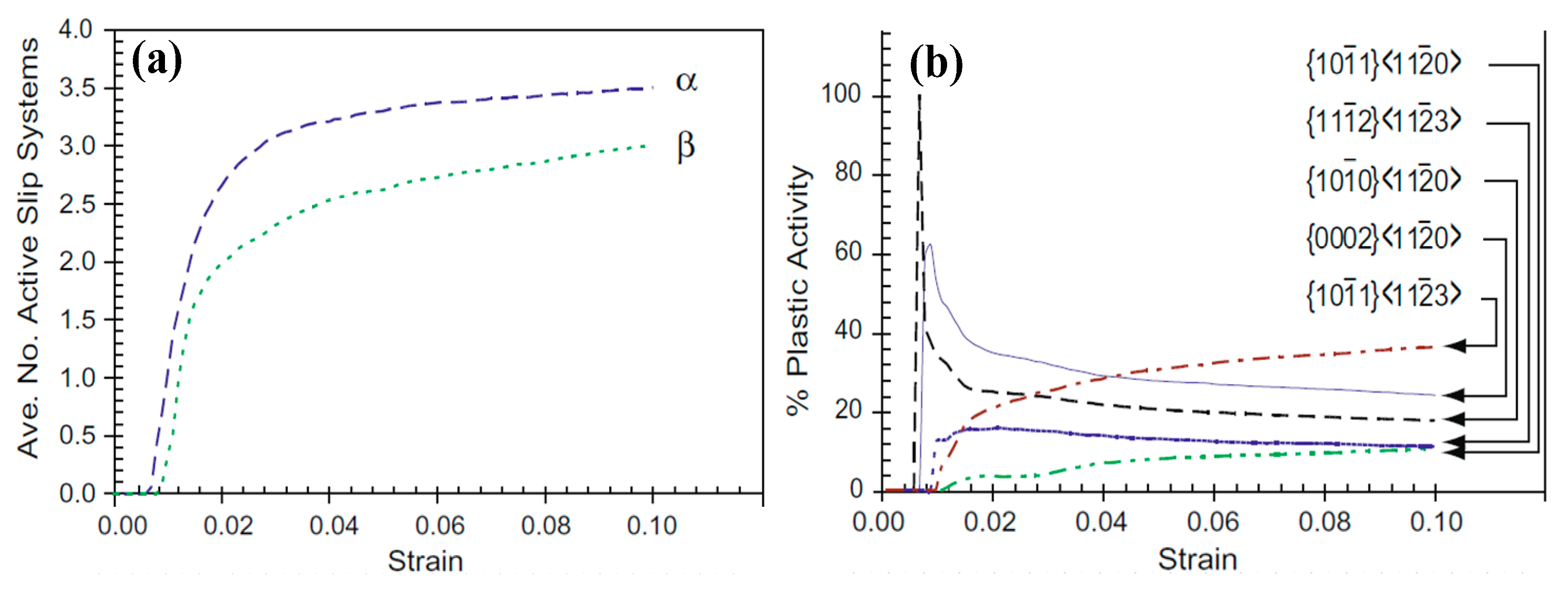
- Salem, A.A.; Kalidindi, S.R.; Semiatin, S.L. Strain hardening due to deformation twinning in a-titanium: Constitutive relations and crystal-plasticity modeling. Acta Mater. 2005, 53, 3495–3502. [Google Scholar] [CrossRef]
- Shahba, A.; Ghosh, S. Crystal plasticity FE modeling of Ti alloys for a range of strain-rates. Part I: A unified constitutive model and flow rule. Int. J. Plast. 2016, 87, 48–68. [Google Scholar] [CrossRef]
- Bobbili, R.; Madhu, V. Flow and fracture characteristics of near alpha titanium alloy. J. Alloys Compd. 2016, 684, 162–170. [Google Scholar] [CrossRef]
- Zherebtsov, S.V.; Kudryavtsev, E.A.; Salishchev, G.A.; Straumal, B.B.; Semiatin, S.L. Microstructure evolution and mechanical behavior of ultrafine Ti-6Al-4V during low-temperature superplastic deformation. Acta Mater. 2016, 121, 152–163. [Google Scholar] [CrossRef]
- Mahajan, Y.; Margolin, H. Deformation associated with surface cracks and alpha particles in an α~β titanium alloy. Scr. Metall. 1979, 13, 451–456. [Google Scholar] [CrossRef]
- Liao, Y.; Bai, J.H.; Chen, F.W.; Xu, G.L.; Cui, Y.W. Microstructural strengthening and toughening mechanisms in Fe-containing Ti-6Al-4V: A comparison between homogenization and aging treated states. J. Mater. Sci. Technol. 2022, 99, 114–126. [Google Scholar] [CrossRef]
- Stapleton, A.M.; Raghunathan, S.L.; Bantounas, I.; Stone, H.J.; Lindley, T.C.; Dye, D. Evolution of lattice strain in Ti-6Al-4V during tensile loading at room temperature. Acta Mater. 2008, 56, 6186–6196. [Google Scholar] [CrossRef]
- Yu, W.X.; Li, M.Q.; Luo, J. Effect of processing parameters on microstructure and mechanical properties in high temperature deformation of Ti-6Al-4V alloy. Rare Met. Mater. Eng. 2009, 38, 19–24. [Google Scholar] [CrossRef]
- Castany, P.; Pettinari-Sturme, F.; Crestou, J.; Douin, J.; Coujou, A. Experimental study of dislocation mobility in a Ti-6Al-4V alloy. Acta Mater. 2007, 55, 6284–6291. [Google Scholar] [CrossRef]
- Li, X.F.; Ji, B.Y.; Zhou, Q.; Chen, J.; Gao, P. Influence of grain size on electrically assisted tensile behavior of Ti-6Al-4V alloy. J. Mater. Eng. Perform. 2016, 25, 4514–4520. [Google Scholar] [CrossRef]
- Ao, D.W.; Chu, X.R.; Gao, J.; Yang, Y.; Lin, S. Experimental investigation on the deformation behaviors of Ti-6Al-4V sheet in electropulsing-assisted incremental forming. Int. J. Adv. Manuf. Technol. 2019, 104, 4243–4254. [Google Scholar] [CrossRef]
- Zhang, D.J.; Cui, Z.S.; Ruan, X.Y.; Li, Y.Q. Sheet springback prediction based on non-linear combined hardening rule and Barlat 89’s yielding function. Comp. Mater. Sci. 2006, 1003, 1218–1225. [Google Scholar]
- Chen, J.; Xiao, Y.Z.; Ding, W.; Zhu, X.H. Describing the non-saturating cyclic hardening behavior with a newly developed kinematic hardening model and its application in springback prediction of DP sheet metals. J. Mater. Process. Technol. 2015, 215, 151–158. [Google Scholar] [CrossRef]
- Li, H.Z.; Dong, X.H.; Shen, Y.; Diehl, A.; Hagenah, H.; Engel, U.; Merklein, M. Size effect on springback behavior due to plastic strain gradient hardening in microbending process of pure aluminum foils. Mater. Sci. Eng. A 2010, 527, 4497–4504. [Google Scholar] [CrossRef]
- He, D.H.; Li, D.S.; Li, X.Q.; Jin, C.H. Optimization on springback reduction in cold stretch forming of titanium-alloy aircraft skin. Trans. Nonferrous Met. Soc. China 2010, 20, 2350–2357. [Google Scholar] [CrossRef]
- Xue, X.; Liao, J.; Vincze, G.; Pereira, A.B.; Barlat, F. Experimental assessment of nonlinear elastic behaviour of dual-phase steels and application to springback prediction. Int. J. Mech. Sci. 2016, 117, 1–15. [Google Scholar] [CrossRef]
- Gardiner, F.J. The springback of metals. Trans. ASM 1957, 79, 1–9. [Google Scholar]
- Zang, S.L.; Lee, M.G.; Kim, J.H. Evaluating the significance of hardening behavior and unloading modulus under strain reversal in sheet springback prediction. Int. J. Mech. Sci. 2013, 77, 194–204. [Google Scholar] [CrossRef]
- Aerens, R.; Vorkov, V.; Duflou, J.R. Springback prediction and elasticity modulus variation. In Proceedings of the 18th International Conference on Sheet Metal, Palermo, Italy, 1–4 April 2019; Volume 29, pp. 185–192. [Google Scholar]
- Vladimirov Ivaylo, N.; Pietryga, M.P.; Reese, S. On the modelling of non-linear kinematic hardening at finite strains with application to springback-Comparison of time integration algorithms. Int. J. Numer. Meth. Eng. 2008, 75, 1–28. [Google Scholar] [CrossRef]
- Sanchez, L.R. Modeling of springback, strain rate and Bauschinger effects for two-dimensional steady state cyclic flow of sheet metal subjected to bending under tension. Int. J. Mech. Sci. 2010, 52, 429–439. [Google Scholar] [CrossRef]
- Welo, J.; Ma, T. Analytical springback assessment in flexible stretch bending of complex shapes. Int. J. Mach. Tool. Manuf. 2021, 160, 103653. [Google Scholar]
- Huang, C.; Xiang, Z.Q.; Mao, Y.S.; Zhang, S.X. An improved study on Gardiner’s work based on elastoplastic analysis considering deformation history. Int. J. Mech. Sci. 2017, 130, 111–118. [Google Scholar] [CrossRef]
- Jin, L.; Yang, Y.F.; Li, R.Z.; Cui, Y.W.; Jamil, M.; Li, L. Study on springback straightening after bending of the U-Section of TC4 material under high-temperature conditions. Materials 2020, 13, 1895. [Google Scholar] [CrossRef]
- Mehrabi, H.; Yang, C.H.; Wang, B.L. Investigation on springback behaviours of hexagonal close-packed sheet metals. Appl. Math. Model. 2021, 92, 149–175. [Google Scholar] [CrossRef]
- Zhang, D.J.; Cui, Z.S.; Ruan, X.Y.; Li, Y.Q. An analytical model for predicting springback and side wall curl of sheet after U-bending. Comp. Mater. Sci. 2007, 38, 707–715. [Google Scholar] [CrossRef]
- Nanu, N.; Brabie, G. Analytical model for prediction of springback parameters in the case of U stretch–bending process as a function of stresses distribution in the sheet thickness. Int. J. Mech. Sci. 2012, 64, 11–21. [Google Scholar] [CrossRef]
- Lee, M.G.; Kim, J.H.; Chung, K.; Kim, S.J.; Wagoner, R.H.; Kim, H.Y. Analytical springback model for lightweight hexagonal close-packed sheet metal. Int. J. Plast. 2009, 25, 399–419. [Google Scholar] [CrossRef]
- Guo, X.N.; Xu, H.; Zeng, Q.; Pet, T. Springback characteristics of arched aluminum alloy gusset plate after stamping forming. Thin-Wall. Struct. 2021, 159, 107294. [Google Scholar] [CrossRef]
- Cai, Z.Y.; Wang, S.H.; Li, M.Z. Numerical investigation of multi-point forming process for sheet metal: Wrinkling, dimpling and springback. Int. J. Adv. Manuf. Technol. 2008, 37, 927–936. [Google Scholar] [CrossRef]
- Badr, O.M.; Rolfe, B.; Zhang, P.; Weiss, M. Applying a new constitutive model to analyse the springback behaviour of titanium in bending and roll forming. Int. J. Mech. Sci. 2017, 128–129, 389–400. [Google Scholar] [CrossRef]
- Jiang, B.; Yang, W.B.; Zhang, Z.Y.; Li, X.F.; Ren, X.P.; Wang, Y.Q. Numerical simulation and experiment of electrically-assisted incremental forming of thin TC4 titanium alloy sheet. Materials 2020, 13, 1335. [Google Scholar] [CrossRef]
- Li, X.F.; Zhou, Q.; Zhao, S.J.; Chen, J. Effect of pulse current on bending behavior of Ti6Al4V alloy. In Proceedings of the 11th International Conference on Technolnology of Plasticity, Nagoya, Japan, 19–24 October 2014; Volume 81, pp. 1799–1804. [Google Scholar]
- Odenberger, E.L.; Pederson, R.; Oldenburg, M. Finite element modeling and validation of springback and stress relaxation in the thermo-mechanical forming of thin Ti-6Al-4V sheets. Int. J. Adv. Manuf. Technol. 2019, 104, 3439–3455. [Google Scholar] [CrossRef]
- Li, F.Q.; Mo, J.H. Springback analysis of TC4 titanium alloy complex part with double curvature under single point incremental forming process. Adv. Mater. Res. 2012, 468–471, 1094–1098. [Google Scholar] [CrossRef]
- Badr, O.M.; Rolfe, B.; Hodgson, P.; Weiss, M. Forming of high strength titanium sheet at room temperature. Mater. Des. 2015, 66, 618–626. [Google Scholar] [CrossRef]
- Leacock, A.G.; Volk, S.Q.G.; McCracken, D.; Brown, D. The influence of strain rate on the springback of commercially pure titanium in a stretch forming operation. Key Eng. Mater. 2015, 639, 107–114. [Google Scholar] [CrossRef]
- Cui, X.H.; Du, Z.H.; Xiao, A.; Yan, Z.Q.; Qiu, D.Y.; Yu, H.L.; Chen, B.G. Electromagnetic partitioning forming and springback control in the fabrication of curved parts. J. Mater. Process. Technol. 2021, 288, 116889. [Google Scholar] [CrossRef]
- Golovashchenko, S.F.; Gillard, A.J.; Mamutov, A.V.; Ibrahim, R. Pulsed electrohydraulic springback calibration of parts stamped from advanced high strength steel. J. Mater. Process. Technol. 2014, 214, 2796–2810. [Google Scholar] [CrossRef]
- Li, H.; Xu, Y.; Chen, S.F.; Song, H.W.; Zhang, S.H. Springback inhibition of Ti-6Al-4V sheet with impact hydroforming at room temperature. In Proceedings of the International Deep-Drawing Research Group Conference (IDDRG 2022), Lorient, France, 6–10 June 2022; Volume 1238, p. 012076. [Google Scholar]
- Sofinowski, K.; Šmíd, M.; van Petegem, S.; Rahimi, S.; Connolley, T.; van Swygenhoven, H. In situ characterization of work hardening and springback in grade 2α-titanium under tensile load. Acta. Mater. 2019, 181, 87–98. [Google Scholar] [CrossRef]
- Khayatzadeh, S.; Rahimi, S.; Blackwell, P. Effect of plastic deformation on elastic and plastic recovery in CP-titanium. Key Eng. Mater. 2016, 716, 891–896. [Google Scholar] [CrossRef]
- Khayatzadeh, S.; Thomas, M.J.; Millet, Y.; Rahimi, S. Characterisation and modeling of in-plane springback in a commercially pure titanium (CP-Ti). J. Mater. Sci. 2018, 53, 6872–6892. [Google Scholar] [CrossRef]
- Zhao, X.F.; Niinomi, M.; Nakai, M.; Hieda, J.; Ishimoto, T.; Nakano, T. Optimization of Cr content of metastable β-type Ti-Cr alloys with changeable Young’s modulus for spinal fixation applications. Acta Biomater. 2012, 8, 2392–2400. [Google Scholar] [CrossRef]
- Ao, D.W.; Chu, X.R.; Lin, S.X.; Yang, Y.; Gao, J. Hot tensile behaviors and microstructure evolution of Ti-6Al-4V titanium alloy under electropulsing. Acta Metall. Sin. (Engl. Lett.) 2018, 31, 1287–1296. [Google Scholar] [CrossRef]
- Wang, L.F.; Huang, G.S.; Zhang, H.; Wang, Y.X.; Yin, L. Evolution of springback and neutral layer of AZ31B magnesium alloy V-bending under warm forming conditions. J. Mater. Process. Technol. 2013, 213, 844–850. [Google Scholar] [CrossRef]
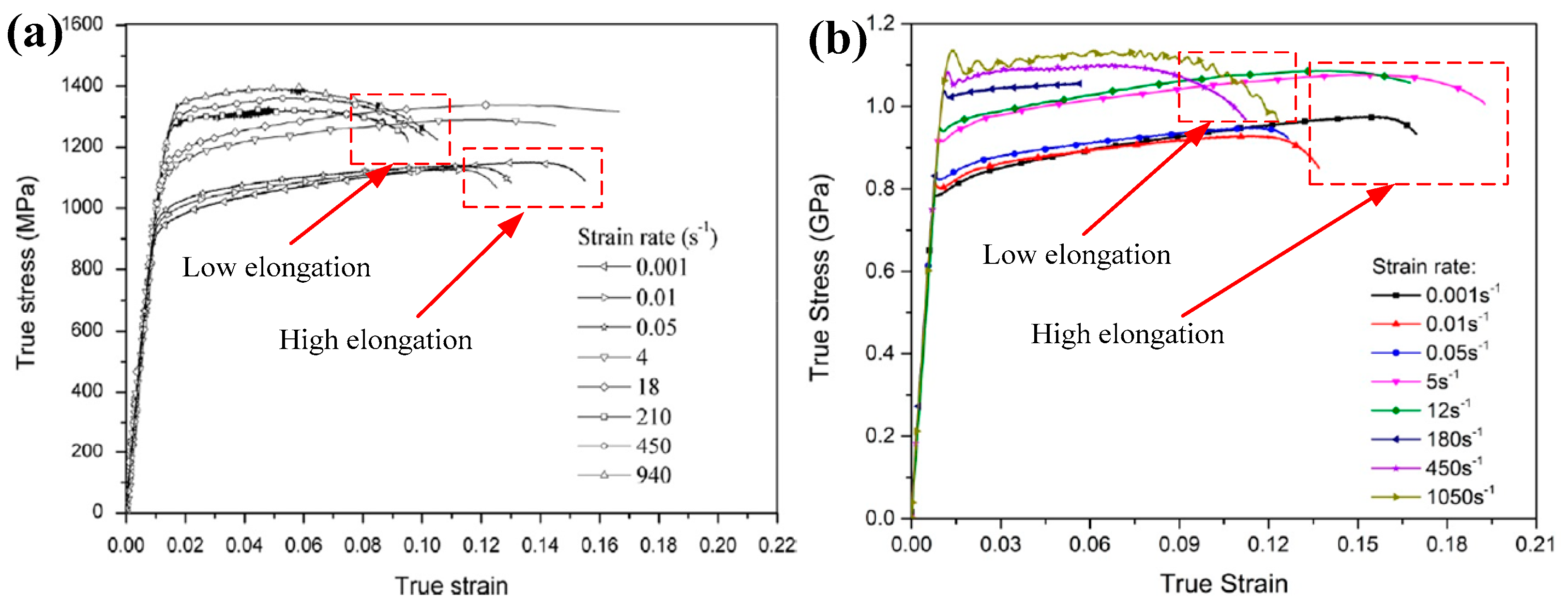
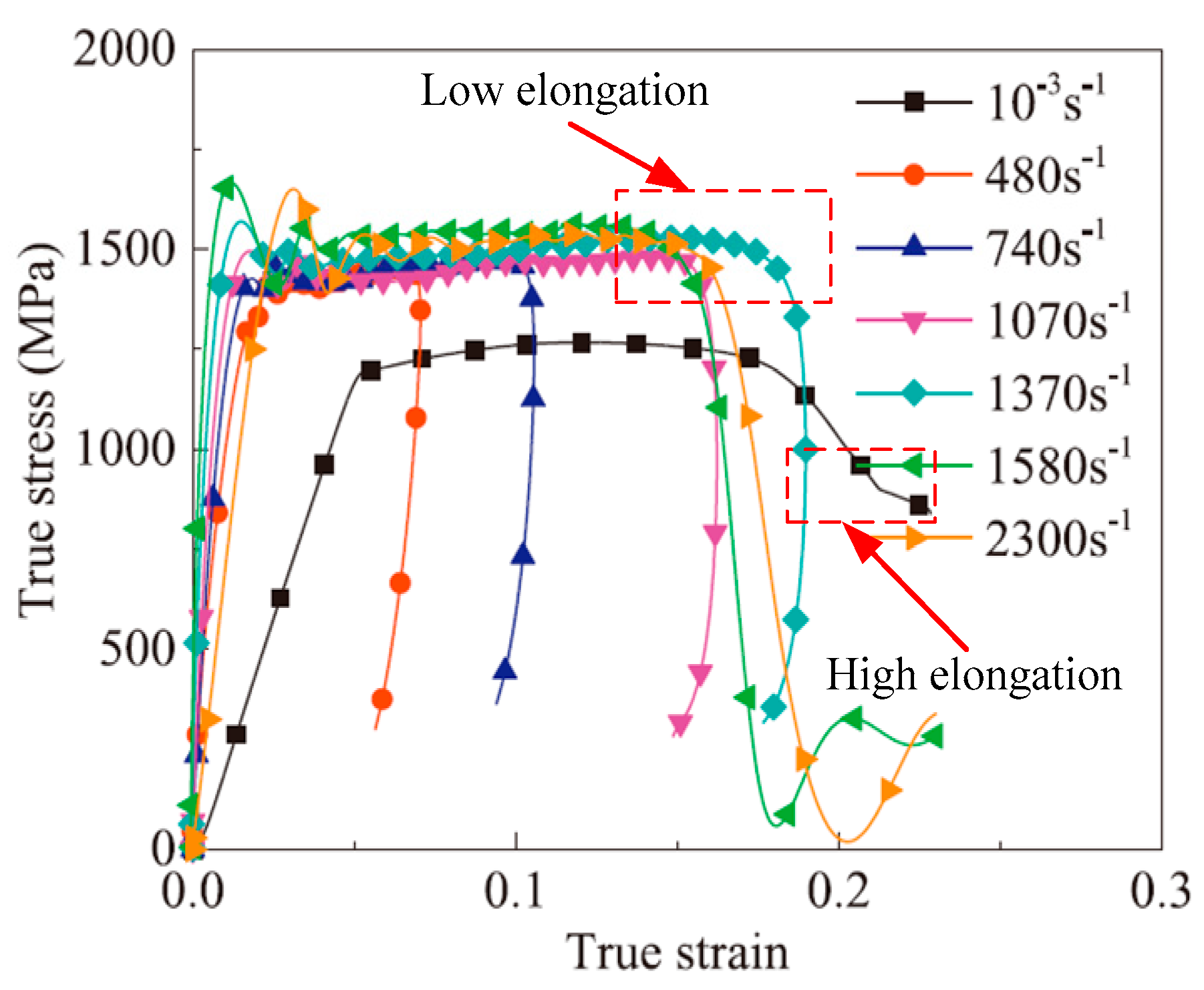
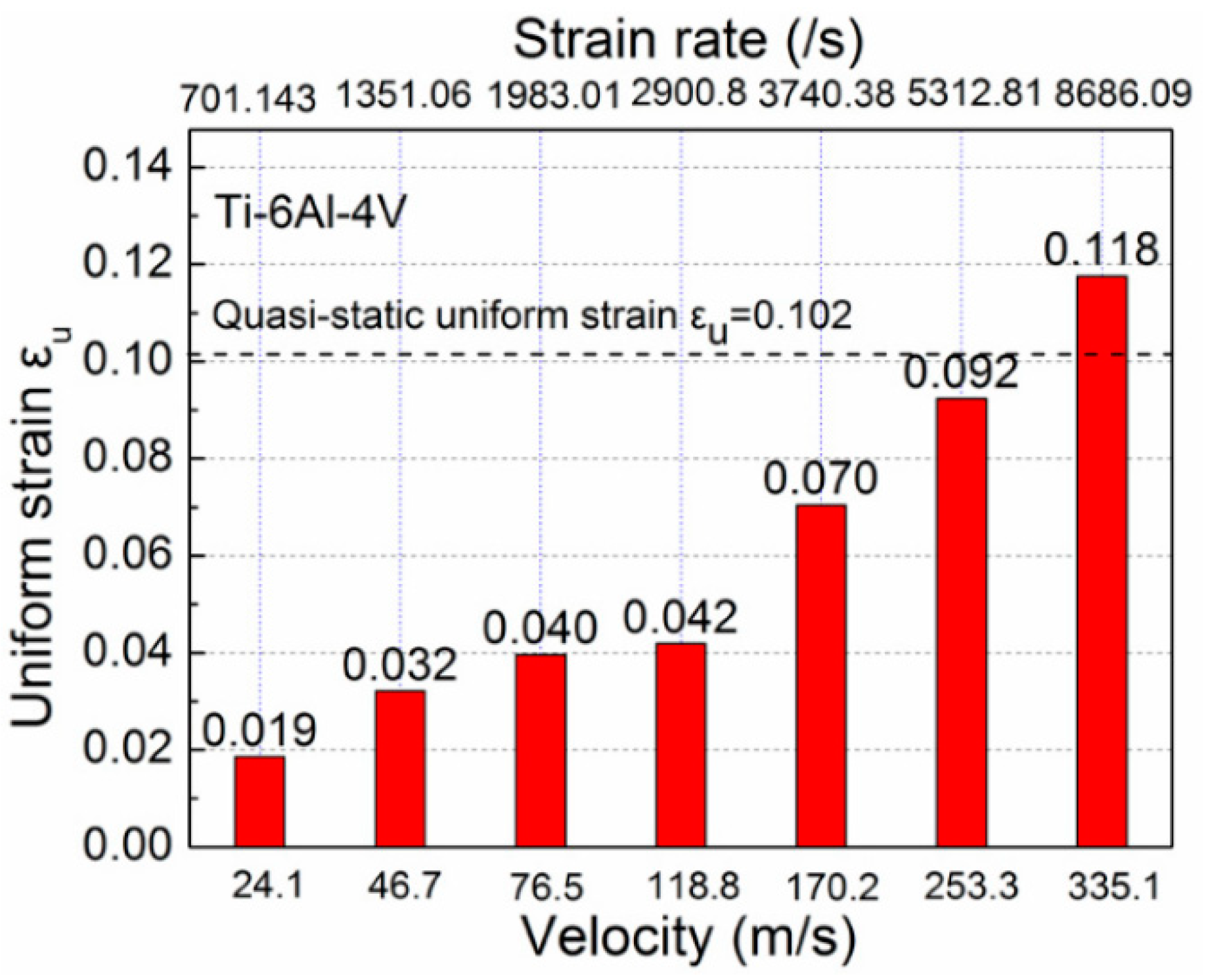
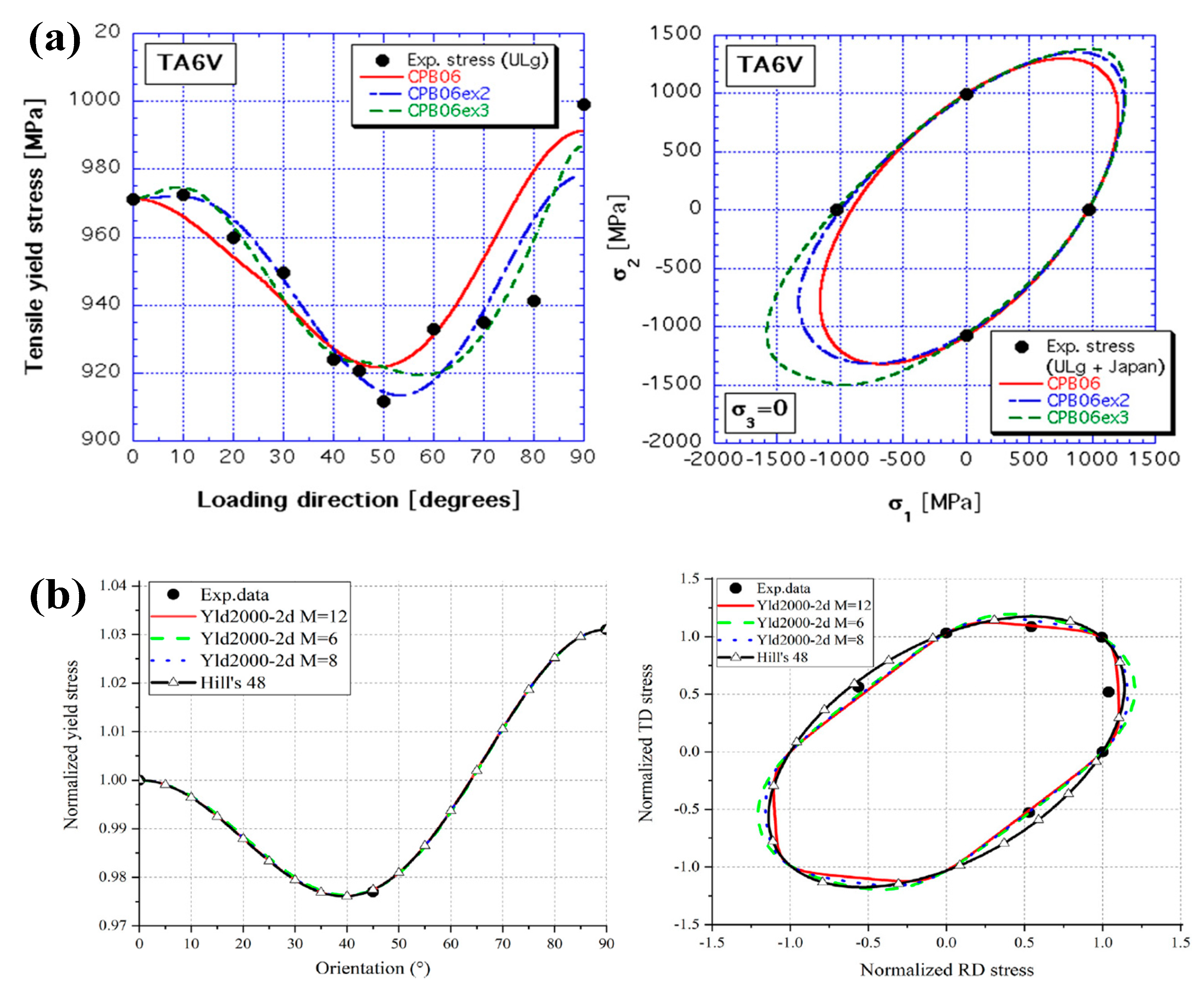







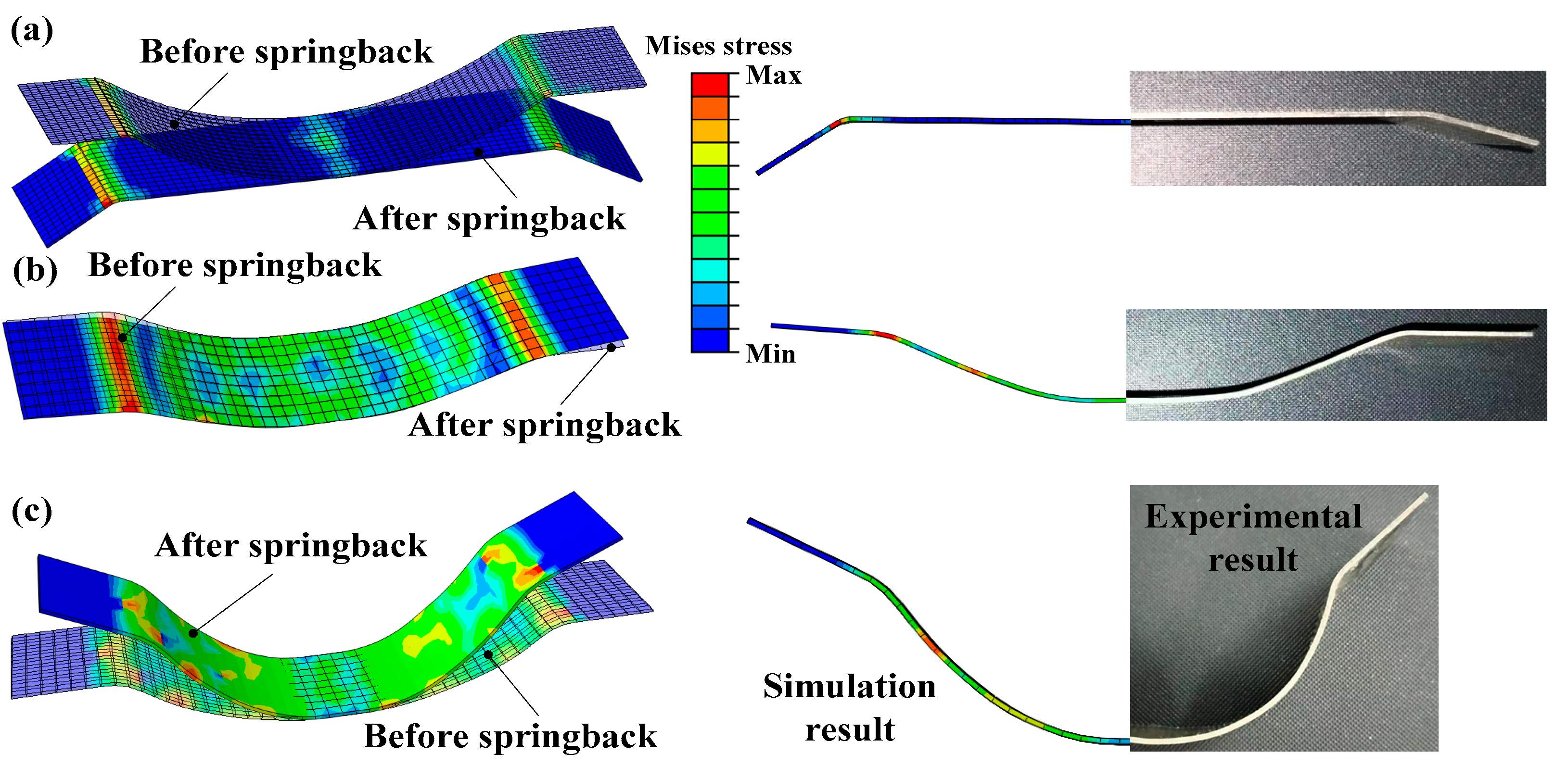
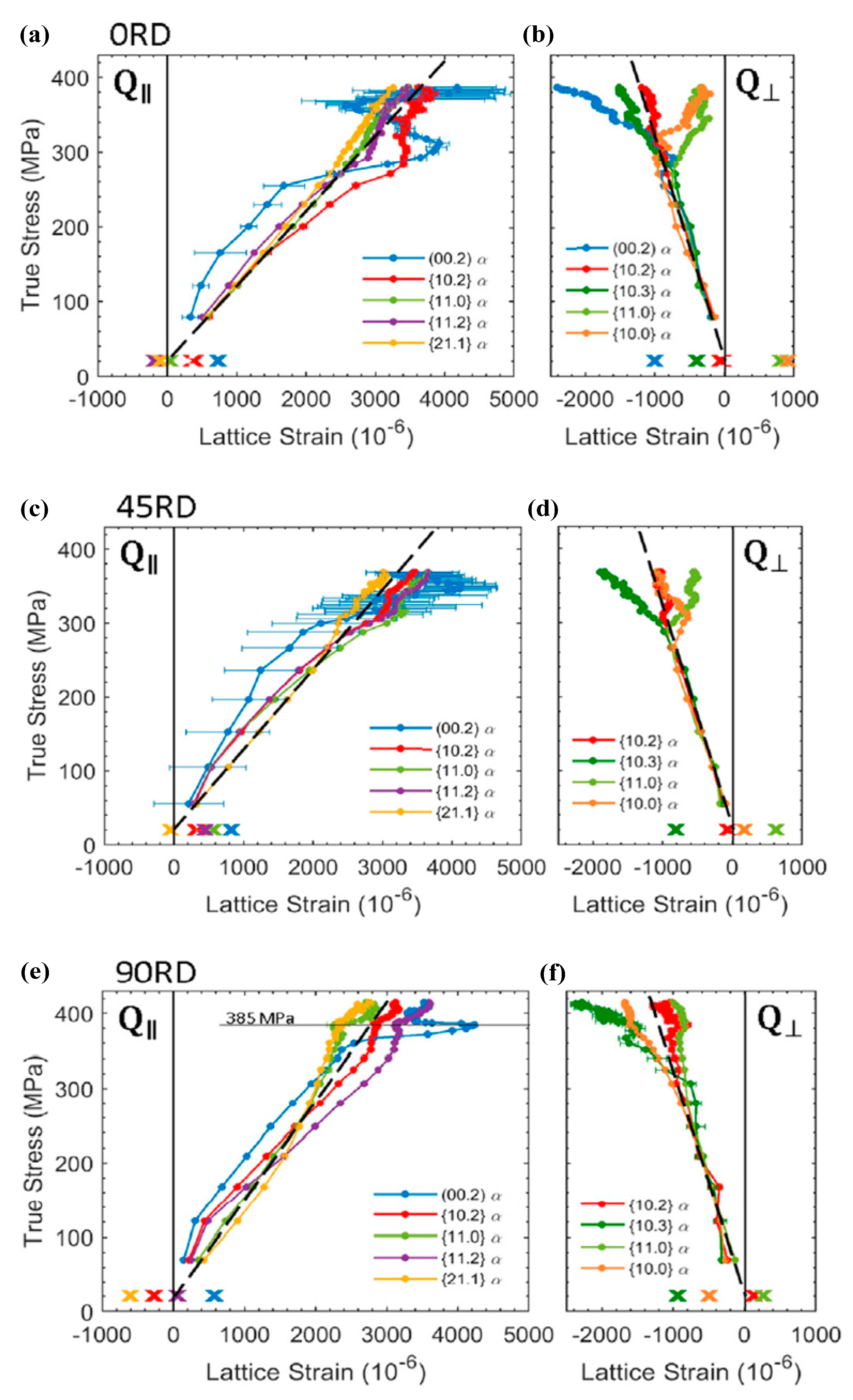
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Chen, S.-F.; Zhang, S.-H.; Xu, Y.; Song, H.-W. Deformation Characteristics, Formability and Springback Control of Titanium Alloy Sheet at Room Temperature: A Review. Materials 2022, 15, 5586. https://doi.org/10.3390/ma15165586
Li H, Chen S-F, Zhang S-H, Xu Y, Song H-W. Deformation Characteristics, Formability and Springback Control of Titanium Alloy Sheet at Room Temperature: A Review. Materials. 2022; 15(16):5586. https://doi.org/10.3390/ma15165586
Chicago/Turabian StyleLi, Hao, Shuai-Feng Chen, Shi-Hong Zhang, Yong Xu, and Hong-Wu Song. 2022. "Deformation Characteristics, Formability and Springback Control of Titanium Alloy Sheet at Room Temperature: A Review" Materials 15, no. 16: 5586. https://doi.org/10.3390/ma15165586
APA StyleLi, H., Chen, S. -F., Zhang, S. -H., Xu, Y., & Song, H. -W. (2022). Deformation Characteristics, Formability and Springback Control of Titanium Alloy Sheet at Room Temperature: A Review. Materials, 15(16), 5586. https://doi.org/10.3390/ma15165586








