Chirality in the Solid State: Chiral Crystal Structures in Chiral and Achiral Space Groups
Abstract
:1. Introduction
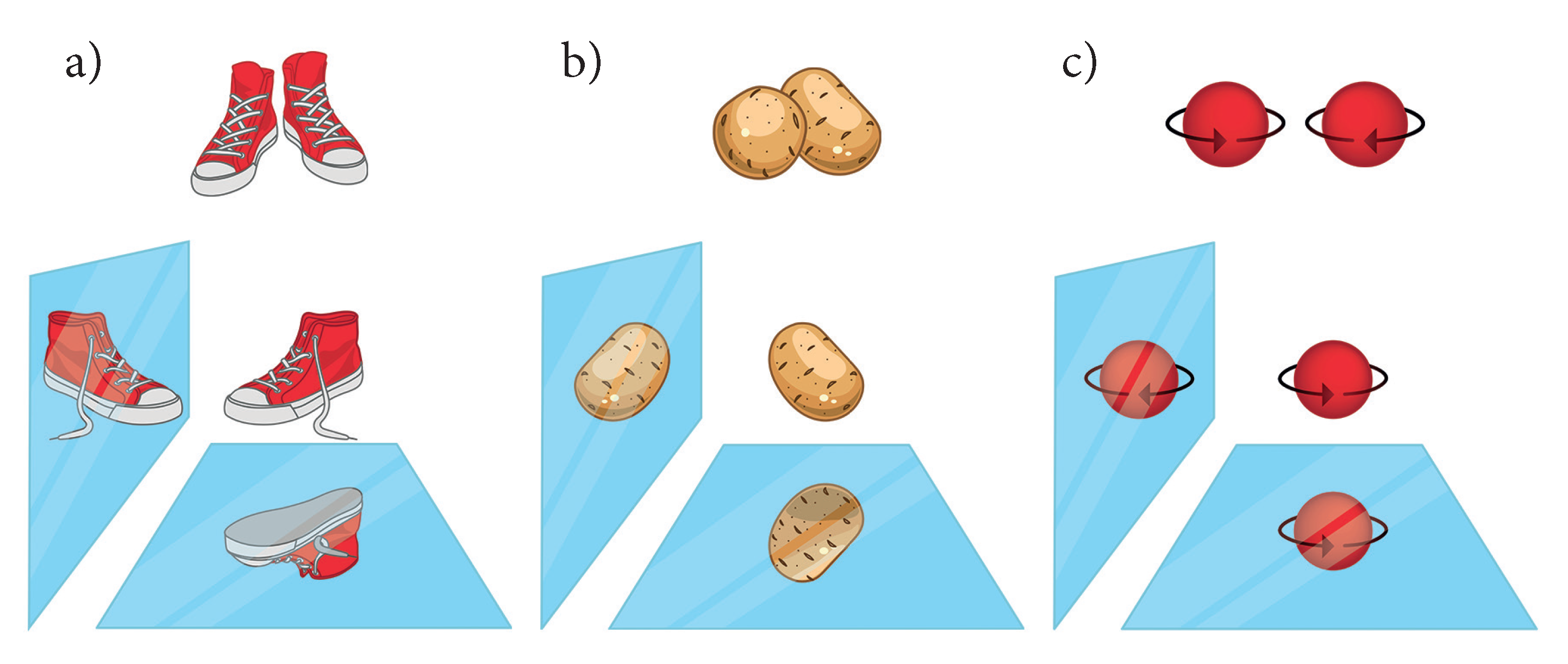
2. Chirality in Three Dimensions
3. Chirality in Two Dimensions
4. Chirality Measures
5. Chiral Systems: From Crystalline Elements to Compounds
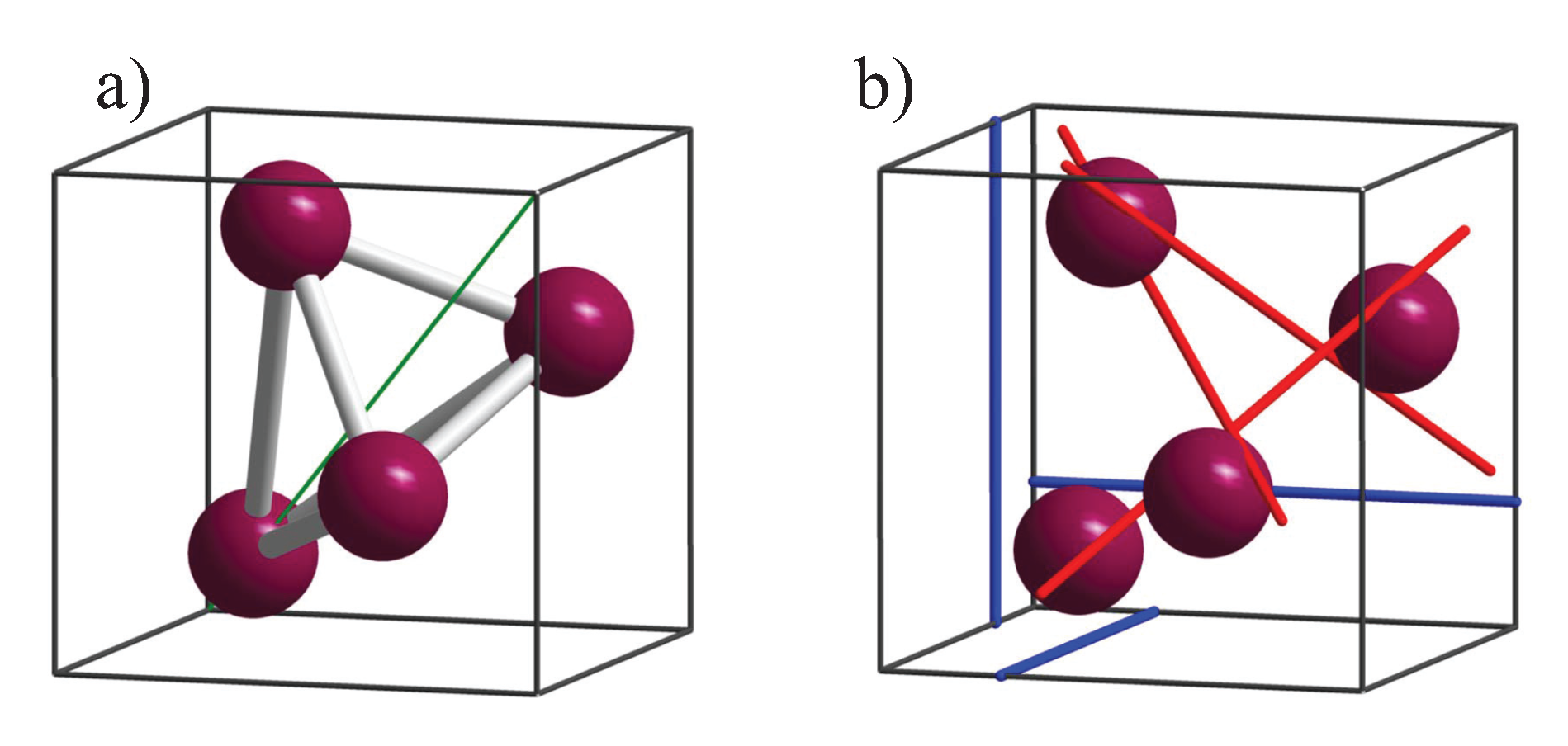
5.1. Elements with Chiral Structures
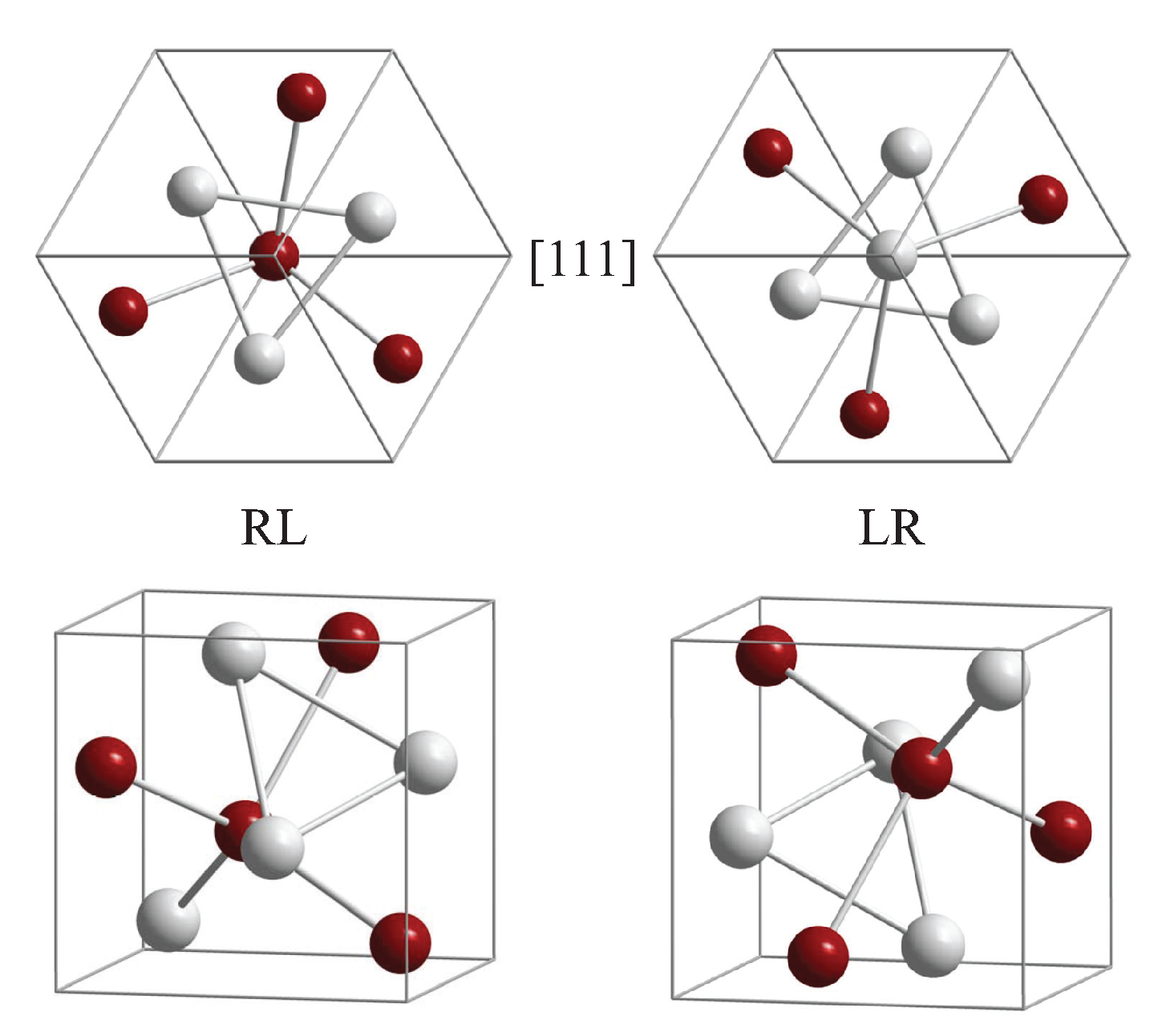
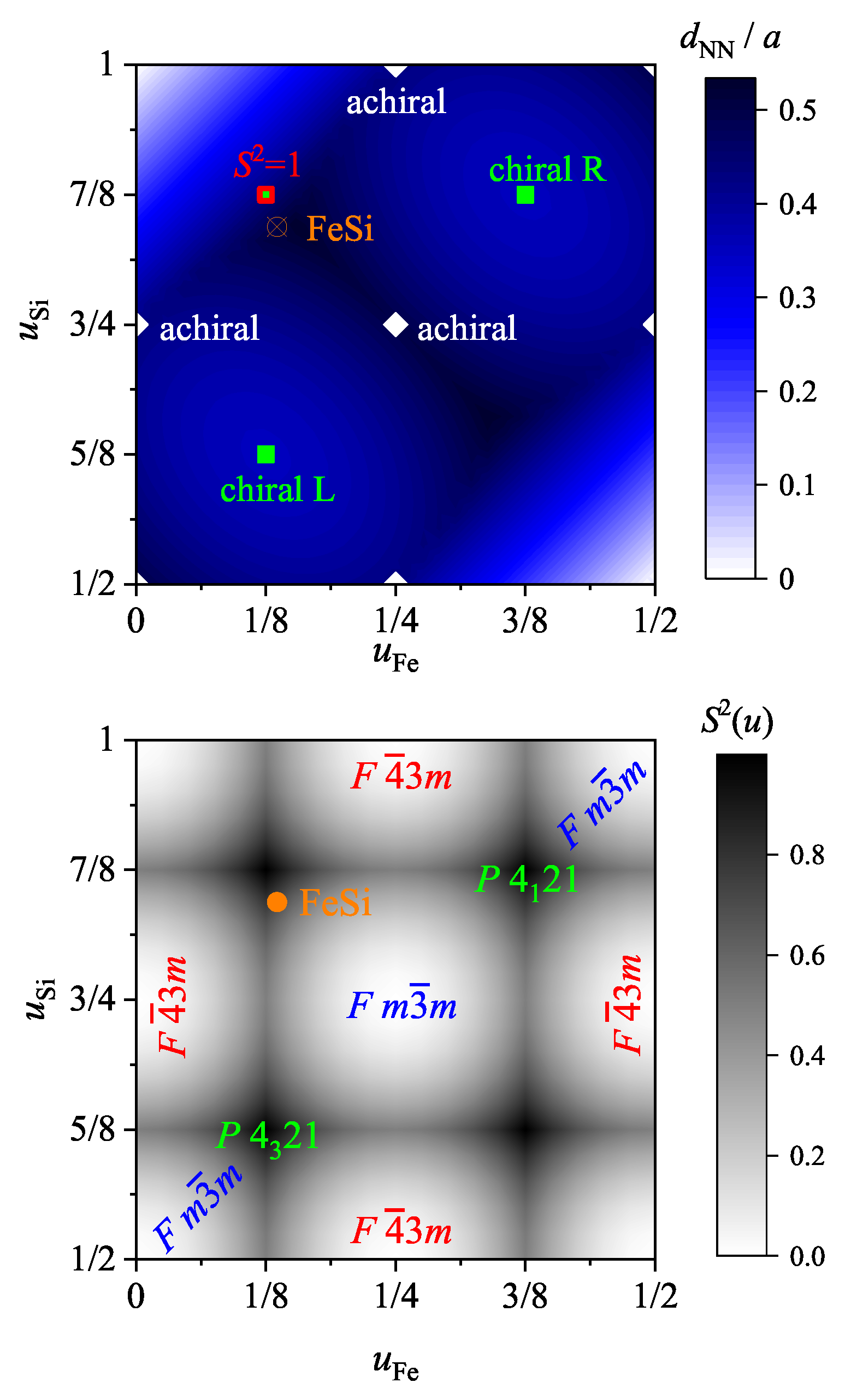
5.2. Compounds with Chiral, Cubic Structures
5.3. Compounds with Tetragonal Chiral Structures
5.4. Compounds with Hexagonal or Trigonal, Chiral Structures
6. Chirality at Solid Surfaces
- achiral bulk with a chiral surface,
- chiral bulk with an achiral surface,
- chiral bulk with a chiral surface,
- achiral bulk with an achiral surface.
6.1. Achiral Bulk with Chiral Surface
6.2. Surfaces of Chiral Bulk Materials
7. Electronic Structure and Chirality
7.1. Electronic Structure of Se
7.2. Electronic Structure of FeSi and Other Compounds with B20 Structure
7.3. Berry Curvature and Chirality
7.4. Circular Dichroism, Chirality, and Electronic Structure
8. Discussion, Summary, and Conclusions
- (I)
- chirality, chirality measure, chirality sense, handedness, and helicity;
- (II)
- chiral structures and chiral crystallographic space groups;
- (III)
- chirality in two and three dimensions;
- (IV)
- material properties depending on chirality measures or chirality sense.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. First Principles Calculations
Appendix B. Relation Between Chiral Structures, Symmorphic Space Groups, and Topological Spaces
| Crystal System | Space Group |
|---|---|
| Triclinic | |
| Monoclinic | , |
| Orthorhombic | , , , |
| Tetragonal | , , , |
| Trigonal | , , , , |
| Hexagonal | , |
| Cubic | , , , , |
References
- Klapper, H.; Hahn, T. Point-group symmetry and physical properties of crystals. In International Tables for Crystallography; International Union of Crystallography: London, UK, 2006; Volume A, Chapter 10.2; pp. 804–808. [Google Scholar]
- Authier, A. Introduction to the properties of tensors. In International Tables for Crystallography; International Union of Crystallography: London, UK, 2006; Volume D, Chapter 1.1; pp. 3–33. [Google Scholar]
- Thomson (Lord Kelvin), W. The Molecular Tactics of a Crystal; Clarendon Press: Oxford, UK, 1894. [Google Scholar]
- Kelvin, L. Baltimore Lectures on Molecular Dynamics and Wave Theory of Light; C. J. Clay and Sons; Cambridge University Press Warehouse: London, UK, 1904. [Google Scholar]
- Moss, G.P. Basic Terminology of Stereochemistry (IUPAC Recommendations 1996). Pure Appl. Chem. 1996, 68, 2193. [Google Scholar] [CrossRef]
- Ruch, E. Algebraic Aspects of the Chirality Phenomenon in Chemistry. Acc. Chem. Res. 1972, 5, 49. [Google Scholar] [CrossRef]
- Cintas, P. Tracing the Origins and Evolution of Chirality and Handedness in Chemical Language. Angew. Chem. Int. Ed. 2007, 46, 4016. [Google Scholar] [CrossRef] [PubMed]
- Ruch, E. Chiral Derivatives of Achiral Molecules: Standard Classes and the Problem of a Right-Left Classification. Angew. Chem. Int. Ed. 1977, 16, 65. [Google Scholar] [CrossRef]
- King, R.B. Chirality and handedness. Ann. N. Y. Acad. Sci. 2003, 988, 158. [Google Scholar] [CrossRef]
- Barron, L.D. True and false chirality and parity violation. Chem. Phys. Lett. 1986, 123, 423. [Google Scholar] [CrossRef]
- Barron, L.D. False Chirality, Absolute Enantioselection and CP Violation: Pierre Curie’s Legacy. Magnetochemistry 2020, 6, 5. [Google Scholar] [CrossRef]
- Mislow, K. Molecular Chirality. In Topics in Stereochemistry; Denmark, S.E., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1999; Volume 22, p. 1. [Google Scholar]
- Togawa, Y.; Kousaka, Y.; Inoue, K.; Kishine, J.I. Symmetry, Structure, and Dynamics of Monoaxial Chiral Magnets. J. Phys. Soc. Jpn. 2016, 85, 112001. [Google Scholar] [CrossRef]
- Cheong, S.W.; Xu, X. Magnetic chirality. NPJ Quantum Mater. 2022, 40, 1. [Google Scholar] [CrossRef]
- Inoue, K. Chiral Magnetism: Coupling Static and Dynamic Chirality. Chem. Lett. 2021, 50, 742. [Google Scholar] [CrossRef]
- Train, C.; Gruselle, M.; Verdaguer, M. The fruitful introduction of chirality and control of absolute configurations in molecular magnets. Chem. Soc. Rev. 2011, 40, 3297. [Google Scholar] [CrossRef]
- Nespolo, M.; Aroyo, M.I.; Souvignier, B. Crystallographic shelves: Space-group hierarchy explained. J. Appl. Crystallogr. 2018, 51, 1481. [Google Scholar] [CrossRef]
- Dryzun, C.; Avnir, D. On the abundance of chiral crystals. Chem. Commun. 2012, 48, 5874. [Google Scholar] [CrossRef]
- Bader, H. Screw Axes of Symmetry and their Symbols. Am. Mineral. 1949, 34, 752. [Google Scholar]
- Villars, P.; Cenzual, K. Pearson’s Crystal Data—Crystal Structure Database for Inorganic Compounds Release 2019/2020; ASM International, The Materials Information Company: Materials Park, OH, USA, 2020. [Google Scholar]
- Glazer, A.M.; Stadnicka, K. On the Use of the Term ’Absolute’ in Crystallography. Acta Cryst. 1989, A45, 234. [Google Scholar] [CrossRef]
- Aroyo, M.I. International Tables for Crystallography Volume A: Space-Group Symmetry; International Union of Crystallography: London, UK, 2016. [Google Scholar]
- Shiozaki, K.; Sato, M.; Gomi, K. Topological crystalline materials: General formulation, module structure, and wallpaper groups. Phys. Rev. B 2017, 95, 235425. [Google Scholar] [CrossRef]
- Flack, H.D.; Bernardinelli, G. Absolute structure and absolute configuration. Acta Cryst. 1999, A55, 908. [Google Scholar] [CrossRef]
- Flack, H.D. Chiral and Achiral Crystal Structures. Helv. Chim. Acta 2003, 96, 905. [Google Scholar] [CrossRef]
- Cahn, R.S.; Ingold, S.C.; Prelog, V. Spezifikation der molekularen Chiralitat. Angew. Chem. 1966, 78, 413. [Google Scholar] [CrossRef]
- Prelog, V. Chirality in Chemistry. Science 1976, 193, 17. [Google Scholar] [CrossRef]
- Buda, A.B.; Heyde, T.A.; Mislow, K. On Quantifying Chirality. Angew. Chem. Int. Ed. 1992, 31, 989. [Google Scholar] [CrossRef]
- Gilat, G. On quantifying chirality-Obstacles and problems towards unification. J. Math. Chem. 1994, 15, 197. [Google Scholar] [CrossRef]
- Weinberg, N.; Mislow, K. A unification of chirality measures. J. Math. Chem. 1995, 17, 35. [Google Scholar] [CrossRef]
- Petitjean, M. Chirality and Symmetry measures: A Transdisciplinary Review. Entropy 2003, 5, 271. [Google Scholar] [CrossRef]
- Fowler, P.W. Quantification of chirality: Attempting the impossible. Symmetry Cult. Sci. 2005, 16, 321. [Google Scholar]
- Alemany, P.; Casanova, D.; Alvarez, S.; Dryzun, C.; Avnir, D. Continuous Symmetry Measures: A New Tool in Quantum Chemeistry. In Reviews in Computational Chemistry; Parrill, A.L., Lipkowitz, K.B., Eds.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2017; Volume 30, p. 290. [Google Scholar]
- Weinberg, N.; Mislow, K. Distance functions as generators of chirality measures. J. Math. Chem. 1993, 14, 427. [Google Scholar] [CrossRef]
- Zimpel, Z. A geometrical approach to the degree of chirality and asymmetry. J. Math. Chem. 1993, 14, 451. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous Symmetry Measures. J. Am. Chem. Soc. 1992, 114, 7843. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Avnir, D. Continuous Symmetry Measures. 4. Chirality. J. Am. Chem. Soc. 1995, 117, 462. [Google Scholar] [CrossRef]
- Alvarez, S.; Alemanyband, P.; Avnir, D. Continuous chirality measures in transition metal chemistr. Chem. Soc. Rev. 2005, 34, 313. [Google Scholar] [CrossRef]
- Pinsky, M.; Dryzun, C.; Casanova, D.; Alemany, P.; Avnir, D. Analytical methods for calculating Continuous Symmetry Measures and the Chirality Measure. J. Comput. Chem. 2008, 29, 2712. [Google Scholar] [CrossRef]
- Dryzun, C.; Zait, A.; Avnir, D. Quantitative symmetry and chirality—A fast computational algorithm for large structures: Proteins, macromolecules, nanotubes, and unit cells. J. Comput. Chem. 2011, 32, 2526. [Google Scholar] [CrossRef]
- Buda, A.B.; Mislow, K. A Hausdorff chirality measure. J. Am. Chem. Soc. 1992, 114, 6006. [Google Scholar] [CrossRef]
- Yewande, E.O.; Neal, M.P.; Low, R. The Hausdorff chirality measure and a proposed Hausdorff structure measure. Mol. Phys. 2009, 107, 281. [Google Scholar] [CrossRef]
- Cosse-Barbi, A.; Raji, M. Constrained and Unconstrained Chirality Functions. A New Method, Going from Discrete to Continuous Space, to Find the Best Overlap Between Enantiomer Atoms. Struct. Chem. 1997, 8, 409. [Google Scholar] [CrossRef]
- Ewald, P.P.; Hermann, C. Strukturbericht; Akademische Verlagsgesellschaft M.B.H.: Leipzig, Germany, 1931. [Google Scholar]
- Connelly, N.G.; Damhus, T.; Hartshorn, R.M.; Hutton, A.T. (Eds.) Nomenclature of Inorganic Chemistry; The Royal Society of Chemistry: London, UK, 2005. [Google Scholar]
- Akahama, Y.; Kobayashi, M.; Kawamura, H. Structural studies of pressure-induced phase transitions in selenium up to 150 GPa. Phys. Rev. B 1993, 47, 20. [Google Scholar] [CrossRef]
- Keller, R.; Holzapfel, W.B.; Schulz, H. Effect of yressnre on the atom yositions in Se anti Te. Phys. Rev. B 1977, 16, 4404. [Google Scholar] [CrossRef]
- Sanchez, D.S.; Belopolski, I.; Cochran, T.A.; Xu, X.; Yin, J.X.; Chang, G.; Xie, W.; Manna, K.; Süß, V.; Huang, C.Y.; et al. Topological chiral crystals with helicoid-arc quantum states. Nature 2019, 567, 500. [Google Scholar] [CrossRef]
- Schröter, N.B.M.; Pei, D.; Vergniory, M.G.; Sun, Y.; Manna, K.; de Juan, F.; Krieger, J.A.; Süß, V.; Schmidt, M.; Dudin, P.; et al. Chiral topological semimetal with multifold band crossings and long Fermi arcs. Nat. Phys. 2019, 15, 759. [Google Scholar] [CrossRef]
- Vescoli, V.; Degiorgi, L.; Buschinger, B.; Guth, W.; Geibel, C.; Steglich, F. The Optical properties of RuSi: Kondo insulator or conventional semiconductor. Solid State Commun. 1998, 105, 367. [Google Scholar] [CrossRef]
- Dmitriev, V.; Chernyshov, D.; Grigoriev, S.; Dyadkin, V. A chiral link between structure and magnetism in MnSi. J. Phys. Condens. Matter 2012, 24, 366005. [Google Scholar] [CrossRef]
- Burkhardt, U.; Borrmann, H.; Moll, P.; Schmidt, M.; Grin, Y.; Winkelmann, A. Absolute Structure from Scanning Electron Microscopy. Sci. Rep. 2020, 10, 4065. [Google Scholar] [CrossRef]
- Placa, S.J.L.; Hamilton, W.C. Refinement of the crystal structure of alpha-N2. Acta Crystallogr. B 1972, 28, 984. [Google Scholar] [CrossRef]
- Krupskii, I.N.; Prokhvatilov, A.I.; Verkin, B.I.; Erenburg, A.I.; Yantsevich, L.D. Structure and Thermal Expansion of alpha-CO. Phys. Status Solidi A 1973, 19, 519. [Google Scholar] [CrossRef]
- Buschow, K.H.J.; Velge, W.A.J.J. Phase Relations and Intermetallic Compounds in the Lanthanum-Cobalt System. J. Less-Common Met. 1967, 13, 11. [Google Scholar] [CrossRef]
- Okamoto, H. Section III: Supplemental Literature Review: Co-La (Cobalt-Lanthanum). J. Phase Equ. Diff. 2009, 30, 408. [Google Scholar] [CrossRef]
- Otto, M.J.; van Woerden, R.A.M.; van der Valk, P.J.; Wijngaard, J.; van Bruggen, C.F.; Haas, C.; Buschow, K.H.J. Half-metallic ferromagnets: I. Structure and magnetic properties of NiMnSb and related inter-metallic compounds. J. Phys. Condens. Matter 1989, 1, 2341. [Google Scholar] [CrossRef]
- Chevalier, B.; Lejay, P.; Cole, A.; Vlasse, M.; Etourneau, J. Crystal Structure, superconducting and magnetic properties of new ternary silicides LaRhSi, LaIrSi and NdIrSi. Solid State Comm. 1982, 41, 801. [Google Scholar] [CrossRef]
- Vergniory, M.G.; Elcoro, L.; Felser, C.; Regnault, N.; Bernevig, B.A.; Wang, Z. A complete catalogue of high-quality topological materials. Nature 2019, 566, 480. [Google Scholar] [CrossRef]
- Riva, S. Chirality in metals: An asymmetrical journey among advanced functional materials. Mater. Sci. Technol. 2017, 33, 795. [Google Scholar] [CrossRef]
- Halasyaman, P.S.; Poeppelmeier, K.R. Noncentrosymmetric Oxides. Chem. Mater. 1998, 10, 2753. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Miao, J.; Li, J.; Zhu, X.; Chen, R.; Tang, Z.; Pan, R.; He, T.; Cheng, J. Chiral Transition Metal Oxides: Synthesis, Chiral Origins, and Perspectives. Adv. Mater. 2020, 32, 1905585. [Google Scholar] [CrossRef]
- Kuang, H.; Xu, C.; Tang, Z. Emerging Chiral Materials. Adv. Mater. 2020, 32, 2005110. [Google Scholar] [CrossRef]
- Hazen, R.M.; Sholl, D.S. Chiral selection on inorganic crystalline surfaces. Nat. Mater. 2003, 2, 367. [Google Scholar] [CrossRef]
- Im, S.W.; Ahn, H.Y.; Kim, R.M.; Cho, N.H.; Kim, H.; Lim, Y.C.; Lee, H.E.; Nam, K.T. Chiral Surface and Geometry of Metal Nanocrystals. Adv. Mater. 2020, 32, 1905758. [Google Scholar] [CrossRef]
- Chen, T.; Wang, D.; Wan, L.J. Two-dimensional chiral molecular assembly on solid surfaces: Formation and regulation. Natl. Sci. Rev. 2015, 2, 205. [Google Scholar] [CrossRef]
- McFadden, C.F.; Cremer, P.S.; Gellman, A.J. Adsorption of Chiral Alcohols on “Chiral” Metal Surfaces. Langmuir 1996, 12, 2483. [Google Scholar] [CrossRef]
- Jenkins, S.J.; Pratt, S.J. Beyond the surface atlas: A roadmap and gazetteer for surface symmetry and structure. Surf. Sci. Rep. 2007, 62, 373. [Google Scholar] [CrossRef]
- Hermann, K. Crystallography and Surface Structure, second, revised and expanded edition ed.; Wiley-VCH Verlag: Weinheim, Germany, 2017. [Google Scholar]
- Vocadlo, L.; Price, G.D.; Wood, I.G. Crystal structure, compressibility and possible phase transitions in e-FeSi studied by first principles pseudopotential calculations. Acta Cryst. 1999, B55, 484. [Google Scholar] [CrossRef]
- Kübler, J.; Yan, B.; Felser, C. Non-vanishing Berry phase in chiral insulators. EPL (Europhys. Lett.) 2013, 104, 30001. [Google Scholar] [CrossRef]
- Bradlyn, B.; Cano, J.; Wang, Z.; Vergniory, M.G.; Felser, C.; Cava, R.J.; Bernevig, B.A. Beyond Dirac and Weyl fermions: Unconventional quasiparticles in conventional crystals. Science 2016, 353, aaf5037. [Google Scholar] [CrossRef]
- Rao, Z.; Li, H.; Zhang, T.; Tian, S.; Li, C.; Fu, B.; Tang, C.; Wang, L.; Li, Z.; Fan, W.; et al. Observation of unconventional chiral fermions with long Fermi arcs in CoS. Nature 2019, 567, 496. [Google Scholar] [CrossRef]
- Takane, D.; Wang, Z.; Souma, S.; Nakayama, K.; Nakamura, T.; Oinuma, H.; Nakata, Y.; Iwasawa, H.; Cacho, C.; Kim, T.; et al. Observation of Chiral Fermions with a Large Topological Charge and Associated Fermi-Arc Surface States in CoSi. Phys. Rev. Lett. 2019, 122, 76402. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal Phase Factors Accompanying Adiabatic Changes. Proc. R. Soc. A 1984, 392, 45. [Google Scholar]
- Chang, M.C.; Niu, Q. Berry curvature, orbital moment, and effective quantum theory of electrons in electromagnetic fields. J. Phys. Condens. Matter 2008, 20, 193202. [Google Scholar] [CrossRef]
- Gradhand, M.; Fedorov, D.V.; Pientka, F.; Zahn, P.; Mertig, I.; Gyöorffy, B.L. First-principle calculations of the Berry curvature of Bloch states for charge and spin transport of electron. J. Phys. Condens. Matter 2012, 24, 213202. [Google Scholar] [CrossRef]
- Tsirkin, S.S.; Puente, P.A.; Souza, I. Gyrotropic effects in trigonal tellurium studied from first principles. Phys. Rev. B 2018, 97, 035158. [Google Scholar] [CrossRef]
- Hüfner, S. Photoelectron Spectroscopy: Principles and Applications, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Suga, S.; Sekiyama, A. Photoelectron Spectroscopy: Bulk and Surface Electronic Structures; Springer Series in Optical Sciences; Springer-Verlag: Berlin Heidelberg, Germany, 2014; Volume 176. [Google Scholar]
- Ritchie, B. Theory of the angular distribution of photoelectrons ejected from optically active molecules and molecular negative ions. Phys. Rev. A 1976, 13, 1411. [Google Scholar] [CrossRef]
- Ritchie, B. Theory of the angular distribution for ejection of photoelectrons from optically active molecules and molecular negative ions. II. Phys. Rev. A 1976, 14, 359. [Google Scholar] [CrossRef]
- Cherepkov, N.A. Circular Dichroism of Molecules in the Continouus Absorption Region. Chem. Phys. Lett. 1982, 87, 344. [Google Scholar] [CrossRef]
- Westphal, C.; Bansmann, J.; Getzlaff, M.; Schönhense, G. Circular Dichroism in the Angular Distribution of Photoelectrons from Oriented CO Molecules. Phys. Rev. Lett. 1989, 63, 151. [Google Scholar] [CrossRef]
- Schönhense, G. Circular Dichroism and Spin Polarization in Photoemission from Adsorbates and Non-Magnetic Solids. Phys. Scr. 1990, T31, 255. [Google Scholar] [CrossRef]
- Feder, R. Directional Photoemission of Polarized Electrons from Adsorbate Systems. Solid State Commun. 1977, 21, 1091. [Google Scholar] [CrossRef]
- Fecher, G.H. The solid surface as origin of circular dichroism in the angular distribution of photoelectrons from spherical states of adsorbates. Europhys. Lett. 1995, 29, 605. [Google Scholar] [CrossRef]
- Fecher, G.H.; Braun, J.; Oelsner, A.; Ostertag, C.; Schönhense, G. Dichroism in Angular Resolved Photoemission from Pt(111). Surf. Rev. Lett. 2002, 9, 883. [Google Scholar] [CrossRef]
- Fedchenko, O.; Medjanik, K.; Chernov, S.; Kutnyakhov, D.; Ellguth, M.; Oelsner, A.; Schönhense, B.; Peixoto, T.R.F.; Lutz, P.; Min, C.H.; et al. 4D texture of circular dichroism in soft-X-ray photoemission from tungsten. New J. Phys. 2019, 21, 13017. [Google Scholar] [CrossRef]
- Kuznetsov, V.V.; Cherepkov, N.A.; Fecher, G.H.; Schönhense, G. Angular Distributions and Dichroism of Photoelectrons ejected from Fixed-In-Space Molecules of Definite Symmetry: Applications to the C2v Symmetry Group. J. Chem. Phys. 2002, 117, 7180. [Google Scholar] [CrossRef]
- Kuznetsov, V.V.; Cherepkov, N.A.; Fecher, G.H.; Schönhense, G. Angular Distributions of Photoelectrons ejected from Fixed-In-Space Molecules of C3v Symmetry Group. J. Chem. Phys. 1999, 110, 9997. [Google Scholar] [CrossRef]
- Kuznetsov, V.; Cherepkov, N.; Raseev, G. Photoionization of adsorbates on sites with non-axial local symmetry. An example of the C4v symmetry group. J. Phys. Condens. Matter 1996, 8, 10327–10345. [Google Scholar] [CrossRef]
- Fecher, G.H.; Kuznetsov, V.V.; Cherepkov, N.A.; Schönhense, G. The Influence of the Symmetry on the Circular Dichroism in Angular Resolved Core-level Photoemission. J. Electron Spectrosc. Relat. Phenom. 2002, 122, 157. [Google Scholar] [CrossRef]
- Goulon, J.; Goulon-Ginet, C.; Rogalev, A.; Gotte, V.; Malgrange, C.; Brouder, C.; Natoli, C.R. X-ray natural circular dichroism in a uniaxial gyrotropic single crystal of LiIO3. J. Chem. Phys. 1998, 108, 6394. [Google Scholar] [CrossRef]
- Lininger, A.; Palermo, G.; Guglielmelli, A.; Nicoletta, G.; Goel, M.; Hinczewski, M.; Strangi, G. Chirality in Light-Matter Interaction. Adv. Mater. 2022, 2107325. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Madsen, G.K.H.; Kvasnicka, D.; Luitz, J.; Laskowski, R.; Tran, F.; Marks, L.D. WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties; Karlheinz Schwarz, Technical Universität Wien: Vienna, Austria, 2019. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Kunes, J.; Arita, R.; Wissgott, P.; Toschi, A.; Ikeda, H.; Held, K. Wien2wannier: From linearized augmented plane waves to maximally localized Wannier functions. Comp. Phys. Commun. 2010, 181, 1888. [Google Scholar] [CrossRef]
- Pizzi, G.; Vitale, V.; Arita, R. Wannier90 as a community code: New features and applications. J. Phys. Condens. Matter 2020, 32, 165902. [Google Scholar] [CrossRef]
- Ebert, H.; Ködderitzsch, D.; Minar, J. Calculating condensed matter properties using the KKR-Green’s function method: Recent developments and applications. Rep. Prog. Phys. 2011, 74, 96501. [Google Scholar] [CrossRef]
- Minar, J.; Braun, J.; Mankovsky, S.; Ebert, H. Calculation of angle-resolved photo emission spectra within the one-step model of photo emission—Recent developments. J. Electron Spectrosc. Relat. Phenom. 2011, 184, 91. [Google Scholar] [CrossRef]
- Braun, J. The theory of angle-resolved ultraviolet photoemission and its applications to ordered materials. Rep. Prog. Phys. 1996, 59, 1267. [Google Scholar] [CrossRef]





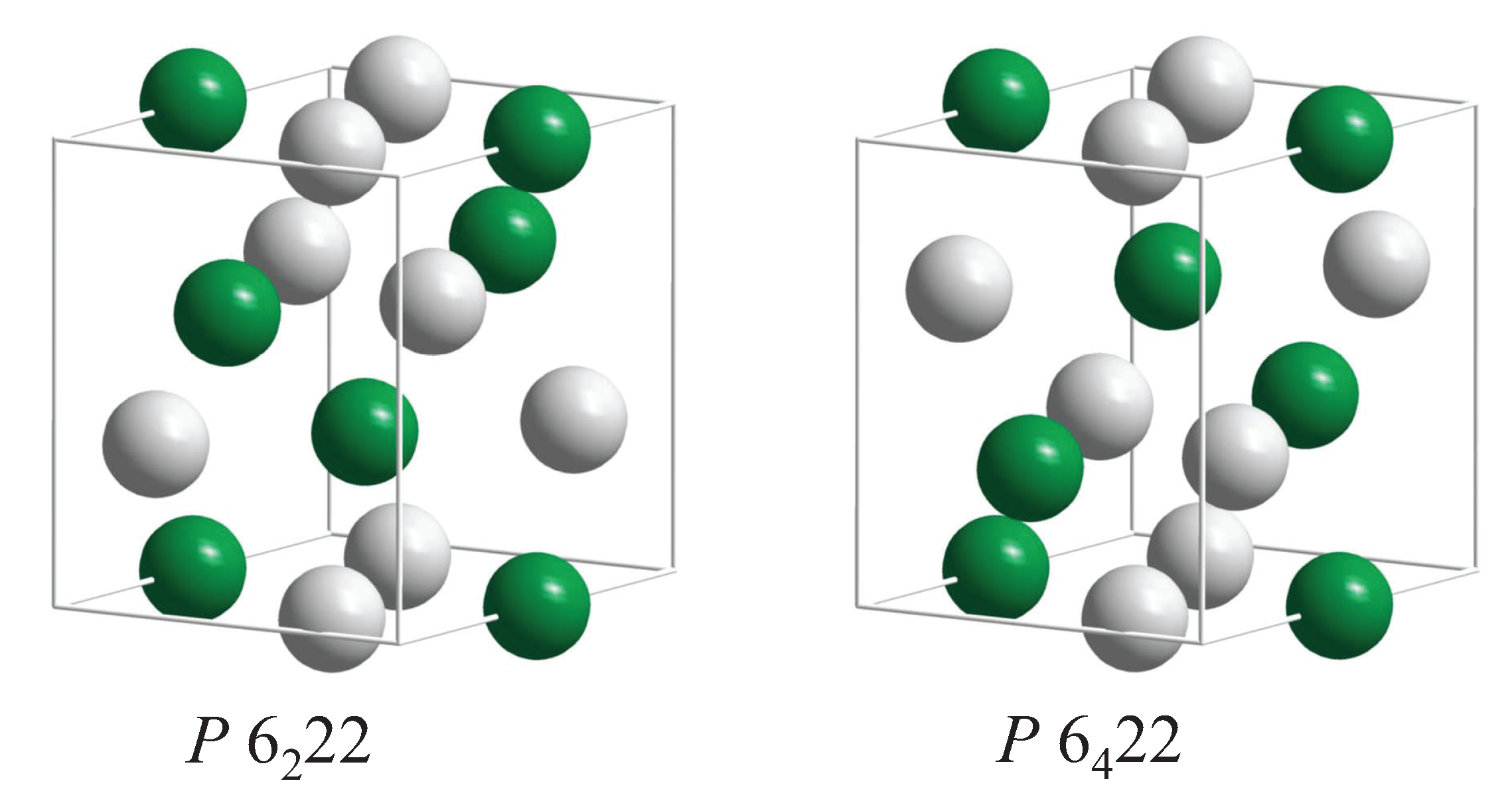





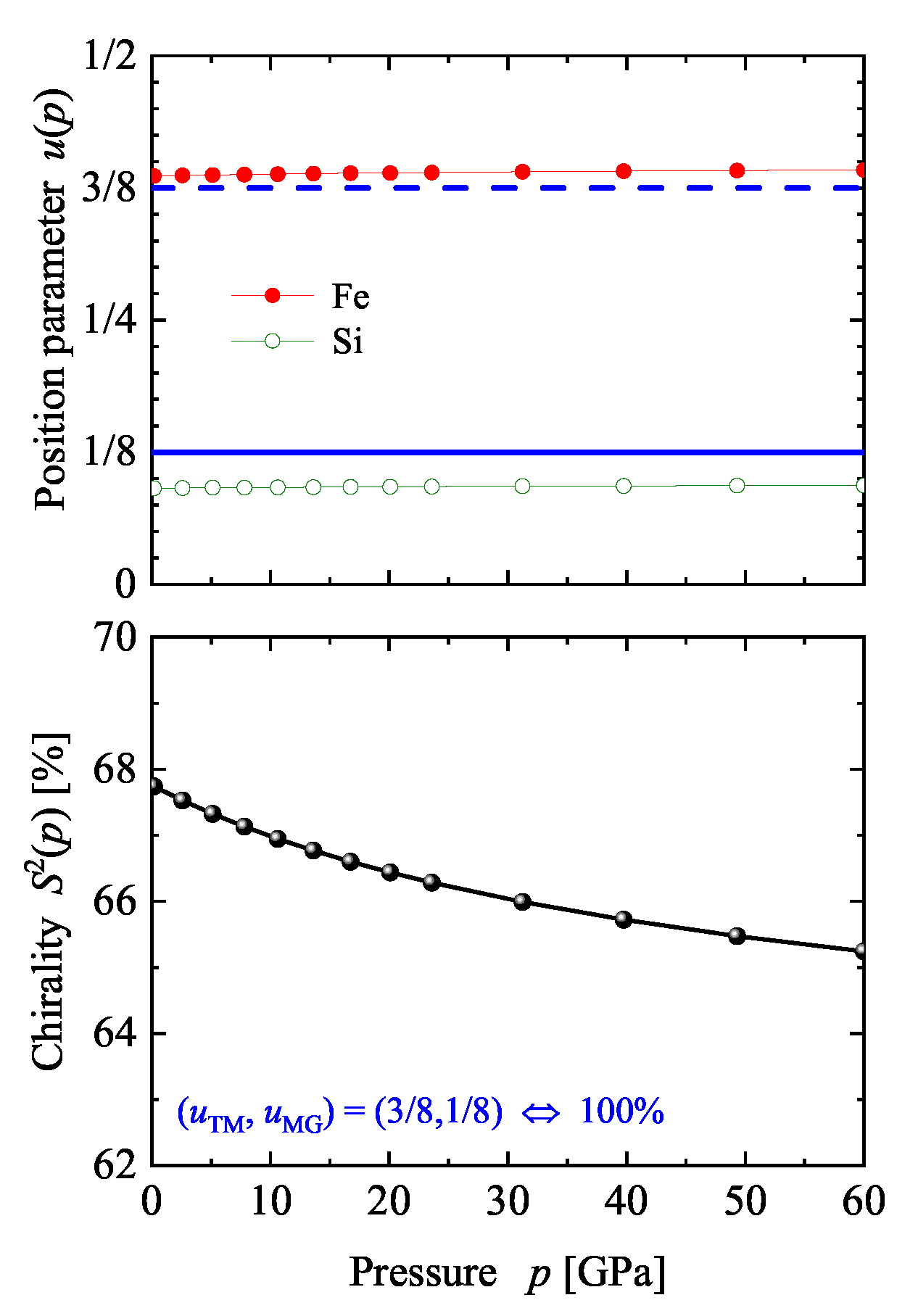



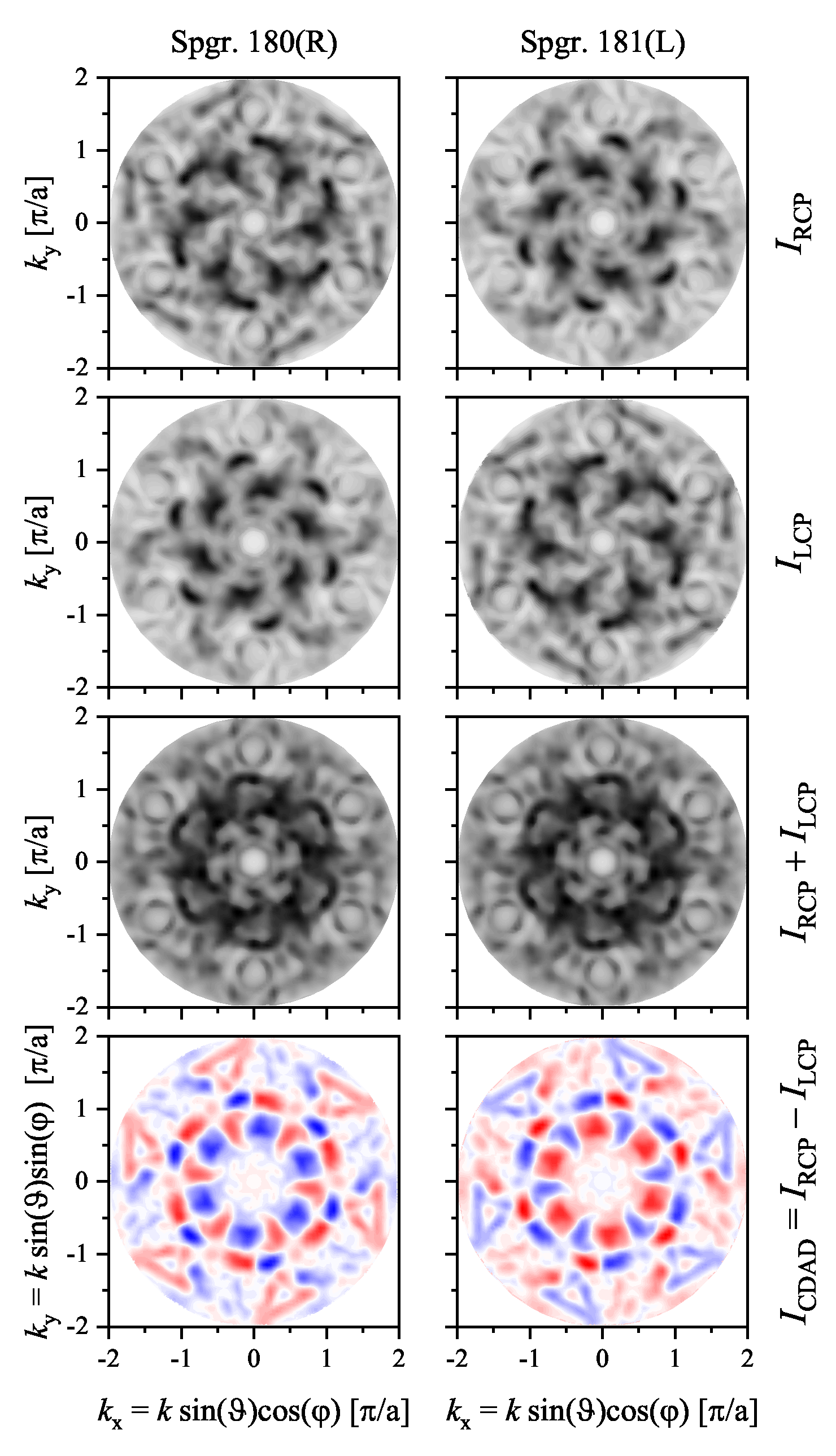
| Property | |||||
|---|---|---|---|---|---|
| No. | Laue Class | E | PY | O | PI |
| 1 | 1, 2, 3, 4, 6 | ⊠ | ⊠ | ⊠ | ⊠ |
| 2 | 222, 32, 422, 622, 23 | ⊠ | ⊠ | ⊠ | |
| 3 | 432 | ⊠ | ⊠ | ||
| 4 | ⊠ | ⊠ | ⊠ | ||
| 5 | ⊠ | ⊠ | |||
| 6 | ⊠ | ⊠ | |||
| 7 | ⊠ | ||||
| Crystal System | Laue Class | Point Group | Hermann-Mauguin Symbol | Space Group Number |
|---|---|---|---|---|
| Triclinic | 1 | 1 | ||
| Monoclinic | 2 | , , | 3–5 | |
| Orthorhombic | 222 | , , , , | 16–… | |
| , , , , | …–24 | |||
| Tetragonal | 4 | , , , , , | 75–80 | |
| 422 | , , , , , , | 89–… | ||
| , , , | …–98 | |||
| Trigonal | 3 | , , , | 143–146 | |
| 32 | , , , , , , | 149–155 | ||
| Hexagonal | 6 | , , , , , | 168–173 | |
| 622 | , , , , , | 177–182 | ||
| Cubic | 23 | T | , , , , | 195–199 |
| 432 | O | , , , , , | 207–… | |
| , , | … –214 |
| Tetragonal | 4 | , | (76,78) | |
| 422 | , | (91,95) | ||
| , | (92,96) | |||
| Trigonal | 3 | , | (144,145) | |
| 32 | , | (151,153) | ||
| , | (152,154) | |||
| Hexagonal | 6 | , | (169,170) | |
| , | (171,172) | |||
| 622 | , | (178,179) | ||
| , | (180,181) | |||
| Cubic | 432 | O | , | (212,213) |
| Crystal System | Laue Class | Point Group | Chiral Axes | Polar Axes |
|---|---|---|---|---|
| Monoclinic | 2 | [001] | [001] | |
| Orthorhombic | 222 | [001], [100], [010] | None | |
| Tetragonal | 4 | [001] | [001] | |
| 422 | [001], [100], [010], | None | ||
| [110], [] | ||||
| Trigonal | 3 | [001] | [001] | |
| 32 | [111], [], | [], | ||
| [], [] | [], [] | |||
| Hexagonal | 6 | [001] | [001] | |
| 622 | [001], [100], [010], | None | ||
| [], [], | ||||
| [210], [120] | ||||
| Cubic | 23 | T | , | |
| 432 | O | , , | None |
| Bravais Lattice | Point Group | Plane Group | Number |
|---|---|---|---|
| Oblique | 1 | ||
| 2 | |||
| Rectangular | 3, 4 | ||
| 6, 7, 8 | |||
| Rhombic | 5 | ||
| 9 | |||
| Square | 10 | ||
| 11, 12 | |||
| Hexagonal | 13 | ||
| 16 | |||
| 14, 15 | |||
| 17 |
| Achiral Group | Polar | WOBr | WOCl | ||
|---|---|---|---|---|---|
| N | 0.049 | 0.0650 | 0.045 | 0.0642 | |
| Y | 0.049 | 0.0654 | 0.045 | 0.0645 | |
| N | 0.049 | 0.0818 | 0.045 | 0.0800 | |
| a [Å] | c [Å] | u | ||
|---|---|---|---|---|
| CrSi | 4.4283 | 6.3680 | 0.1658 | 0.2706 |
| MoSi | 4.6220 | 6.6460 | 0.1642 | 0.2702 |
| NbSi | 4.7974 | 6.5923 | 0.1593 | 0.2690 |
| TaSi | 4.7839 | 6.5700 | 0.1590 | 0.2689 |
| VSi | 4.5726 | 6.3744 | 0.1626 | 0.2698 |
| WSi | 4.6180 | 6.6740 | 0.1640 | 0.2702 |
| NbGe | 4.9670 | 6.7830 | 0.1631 | 0.2699 |
| TaGe | 4.9380 | 6.7300 | 0.1640 | 0.2702 |
| WAl | 4.7422 | 6.6057 | 0.1618 | 0.2696 |
| cubic | [001] | [110] | [111] |
| 212,213 | |||
| 198 | |||
| hexagonal | [0001] | [110] | |
| 180,181 | |||
| 178,179 | |||
| 171,172 | |||
| 169,170 | |||
| trigonal | [001] | [100] | [210] |
| 152,154 | |||
| 151,153 | |||
| 144,145 | |||
| tetragonal | [001] | [100] | [110] |
| 92,96 | |||
| 91,95 | |||
| 76,78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fecher, G.H.; Kübler, J.; Felser, C. Chirality in the Solid State: Chiral Crystal Structures in Chiral and Achiral Space Groups. Materials 2022, 15, 5812. https://doi.org/10.3390/ma15175812
Fecher GH, Kübler J, Felser C. Chirality in the Solid State: Chiral Crystal Structures in Chiral and Achiral Space Groups. Materials. 2022; 15(17):5812. https://doi.org/10.3390/ma15175812
Chicago/Turabian StyleFecher, Gerhard H., Jürgen Kübler, and Claudia Felser. 2022. "Chirality in the Solid State: Chiral Crystal Structures in Chiral and Achiral Space Groups" Materials 15, no. 17: 5812. https://doi.org/10.3390/ma15175812
APA StyleFecher, G. H., Kübler, J., & Felser, C. (2022). Chirality in the Solid State: Chiral Crystal Structures in Chiral and Achiral Space Groups. Materials, 15(17), 5812. https://doi.org/10.3390/ma15175812






