Synthesis and Spatial Order Characterization of Controlled Silica Particle Sizes Organized as Photonic Crystals Arrays
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Instruments for Syntehsis and Sample Preparation
2.3. Characterization Methods
2.4. Synthesis of SiPs
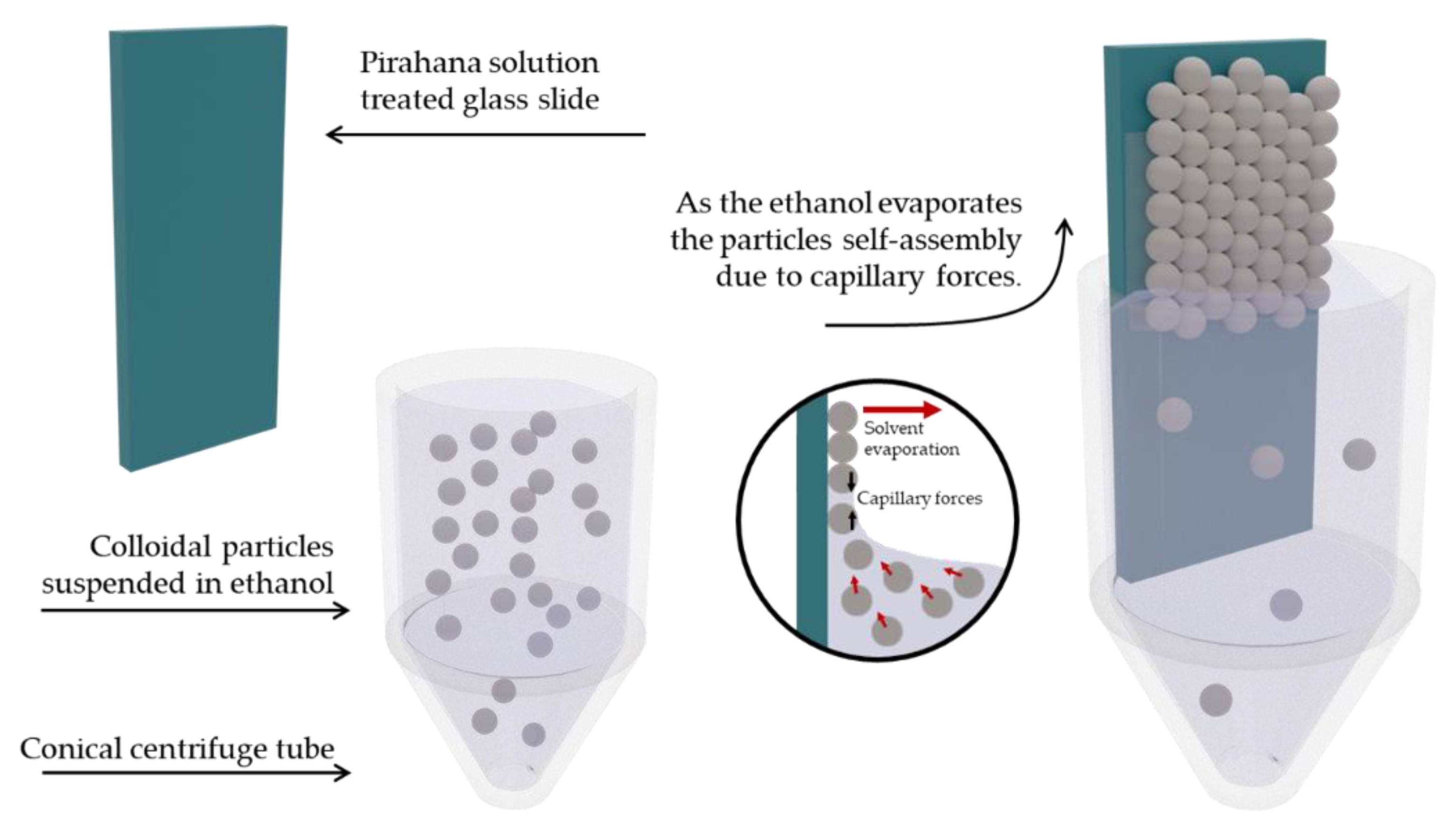
2.5. Preparation of SiPs Based PhC
3. Results and Discussions
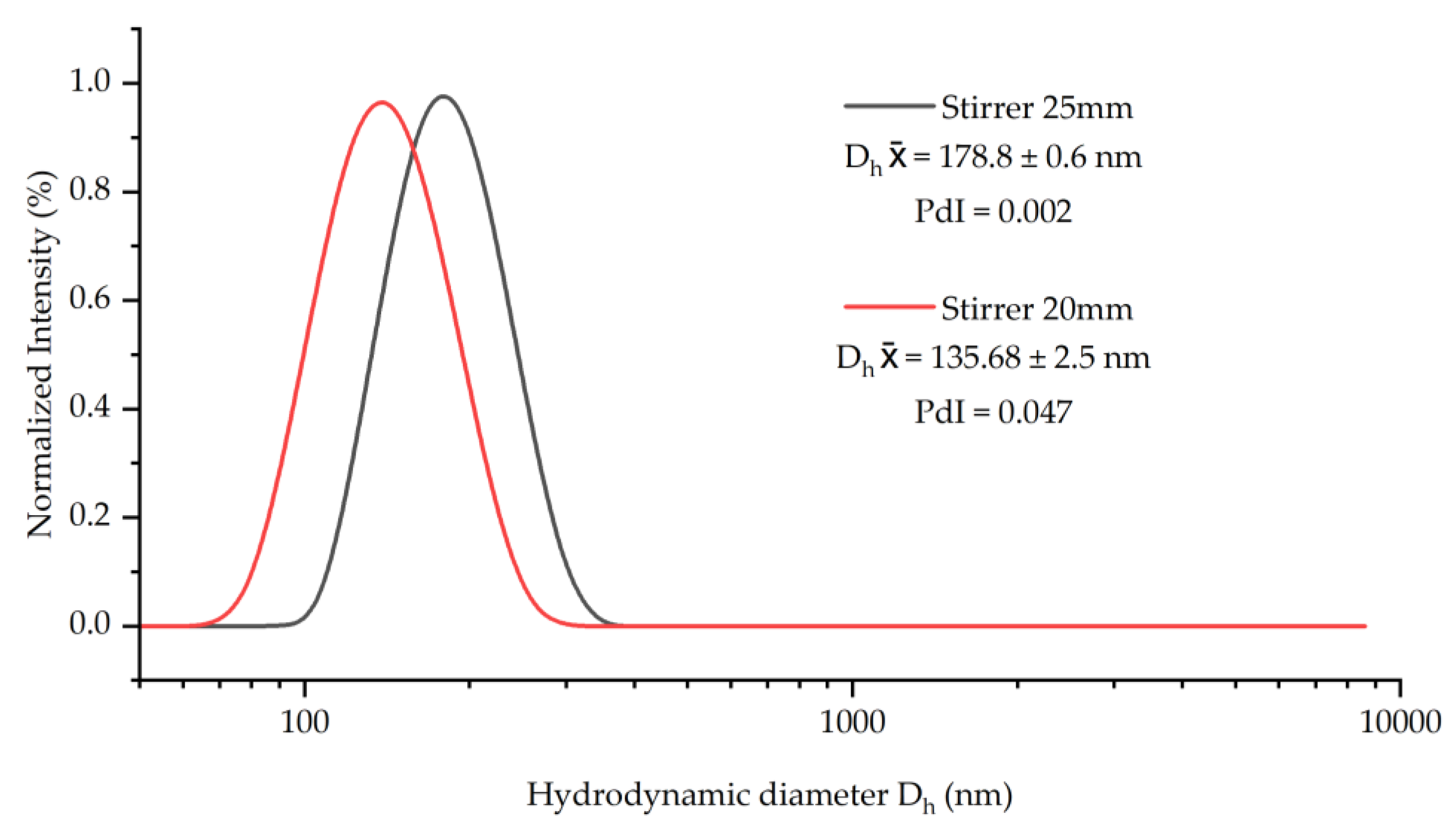
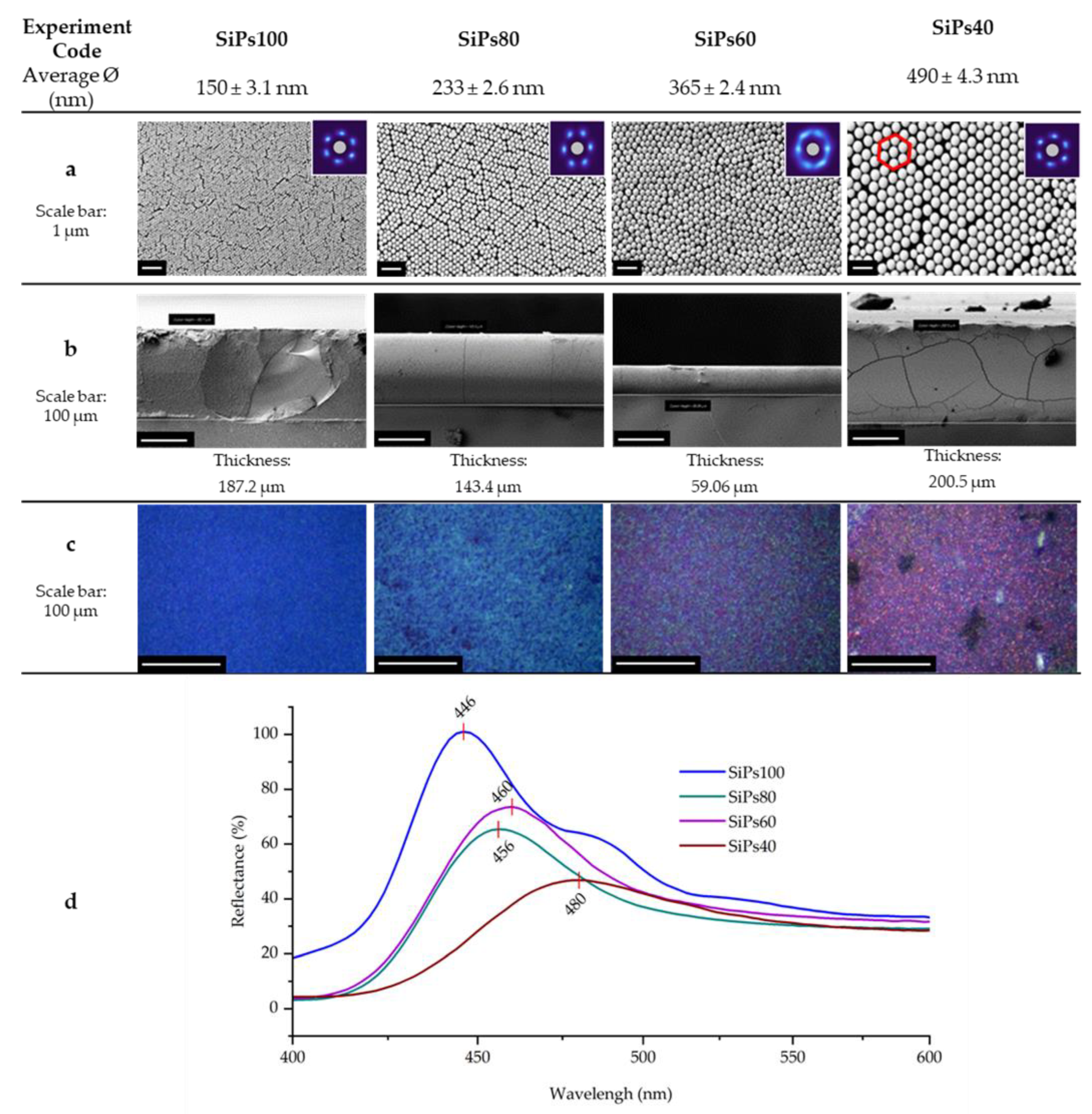
3.1. Synthesis and Characterization of SiPs
3.2. Formation and Characterization of the SiPs PhC
3.2.1. Visual Characterization
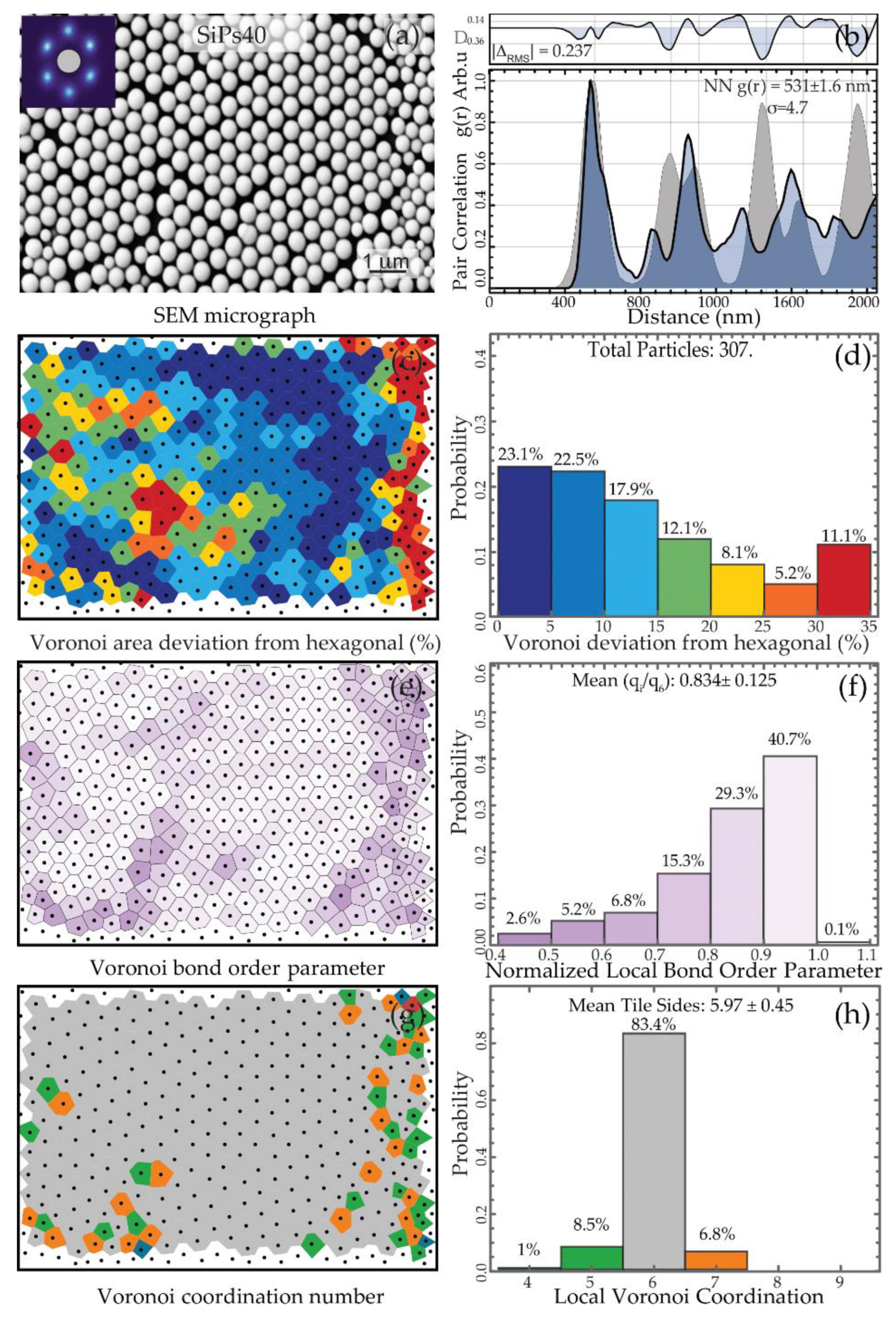
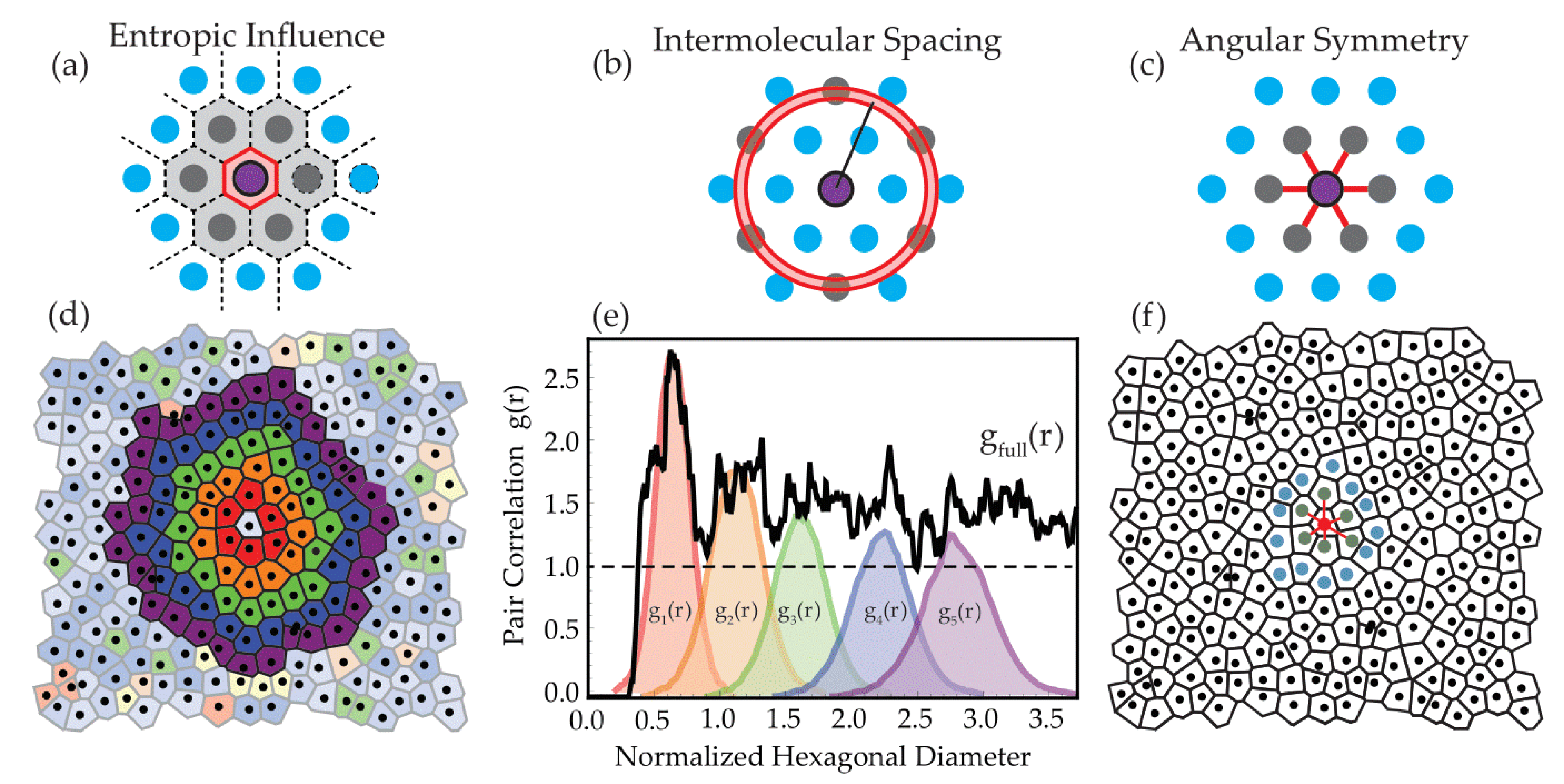
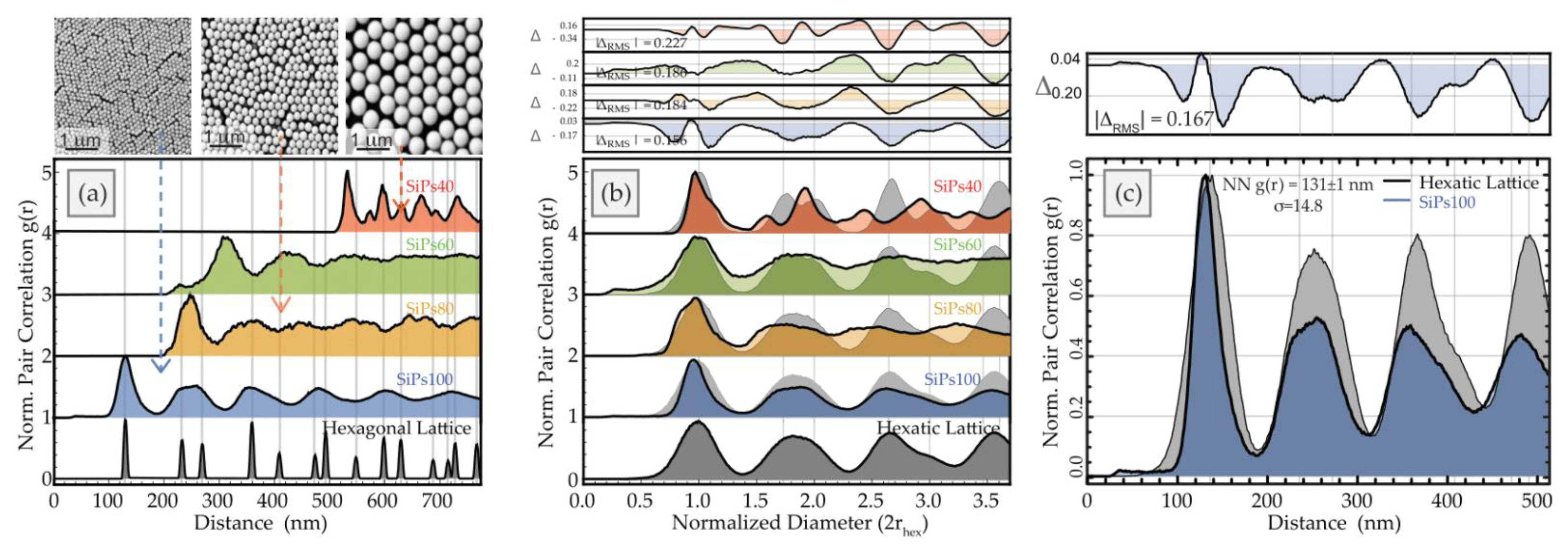
3.2.2. Spatial Statistics Characterization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Fenzl, C.; Hirsch, T.; Wolfbeis, O.S. Photonic crystals for chemical sensing and biosensing. Angew. Chem. Int. Ed. Engl. 2014, 53, 3318–3335. [Google Scholar] [CrossRef]
- Wickham, S.; Poladian, L.; Large, M.; Vukusic, P. Control of iridescence in natural photonic structures: The case of butterfly scales. In Optical Biomimetics; Elsevier: Amsterdam, The Netherlands, 2012; pp. 147–176. ISBN 9781845698027. [Google Scholar]
- Teyssier, J.; Saenko, S.V.; van der Marel, D.; Milinkovitch, M.C. Photonic crystals cause active colour change in chameleons. Nat. Commun. 2015, 6, 6368. [Google Scholar] [CrossRef]
- Masuda, Y.; Itoh, T.; Koumoto, K. Self-assembly patterning of silica colloidal crystals. Langmuir 2005, 21, 4478–4481. [Google Scholar] [CrossRef]
- Stöber, W.; Fink, A.; Bohn, E. Controlled growth of monodisperse silica spheres in the micron size range. J. Colloid Interface Sci. 1968, 26, 62–69. [Google Scholar] [CrossRef]
- Wong, Y.J.; Zhu, L.; Teo, W.S.; Tan, Y.W.; Yang, Y.; Wang, C.; Chen, H. Revisiting the Stöber method: Inhomogeneity in silica shells. J. Am. Chem. Soc. 2011, 133, 11422–11425. [Google Scholar] [CrossRef]
- Murayama, M.; Howe, J.M.; Hidaka, H.; Takaki, S. Atomic-level observation of disclination dipoles in mechanically milled, nanocrystalline Fe. Science 2002, 295, 2433–2435. [Google Scholar] [CrossRef]
- Bogush, G.H.; Tracy, M.A.; Zukoski, C.F. Preparation of monodisperse silica particles: Control of size and mass fraction. J. Non-Cryst. Solids 1988, 104, 95–106. [Google Scholar] [CrossRef]
- Tan, C.G.; Bowen, B.D.; Epstein, N. Production of monodisperse colloidal silica spheres: Effect of temperature. J. Colloid Interface Sci. 1987, 118, 290–293. [Google Scholar] [CrossRef]
- Malay, O.; Yilgor, I.; Menceloglu, Y.Z. Effects of solvent on TEOS hydrolysis kinetics and silica particle size under basic conditions. J. Sol-Gel. Sci. Technol. 2013, 67, 351–361. [Google Scholar] [CrossRef]
- Danaei, M.; Dehghankhold, M.; Ataei, S.; Hasanzadeh Davarani, F.; Javanmard, R.; Dokhani, A.; Khorasani, S.; Mozafari, M.R. Impact of Particle Size and Polydispersity Index on the Clinical Applications of Lipidic Nanocarrier Systems. Pharmaceutics 2018, 10, 57. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mudalige, T.; Qu, H.; van Haute, D.; Ansar, S.M.; Paredes, A.; Ingle, T. Characterization of Nanomaterials. In Nanomaterials for Food Applications; Elsevier: Amsterdam, The Netherlands, 2019; pp. 313–353. ISBN 9780128141304. [Google Scholar]
- Park, T.J.; Lee, S.-K.; Yoo, S.M.; Yang, S.-M.; Lee, S.Y. Development of reflective biosensor using fabrication of functionalized photonic nanocrystals. J. Nanosci. Nanotechnol. 2011, 11, 632–637. [Google Scholar] [CrossRef]
- Wu, Z.; Hu, X.; Tao, C.; Li, Y.; Liu, J.; Yang, C.; Shen, D.; Li, G. Direct and label-free detection of cholic acid based on molecularly imprinted photonic hydrogels. J. Mater. Chem. 2008, 18, 5452. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z.; Zeng, Q.; Huang, Y.; Gu, H.; He, J.; Liu, Y.; Chen, S.; Sun, H.; Lai, J. Visual test for the presence of the illegal additive ethyl anthranilate by using a photonic crystal test strip. Mikrochim. Acta 2019, 186, 685. [Google Scholar] [CrossRef]
- Gao, W.; Rigout, M.; Owens, H. Self-assembly of silica colloidal crystal thin films with tuneable structural colours over a wide visible spectrum. Appl. Surf. Sci. 2016, 380, 12–15. [Google Scholar] [CrossRef]
- Koay, N.; Burgess, I.B.; Kay, T.M.; Nerger, B.A.; Miles-Rossouw, M.; Shirman, T.; Vu, T.L.; England, G.; Phillips, K.R.; Utech, S.; et al. Hierarchical structural control of visual properties in self-assembled photonic-plasmonic pigments. Opt. Express 2014, 22, 27750–27768. [Google Scholar] [CrossRef]
- Shen, Z.; Shi, L.; You, B.; Wu, L.; Zhao, D. Large-scale fabrication of three-dimensional ordered polymer films with strong structure colors and robust mechanical properties. J. Mater. Chem. 2012, 22, 8069. [Google Scholar] [CrossRef]
- Li, H.; Tang, Q.; Cai, F.; Hu, X.; Lu, H.; Yan, Y.; Hong, W.; Zhao, B. Optimized photonic crystal structure for DSSC. Sol. Energy 2012, 86, 3430–3437. [Google Scholar] [CrossRef]
- Liu, W.; Ma, H.; Walsh, A. Advance in photonic crystal solar cells. Renew. Sustain. Energy Rev. 2019, 116, 109436. [Google Scholar] [CrossRef]
- Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef]
- van Dommelen, R.; Fanzio, P.; Sasso, L. Surface self-assembly of colloidal crystals for micro- and nano-patterning. Adv. Colloid Interface Sci. 2018, 251, 97–114. [Google Scholar] [CrossRef]
- Yeo, S.J.; Choi, G.H.; Yoo, P.J. Multiscale-architectured functional membranes utilizing inverse opal structures. J. Mater. Chem. A 2017, 5, 17111–17134. [Google Scholar] [CrossRef]
- Yablonovitch, E.; Gmitter, T.J.; Leung, K.M. Photonic band structure: The face-centered-cubic case employing nonspherical atoms. Phys. Rev. Lett. 1991, 67, 2295–2298. [Google Scholar] [CrossRef]
- Bumstead, M.; Liang, K.; Hanta, G.; Hui, L.S.; Turak, A. disLocate: Tools to rapidly quantify local intermolecular structure to assess two-dimensional order in self-assembled systems. Sci. Rep. 2018, 8, 1554. [Google Scholar] [CrossRef]
- Gao, W.; Rigout, M.; Owens, H. Facile control of silica nanoparticles using a novel solvent varying method for the fabrication of artificial opal photonic crystals. J. Nanopart. Res. 2016, 18, 387. [Google Scholar] [CrossRef]
- Agarwal, U.; Escobedo, F.A. Mesophase behaviour of polyhedral particles. Nat. Mater. 2011, 10, 230–235. [Google Scholar] [CrossRef] [PubMed]
- Timmermans, J. Plastic crystals: A historical review. J. Phys. Chem. Solids 1961, 18, 1–8. [Google Scholar] [CrossRef]
- Bernard, E.P.; Krauth, W. Two-step melting in two dimensions: First-order liquid-hexatic transition. Phys. Rev. Lett. 2011, 107, 155704. [Google Scholar] [CrossRef]
- Williamson, J.J.; Evans, R.M.L. Measuring local volume fraction, long-wavelength correlations, and fractionation in a phase-separating polydisperse fluid. J. Chem. Phys. 2014, 141, 164901. [Google Scholar] [CrossRef] [PubMed]
- Okabe, A.; Boots, B.; Sugihara, K.; Chiu, S.N.; Kendall, D.G. Spatial Tessellations; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000; ISBN 9780470317013. [Google Scholar]
- van Anders, G.; Ahmed, N.K.; Smith, R.; Engel, M.; Glotzer, S.C. Entropically patchy particles: Engineering valence through shape entropy. ACS Nano 2014, 8, 931–940. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, U.; Escobedo, F.A. Effect of quenched size polydispersity on the ordering transitions of hard polyhedral particles. J. Chem. Phys. 2012, 137, 24905. [Google Scholar] [CrossRef] [PubMed]
- Damasceno, P.F.; Engel, M.; Glotzer, S.C. Crystalline assemblies and densest packings of a family of truncated tetrahedra and the role of directional entropic forces. ACS Nano 2012, 6, 609–614. [Google Scholar] [CrossRef]
- Kirkwood, J.G.; Boggs, E.M. The Radial Distribution Function in Liquids. J. Chem. Phys. 1942, 10, 394–402. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Nelson, D.R.; Ronchetti, M. Bond-orientational order in liquids and glasses. Phys. Rev. B 1983, 28, 784–805. [Google Scholar] [CrossRef]
- Magonov, S.N. Surface Analysis with STM and AFM: Experimental and Theoretical Aspects of Image Analysis; VCH: Weinheim, Germany; New York, NY, USA, 2008; ISBN 9783527615100. [Google Scholar]
- Bharati, M.H.; Liu, J.; MacGregor, J.F. Image texture analysis: Methods and comparisons. Chemom. Intell. Lab. Syst. 2004, 72, 57–71. [Google Scholar] [CrossRef]
- Rankin, D.W.H.; Morrison, C.A.; Mitzel, N.W. Structural Methods in Molecular Inorganic Chemistry; Wiley: Chichester, West Sussex, UK, 2013; ISBN 9781118462881. [Google Scholar]
- Ladd, M.; Palmer, R. Structure Determination by X-ray Crystallography; Springer US: Boston, MA, USA, 2013; ISBN 978-1-4614-3956-1. [Google Scholar]
- Barón, M. Definitions of basic terms relating to low-molar-mass and polymer liquid crystals (IUPAC Recommendations 2001). Pure Appl. Chem. 2001, 73, 845–895. [Google Scholar] [CrossRef]
- Lobmeyer, D.M.; Biswal, S.L. Grain boundary dynamics driven by magnetically induced circulation at the void interface of 2D colloidal crystals. Sci. Adv. 2022, 8, eabn5715. [Google Scholar] [CrossRef]

| Experiment Code | EtOH (mL) | Average Diameter 1 ⌀ (nm) | Hydrodynamic Average Diameter 2 Dh (nm) | PDI 2 |
|---|---|---|---|---|
| SiPs100 | 100 | 150 ± 3.1 | 178.8 ± 0.6 | 0.002 |
| SiPs80 | 80 | 233 ± 2.6 | 242.7 ± 2.2 | 0.020 |
| SiPs60 | 60 | 365 ± 2.4 | 396.3 ± 2.3 | 0.022 |
| SiPs40 | 40 | 490 ± 4.3 | 518.5 ± 4.2 | 0.034 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Estrada Alvarez, S.A.; Guger, I.; Febbraro, J.; Turak, A.; Lin, H.-R.; Salinas, Y.; Brüggemann, O. Synthesis and Spatial Order Characterization of Controlled Silica Particle Sizes Organized as Photonic Crystals Arrays. Materials 2022, 15, 5864. https://doi.org/10.3390/ma15175864
Estrada Alvarez SA, Guger I, Febbraro J, Turak A, Lin H-R, Salinas Y, Brüggemann O. Synthesis and Spatial Order Characterization of Controlled Silica Particle Sizes Organized as Photonic Crystals Arrays. Materials. 2022; 15(17):5864. https://doi.org/10.3390/ma15175864
Chicago/Turabian StyleEstrada Alvarez, Silvia Adriana, Isabella Guger, Jana Febbraro, Ayse Turak, Hong-Ru Lin, Yolanda Salinas, and Oliver Brüggemann. 2022. "Synthesis and Spatial Order Characterization of Controlled Silica Particle Sizes Organized as Photonic Crystals Arrays" Materials 15, no. 17: 5864. https://doi.org/10.3390/ma15175864
APA StyleEstrada Alvarez, S. A., Guger, I., Febbraro, J., Turak, A., Lin, H.-R., Salinas, Y., & Brüggemann, O. (2022). Synthesis and Spatial Order Characterization of Controlled Silica Particle Sizes Organized as Photonic Crystals Arrays. Materials, 15(17), 5864. https://doi.org/10.3390/ma15175864









