Experimental Study and Calculation Methods of Shear Capacity for High-Strength Reinforced Concrete Full-Scale Deep Beams
Abstract
:1. Introduction
2. Experimental Study
2.1. Materials
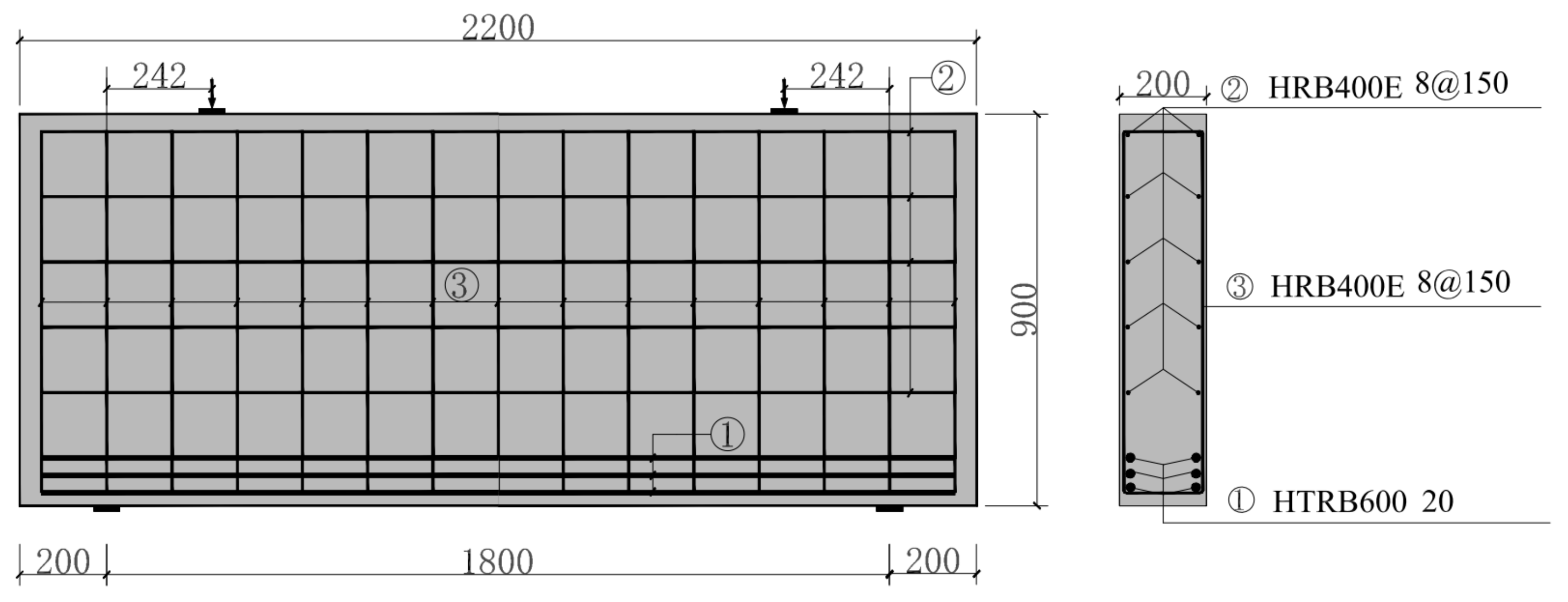
2.2. Specimen Preparation
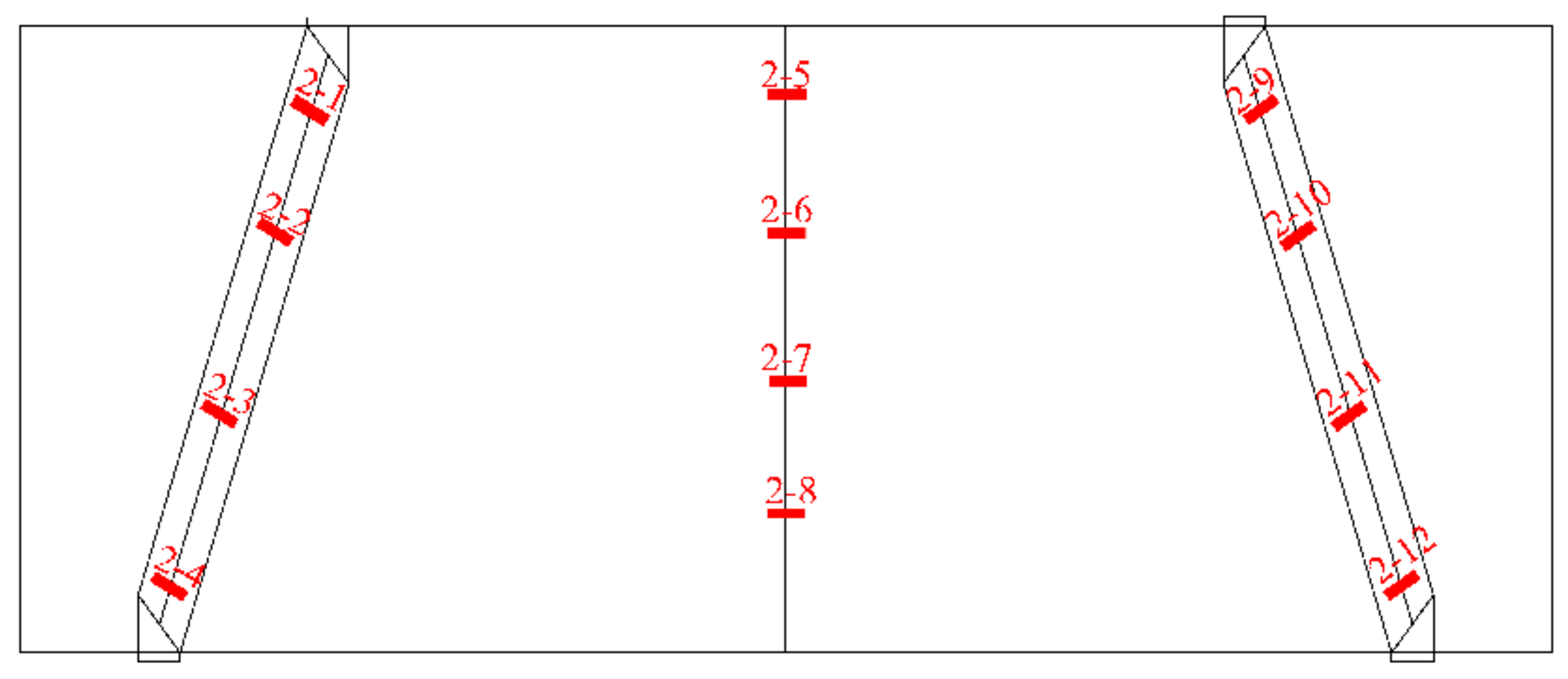
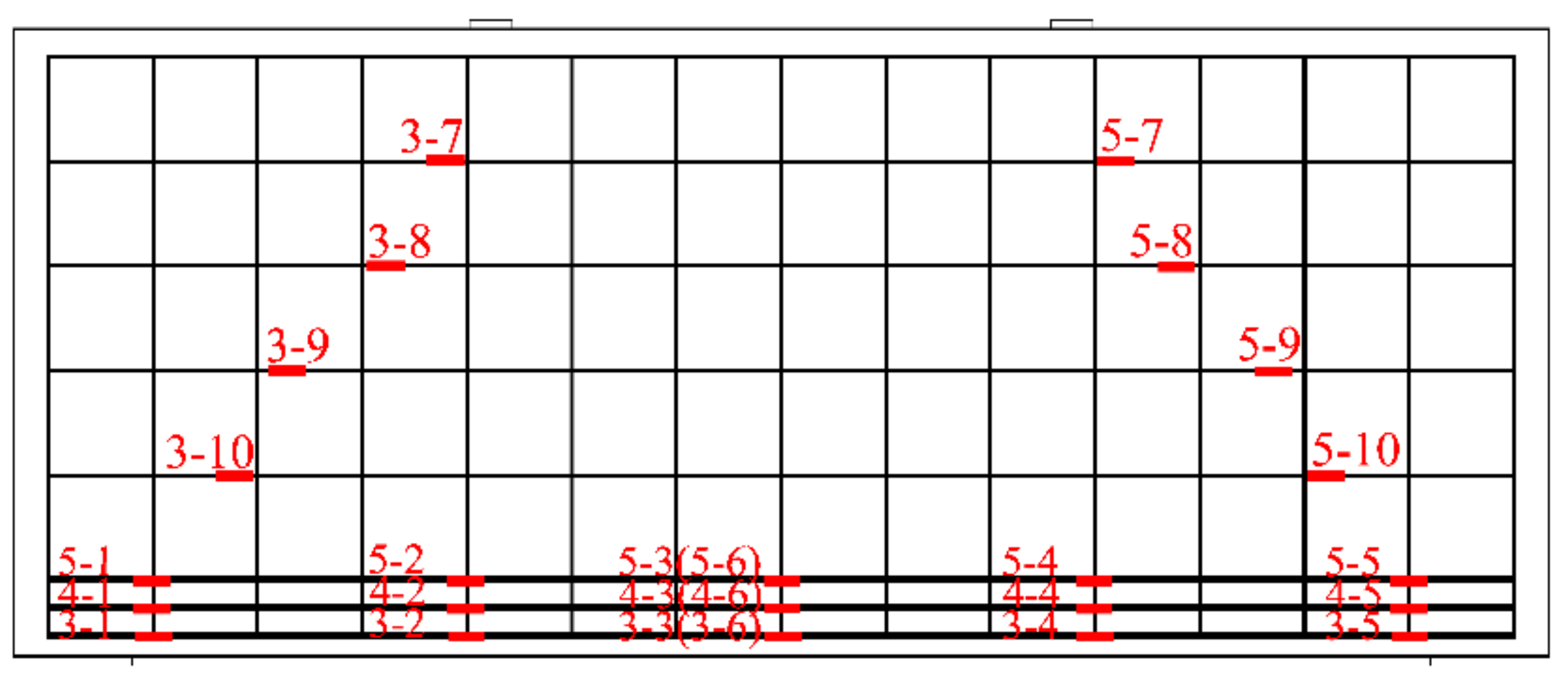
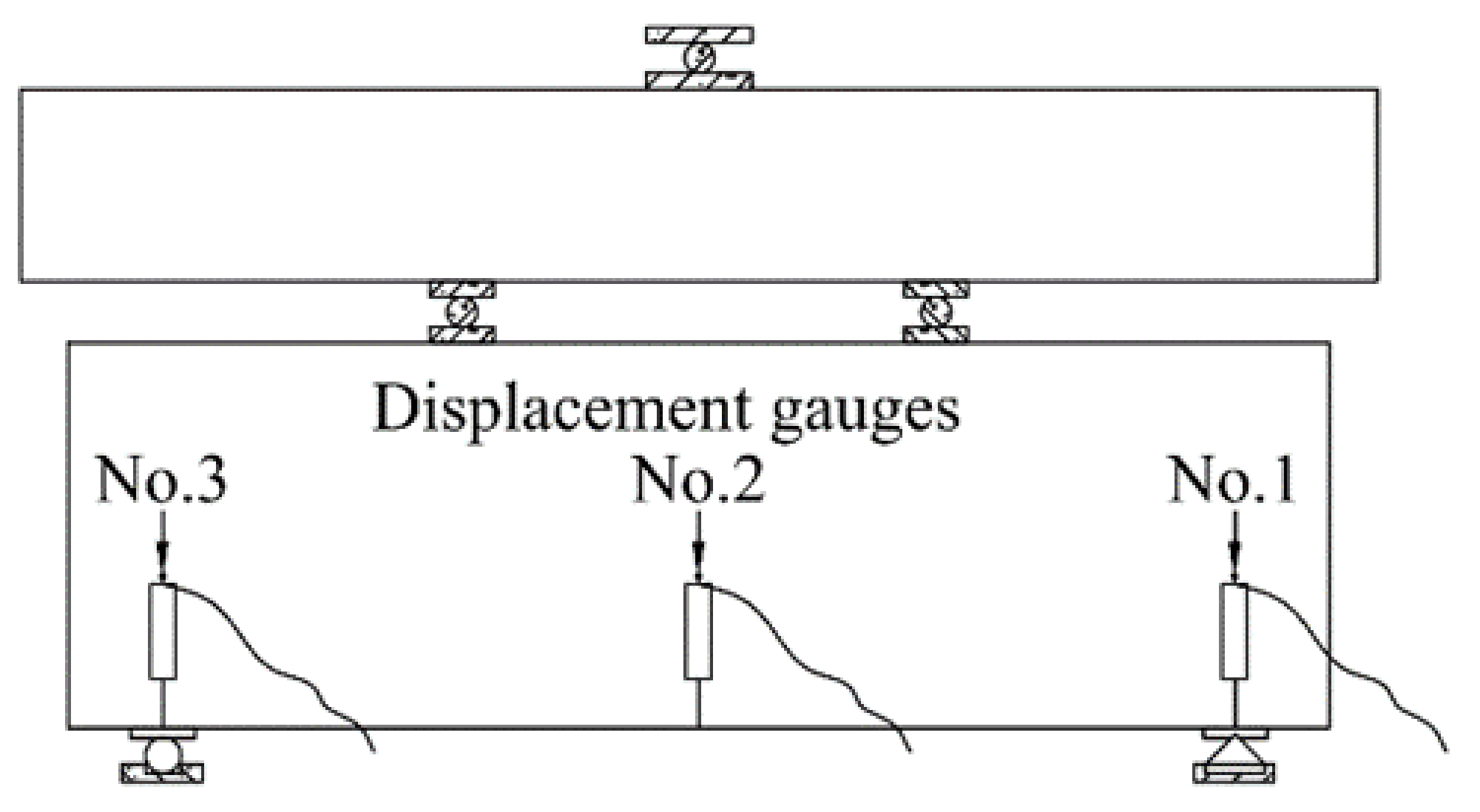
2.3. Test Instrumentation and Procedures
3. Test results and Discussion
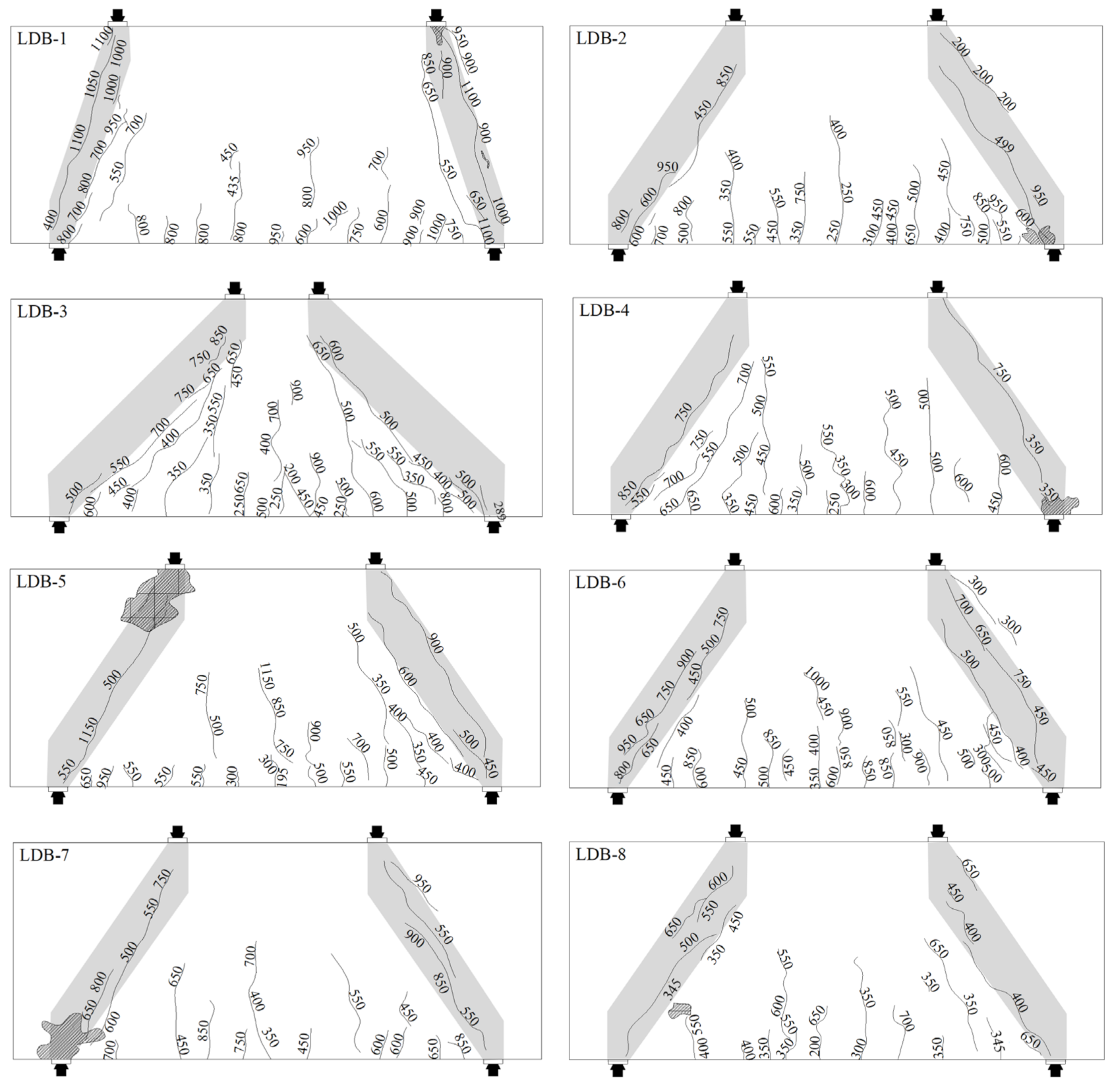
3.1. Crack and Failure Modes
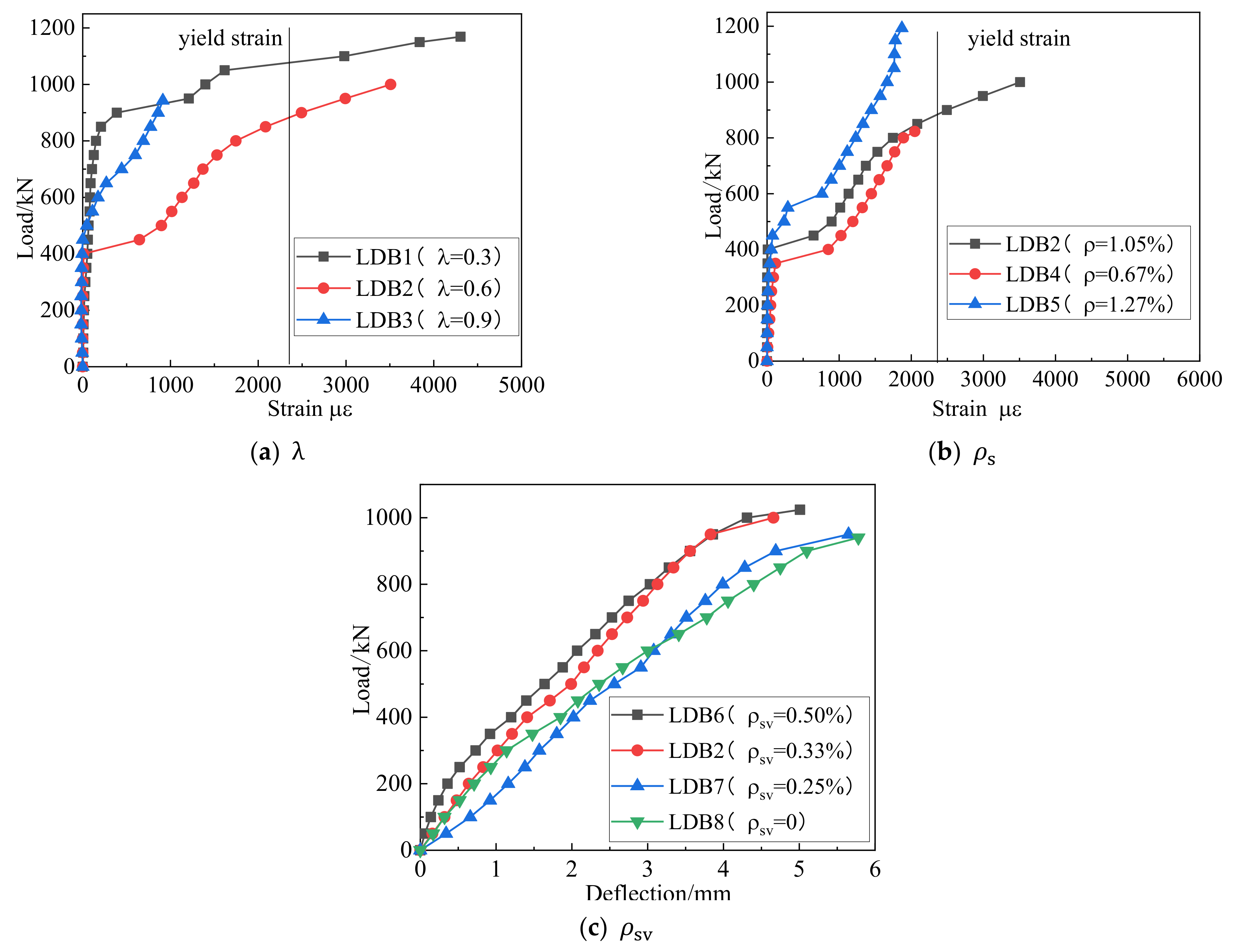
3.2. Load–Deflection Response
3.3. Cracking and Ultimate Shear Strengths
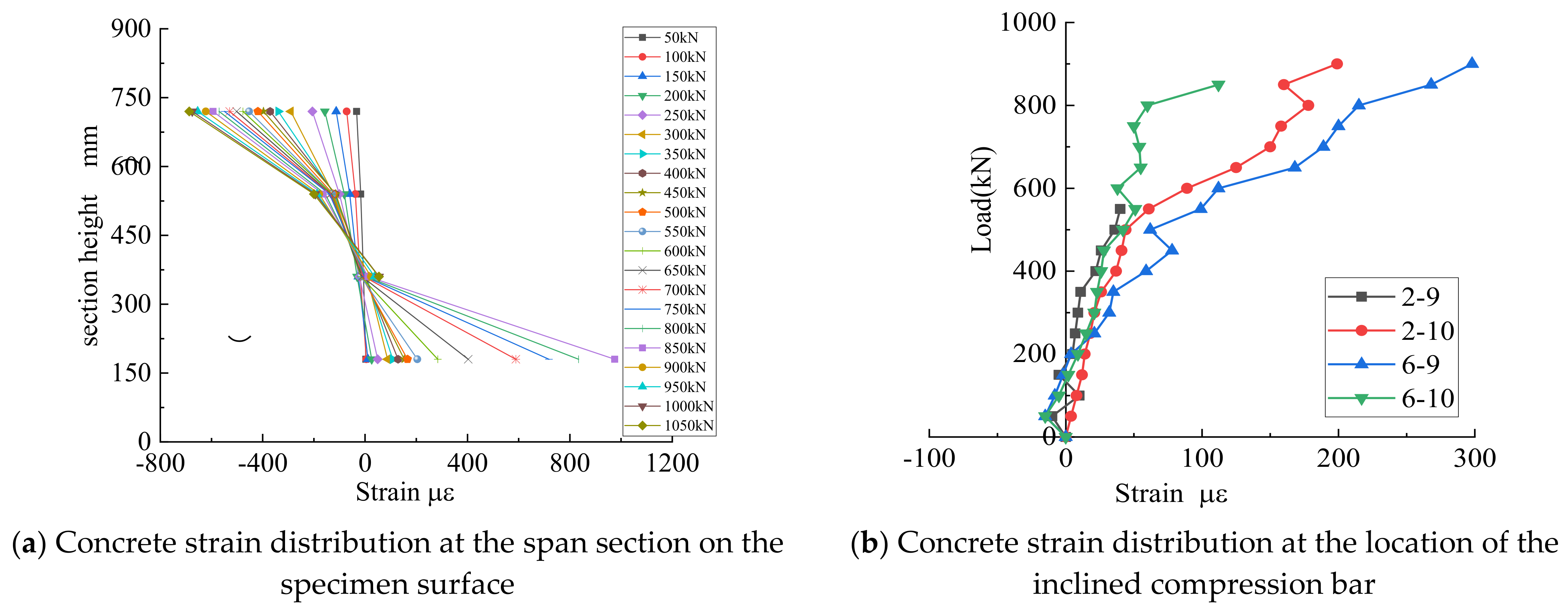
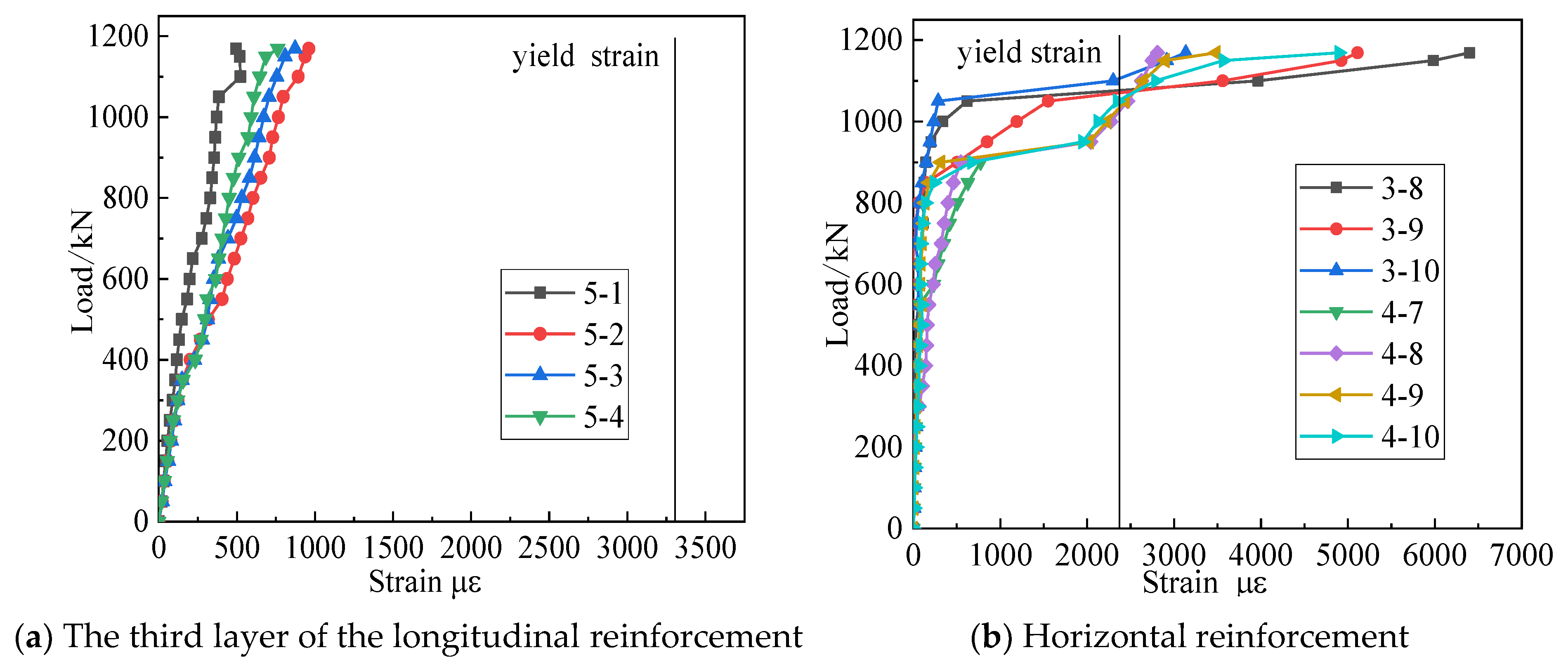
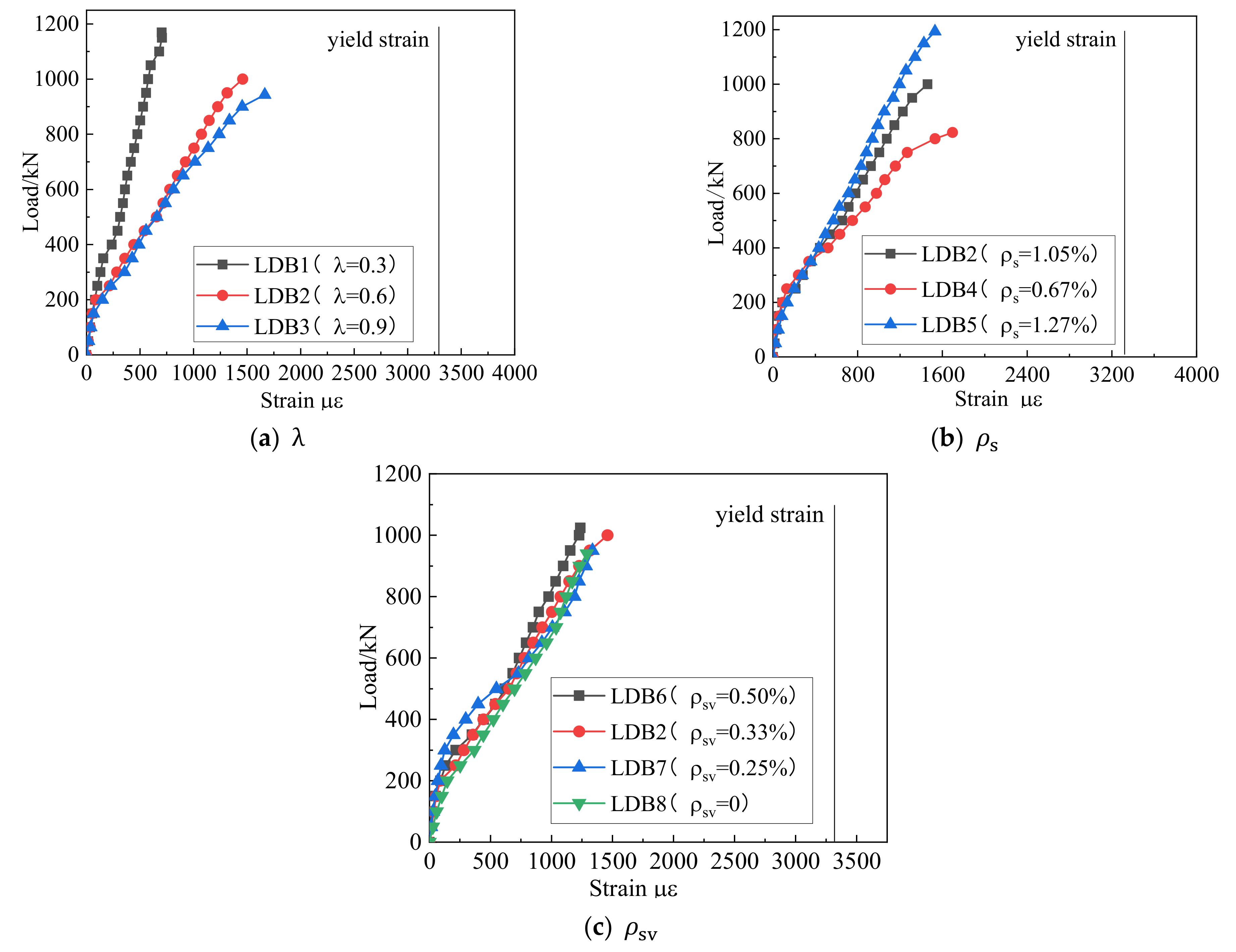
3.4. Reinforcement Strain Response
4. Comparisons with STMs
4.1. American ACI 318-19 Code
4.2. Canadian CSAA23.3-19 Code
4.3. European EC Code
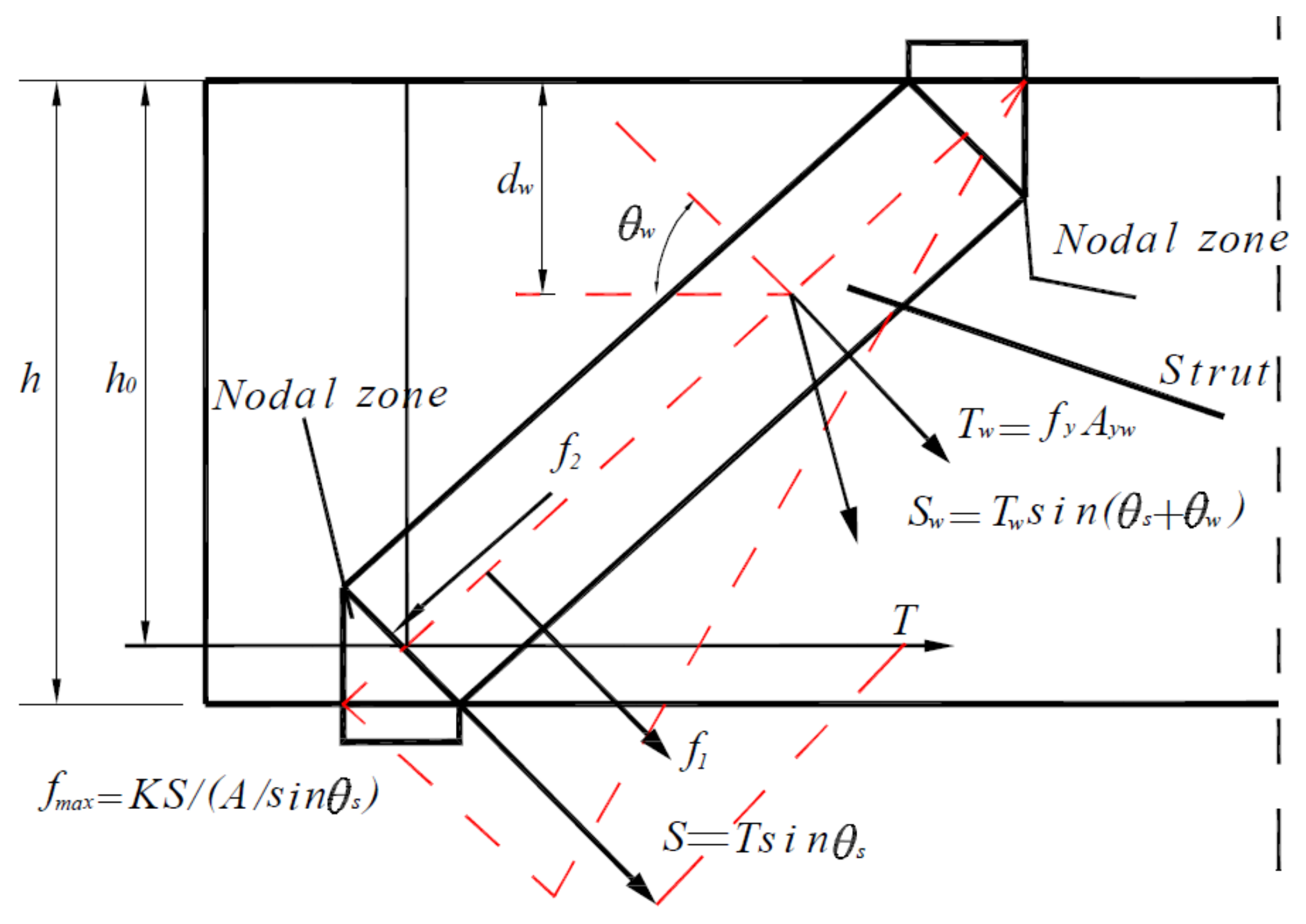
4.4. The Tan–Tan Model
4.5. The Tan–Cheng Model
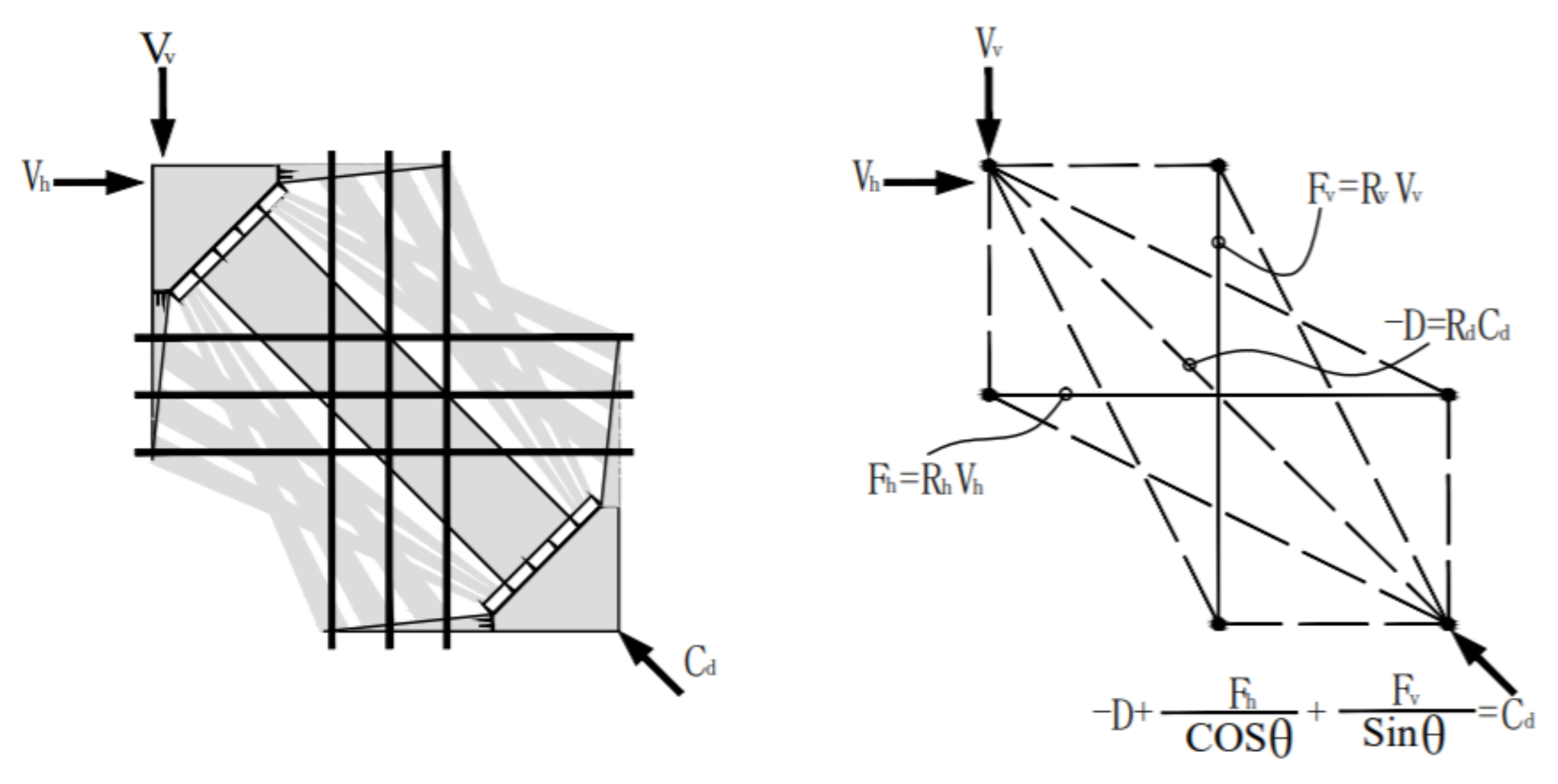
4.6. SSTM
4.7. SSSTM
4.8. Comparison of Shear Design Equations
5. Conclusions
- The failure mode of the deep beam is the crushing of the inclined compression bar. At the beginning, the bending crack appears at the mid-span, and the load is about 16–37% of the ultimate load. Subsequently, inclined cracks appear between the bearing and the loading point, and the load is about 29–52% of the ultimate load. The failure of deep beams is caused by the penetration of oblique cracks, showing the nature of brittle failure.
- The shear span-depth ratio is the most important parameter affecting the shear capacity of high-strength reinforced concrete deep beams. With the increase of shear span ratio, the shear capacity of deep beams decreases significantly. When the shear span ratio increases from 0.3 to 0.9, the shear bearing capacity decreases by 19.3%. The number of longitudinal bars at the bottom also significantly affects the shear capacity of deep beams. When the ratio of longitudinal bars increases from 0.67% to 1.05%, the shear capacity increases by 14.6%. In addition, the presence of shear reinforcement is critical for controlling crack propagation and providing ductility for deep beams.
- The effective coefficient is determined by the compressive strength of concrete, but it is also affected by the shear span depth ratio. ACI 318-19, EC2 and CSA codes ignore the influence of these two parameters when estimating the effective concrete strength of the inclined compression bar, thus leading to non-conservative prediction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| shear span-to-depth ratio, dimensionless | tensile strain of the longitudinal reinforcement, dimensionless | ||
| longitudinal reinforcement ratio, dimensionless | minimum value of the angle between the compression strut and the node | ||
| stirrup reinforcement ratio, dimensionless | height of the bottom nodal zone, mm | ||
| cube compressive strength of concretet, MPa | height of the top nodal zone, mm | ||
| prism compressive strength of concretet, MPa | ultimate load of concrete when damaged along the diagonal compression strut, kN | ||
| tensile strength of concretet, MPa | |||
| elastic modulus of concrete, MPa | resistance of the diagonal compression strut to splitting damage, kN | ||
| diameters of steel reinforcement, mm | compressive strength of the concretet, MPa | ||
| specified yield strength for reinforcementt, MPa | yield strength of the webt, MPa | ||
| ultimate strength for reinforcementt, MPa | yield strength of the longitudinal reinforcement | ||
| modulus of elasticity of reinforcement, MPa | |||
| cracking load of the normal section, kN | |||
| diagonal cracking load, kN | |||
| ultimate load, kN | |||
| shear bearing force of the deep beam, kN | depth from the intersection of the leftline of the web and the diagonal compression strut to the top of the beam, mm | ||
| minimum angle between the concrete diagonal strut and the steel tie connected to it, and the American code stipulates it should not be less than 25° | diagonal compression force, kN | ||
| normal shear force of the concrete strut | vertical shear force shear force, kN | ||
| nominal compressive strength of the concrete strut, MPa | horizontal shear force shear force, kN | ||
| strength reduction coefficient after cracking of the strut, dimensionless | tension force in the vertical ties, kN | ||
| strength coefficient by the influence of concrete confinement on the effective compressive strength of a strut or node, dimensionless | tension force in the horizontal ties, kN | ||
| maximum compressive stress | |||
| width of the specimen section, mm | average principal stress of concrete in the d-direction | ||
| width of the diagonal strut, mm | softening coefficient, dimensionless | ||
| height of the bottom nodal, mm | average principal stresses in the d-direction | ||
| top nodal zone, mm | average principal stresses in the r-direction | ||
| width of the loading steel plate, mm | averaged normal strains in the h-direction | ||
| averaged normal strains in the v-direction | |||
| horizontal tie indexes, dimensionless | horizontal tie index with sufficient horizontal reinforcement, dimensionless | ||
| vertical tie indexes, dimensionless | vertical tie index with sufficient vertical reinforcement, dimensionless | ||
| balanced amount of the horizontal tie force, kN | balance amount of the vertical reinforcement force, kN |
References
- American Concrete Institute–American Society of Civil Engineers (ACI–ASCE) Committee 445. Recent approaches to shear design of structural concrete. J. Struct. Eng. 1998, 119, 1375–1417. [Google Scholar]
- ACI. ACI 318-19 & ACI 318R-19: Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]
- Kani, G.N.J. How safe our large reinforced concrete beams. ACI Struct. J. 1967, 64, 128–141. [Google Scholar]
- Rogowsky, D.M.; MacGregor, J.G.; Ong, S. Tests of Reinforced Concrete Deep Beams. ACI Struct. J. 1984, 83, 614–623. [Google Scholar]
- Tan, K.H.; Kong, F.K.; Teng, S.; Guan, L. High-strength concrete deep beams with effective span and shear span variations. ACI Struct. J. 1995, 92, 395–405. [Google Scholar]
- Foster, S.J.; Gilbert, R.I. Experimental Studies on High-Strength Concrete Deep Beams. ACI Struct. J. 1998, 95, 382–390. [Google Scholar]
- Oh, J.; Shin, S. Shear Strength of Reinforced High-Strength Concrete Deep Beams. ACI Struct. J. 2001, 98, 164–173. [Google Scholar]
- Lu, W.; Lin, I.; Yu, H. Shear Strength of Reinforced Concrete Deep Beams. ACI Struct. J. 2013, 110, 671–680. [Google Scholar]
- Shuraim, A.B.; El-Sayed, A.K. Experimental verification of strut and tie model for HSC deep beams without shear reinforcement. Eng Struct. 2016, 117, 71–85. [Google Scholar] [CrossRef]
- Demir, A.; Caglar, N.; Ozturk, H. Parameters affecting diagonal cracking behavior of reinforced concrete deep beams. Eng Struct. 2019, 184, 217–231. [Google Scholar] [CrossRef]
- Cook, W.D.; Mitchell, D. Studies of disturbed regions near discontinuities in reinforced concrete members. ACI Struct. 1988, 85, 206–216. [Google Scholar]
- Schlaich, J.; Schäfer, K. Towards a Consistent Design of Structural Concrete. PCI J. 1987, 32, 74–150. [Google Scholar] [CrossRef]
- MacGregor, J.G.; Wight, J.K. Prentice Hall. In Reinforced Concrete: Mechanics and Design, 7th ed; Pearson Education South Asia: Singapore, 2006; Volume 7, pp. 154–187. [Google Scholar]
- Zhang, J.H.; Li, S.S. Experimental study on shear capacity of high-strength reinforced concrete deep beams with small shear span-depth ratio. Materials 2020, 13, 56–75. [Google Scholar]
- Chen, H.; Yi, W.J.; Hwang, H.J. Cracking strut-and-tie model for shear strength evaluation of reinforced concrete deep beams. Eng. Struct. 2018, 163, 396–408. [Google Scholar] [CrossRef]
- Wu, T.; Wei, H. Shear behavior of large-scale deep beams with lightweight-aggregate concrete. ACI Struct. J. 2020, 117, 75–89. [Google Scholar] [CrossRef]
- Lu, W.Y.; Zhu, J.X. Tests of high-strength concrete deep beams. Mag. Concr. Res. 2019, 4, 184–194. [Google Scholar] [CrossRef]
- Chen, H.; Yi, W.J. Shear strength of reinforced concrete simple and continuous deep beams. ACI Struct. 2019, 116, 31–40. [Google Scholar] [CrossRef]
- Ismail, K.S.; Guadagnini, M.; Pilakoutas, K. Shear Behavior of Reinforced Concrete Deep Beams. Struct. J. 2017, 114, 87–99. [Google Scholar] [CrossRef]
- Quintero, F.C.G.; Parra, M.G. Strength of struts in deep concrete members designed using strut-and-tie method. ACI Struct. J. 2006, 103, 577–586. [Google Scholar]
- Park, J.W.; Kuchma, D. Strut-and-tie model analysis for strength prediction of deep beams. ACI Struct. J. 2007, 104, 657–666. [Google Scholar]
- Varghese, P.C.; Krishnamoorthy, C.S. Strength and behavior of deep reinforced concrete beams. Indian Concr. J. 1966, 40, 104–108. [Google Scholar]
- Watstein, D.; Collins, M.P. Diagonal compression field theory-a rational model for structural concrete in pure shear torsion. ACI Struct. J. 1958, 55, 717–728. [Google Scholar]
- Liu, L.Q.; Wang, J.J.; Han, J.Y.; Zhang, G.X.; Wu, X.L. Experimental study on static performance of reinforced concrete simply-supported deep beams and analysis of compression rod model. Build. Struct. 2013, 34, 137–141. [Google Scholar]
- Mua, S.T.; Hsu, T.T.C. Shear strength predication for deep beams with web reinforcement. ACI Struct. J. 1987, 84, 318–329. [Google Scholar]
- Tang, X.R.; Sun, H.M. Experimental research and design suggestion on static behavior of spatial steel frame concrete simply supported deep beam. Build. Struct. 2010, 31, 108–116. [Google Scholar]
- Vecchio, F.J.; Collins, M.P. The modified compression-field theory for reinforced concrete elements subjected to shear. ACI Struct. J. 1986, 83, 219–231. [Google Scholar]
- ACI Committee 318: Building Code Requirement for Structure Concrete (ACI 318–19) and Commentary; American Concrete Institute: Famington Hills, MI, USA, 2019.
- The European Standard EN 1992-1-1:2004; Eurocode 2, Design of Concrete Structures. British Standards Institution: Brussels, Belgium, 2004.
- CSA A23.3—19; Design of Concrete Structures. Canadian Standards Association: Mississauga, ON, Canada, 2019.
- Tang, C.Y.; Tan, K.H. Interactive mechanical model for shear strength of deep beams. J. Struct. Eng. 2004, 130, 1534–1544. [Google Scholar] [CrossRef]
- Tan, K.H.; Cheng, G.H. Size effect on shear strength of deep beams: Investigating with strut-and-tie model. J. Struct. Eng. 2006, 132, 673–685. [Google Scholar] [CrossRef]
- Hwang, S.J.; Lu, W.Y. Shear strength predication for deep beams. ACI Struct. J. 2000, 97, 367–376. [Google Scholar]
- GB50010-2010; Design Code for Concrete Structures. China Construction Industry Press: Beijing, China, 2010.
- GB50152-92; Standard for Test Method of Concrete Structures. China Architecture & Building Press: Beijing, China, 1992.
- GB/T50081-2002; Standard for Test Methods of Mechanical Properties of Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2002.
- GB/T50152-2012; Standard for Test Method of Concrete Structures. China Architecture & Building Press: Beijing, China, 2012.
- Tan, K.H.; Cheng, G.H.; Cheng, H.K. Size effect in shear strength of large beams-behavior and finite element modeling. Mag. Concr. Res. 2005, 57, 497–509. [Google Scholar] [CrossRef]
- Hwang, S.J.; Lee, H.J. Strength prediction for discontinuity regions failing in diagonal compressions by softened strut-and-tie model. J. Struct. Eng. 2002, 128, 1519–1526. [Google Scholar] [CrossRef]
- Yang, K.H.; Chung, H.S. Influence of shear reinforcement on reinforce concrete continuous deep beams. J. Struct. Eng. 2007, 104, 420–429. [Google Scholar]
- Ma, K.Z.; Qi, T.; Liu, H.J.; Wang, H.B. Shear behavior of hybrid fiber reinforced concrete deep beams. Materials 2018, 11, 2023. [Google Scholar] [CrossRef] [PubMed] [Green Version]








| 59.82 | 42.90 | 3.74 | 34.64 |
| Component Number | ||||||
|---|---|---|---|---|---|---|
| LDB1 | ||||||
| LDB2 | ||||||
| LDB3 | ||||||
| LDB4 | ||||||
| LDB5 | ||||||
| LDB6 | ||||||
| LDB7 | ||||||
| LDB8 |
| Specimen | Failure Model | Failure Form | ||||||
|---|---|---|---|---|---|---|---|---|
| LDB1 | 435 | 550 | 1169 | 37.21% | 47.05% | 3.25 | Diagonal- compression | Crushing- strut |
| LDB2 | 250 | 449 | 1000 | 25.00% | 44.90% | 4.66 | Diagonal- compression | Crushing- strut |
| LDB3 | 200 | 289 | 943 | 21.21% | 30.65% | 6.59 | Diagonal- compression | Crushing- strut |
| LDB4 | 250 | 350 | 823 | 30.38% | 42.53% | 4.44 | Diagonal- compression | Crushing- strut |
| LDB5 | 195 | 350 | 1193.5 | 16.34% | 29.33% | 4.60 | Diagonal- compression | Crushing- strut |
| LDB6 | 350 | 400 | 1024 | 34.18% | 39.06% | 5.01 | Diagonal- compression | Crushing- strut |
| LDB7 | 350 | 500 | 950 | 36.84% | 52.63% | 5.65 | Diagonal- compression | Crushing- strut |
| LDB8 | 200 | 345 | 940 | 27.59% | 47.59% | 5.78 | Diagonal- compression | Diagonal- splitting |
| Specimen | Test Value | |||||||
|---|---|---|---|---|---|---|---|---|
| Vn (kN) | ACI | EC2 | CSA | Tan–Tang | Tan–Cheng | SSTM | SSSTM | |
| LDB1 | 1169 | 1.666 | 2.136 | 1.563 | 1.322 | 1.36 | 0.89 | 0.93 |
| LDB2 | 1000 | 1.295 | 1.661 | 1.489 | 1.246 | 1.243 | 0.92 | 0.98 |
| LDB3 | 943 | 1.303 | 1.671 | 1.958 | 1.377 | 1.342 | 1.01 | 1.09 |
| LDB4 | 823 | 1.08 | 1.385 | 1.239 | 1.156 | 1.112 | 0.78 | 0.93 |
| LDB5 | 1193.5 | 1.535 | 1.969 | 1.767 | 1.425 | 1.448 | 0.99 | 1.10 |
| LDB6 | 1024 | 1.326 | 1.701 | 1.525 | 1.275 | 1.273 | 0.96 | 1.00 |
| LDB7 | 950 | 1.23 | 1.578 | 1.414 | 1.183 | 1.244 | 0.88 | 0.93 |
| LDB8 | 940 | 1.217 | 1.561 | 1.4 | 1.175 | 1.35 | 0.79 | 0.94 |
| Mean | 1.331 | 1.708 | 1.544 | 1.27 | 1.297 | 0.90 | 0.99 | |
| Variance | 0.03 | 0.05 | 0.044 | 0.009 | 0.009 | 0.006 | 0.004 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Wu, Z.; Zhang, J.; Xie, W. Experimental Study and Calculation Methods of Shear Capacity for High-Strength Reinforced Concrete Full-Scale Deep Beams. Materials 2022, 15, 6017. https://doi.org/10.3390/ma15176017
Li S, Wu Z, Zhang J, Xie W. Experimental Study and Calculation Methods of Shear Capacity for High-Strength Reinforced Concrete Full-Scale Deep Beams. Materials. 2022; 15(17):6017. https://doi.org/10.3390/ma15176017
Chicago/Turabian StyleLi, Shushan, Ziwen Wu, Junhong Zhang, and Wei Xie. 2022. "Experimental Study and Calculation Methods of Shear Capacity for High-Strength Reinforced Concrete Full-Scale Deep Beams" Materials 15, no. 17: 6017. https://doi.org/10.3390/ma15176017
APA StyleLi, S., Wu, Z., Zhang, J., & Xie, W. (2022). Experimental Study and Calculation Methods of Shear Capacity for High-Strength Reinforced Concrete Full-Scale Deep Beams. Materials, 15(17), 6017. https://doi.org/10.3390/ma15176017








