Thermo-Mechanical Behavior of Aluminum Matrix Nano-Composite Automobile Disc Brake Rotor Using Finite Element Method
Abstract
:1. Introduction
2. Methodology and Materials
2.1. Materials for Disc Brake Rotor
- The brakes must be strong enough to stop the car in an emergency within a minimum distance.
- During braking, the driver must maintain good vehicle control to prevent skidding.
- The brakes must have improved anti-fade properties, meaning their efficiency should not deteriorate.
- The brakes must have the maximum thermal resistance.
2.2. Matrix Material for Disc Brake Rotor
2.3. Reinforcement Material for Disc Brake Rotor
3. Results and Discussion
3.1. Finite Element Modeling of Disc Brake
3.2. Theoretical Approaches and Calculations of Disc Brake Rotor
- All kinetic energy at disc brake rotor surface is converted into heat energy.
- Single stop braking scenario where the vehicle is taken.
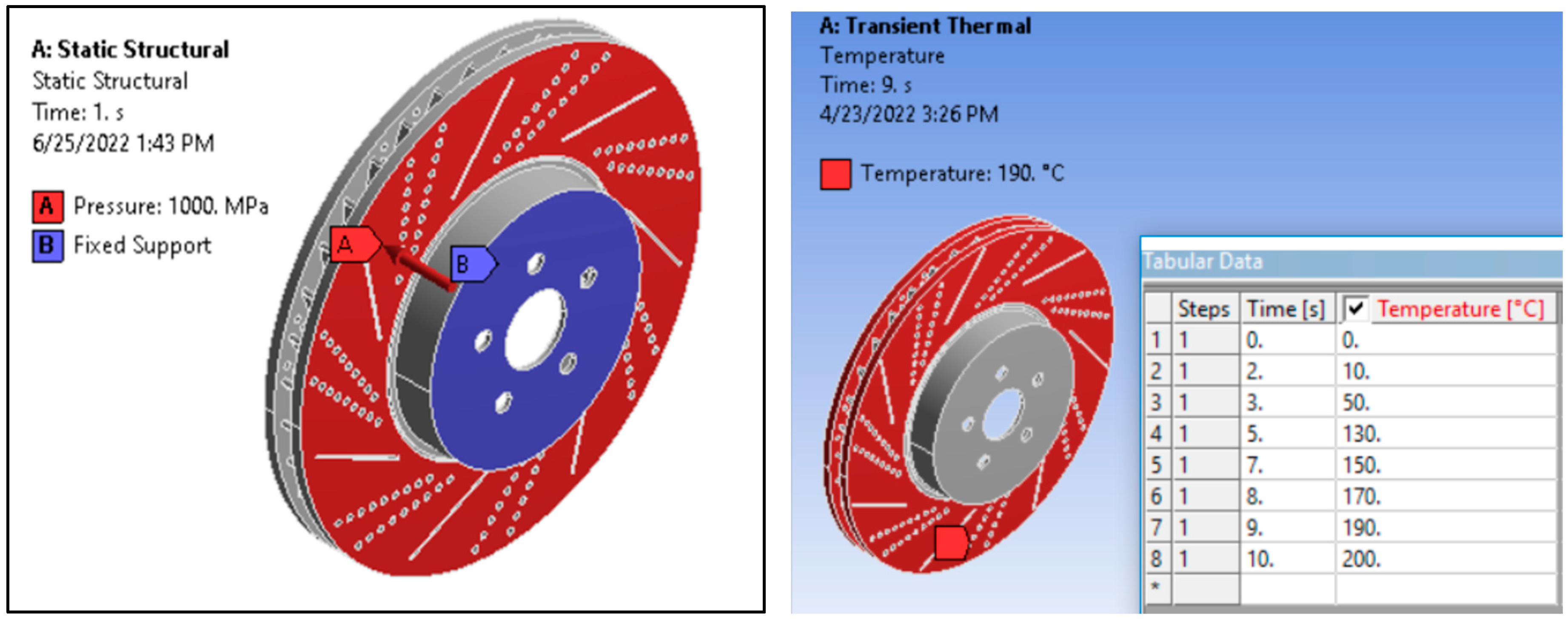
- Maximum value of pressure developed between disc brake rotor and pad is 1 MPa.
- The disc material is considered homogeneous and isotropic so that Young’s modulus, Poisson’s ratio, and the thermal expansion coefficient remain constant.
Braking Energy
- m—mass of vehicle, kg
- v1—velocity at the beginning of braking, m/s
- v2—velocity at the end of braking, m/s
- I—mass moment of inertia of rotor, Kg.m2
- ω1—angular velocity of rotor at the beginning of braking, rad/s
- ω2—angular velocity of rotor at the end of braking, rad/s
- KE—initial kinetic energy of the vehicle.
- m—mass of the vehicle
- I—polar inertial moment of rotating parts.
3.3. Boundary Conditions
3.4. Static Structural Result
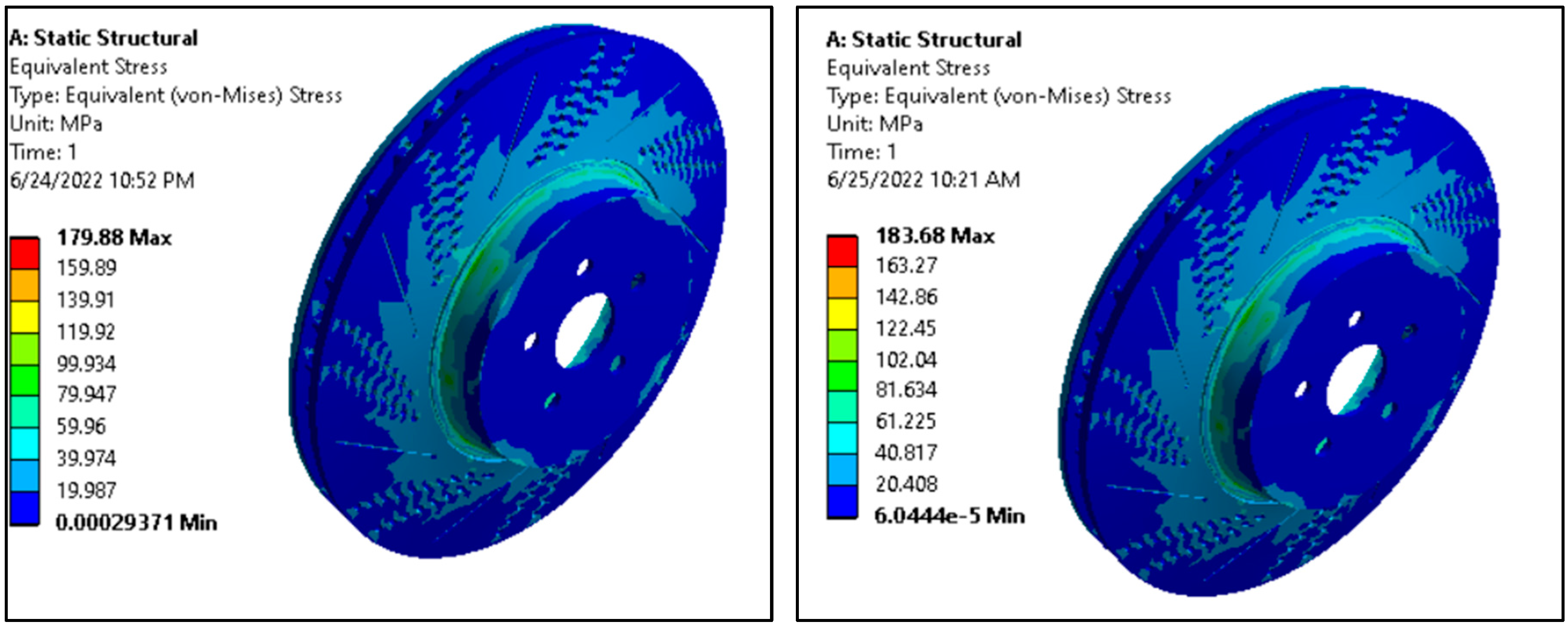
3.4.1. Equivalent (Von Mises) Stress
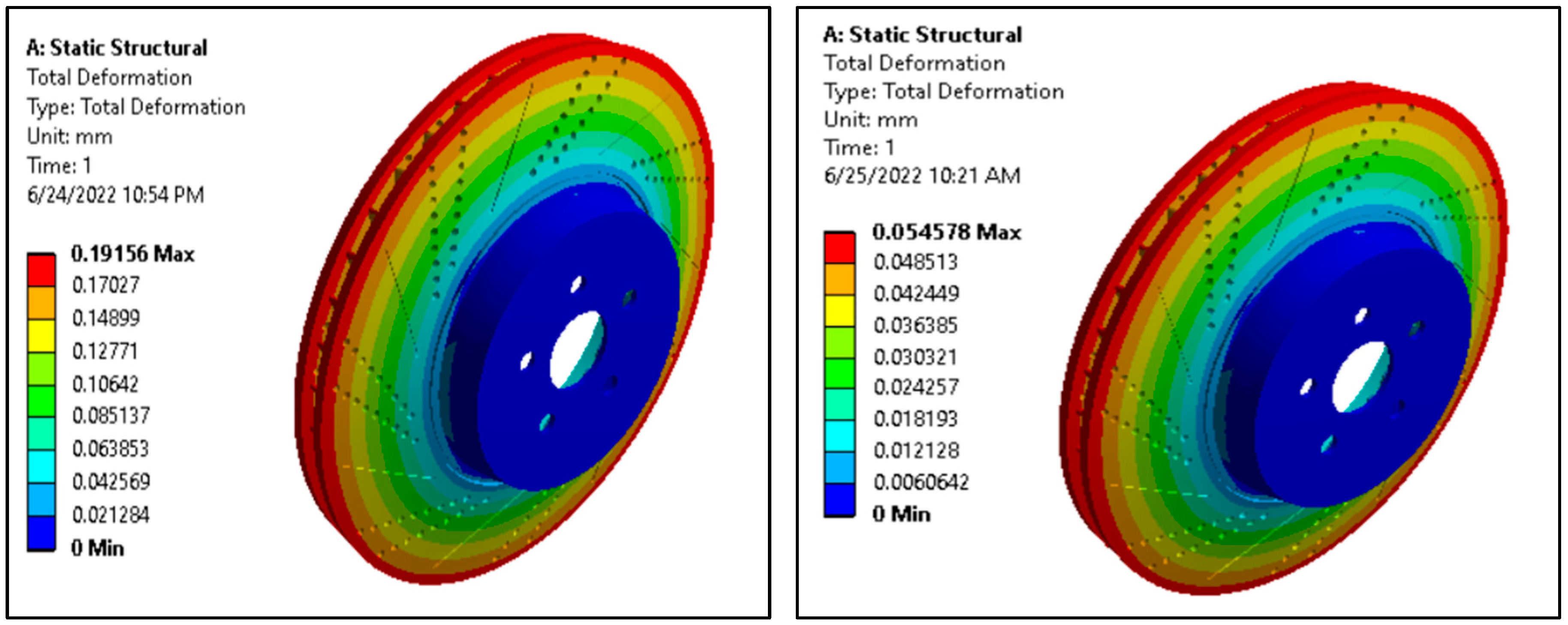
3.4.2. Total Deformation
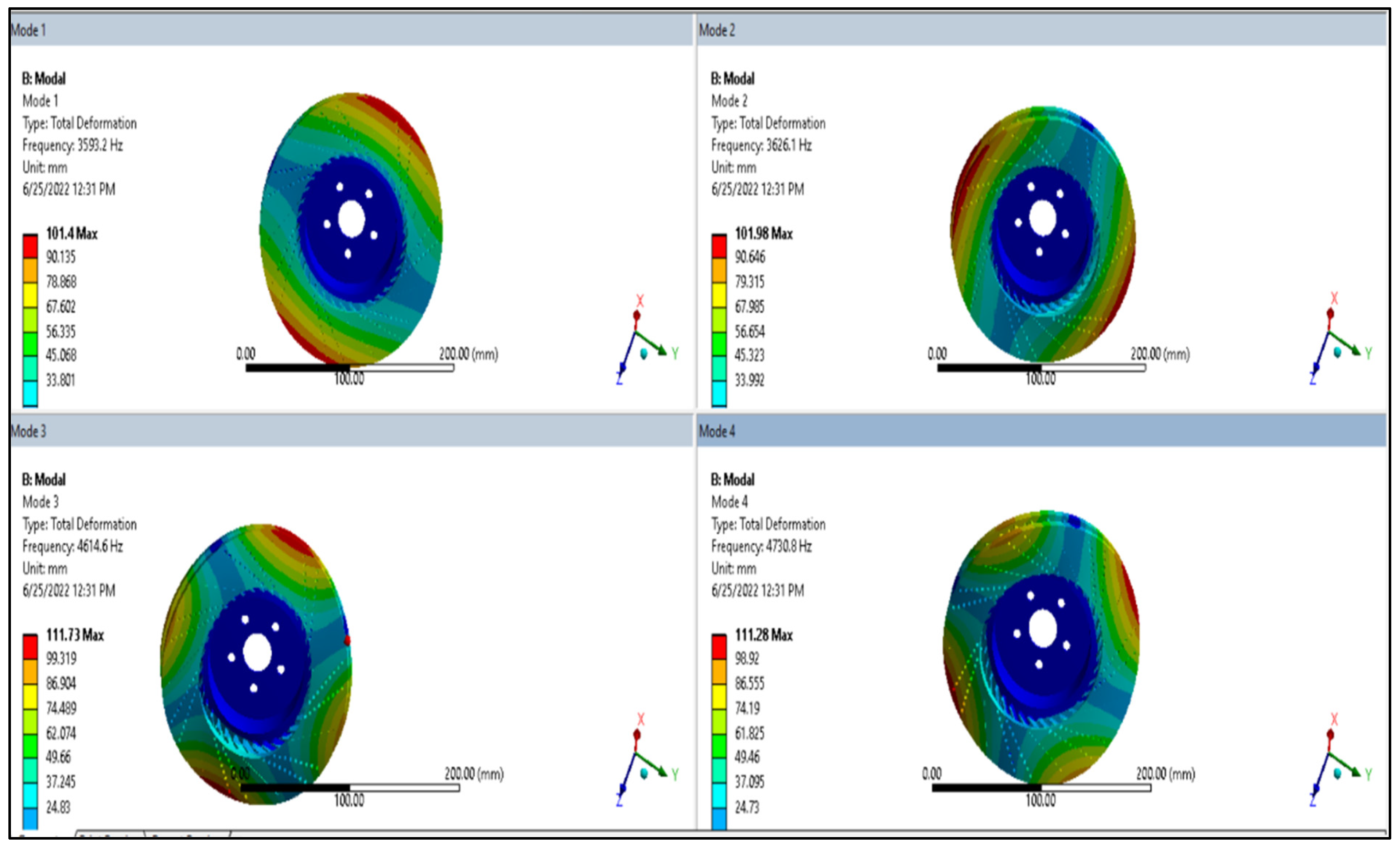
3.5. Dynamic/Modal Analysis of Brake Disc
3.5.1. Mode Shape
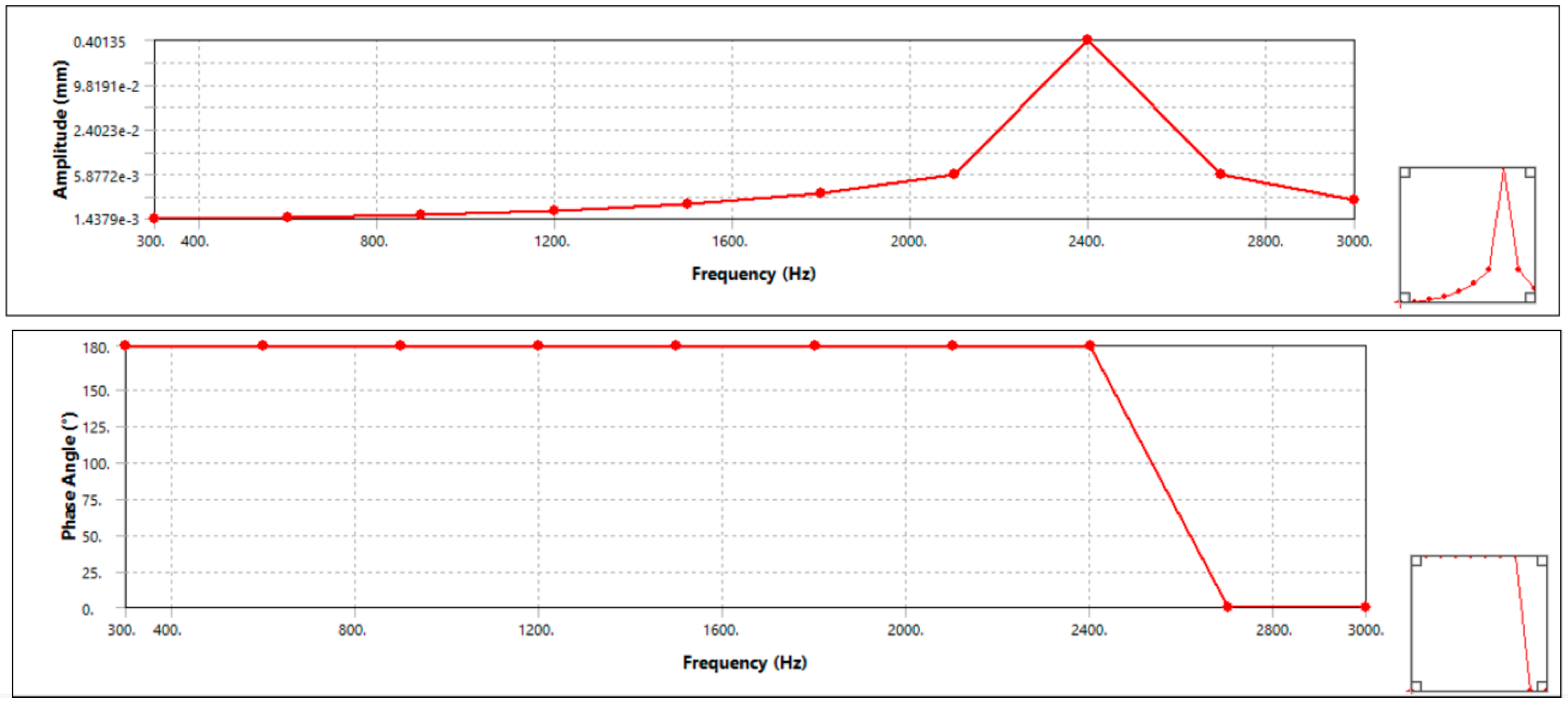
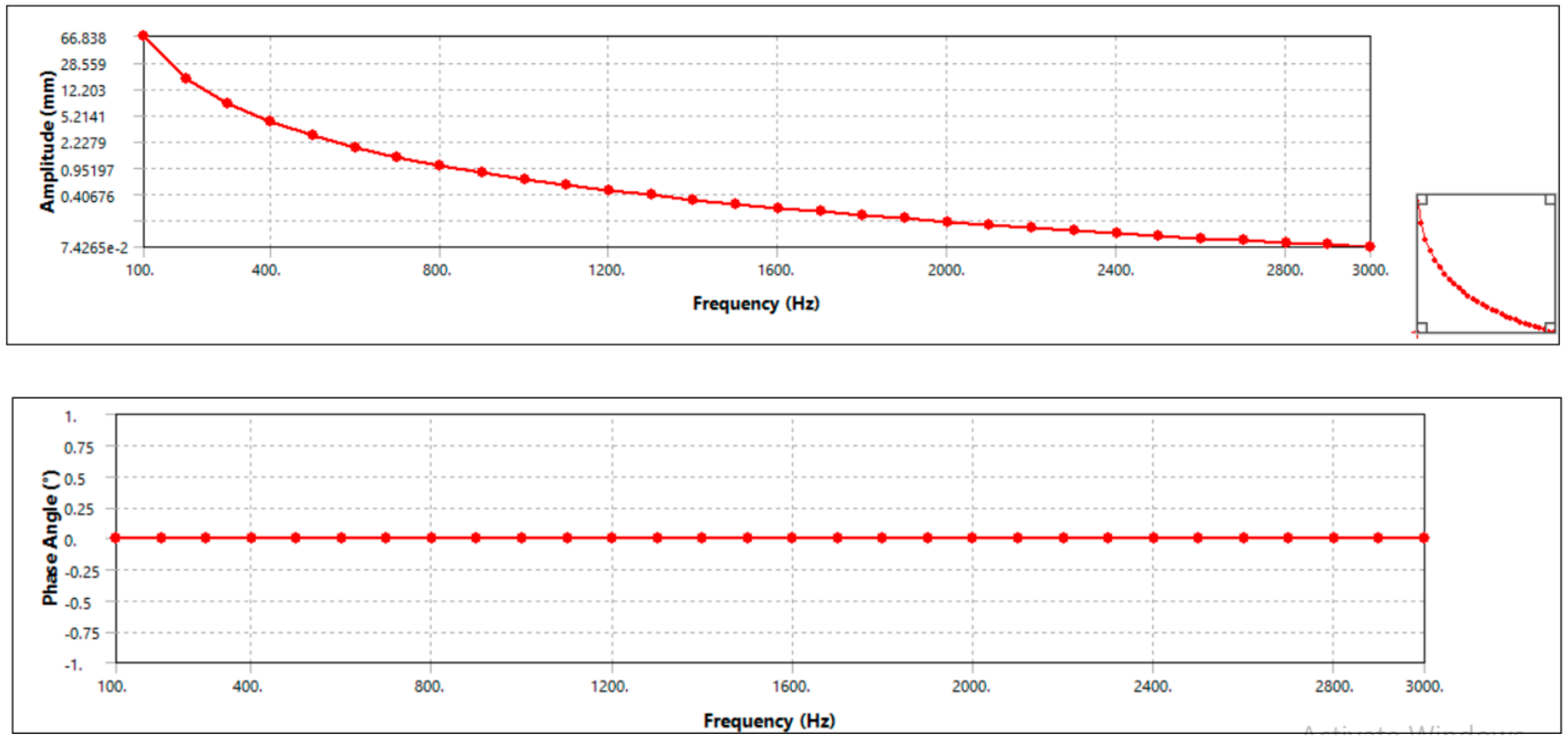
3.5.2. Harmonic Response
3.6. Transient Thermal Analysis
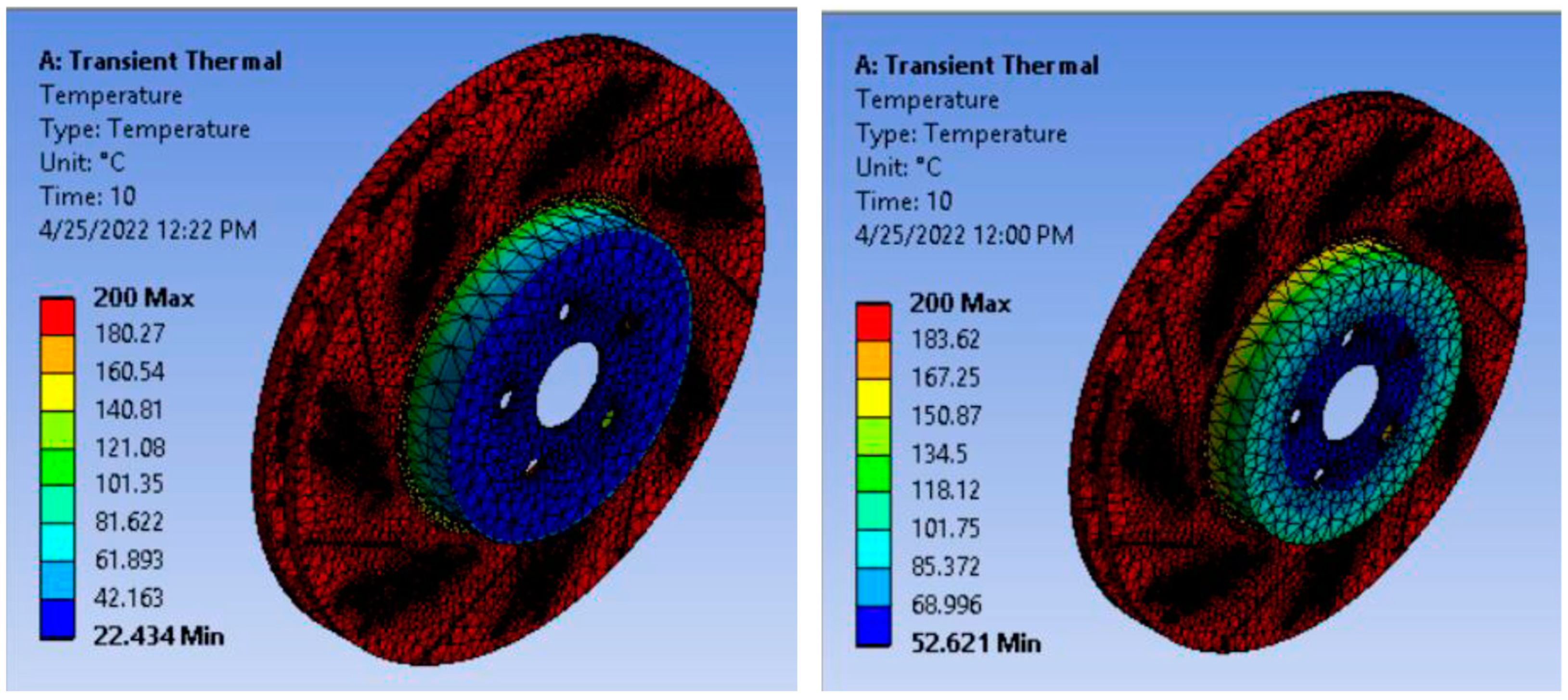
3.6.1. Temperature Distribution
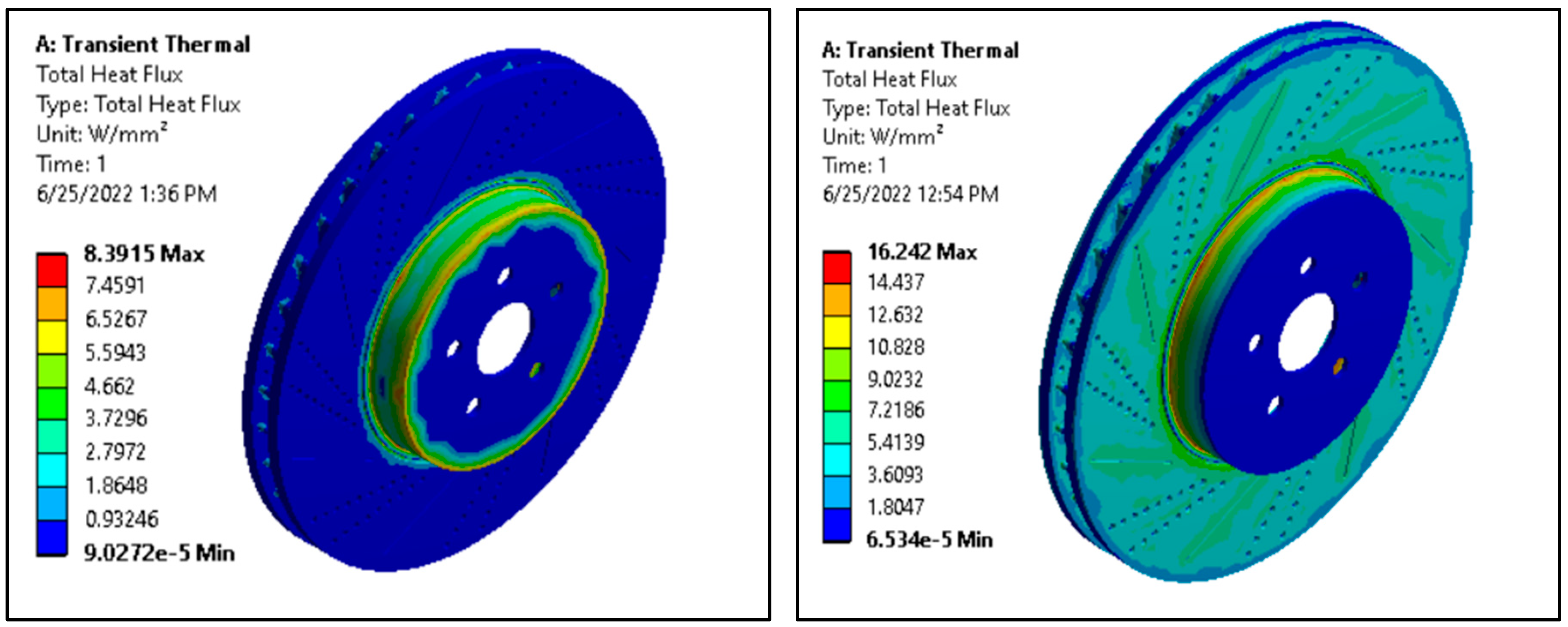
3.6.2. Total Heat Flux
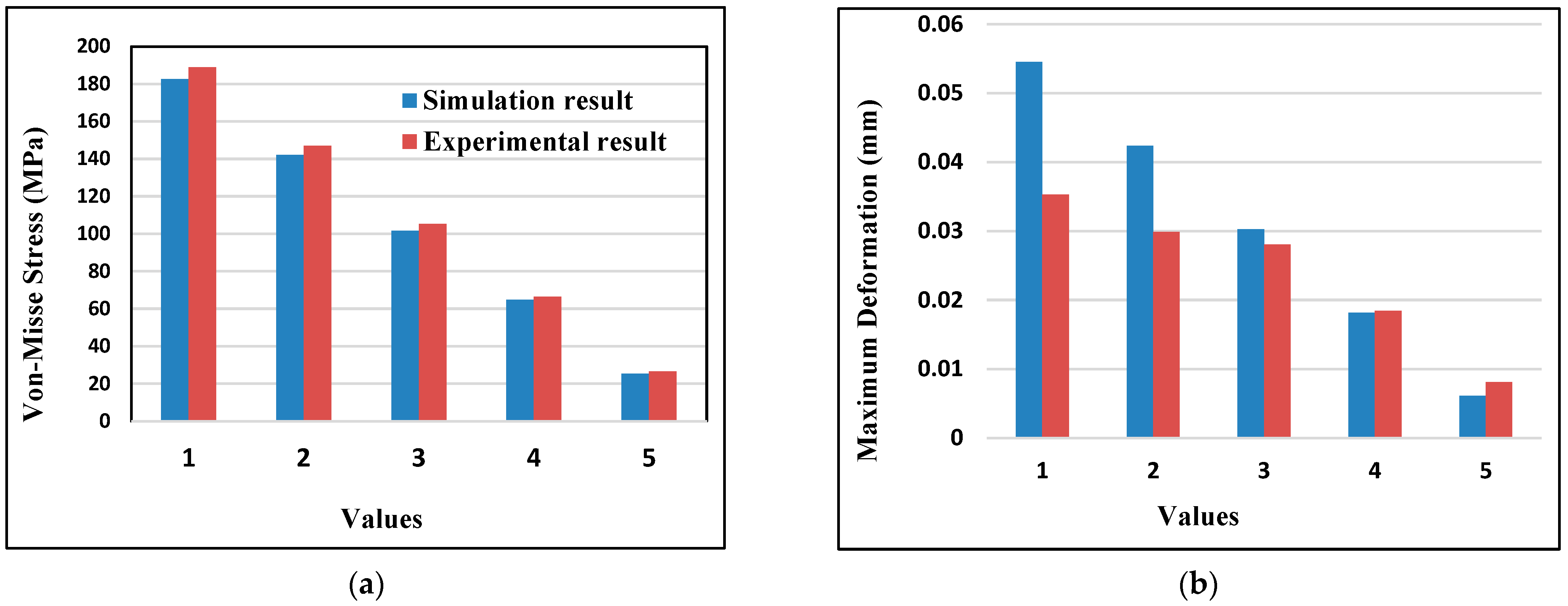
3.7. Validation of Result
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Din, S.H.; Shah, M.A.; Sheikh, N.A.; Butt, M.M. Nano-Composites and their Applications: A review. Charact. Appl. Nanomater. 2020, 3, 875. [Google Scholar] [CrossRef]
- Rashid, A. Overview of disc brakes and related phenomena—A review. Int. J. Veh. Noise Vib. 2014, 10, 257–301. [Google Scholar] [CrossRef]
- Maleque, M.; Adebisi, A.; Shah, Q. Energy and Cost Analysis of Weight Reduction using Composite Brake Rotor. Int. J. Veh. Struct. Syst. 2012, 4, 69–73. [Google Scholar] [CrossRef]
- Fatchurrohman, N.; Marini, C.D.; Suraya, S.; Iqbal, A.A. Investigation of Product Performance of Al-Metal Matrix Composites Brake Disc using Finite Element Analysis. IOP Conf. Ser. Mater. Sci. Eng. 2016, 114, 012107. [Google Scholar] [CrossRef]
- Singh, K.K.; Singh, S.; Shrivastava, A.K. Study of Tribological Behavior of Silicon Carbide Based Aluminium Metal Matrix Composites under Dry and Lubricated Environment. Adv. Mater. Sci. Eng. 2016, 2016, 3813412. [Google Scholar] [CrossRef]
- Maluf, O.; Milan, M.T.; Angeloni, M.; Spinelli, D.; Bose Filho, W.W. Development of Materials for Automotive Disc Brakes. Minerva 2007, 4, 149–158. [Google Scholar]
- Ripin, Z.B.M. Analysis of Disc Brake Squeal Using the Finite Element Method. Ph.D. Thesis, University of Leeds, Leeds, UK, September 1995. [Google Scholar]
- Anand, G.; Amal, K.G.; Athul Varma, S.; Krishnaprasad, C.T.; Rakesh, S. Structural and Thermal Analysis of Brake Disc with Grey Cast Iron and Cenosphere-Aluminium Composite. IRJET 2021, 8, 1092–1097. [Google Scholar]
- Awe, S.A. Developing Material Requirements for Automotive Brake Disc. Mod. Concepts Mater. Sci. 2019, 2, 1–4. [Google Scholar] [CrossRef]
- Nathi, G.M.; Charyulu, T.N.; Gowtham, K.; Satish Reddy, P. Coupled Structual/Thermal Analysis of Disc Brake. Int. J. Res. Eng. Technol. 2012, 1, 539–553. [Google Scholar] [CrossRef]
- Black, T.A.; Fine, C.H.; Sachs, E.M. A Method for Systems Design Using Precedence Relationships: An Application to Automotive Brake Systems; MIT: Cambridge, MA, USA, 1990. [Google Scholar]
- Maleque, M.A.; Dyuti, S.; Rahman, M.M. Material selection method in design of automotive brake disc. In Proceedings of the WCE 2010-World Congress on Engineering, London, UK, 30 June–2 July 2010; Volume 3, pp. 2322–2326. [Google Scholar]
- Shanker, P.S. A review on properties of conventional and metal matrix composite materials in manufacturing of disc brake. Mater. Today Proc. 2018, 5, 5864–5869. [Google Scholar] [CrossRef]
- Hayidso, T.H.; Gemeda, D.O.; Abraham, A.M. Identifying Road Traffic Accidents Hotspots Areas Using GIS in Ethiopia: A Case Study of Hosanna Town. Transp. Telecommun. J. 2019, 20, 123–132. [Google Scholar] [CrossRef]
- Maheshwari, N.; Choudhary, J.; Rath, A.; Shinde, D.; Kalita, K. Finite Element Analysis and Multi-criteria Decision-Making (MCDM)-Based Optimal Design Parameter Selection of Solid Ventilated Brake Disc. J. Inst. Eng. Ser. C 2021, 102, 349–359. [Google Scholar] [CrossRef]
- Kalita, K.; Shinde, D.; Chakraborty, S. Grey wolf optimizer-based design of ventilated brake disc. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 405. [Google Scholar] [CrossRef]
- Shinde, D.; Öktem, H.; Kalita, K.; Chakraborty, S.; Gao, X.-Z. Optimization of Process Parameters for Friction Materials Using Multi-Criteria Decision Making: A Comparative Analysis. Processes 2021, 9, 1570. [Google Scholar] [CrossRef]
- Abdullah, O.I.; Belhocine, A. A thermomechanical model for the analysis of disc brake using the finite element method in frictional contact. J. Eng. Res. 2021. [Google Scholar]
- Thakre, S.; Shahare, A.; Awari, G.K. Investigation of Thermal Response of Disc Brake System: A Review. IOP Conf. Ser. Mater Sci. Eng. 2021, 1170, 012010. [Google Scholar] [CrossRef]
- Stojanović, N.; Abdullah, O.I.; Glišović, J.; Grujic, I.; Dorić, J. Investigation of Thermal Behavior of Brake System Using Alternative Materials. Heat Transf. Res. 2020, 51, 1609–1623. [Google Scholar] [CrossRef]
- Belhocine, A. Finite Element Analysis of Automotive Disk Brake and Pad in Frictional Model Contact. ADMT J. 2014, 7, 27–40. [Google Scholar]
- Jiang, L.; Jiang, Y.; Yu, L.; Yang, H.; Li, Z.; Ding, Y. Thermo-mechanical coupling analyses for al alloy brake discs with Al2O3-SiC (3D)/Al alloy composite wear-resisting surface layer for high-speed trains. Materials 2019, 12, 3155. [Google Scholar] [CrossRef]
- Sharath, B.; Venkatesh, C.; Afzal, A.; Aslfattahi, N.; Aabid, A.; Baig, M.; Saleh, B. Multi Ceramic Particles Inclusion in the Aluminium Matrix and Wear Characterization through Experimental and Response Surface-Artificial Neural Networks. Materials 2021, 14, 2895. [Google Scholar] [CrossRef]
- Baig, M.M.A.; Al-Qutub, A.M.; Allam, I.M.; Patel, F.; Mohammed, A.S. Tribological Performance of Sub-Micron Al2O3-Reinforced Aluminium Composite Brake Rotor Material. Arab. J. Sci. Eng. 2021, 46, 2691–2700. [Google Scholar] [CrossRef]
- Deme, D. Road Traffic Accident in Ethiopia from 2007/08-2017/18. Am. Int. J. Sci. Eng. Res. 2019, 2, 49–59. [Google Scholar] [CrossRef]
- Rajesh, P.V.; Gupta, K.K.; Čep, R.; Ramachandran, M.; Kouřil, K.; Kalita, K. Optimizing Friction Stir Welding of Dissimilar Grades of Aluminium Alloy Using WASPAS. Materials 2022, 15, 1715. [Google Scholar] [CrossRef] [PubMed]
- Belhocine, A.; Bouchetara, M. Investigation of temperature and thermal stress in ventilated disc brake based on 3D thermomechanical coupling model. Ain Shams Eng. J. 2013, 4, 475–483. [Google Scholar] [CrossRef] [Green Version]
- Kalita, K.; Shinde, D.; Thomas, T.T. Non-dimensional Stress Analysis of an Orthotropic Plate. Mater. Today Proc. 2015, 2, 3527–3533. [Google Scholar] [CrossRef]
- Kalita, K.; Shinde, D.; Haldar, S. Analysis on Transverse Bending of Rectangular Plate. Mater. Today Proc. 2015, 2, 2146–2154. [Google Scholar] [CrossRef]
- Belhocine, A.; Bouchetara, M. Structural and Thermal Analysis of Automotive Disc Brake Rotor. Arch. Mech. Eng. 2014, 61, 89–113. [Google Scholar] [CrossRef]
- Belhocine, A.; Abu Bakar, A.R.; Abdullah, O. Structural and Contact Analysis of Disc Brake Assembly During Single Stop Braking Event. Trans. Indian Inst. Met. 2014, 68, 403–410. [Google Scholar] [CrossRef]
- Ishak, M.R.; Abu Bakar, A.R.; Belhocine, A.; Taib, J.M.; Omar, W.Z.W. Brake torque analysis of fully mechanical parking brake system: Theoretical and experimental approach. Measurement 2016, 94, 487–497. [Google Scholar] [CrossRef]
- Stojanovic, B.; Glisovic, J. Application of Ceramic Matrix Composite in Automotive Industry. Encycl. Mater. Compos. 2020, 2, 275–292. [Google Scholar] [CrossRef]
- Ahmed, G.M.S.; Algarni, S. Design, Development and FE Thermal Analysis of a Radially Grooved Brake Disc Developed through Direct Metal Laser Sintering. Materials 2018, 11, 1211. [Google Scholar] [CrossRef]
- Seelam, A.B.; Hussain, N.A.Z.; Krishanmurthy, S.H. Design and analysis of disc brake system in high speed vehicles. Int. J. Simul. Multidiscip. Des. Optim. 2021, 12, 19. [Google Scholar] [CrossRef]
- Belhocine, A.; Omar, W.Z.W. A numerical parametric study of mechanical behavior of dry contact slipping on the disc–pads interface. Alex. Eng. J. 2016, 55, 1127–1141. [Google Scholar] [CrossRef]
- Chavan, C.B.; More, A.S.; Patil, N.N.; Baskar, P. Static structural and thermal analysis of brake disc with different cut patterns. J. Appl. Res. Technol. 2018, 16, 41–52. [Google Scholar] [CrossRef] [Green Version]
- Bhat, A.; Pal, B.; Dandotiya, D. Structural Analysis of a Two-Wheeler Disc Brake. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1013, 012024. [Google Scholar] [CrossRef]
- Gurram, P.; Komakula, S.A.; Kumar, G.V. Design and analysis of vented disc brake rotor. Int. J. Appl. Eng. Res. 2019, 14, 2228–2233. [Google Scholar]


| Brake Rotor Parameter Name | Parameter Value (Units) |
|---|---|
| The outer diameter of the disc rotor (Do) | 0.302 (m) |
| The inner diameter of the disc rotor (Di) | 0.100 (m) |
| Number of holes | 6 |
| Thickness of disc brake rotors | 0.048 (m) |
| Drilled hole diameter | 0.010 (m) |
| Top speed (V) | 52.78 (m/s) |
| Wheel base | 0.2730 (m) |
| Wheel diameter | 0.68(m) |
| Materials | Von Mises Stress (MPa) | Allowable Stress (MPa) |
|---|---|---|
| Aluminum alloy disc | 179.88 | 310 |
| Aluminum matrix nano-composite disc | 183.68 | 845.21 |
| Time (s) | Aluminum Alloy Disk | AMNCs Disk | ||
|---|---|---|---|---|
| Minimum (°C) | Maximum (°C) | Minimum (°C) | Maximum (°C) | |
| 1. | 5 | 22 | 5 | 21.92 |
| 2. | 9.98 | 21.99 | 9.55 | 21.71 |
| 3. | 20.82 | 50 | 20.78 | 50 |
| 4. | 21.85 | 90 | 21.68 | 90 |
| 5. | 21.97 | 130 | 22.90 | 130 |
| 6. | 21.99 | 140 | 25.62 | 140 |
| 7. | 22.01 | 150 | 30.05 | 150 |
| 8. | 22.08 | 170 | 36.12 | 170 |
| 9. | 22.20 | 190 | 43.70 | 190 |
| 10. | 22.43 | 200 | 52.62 | 200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sivaprakasam, P.; Abebe, E.; Čep, R.; Elangovan, M. Thermo-Mechanical Behavior of Aluminum Matrix Nano-Composite Automobile Disc Brake Rotor Using Finite Element Method. Materials 2022, 15, 6072. https://doi.org/10.3390/ma15176072
Sivaprakasam P, Abebe E, Čep R, Elangovan M. Thermo-Mechanical Behavior of Aluminum Matrix Nano-Composite Automobile Disc Brake Rotor Using Finite Element Method. Materials. 2022; 15(17):6072. https://doi.org/10.3390/ma15176072
Chicago/Turabian StyleSivaprakasam, Palani, Esayas Abebe, Robert Čep, and Muniyandy Elangovan. 2022. "Thermo-Mechanical Behavior of Aluminum Matrix Nano-Composite Automobile Disc Brake Rotor Using Finite Element Method" Materials 15, no. 17: 6072. https://doi.org/10.3390/ma15176072
APA StyleSivaprakasam, P., Abebe, E., Čep, R., & Elangovan, M. (2022). Thermo-Mechanical Behavior of Aluminum Matrix Nano-Composite Automobile Disc Brake Rotor Using Finite Element Method. Materials, 15(17), 6072. https://doi.org/10.3390/ma15176072







