Concrete with a High Content of End-of-Life Tire Materials for Flexural Strengthening of Reinforced Concrete Structures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Static Loading
2.1.1. Loading under Compression
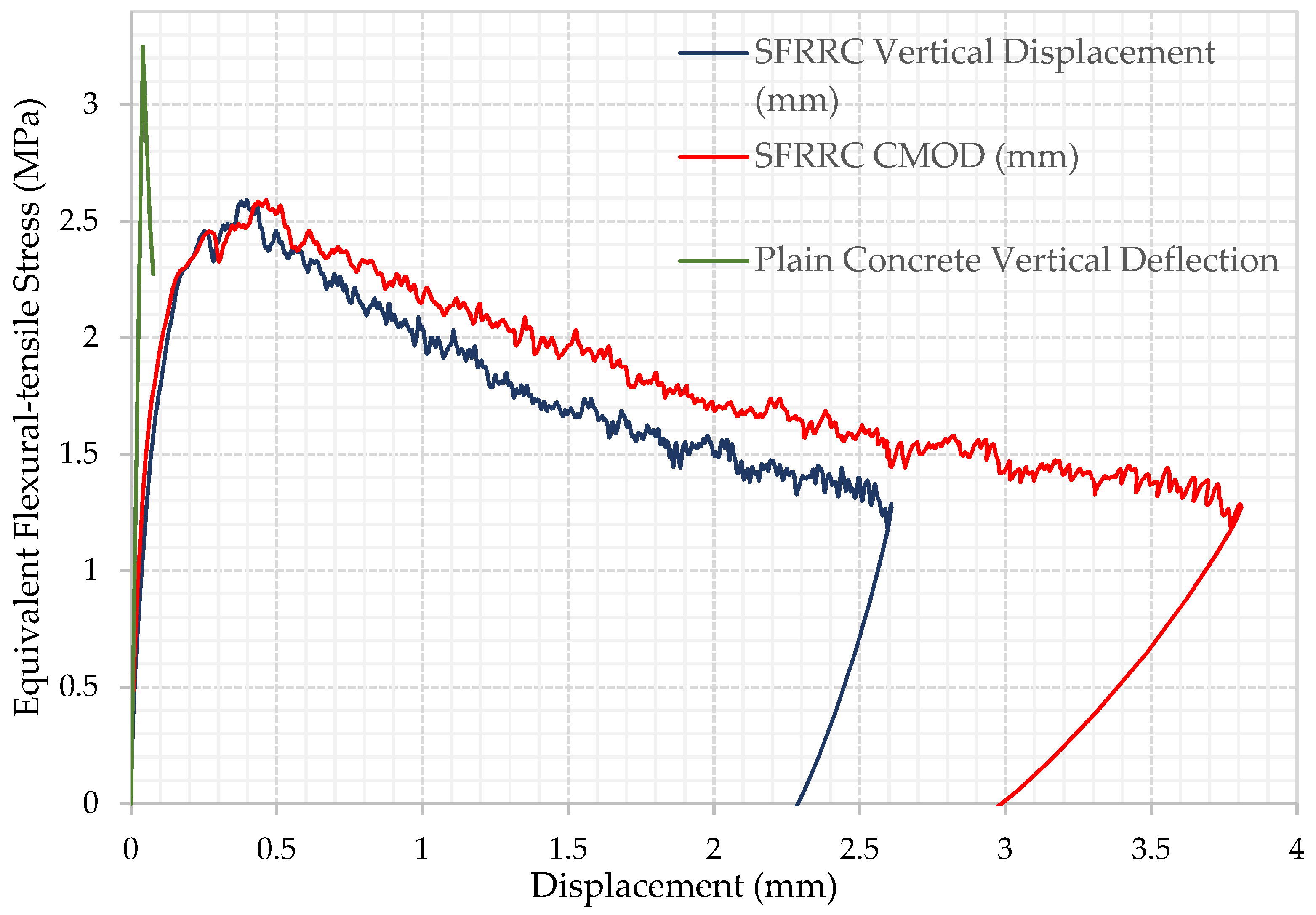
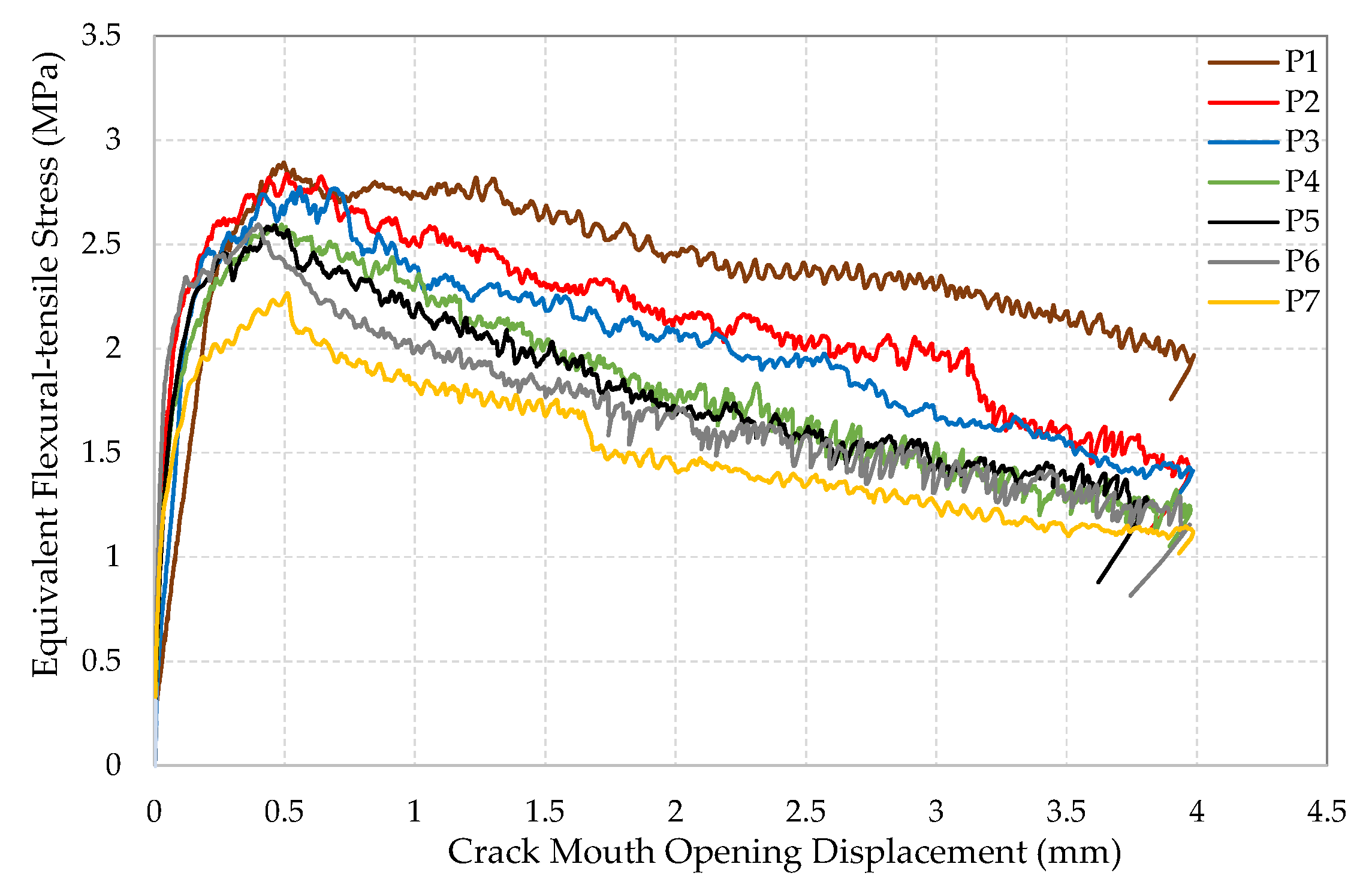
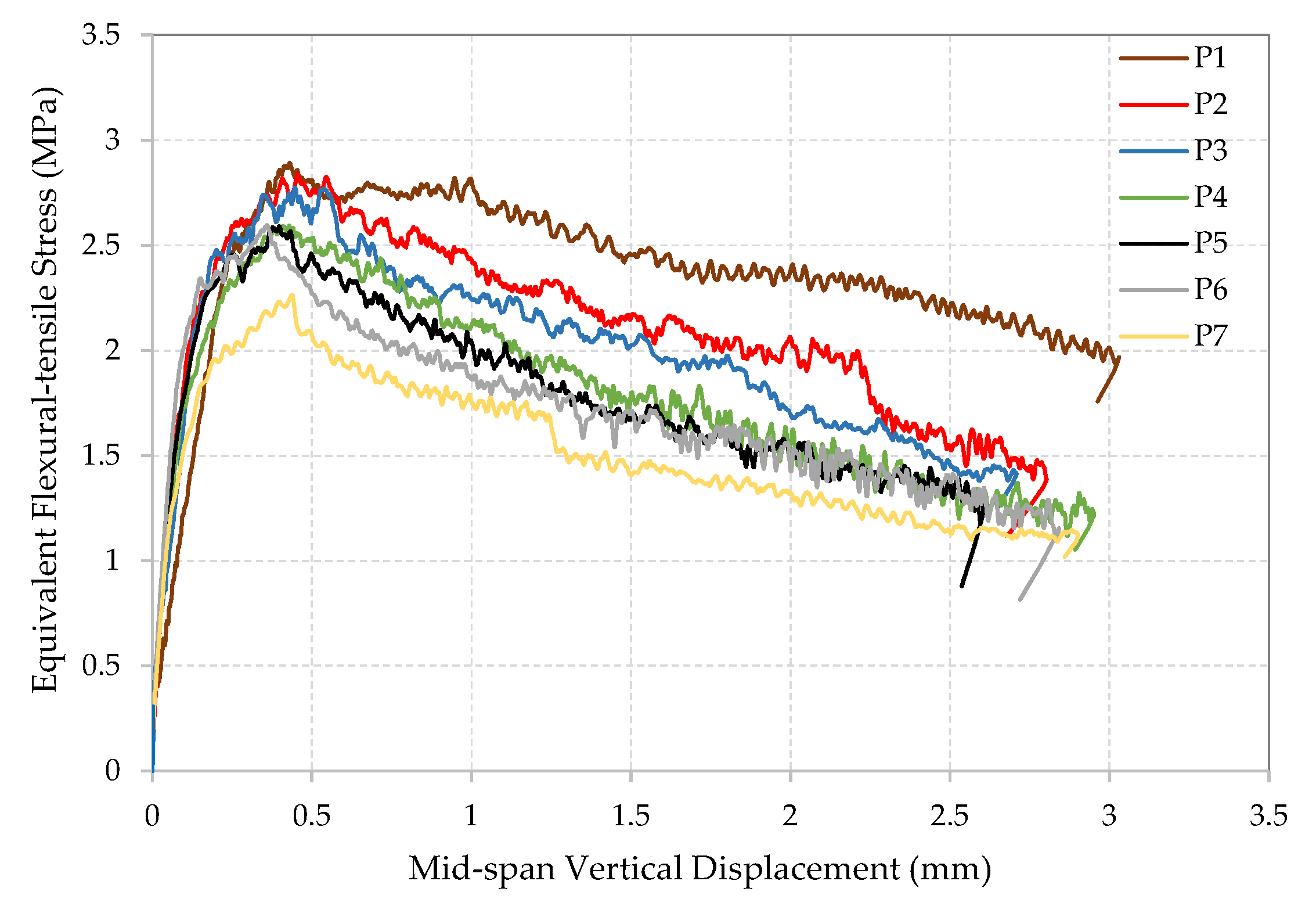
2.1.2. Loading under Bending
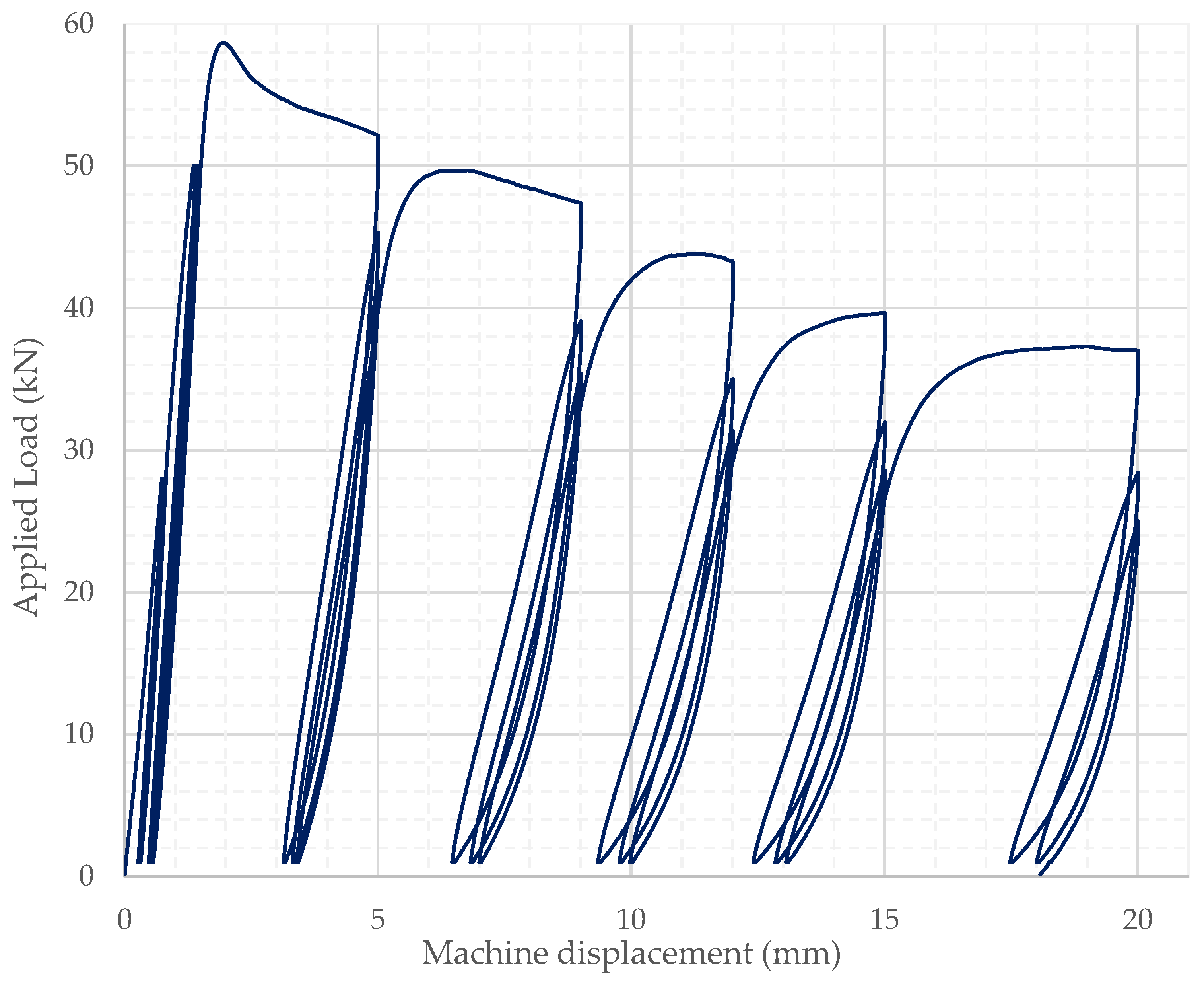
2.2. Cyclic Compressive Loading
2.3. Impact Loading
2.4. Durability Testing
2.4.1. Chloride Corrosion Exposure
2.4.2. Freeze–Thaw Resistance
3. Experimental Results and Discussion
3.1. Static Loading
3.1.1. Loading under Compression
3.1.2. Loading under Bending
3.2. Cyclic Compressive Loading
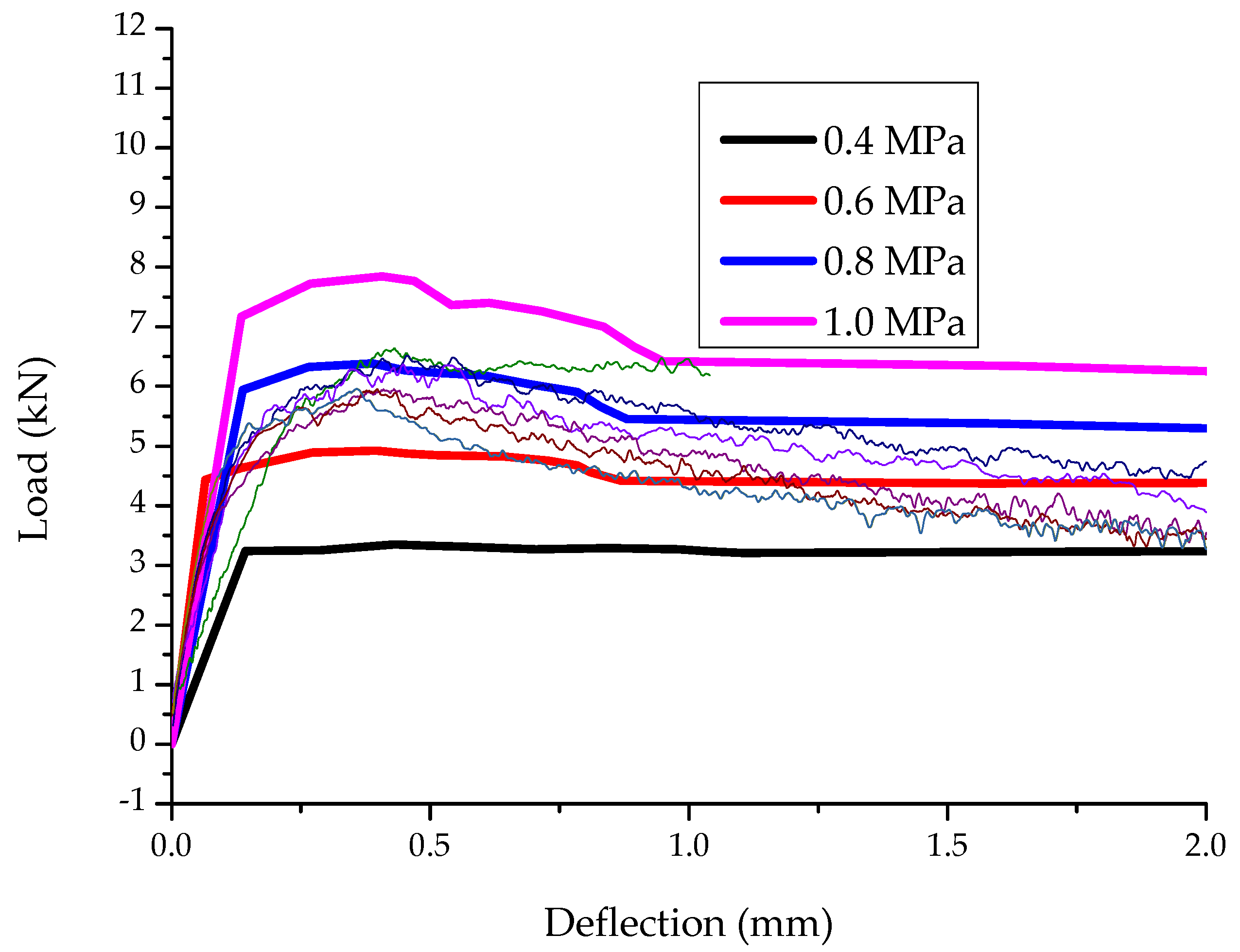
3.3. Impact Loading
3.4. Durability Testing
3.4.1. Chloride Corrosion Resistance
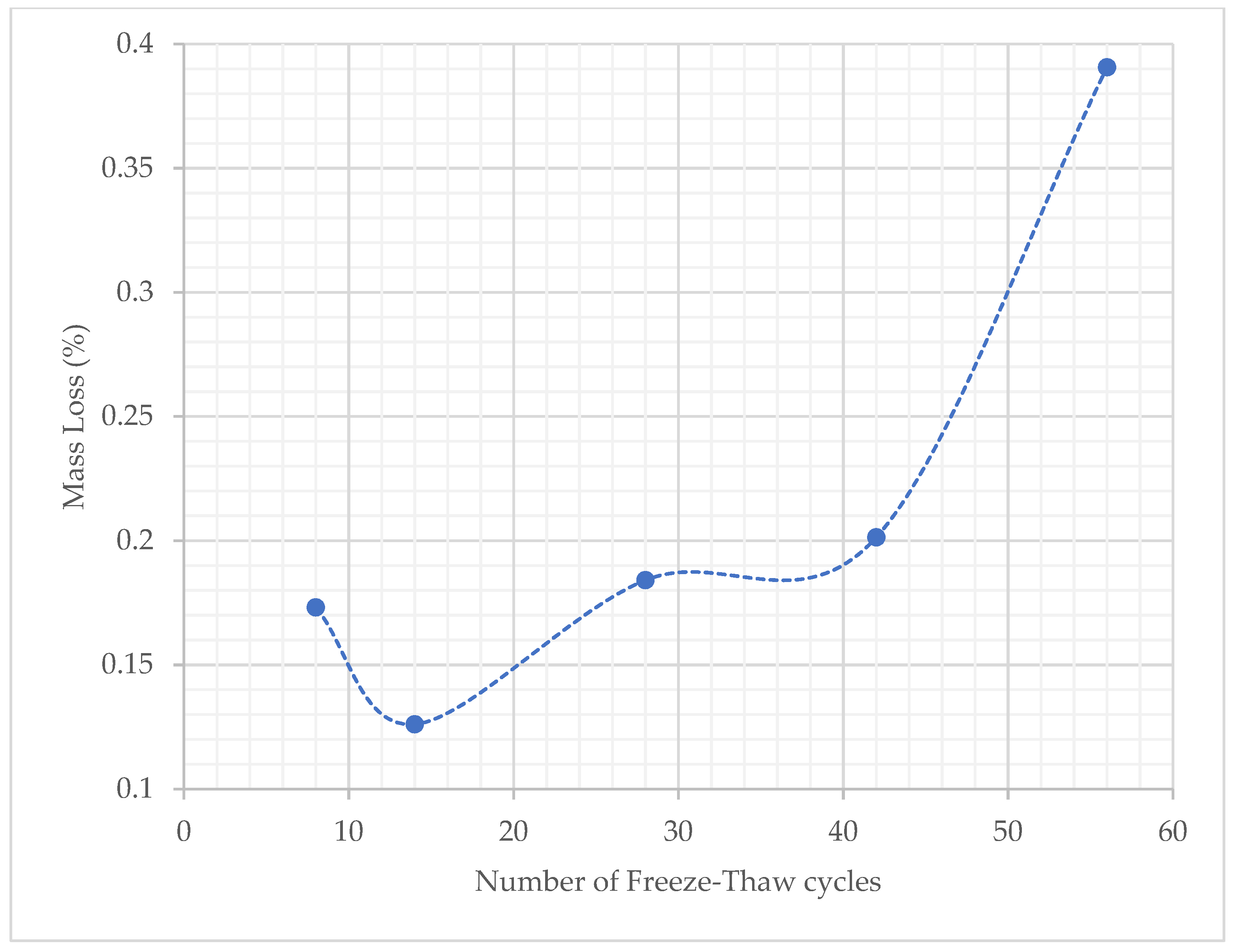
3.4.2. Freeze–Thaw Resistance
4. Numerical Study on the Efficiency of SFRRC as a Strengthening Material
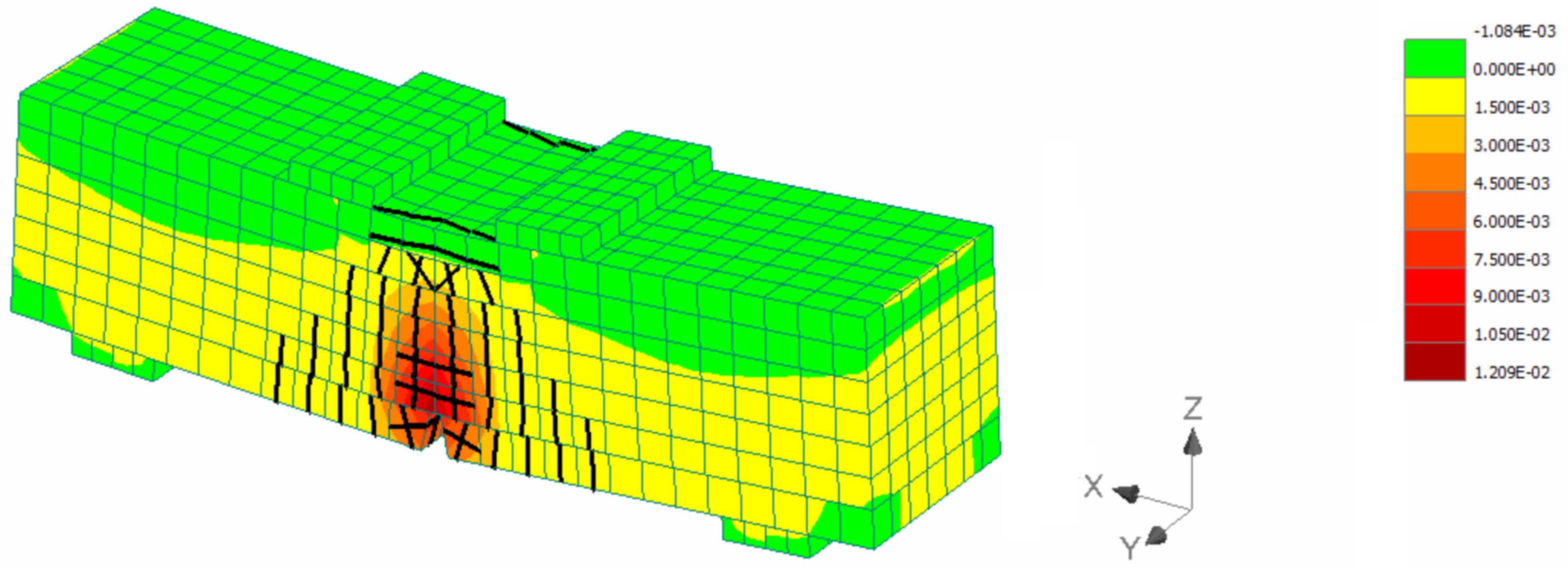
4.1. SFRCC Numerical Modeling
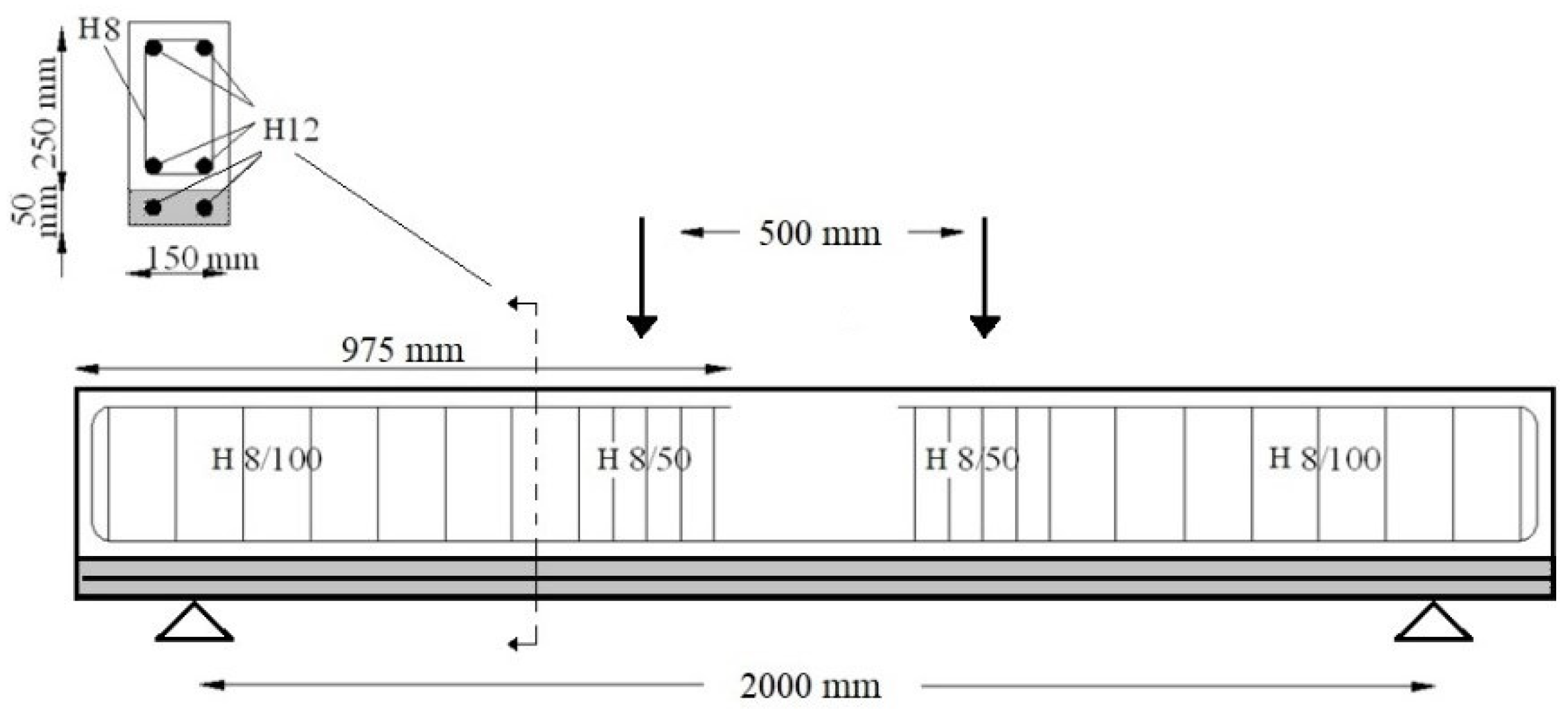
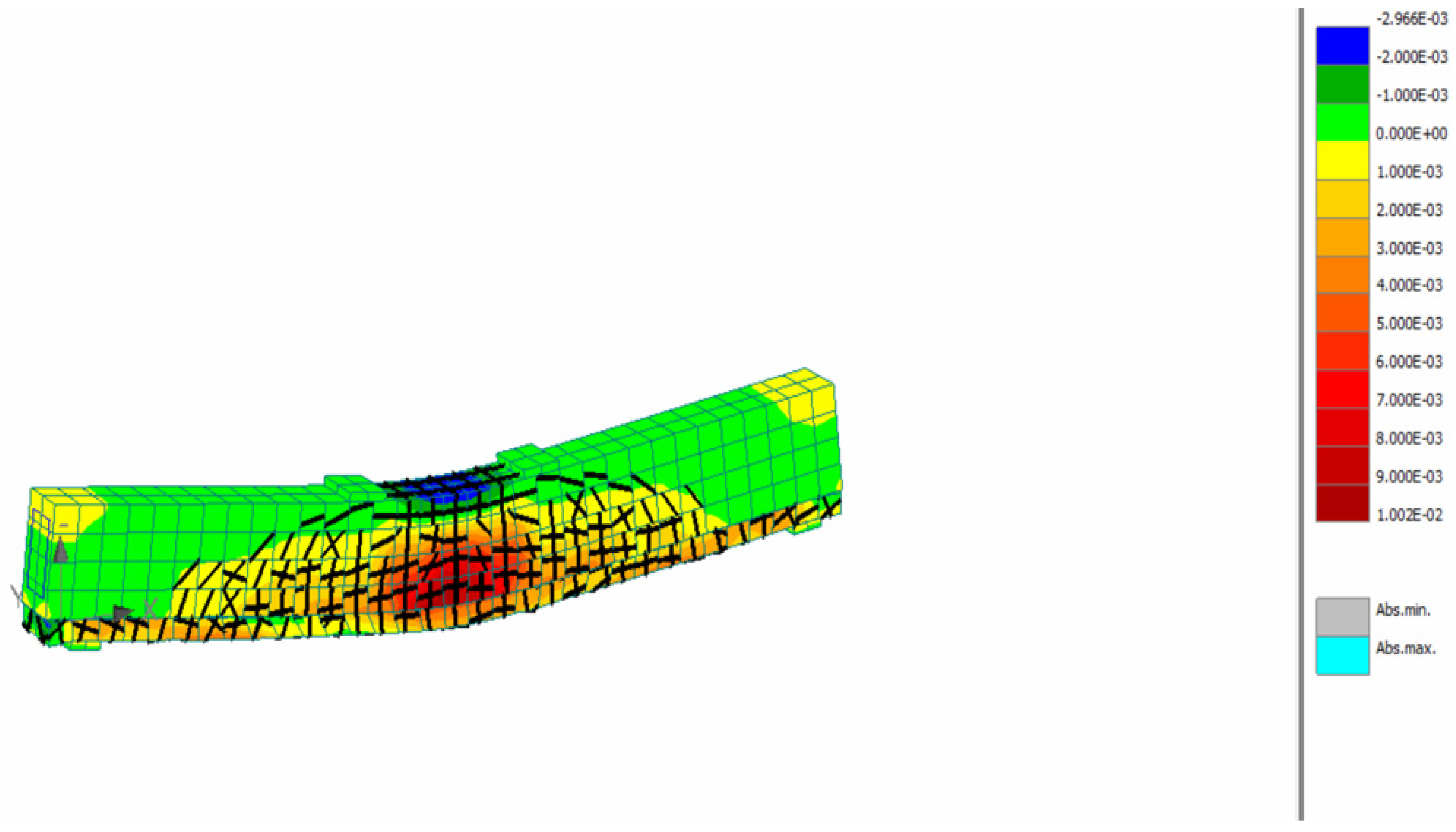
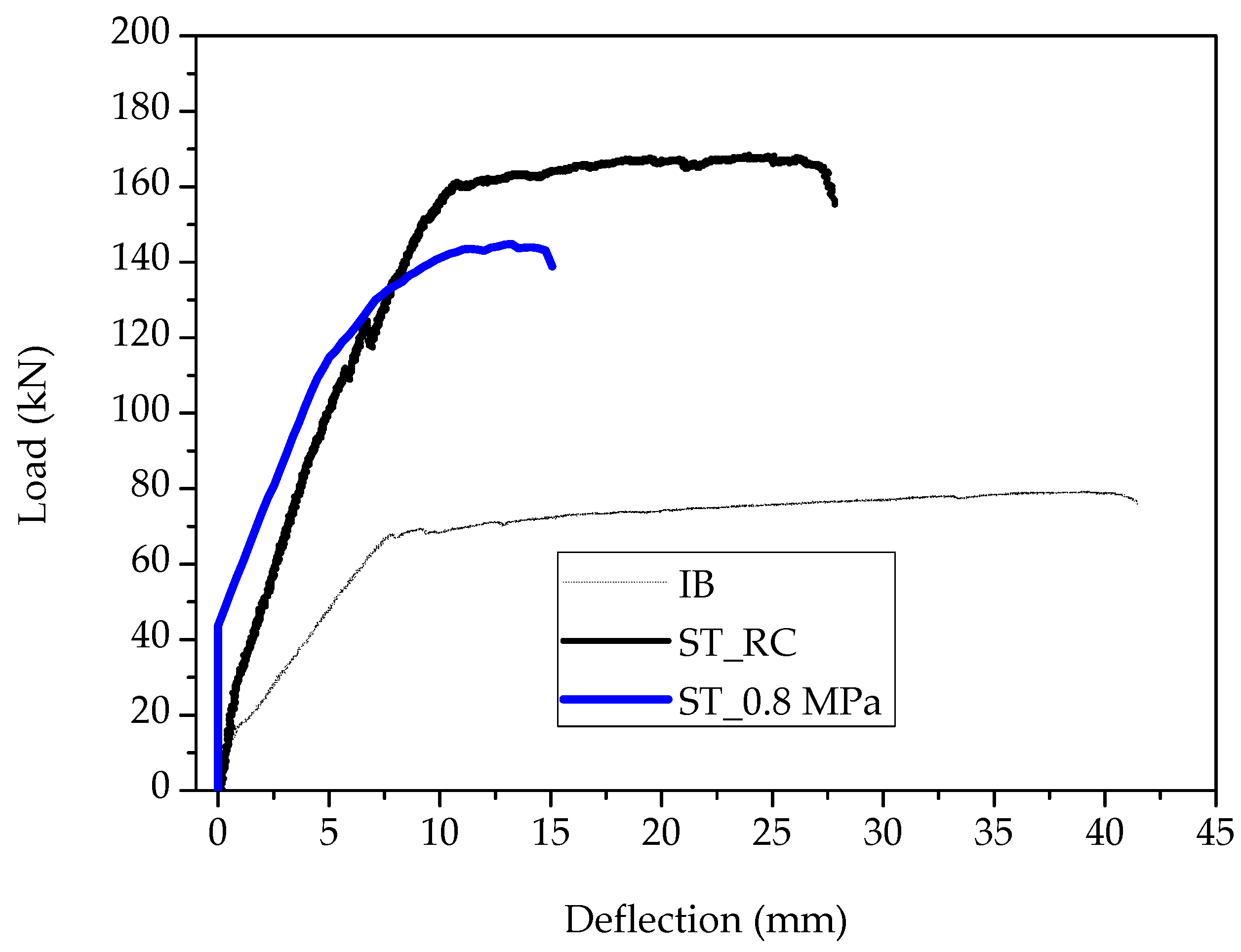
4.2. Strengthening of Reinforced Concrete Beams Using SFRRC Layer
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- United Nations Conference on Trade and Development (UNCTAD). Circular Economy: The New Normal? UNCTAD: Geneva, Switzerland, 2018. [Google Scholar]
- Ismail, M.K.; Hassan, A.A.A. Impact resistance and mechanical properties of self-consolidating rubberized concrete reinforced with steel fibers. J. Mater. Civ. Eng. 2017, 29, 04016193. [Google Scholar] [CrossRef]
- Ozbay, E.; Lachemi, M.; Sevim, U.K. Compressive strength, abrasion resistance and energy absorption capacity of rubberized concretes with and without slag. Mater. Struct./Mater. Constr. 2011, 44, 1297–1307. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H.; Hajirasouliha, I.; Guadagnini, M.; Pilakoutas, K. Tensile stress-strain characteristics of rubberised concrete from flexural tests. Constr. Build. Mater. 2020, 236, 117591. [Google Scholar] [CrossRef]
- Pajak, M.; Krystek, M.; Zakrzewski, M.; Domski, J. Laboratory investigation and numerical modelling of concrete reinforced with recycled steel fibers. Materials 2021, 14, 1828. [Google Scholar] [CrossRef]
- Polydorou, T.; Constantinides, G.; Neocleous, K.; Kyriakides, N.; Koutsokeras, L.; Chrysostomou, C.; Hadjimitsis, D. Effects of pre-treatment using waste quarry dust on the adherence of recycled tyre rubber particles to cementitious paste in rubberised concrete. Constr. Build. Mater. 2020, 254, 119325. [Google Scholar] [CrossRef]
- Brühwiler, E.; Denarié, E. Rehabilitation of concrete structures using Ultra-High Performance Fibre Reinforced Concrete. In Proceedings of the Second International Symposium on Ultra High Performance Concrete, Kessel, Germany, 5–7 March 2008; pp. 1–8. [Google Scholar]
- Al-Osta, M.A.; Isa, M.N.; Baluch, M.H.; Rahman, M.K. Flexural behavior of reinforced concrete beams strengthened with ultra-high performance fiber reinforced concrete. Constr. Build. Mater. 2017, 134, 279–296. [Google Scholar] [CrossRef]
- Lampropoulos, A.P.; Paschalis, S.A.; Tsioulou, O.T.; Dritsos, S.E. Strengthening of reinforced concrete beams using ultra high performance fibre reinforced concrete (UHPFRC). Eng. Struct. 2016, 106, 370–384. [Google Scholar] [CrossRef]
- Paschalis, S.A.; Lampropoulos, A.P.; Tsioulou, O. Experimental and numerical study of the performance of Ultra High Performance Fiber Reinforced Concrete-Reinforced Concrete for the flexural strengthening of full scale members. Constr. Build. Mater. 2018, 186, 351–366. [Google Scholar] [CrossRef]
- Ana, B.; Dubravka, B.; Marijan, S. Hybrid Fiber–Reinforced Concrete with Unsorted Recycled-Tire Steel Fibers. J. Mater. Civ. Eng. 2017, 29, 6017005. [Google Scholar]
- Hu, H.; Papastergiou, P.; Angelakopoulos, H.; Guadagnini, M.; Pilakoutas, K. Mechanical properties of SFRC using blended Recycled Tyre Steel Cords (RTSC) and Recycled Tyre Steel Fibres (RTSF). Constr. Build. Mater. 2018, 187, 553–564. [Google Scholar] [CrossRef]
- Lavagna, L.; Nisticò, R.; Sarasso, M.; Pavese, M. An analytical mini-review on the compression strength of rubberized concrete as a function of the amount of recycled tires crumb rubber. Materials 2020, 13, 1234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bignozzi, M.C.; Sandrolini, F. Tyre rubber waste recycling in self-compacting concrete. Cem. Concr. Res. 2006, 36, 735–739. [Google Scholar] [CrossRef]
- Hisham, B.; Bakar, A.; Noaman, A.T.; Akil, H.M. Cumulative Effect of Crumb Rubber and Steel Fiber on the Flexural Toughness of Concrete. Eng. Technol. Appl. Sci. Res. 2017, 7, 1345–1352. [Google Scholar]
- Najim, K.B.; Hall, M.R. Mechanical and dynamic properties of self-compacting crumb rubber modified concrete. Constr. Build. Mater. 2012, 27, 521–530. [Google Scholar] [CrossRef]
- Graeff, A.G.; Pilakoutas, K.; Neocleous, K.; Peres, M.V.N.N. Fatigue resistance and cracking mechanism of concrete pavements reinforced with recycled steel fibres recovered from post-consumer tyres. Eng. Struct. 2012, 45, 385–395. [Google Scholar] [CrossRef]
- Alsaif, A.; Koutas, L.; Bernal, S.A.; Guadagnini, M.; Pilakoutas, K. Mechanical performance of steel fibre reinforced rubberised concrete for flexible concrete pavements. Constr. Build. Mater. 2018, 172, 533–543. [Google Scholar] [CrossRef]
- AbdelAleem, B.H.; Hassan, A.A.A. Use of rubberized engineered cementitious composite in strengthening flexural concrete beams. Eng. Struct. 2022, 262, 114304. [Google Scholar] [CrossRef]
- Raffoul, S.; Garcia, R.; Pilakoutas, K.; Guadagnini, M.; Medina, N.F. Optimisation of rubberised concrete with high rubber content: An experimental investigation. Constr. Build. Mater. 2016, 124, 391–404. [Google Scholar] [CrossRef]
- EN 197-1:2011; Cement—Part 1: Composition, Specifications and Conformity Criteria for Common Cements. European Committee for Standardization: Brussels, Belgium, 2007.
- EN 450-1:2012; Fly Ash for Concrete Part 1: Definition, Specifications and Conformity Criteria. European Committee for Standardization: Brussels, Belgium, 2012.
- EN 13263-1; Silica Fume for Concrete. CEN (European Commitee for Standardization): Brussels, Belgium, 2005.
- EN 934-2:2009; Admixtures for Concrete, Mortar and Grout. CEN (European Commitee for Standardization): Brussels, Belgium, 2009.
- EN 1097-6:2013; Tests for Mechanical and Physical Properties of Aggregates—Part 6: Determination of Particle Density and Water Absorption. CEN (European Commitee for Standardization): Brussels, Belgium, 2013.
- Twincon Ltd. Technical Data Sheet Product: Reused Tyre Steel Fibre (RTSF); Twincon Ltd.: Sheffield, UK, 2018. [Google Scholar]
- EN 206:2013+A1:2016; Concrete—Specification, Performance, Production and Conformity. CEN (European Commitee for Standardization): Brussels, Belgium, 2016.
- EN 12390-3:2009/AC:2011; Testing Hardened Concrete—Part 3: Compressive Strength of Test Specimens. CEN (European Commitee for Standardization): Brussels, Belgium, 2011.
- BS1881-121:1983; Testing Concrete—Part 121: Method for Determination of Static Modulus of Elasticity in Compression. British Standards Institution (BSI): London, UK, 1983.
- JSCE-SF4; Method of Tests for Flexural Strength and Flexural Toughness of Steel Fiber Reinforced Concrete. JSI: Tokyo, Japan, 2016.
- Vandewalle, L.; Nemegeer, D.; Balázs, G.L.; Barr, B.; Barros, J.A.O.; Bartos, P.; Banthia, N.; Criswell, M.; Denarie, E.; di Prisco, M.; et al. RILEM RILEM TC 162-TDF: “Test and design methods for steel fibre reinforced concrete” σ-ε-design method (final recommendation). Mater. Struct./Mater. Constr. 2003, 36, 560–567. [Google Scholar]
- EN 14651; Test Method for Metallic Fibered Concrete—Measuring the Flexural Tensile Strength (Limit of Proportionality (LOP), Residual). CEN (European Commitee for Standardization): Brussels, Belgium, 2007.
- BSI PD CEN/TS 12390-9:2016; Testing Hardened Concrete—Freeze-Thaw Resistance with De-Icing Salts—Scaling. CEN (European Commitee for Standardization): Brussels, Belgium, 2016; p. 36.
- Nisticò, R.; Lavagna, L.; Boot, E.A.; Ivanchenko, P.; Lorusso, M.; Bosia, F.; Pugno, N.M.; D’Angelo, D.; Pavese, M. Improving rubber concrete strength and toughness by plasma-induced end-of-life tire rubber surface modification. Plasma Processes Polym. 2021, 18, 2100081. [Google Scholar] [CrossRef]
- American Wood Council. Beam Design Formulas With Shear and Moment Diagrams. Design AID No. 6; American Wood Council: Washington, DC, USA, 2005; Volume 20. [Google Scholar]
- fib Special Activity Group 5. fib Bulletin 55: Model Code 2010; fib: Lausanne, Switzerland, 2010. [Google Scholar]
- fib Special Activity Group 5. fib Bulletin 56: Model Code 2010; fib: Lausanne, Switzerland, 2010. [Google Scholar]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2007; ISBN 013156174X. [Google Scholar]
- EN 1998-1:2004; Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
- SS 137244:2019; Betongprovning—Hårdnad betong—Avflagning vid frysning Concrete testing—Hardened concrete—Scaling at freezing. SIS: Stockholm, Sweden, 2005.
- Pryl, D.; Červenka, J. ATENA Program Documentation Part 1; Cervenka Consulting: Prague, Czech, 2013. [Google Scholar]
- Tsioulou, O.T.; Lampropoulos, A.P.; Dritsos, S.E. Experimental investigation of interface behaviour of RC beams strengthened with concrete layers. Constr. Build. Mater. 2013, 40, 50–59. [Google Scholar] [CrossRef]








| Mix Constituent | SFRRC Mix Amount (kg/m3) | Plain Concrete Mix Amount (kg/m3) |
|---|---|---|
| Cement CEM I 52,5 N | 400.00 | 400.00 |
| Silica Fume (micro-silica) | 100.00 | 100.00 |
| Fine Mineral Aggregate | 310.50 | 573.70 |
| Coarse Mineral Aggregate | 378.00 | 1147.50 |
| Fine Rubber Particles | 169.70 | 0.00 |
| Coarse Rubber Particles | 207.00 | 0.00 |
| Recycled Tire Steel Fibers | 25.00 | 0.00 |
| Water | 225.00 | 225.00 |
| Superplasticizer | 3.61 | 3.61 |
| Experimental Procedure | Average Value | Variance |
|---|---|---|
| Cylinder Compressive Strength | 3.499 MPa | 0.274 |
| Cube Compressive Strength | 8.201 MPa | 0.388 |
| Cylinder Modulus of Elasticity | 3.263 GPa | 0.408 |
| Average Flexural Residual Strength fRi (MPa) | CoV of Flexural Residual Strength fRi (MPa) | CMOD (mm) | |
|---|---|---|---|
| fR1 | 2.57 | 0.08 | 0.5 |
| fR2 | 2.05 | 0.17 | 1.5 |
| fR3 | 1.78 | 0.19 | 2.5 |
| fR4 | 1.45 | 0.25 | 3.5 |
| Damping Ratio, ζ | Frequency, f (Hz) | ||
|---|---|---|---|
| Average | Variance | Average | Variance |
| 0.118 | 0.243 | 81.00 | 0.096 |
| Cycle Duration (Days) | NaCl Solution % Concentration | Average Mass Loss (%) | Coefficient of Variation |
|---|---|---|---|
| 56 (28 in/28 out) | 3 | 0.98 | 0.067 |
| 112 (56 in/56 out) | 3 | 1.29 | 0.026 |
| 168 (84 in/84 out) | No NaCl | 1.23 | 0.043 |
| 168 (84 in/84 out) | 3 | 1.04 | 0.085 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polydorou, T.; Kyriakides, N.; Lampropoulos, A.; Neocleous, K.; Votsis, R.; Tsioulou, O.; Pilakoutas, K.; Hadjimitsis, D.G. Concrete with a High Content of End-of-Life Tire Materials for Flexural Strengthening of Reinforced Concrete Structures. Materials 2022, 15, 6150. https://doi.org/10.3390/ma15176150
Polydorou T, Kyriakides N, Lampropoulos A, Neocleous K, Votsis R, Tsioulou O, Pilakoutas K, Hadjimitsis DG. Concrete with a High Content of End-of-Life Tire Materials for Flexural Strengthening of Reinforced Concrete Structures. Materials. 2022; 15(17):6150. https://doi.org/10.3390/ma15176150
Chicago/Turabian StylePolydorou, Thomaida, Nicholas Kyriakides, Andreas Lampropoulos, Kyriacos Neocleous, Renos Votsis, Ourania Tsioulou, Kypros Pilakoutas, and Diofantos G. Hadjimitsis. 2022. "Concrete with a High Content of End-of-Life Tire Materials for Flexural Strengthening of Reinforced Concrete Structures" Materials 15, no. 17: 6150. https://doi.org/10.3390/ma15176150







