Experimental and Numerical Studies on Fixed Steel Sheets Subjected to Underwater Explosion
Abstract
:1. Introduction
2. Experimental Program
2.1. Overview of Test
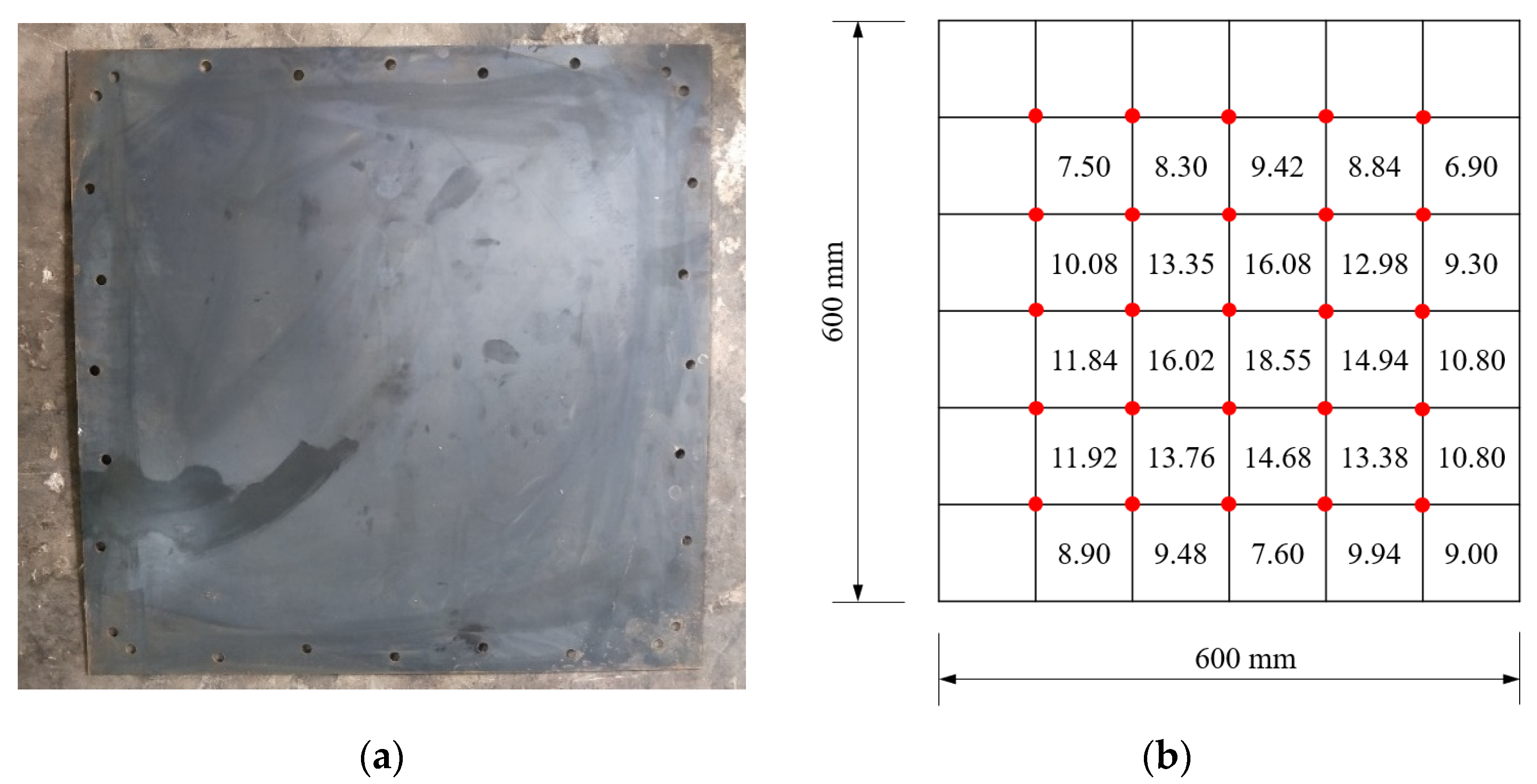
2.2. Test Setup and Instruments
3. Test Results and Discussion
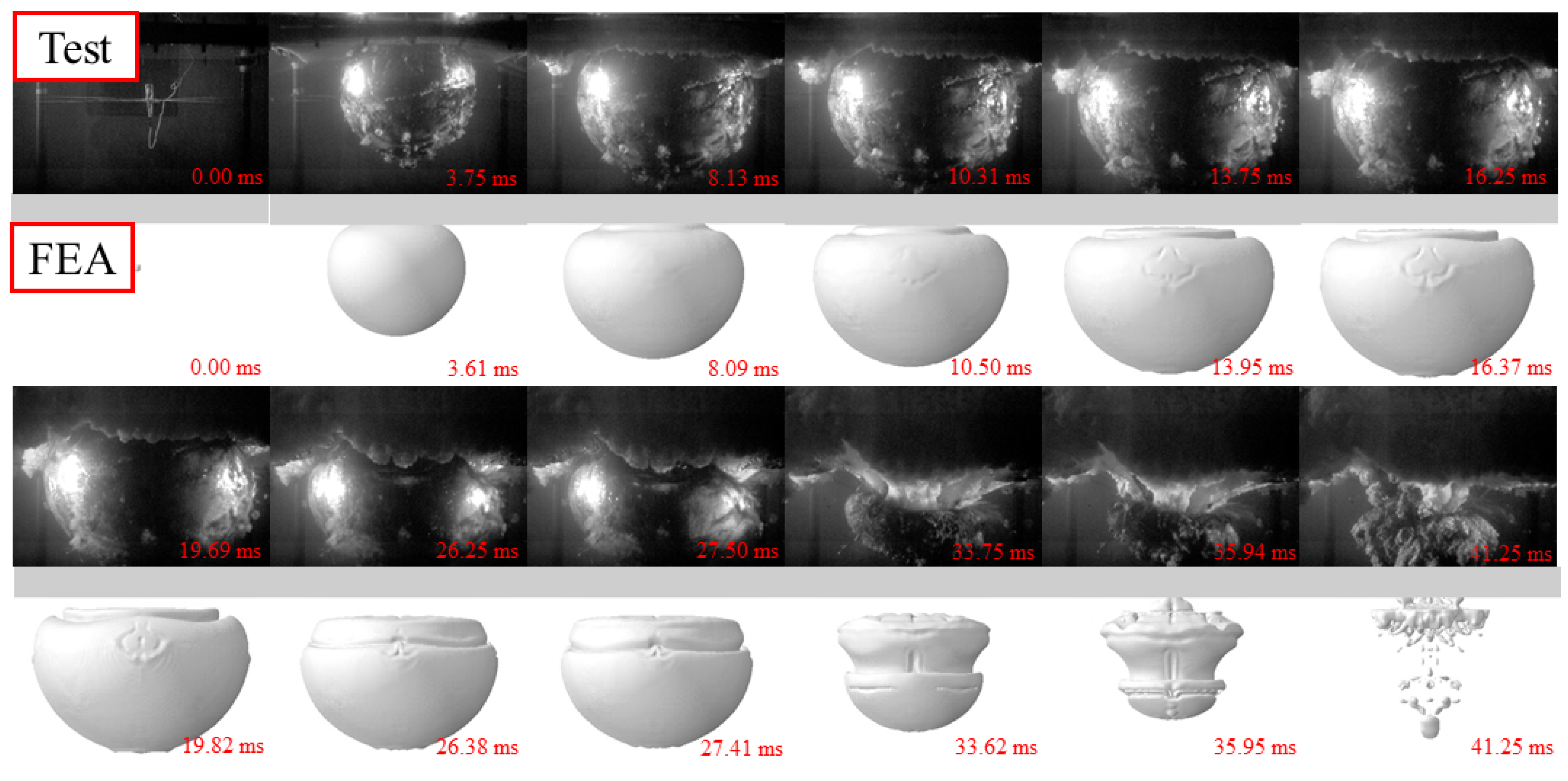
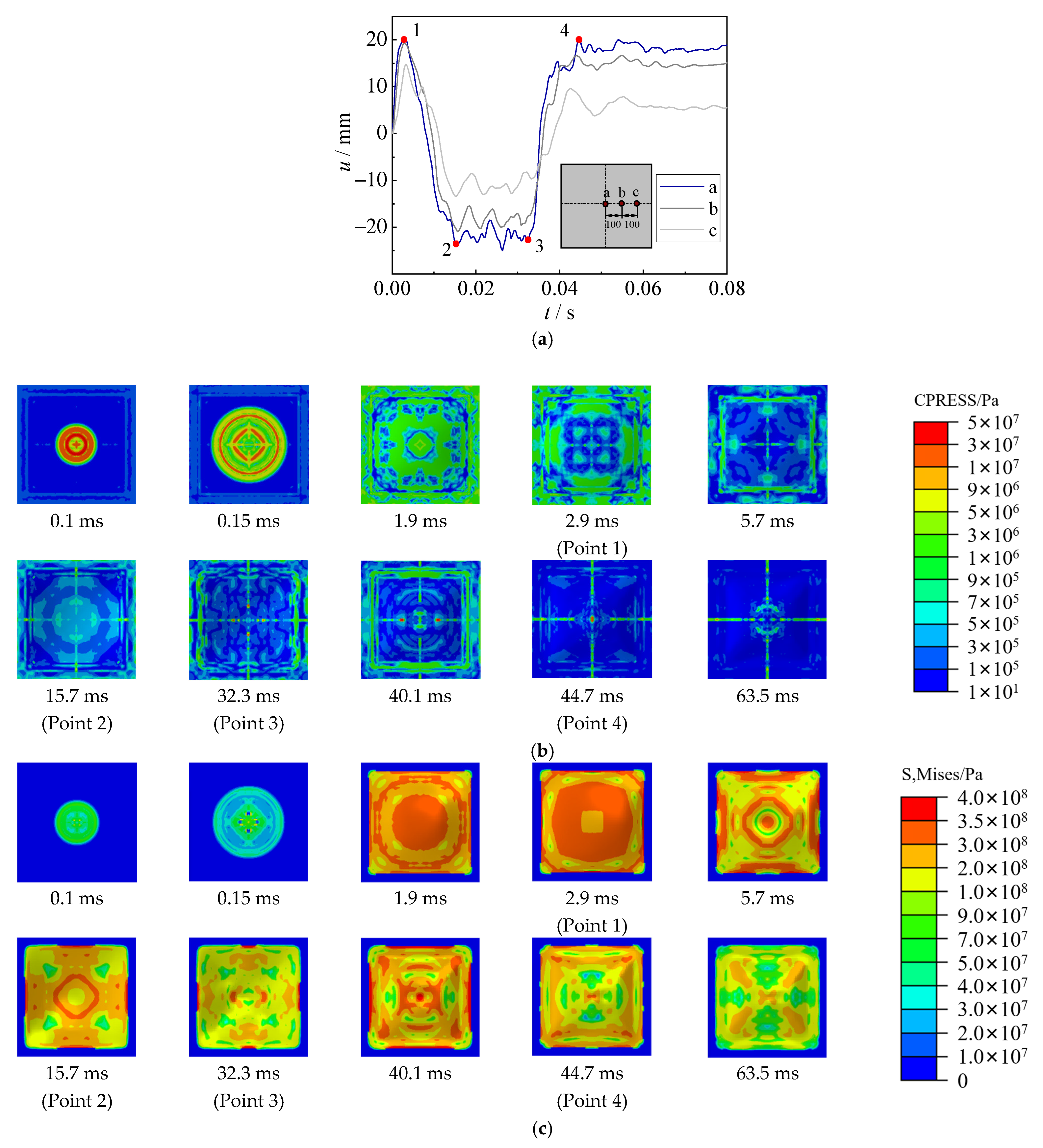
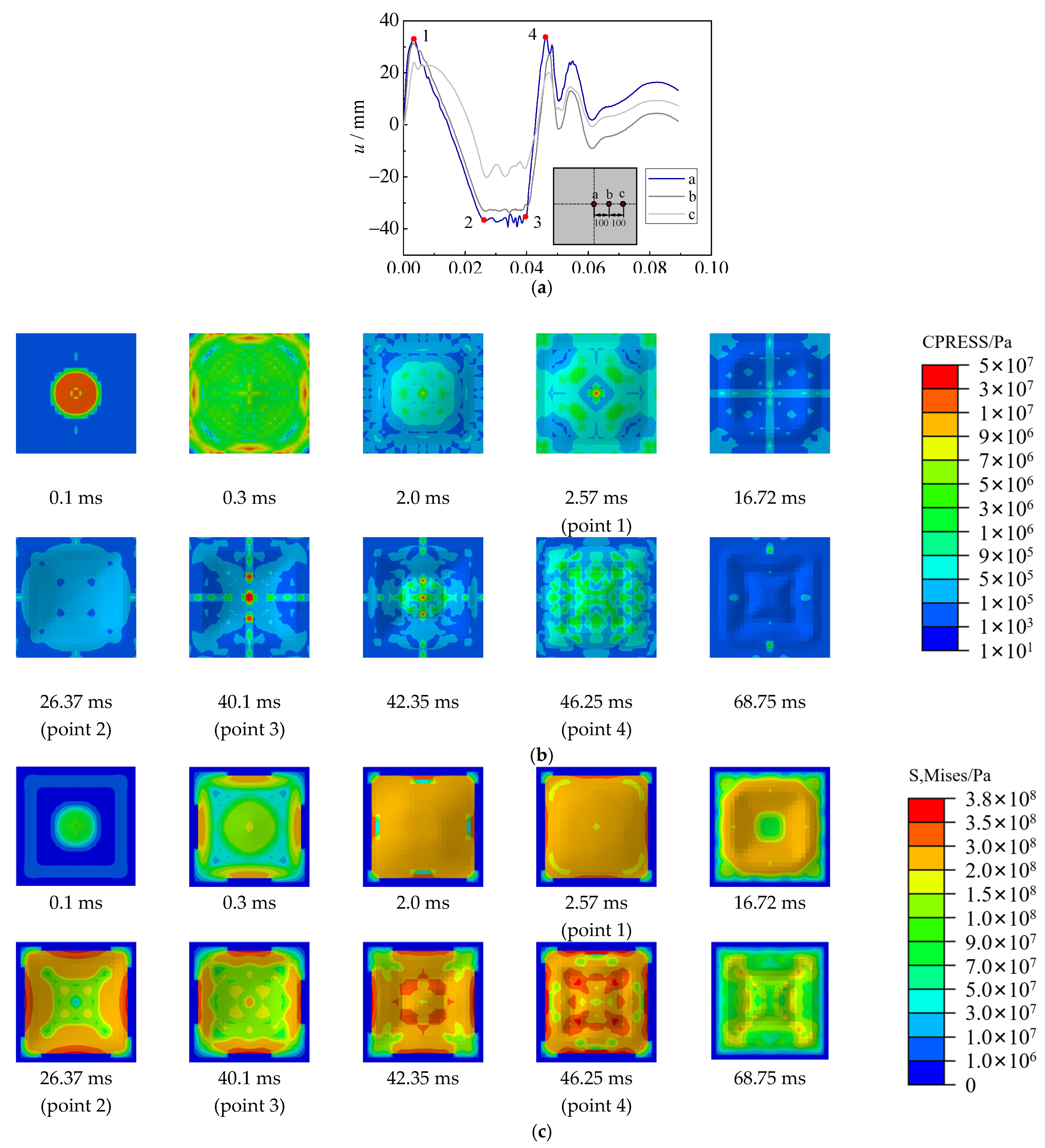
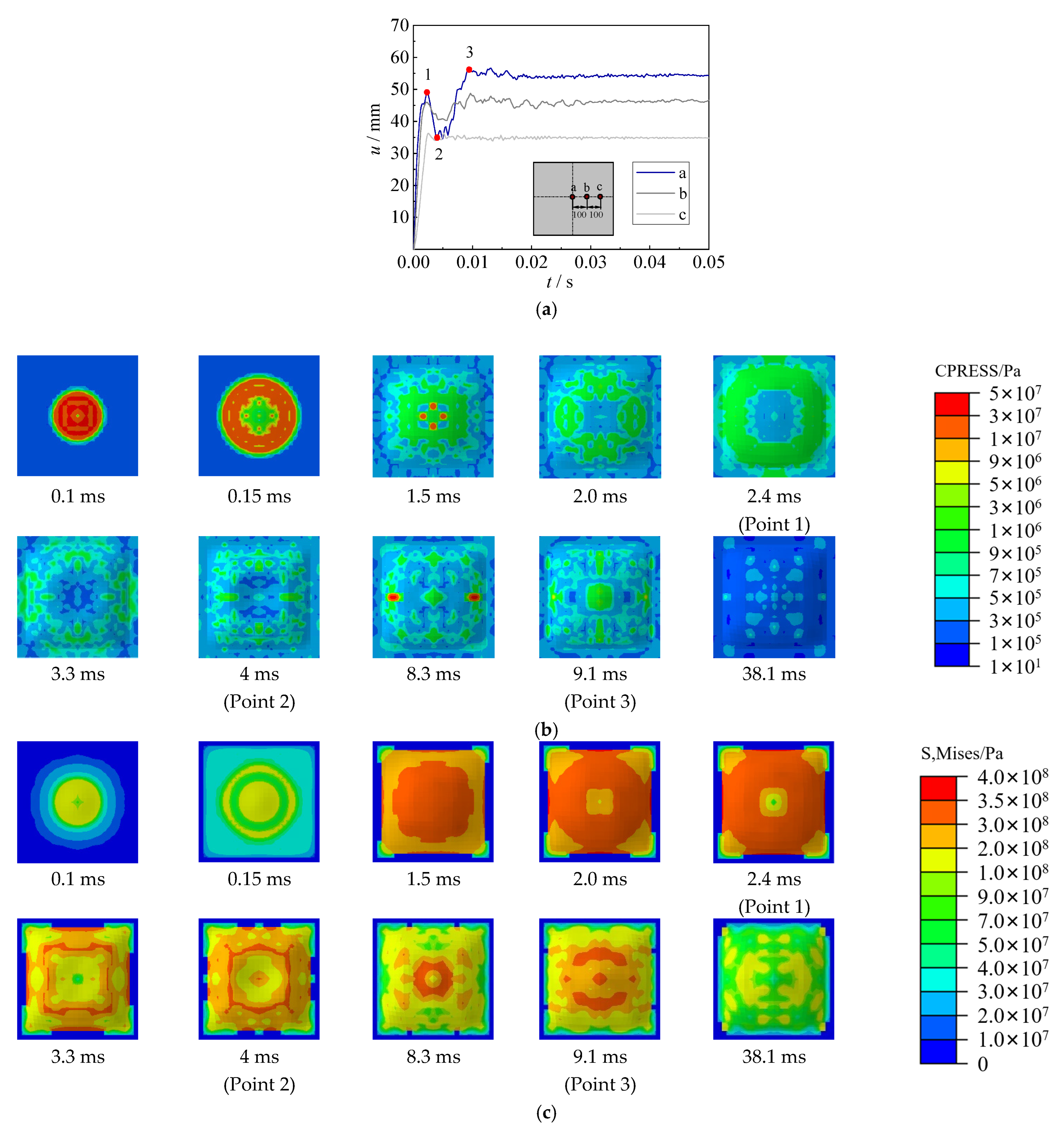
3.1. Process of Underwater Explosion
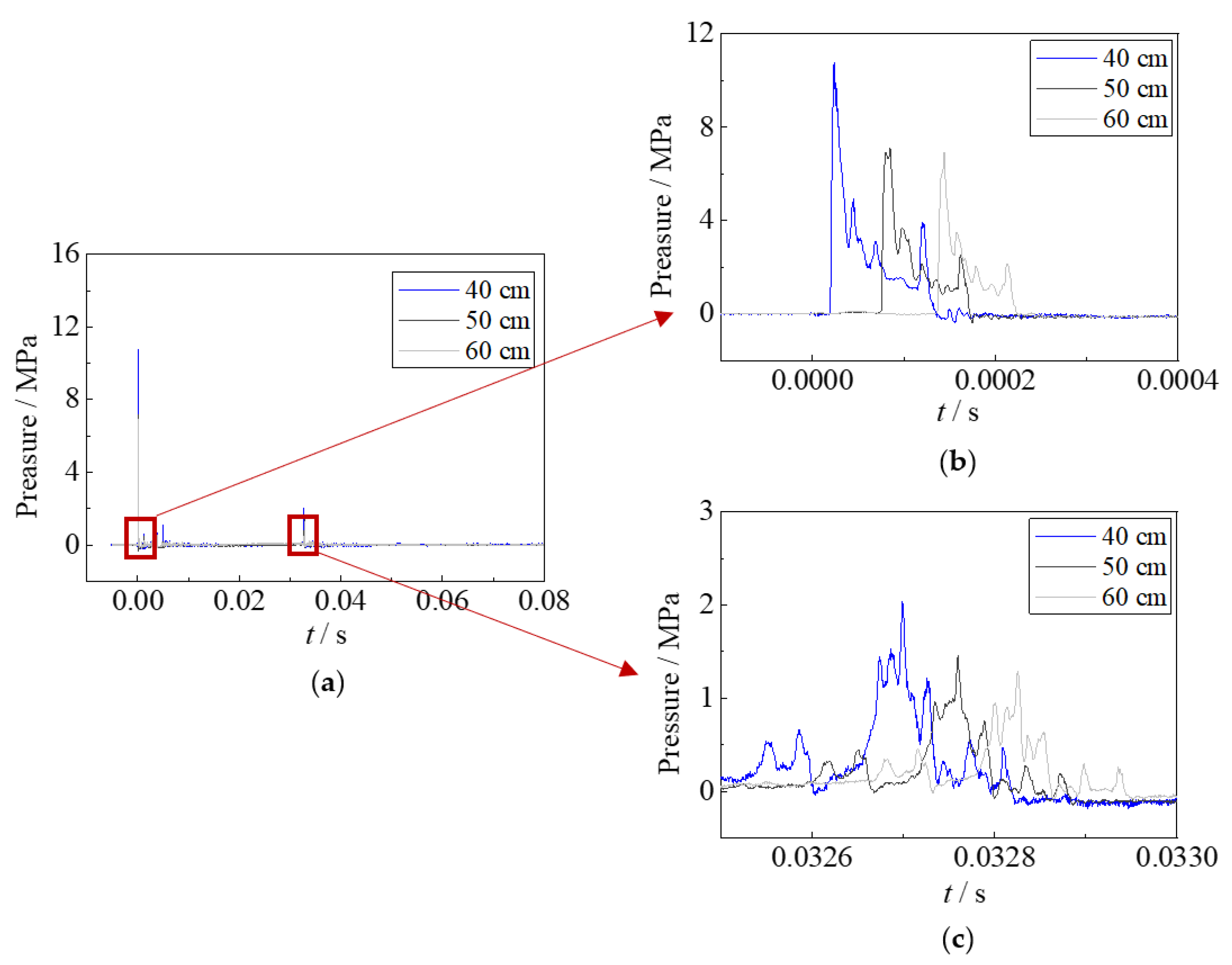
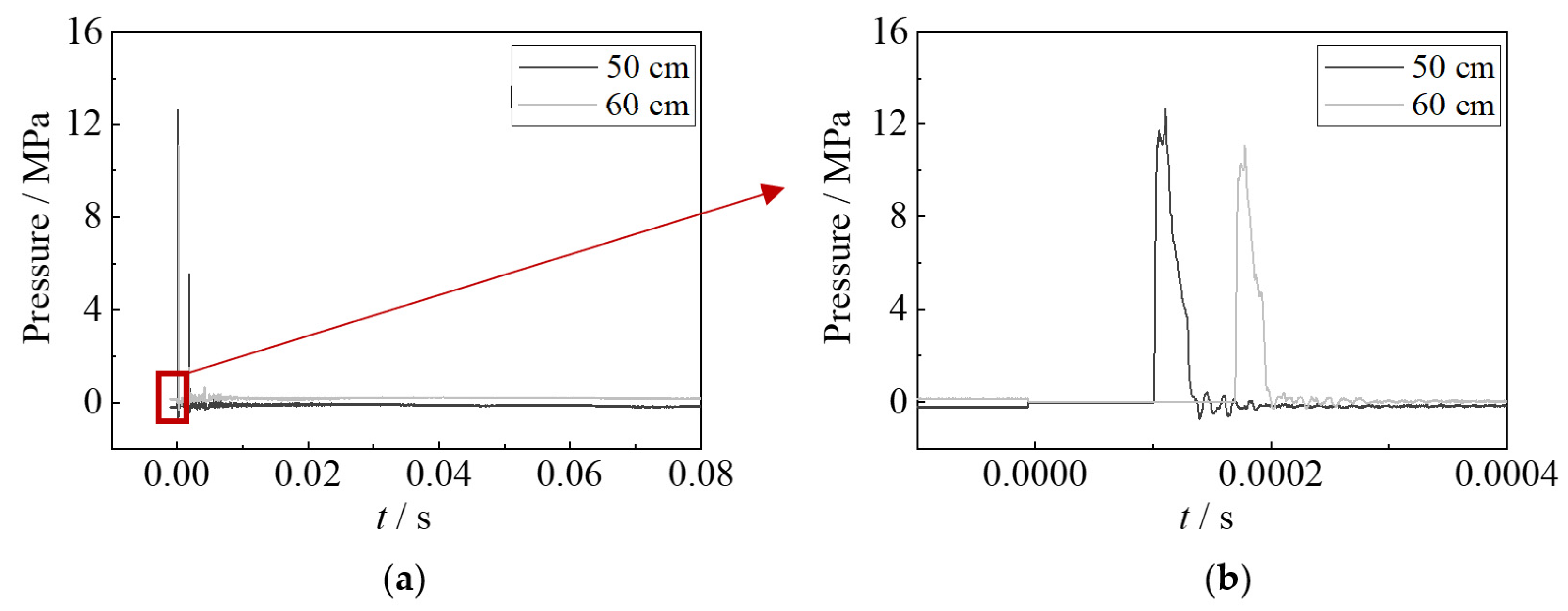
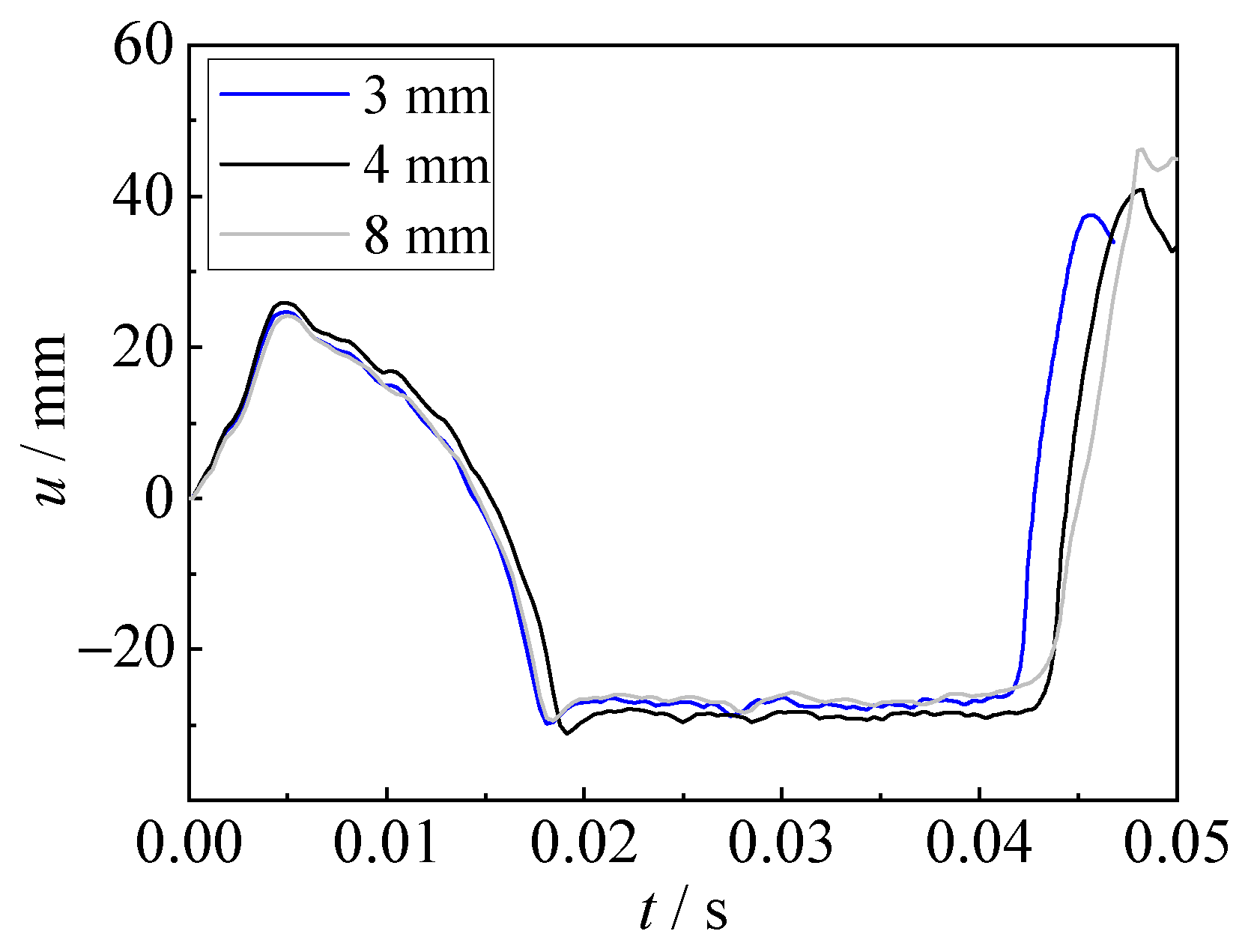
3.2. Impulsive Pressure
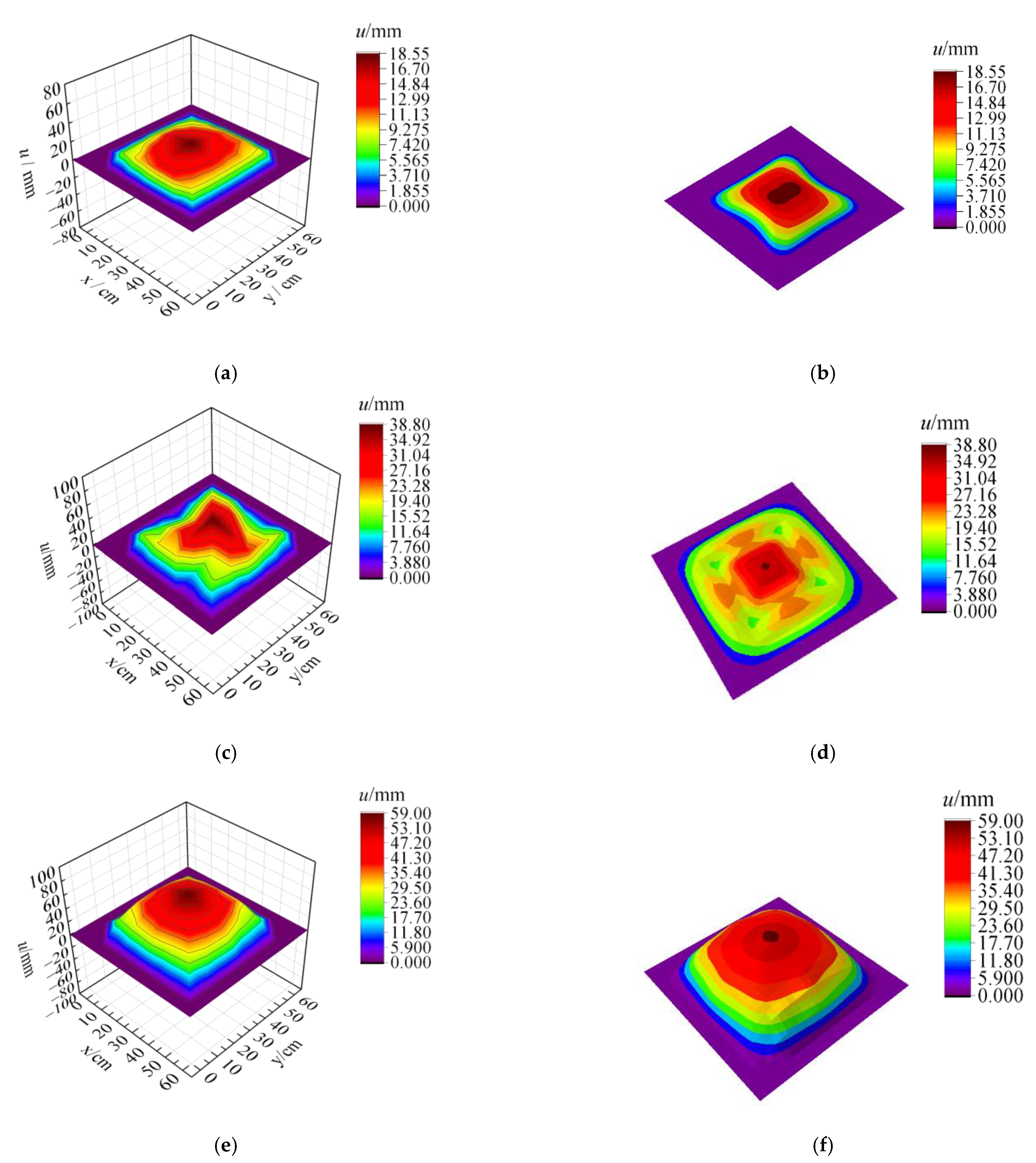
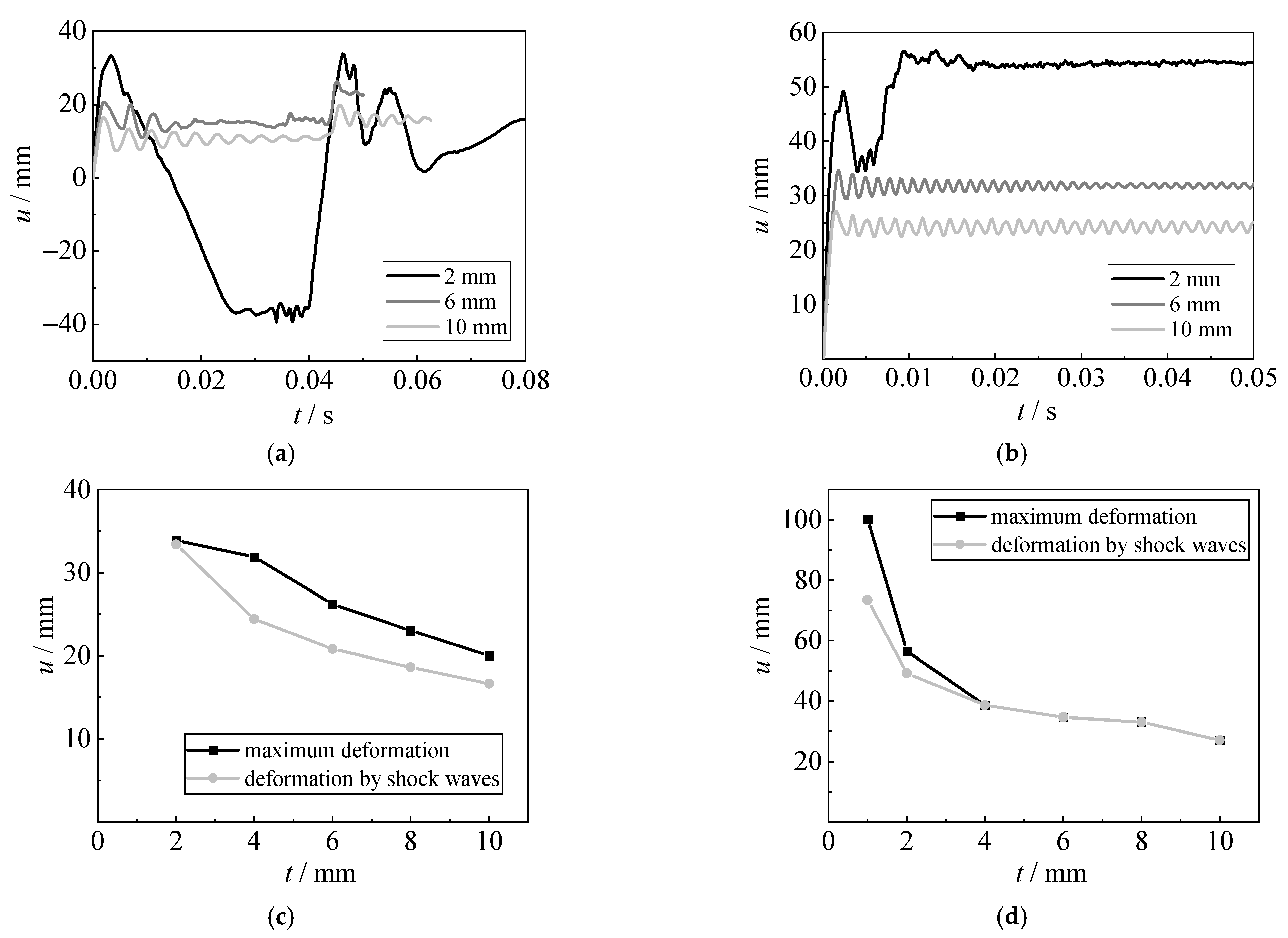
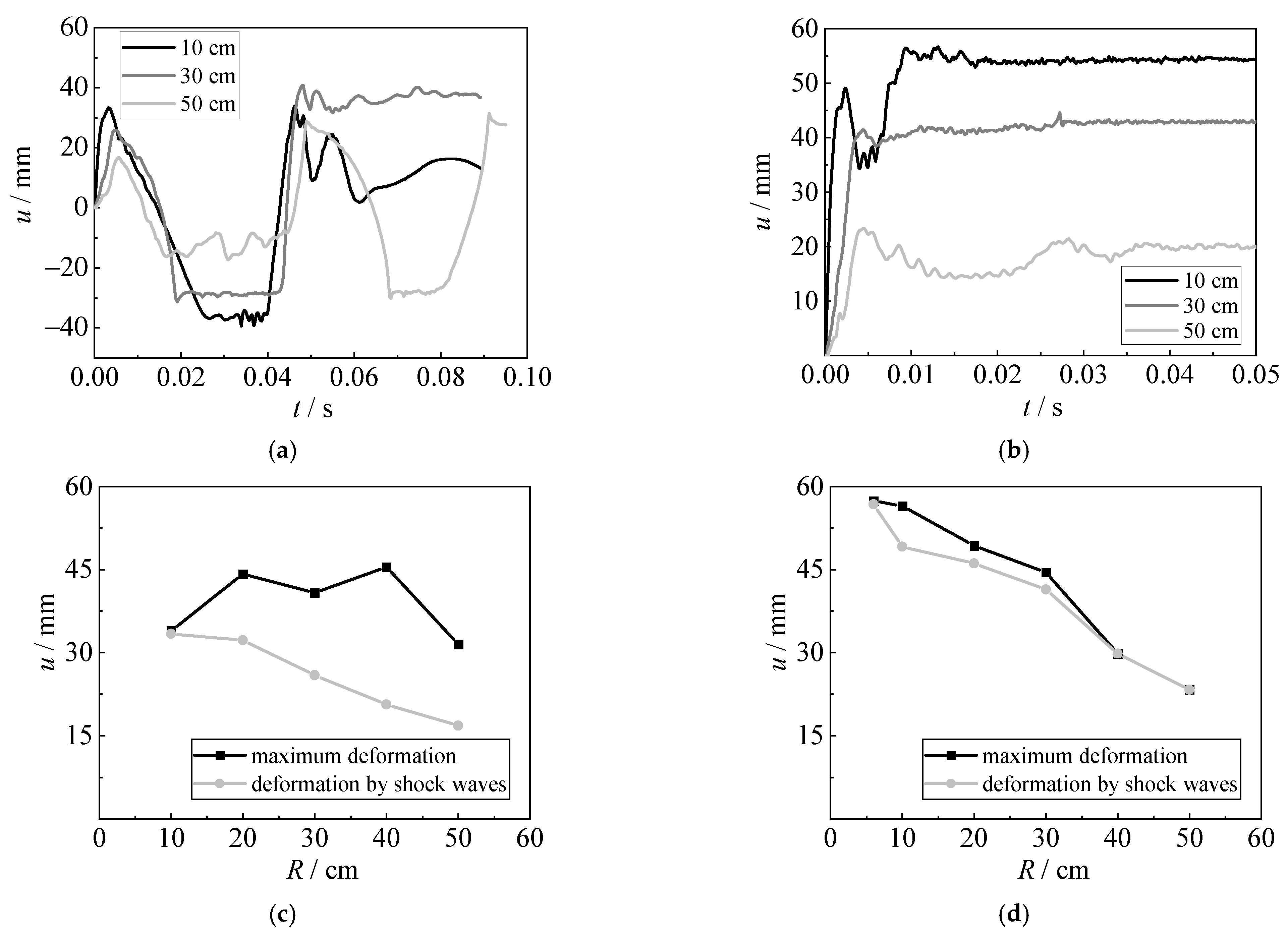
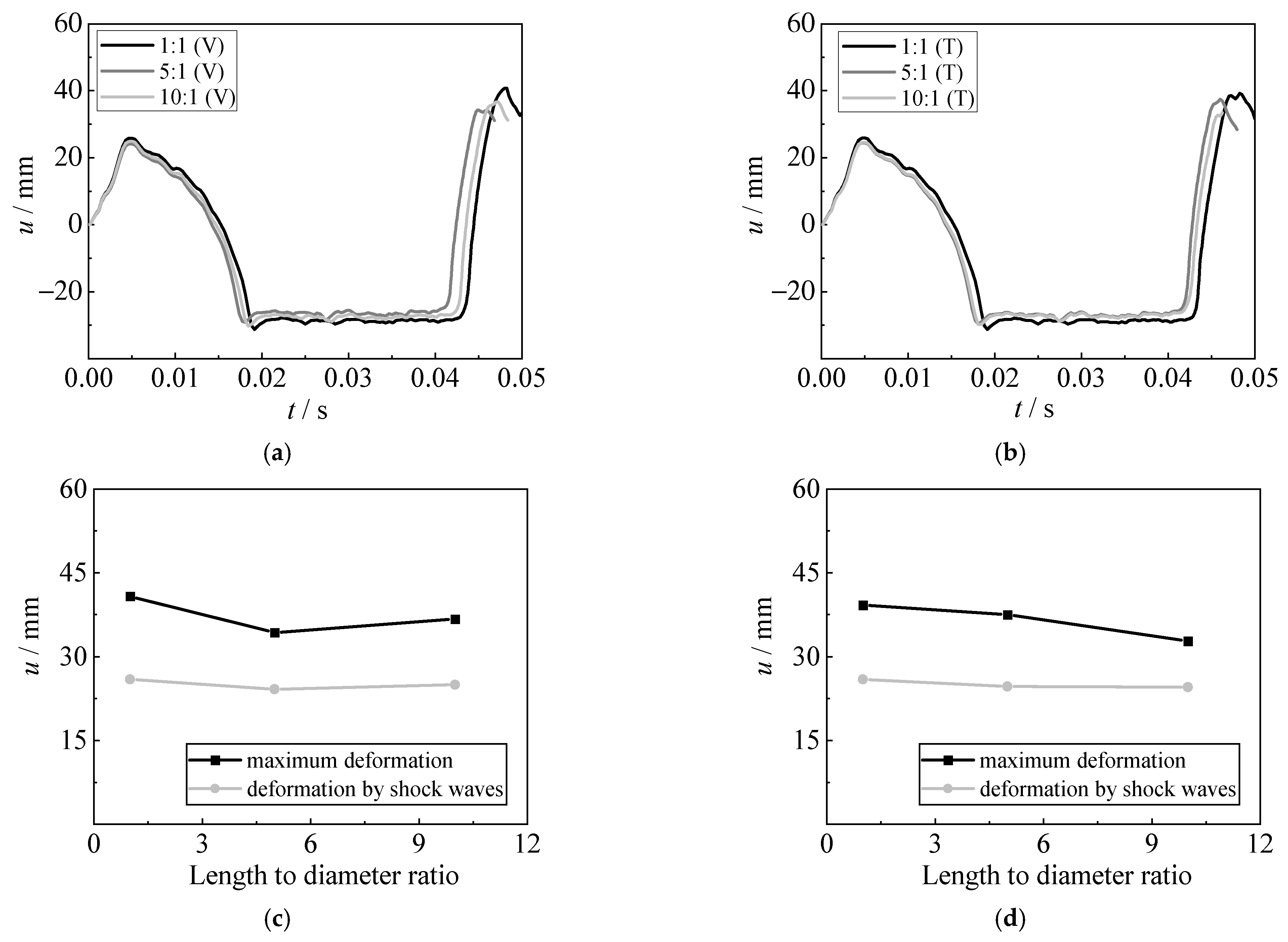
3.3. Deformation
4. Finite Element Analysis
4.1. Establishment of FE Model
4.1.1. Details of FE Model
4.1.2. Equation of State
- (1)
- Water
- (2)
- Air
- (3)
- Detonation
4.1.3. Dynamic Constitutive Model of Steel
4.2. FE Model Benchmarking
4.3. Mechanism of Underwater Explosion
4.4. Parametric Analysis
4.4.1. Effect of Steel Grade
4.4.2. Effect of Plate Thickness
4.4.3. Effect of Detonation Distance
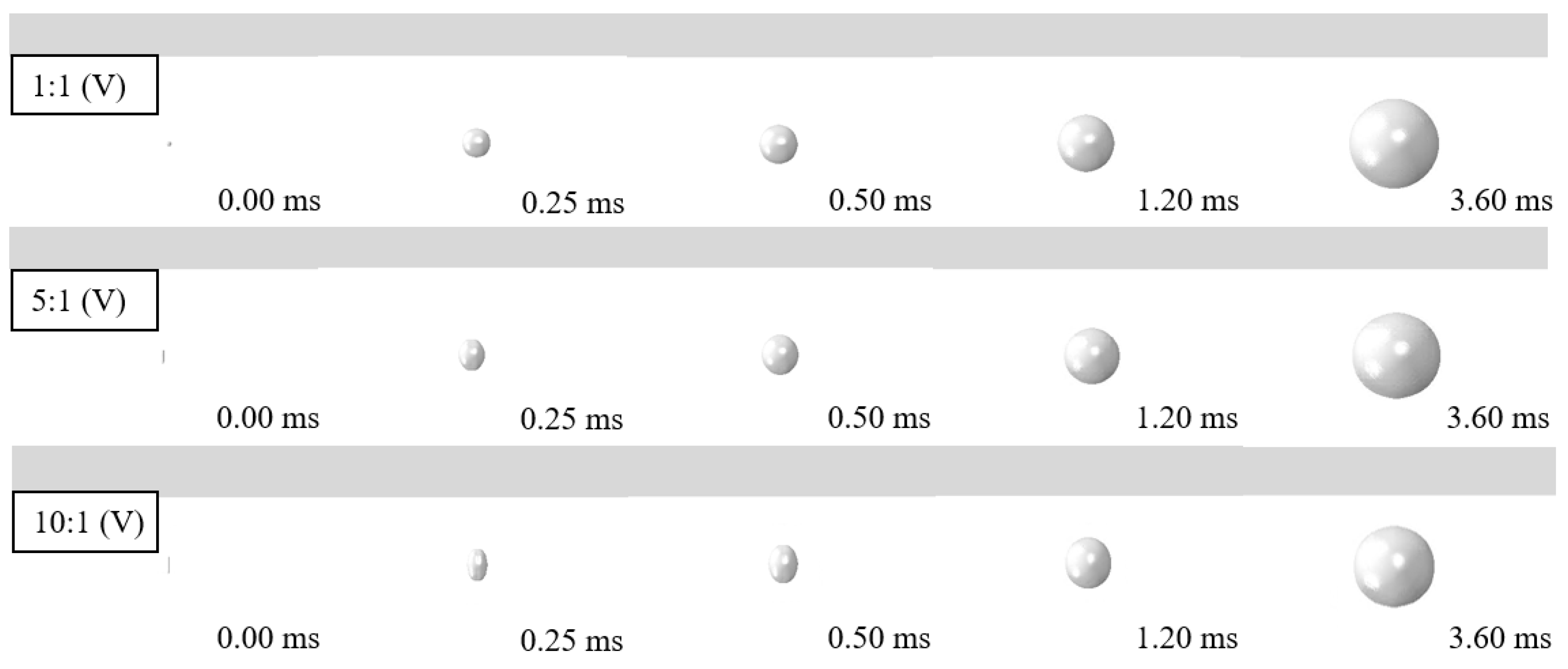
4.4.4. Effect of Shape and Position of the Charge
5. Conclusions
- 1.
- The steel sheet shows a process of hogging deformation, sagging deformation, and hogging deformation again, due to the actions of shock waves, bubble expansion, bubble collapse, and bubble pulsation. The air may be sucked into the bubble during the hogging process, making the bubble collapse earlier and resulting in a relatively lower sagging deformation for the explosions with a large charge weight of TNT.
- 2.
- The time duration of the impulsive pressure of bubble pulsation is relatively large, which is approximately three times that of shock waves. Although the impulsive pressure of bubble pulsation is lower than that of shock waves, the deformation caused by bubble pulsation is larger than that by the shock waves, owing to the large time duration of bubble pulsation.
- 3.
- The damage to the steel plate gradually decreases, with the increase in steel strength, plate thickness, and detonation distance. Using higher-strength steel and thicker steel sheet can reduce the deformation and improve the blast capacity of the steel sheet, especially for the deformation caused by bubble pulsation. The action of bubble pulsation becomes larger when the detonation distance increases to bubble radius (about 40 cm), resulting in the largest deformation. A limited influence on the dynamic behavior of steel sheets subjected to various shapes and positions of the charge was observed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cole, R.H. Underwater Explosion; Princeton University Press: Princeton, NJ, USA, 1948. [Google Scholar]
- Geers, T.L.; Hunter, K.S. An integrated wave-effects model for an underwater explosion bubble. J. Acoust. Soc. Am. 2002, 111, 1584–1601. [Google Scholar] [CrossRef] [PubMed]
- Klaseboer, E.; Hung, K.C.; Wang, C.; Wang, C.W.; Khoo, B.C.; Boyce, P.; Debono, S.; Charlier, H. Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure. J. Fluid Mech. 2005, 537, 387–413. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Wang, Y.X.; Zhao, H.F.; Qian, H.F.; Mou, J.L. An experimental study on the dynamic response of a hull girder subjected to near field underwater explosion. Mar. Struct. 2015, 44, 43–60. [Google Scholar] [CrossRef]
- Zong, Z.; Zhao, Y.J.; Li, H.T. A numerical study of whole ship structural damage resulting from close-in underwater explosion shock. Mar. Struct. 2013, 31, 24–43. [Google Scholar] [CrossRef]
- Rajendran, R.; Narasimhan, K. Damage prediction of clamped circular plates subjected to contact underwater explosion. Int. J. Impact Eng. 2001, 25, 373–386. [Google Scholar] [CrossRef]
- Wu, W.B.; Zhang, A.M.; Liu, Y.L.; Wang, S.P. Local discontinuous Galerkin method for far-field underwater explosion shock wave and cavitation. Appl. Ocean Res. 2019, 87, 102–110. [Google Scholar] [CrossRef]
- Jen, C.Y. Coupled acoustic–structural response of optimized ring-stiffened hull for scaled down submerged vehicle subject to underwater explosion. Theor. Appl. Fract. Mec. 2009, 52, 96–110. [Google Scholar] [CrossRef]
- Zhang, A.M.; Wang, S.P.; Huang, C.; Wang, B. Influences of initial and boundary conditions on underwater explosion bubble dynamics. Eur. J. Mech. B Fluids 2013, 42, 69–91. [Google Scholar] [CrossRef]
- Liu, N.N.; Cui, P.; Ren, S.F.; Zhang, A.M. Study on the interactions between two identical oscillation bubbles and a free surface in a tank. Phys. Fluids 2017, 29, 052104. [Google Scholar] [CrossRef]
- Wang, L.K.; Zhang, Z.F.; Shi, P. Pressure characteristics of bubble collapse near a rigid wall in compressible fluid. Appl. Ocean Res. 2016, 59, 183–192. [Google Scholar] [CrossRef]
- Liu, L.T.; Gan, N.; Wang, J.X.; Zhang, Y.F. Study on bubble collapse near a solid wall under different hyper gravity environments. Ocean Eng. 2021, 221, 108563. [Google Scholar] [CrossRef]
- Zhang, N.; Zong, Z. The effect of rigid-body motions on the whipping response of a ship hull subjected to an underwater bubble. J. Fluids Struct. 2011, 27, 1326–1336. [Google Scholar] [CrossRef]
- Klaseboer, E.; Khoo, B.C.; Hung, K.C. Dynamics of an oscillating bubble near a floating structure. J. Fluids Struct. 2005, 10, 395–412. [Google Scholar] [CrossRef]
- He, M.; Wang, S.P.; Ren, S.F.; Zhang, F. Numerical study of effects of stand-off distance and gravity on large scale bubbles near a breach. Appl. Ocean Res. 2021, 117, 102946. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Yao, X.L.; Cui, X.W.; Li, S.Y.; Liu, L.T. Study on the quantitative law of wall pressure caused by mini-charge underwater explosion bubble. Ocean Eng. 2020, 213, 107552. [Google Scholar]
- Liu, L.T.; Yao, X.L.; Zhang, A.M.; Sun, B.S. Research on the estimate formulas for underwater explosion bubble jet parameters. Ocean Eng. 2018, 164, 563–576. [Google Scholar] [CrossRef]
- Tian, Z.L.; Liu, Y.L.; Zhang, A.M.; Tao, L.; Chen, L. Jet development and impact load of underwater explosion bubble on solid wall. Appl. Ocean Res. 2022, 95, 102013. [Google Scholar] [CrossRef]
- Cui, P.; Zhang, A.M.; Wang, S.P. Small-charge underwater explosion bubble experiments under various boundary conditions. Phys. Fluids 2016, 28, 117103. [Google Scholar] [CrossRef]
- Zhang, A.M.; Zhou, W.X.; Wang, S.P.; Feng, L.H. Dynamic response of the non-contact underwater explosion on naval equipment. Mar. Struct. 2011, 24, 396–411. [Google Scholar]
- Jiang, X.W.; Zhang, W.; Li, D.C.; Chen, T.; Tang, Y.; Guo, Z.T. Experimental analysis on dynamic response of pre-cracked aluminum plate subjected to underwater explosion shock loadings. Thin-Walled Struct. 2020, 159, 107256. [Google Scholar] [CrossRef]
- Leblanc, J.; Shukla, A. Underwater explosion response of curved composite plates. Compos. Struct. 2015, 134, 716–725. [Google Scholar] [CrossRef]
- Jin, Z.Y.; Yin, C.Y.; Chen, Y.; Hua, H.X. Numerical study on the interaction between underwater explosion bubble and a moveable plate with basic characteristics of a sandwich structure. Ocean Eng. 2018, 164, 508–520. [Google Scholar] [CrossRef]
- Zhang, A.M.; Yao, X.L.; Li, J. The interaction of an underwater explosion bubble and an elastic–plastic structure. Appl. Ocean Res. 2008, 30, 159–171. [Google Scholar] [CrossRef]
- Li, S.; Khoo, B.C.; Zhang, A.M.; Wang, S. Bubble-sphere interaction beneath a free surface. Ocean Eng. 2018, 169, 469–483. [Google Scholar] [CrossRef]
- Li, S.; Meer, D.V.D.; Zhang, A.M.; Prosperetti, A.; Lohse, D. Modelling large scale airgun-bubble dynamics with highly non-spherical features. Int. J. Multiphas. Flow 2020, 122, 103143. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, A.M.; Cui, P.; Li, T. Simulation of air gun bubble motion in the presence of air gun body based on the finite volume method. Appl. Ocean Res. 2020, 97, 102095. [Google Scholar] [CrossRef]
- Gan, N.; Liu, L.T.; Yao, X.L.; Wang, J.X.; Wu, W.B. Experimental and numerical investigation on the dynamic response of a simplified open floating slender structure subjected to underwater explosion bubble. Ocean Eng. 2020, 219, 108308. [Google Scholar] [CrossRef]
- Lee, E.L.; Hornig, H.C. Equation of state of detonation product gases. Symp. Int. Combust. 1969, 12, 493–499. [Google Scholar] [CrossRef]
- Yang, X.Q.; Yang, H.; Gardner, L.; Wang, Y.Y. A continuous dynamic constitutive model for normal-and high-strength structural steels. J. Constr. Steel Res. 2022, 192, 107254. [Google Scholar] [CrossRef]




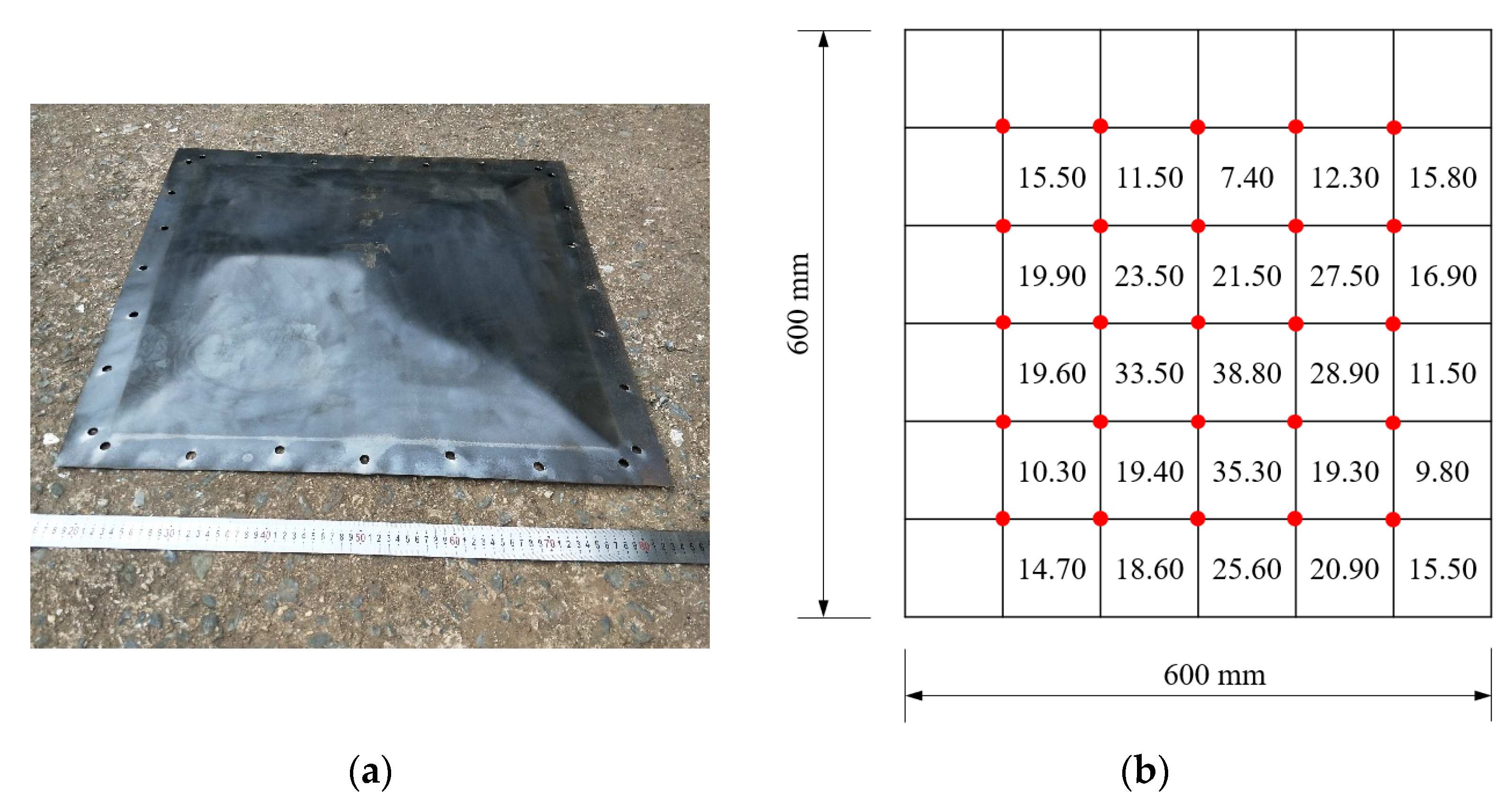
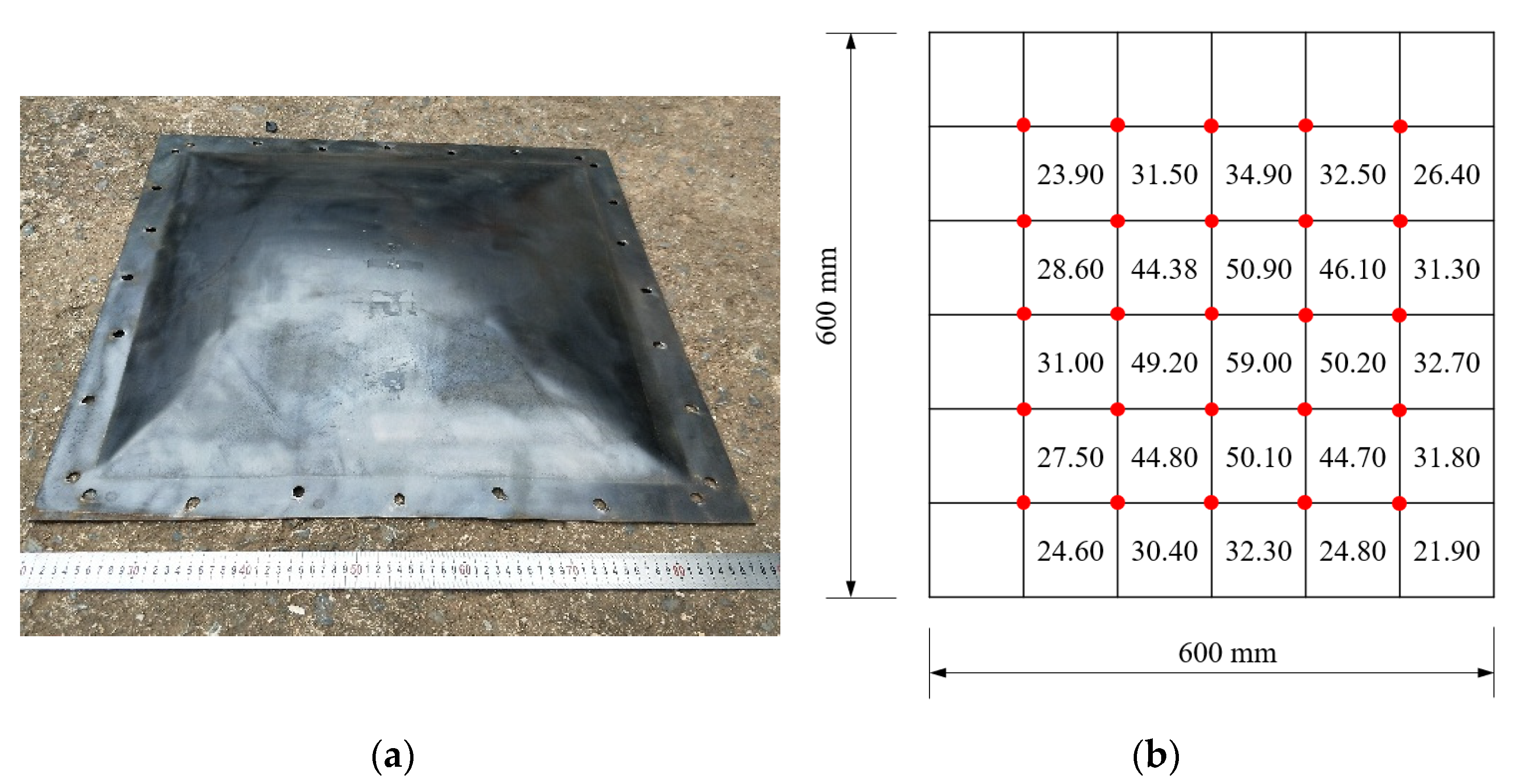



| No. | Specimen Dimension (B × B × ts mm) | Steel Grade | Charge Type | R (mm) | W (g) |
|---|---|---|---|---|---|
| 1 | 600 × 600 × 2 | Q235 | TNT | 100 | 2.5 |
| 2 | 5 | ||||
| 3 | 10 |
| No. | Parameters | Dimensions (B × B mm) | Length-to-Diameter Ratio of the Charge | W (g) | Steel Grade | Thickness ts (mm) | R (mm) |
|---|---|---|---|---|---|---|---|
| 1 | Steel grade | 600 × 600 | 1:1 (V) | 10 | Q235 | 2 | 100 |
| 2 | Q355 | ||||||
| 3 | Q460 | ||||||
| 4 | Q550 | ||||||
| 5 | Q690 | ||||||
| 6 | 1:1 (V) | 5 | Q235 | 2 | 100 | ||
| 7 | Q355 | ||||||
| 8 | Q460 | ||||||
| 9 | Q550 | ||||||
| 10 | Q690 | ||||||
| 11 | Thickness | 600 × 600 | 1:1 (V) | Q235 | 1 | 100 | |
| 12 | 4 | ||||||
| 13 | 10 | 6 | |||||
| 14 | 8 | ||||||
| 15 | 10 | ||||||
| 16 | 1:1 (V) | 5 | Q235 | 4 | 100 | ||
| 17 | 6 | ||||||
| 18 | 8 | ||||||
| 19 | 10 | ||||||
| 20 | Detonation distance | 600 × 600 | 1:1 (V) | 10 | Q235 | 2 | 60 |
| 21 | 200 | ||||||
| 22 | 300 | ||||||
| 23 | 400 | ||||||
| 24 | 500 | ||||||
| 25 | 1:1 (V) | 5 | Q235 | 2 | 200 | ||
| 26 | 300 | ||||||
| 27 | 400 | ||||||
| 28 | 500 | ||||||
| 29 | Length-to-diameter ratio | 600 × 600 | 1:1 (T) | 5 | Q235 | 2 | 300 |
| 30 | 5:1 (V) | ||||||
| 31 | 5:1 (T) | ||||||
| 32 | 10:1 (V) | ||||||
| 33 | 10:1 (T) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Qin, J.; Deng, S.; Meng, X.; Huang, R.; Yang, X. Experimental and Numerical Studies on Fixed Steel Sheets Subjected to Underwater Explosion. Materials 2022, 15, 6419. https://doi.org/10.3390/ma15186419
Chen S, Qin J, Deng S, Meng X, Huang R, Yang X. Experimental and Numerical Studies on Fixed Steel Sheets Subjected to Underwater Explosion. Materials. 2022; 15(18):6419. https://doi.org/10.3390/ma15186419
Chicago/Turabian StyleChen, Si, Jian Qin, Shuo Deng, Xiangyao Meng, Ruiyuan Huang, and Xiaoqiang Yang. 2022. "Experimental and Numerical Studies on Fixed Steel Sheets Subjected to Underwater Explosion" Materials 15, no. 18: 6419. https://doi.org/10.3390/ma15186419
APA StyleChen, S., Qin, J., Deng, S., Meng, X., Huang, R., & Yang, X. (2022). Experimental and Numerical Studies on Fixed Steel Sheets Subjected to Underwater Explosion. Materials, 15(18), 6419. https://doi.org/10.3390/ma15186419





