Influence of the Heterogeneity of the Core Material on the Local Instability of a Sandwich Panel
Abstract
:1. Introduction
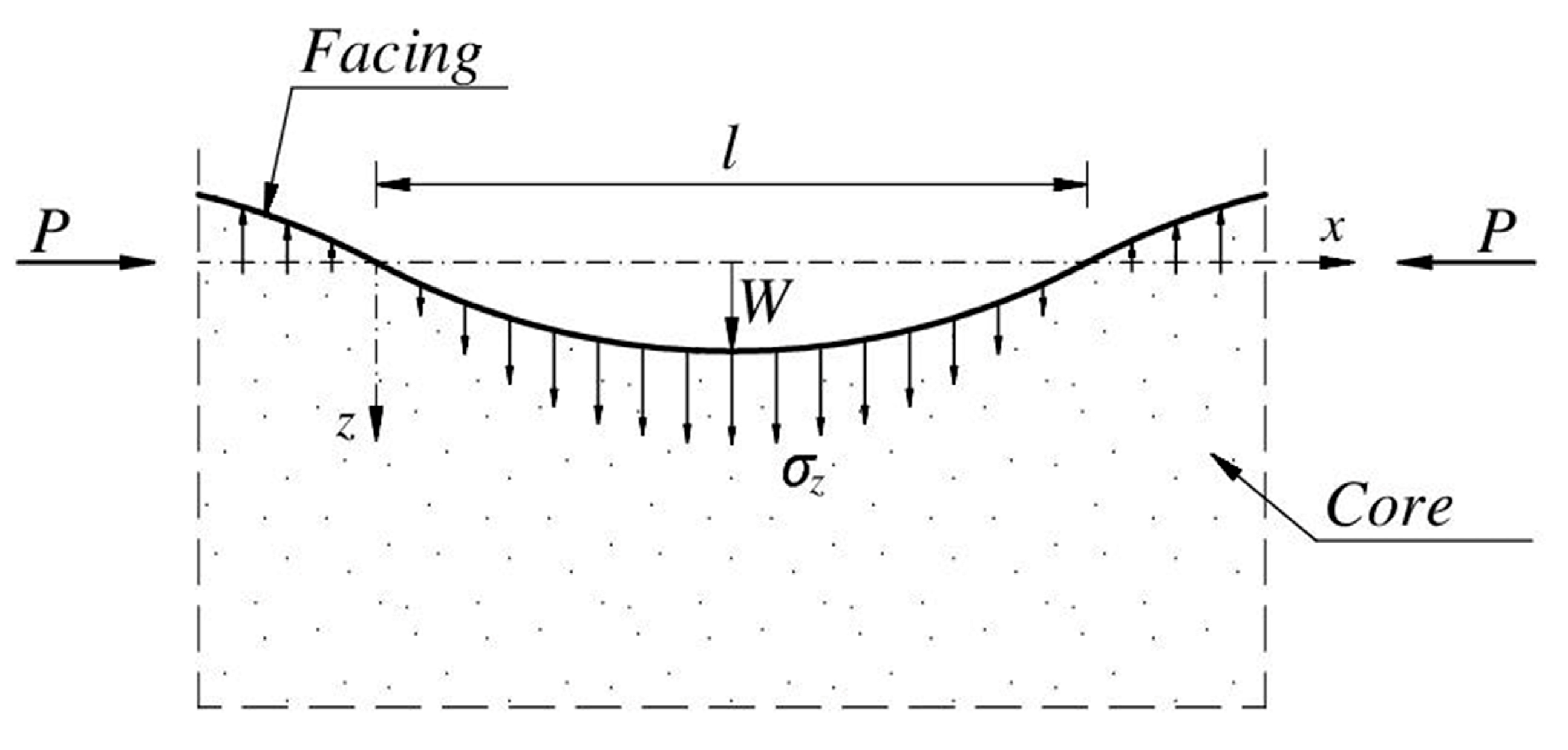
2. Formulation of the Problem
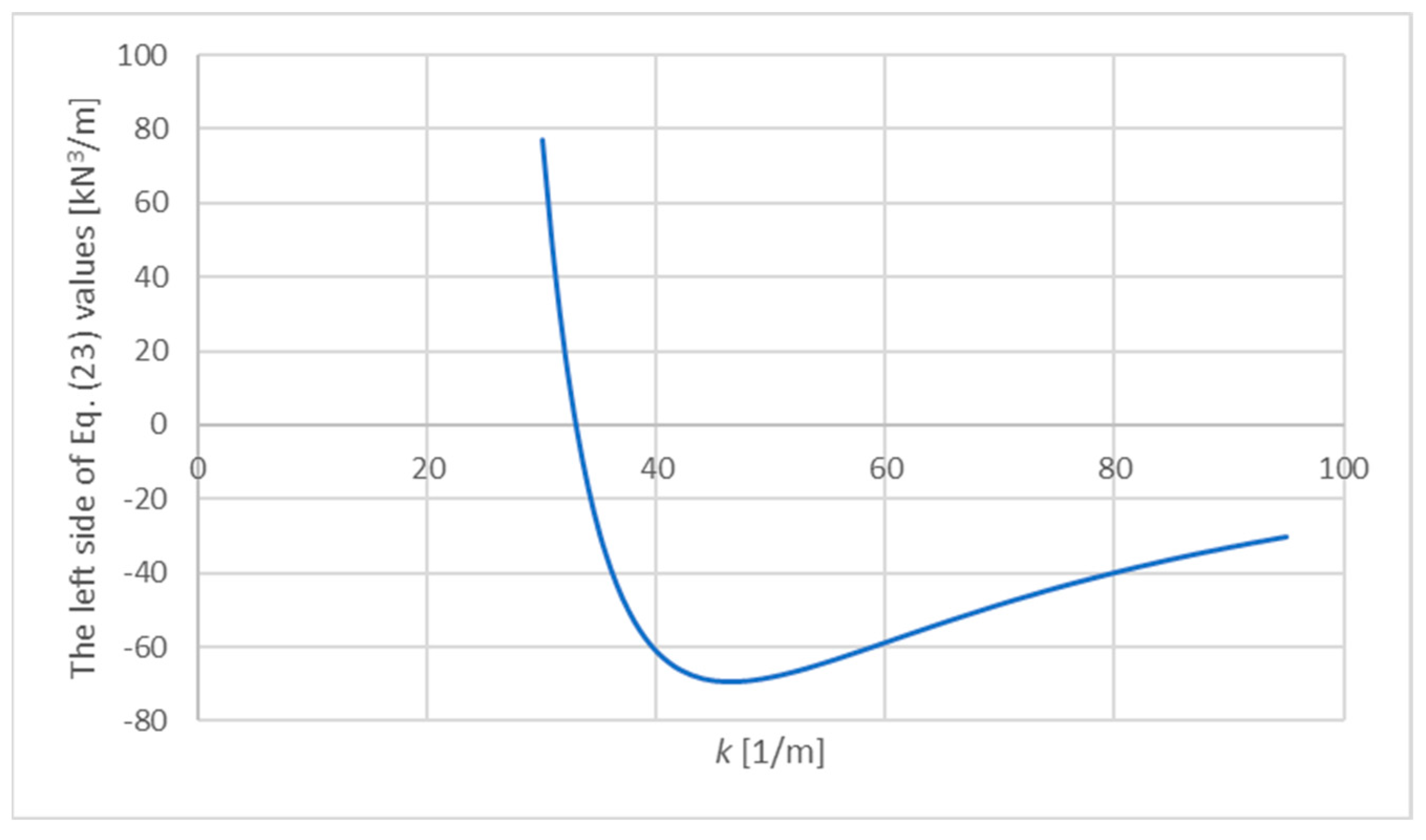
3. Determination of the Wrinkling Stress
3.1. General Equations
3.2. Exponential Function of Material Parameters
3.3. Polynomial Function of Material Parameters
4. Examples
4.1. Material Parameters
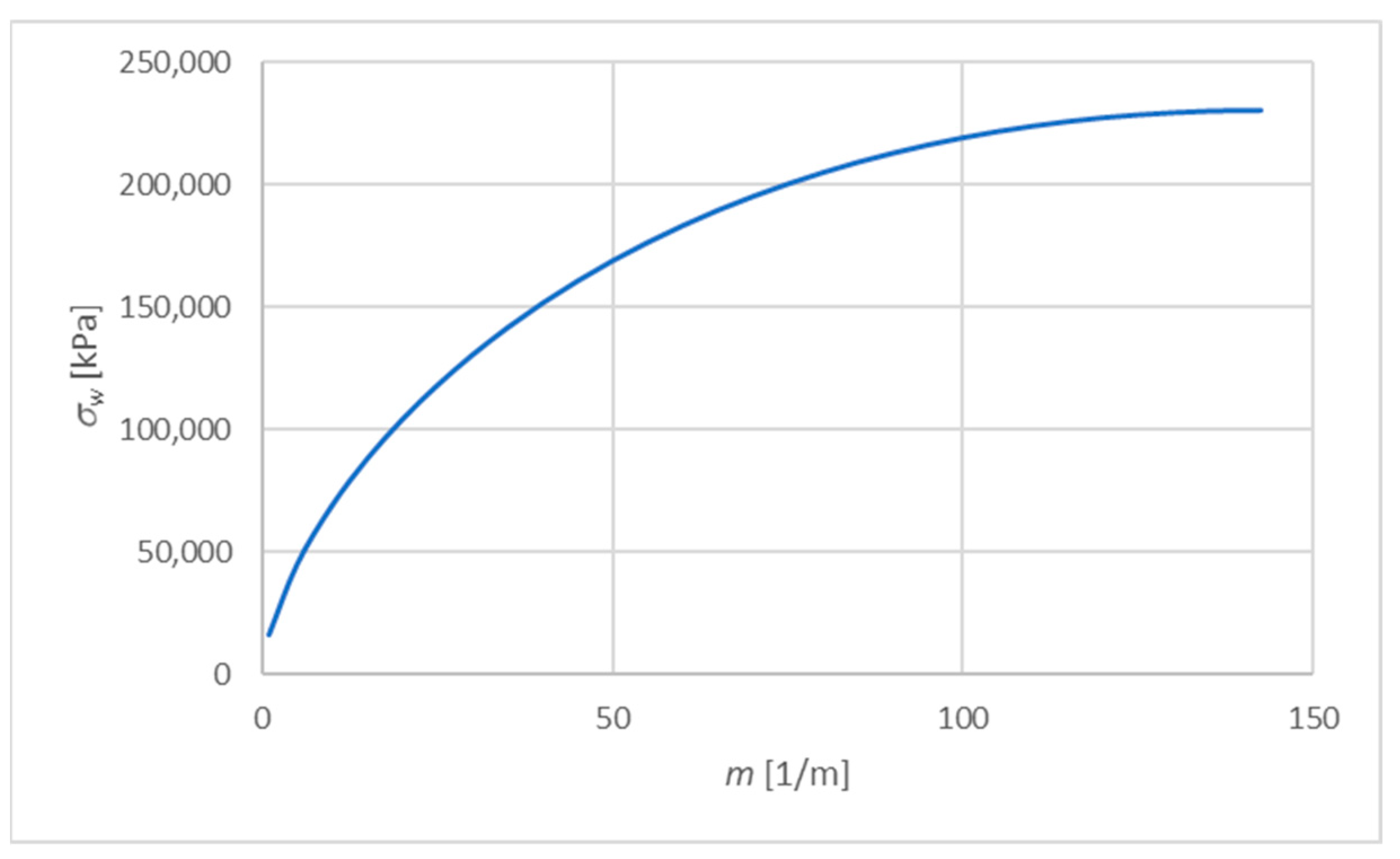
4.2. The Exponential Function
4.3. The Polynomial Function
4.4. Comparison of the Results
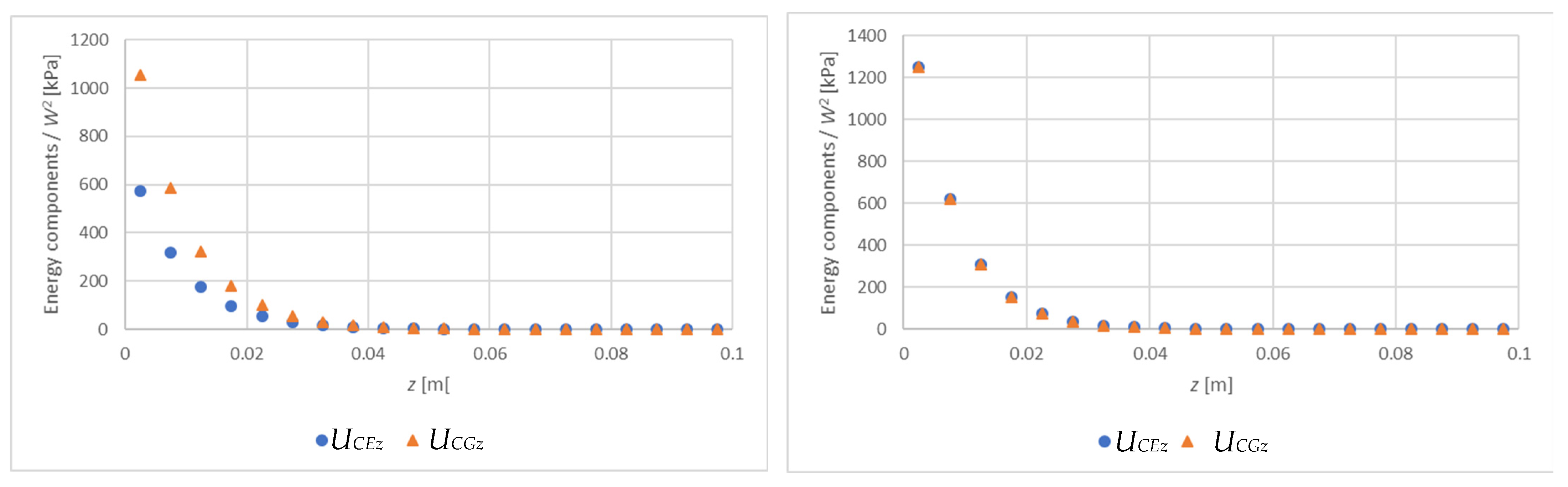
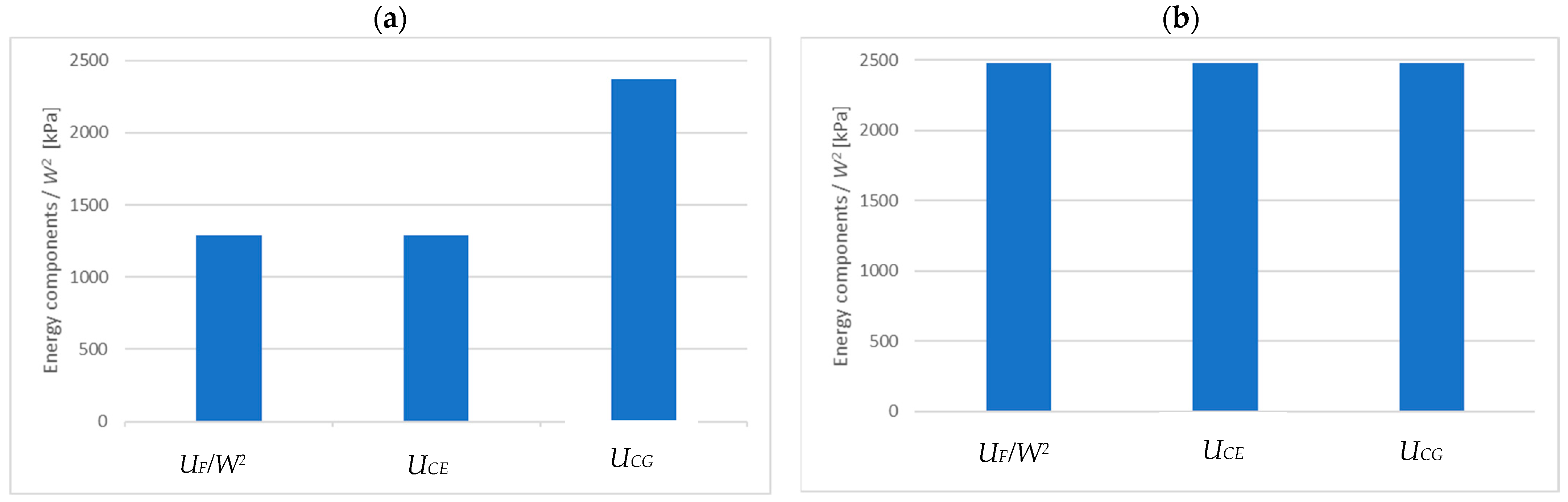
5. Energy Considerations
6. Optimal Distribution of Material Parameters
7. Conclusions
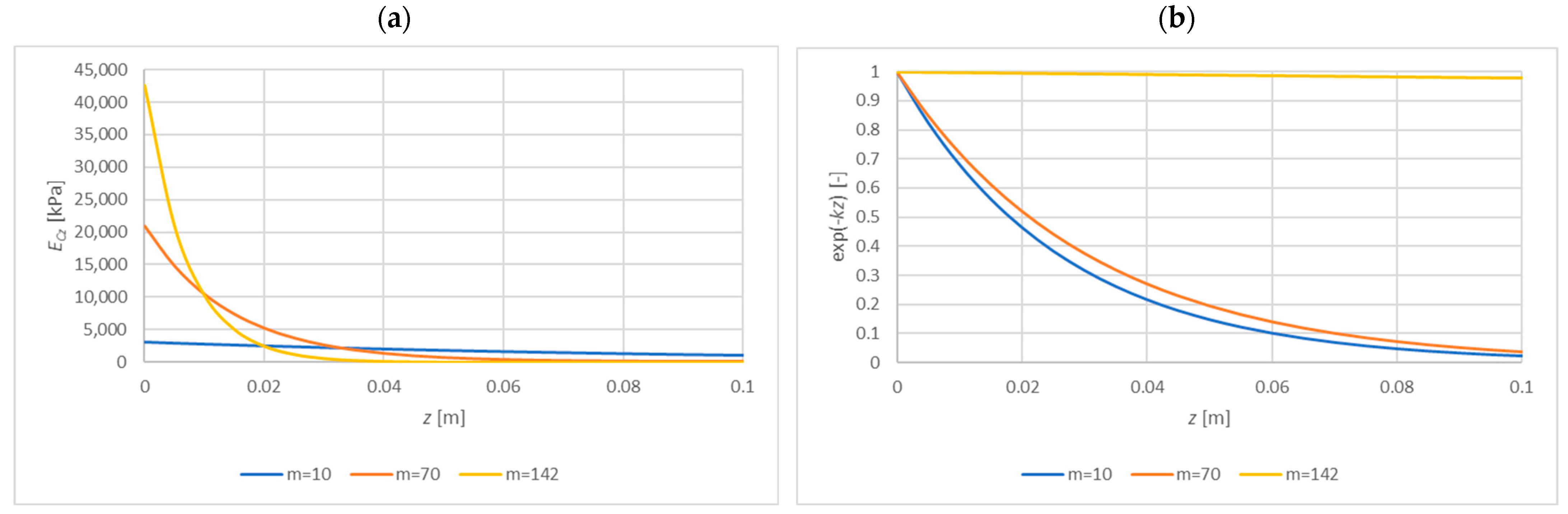
- More than 90% of the strain energy of the core is stored to a depth of about 2 cm from the facing, which means that the value of the wrinkling stress is mainly determined by the layer adjacent to the facing;
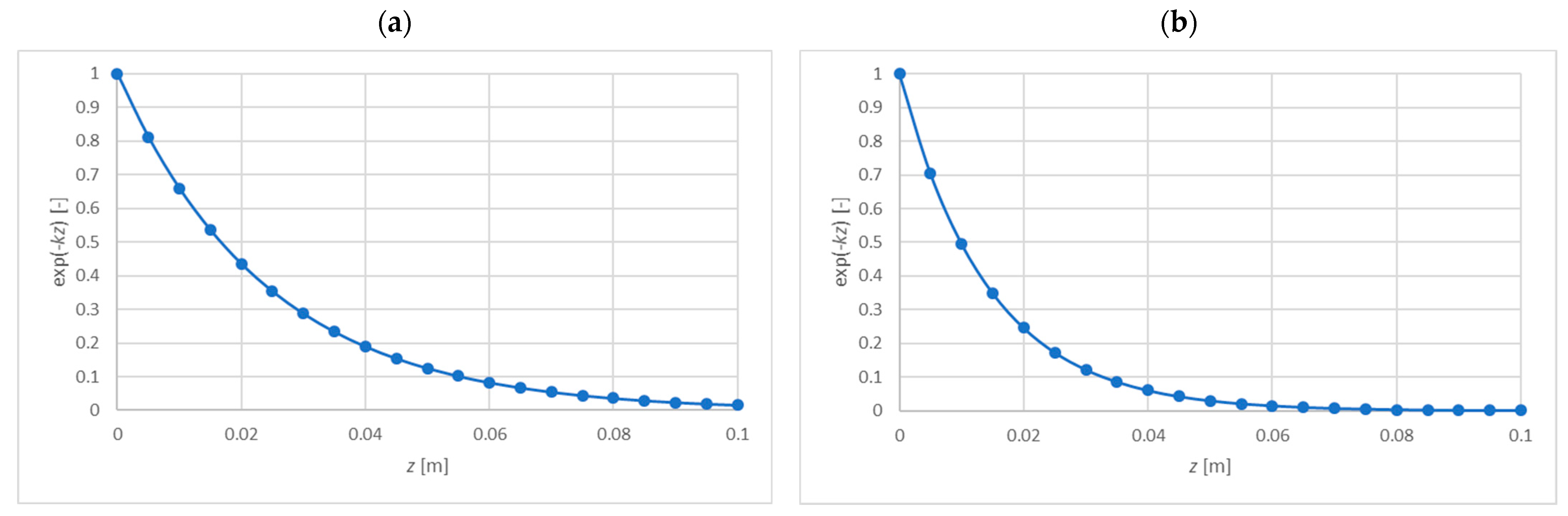
- Core deformation is reduced by 90% at a depth of 6 cm (core with variable parameters) or at a depth of 3.5 cm (core with constant parameters), which means that considering the theoretical case of an infinitely thick core is acceptable in most cases;
- The strain energy of the facing deformation is always equal to the normal strain energy of the core; the shear strain energy of the core is equal to them only when the core parameters are constant across the thickness;
- In the case of non-linear (disappearing with thickness) distribution of core material parameters, the shear strain energy of the core has a decisive influence on the wrinkling stress.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hoff, N.J.; Mautner, S.E. Buckling of Sandwich Type Panels. J. Aeronaut. Sci. 1945, 12, 285–297. [Google Scholar] [CrossRef]
- Plantema, F.J. Sandwich Construction; The Bending and Buckling of Sandwich Beams, Plates and Shells; John Wiley & Sons, Inc.: New York, NY, USA, 1966. [Google Scholar]
- Allen, H.G. Analysis and Design of Structural Sandwich Panels; Pergamon Press: Oxford, UK, 1969. [Google Scholar]
- Norris, C.B.; Ericksen, W.S.; March, H.W.; Smith, C.B.; Boller, K.H. Wrinkling of the Facing of Sandwich Construction Subjected to Edgewise Compression; Report No. 1810; Forest Products Laboratory: Madison, WI, USA, 1961. [Google Scholar]
- Vonach, W.K.; Rammerstorfer, F.G. Wrinkling of thick orthotropic sandwich plates under general loading conditions. Arch. Appl. Mech. 2000, 70, 338–348. [Google Scholar] [CrossRef]
- Birman, V.; Bert, C.W. Wrinkling of composite-facing sandwich panels under biaxial loading. J. Sandw. Struct. Mater. 2004, 6, 217–237. [Google Scholar] [CrossRef]
- Fagerberg, L.; Zenkert, D. Effects of anisotropy and multiaxial loading on the wrinkling of sandwich panels. J. Sandw. Struct. Mater. 2005, 7, 177–194. [Google Scholar] [CrossRef]
- Lopatin, A.; Morozov, E. Symmetrical facing wrinkling of composite sandwich panels. J. Sandw. Struct. Mater. 2008, 10, 475–497. [Google Scholar] [CrossRef]
- Frostig, Y. On wrinkling of a sandwich panel with a compliant core and self-equilibrated loads. J. Sandw. Struct. Mater. 2011, 13, 663–679. [Google Scholar] [CrossRef]
- Hohe, J.; Librescu, L. Recent results on the effect of the transverse core compressibility on the static and dynamic response of sandwich structures. Compos. Part B Eng. 2008, 39, 108–119. [Google Scholar] [CrossRef]
- Phan, C.N.; Bailey, N.W.; Kardomateas, G.A.; Battley, M.A. Wrinkling of sandwich wide panels/beams based on the extended high-order sandwich panel theory: Formulation, comparison with elasticity and experiments. Arch. Appl. Mech. 2012, 82, 1585–1599. [Google Scholar] [CrossRef]
- Birman, V.; Vo, N. Wrinkling in sandwich structures with a functionally graded core. J. Appl. Mech. 2017, 84, 021002. [Google Scholar] [CrossRef]
- Hassinen, P.; Misiek, T. Einfluss von Inhomogenitäten im Kernwerkstoff von Sandwichelementen auf die Tragfähigkeit. Stahlbau 2012, 81, 935–943. [Google Scholar] [CrossRef]
- Jasion, P.; Magnucki, K. Face wrinkling of sandwich beams under pure bending. J. Theor. Appl. Mech. 2012, 50, 933–941. [Google Scholar]
- Frostig, Y.; Birman, V.; Kardomateas, G.A. Non-linear wrinkling of a sandwich panel with functionally graded core—Extended high-order approach. Int. J. Solids Struct. 2018, 148, 122–139. [Google Scholar] [CrossRef]
- Li, B.; Cao, Y.P.; Feng, X.Q.; Gao, H. Mechanics of morphological instabilities and surface wrinkling in soft materials: A review. Soft Matter 2012, 8, 5728–5745. [Google Scholar] [CrossRef]
- Lv, H.; Deng, J.; Ren, Y.; Zhang, H.; Zhang, W.; Zhang, M.; Liu, H.; Gu, B. Preparation and Band Gap Characteristics of Composite Film/Substrate Instability System. Materials 2022, 15, 6248. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; He, L.; Ni, Y. Tunable hierarchical wrinkling: From models to applications. J. Appl. Phys. 2020, 127, 111101. [Google Scholar] [CrossRef]
- Li, M.; Hakimi, N.; Perez, R.; Waldman, S.; Kozinski, J.A.; Hwang, D.K. Microarchitecture for a Three-Dimensional Wrinkled Surface Platform. Adv. Mater. 2015, 27, 1880–1886. [Google Scholar] [CrossRef] [PubMed]
- Lou, J.; Zhang, J.; Wang, D.; Fan, X. Improving the Dyeability and Anti-Wrinkle Properties of Cotton Fabric via Oxidized Raffinose. Appl. Sci. 2021, 11, 4641. [Google Scholar] [CrossRef]
- Studziński, R. Optimal design of sandwich panels with hybrid core. J. Sandw. Struct. Mater. 2019, 21, 2181–2193. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, H.; Xing, S. Mechanical performances of metal-polymer sandwich structures with 3D-printed lattice cores subjected to bending load. Arch. Civ. Mech. Eng. 2020, 20, 1–17. [Google Scholar] [CrossRef]
- Pozorska, J.; Pozorski, Z. The Influence of the Core Orthotopy on the Wrinkling of Sandwich Panels. J. Appl. Math. Comput. Mech. 2015, 14, 133–138. [Google Scholar] [CrossRef]
- Pozorski, Z.; Pozorska, J.; Kreja, I.; Smakosz, Ł. On Wrinkling in Sandwich Panels with an Orthotropic Core. Materials 2021, 14, 5043. [Google Scholar] [CrossRef] [PubMed]
- Hammarberg, S.; Kajberg, J.; Larsson, S.; Moshfegh, R.; Jonsén, P. Novel Methodology for Experimental Characterization of Micro-Sandwich Materials. Materials 2021, 14, 4396. [Google Scholar] [CrossRef] [PubMed]
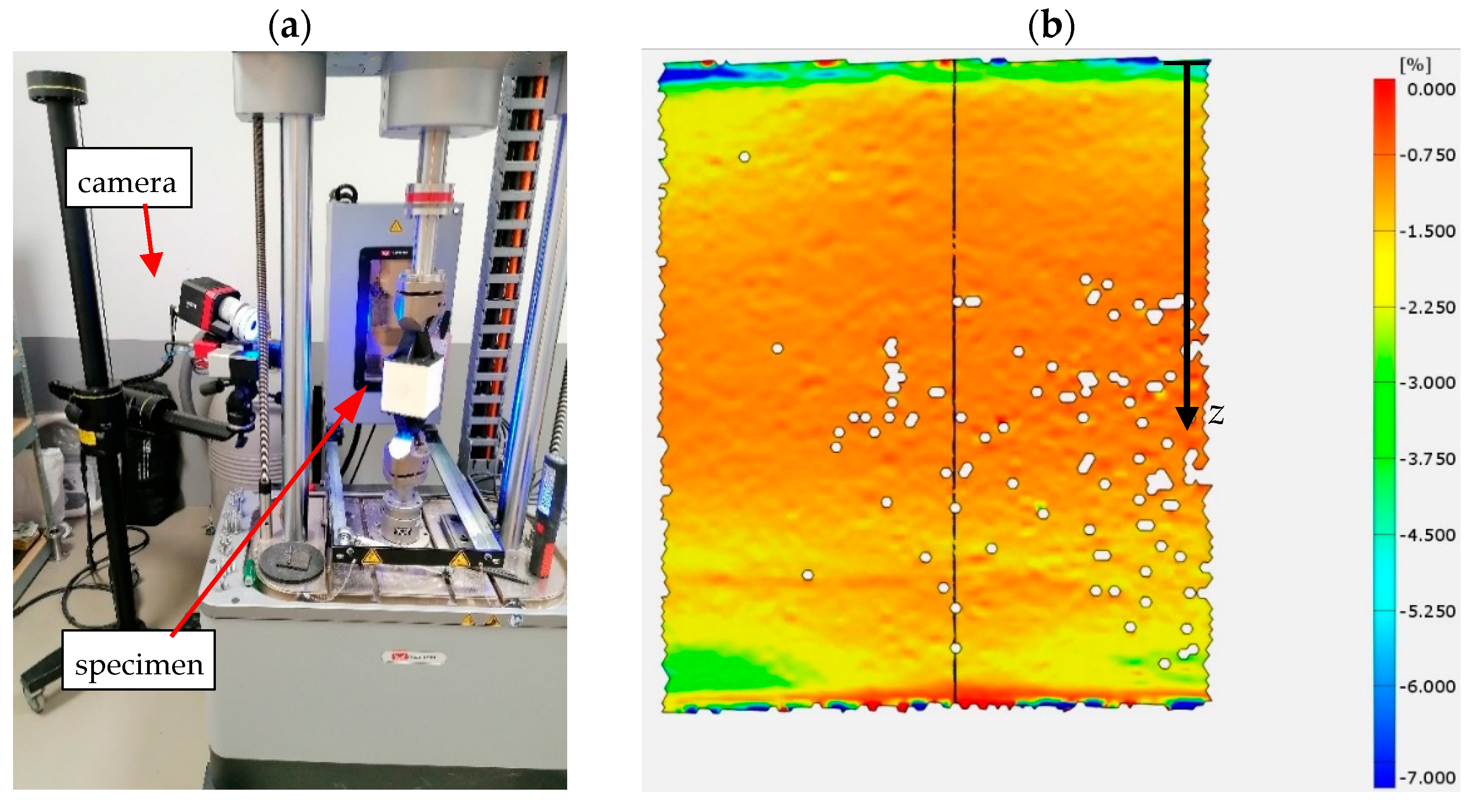
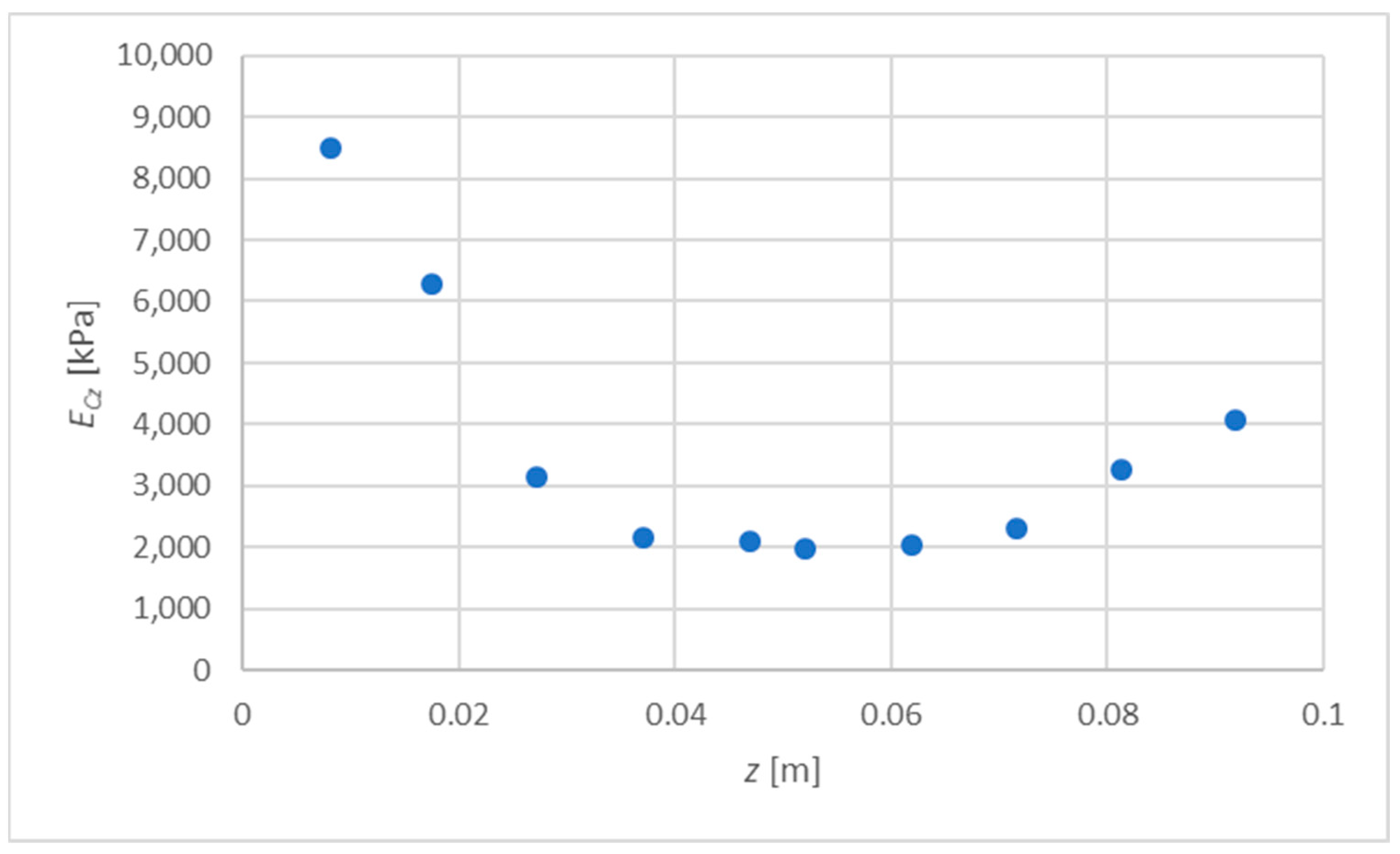
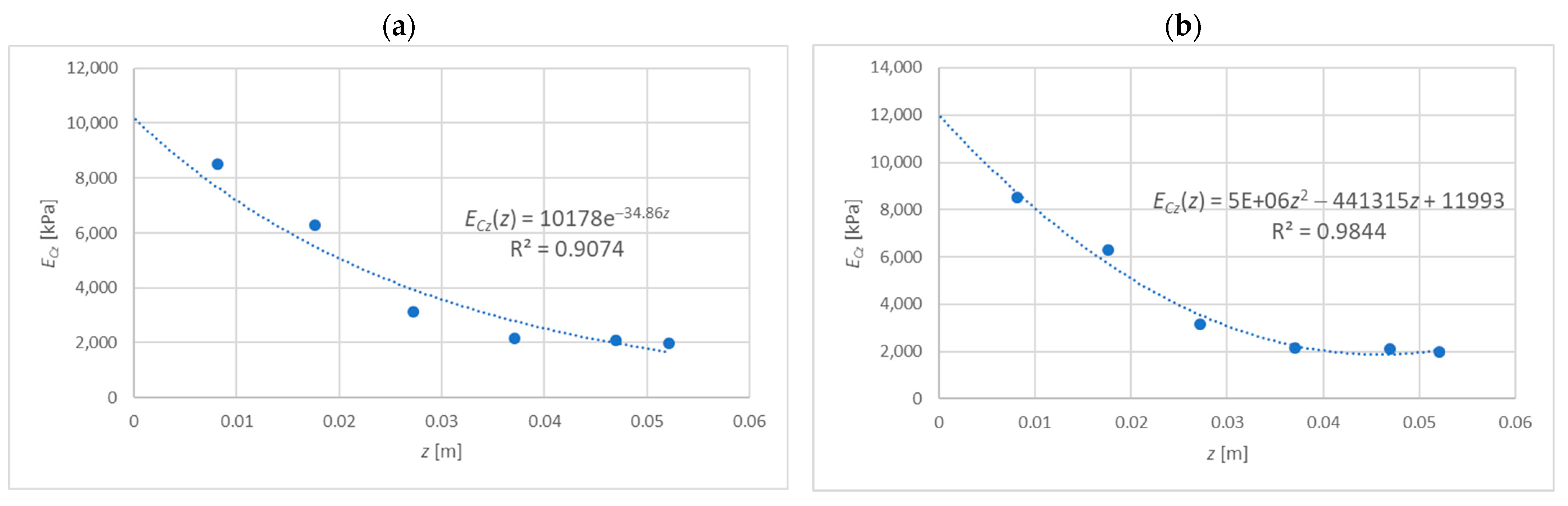
| [m] | 0.00814 | 0.0176 | 0.0272 | 0.0371 | 0.0470 | 0.0521 |
| [kPa] | 8509 | 6282 | 3146 | 2173 | 2093 | 1994 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pozorski, Z.; Pozorska, J. Influence of the Heterogeneity of the Core Material on the Local Instability of a Sandwich Panel. Materials 2022, 15, 6687. https://doi.org/10.3390/ma15196687
Pozorski Z, Pozorska J. Influence of the Heterogeneity of the Core Material on the Local Instability of a Sandwich Panel. Materials. 2022; 15(19):6687. https://doi.org/10.3390/ma15196687
Chicago/Turabian StylePozorski, Zbigniew, and Jolanta Pozorska. 2022. "Influence of the Heterogeneity of the Core Material on the Local Instability of a Sandwich Panel" Materials 15, no. 19: 6687. https://doi.org/10.3390/ma15196687







