Elastic Properties of Open Cell Metallic Foams—Modeling of Pore Size Variation Effect
Abstract
1. Introduction
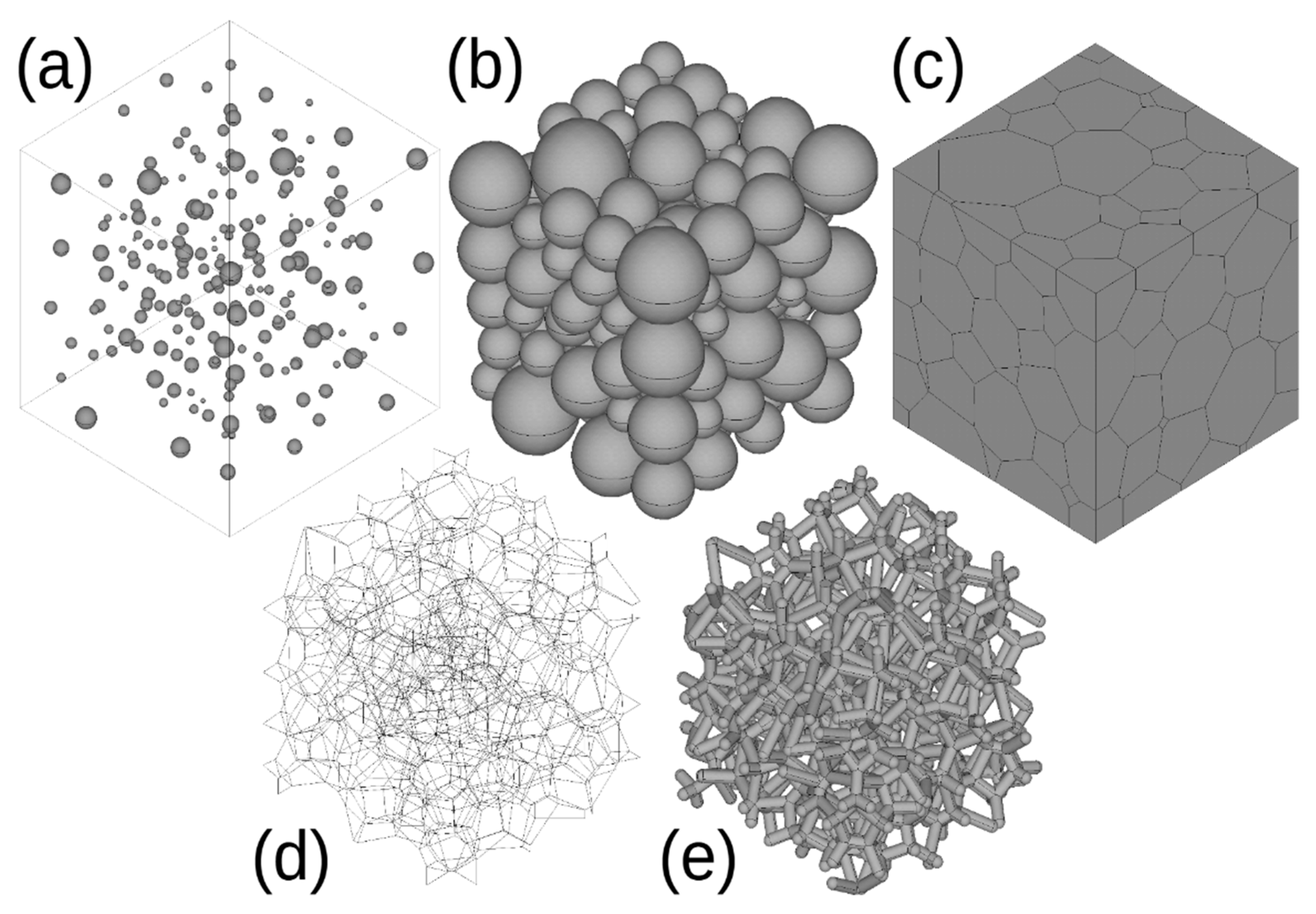
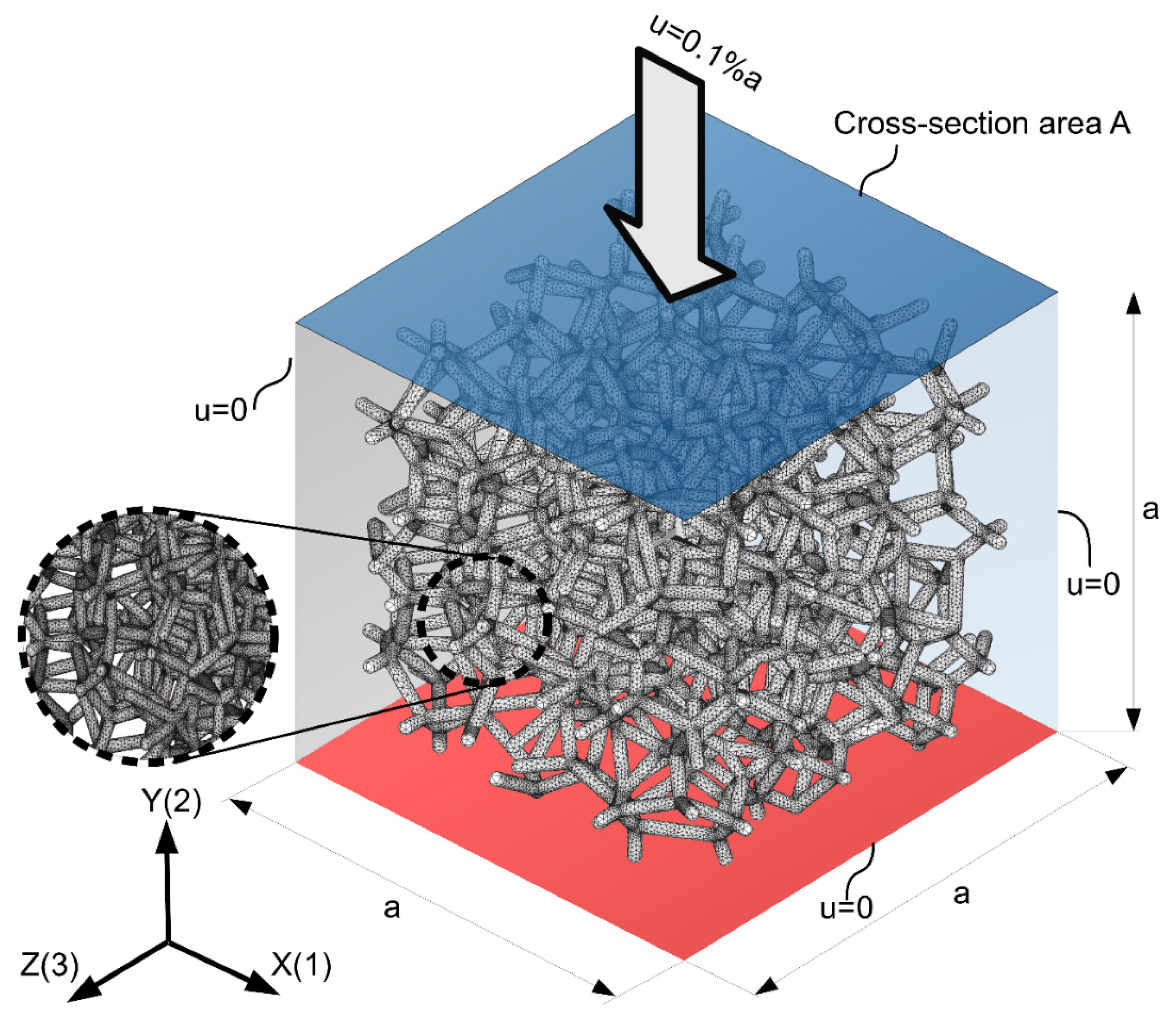
2. Materials and Methods
3. Results and Discussion
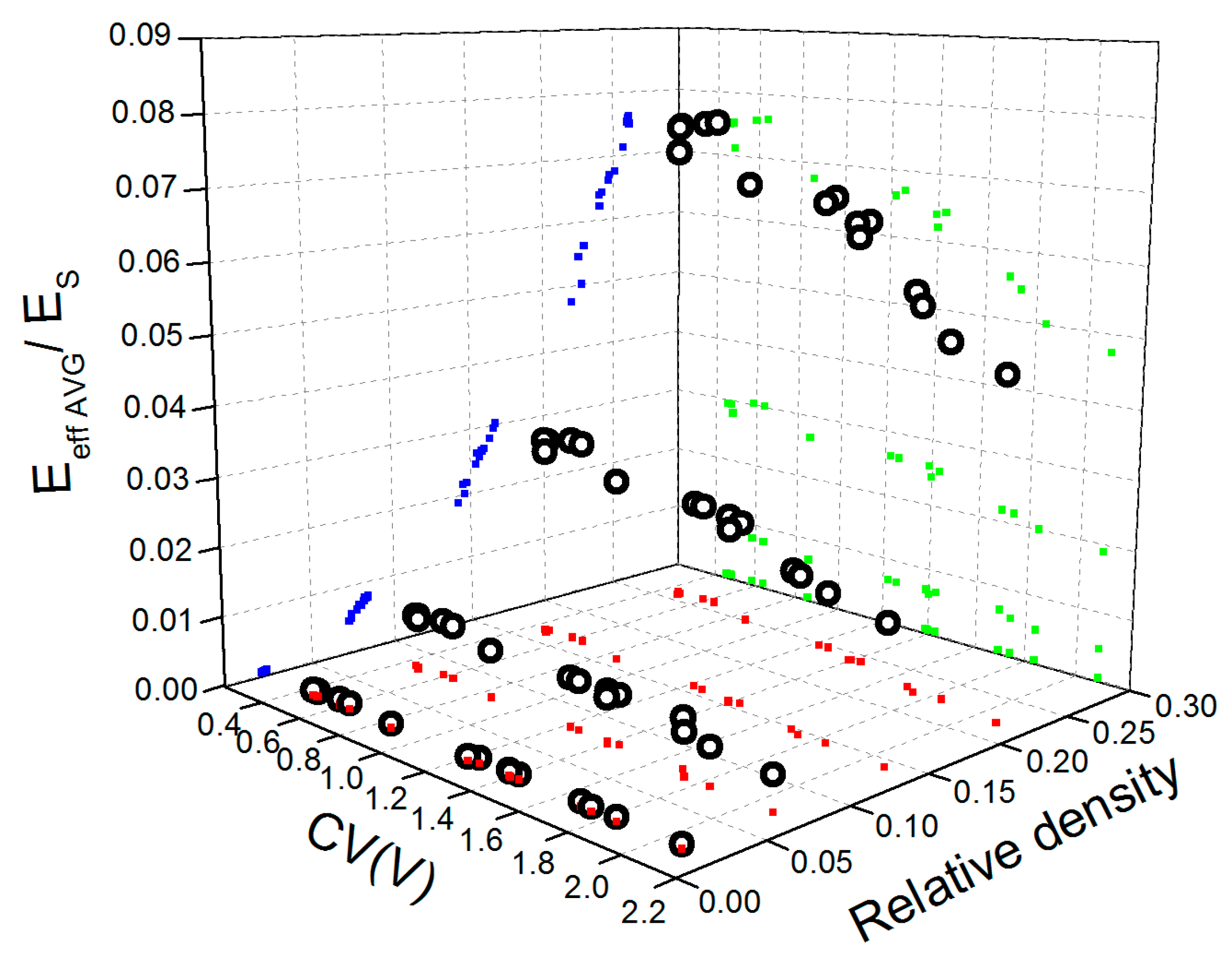
3.1. Effective Young’s Modulus of Aluminum Open-Cell Foams
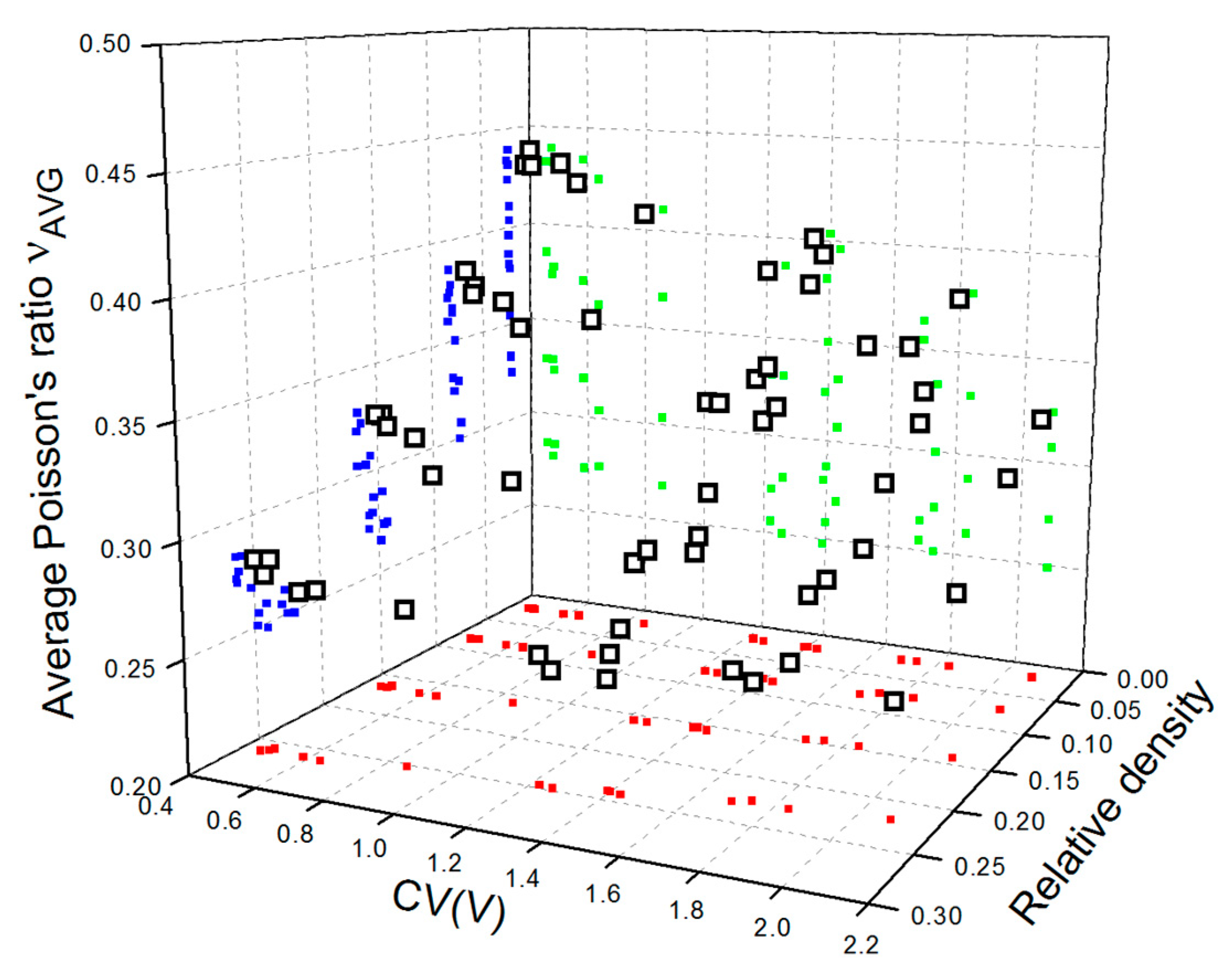
3.2. Effective Poisson’s Ratio of Aluminum Open-Cell Foams
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Lu, S.; Zhang, M.; Guo, S.; Hur, B.; Yue, X. Numerical Investigation of Impact Behavior of Strut-Based Cellular Structures Designed by Spatial Voronoi Tessellation. Metals 2022, 12, 1189. [Google Scholar] [CrossRef]
- Cwieka, K.; Wejrzanowski, T.; Kurzydlowski, K.J. Incorporation of the Pore Size Variation to Modeling of the Elastic Behaviour of Metallic Open-Cell Foams. Arch. Metall. Mater. 2017, 62, 269–272. [Google Scholar] [CrossRef][Green Version]
- Skibinski, J.; Cwieka, K.; Ibrahim, S.H.; Wejrzanowski, T. Influence of Pore Size Variation on Thermal Conductivity of Open-Porous Foams. Materials 2019, 12, 2017. [Google Scholar] [CrossRef]
- Zhang, M.; Shang, J.; Guo, S.; Hur, B.; Yue, X. Numerical Investigation of Effective Thermal Conductivity of Strut-Based Cellular Structures Designed by Spatial Voronoi Tessellation. Materials 2020, 14, 138. [Google Scholar] [CrossRef] [PubMed]
- Skibinski, J.; Cwieka, K.; Kowalkowski, T.; Wysocki, B.; Wejrzanowski, T.; Kurzydlowski, K.J. The influence of pore size variation on the pressure drop in open-cell foams. Mater. Des. 2015, 87, 650–655. [Google Scholar] [CrossRef]
- Regulski, W.; Szumbarski, J.; Łaniewski-Wołłk, Ł.; Gumowski, K.; Skibiński, J.; Wichrowski, M.; Wejrzanowski, T. Pressure drop in flow across ceramic foams—A numerical and experimental study. Chem. Eng. Sci. 2015, 137, 320–337. [Google Scholar] [CrossRef]
- Banhart, J. Aluminium foams for lighter vehicles. Int. J. Veh. Des. 2005, 37, 114. [Google Scholar] [CrossRef]
- Banhart, J. Manufacture, characterization and application of cellular metals and metal foams. Manuf. Prog Mater. Sci. 2001, 46, 559–632. [Google Scholar] [CrossRef]
- Crupi, V.; Epasto, G.; Guglielmino, E. Impact Response of Aluminum Foam Sandwiches for Light-Weight Ship Structures. Metals 2011, 1, 98–112. [Google Scholar] [CrossRef]
- Raza, M.R.; Sulong, A.B.; Muhamad, N.; Akhtar, M.N.; Rajabi, J. Effects of binder system and processing parameters on formability of porous Ti/HA composite through powder injection molding. Mater. Des. 2015, 87, 386–392. [Google Scholar] [CrossRef]
- Arenas, M.; Crocker, J. Recent Trends in Porous Sound-Absorbing Materials. Noise Vib. Control Mag. 2010, 12–17. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.454.5923&rep=rep1&type=pdf (accessed on 20 September 2022).
- Crocker, M.J.; Arenas, J.P. Use of sound-absorbing materials. In Handbook of Noise and Vibration Control; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; pp. 696–713. [Google Scholar] [CrossRef]
- Han, F.; Seiffert, G.; Zhao, Y.; Gibbs, B. Acoustic absorption behaviour of an open-celled aluminium foam. J. Phys. D Appl. Phys. 2003, 36, 294–302. [Google Scholar] [CrossRef]
- Lu, T.J.; Stone, H.A.; Ashby, M.F. Heat transfer in open-cell metal foams. Acta Mater. 1998, 46, 3619–3635. [Google Scholar] [CrossRef]
- Barg, S.; Soltmann, C.; Schwab, A.; Koch, D.; Schwieger, W.; Grathwohl, G. Novel open cell aluminum foams and their use as reactive support for zeolite crystallization. J. Porous Mater. 2011, 18, 89–98. [Google Scholar] [CrossRef]
- Edouard, D.; Lacroix, M.; Huu, C.P.; Luck, F. Pressure drop modeling on SOLID foam: State-of-the art correlation. Chem. Eng. J. 2008, 144, 299–311. [Google Scholar] [CrossRef]
- Srivastava, V.C.; Sahoo, K.L. Processing, stabilization and applications of metallic foams. Art of science. Mater. Sci. 2007, 25, 733–753. [Google Scholar]
- Kakutkina, N.A.; Korzhavin, A.A.; Namyatov, I.G.; Rychkov, A.D. Flame propagation through the header of an in-line flame arrester, Combust. Explos. Shock Waves 2007, 43, 391–404. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.W.; Li, J.G.; Sun, X.D. Preparation and mechanical property of a novel 3D porous magnesium scaffold for bone tissue engineering. Mater. Sci. Eng. C 2014, 42, 362–367. [Google Scholar] [CrossRef]
- Alaboodi, A.S.; Sivasankaran, S. Experimental design and investigation on the mechanical behavior of novel 3D printed biocompatibility polycarbonate scaffolds for medical applications. J. Manuf. Process. 2018, 35, 479–491. [Google Scholar] [CrossRef]
- Veyhl, C.; Belova, I.V.; Murch, G.E.; Fiedler, T. Finite element analysis of the mechanical properties of cellular aluminium based on micro-computed tomography. Mater. Sci. Eng. A 2011, 528, 4550–4555. [Google Scholar] [CrossRef]
- Zhu, X.; Ai, S.; Fang, D.; Liu, B.; Lu, X. A novel modeling approach of aluminum foam based on MATLAB image processing. Comput. Mater. Sci. 2014, 82, 451–456. [Google Scholar] [CrossRef]
- Geißendörfer, M.; Liebscher, A.; Proppe, C.; Redenbach, C.; Schwarzer, D. Stochastic multiscale modeling of metal foams. Probab. Eng. Mech. 2014, 37, 132–137. [Google Scholar] [CrossRef]
- Drach, B.; Tsukrov, I.; Trofimov, A. Comparison of full field and single pore approaches to homogenization of linearly elastic materials with pores of regular and irregular shapes. Int. J. Solids Struct. 2016, 96, 48–63. [Google Scholar] [CrossRef]
- Liu, R.; Antoniou, A. A relationship between the geometrical structure of a nanoporous metal foam and its modulus. Acta Mater. 2013, 61, 2390–2402. [Google Scholar] [CrossRef]
- Pia, G.; Delogu, F. On the elastic deformation behavior of nanoporous metal foams. Scr. Mater. 2013, 69, 781–784. [Google Scholar] [CrossRef]
- An, Y.; Wen, C.; Hodgson, P.D.; Yang, C. Investigation of cell shape effect on the mechanical behaviour of open-cell metal foams. Comput. Mater. Sci. 2012, 55, 1–9. [Google Scholar] [CrossRef]
- Wieding, J.; Wolf, A.; Bader, R. Numerical optimization of open-porous bone scaffold structures to match the elastic properties of human cortical bone. J. Mech. Behav. Biomed. Mater. 2014, 37, 56–68. [Google Scholar] [CrossRef]
- Jung, A.; Diebels, S. Modelling of Metal Foams by a Modified Elastic Law. Mech. Mater. 2016, 101, 61–70. [Google Scholar] [CrossRef]
- Redenbach, C.; Shklyar, I.; Andrä, H. Laguerre tessellations for elastic stiffness simulations of closed foams with strongly varying cell sizes. Int. J. Eng. Sci. 2012, 50, 70–78. [Google Scholar] [CrossRef]
- Zhu, H.X.; Hobdell, J.R.; Windle, A.H. Effects of cell irregularity on the elastic properties of open-cell foams. Acta Mater. 2000, 48, 4893–4900. [Google Scholar] [CrossRef]
- Köll, J.; Hallström, S. Elastic properties of equilibrium foams. Acta Mater. 2016, 113, 11–18. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Kraynik, A.M.; Warren, W.E. The elastic behavior of low-density cellular plastics. In Low Density Cell; Hilyard, N.C., Cunningham, A., Eds.; Springer: Dordrecht, The Netherlands, 1994; pp. 187–225. [Google Scholar] [CrossRef]
- Roberts, A.P.; Garboczi, E.J. Elastic properties of model random three-dimensional open- cell solid. J. Mech. Phys. Solids 2002, 50, 33–55. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, A.G.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N.G. Metal Foams; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar] [CrossRef]
- Aurenhammer, F. Power Diagrams: Properties, Algorithms and Applications. SIAM J. Comput. 1987, 16, 78–96. [Google Scholar] [CrossRef]
- Redenbach, C. Microstructure models for cellular materials. Comput. Mater. Sci. 2009, 44, 1397–1407. [Google Scholar] [CrossRef]
- Fan, Z.; Wu, Y.; Zhao, X.; Lu, Y. Simulation of polycrystalline structure with Voronoi diagram in Laguerre geometry based on random closed packing of spheres. Comput. Mater. Sci. 2004, 29, 301–308. [Google Scholar] [CrossRef]
- Wejrzanowski, T.; Skibinski, J.; Szumbarski, J.; Kurzydlowski, K.J. Structure of foams modeled by Laguerre-Voronoi tessellations. Comput. Mater. Sci. 2013, 67, 216–221. [Google Scholar] [CrossRef]
- Wejrzanowski, T.; Skibinski, J.; Madej, L.; Kurzydlowski, K.J. Modeling structures of cellular materials for application at various length-scales. Comput. Methods Mater. Sci. 2013, 13, 493–500. [Google Scholar]
- Fiedler, T.; Belova, I.V.; Murch, G.E. μ-CT-based finite element analysis on imperfections in open-celled metal foam: Mechanical properties. Scr. Mater. 2012, 67, 455–458. [Google Scholar] [CrossRef]
- Jung, A.; Diebels, S. Microstructural characterisation and experimental determination of a multiaxial yield surface for open-cell aluminium foams. Mater. Des. 2017, 131, 252–264. [Google Scholar] [CrossRef]
- Belardi, V.G.; Fanelli, P.; Trupiano, S.; Vivio, F. Multiscale analysis and mechanical characterization of open-cell foams by simplified FE modeling. Eur. J. Mech. A/Solids 2021, 89, 104291. [Google Scholar] [CrossRef]
- Kanahashi, H.; Mukai, T.; Nieh, T.G.; Aizawa, T.; Higashi, K. Effect of Cell Size on the Dynamic Compressive Properties of Open-Celled Aluminum Foams. Mater. Trans. 2002, 43, 2548–2553. [Google Scholar] [CrossRef][Green Version]
- Larner, M.; Acker, J.; Dávila, L.P. The random porous structure and mechanical response of lightweight aluminum foams. MRS Proc. 2014, 1662, 3–9. [Google Scholar] [CrossRef]
- Veale, P.J. Investigation of the Behavior of Open Cell Aluminum Foam. Master’s Thesis, University of Massachusetts, Amherst, MA, USA, 2011. Available online: http://scholarworks.umass.edu/theses’/443 (accessed on 20 September 2022).
- ERG. Duocel® Aluminum Foam. Available online: https://www.duocelfoam.com/ (accessed on 20 September 2022).
- Mills, N.J. The high strain mechanical response of the wet Kelvin model for open-cell foams. Int. J. Solids Struct. 2007, 44, 51–65. [Google Scholar] [CrossRef]
- Buffel, B.; Desplentere, F.; Bracke, K.; Verpoest, I. Modelling open cell-foams based on the Weaire-Phelan unit cell with a minimal surface energy approach. Int. J. Solids Struct. 2014, 51, 3461–3470. [Google Scholar] [CrossRef]
- Gong, L.; Kyriakides, S.; Jang, W.Y. Compressive response of open-cell foams. Part I: Morphology and elastic properties. Int. J. Solids Struct. 2005, 42, 1355–1379. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ćwieka, K.; Skibiński, J. Elastic Properties of Open Cell Metallic Foams—Modeling of Pore Size Variation Effect. Materials 2022, 15, 6818. https://doi.org/10.3390/ma15196818
Ćwieka K, Skibiński J. Elastic Properties of Open Cell Metallic Foams—Modeling of Pore Size Variation Effect. Materials. 2022; 15(19):6818. https://doi.org/10.3390/ma15196818
Chicago/Turabian StyleĆwieka, Karol, and Jakub Skibiński. 2022. "Elastic Properties of Open Cell Metallic Foams—Modeling of Pore Size Variation Effect" Materials 15, no. 19: 6818. https://doi.org/10.3390/ma15196818
APA StyleĆwieka, K., & Skibiński, J. (2022). Elastic Properties of Open Cell Metallic Foams—Modeling of Pore Size Variation Effect. Materials, 15(19), 6818. https://doi.org/10.3390/ma15196818








