Predicting the Response of RC Beam from a Drop-Weight Using Gene Expression Programming
Abstract
:1. Introduction
2. Research Significance
3. Assumptions
- The shape of the impactor is considered not to influence the impact behavior of RC beams;
- The impact event is so fast that the damping of the impacted component can be neglected;
- The bearing plates are normally provided to distribute the impact load and avoid localized failure. This influence of the bearing plate is ignored;
- The impact force is applied perpendicular to the longitudinal axis of the beam;
- No provision is made in the proposed model for incorporating special anchored reinforcement.
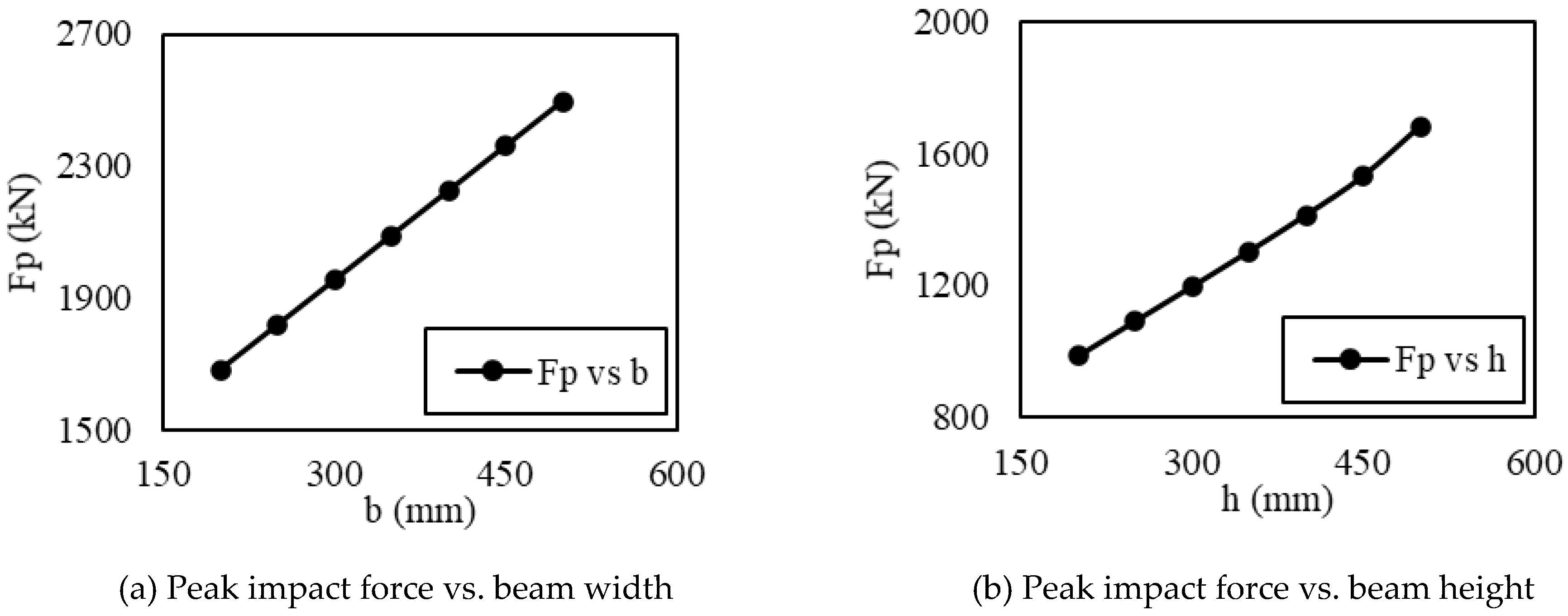
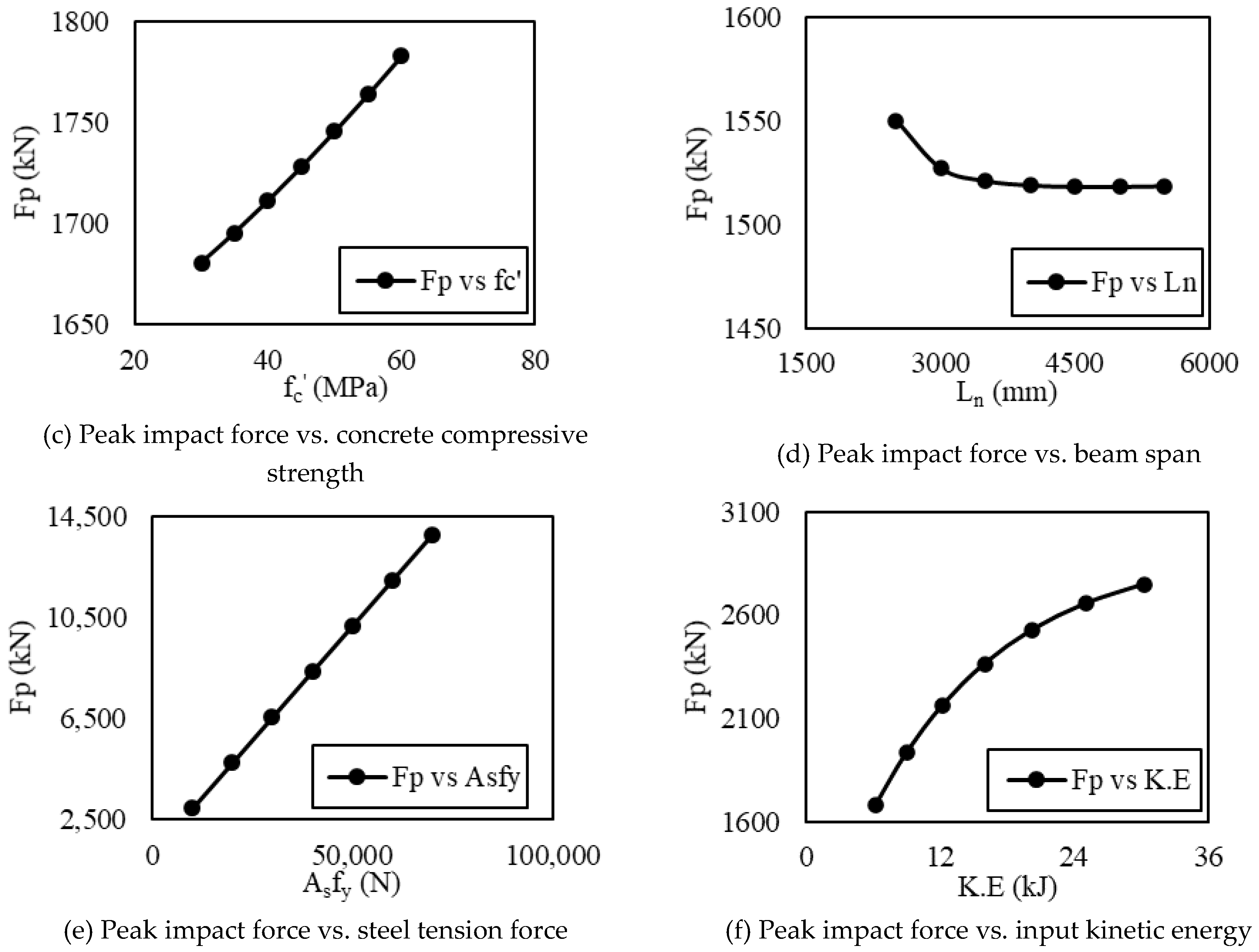
4. Discussion of Influencing Parameters
5. Experimental Database
Distribution of Key Influence Parameters
6. Previous Models to Evaluate the Peak Impact Force on RC Beam
6.1. Zhao et al. Model
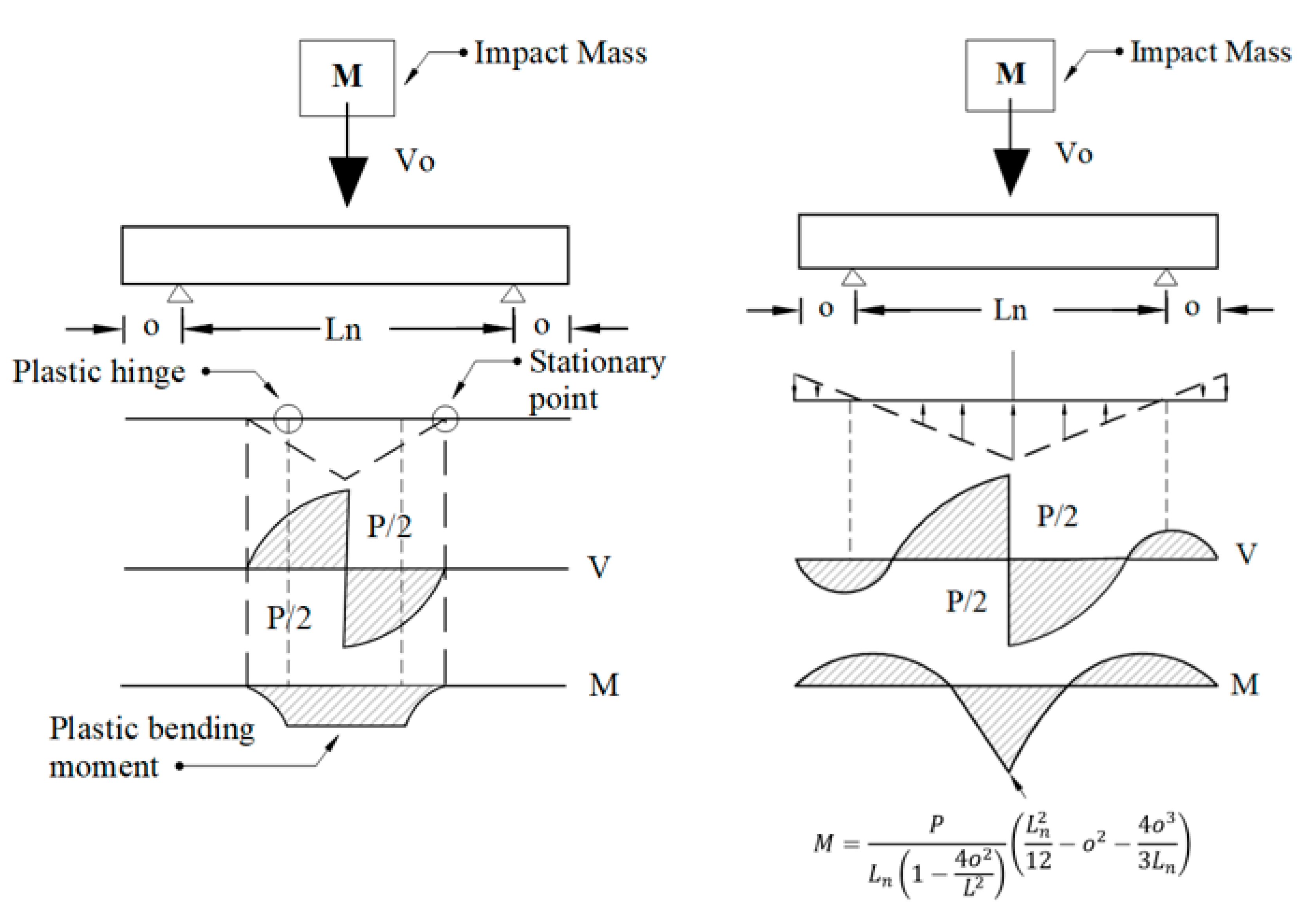
6.2. Pham and Hao Model
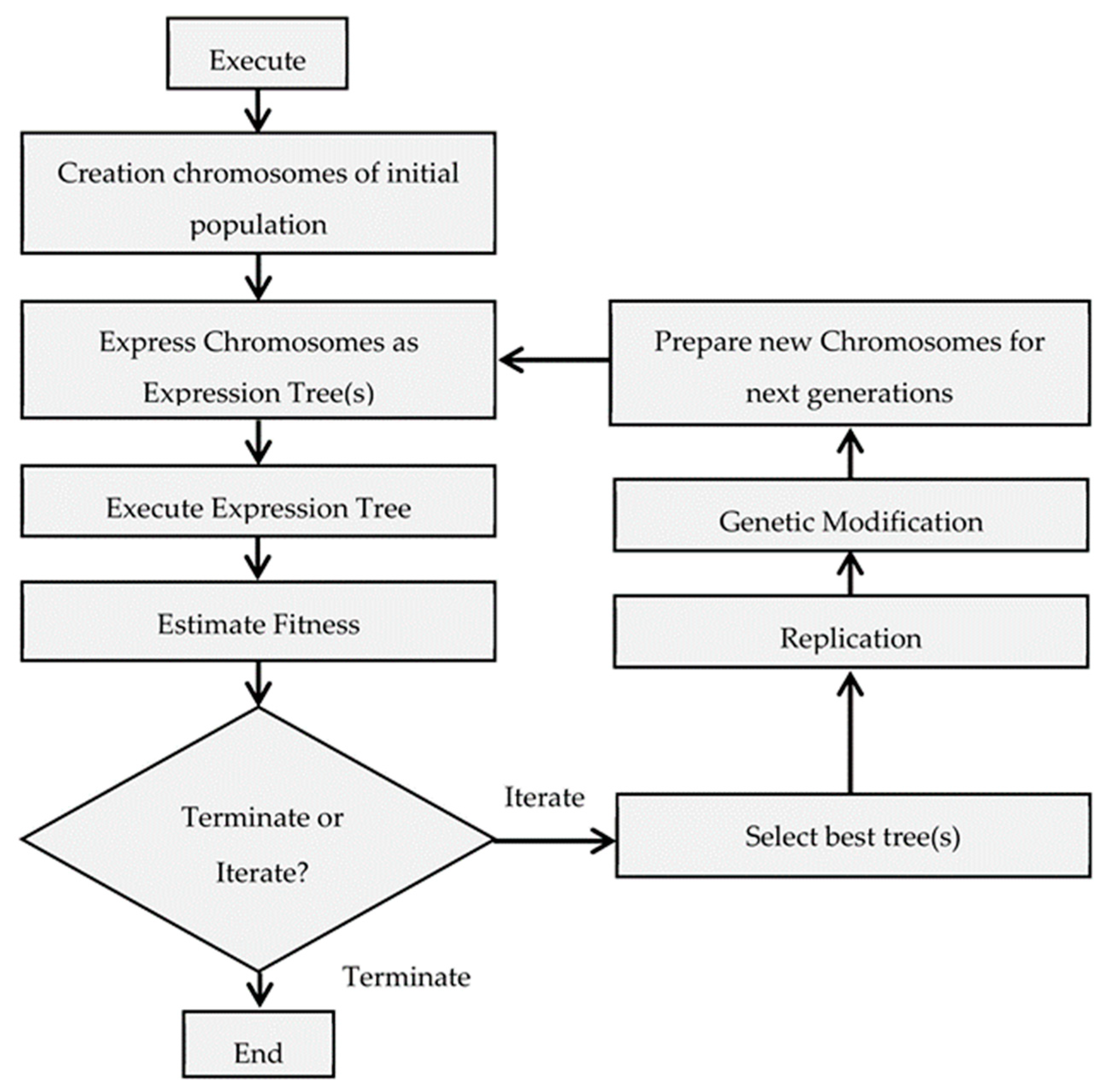
7. GEP Algorithm
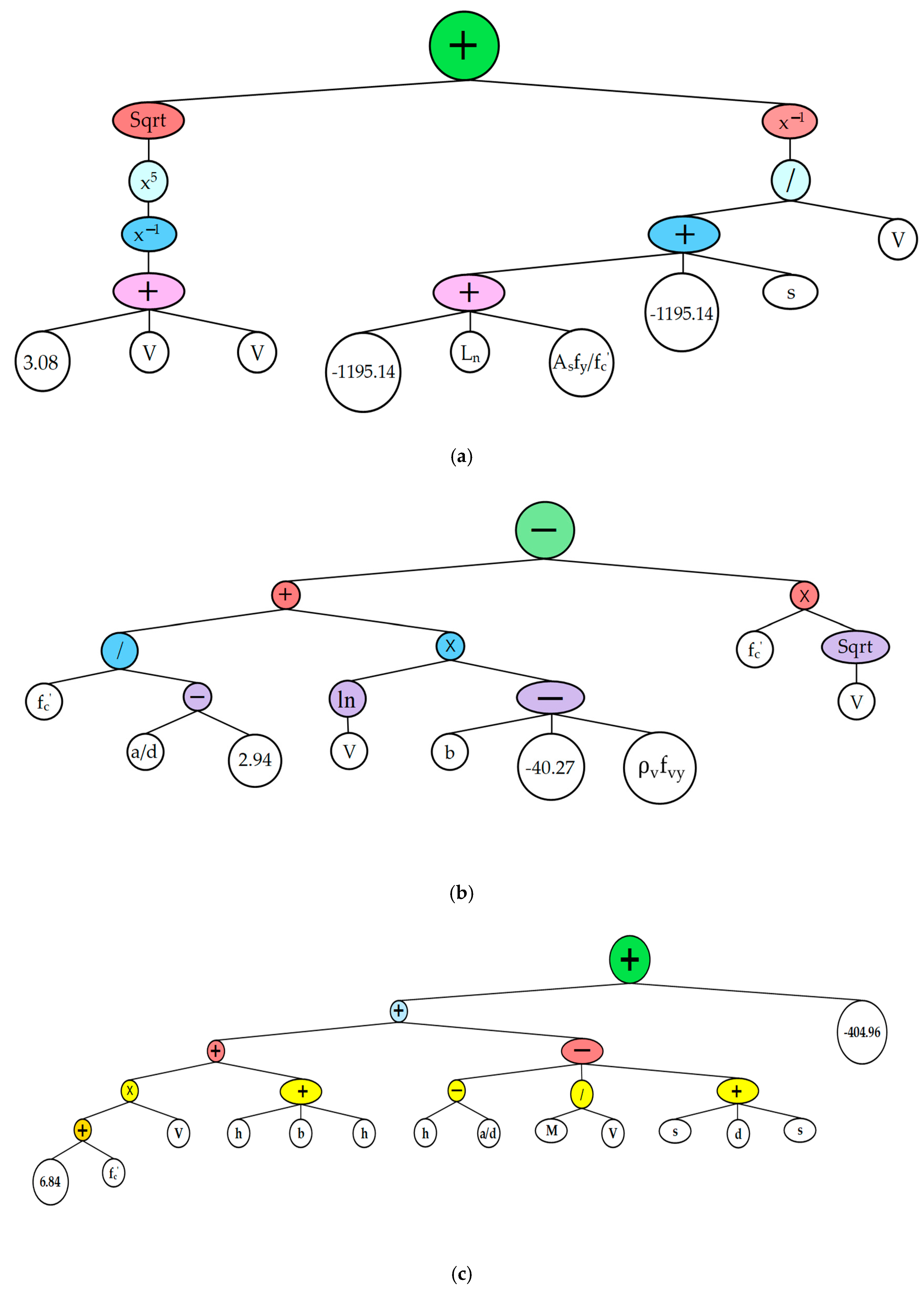
8. Proposed GEP Model for Estimating Peak Impact Force
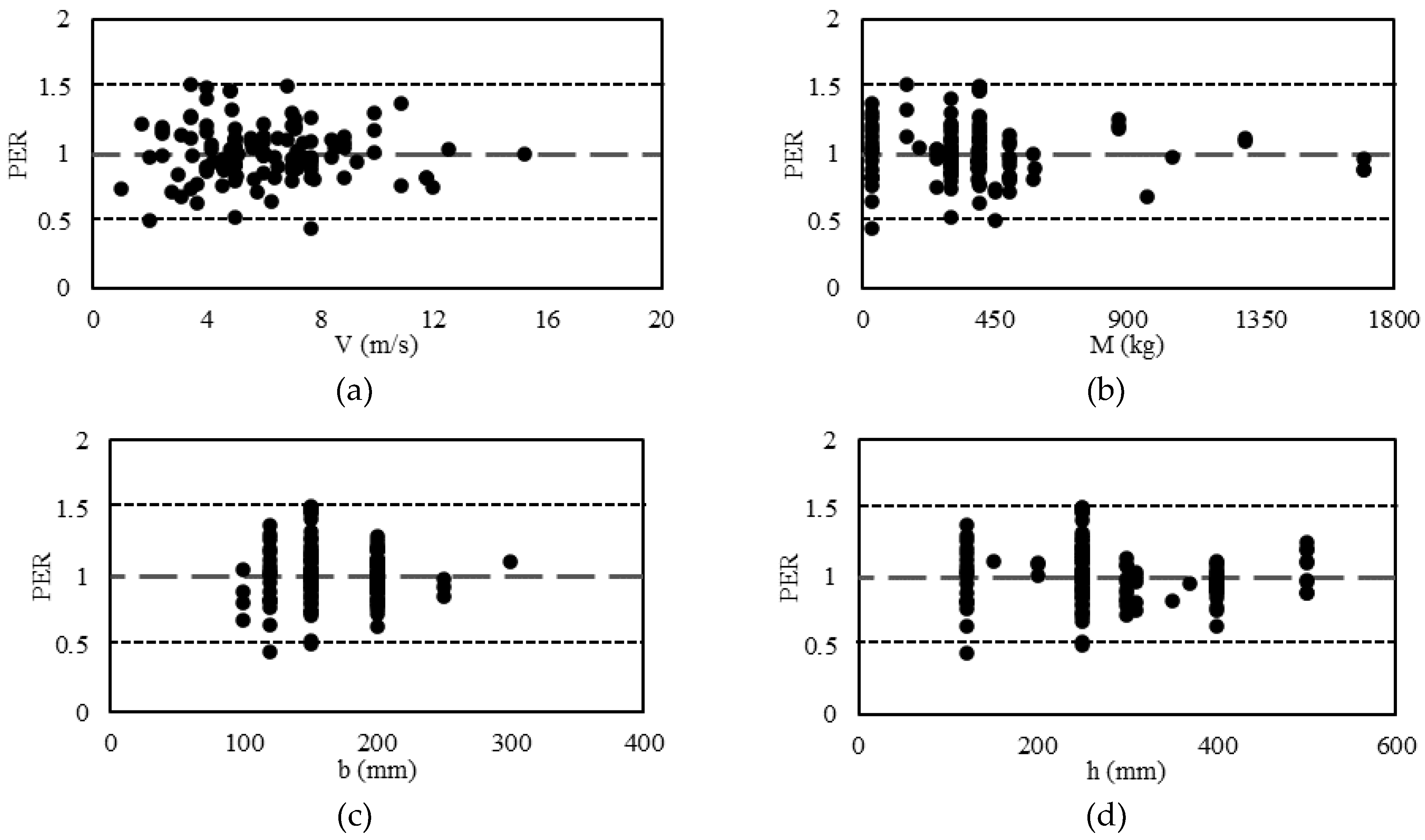
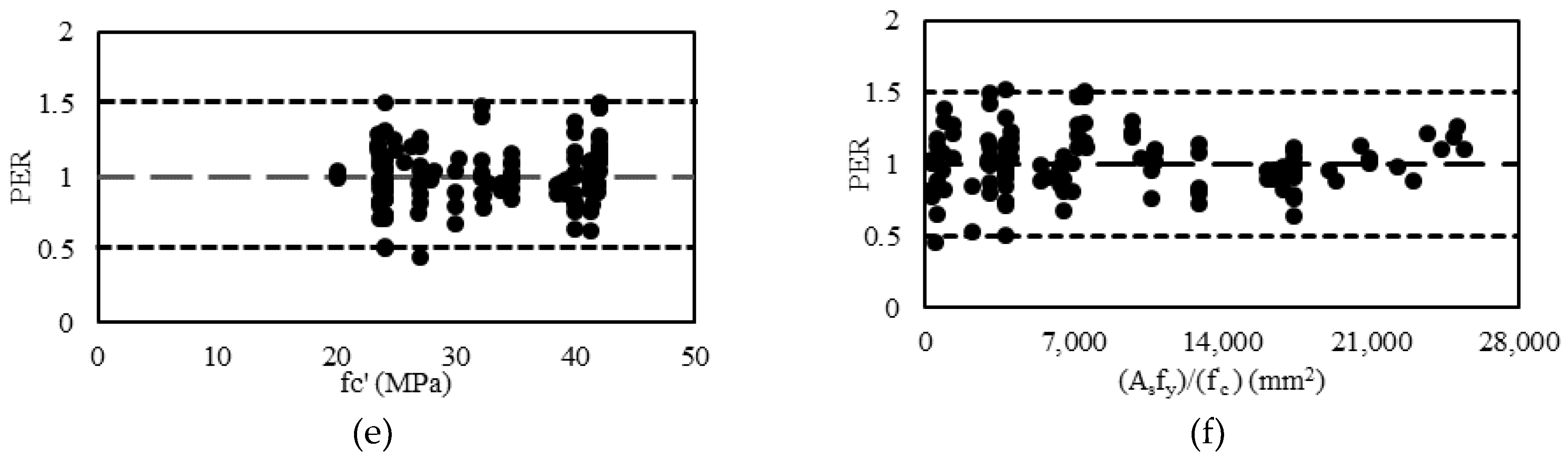
9. Accuracy of the Proposed Model
10. Development of a Numerical Model
10.1. Experimental Program Bhatti
10.2. Response of RC Beam Predicted by ABAQUS
11. Results and Discussions
11.1. Peak Impact Force on RC Beam
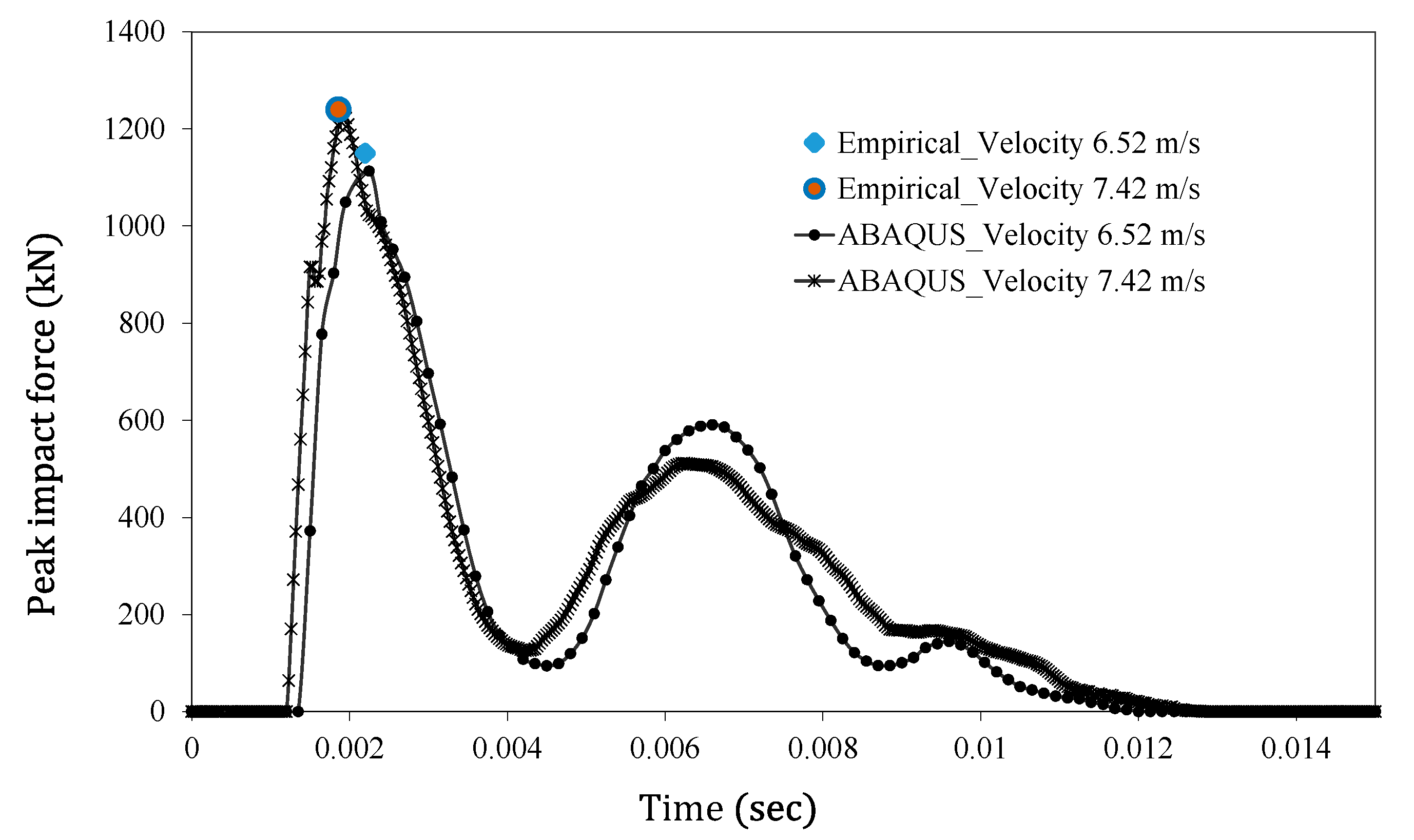
11.2. Numerical Verification of Empirical Model
11.3. Practical Implementation
12. Conclusions
- An increase in the influencing factors, such as the concrete compressive strength, the steel bar tensile strength, the longitudinal reinforcement ratio, the geometric dimension of beam cross-section, and the input kinetic energy results in attracting more impact force. Contrarily, an increase in the beam span results in attracting less impact force;
- The proposed empirical equation can accurately determine the impact force by incorporating all the aforementioned influencing factors. In addition, the influencing parameters in the model are consistently related to the experimental data;
- The predictive ability of the proposed model is indicated by the coefficient of determination, performance factor, and the average absolute error (98%, 1.01, and 15.2%, respectively);
- The proposed model can approximate the transmitted impact force to the RC beam more closely than an available analytical model and an artificial neural network-based model. A comparison is made with two different models to evidence the predictive ability of the developed model;
- The proposed model is also validated by comparing the results with the FE simulation, using an ABAQUS/Explicit solver, which was developed on existing experimental results. The model gives good agreement with the numerical results showing less than 4% error;
- Overall, the proposed regression model offers an excellent predictive tool for determining the peak impact force transmitted to RC beams subjected to impact. Surely, the predictability of the current model has been improved by incorporating the important influencing parameters, such as the properties of shear and longitudinal reinforcement. This impact force can be employed for determining the bending and shear design of these beams, which is useful design information in terms of sizing and detailing of RC beams under impact loading;
- In future work, experiments will be performed to further validate the empirical formulation with varying impactor mass, striking velocity, and steel reinforcement in an RC beam. Additionally, the ABAQUS formulation will be improved by adopting actual stress–strain curves to accurately simulate the tested beams.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| ID | Geometric Size | Concrete | Longitudinal Reinforcement | Shear Reinforcement | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| b (mm) | h (mm) | L (mm) | Ln (mm) | a (mm) | F’c (Mpa) | As (mm2) | Fy (Mpa) | A’s (mm) | F’y (Mpa) | Fvy (Mpa) | Ratio % | |
| A37 | 200 | 400 | 2400 | 2000 | 50 | 41.2 | 1924 | 373 | 1924 | 373 | 373 | 0.21 |
| A46 | 200 | 400 | 2400 | 2000 | 50 | 41.2 | 1924 | 373 | 1924 | 373 | 373 | 0.21 |
| A56 | 200 | 400 | 2400 | 2000 | 50 | 41.2 | 1924 | 373 | 1924 | 373 | 373 | 0.21 |
| A65 | 200 | 400 | 2400 | 2000 | 50 | 41.2 | 1924 | 373 | 1924 | 373 | 373 | 0.21 |
| A74 | 200 | 400 | 2400 | 2000 | 50 | 41.2 | 1924 | 373 | 1924 | 373 | 373 | 0.21 |
| A84 | 200 | 400 | 2400 | 2000 | 50 | 41.2 | 1924 | 373 | 1924 | 373 | 373 | 0.21 |
| B37 | 200 | 400 | 2400 | 2000 | 50 | 41.2 | 1924 | 373 | 1924 | 373 | 373 | 0.42 |
| B46 | 200 | 400 | 2400 | 2000 | 50 | 41.2 | 1924 | 373 | 1924 | 373 | 373 | 0.42 |
| B65 | 200 | 400 | 2400 | 2000 | 50 | 41.2 | 1924 | 373 | 1924 | 373 | 373 | 0.42 |
| B74 | 200 | 400 | 2400 | 2000 | 50 | 41.2 | 1924 | 373 | 1924 | 373 | 373 | 0.42 |
| B84 | 200 | 400 | 2400 | 2000 | 50 | 41.2 | 1924 | 373 | 1924 | 373 | 373 | 0.42 |
| B93 | 200 | 400 | 2400 | 2000 | 50 | 41.2 | 1924 | 373 | 1924 | 373 | 373 | 0.42 |
| S1616-1 | 150 | 250 | 1700 | 1400 | 40 | 42.0 | 402 | 426 | 402 | 426 | 295 | 1.40 |
| S1616-2 | 150 | 250 | 1700 | 1400 | 40 | 42.0 | 402 | 426 | 402 | 426 | 295 | 1.40 |
| S1616-3 | 150 | 250 | 1700 | 1400 | 40 | 42.0 | 402 | 426 | 402 | 426 | 295 | 1.40 |
| S1616-4 | 150 | 250 | 1700 | 1400 | 40 | 42.0 | 402 | 426 | 402 | 426 | 295 | 1.40 |
| S1322-1 | 150 | 250 | 1700 | 1400 | 40 | 42.0 | 760 | 397 | 265 | 397 | 295 | 1.40 |
| S1322-2 | 150 | 250 | 1700 | 1400 | 40 | 42.0 | 760 | 397 | 265 | 397 | 295 | 1.40 |
| S1322-3 | 150 | 250 | 1700 | 1400 | 40 | 42.0 | 760 | 397 | 265 | 397 | 295 | 1.40 |
| S1322-4 | 150 | 250 | 1700 | 1400 | 40 | 42.0 | 760 | 397 | 265 | 397 | 295 | 1.40 |
| S2222-1 | 150 | 250 | 1700 | 1400 | 40 | 42.0 | 760 | 418 | 760 | 418 | 295 | 1.40 |
| S2222-2 | 150 | 250 | 1700 | 1400 | 40 | 42.0 | 760 | 418 | 760 | 418 | 295 | 1.40 |
| S2222-3 | 150 | 250 | 1700 | 1400 | 40 | 42.0 | 760 | 418 | 760 | 418 | 295 | 1.40 |
| S2222-4 | 150 | 250 | 1700 | 1400 | 40 | 42.0 | 760 | 418 | 760 | 418 | 295 | 1.40 |
| A1 | 150 | 250 | 1400 | 1000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A2-1 | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A2-2 | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A2-3 | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A2-4 | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A2-5 | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A2-6 | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A2-7 | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A2-8 | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A2-9 | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A2-10 | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A2-11 | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A2-12 | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A2-13 | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A2-14 | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| A4 | 150 | 250 | 4400 | 4000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| B | 300 | 150 | 2400 | 2000 | 40 | 24.0 | 530 | 345 | 530 | 345 | 295 | 0.75 |
| C | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 402 | 345 | 402 | 345 | 295 | 0.75 |
| D | 150 | 250 | 2400 | 2000 | 40 | 24.0 | 157 | 345 | 157 | 345 | 295 | 0.75 |
| E | 150 | 400 | 2400 | 2000 | 40 | 24.0 | 265 | 345 | 265 | 345 | 295 | 0.75 |
| F | 150 | 400 | 2400 | 2000 | 40 | 24.0 | 157 | 345 | 157 | 345 | 295 | 0.75 |
| G1-1 | 200 | 300 | 3400 | 3000 | 40 | 33.7 | 567 | 379 | 567 | 379 | 295 | 0.07 |
| G1-1S | 200 | 300 | 3400 | 3000 | 40 | 33.7 | 567 | 379 | 567 | 379 | 295 | 0.07 |
| G2-1 | 150 | 250 | 2400 | 2000 | 40 | 32.2 | 265 | 373 | 265 | 373 | 295 | 0.13 |
| G2-2 | 150 | 250 | 2400 | 2000 | 40 | 32.2 | 265 | 373 | 265 | 373 | 295 | 0.13 |
| G2-3 | 150 | 250 | 2400 | 2000 | 40 | 32.2 | 265 | 373 | 265 | 373 | 295 | 0.13 |
| G2L-1 | 150 | 250 | 2400 | 2000 | 40 | 32.2 | 265 | 373 | 265 | 373 | 295 | 0.13 |
| G2L-2 | 150 | 250 | 2400 | 2000 | 40 | 32.2 | 265 | 373 | 265 | 373 | 295 | 0.13 |
| G2L-3 | 150 | 250 | 2400 | 2000 | 40 | 32.2 | 265 | 373 | 265 | 373 | 295 | 0.13 |
| G3-1 | 150 | 250 | 2400 | 2000 | 40 | 34.6 | 265 | 393 | 265 | 393 | 295 | 0.13 |
| G3-2 | 150 | 250 | 2400 | 2000 | 40 | 34.6 | 265 | 393 | 265 | 393 | 295 | 0.13 |
| G3-3 | 150 | 250 | 2400 | 2000 | 40 | 34.6 | 265 | 393 | 265 | 393 | 295 | 0.13 |
| G4-1 | 150 | 250 | 2400 | 2000 | 40 | 32.3 | 265 | 373 | 265 | 373 | 295 | 0.13 |
| G4-2 | 150 | 250 | 2400 | 2000 | 40 | 32.3 | 265 | 373 | 265 | 373 | 295 | 0.13 |
| G5-1 | 200 | 300 | 3400 | 3000 | 40 | 39.2 | 567 | 379 | 567 | 379 | 295 | 0.07 |
| G5-2 | 200 | 300 | 3400 | 3000 | 40 | 39.2 | 567 | 379 | 567 | 379 | 295 | 0.07 |
| G6-1 | 250 | 250 | 2400 | 2000 | 40 | 34.7 | 567 | 392 | 567 | 392 | 295 | 0.13 |
| G7-1 | 250 | 250 | 3400 | 3000 | 40 | 34.7 | 567 | 392 | 567 | 392 | 295 | 0.09 |
| G7-2 | 250 | 250 | 3400 | 3000 | 40 | 34.7 | 567 | 392 | 567 | 392 | 295 | 0.09 |
| G8-1 | 200 | 200 | 2400 | 2000 | 40 | 34.7 | 982 | 383 | 982 | 383 | 295 | 0.16 |
| G9-1 | 200 | 200 | 3400 | 3000 | 40 | 34.7 | 982 | 383 | 982 | 383 | 295 | 0.12 |
| G9-2 | 200 | 200 | 3400 | 3000 | 40 | 34.7 | 982 | 383 | 982 | 383 | 295 | 0.12 |
| G10-1 | 200 | 250 | 3400 | 3000 | 40 | 23.5 | 567 | 404 | 567 | 404 | 295 | 0.09 |
| G10-2 | 200 | 250 | 3400 | 3000 | 40 | 23.5 | 567 | 404 | 567 | 404 | 295 | 0.09 |
| G10-3 | 200 | 250 | 3400 | 3000 | 40 | 23.5 | 567 | 404 | 567 | 404 | 295 | 0.09 |
| G10-4 | 200 | 250 | 3400 | 3000 | 40 | 23.5 | 567 | 404 | 567 | 404 | 295 | 0.09 |
| G11-1 | 200 | 300 | 3100 | 2700 | 50 | 23.6 | 760 | 401 | 760 | 401 | 295 | 0.08 |
| G11-2 | 200 | 300 | 3100 | 2700 | 50 | 23.6 | 760 | 401 | 760 | 401 | 295 | 0.08 |
| G11-3 | 200 | 300 | 3100 | 2700 | 50 | 23.6 | 760 | 401 | 760 | 401 | 295 | 0.08 |
| G11-4 | 200 | 300 | 3100 | 2700 | 50 | 23.6 | 760 | 401 | 760 | 401 | 295 | 0.08 |
| G11-5 | 200 | 300 | 3100 | 2700 | 50 | 23.6 | 760 | 401 | 760 | 401 | 295 | 0.08 |
| G11-6 | 200 | 300 | 3100 | 2700 | 50 | 23.6 | 760 | 401 | 760 | 401 | 295 | 0.08 |
| G12-1 | 200 | 300 | 3100 | 2700 | 50 | 23.6 | 1473 | 407 | 1473 | 407 | 295 | 0.08 |
| G13-1 | 200 | 400 | 3100 | 2700 | 50 | 23.6 | 982 | 406 | 982 | 406 | 295 | 0.06 |
| G14-1 | 200 | 350 | 3100 | 2700 | 50 | 23.6 | 982 | 406 | 982 | 406 | 295 | 0.07 |
| G15-1 | 200 | 400 | 3100 | 2700 | 50 | 23.6 | 982 | 406 | 982 | 406 | 295 | 0.06 |
| G16-1 | 200 | 370 | 3100 | 2700 | 50 | 23.6 | 982 | 406 | 982 | 406 | 295 | 0.06 |
| B-1700-4.60 | 200 | 500 | 6000 | 5000 | 40 | 27.0 | 1257 | 495 | 402 | 495 | 344 | 0.09 |
| B-1052-6.40 | 200 | 500 | 6000 | 5000 | 40 | 27.9 | 1257 | 495 | 402 | 495 | 344 | 0.09 |
| B-868-7.14 | 200 | 500 | 6000 | 5000 | 40 | 24.8 | 1257 | 495 | 402 | 495 | 344 | 0.09 |
| C-1700-4.60 | 200 | 500 | 4000 | 3000 | 40 | 32.1 | 1257 | 495 | 402 | 495 | 344 | 0.09 |
| C-1300-5.56 | 200 | 500 | 4000 | 3000 | 40 | 30.3 | 1257 | 495 | 402 | 495 | 344 | 0.09 |
| C-868-7.14 | 200 | 500 | 4000 | 3000 | 40 | 26.3 | 1257 | 495 | 402 | 495 | 344 | 0.09 |
| D-1700-4.60 | 200 | 500 | 4000 | 3000 | 40 | 32.7 | 1257 | 495 | 402 | 495 | 344 | 0.19 |
| D-1300-5.56 | 200 | 500 | 4000 | 3000 | 40 | 25.6 | 1257 | 495 | 402 | 495 | 344 | 0.19 |
| D-868-7.14 | 200 | 500 | 4000 | 3000 | 40 | 25.0 | 1257 | 495 | 402 | 495 | 344 | 0.19 |
| BD1 | 150 | 310 | 2700 | 1860 | 33 | 28.1 | 603 | 477 | 603 | 477 | 550 | 0.22 |
| BD2 | 150 | 310 | 2700 | 1860 | 33 | 26.9 | 603 | 477 | 603 | 477 | 550 | 0.22 |
| BD3 | 150 | 310 | 2700 | 1860 | 33 | 26.9 | 603 | 477 | 603 | 477 | 550 | 0.22 |
| BD4 | 150 | 310 | 2700 | 1860 | 33 | 41.4 | 603 | 477 | 603 | 477 | 550 | 0.22 |
| BD5 | 150 | 310 | 2700 | 1860 | 33 | 41.4 | 603 | 477 | 603 | 477 | 550 | 0.22 |
| A-1 | 100 | 250 | 3000 | 2500 | 28 | 30.0 | 402 | 490 | 402 | 490 | 340 | 0.38 |
| A-2 | 100 | 250 | 3000 | 2500 | 28 | 30.0 | 402 | 490 | 402 | 490 | 340 | 0.38 |
| A-3 | 100 | 250 | 3000 | 2500 | 28 | 30.0 | 402 | 490 | 402 | 490 | 340 | 0.38 |
| A-4 | 100 | 250 | 3000 | 2500 | 28 | 30.0 | 402 | 490 | 402 | 490 | 340 | 0.38 |
| B-0-00 | 200 | 400 | 2800 | 2400 | 42.5 | 41.9 | 1473 | 460 | 402 | 460 | 0 | 0.00 |
| B-0-25 | 200 | 400 | 2800 | 2400 | 42.5 | 41.9 | 1473 | 460 | 402 | 460 | 314 | 0.25 |
| B-0-50 | 200 | 400 | 2800 | 2400 | 42.5 | 41.9 | 1473 | 460 | 402 | 460 | 314 | 0.50 |
| BD1 | 150 | 310 | 3000 | 1860 | 33 | 45.8 | 603 | 394 | 0 | 394 | 0 | 0.00 |
| BD2 | 150 | 310 | 3000 | 1860 | 33 | 45.8 | 603 | 394 | 0 | 394 | 0 | 0.00 |
| BD3 | 150 | 310 | 3000 | 1860 | 33 | 45.8 | 603 | 394 | 0 | 394 | 0 | 0.00 |
| BD4 | 150 | 310 | 3000 | 1860 | 33 | 45.8 | 603 | 394 | 0 | 394 | 0 | 0.00 |
| BD5 | 150 | 310 | 3000 | 1860 | 33 | 45.8 | 603 | 394 | 0 | 394 | 0 | 0.00 |
| B1 | 200 | 400 | 2800 | 2400 | 42 | 20.1 | 982 | 429 | 402 | 429 | 314 | 0.50 |
| B2 | 200 | 400 | 2800 | 2400 | 42 | 20.1 | 982 | 429 | 402 | 429 | 314 | 0.50 |
| B3 | 200 | 400 | 2800 | 2400 | 42 | 20.1 | 982 | 429 | 402 | 429 | 314 | 0.50 |
| B4 | 200 | 400 | 2800 | 2400 | 42 | 38.5 | 1473 | 429 | 402 | 429 | 0 | 0.00 |
| B5 | 200 | 400 | 2800 | 2400 | 42 | 38.5 | 1473 | 429 | 402 | 429 | 314 | 0.50 |
| B6 | 200 | 400 | 2800 | 2400 | 42 | 38.5 | 1473 | 429 | 402 | 429 | 314 | 0.25 |
| 10-C27-4 | 120 | 120 | 1800 | 1200 | 27 | 157 | 235 | 157 | 235 | 235 | 0.5 | |
| 6-C40-5 | 120 | 120 | 1800 | 1200 | 40 | 56.52 | 235 | 56.52 | 235 | 235 | 0.5 | |
| 6-C40-6 | 120 | 120 | 1800 | 1200 | 40 | 56.52 | 235 | 56.52 | 235 | 235 | 0.5 | |
| 6-C40-7 | 120 | 120 | 1800 | 1200 | 40 | 56.52 | 235 | 56.52 | 235 | 235 | 0.5 | |
| 6-C40-8 | 120 | 120 | 1800 | 1200 | 40 | 56.52 | 235 | 56.52 | 235 | 235 | 0.5 | |
| 8-C40-2 | 120 | 120 | 1800 | 1200 | 40 | 101 | 235 | 101 | 235 | 235 | 0.5 | |
| 8-C40-3 | 120 | 120 | 1800 | 1200 | 40 | 101 | 235 | 101 | 235 | 235 | 0.5 | |
| 8-C40-4 | 120 | 120 | 1800 | 1200 | 40 | 101 | 235 | 101 | 235 | 235 | 0.5 | |
| 8-C40-5 | 120 | 120 | 1800 | 1200 | 40 | 101 | 235 | 101 | 235 | 235 | 0.5 | |
| 10-C40-5 | 120 | 120 | 1800 | 1200 | 40 | 157 | 235 | 157 | 235 | 235 | 0.5 | |
| 10-C40-6 | 120 | 120 | 1800 | 1200 | 40 | 157 | 235 | 157 | 235 | 235 | 0.5 | |
| 10-C40-7 | 120 | 120 | 1800 | 1200 | 40 | 157 | 235 | 157 | 235 | 235 | 0.5 | |
| ID | Hammer | Test Results | Reference | |||
|---|---|---|---|---|---|---|
| V (m/s) | M (kg) | FP (kN) | Smax (mm) | Failure Model | ||
| A37 | 3.67 | 400 | 750 | 8.1 | Flexure | [8] |
| A46 | 4.58 | 400 | 880 | 10.1 | Flexure | |
| A56 | 5.61 | 400 | 1000 | 13.1 | Flexure-shear | |
| A65 | 6.52 | 400 | 1110 | 16.0 | Shear | |
| A74 | 7.42 | 400 | 1290 | 22.0 | Shear | |
| A84 | 8.4 | 400 | 1400 | 24.4 | Shear | |
| B37 | 3.67 | 400 | 760 | 7.5 | Flexure | |
| B46 | 4.58 | 400 | 900 | 11.3 | Flexure-shear | |
| B65 | 6.52 | 400 | 1200 | 16.0 | Shear | |
| B74 | 7.42 | 400 | 1280 | 19.8 | Flexure-shear | |
| B84 | 8.4 | 400 | 1416 | 24.0 | Flexure-shear | |
| B93 | 9.3 | 400 | 1575 | 28.0 | Flexure-shear | |
| S1616-1 | 1.73 | 400 | 125 | 5.9 | None | [4] |
| S1616-2 | 2.45 | 400 | 180 | 11.0 | None | |
| S1616-3 | 3.46 | 400 | 248 | 20.1 | Flexure | |
| S1616-4 | 4.85 | 400 | 317 | 36.2 | Flexure | |
| S1322-1 | 2.45 | 400 | 190 | 7.8 | None | |
| S1322-2 | 3.46 | 400 | 260 | 11.4 | Flexure | |
| S1322-3 | 4.85 | 400 | 305 | 23.5 | Flexure | |
| S1322-4 | 6.86 | 400 | 340 | 27.0 | Flexure | |
| S2222-1 | 2.45 | 400 | 200 | 7.0 | None | |
| S2222-2 | 3.46 | 400 | 260 | 11.0 | Flexure | |
| S2222-3 | 4.85 | 400 | 313 | 21.4 | Flexure | |
| S2222-4 | 6.86 | 400 | 388 | 31.8 | Flexure | |
| A1 | 5 | 300 | 434 | 24.1 | n/p | [23] |
| A2-1 | 3.46 | 150 | 321 | 13.6 | Flexure | |
| A2-2 | 2.45 | 300 | 293 | 25.4 | Flexure | |
| A2-3 | 2 | 450 | 245 | 37.0 | Flexure | |
| A2-4 | 4.9 | 150 | 453 | 16.3 | Flexure | |
| A2-5 | 3.5 | 300 | 417 | 31.6 | Flexure | |
| A2-6 | 2.8 | 450 | 346 | 43.7 | Flexure | |
| A2-7 | 6 | 150 | 573 | 17.9 | Flexure | |
| A2-8 | 4.24 | 300 | 513 | 33.3 | Flexure | |
| A2-9 | 3.46 | 450 | 445 | 48.4 | Flexure | |
| A2-10 | 1 | 300 | 65 | 4.5 | Flexure | |
| A2-11 | 2 | 300 | 253 | 12.6 | Flexure | |
| A2-12 | 3 | 300 | 426 | 26.9 | Flexure | |
| A2-13 | 4 | 300 | 489 | 41.4 | Flexure | |
| A2-14 | 5 | 300 | 466 | 58.3 | Flexure | |
| A4 | 5 | 300 | 452 | 114.9 | n/p | |
| B | 5 | 300 | 667 | 77.0 | n/p | |
| C | 5 | 300 | 650 | 42.4 | n/p | |
| D | 5 | 300 | 639 | 94.0 | n/p | |
| E | 5 | 300 | 742 | 29.1 | n/p | |
| F | 5 | 300 | 664 | 43.9 | n/p | |
| G1-1 | 7 | 300 | 1496 | 64.3 | n/p | [2] |
| G1-1S | 7 | 300 | 1601 | 58.0 | n/p | |
| G2-1 | 4 | 300 | 510 | 28.3 | n/p | |
| G2-2 | 5 | 300 | 779 | 44.0 | n/p | |
| G2-3 | 6 | 300 | 854 | 57.0 | n/p | |
| G2L-1 | 4 | 400 | 447 | 44.2 | Flexure | |
| G2L-2 | 5 | 400 | 668 | 66.8 | Flexure | |
| G2L-3 | 6 | 400 | 787 | 89.7 | Flexure | |
| G3-1 | 4 | 300 | 609 | 36.7 | n/p | |
| G3-2 | 5 | 300 | 770 | 52.0 | n/p | |
| G3-3 | 6 | 300 | 839 | 70.6 | n/p | |
| G4-1 | 4 | 300 | 800 | 39.7 | n/p | |
| G4-2 | 5 | 300 | 986 | 56.1 | n/p | |
| G5-1 | 6 | 400 | 1313 | 63.5 | Flexure | |
| G5-2 | 7 | 400 | 1557 | 83.4 | Flexure | |
| G6-1 | 5 | 300 | 1336 | 26.4 | n/p | |
| G7-1 | 5 | 300 | 1243 | 45.8 | n/p | |
| G7-2 | 6 | 300 | 1588 | 60.9 | n/p | |
| G8-1 | 6 | 300 | 1192 | 36.5 | n/p | |
| G9-1 | 5 | 300 | 931 | 43.2 | n/p | |
| G9-2 | 6 | 300 | 1103 | 57.9 | n/p | |
| G10-1 | 4 | 300 | 751 | 33.7 | None | |
| G10-2 | 5 | 300 | 922 | 49.5 | Flexure | |
| G10-3 | 6 | 300 | 1017 | 67.8 | Flexure | |
| G10-4 | 7 | 300 | 1042 | 83.9 | Flexure | |
| G11-1 | 3.13 | 500 | 703 | 20.5 | n/p | |
| G11-2 | 4.2 | 500 | 971 | 33.2 | n/p | |
| G11-3 | 5.05 | 500 | 1462 | 43.1 | n/p | |
| G11-4 | 5.78 | 500 | 1878 | 55.5 | n/p | |
| G11-5 | 6.42 | 500 | 1765 | 67.2 | n/p | |
| G11-6 | 7 | 500 | 1907 | 83.4 | n/p | |
| G12-1 | 7.67 | 500 | 1675 | 85.4 | n/p | |
| G13-1 | 7.67 | 500 | 2150 | 60.6 | n/p | |
| G14-1 | 7.67 | 500 | 2258 | 63.7 | n/p | |
| G15-1 | 7.67 | 500 | 2063 | 40.5 | n/p | |
| G16-1 | 7.67 | 500 | 2023 | 52.9 | n/p | |
| B-1700-4.60 | 4.6 | 1700 | 1360 | 83.7 | Flexure | [24] |
| B-1052-6.40 | 6.4 | 1052 | 1900 | 79.3 | Flexure-shear | |
| B-868-7.14 | 7.14 | 868 | 1450 | 209.0 | Shear | |
| C-1700-4.60 | 4.6 | 1700 | 1380 | 118.0 | Shear | |
| C-1300-5.56 | 5.56 | 1300 | 1500 | 67.4 | Shear | |
| C-868-7.14 | 7.14 | 868 | 1780 | 67.9 | Shear | |
| D-1700-4.60 | 4.6 | 1700 | 1380 | 41.5 | Flexure | |
| D-1300-5.56 | 5.56 | 1300 | 1500 | 48.0 | Flexure | |
| D-868-7.14 | 7.14 | 868 | 1780 | 47.5 | Flexure-shear | |
| BD1 | 4.15 | 253 | 891 | 12.0 | Flexure | [40] |
| BD2 | 7.11 | 253 | 1396 | 24.0 | Flexure | |
| BD3 | 11.96 | 253 | 1940 | 75.0 | Shear | |
| BD4 | 7.81 | 578 | 1466 | 80.0 | Flexure | |
| BD5 | 5.1 | 578 | 983 | 38.0 | Flexure-shea | |
| A-1 | 3.12 | 968 | 260 | 81.0 | Flexure | [41] |
| A-2 | 4 | 587 | 420 | 74.0 | Flexure | |
| A-3 | 5.7 | 392 | 790 | 83.6 | Flexure | |
| A-4 | 8.5 | 197 | 800 | 89.5 | Flexure | |
| B-0-00 | 7.2 | 393 | 2014 | 142.6 | Shear | [39] |
| B-0-25 | 7.2 | 393 | 2214 | 31.4 | Flexure-shear | |
| B-0-50 | 7.2 | 393 | 1948 | 20.3 | Flexure | |
| BD1 | 4.43 | 333 | 912 | n/p | Shear | [49] |
| BD2 | 8.85 | 333 | 1708 | n/p | Shear | |
| BD3 | 5.71 | 200 | 1184 | n/p | Shear | |
| BD4 | 4.43 | 200 | 768 | n/p | Flexure | |
| BD5 | 5.71 | 200 | 1360 | n/p | Flexure-shea | |
| B1 | 5.9 | 253 | 1500 | 12.4 | Flexure-shear | [42] |
| B2 | 15.2 | 253 | 2203 | 79.8 | Flexure | |
| B3 | 7.2 | 393 | 1689 | 44.8 | Flexure | |
| B4 | 7.2 | 393 | 2014 | 142.6 | Shear | |
| B5 | 7.2 | 393 | 1948 | 20.3 | Flexure | |
| B6 | 7.2 | 393 | 2214 | 31.4 | Flexure-shear | |
| 10-C27-4 | 8.85 | 33.6 | 141.97 | 28.66 | n/p | [38] |
| 6-C40-5 | 9.9 | 33.6 | 202.2 | 62.65 | n/p | |
| 6-C40-6 | 10.84 | 33.6 | 267.7 | 87.74 | n/p | |
| 6-C40-7 | 11.71 | 33.6 | 230.71 | 119.07 | n/p | |
| 6-C40-8 | 12.52 | 33.6 | 224.75 | 119.11 | n/p | |
| 8-C40-2 | 6.26 | 33.6 | 151.73 | 22.94 | n/p | |
| 8-C40-3 | 7.67 | 33.6 | 182.59 | 35.65 | n/p | |
| 8-C40-4 | 8.85 | 33.6 | 203.26 | 35.14 | n/p | |
| 8-C40-5 | 9.9 | 33.6 | 234.5 | 38.82 | n/p | |
| 10-C40-5 | 9.9 | 33.6 | 245.8 | 33.7 | n/p | |
| 10-C40-6 | 10.84 | 33.6 | 248.56 | 45.22 | n/p | |
| 10-C40-7 | 11.71 | 33.6 | 183.3 | 62.5 | n/p | |
References
- Cotsovos, D. A simplified approach for assessing the load-carrying capacity of reinforced concrete beams under concentrated load applied at high rates. Int. J. Impact Eng. 2010, 37, 907–917. [Google Scholar] [CrossRef]
- Kishi, N.; Mikami, H. Empirical Formulas for Designing Reinforced Concrete Beams under Impact Loading. ACI Struct. J. 2012, 109, 509–519. [Google Scholar] [CrossRef]
- Pham, T.M.; Hao, H. Prediction of the impact force on reinforced concrete beams from a drop weight. Adv. Struct. Eng. 2016, 19, 1710–1722. [Google Scholar] [CrossRef]
- Fujikake, K.; Li, B.; Soeun, S. Impact Response of Reinforced Concrete Beam and Its Analytical Evaluation. J. Struct. Eng. 2009, 135, 938–950. [Google Scholar] [CrossRef]
- Yi, W.-J.; Zhao, D.-B.; Kunnath, S.K. Simplified Approach for Assessing Shear Resistance of Reinforced Concrete Beams under Impact Loads. ACI Struct. J. 2016, 113, 747–756. [Google Scholar] [CrossRef]
- Zhao, D.-B.; Yi, W.-J.; Kunnath, S.K. Numerical simulation and shear resistance of reinforced concrete beams under impact. Eng. Struct. 2018, 166, 387–401. [Google Scholar] [CrossRef]
- Zhao, W.; Qian, J.; Jia, P. Peak Response Prediction for RC Beams under Impact Loading. Shock Vib. 2019, 2019, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Bhatti, A.Q.; Kishi, N.; Mikami, H.; Ando, T. Elasto-plastic impact response analysis of shear-failure-type RC beams with shear rebars. Mater. Des. 2009, 30, 502–510. [Google Scholar] [CrossRef]
- Saatci, S.; Vecchio, F.J. Nonlinear Finite Element Modeling of Reinforced Concrete Structures under Impact Loads. ACI Struct. J. 2009, 106, 717–725. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Chen, W.; Pham, T.M.; Hao, H. Analytical and numerical studies on impact force profile of RC beam under drop weight impact. Int. J. Impact Eng. 2021, 147, 103743. [Google Scholar] [CrossRef]
- Das Adhikary, S.; Li, B.; Fujikake, K. Dynamic behavior of reinforced concrete beams under varying rates of concentrated loading. Int. J. Impact Eng. 2012, 47, 24–38. [Google Scholar] [CrossRef]
- Qasrawi, Y.; Heffernan, P.J.; Fam, A. Dynamic behaviour of concrete filled FRP tubes subjected to impact loading. Eng. Struct. 2015, 100, 212–225. [Google Scholar] [CrossRef]
- Goldston, M.; Remennikov, A.; Sheikh, M.N. Experimental investigation of the behaviour of concrete beams reinforced with GFRP bars under static and impact loading. Eng. Struct. 2016, 113, 220–232. [Google Scholar] [CrossRef] [Green Version]
- Pham, T.M.; Hao, H. Review of Concrete Structures Strengthened with FRP Against Impact Loading. Structures 2016, 7, 59–70. [Google Scholar] [CrossRef] [Green Version]
- Saatçi, S.; Vecchio, F.J. Effects of Shear Mechanisms on Impact Behavior of Reinforced Concrete Beams. ACI Struct. J. 2009, 106, 78–86. [Google Scholar] [CrossRef] [Green Version]
- Kishi, N.; Mikami, H.; Matsuoka, K.; Ando, T. Impact behavior of shear-failure-type RC beams without shear rebar. Int. J. Impact Eng. 2002, 27, 955–968. [Google Scholar] [CrossRef]
- Chen, S.; Li, Q.; Liu, Y.; Xia, J.; Xue, Z. Dynamic elastoplastic analysis using the meshless local natural neighbor interpolation method. Int. J. Comput. Methods 2011, 08, 463–481. [Google Scholar] [CrossRef]
- Pham, T.M.; Hao, H. Plastic hinges and inertia forces in RC beams under impact loads. Int. J. Impact Eng. 2017, 103, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Jones, N. Plastic Failure of Ductile Beams Loaded Dynamically. J. Eng. Ind. 1976, 98, 131–136. [Google Scholar] [CrossRef]
- Khan, A.; Smith, D.L.; Izzuddin, B.A. Investigation of rigid-plastic beams subjected to impact using linear complementarity. Eng. Struct. 2013, 50, 137–148. [Google Scholar] [CrossRef]
- Das Adhikary, S.; Li, B.; Fujikake, K. Effects of High Loading Rate on Reinforced Concrete Beams. ACI Struct. J. 2014, 111, 651–660. [Google Scholar] [CrossRef]
- Fujikake, K.; Senga, T.; Ueda, N.; Ohno, T.; Katagiri, M. Study on Impact Response of Reactive Powder Concrete Beam and Its Analytical Model. J. Adv. Concr. Technol. 2006, 4, 99–108. [Google Scholar] [CrossRef] [Green Version]
- Tachibana, S.; Masuya, H.; Nakamura, S. Performance based design of reinforced concrete beams under impact. Nat. Hazards Earth Syst. Sci. 2010, 10, 1069–1078. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.-B.; Yi, W.-J.; Kunnath, S.K. Shear Mechanisms in Reinforced Concrete Beams under Impact Loading. J. Struct. Eng. 2017, 143, 04017089. [Google Scholar] [CrossRef]
- Das Adhikary, S.; Li, B.; Fujikake, K. Low Velocity Impact Response of Reinforced Concrete Beams: Experimental and Numerical Investigation. Int. J. Prot. Struct. 2015, 6, 81–111. [Google Scholar] [CrossRef]
- Yan, P.; Zhang, J.; Fang, Q.; Zhang, Y. Numerical simulation of the effects of falling rock’s shape and impact pose on impact force and response of RC slabs. Constr. Build. Mater. 2018, 160, 497–504. [Google Scholar] [CrossRef]
- Zhang, C.; Gholipour, G.; Mousavi, A.A. Nonlinear dynamic behavior of simply-supported RC beams subjected to combined impact-blast loading. Eng. Struct. 2018, 181, 124–142. [Google Scholar] [CrossRef]
- Li, H.; Chen, W.; Hao, H. Influence of drop weight geometry and interlayer on impact behavior of RC beams. Int. J. Impact Eng. 2019, 131, 222–237. [Google Scholar] [CrossRef]
- Fan, W.; Liu, B.; Huang, X.; Sun, Y. Efficient modeling of flexural and shear behaviors in reinforced concrete beams and columns subjected to low-velocity impact loading. Eng. Struct. 2019, 195, 22–50. [Google Scholar] [CrossRef]
- Ando, T.; Kishi, N.; Mikami, H.; Sato, M.; Matsuoka, K.G. Experimental study on impact resistance of bending failure type of RC beams. In Proceedings of the 7th East Asia-Pacific Conference on Structural Engineering & Construction, Kochi, Japan, 27–29 August 1999; pp. 1075–1080. [Google Scholar]
- Kishi, N.; Mikami, H.; Matsuoka, K.-I.G.; Ando, T. An empirical impact resistant design formula of rc beams with statically bending failure mode. Doboku Gakkai Ronbunshu 2000, 2000, 177–190. [Google Scholar] [CrossRef]
- Das Adhikary, S.; Li, B.; Fujikake, K. Parametric study of RC beams under a wide range of loading rates. Proc. Inst. Civ. Eng.-Struct. Build. 2015, 168, 729–746. [Google Scholar] [CrossRef]
- Soleimani, S.M.; Banthia, N.; Mindess, S. Behavior of RC beams under impact loading: Some new findings. In Proceedings of the 6th International Conference on Fracture Mechanics of Concrete and Concrete Structures, Catania, Italy, 17–22 June 2007; Volume 2, pp. 867–874. [Google Scholar]
- Hughes, B.P.; Mahmood, A.T. Impact behaviour of prestressed concrete beams in flexure. Mag. Concr. Res. 1984, 36, 157–164. [Google Scholar] [CrossRef]
- Louw, J.; Maritz, G.; Loedolff, M. The behaviour of RC columns under impact loading. Civ. Eng. Siviele Ing. 1992, 34, 371–378. [Google Scholar]
- May, I.M.; Chen, Y.; Owen, D.R.J.; Feng, Y.; Thiele, P.J. Reinforced concrete beams under drop-weight impact loads. Comput. Concr. 2006, 3, 79–90. [Google Scholar] [CrossRef]
- Zhan, T.; Wang, Z.; Ning, J. Failure behaviors of reinforced concrete beams subjected to high impact loading. Eng. Fail. Anal. 2015, 56, 233–243. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, R.; Dou, G.; Xu, J.; Du, X. Experimental and numerical study of reinforced concrete beams with steel fibers subjected to impact loading. Int. J. Damage Mech. 2017, 27, 1058–1083. [Google Scholar] [CrossRef]
- Xu, B.; Zeng, X. Experimental study on the behaviors of reinforced concrete beams under impact loadings. China Civ. Eng. J. 2014, 47, 41–51. [Google Scholar]
- Zhao, D.B.; Yi, W.J. Anti-impact behavior and design method for RC beams. J. Vib. Shock 2015, 34, 139–145. [Google Scholar] [CrossRef]
- Dou, G.; Du, X.; Li, L. Experimental study on the behavior of high strength reinforced concrete beams under impact load. J. Tianjin Univ. 2014, 47, 1072–1080. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Tariq, M.; Khan, A.; Ullah, A.; Zamin, B.; Kashyzadeh, K.R.; Ahmad, M. Gene Expression Programming for Estimating Shear Strength of RC Squat Wall. Buildings 2022, 12, 918. [Google Scholar] [CrossRef]
- Tariq, M.; Khan, A.; Shayanfar, J.; Hanif, M.U.; Ullah, A. A regression model for predicting the shear strength of RC knee joint subjected to opening and closing moment. J. Build. Eng. 2021, 41, 102727. [Google Scholar] [CrossRef]
- Tariq, M.; Khan, A.; Ullah, A.; Shayanfar, J.; Niaz, M. Improved Shear Strength Prediction Model of Steel Fiber Reinforced Concrete Beams by Adopting Gene Expression Programming. Materials 2022, 15, 3758. [Google Scholar] [CrossRef] [PubMed]
- Ilie, I.; Dittrich, P.; Carvalhais, N.; Jung, M.; Heinemeyer, A.; Migliavacca, M.; Morison, J.I.L.; Sippel, S.; Subke, J.-A.; Wilkinson, M.; et al. Reverse engineering model structures for soil and ecosystem respiration: The potential of gene expression programming. Geosci. Model Dev. 2017, 10, 3519–3545. [Google Scholar] [CrossRef] [Green Version]
- Teodorescu, L.; Sherwood, D. High Energy Physics event selection with Gene Expression Programming. Comput. Phys. Commun. 2008, 178, 409–419. [Google Scholar] [CrossRef]
- Kose, M.M.; Kayadelen, C. Modeling of transfer length of prestressing strands using genetic programming and neuro-fuzzy. Adv. Eng. Softw. 2010, 41, 315–322. [Google Scholar] [CrossRef]
- Zeng, X.; Xu, B. Experimental study on the impact-resistant behavior of RC beams without shear-resistant rebar. China Civ. Eng. J. 2012, 45, 63–73. [Google Scholar]




| Parameters | Ranges |
|---|---|
| Velocity (V) | 1–16 (m/s) |
| Mass (M) | 33–1700 (kg) |
| ) | 20–42 (MPa) |
| Net span length (Ln) | 1000–5000 (mm) |
| Beam width (b) | 100–300 (mm) |
| Beam height (h) | 120–500 (mm) |
| Tensile reinforcement ratio | 0.29–3.1 (%) |
| Shear reinforcement ratio | 0–1.4 (%) |
| Function Set | ln, +, −, /, x, sqrt, x2,3,4,5 |
|---|---|
| Chromosomes | 110 |
| Head size | 11 |
| Linking function | Addition |
| Number of genes | 3 |
| Mutation rate | 0.0014 |
| Inversion rate | 0.1 |
| One-point recombination rate | 0.0027 |
| Two-point recombination rate | 0.0027 |
| Gene recombination rate | 0.0027 |
| Gene transposition rate | 0.0027 |
| Constants per gene | 10 |
| Lower/upper bound of constants | −20/20 |
| Parameters | Values |
|---|---|
| (MPa) | 4.12 |
| Dilation angle (degrees) | 35 |
| Eccentricity | 0.10 |
| Bi-axial to uni-axial strength ratio | 1.16 |
| Second stress invariant ratio | 0.667 |
| Viscosity parameter | 0.01 |
| Experimental Results | ABAQUS Results | GEP Results | |
|---|---|---|---|
| Peak Impact force on the beam (kN) [Striker velocity 6.52 m/s] | 1110 | 1113 | 1150 |
| Peak Impact force on the beam (kN) [Striker velocity 7.42 m/s] | 1290 | 1229 | 1240 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tariq, M.; Khan, A.; Ullah, A. Predicting the Response of RC Beam from a Drop-Weight Using Gene Expression Programming. Materials 2022, 15, 6910. https://doi.org/10.3390/ma15196910
Tariq M, Khan A, Ullah A. Predicting the Response of RC Beam from a Drop-Weight Using Gene Expression Programming. Materials. 2022; 15(19):6910. https://doi.org/10.3390/ma15196910
Chicago/Turabian StyleTariq, Moiz, Azam Khan, and Asad Ullah. 2022. "Predicting the Response of RC Beam from a Drop-Weight Using Gene Expression Programming" Materials 15, no. 19: 6910. https://doi.org/10.3390/ma15196910
APA StyleTariq, M., Khan, A., & Ullah, A. (2022). Predicting the Response of RC Beam from a Drop-Weight Using Gene Expression Programming. Materials, 15(19), 6910. https://doi.org/10.3390/ma15196910






