Analysis and Suppression of Thermal Magnetic Noise of Ferrite in the SERF Co-Magnetometer
Abstract
:1. Introduction
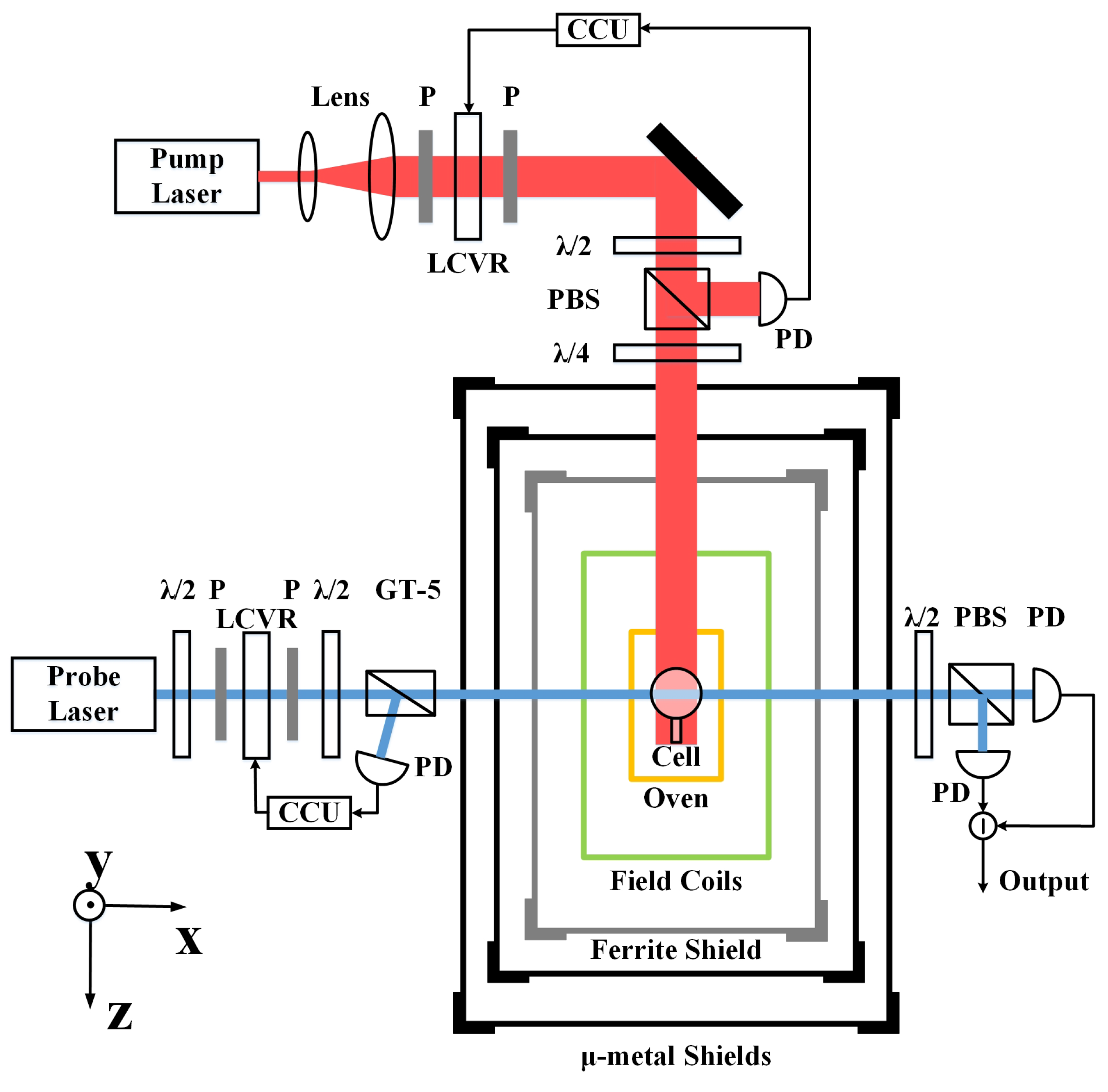
2. Methods
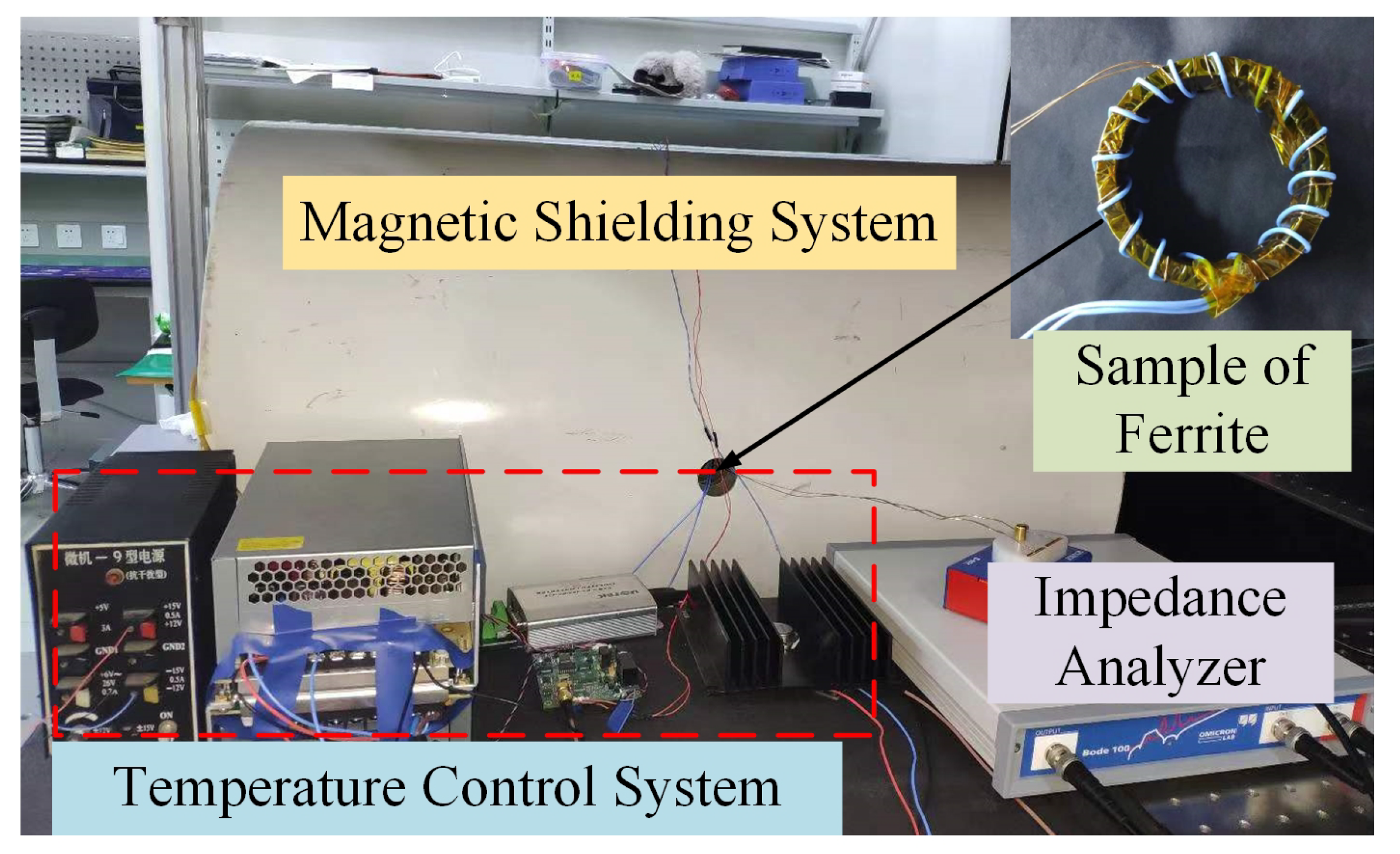
3. Experimental Setup
4. Results and Analysis
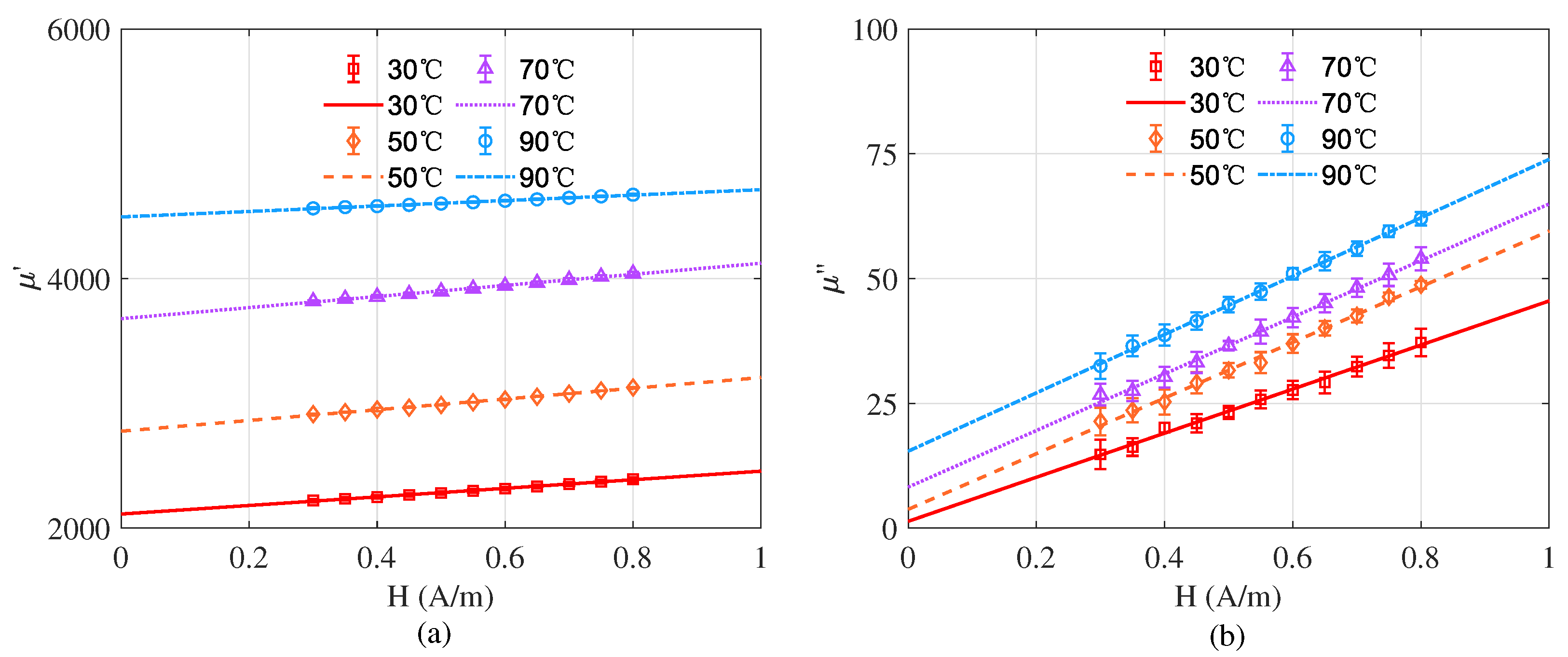
4.1. Measurement of Ferrite Complex Permeability at Different Temperatures
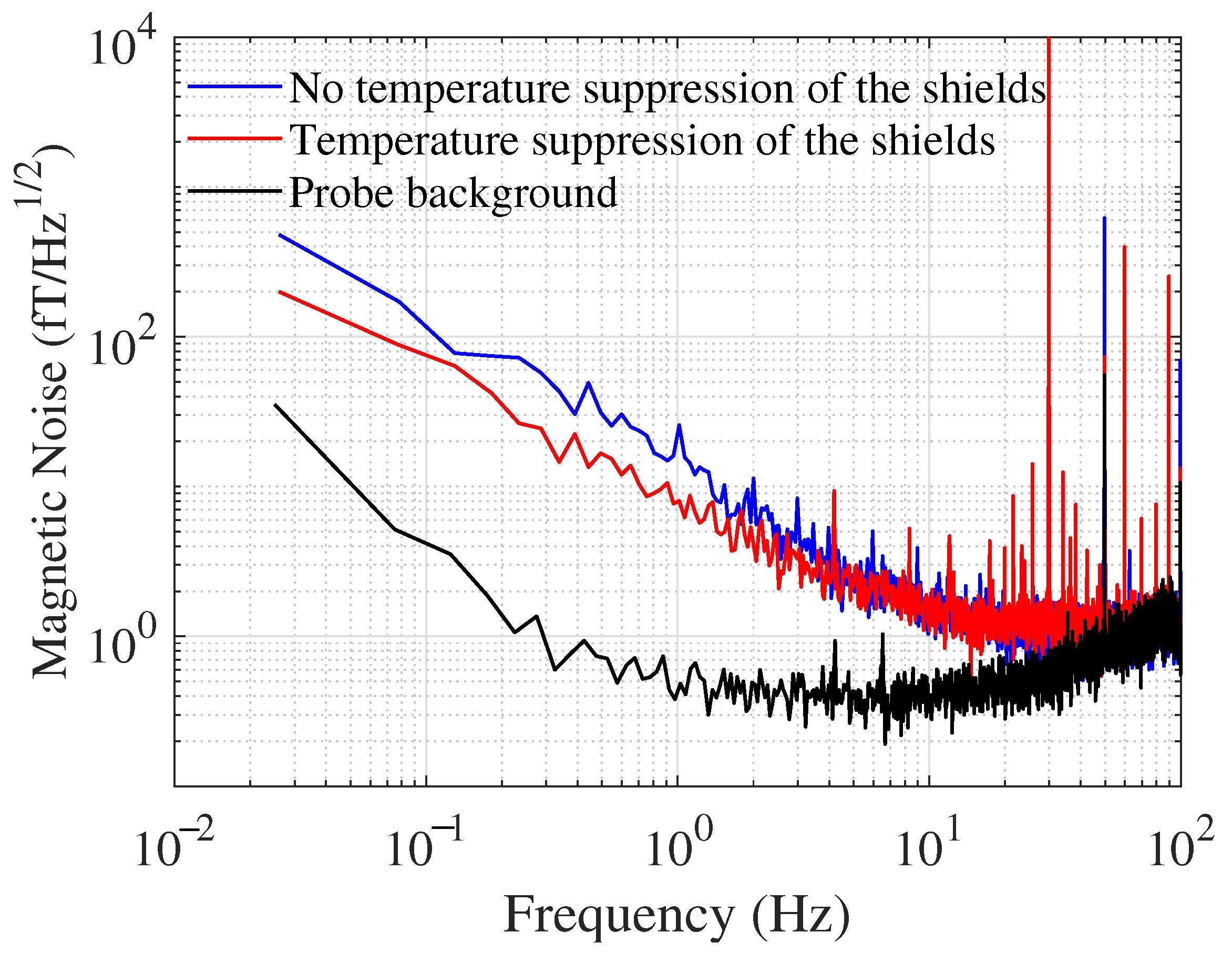
4.2. Magnetic Noise Measurement
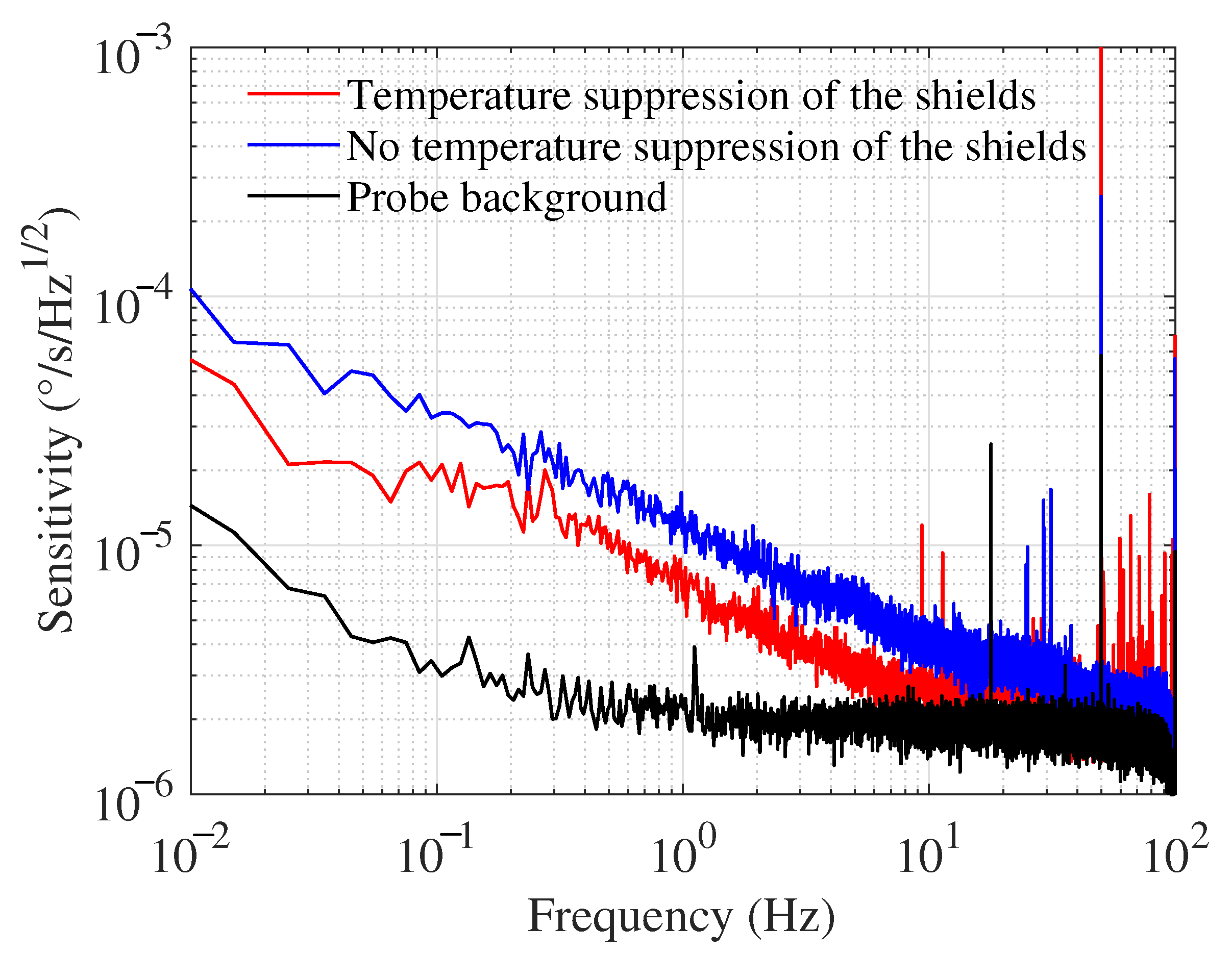
4.3. Sensitivity Measurement of SERF Co-Magnetometer
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
Abbreviations
| SERF | Spin-Exchange Relaxation Free |
Appendix A
Principle of Complex Magnetic Permeability Measurement
| Trem | Description |
|---|---|
| inductance of the sample | |
| effective magnetic circuit length | |
| effective cross-sectional area | |
| N | number of turns of the winding |
| resistance value containing the resistance of the test coil | |
| resistance value of the measurement coil | |
| f | test frequency |
References
- Bear, D.; Stoner, R.E.; Walsworth, R.L.; Kostelecky, V.A.; Lane, C.D. Limit on Lorentz and CPT Violation of the Neutron Using a Two-Species Noble-Gas Maser. Phys. Rev. Lett. 2002, 89, 209902. [Google Scholar] [CrossRef]
- Brown, I.M. A New Limit on Lorentz-and CPT -Violating Neutron Spin Interactions Using a K-3He Comagnetometer. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2011. [Google Scholar]
- Allred, J.C.; Lyman, R.N.; Kornack, T.W.; Romalis, M.V. High-Sensitivity Atomic Magnetometer Unaffected by Spin-Exchange Relaxation. Phys. Rev. Lett. 2002, 89, 130801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kominis, I.K.; Kornack, T.W.; Allred, J.C.; Romalis, M.V. A Subfemtotesla Multichannel Atomic Magnetometer. Nature 2003, 422, 596–599. [Google Scholar] [CrossRef] [PubMed]
- Dang, H.B.; Maloof, A.C.; Romalis, M.V. Ultrahigh sensitivity magnetic field and magnetization measurements with an atomic magnetometer. Appl. Phys. Lett. 2010, 97, 151110. [Google Scholar] [CrossRef] [Green Version]
- Kornack, T.W.; Romalis, M.V. Dynamics of Two Overlapping Spin Ensembles Interacting by Spin Exchange. Phys. Rev. Lett. 2002, 89, 253002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kornack, T.W.; Ghosh, R.K.; Romalis, M.V. Nuclear Spin Gyroscope Based on an Atomic Comagnetometer. Phys. Rev. Lett. 2005, 95, 230801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boto, E.; Holmes, N.; Leggett, J.; Roberts, G.; Shah, V.; Meyer, S.S.; Munoz, L.D.; Mullinger, K.J.; Tierney, T.M.; Bestmann, S.; et al. Moving magnetoencephalography towards real-world applications with a wearable system. Nature 2018, 555, 657–661. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Savukov, I.; Kim, Y.J.; Shah, V.; Boshier, M.G. High-sensitivity operation of single-beam optically pumped magnetometer in a kHz frequency range. Meas. Sci. Technol. 2017, 28, 035104. [Google Scholar] [CrossRef]
- Fan, W.; Quan, W.; Liu, F.; Xing, L.; Liu, G. Suppression of the Bias Error Induced by Magnetic Noise in a Spin-Exchange Relaxation-Free Gyroscope. IEEE Sensors J. 2019, 19, 9712–9721. [Google Scholar] [CrossRef]
- Pang, H.; Duan, L.; Quan, W.; Wang, J.; Wu, W.; Fan, W.; Liu, F. Design of Highly Uniform Three Dimensional Spherical Magnetic Field Coils for Atomic Sensors. IEEE Sens. J. 2020, 20, 11229–11236. [Google Scholar] [CrossRef]
- Pang, H.; Fan, W.; Huang, J.; Liu, F.; Liu, S.; Quan, W. A Highly Sensitive In-Situ Magnetic Field Fluctuation Measurement Method Based on Nuclear-Spin Depolarization in an Atomic Comagnetometer. IEEE Trans. Instrum. Meas. 2022, 71, 9505408. [Google Scholar] [CrossRef]
- Ma, D.; Ding, M.; Lu, J.; Yao, H.; Zhao, J.; Yang, K.; Cai, J.; Han, B. Study of Shielding Ratio of Cylindrical Ferrite Enclosure with Gaps and Holes. IEEE Sens. J. 2019, 19, 6085–6092. [Google Scholar] [CrossRef]
- Fu, Y.; Sun, J.; Ruan, J.; Quan, W. A Nanocrystalline Shield for High Precision Co-magnetometer Operated in Spin-Exchange Relaxation-Free Regime. Sens. Actuators A-Phys. 2022, 339, 113487. [Google Scholar] [CrossRef]
- Paperno, E.; Romalis, M.V.; Noam, Y. Optimization of five-shell axial magnetic shields having openings in the end-caps. IEEE Trans. Magn. 2004, 40, 2170–2172. [Google Scholar] [CrossRef]
- Fan, W.; Quan, W.; Liu, F.; Pang, H.; Xing, L.; Liu, G. Performance of Low-Noise Ferrite Shield in a K-Rb-21Ne Co-Magnetometer. IEEE Sens. J. 2019, 20, 2543–2549. [Google Scholar] [CrossRef]
- Munger, C.T. Magnetic Johnson noise constraints on electron electric dipole moment experiments. Phys. Rev. A 2005, 72, 012506. [Google Scholar] [CrossRef] [Green Version]
- Silveyra, J.M.; Ferrara, E.; Huber, D.L.; Monson, T.C. Soft magnetic materials for a sustainable and electrified world. Science 2018, 362, 418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kornack, T.W.; Smullin, S.J.; Lee, S.K.; Romalis, M.V. A Low-Noise Ferrite Magnetic Shield. Appl. Phys. Lett. 2007, 90, 223501. [Google Scholar] [CrossRef] [Green Version]
- Jia, Y.C.; Liu, Z.C.; Zhou, B.Q.; Liang, X.Y.; Wu, W.F.; Peng, J.P.; Ding, M.; Zhai, Y.Y.; Fang, J.C. Pump Beam Influence on Spin Polarization Homogeneity in the Nuclear Magnetic Resonance Gyroscope. J. Phys. D-Appl. Phys. 2019, 52, 355001. [Google Scholar]
- Liu, L.B.; Yan, Y.; Ngo, K.D.T.; Lu, G.Q. NiCuZn Ferrite Cores by Gelcasting: Processing and Properties. IEEE Trans. Ind. Appl. 2017, 53, 5728–5733. [Google Scholar] [CrossRef]
- Dobak, S.; Beatrice, C.; Tsakaloudi, V.; Fiorillo, F. Magnetic Losses in Soft Ferrites. Magnetochemistry 2022, 8, 60. [Google Scholar] [CrossRef]
- Lee, S.K.; Romalis, M.V. Calculation of Magnetic Field Noise From High-Permeability Magnetic Shields and Conducting Objects with Simple Geometry. J. Appl. Phys. 2008, 103, 084904. [Google Scholar] [CrossRef] [Green Version]
- Ma, D.; Lu, J.; Fang, X.; Yang, K.; Wang, K.; Zhang, N.; Han, B.; Ding, M. Parameter Modeling Analysis of a Cylindrical Ferrite Magnetic Shield to Reduce Magnetic Noise. IEEE Trans. Ind. Electron. 2022, 69, 991–998. [Google Scholar] [CrossRef]
- Yang, K.; Lu, J.; Ding, M.; Zhao, J.; Ma, D.; Li, Y.; Xing, B.; Han, B.; Fang, J. Improved Measurement of the Low-Frequency Complex Permeability of Ferrite Annulus for Low-Noise Magnetic Shielding. IEEE Access 2019, 7, 126059–126065. [Google Scholar] [CrossRef]
- Lu, J.; Ma, D.; Yang, K.; Quan, W.; Zhao, J.; Xing, B.; Han, B.; Ding, M. Study of Magnetic Noise of a Multi-Annular Ferrite Shield. IEEE Access 2020, 8, 40918–40924. [Google Scholar] [CrossRef]
- Pczkowski, P.; Zachariasz, P.; Kowalik, M.; Tokarz, W.; Naik, S.P.K.; Żukrowski, J.; Jastrzębski, C.; Dadiel, L.J.; Tabiś, W.; Gondek, Ł. Iron diffusivity into superconducting YBa2Cu3O7-δ at oxygen-assisted sintering: Structural, magnetic, and transport properties. J. Eur. Ceram. Soc. 2021, 41, 7085–7097. [Google Scholar] [CrossRef]
- Chrobak, M.; Woch, W.M.; Szwachta, G.; Zalecki, R.; Gondek, Ł.; Kołodziejczyk, A.; Kusiński, J. Thermal Fluctuations in YBCO Thin Film on MgO Substrate. ACTA Phys. Pol. A 2014, 126, A88–A91. [Google Scholar] [CrossRef]
- Fiorillo, F.; Beatrice, C.; Coisson, M.; Zhemchuzhna, L. Loss and Permeability Dependence on Temperature in Soft Ferrites. IEEE Trans. Magn. 2009, 45, 4242–4245. [Google Scholar] [CrossRef]
- Sidles, J.A.; Garbini, J.L.; Dougherty, W.M.; Chao, S.H. The classical and quantum theory of thermal magnetic noise, with applications in spintronics and quantum microscopy. Proc. IEEE 2003, 91, 799–816. [Google Scholar] [CrossRef]
- Fan, W.; Quan, W.; Zhang, W.; Xing, L.; Liu, G. Analysis on the Magnetic Field Response for Nuclear Spin Co-magnetometer Operated in Spin-Exchange Relaxation-Free Regime. IEEE Access 2019, 7, 28574–28580. [Google Scholar] [CrossRef]

| Temperature (C) | at 1 Hz (fT/Hz) | ||
|---|---|---|---|
| 30 | 2113.4 | 1.37 | 7.45 |
| 50 | 2777.3 | 3.77 | 9.77 |
| 70 | 3679.0 | 8.23 | 11.22 |
| 90 | 4494.6 | 15.42 | 12.93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, H.; Liu, F.; Fan, W.; Wu, J.; Yuan, Q.; Wu, Z.; Quan, W. Analysis and Suppression of Thermal Magnetic Noise of Ferrite in the SERF Co-Magnetometer. Materials 2022, 15, 6971. https://doi.org/10.3390/ma15196971
Pang H, Liu F, Fan W, Wu J, Yuan Q, Wu Z, Quan W. Analysis and Suppression of Thermal Magnetic Noise of Ferrite in the SERF Co-Magnetometer. Materials. 2022; 15(19):6971. https://doi.org/10.3390/ma15196971
Chicago/Turabian StylePang, Haoying, Feng Liu, Wengfeng Fan, Jiaqi Wu, Qi Yuan, Zhihong Wu, and Wei Quan. 2022. "Analysis and Suppression of Thermal Magnetic Noise of Ferrite in the SERF Co-Magnetometer" Materials 15, no. 19: 6971. https://doi.org/10.3390/ma15196971
APA StylePang, H., Liu, F., Fan, W., Wu, J., Yuan, Q., Wu, Z., & Quan, W. (2022). Analysis and Suppression of Thermal Magnetic Noise of Ferrite in the SERF Co-Magnetometer. Materials, 15(19), 6971. https://doi.org/10.3390/ma15196971






