Distribution of Order Parameter in Solids under High Pressure Torsion
Abstract
:1. Introduction
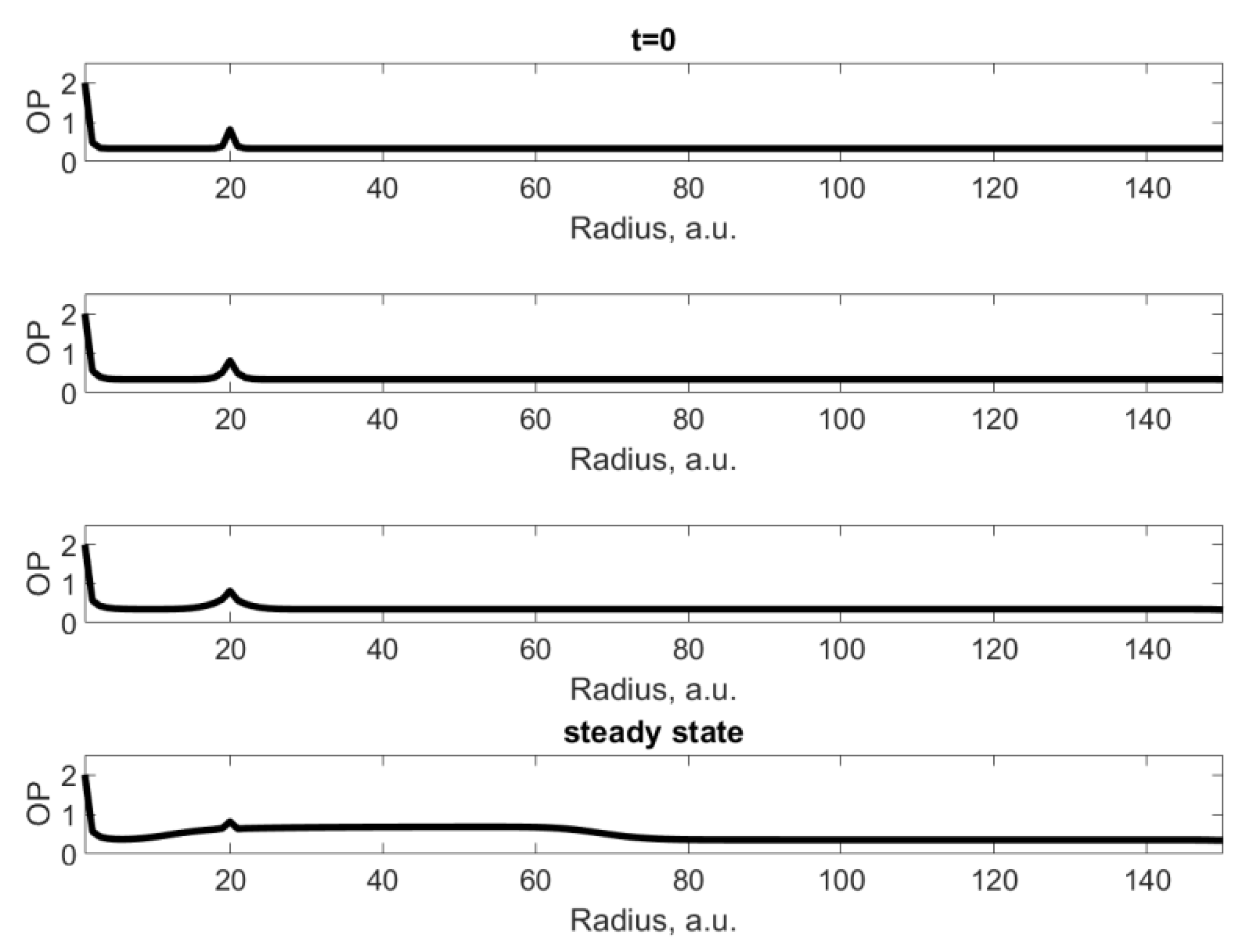
2. Evolution of Order Parameter and Steady State during HPT
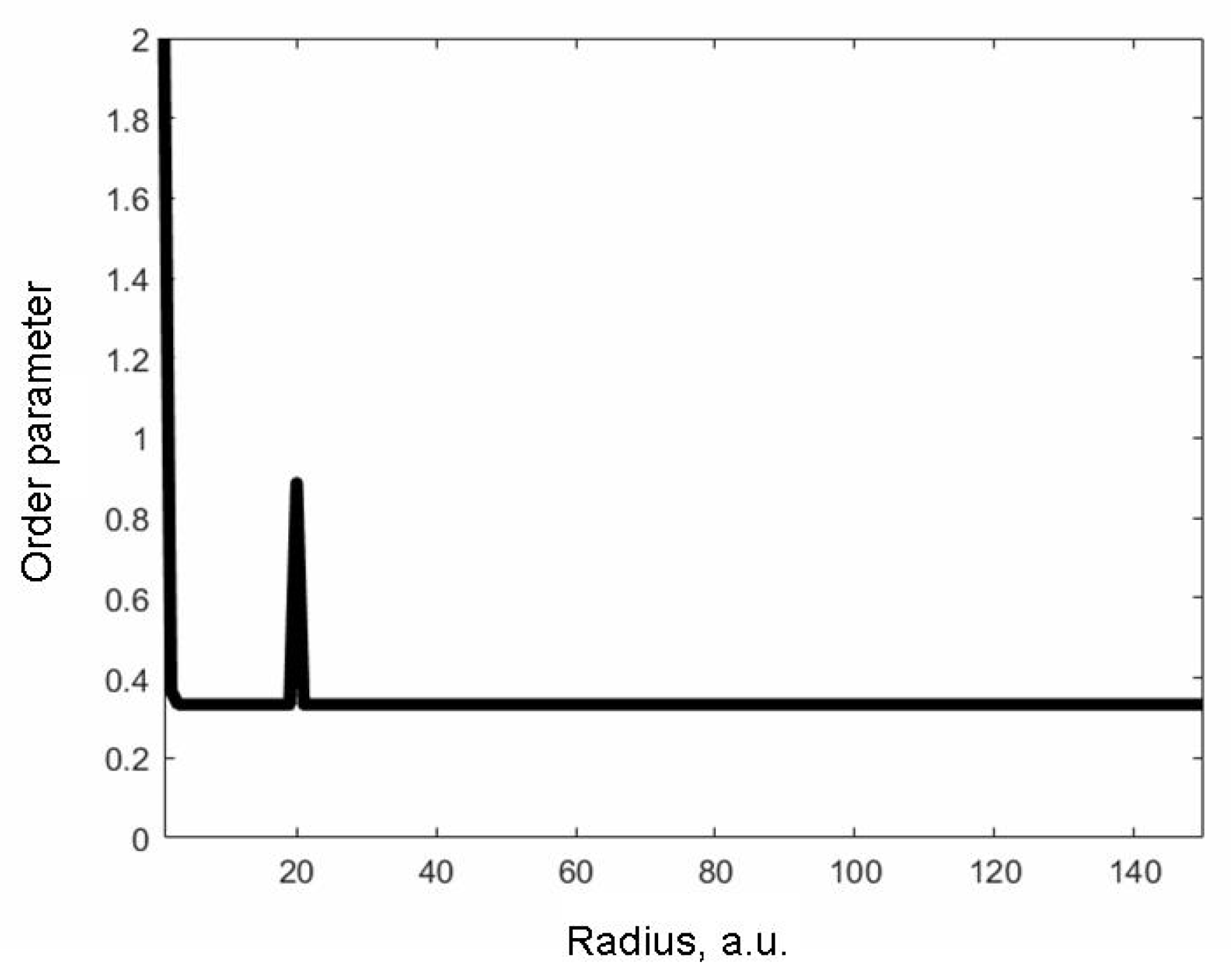
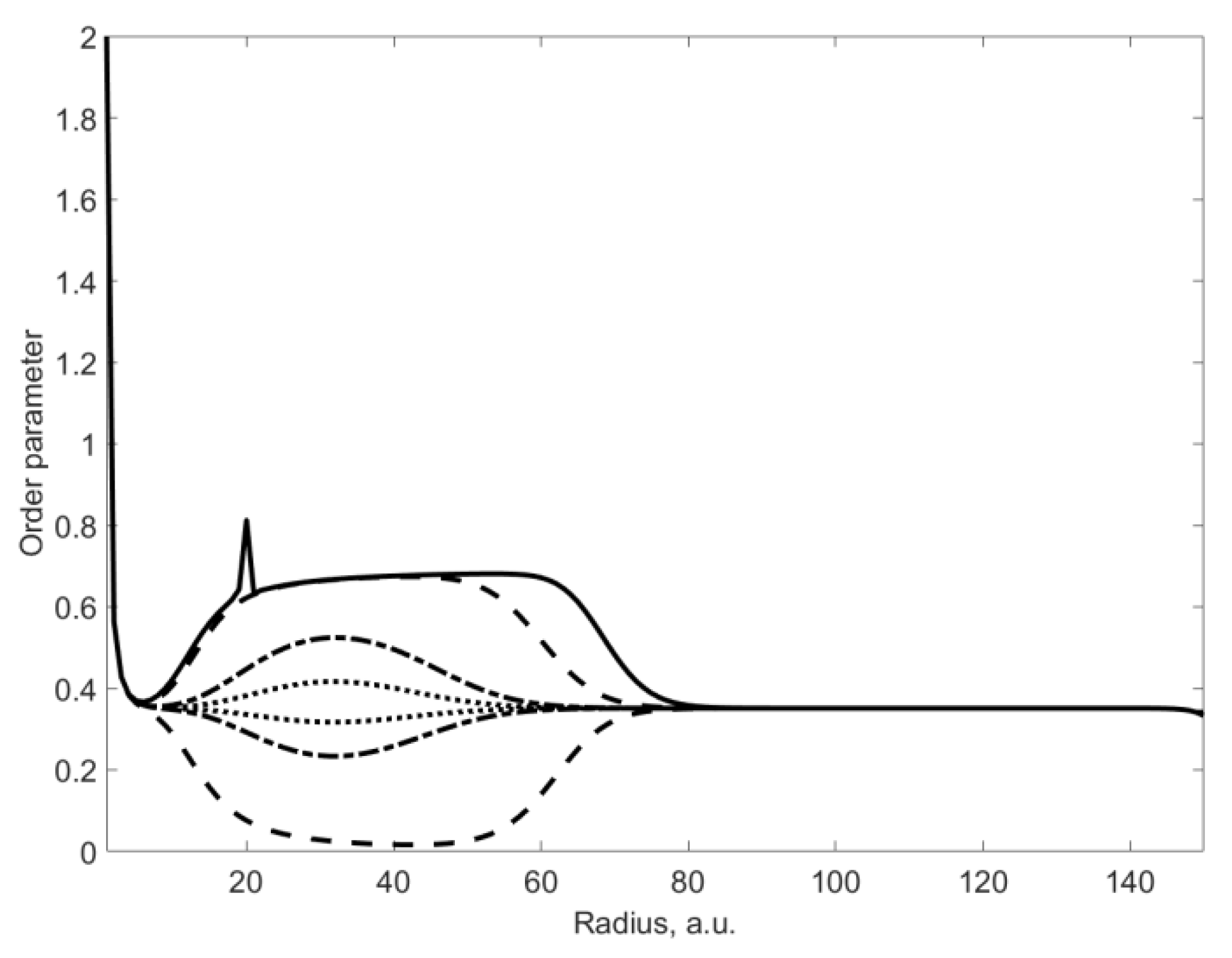
3. Distribution of Order Parameter in the HPT Sample
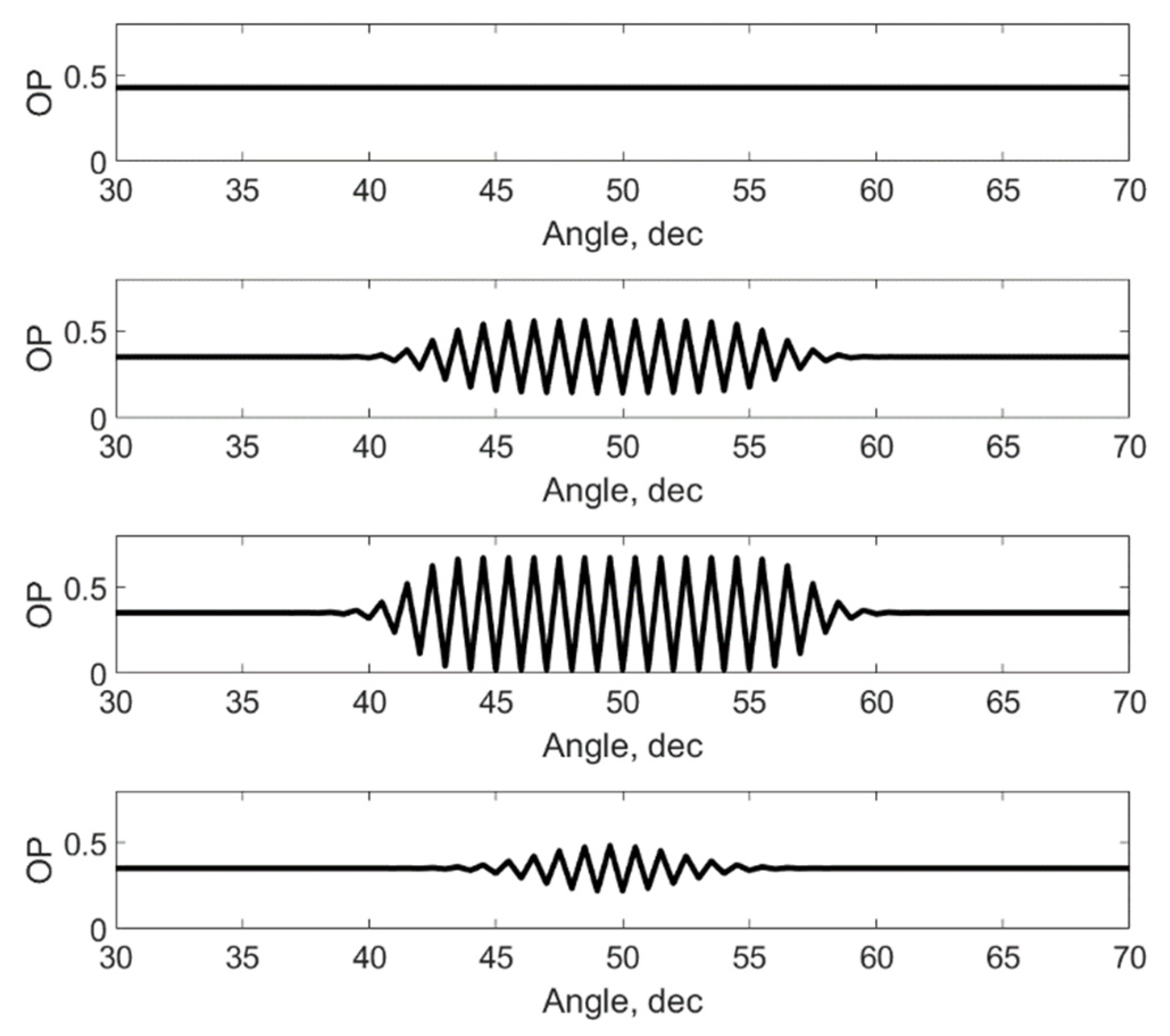
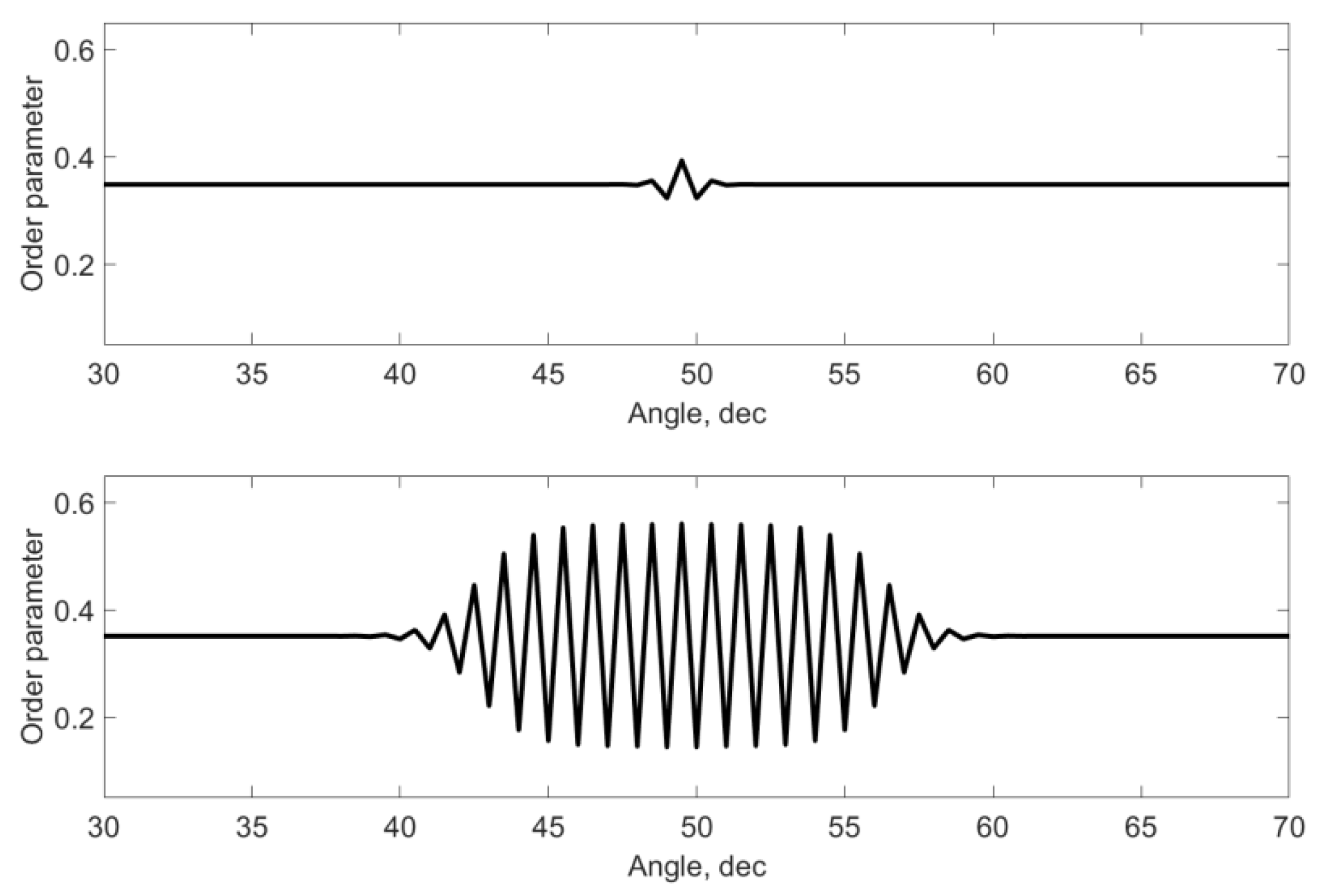
4. Influence of the Higher-Order Invariants
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gleser, A.M.; Metlov, L.S. Physics of megaplastic (severe) deformation in solids. Phys. Solid State 2010, 52, 1162–1169. [Google Scholar] [CrossRef]
- Straumal, B.B.; Kilmametov, A.R.; Ivanisenko, Y.; Gornakova, A.S.; Mazilkin, A.A.; Kriegel, M.J.; Fabrichnaya, O.B.; Baretzky, B.; Hahn, H. Phase transformations in Ti–Fe alloys induced by high pressure torsion. Adv. Eng. Mater. 2015, 17, 1835–1841. [Google Scholar] [CrossRef]
- Straumal, B.B.; Gornakova, A.S.; Mazilkin, A.A.; Fabrichnaya, O.B.; Kriegel, M.J.; Baretzky, B.; Jiang, J.-Z.; Dobatkin, S.V. Phase transformations in the severely plastically deformed Zr–Nb alloys. Mater. Lett. 2012, 81, 225–228. [Google Scholar] [CrossRef]
- Kulagin, R.; Beygelzimer, Y.; Ivanisenko, Y.; Mazilkin, A.; Straumal, B.; Hahn, H. Instabilities of interfaces between dissimilar metals induced by high pressure torsion. Mater. Lett. 2018, 222, 172–175. [Google Scholar] [CrossRef]
- Borchers, C.; Garve, C.; Tiegel, M.; Deutges, M.; Herz, A.; Edalati, K.; Pippan, R.; Horita, Z.; Kirchheim, R. Nanocrystalline steel obtained by mechanical alloying of iron and graphite subsequently compacted by high-pressure torsion. Acta Mater. 2015, 97, 207–215. [Google Scholar] [CrossRef]
- Lee, S.; Horita, Z. High-pressure torsion for pure chromium and niobium. Mater. Trans. 2012, 53, 38–45. [Google Scholar] [CrossRef] [Green Version]
- Edalati, K.; Toh, S.; Watanabe, M.; Horita, Z. In situ production of bulk intermetal-lic-based nanocomposites and nanostructured intermetallics by high-pressure torsion. Scr. Mater. 2012, 66, 386–389. [Google Scholar] [CrossRef]
- Cubero-Sesin, J.M.; Horita, Z. Strengthening via microstructure refinement in bulk Al4 mass: % Fe alloy using high-pressure torsion. Mater. Trans. 2012, 53, 46–55. [Google Scholar] [CrossRef] [Green Version]
- Bryła, K.; Morgiel, J.; Faryna, M.; Edalati, K.; Horita, Z. Effect of high-pressure torsion on grain refinement, strength enhancement and uniform ductility of EZ magnesium alloy. Mater. Lett. 2018, 212, 323–326. [Google Scholar] [CrossRef]
- Edalati, K.; Lee, D.J.; Nagaoka, T.; Arita, M.; Kim, H.S.; Horita, Z.; Pippan, R. Real hy-drostatic pressure in high-pressure torsion measured by bismuth phase transformations and FEM simulations. Mater. Trans. 2016, 57, 533–538. [Google Scholar] [CrossRef]
- Edalati, K.; Horita, Z. High-pressure torsion of pure metals: Influence of atomic bond parameters and stacking fault energy on grain size and correlation with hardness. Acta Mater. 2011, 59, 6831–6836. [Google Scholar] [CrossRef]
- Edalati, K.; Horita, Z.; Furuta, T.; Kuramoto, S. Dynamic recrystallization and recovery during high-pressure torsion: Experimental evidence by torque measurement using ring specimens. Mater. Sci. Eng. A 2013, 559, 506–509. [Google Scholar] [CrossRef]
- Beygelzimer, Y.; Kulagin, R.; Toth, L.S.; Ivanisenko, Y. The self-similarity theory of high pressure torsion. Beilstein J. Nanotechnol. 2016, 7, 1267–1277. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kulagin, R.; Beygelzimer, Y.; Ivanisenko, Y.; Mazilkin, A.; Hahn, H. High pressure torsion: From laminar flow to turbulence. IOP Conf. Ser. Mater. Sci. Eng. 2017, 194, 012045. [Google Scholar] [CrossRef]
- Straumal, B.B.; Kilmametov, A.R.; Ivanisenko, Y.; Mazilkin, A.A.; Kogtenkova, O.A.; Kurmanaeva, L.; Korneva, A.; Zięba, P.; Baretzky, B. Phase transitions induced by severe plastic deformation: Steady-state and equifinality. Int. J. Mater. Res. 2015, 106, 657–664. [Google Scholar] [CrossRef]
- Metlov, L. Nonequilibrium thermodynamics of a two-defect system under severe load. Phys. Rev. E. 2014, 90, 022124. [Google Scholar] [CrossRef] [Green Version]
- Straumal, B.B.; Protasova, S.G.; Mazilkin, A.A.; Rabkin, E.; Goll, D.; Schütz, G.; Baretzky, B.; Valiev, R. Deformation-driven formation of equilibrium phases in the Cu–Ni alloys. J. Mater. Sci. 2012, 47, 360–367. [Google Scholar] [CrossRef]
- Straumal, B.B.; Kilmametov, A.R.; Ivanisenko, Y.; Kurmanaeva, L.; Baretzky, B.; Kucheev, Y.O.; Zięba, P.; Korneva, A.; Molodov, D.A. Phase transitions during high pressure torsion of Cu–Co alloys. Mater. Lett. 2014, 118, 111–114. [Google Scholar] [CrossRef]
- Straumal, B.B.; Kilmametov, A.R.; Baretzky, B.; Kogtenkova, O.A.; Straumal, P.B.; Litynska-Dobrzynska, L.; Chulist, R.; Korneva, A.; Zieba, P. High pressure torsion of Cu–Ag and Cu–Sn alloys: Limits for solubility and dissolution. Acta Mater. 2020, 195, 184–198. [Google Scholar] [CrossRef]
- Straumal, B.; Kilmametov, A.; Korneva, A.; Zięba, P.; Zavorotnev, Y.; Metlov, L.; Popova, O.; Baretzky, B. The Enrichment of (Cu, Sn) Solid Solution Driven by High-Pressure Torsion. Crystals 2021, 11, 766. [Google Scholar] [CrossRef]
- Korneva, A.; Kilmametov, A.; Zavorotnev, Y.; Metlov, L.; Popova, O.; Baretzky, B. The enrichment of solid solution in a two-phase alloy during the high pressure torsion. Mater. Lett. 2021, 302, 130386. [Google Scholar] [CrossRef]
- Metlov, L.; Gordey, M. Nonequilibrium evolution thermodynamics of poly- and two-components alloys affected by severe plastic deformation. J. Phys. Cond. Mat. 2021, 2052, 012026. [Google Scholar] [CrossRef]
- Zavorotnev, Y.D.; Metlov, L.S.; Tomashevskaya, E.Y. Establishment of a Steady State upon Imposition of severe plastic torsion deformation in two-component crystal. Phys. Solid State 2022, 64, 462. [Google Scholar] [CrossRef]
- Li, Z.; Wang, K.; Li, W.; Yan, S.; Chen, F.; Peng, S. Analysis of surface pressure pulsation characteristics of centrifugal pump magnetic liquid sealing film. Front. Energy Res. 2022, 10, 937299. [Google Scholar] [CrossRef]
- Xu, X.; Niu, D.; Peng, L.; Zheng, S.; Qiu, J. Hierarchical multi-objective optimal planning model of active distribution network considering distributed generation and demand-side response. Sust. Energy Technol. Assess. 2022, 53, 102438. [Google Scholar] [CrossRef]
- Xie, X.; Sun, Y. A piecewise probabilistic harmonic power flow approach in unbalanced residential distribution systems. Electr. Power Energy Syst. 2022, 141, 108114. [Google Scholar] [CrossRef]
- Generalov, D.; Tsvetova, E.; Fedorov, R.; Kovalnogov, V.; Simos, T.E. A two-step singularly P-stable method with high phase and large stability properties for problems in chemistry. J. Math. Chem. 2022, 60, 475–501. [Google Scholar] [CrossRef]
- Wang, H.; Wu, X.; Zheng, X.; Yuan, X. Virtual voltage vector based model predictive control for a nine-phase open-end winding PMSM with a common DC bus. IEEE Trans. Ind. Electr. 2022, 69, 5386–5397. [Google Scholar] [CrossRef]
- Zykov, V.S.; Morozova, O.L. Modeling of spiral waves in the round exitable me-dium. Math. Model. 1994, 6, 61–73. (In Russian) [Google Scholar]
- Elkin, Y.E. Autowave processes. Matem. Biol. Inform. 2006, 1, 27–40. (In Russian) [Google Scholar]
- Khomenko, V.; Troshchenko, D.; Metlov, L. Effect of stochastic processes on struc-ture formation in nanocrystalline materials under severe plastic deformation. Phys. Rev. E. 2019, 100, 022110. [Google Scholar] [CrossRef] [PubMed]
- Pitaevskii, L.P.; Lifshitz, E.M.; Sykes, J.B. Course of Theoretical Physics: Physical Kinetics; Elsevier: Amsterdam, The Netherlands, 2017; p. 465. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Straumal, P.; Zavorotnev, Y.; Metlov, L.; Popova, O. Distribution of Order Parameter in Solids under High Pressure Torsion. Materials 2022, 15, 6970. https://doi.org/10.3390/ma15196970
Straumal P, Zavorotnev Y, Metlov L, Popova O. Distribution of Order Parameter in Solids under High Pressure Torsion. Materials. 2022; 15(19):6970. https://doi.org/10.3390/ma15196970
Chicago/Turabian StyleStraumal, Petr, Yuri Zavorotnev, Leonid Metlov, and Olga Popova. 2022. "Distribution of Order Parameter in Solids under High Pressure Torsion" Materials 15, no. 19: 6970. https://doi.org/10.3390/ma15196970
APA StyleStraumal, P., Zavorotnev, Y., Metlov, L., & Popova, O. (2022). Distribution of Order Parameter in Solids under High Pressure Torsion. Materials, 15(19), 6970. https://doi.org/10.3390/ma15196970





