Experimental and Numerical Study of Static Behavior of Precast Segmental Hollow Bridge Piers
Abstract
:1. Introduction
2. Experimental Program
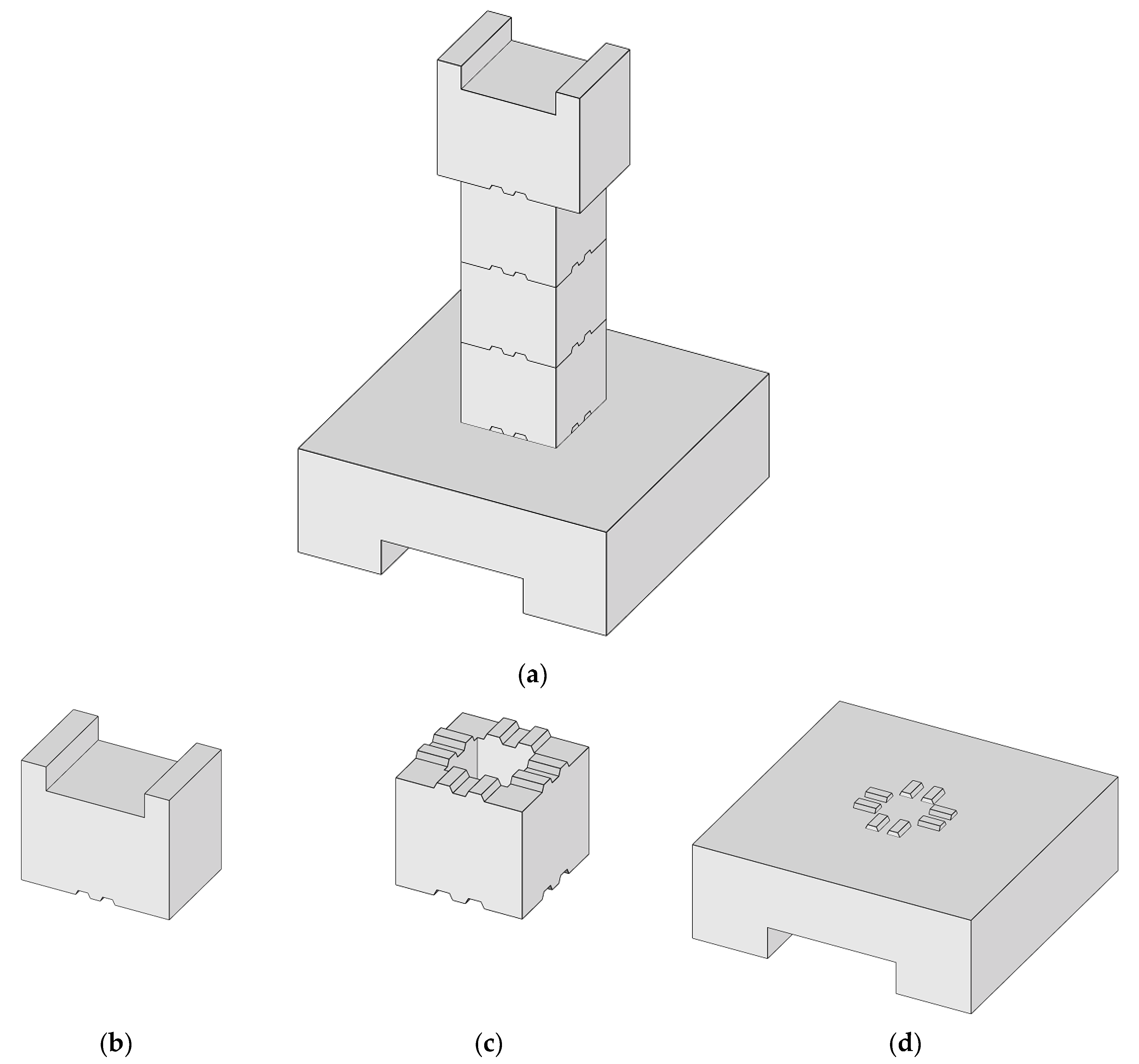
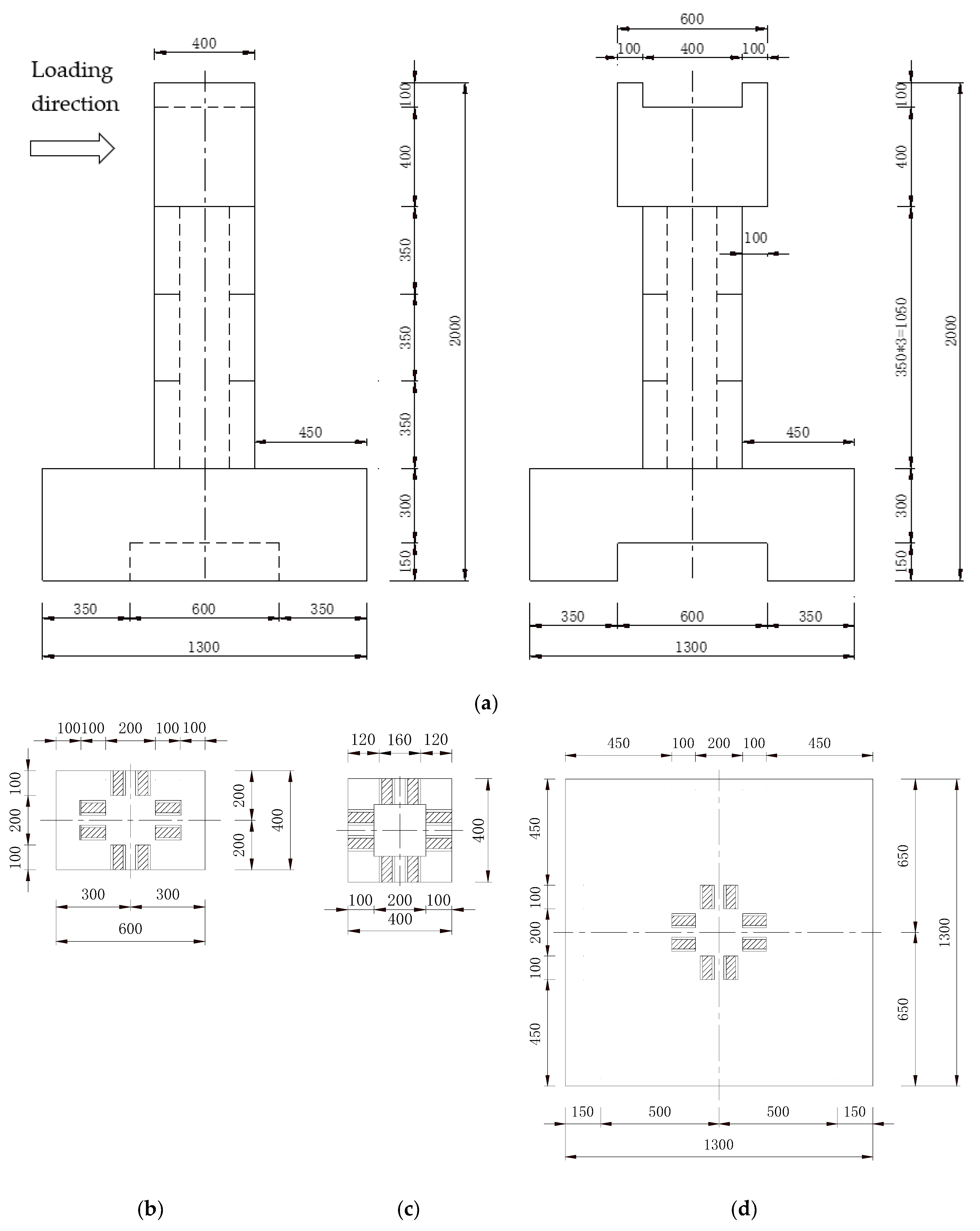
2.1. Specimen Design
2.2. Material Properties
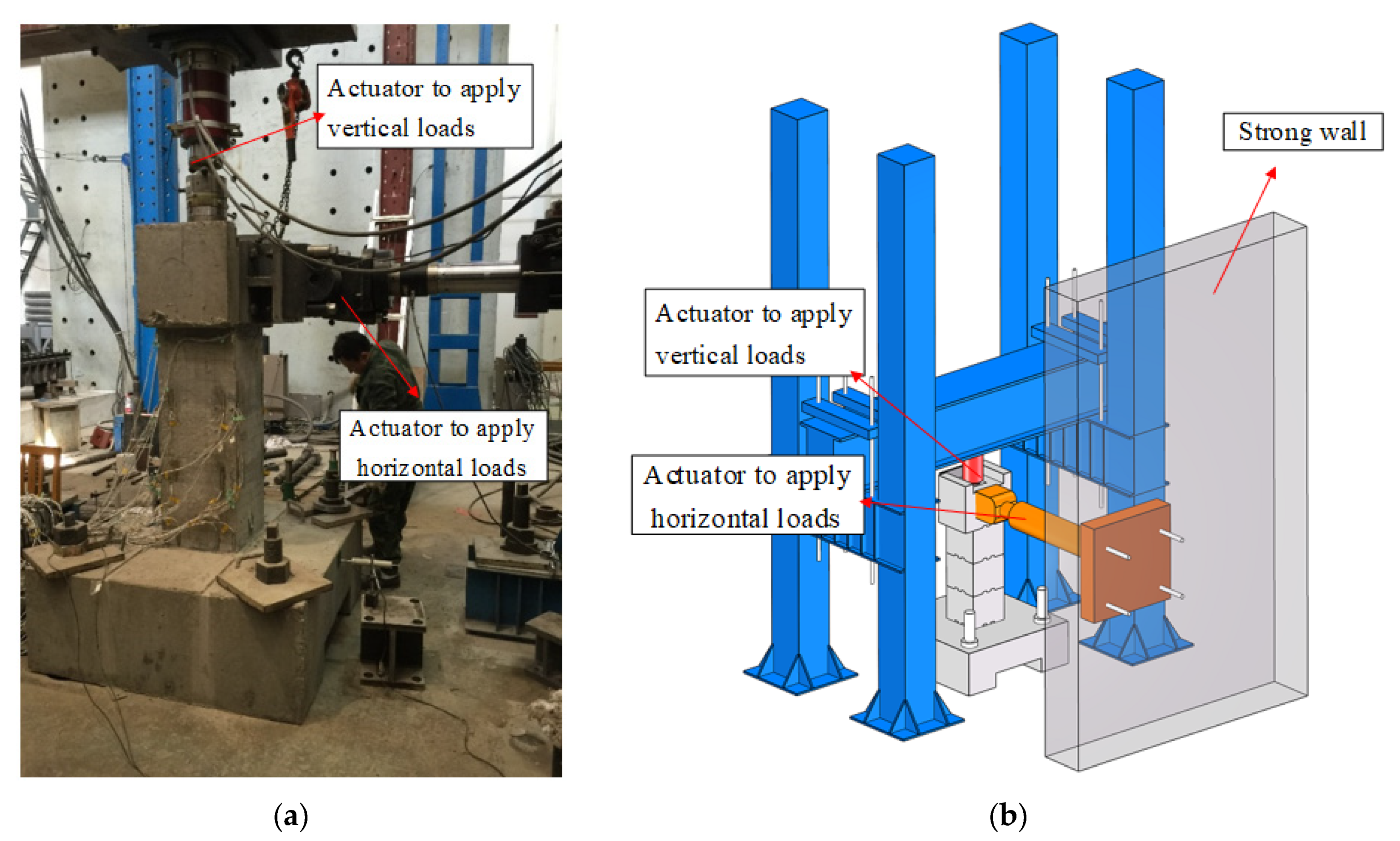
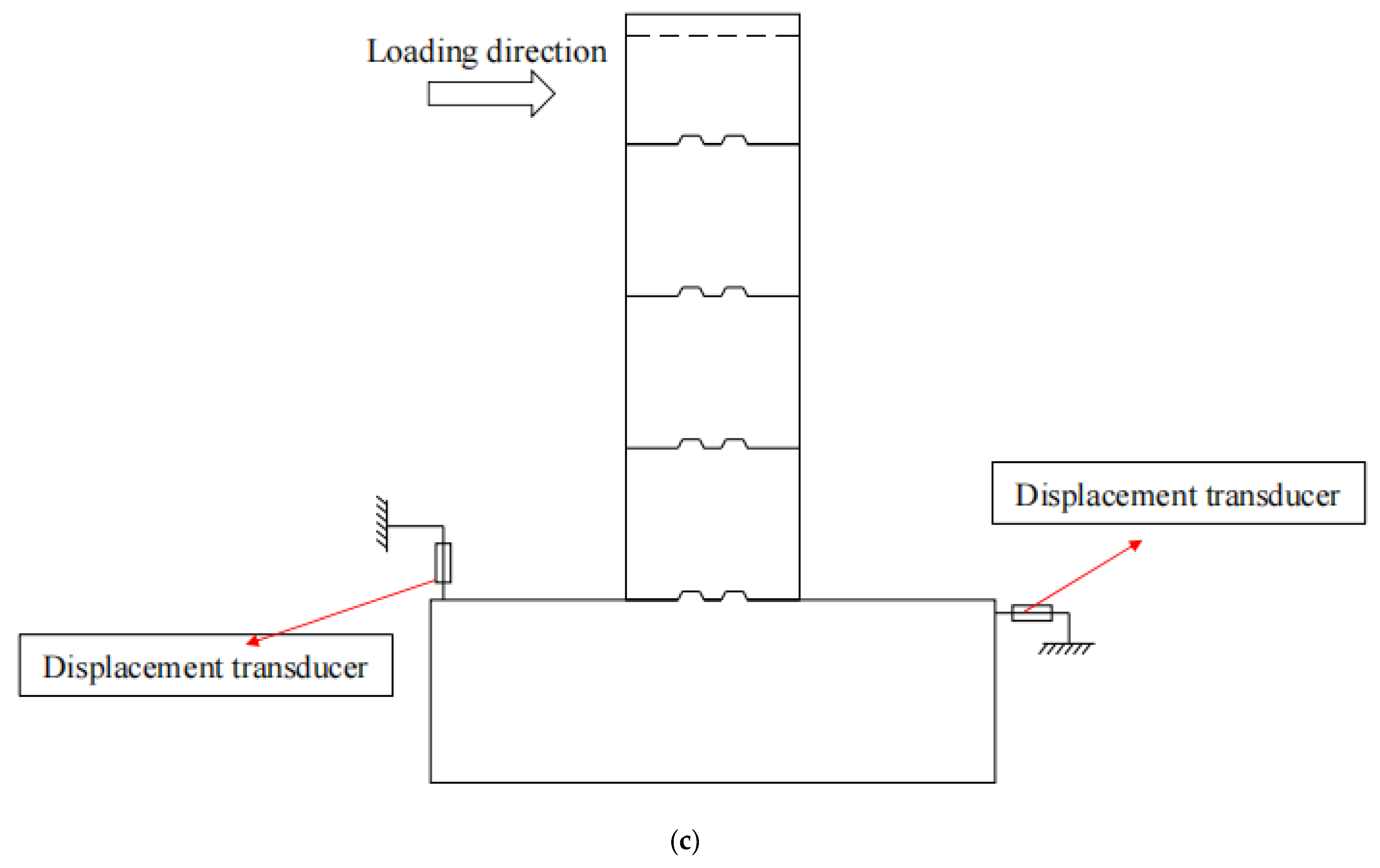
2.3. Test Setup
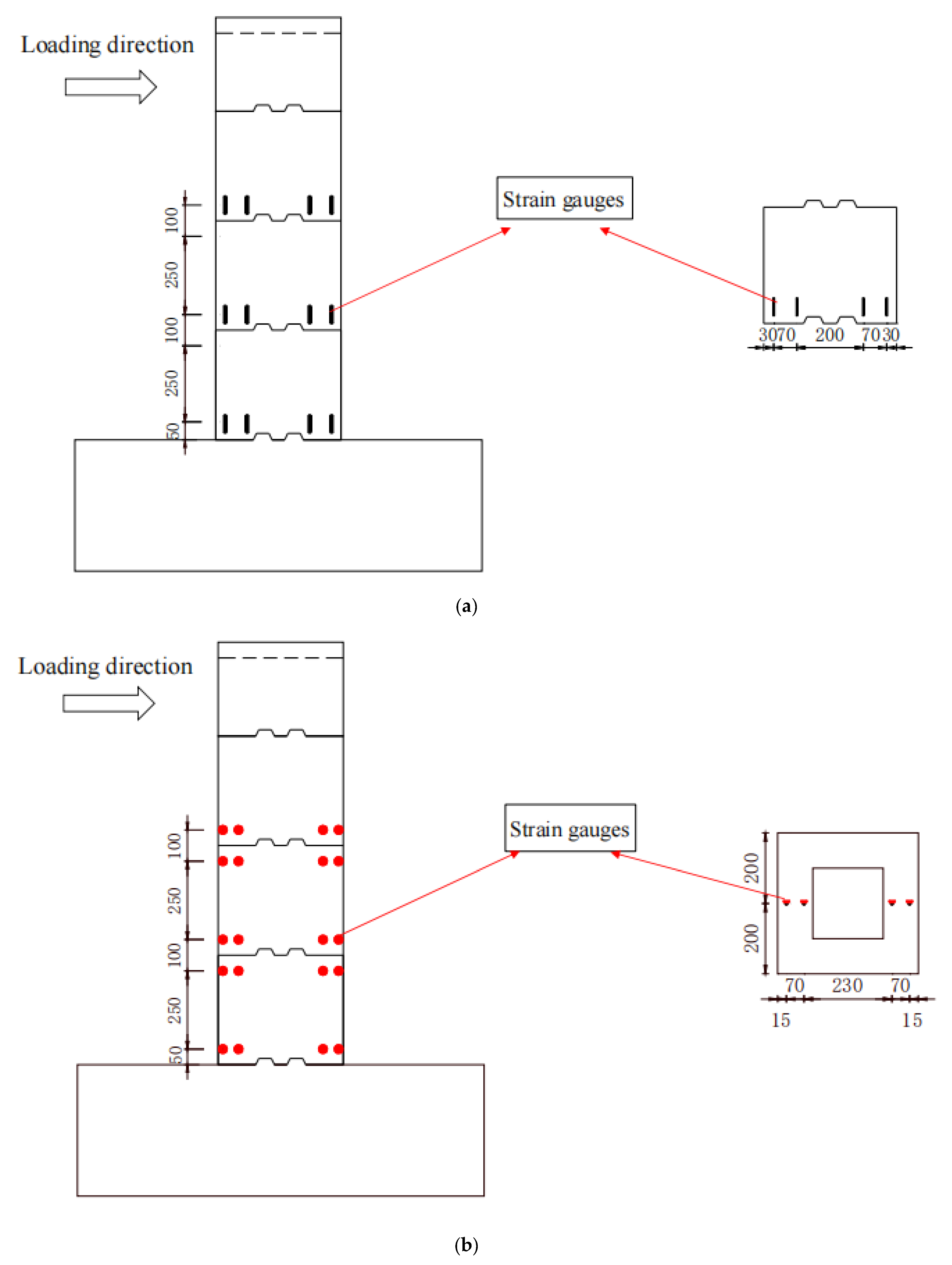
2.4. Instrumentation
3. Test Results
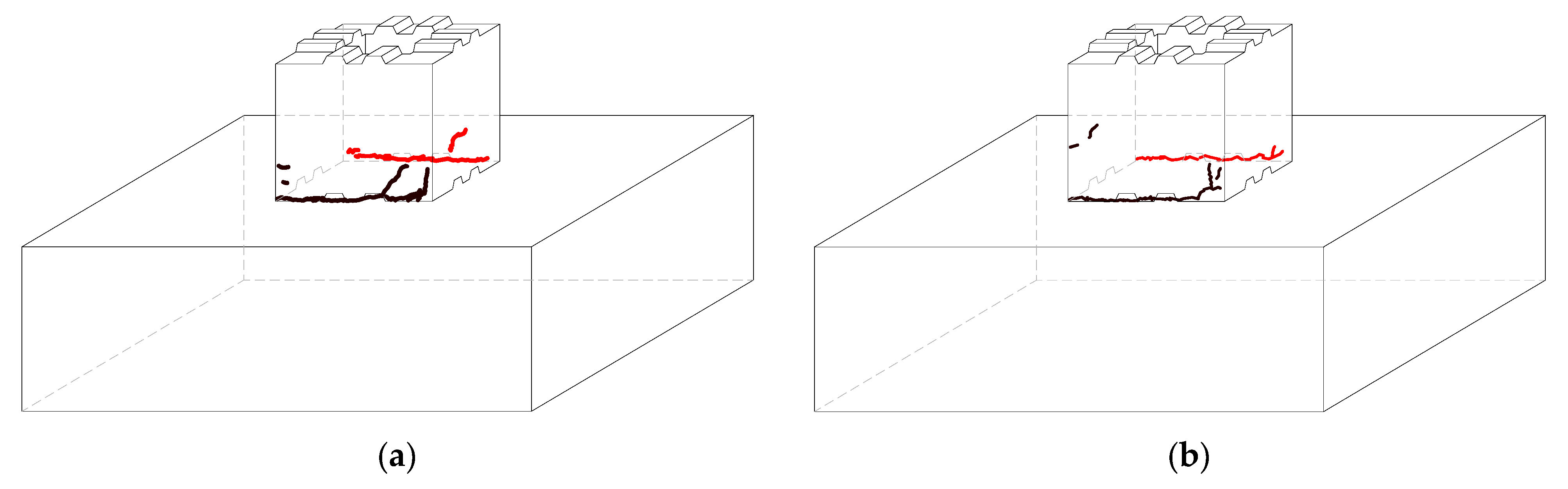
3.1. General Observations and Failure Modes
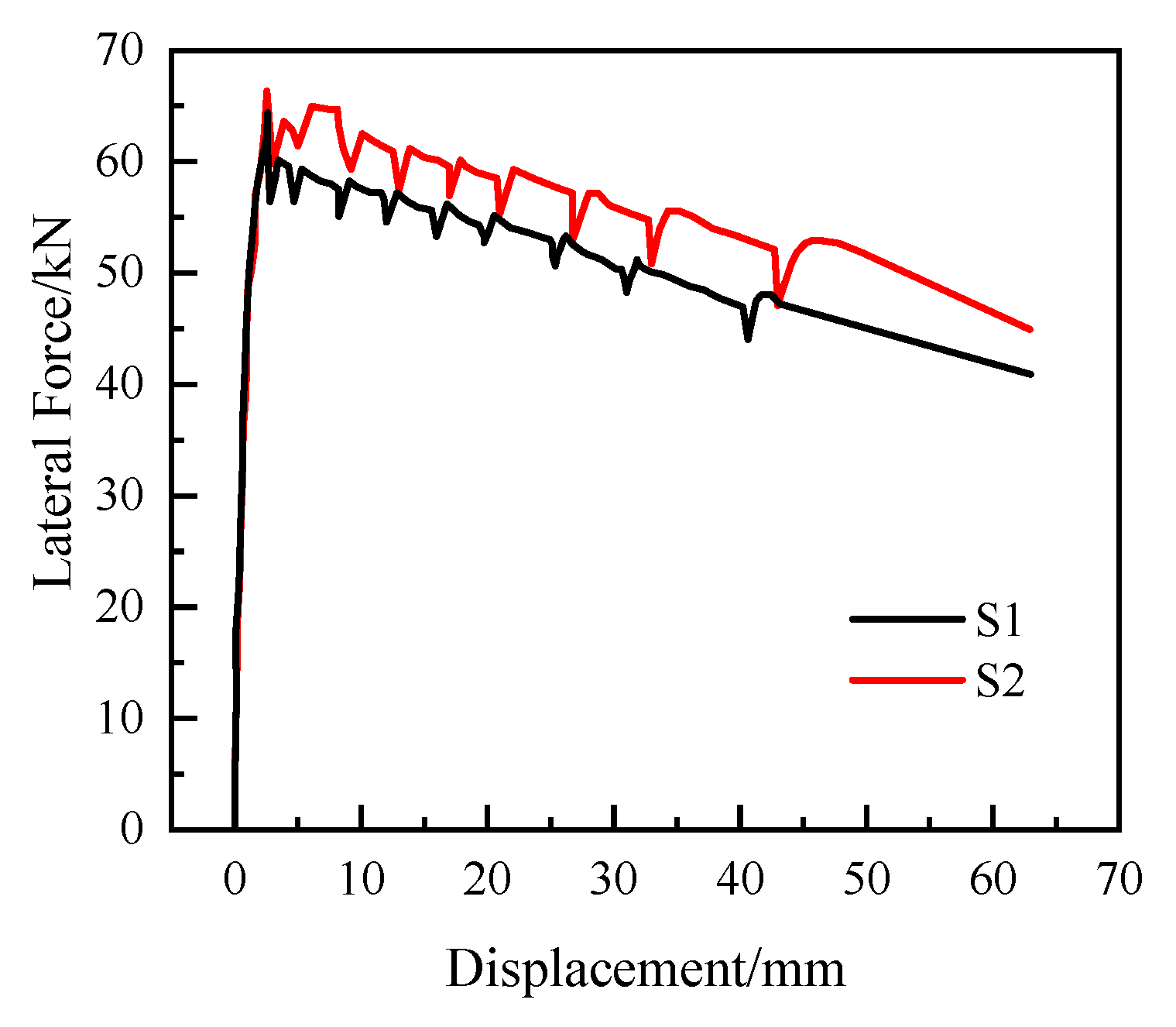
3.2. Load–Deflection Curves
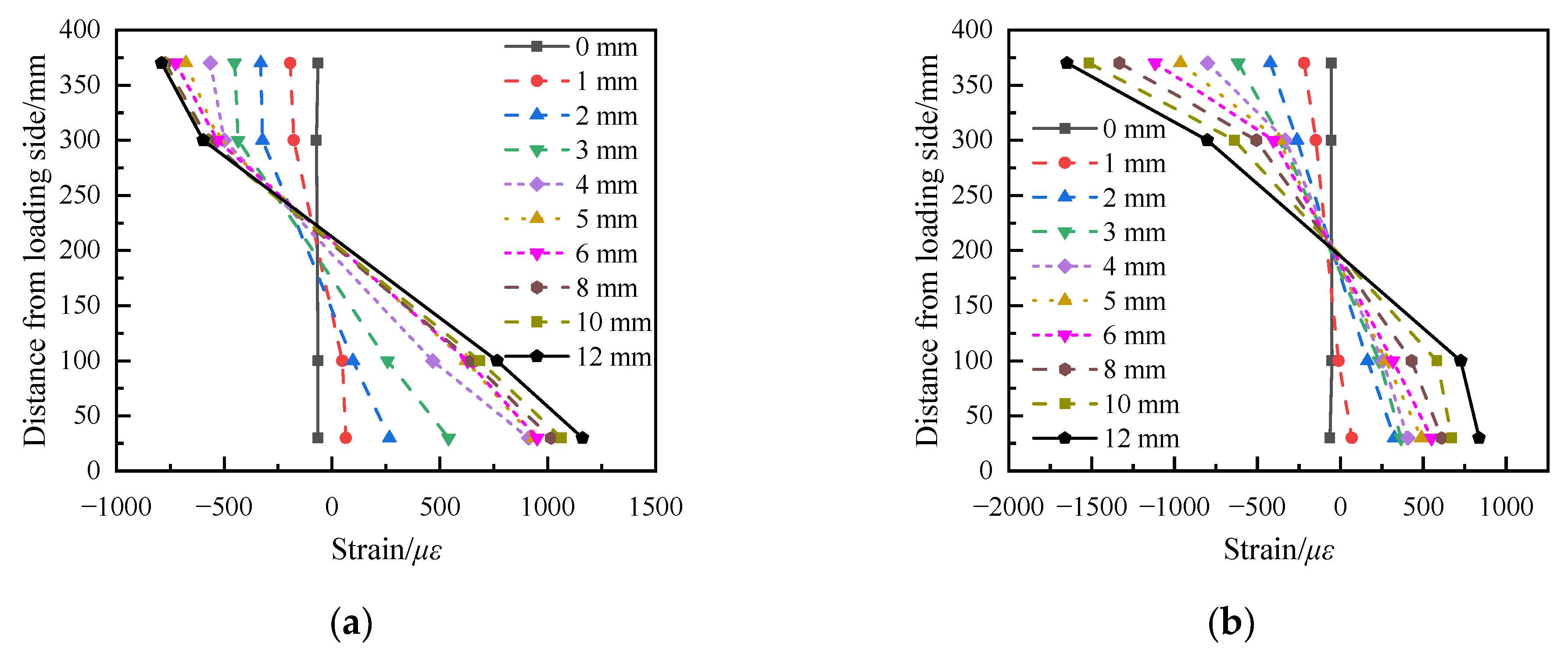
3.3. Load–Strain Response
4. Finite Element Analysis
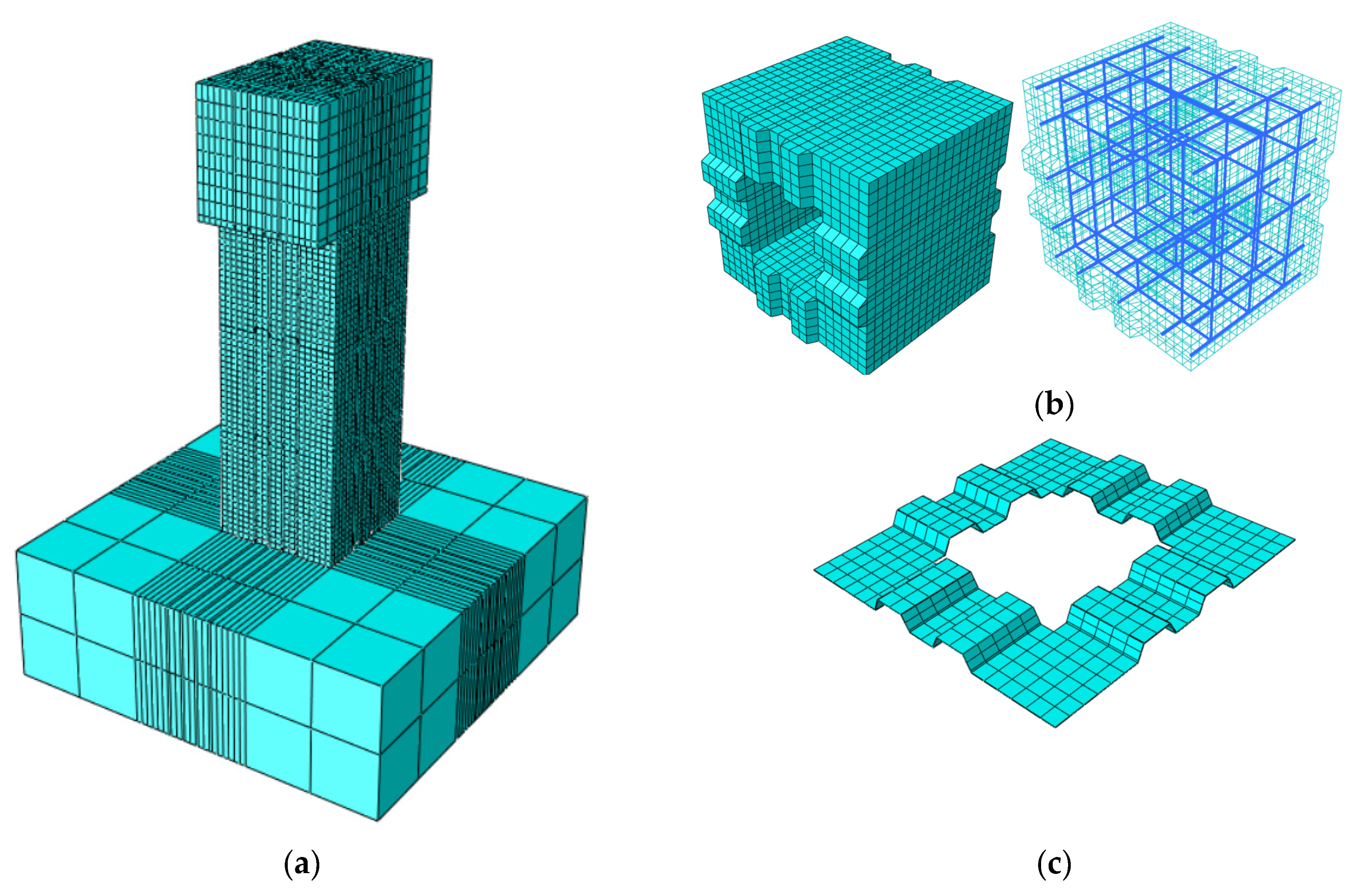
4.1. Finite Element Model
4.1.1. Finite Element Modeling
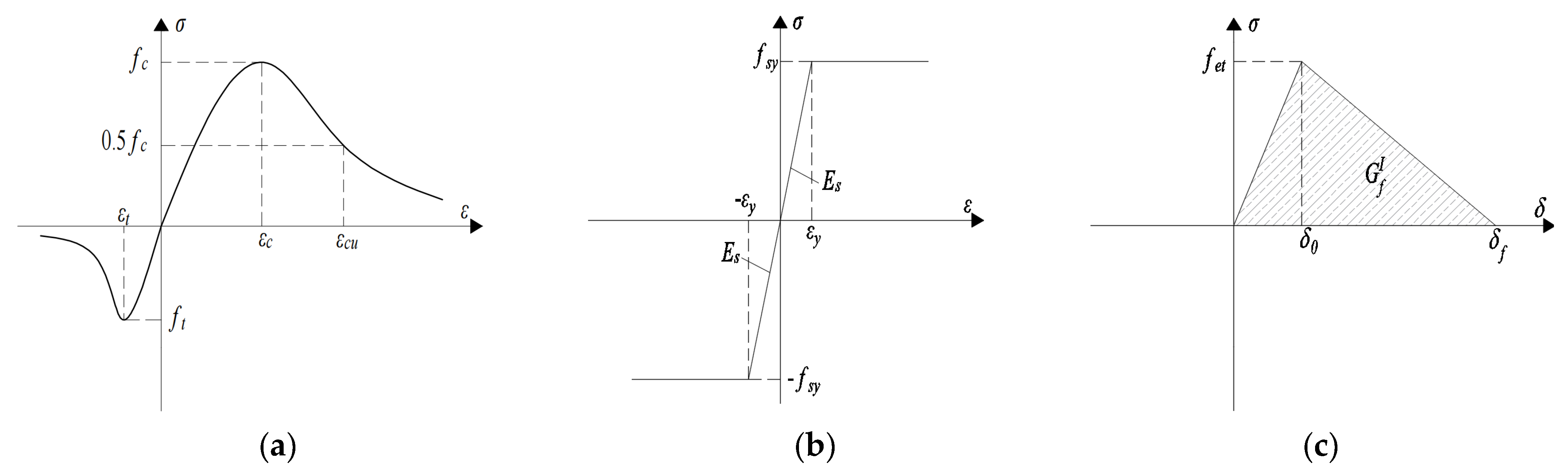
4.1.2. Material Constitutive Relationship
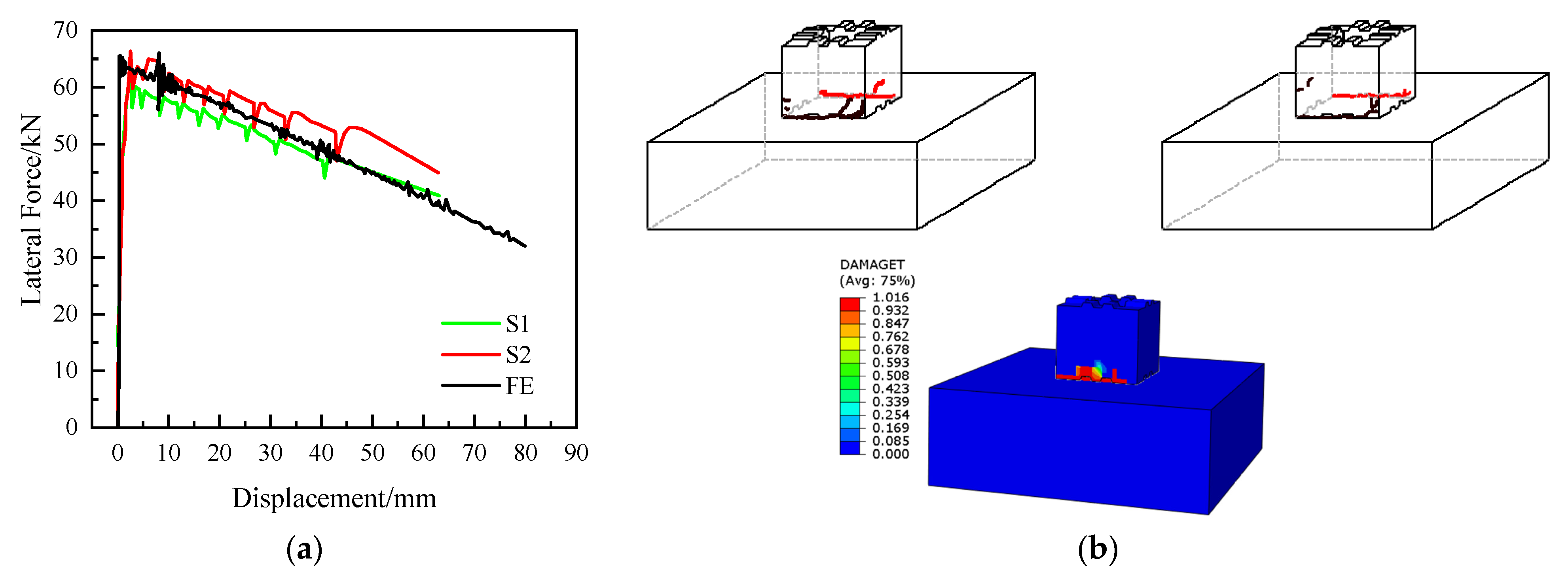
4.2. Comparison of Test Results and FEM Analyses
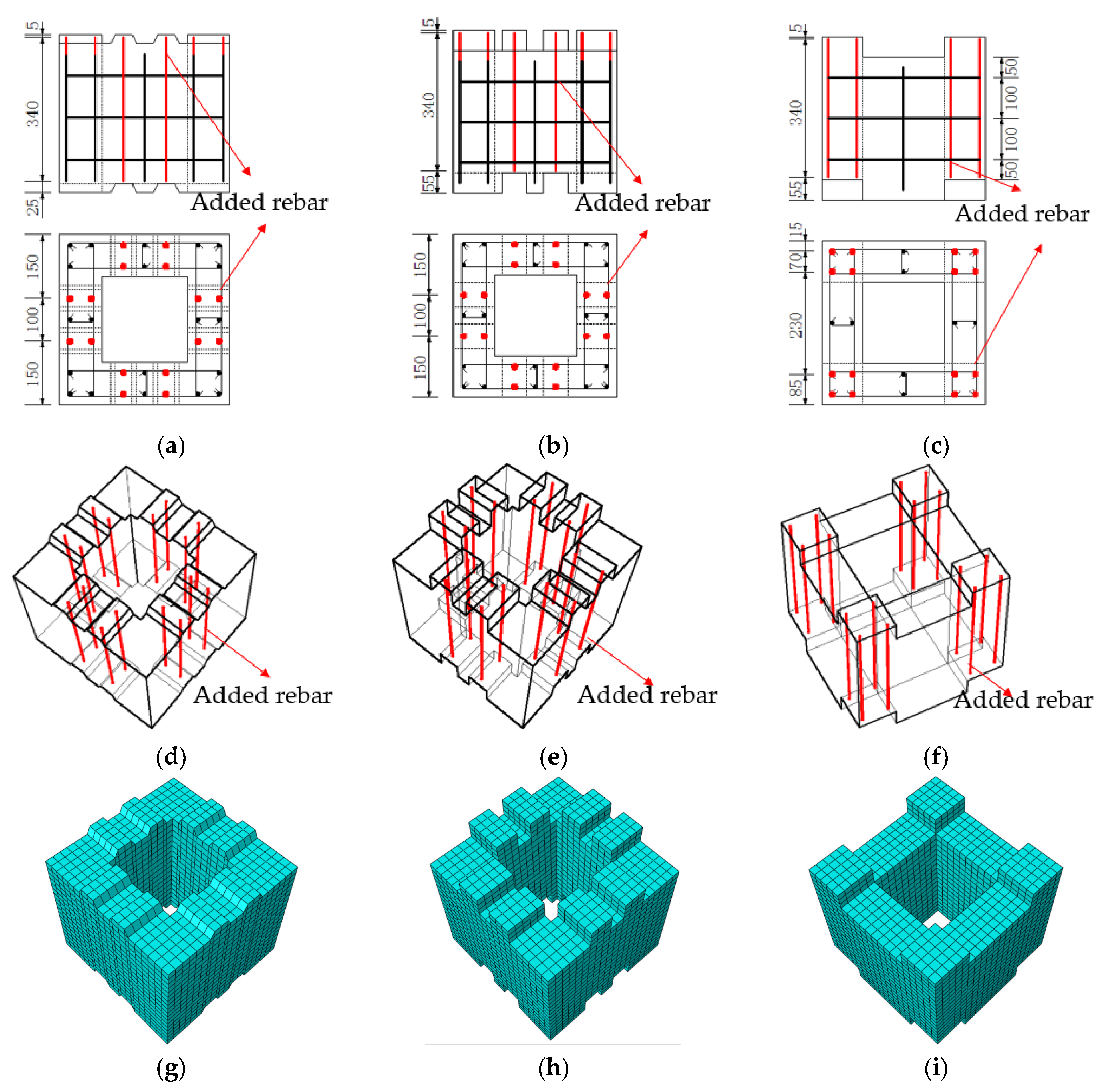
4.3. Optimizing the Design of Segmental Prefabricated Hollow Piers
4.3.1. Optimization of the Design Scheme
4.3.2. Analysis of Finite Element Simulation Results
5. Conclusions
- (1)
- The segmental prefabricated assembled hollow pier force behavior is similar to that of cantilevered bending members. The specimens present brittle damage characteristics after the destruction of the structure at the bottom of the pier pressure edge as the axis of the rigid body rotation.
- (2)
- During the test loading process, the bonding between the segments is good, except for the pier bottom damage surface of the rest of the bonding surface, which has no relative displacement. At the cracked damaged surface at the pier bottom, the connection bonds are always firmly connected to the key slot of the corresponding section.
- (3)
- The finite element model of precast segmental hollow piers was established, and the cohesive unit was used to simulate the adhesive joints between segments. The model calculation results are in good agreement with the test results and can effectively predict the load-displacement response of precast segmental hollow piers.
- (4)
- Three optimized design solutions are proposed. The finite element simulation proves all three optimized design solutions show better overall ductility than the original solution and can effectively improve the performance of segmental precast hollow piers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shahawy, M. Prefabricated Bridge Elements and Systems to Limit Traffic Disruption during Construction; Transportation Research Board: Washington, DC, USA, 2003. [Google Scholar]
- Farooq, R.; Ghumman, A.R.; Tariq, M.A.U.R.; Ahmed, A.; Jadoon, K.Z. Optimal octagonal hooked collar countermeasure to reduce scour around a single bridge pier. Period. Polytech. Civ. Eng. 2020, 64, 1026–1037. [Google Scholar] [CrossRef]
- Rad, M.M.; Ibrahim, S.K.; Lógó, J. Limit design of reinforced concrete haunched beams by the control of the residual plastic deformation. Structures 2022, 39, 987–996. [Google Scholar]
- Liu, S.; Yu, T.; Yin, S.; Bui, T.Q. Size and surface effects on mechanical behavior of thin nanoplates incorporating microstructures using isogeometric analysis. Comput. Struct. 2019, 212, 173–187. [Google Scholar] [CrossRef]
- Dániel, H.; Habashneh, M.; Rad, M.M. Reliability-based numerical analysis of glulam beams reinforced by CFRP plate. Sci. Rep. 2022, 12, 13587. [Google Scholar] [CrossRef] [PubMed]
- Aksoylu, C.; Özkılıç, Y.O.; Yazman, Ş.; Gemi, L.; Arslan, M.H. Experimental and Numerical Investigation of Load Bearing Capacity of Thinned End Precast Purlin Beams and Solution Proposals. Tek. Dergi. 2021, 614, 10823–10858. [Google Scholar]
- Özkılıç, Y.O.; Aksoylu, C.; Arslan, M.H. Experimental and numerical investigations of steel fiber reinforced concrete dapped-end purlins. J. Build. Eng. 2021, 36, 102119. [Google Scholar] [CrossRef]
- Aksoylu, C.; Özkılıç, O.Y.; Arslan, H.M. Damages on prefabricated concrete dapped-end purlins due to snow loads and a novel reinforcement detail. Eng. Struct. 2020, 225, 111225. [Google Scholar] [CrossRef]
- Özkılıç, Y.O.; Aksoylu, C.; Gemi, L.; Arslan, M.H. Behavior of CFRP-strengthened RC beams with circular web openings in shear zones: Numerical study. Structures 2022, 41, 1369–1389. [Google Scholar] [CrossRef]
- Özkılıç, Y.O.; Aksoylu, C.; Arslan, M.H. Numerical evaluation of effects of shear span, stirrup spacing and angle of stirrup on reinforced concrete beam behaviour. Struct. Eng. Mech. Int. J. 2021, 79, 309–326. [Google Scholar]
- Özkılıç, Y.O.; Yazman, Ş.; Aksoylu, C.; Arslan, M.H.; Gemi, L. Numerical investigation of the parameters influencing the behavior of dapped end prefabricated concrete purlins with and without CFRP strengthening. Constr. Build. Mater. 2021, 275, 122173. [Google Scholar] [CrossRef]
- Billington, S.L.; Barnes, R.W.; Breen, J.E. A precast segmental substructure system for standard bridges. PCI J. 1999, 44, 56–73. [Google Scholar] [CrossRef]
- Ou, Y.-C.; Chiewanichakorn, M.; Aref, A.J.; Lee, G.C. Seismic performance of segmental precast unbonded posttensioned concrete bridge columns. J. Struct. Eng. N. Y. 2007, 133, 1636. [Google Scholar] [CrossRef]
- Podolny, W.; Muller, J.M. Construction and Design of Prestressed Concrete Segmental Bridges; Krieger Publishing Company: New York, NY, USA, 1992. [Google Scholar]
- Nasir, S.; Gupta, S.; Umehara, H.; Hirasawa, I. An efficient method for the construction of bridge piers. Eng. Struct. 2001, 23, 1142–1151. [Google Scholar] [CrossRef]
- Hieber, D.; Wacker, J.; Eberhard, M.; Stanton, J. State-of-the-Art on Precast Concrete Systems for Rapid Construction of Bridges; Washington State Transportation Center: Washington, DC, USA, 2005.
- Hieber, D.G.; Wacker, J.M.; Eberhard, M.O.; Stanton, J.F. Precast Concrete Pier Systems for Rapid Construction of Bridges in Seismic Regions; University of Washington Seattle: Washington, DC, USA, 2005. [Google Scholar]
- Nishiyama, M.; Watanabe, F. Seismic performance of precast column-foundation connection assembled by post-tensioning. In Proceedings of the Advanced Materials for Construction of Bridges, Buildings, and Other Structures III, Davos, Switzerland, 12 September 2003. [Google Scholar]
- Mander, J.B.; Cheng, C.-T. Seismic Resistance of Bridge Piers Based on Damage Avoidance Design; National Center for Earthquake Engineering Research (NCEER): Taipei, Taiwan, 1997; p. 109.
- Billington, S.; Barnes, R.; Breen, J. A Precast Substructure Design for Standard Bridge Systems; University of Texas at Austin, Center for Transportation Research: Austin, TX, USA, 1998. [Google Scholar]
- Billington, S.; Barnes, R.; Breen, J. Alternate substructure systems for standard highway bridges. J. Bridge Eng. 2001, 6, 87–94. [Google Scholar] [CrossRef]
- Billington, S.L.; Yoon, J. Cyclic response of unbonded posttensioned precast columns with ductile fiber-reinforced concrete. J. Bridge Eng. 2004, 9, 353–363. [Google Scholar] [CrossRef]
- Hewes, J.T. Seismic Design and Performance of Precast Concrete Segmental Bridge Columns; University of California: San Diego, CA, USA, 2002. [Google Scholar]
- Ou, Y.-C. Precast Segmental Post-Tensioned Concrete Bridge Columns for Seismic Regions; State University of New York at Buffalo: Buffalo, NY, USA, 2007. [Google Scholar]
- Palermo, A.; Pampanin, S.; Marriott, D. Design, modeling, and experimental response of seismic resistant bridge piers with posttensioned dissipating connections. J. Struct. Eng. 2007, 133, 1648–1661. [Google Scholar] [CrossRef]
- Kim, T.-H.; Lee, K.-M.; Yoon, C.; Shin, H.M. Inelastic behavior and ductility capacity of reinforced concrete bridge piers under earthquake. II: Numerical validation. J. Struct. Eng. 2003, 129, 1208–1219. [Google Scholar] [CrossRef]
- Kim, T.-H.; Lee, K.-M.; Yoon, C.; Shin, H.M. Inelastic behavior and ductility capacity of reinforced concrete bridge piers under earthquake. I: Theory and formulation. J. Struct. Eng. 2003, 129, 1199–1207. [Google Scholar] [CrossRef]
- Kurama, Y.; Pessiki, S.; Sause, R.; Lu, L.-W. Seismic behavior and design of unbonded post-tensioned precast concrete walls. PCI J. 1999, 44, 72–89. [Google Scholar] [CrossRef]
- Dawood, H.; ElGawady, M.; Cofer, W. Seismic Behavior and Design of Segmental Precast Post-Tensioned Concrete Piers; Transportation Northwest (Organization): Washington, DC, USA, 2011. [Google Scholar]
- CJJ/T 111-2006; Technical Specification for Construction of Span by Span Method of Precast Segment in Presstressed Concrete Bridge. Ministry of Construction of the People’s Republic of China: Beijing, China, 2006.
- GB 50728-2011; Technical Code for Safety Appraisal of Engineering Structural Strengthening Materials. Ministry of Housing and Urban-Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2011.
- GB 50010-2010 (Modified in 2015); Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2015.






| Material | Weight |
|---|---|
| C50 (kg/m3) | |
| Cement | 478 |
| Fine sand | 610 |
| Water | 172 |
| Superplasticizer | 3.59 |
| Coarse aggregate | 1.186 |
| Mix | fc (Mpa) | ft (Mpa) | Ec (Gpa) |
|---|---|---|---|
| C50 | 35.5 | 2.74 | 35.1 |
| Materials | Compressive Stress (Mpa) | Tensile Strength (Mpa) | Elasticity Modulus (Gpa) |
|---|---|---|---|
| Epoxy | 82 | 32 | 4.5 |
| Materials | fsy (Mpa) | fsu (Mpa) | Es (Gpa) |
|---|---|---|---|
| HPB300 | 320 | 416 | 210.5 |
| HRB335 | 345 | 511 | 203.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Peng, W.-Q.; Zhu, L.; Gao, C.; Tang, Y.-D.; Zhou, Y.-W.; Su, W.; Zeng, B. Experimental and Numerical Study of Static Behavior of Precast Segmental Hollow Bridge Piers. Materials 2022, 15, 6991. https://doi.org/10.3390/ma15196991
Lu W, Peng W-Q, Zhu L, Gao C, Tang Y-D, Zhou Y-W, Su W, Zeng B. Experimental and Numerical Study of Static Behavior of Precast Segmental Hollow Bridge Piers. Materials. 2022; 15(19):6991. https://doi.org/10.3390/ma15196991
Chicago/Turabian StyleLu, Wenliang, Wen-Qiang Peng, Li Zhu, Cong Gao, Ya-Dong Tang, Yue-Wu Zhou, Wei Su, and Bing Zeng. 2022. "Experimental and Numerical Study of Static Behavior of Precast Segmental Hollow Bridge Piers" Materials 15, no. 19: 6991. https://doi.org/10.3390/ma15196991
APA StyleLu, W., Peng, W.-Q., Zhu, L., Gao, C., Tang, Y.-D., Zhou, Y.-W., Su, W., & Zeng, B. (2022). Experimental and Numerical Study of Static Behavior of Precast Segmental Hollow Bridge Piers. Materials, 15(19), 6991. https://doi.org/10.3390/ma15196991





